Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Materials and Methods
3. Results
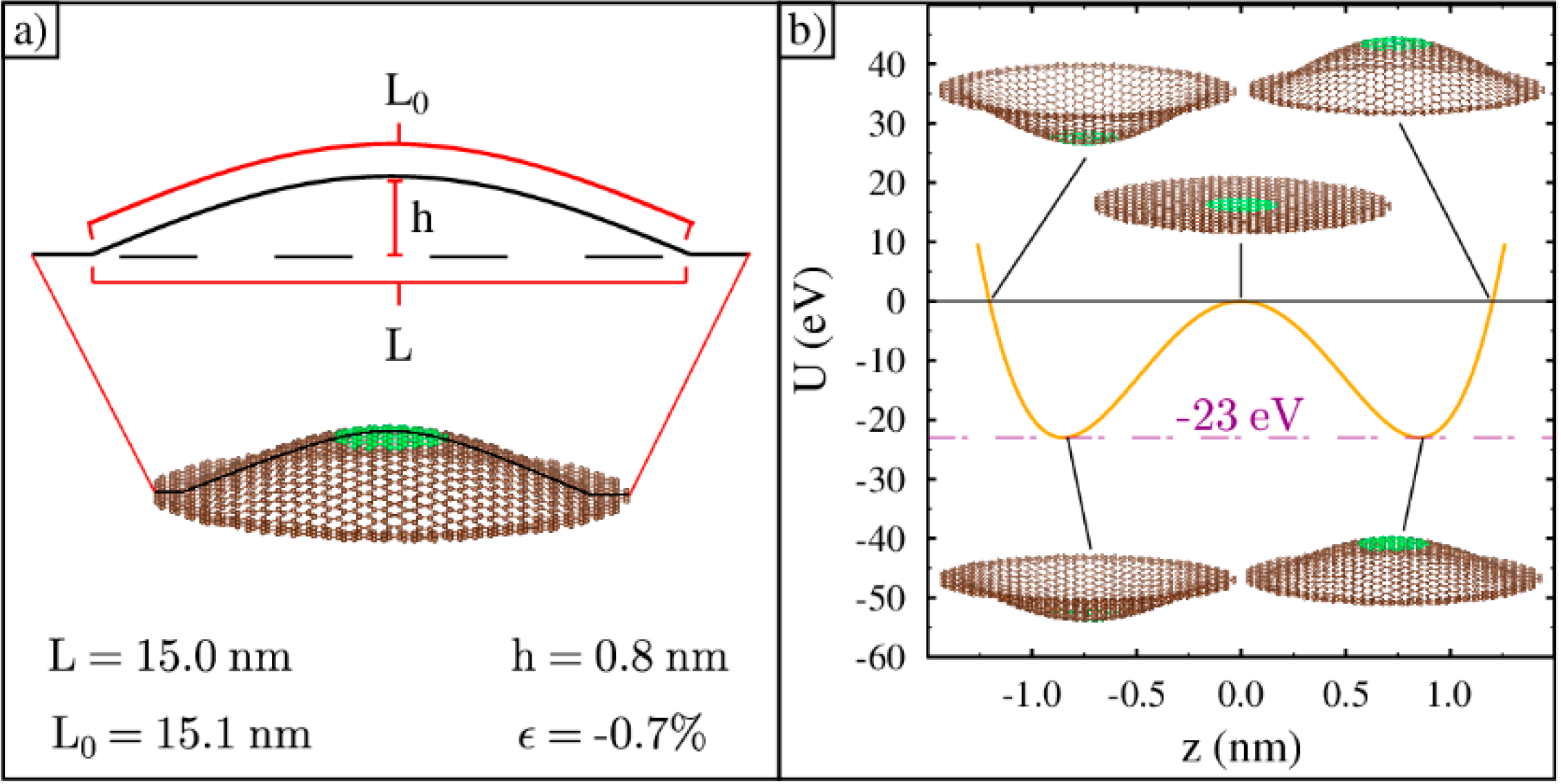
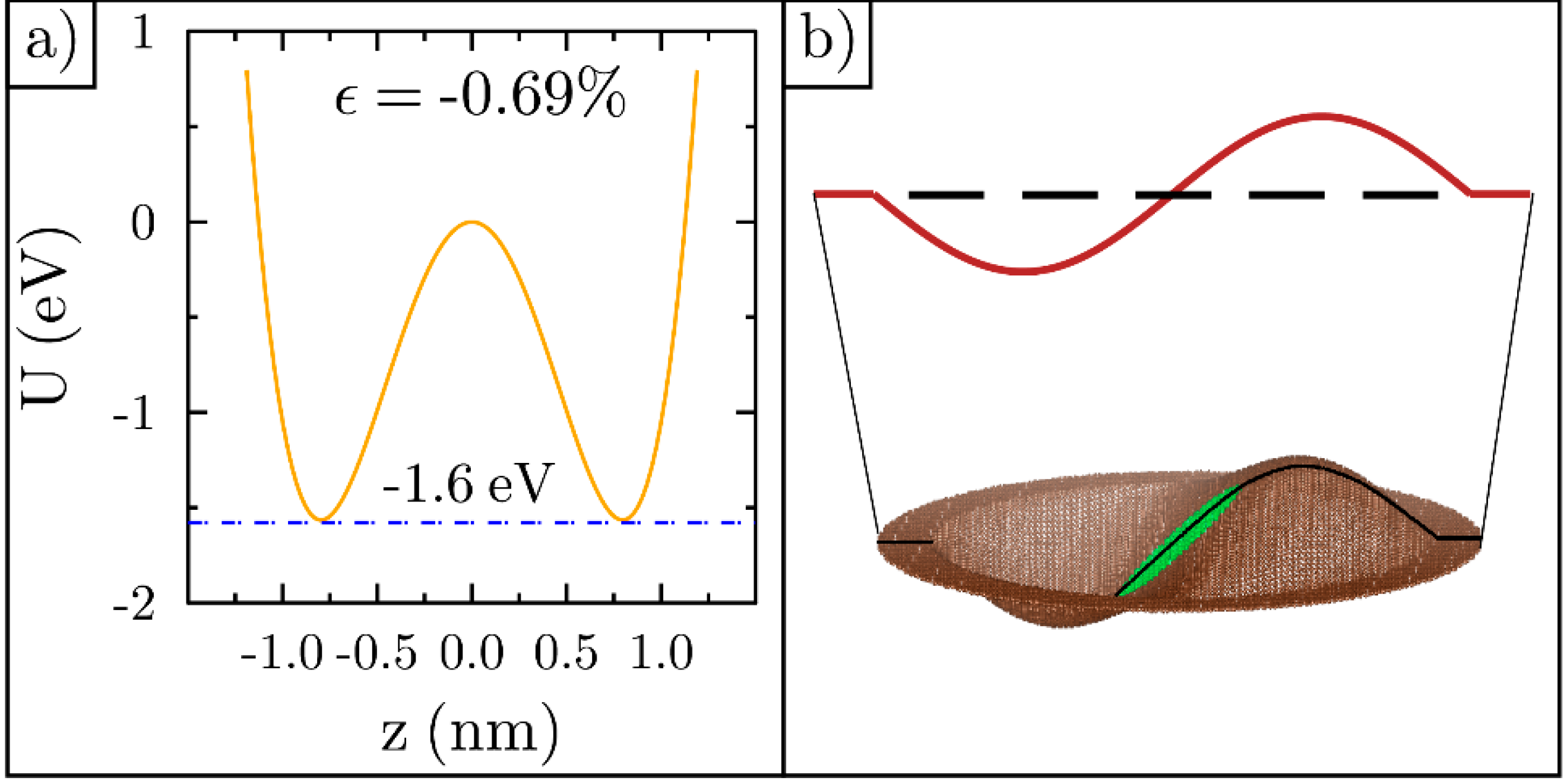
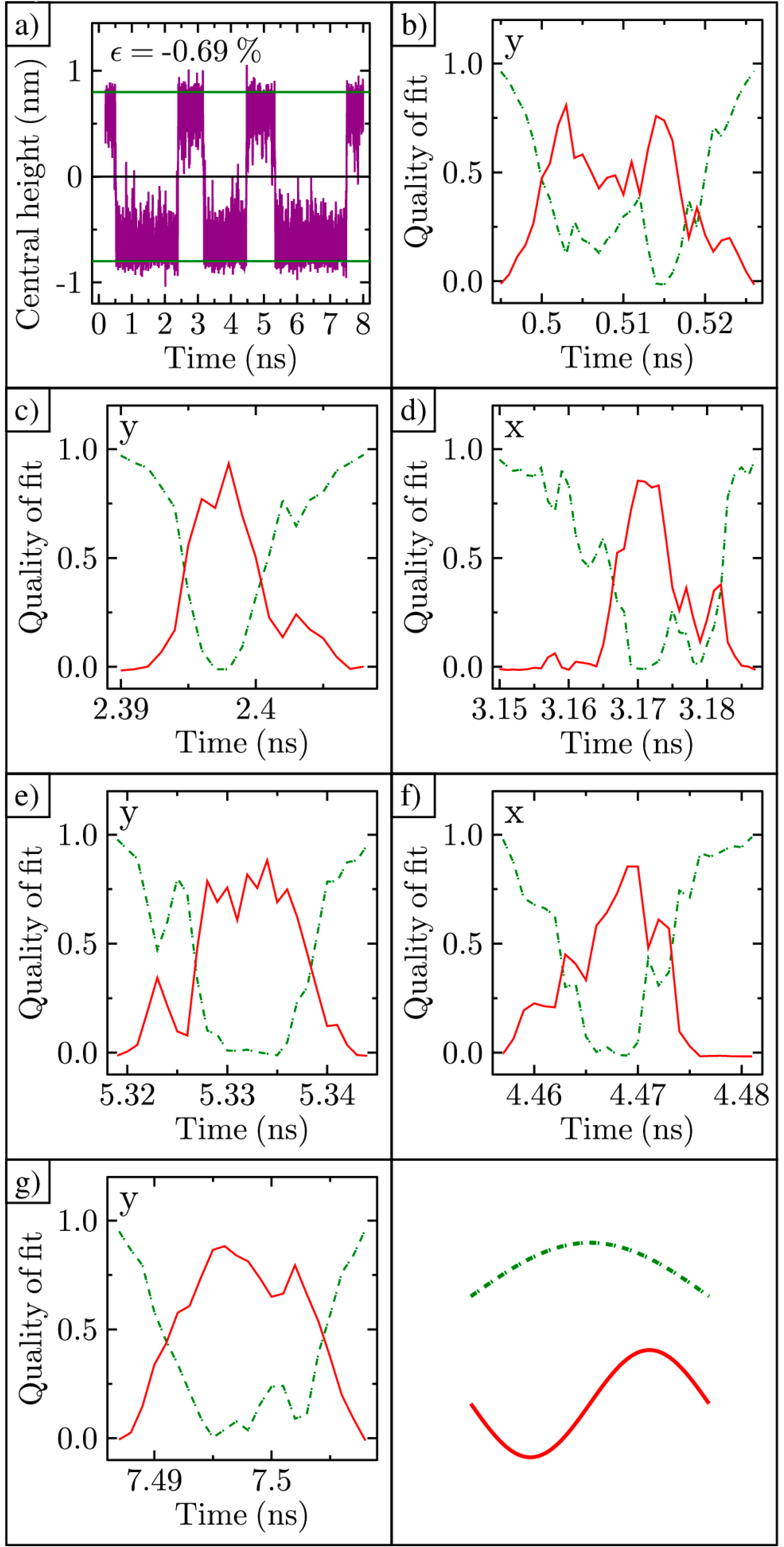
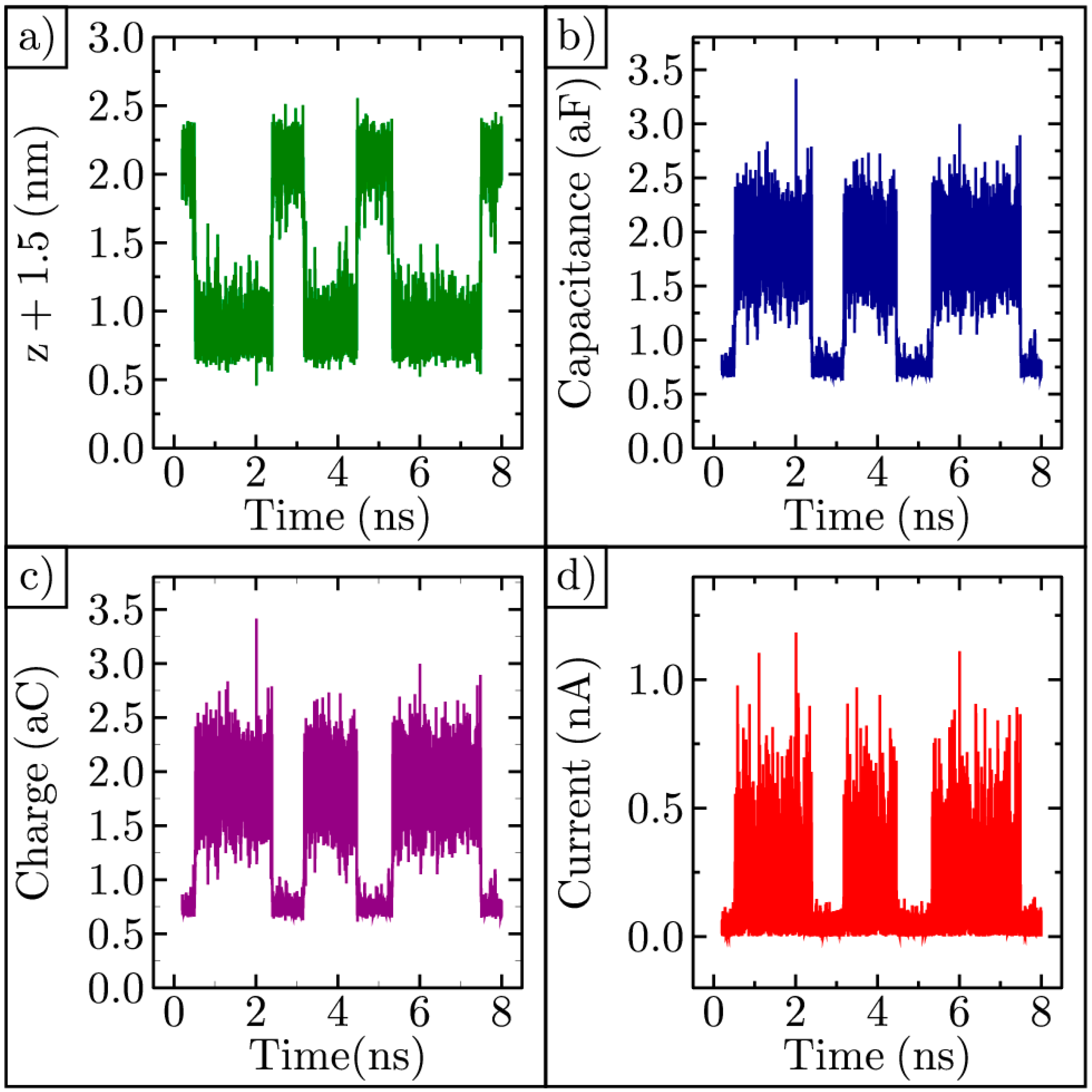
3.1. A. Bistable Ripples
3.2. B. Average Time between Inversion
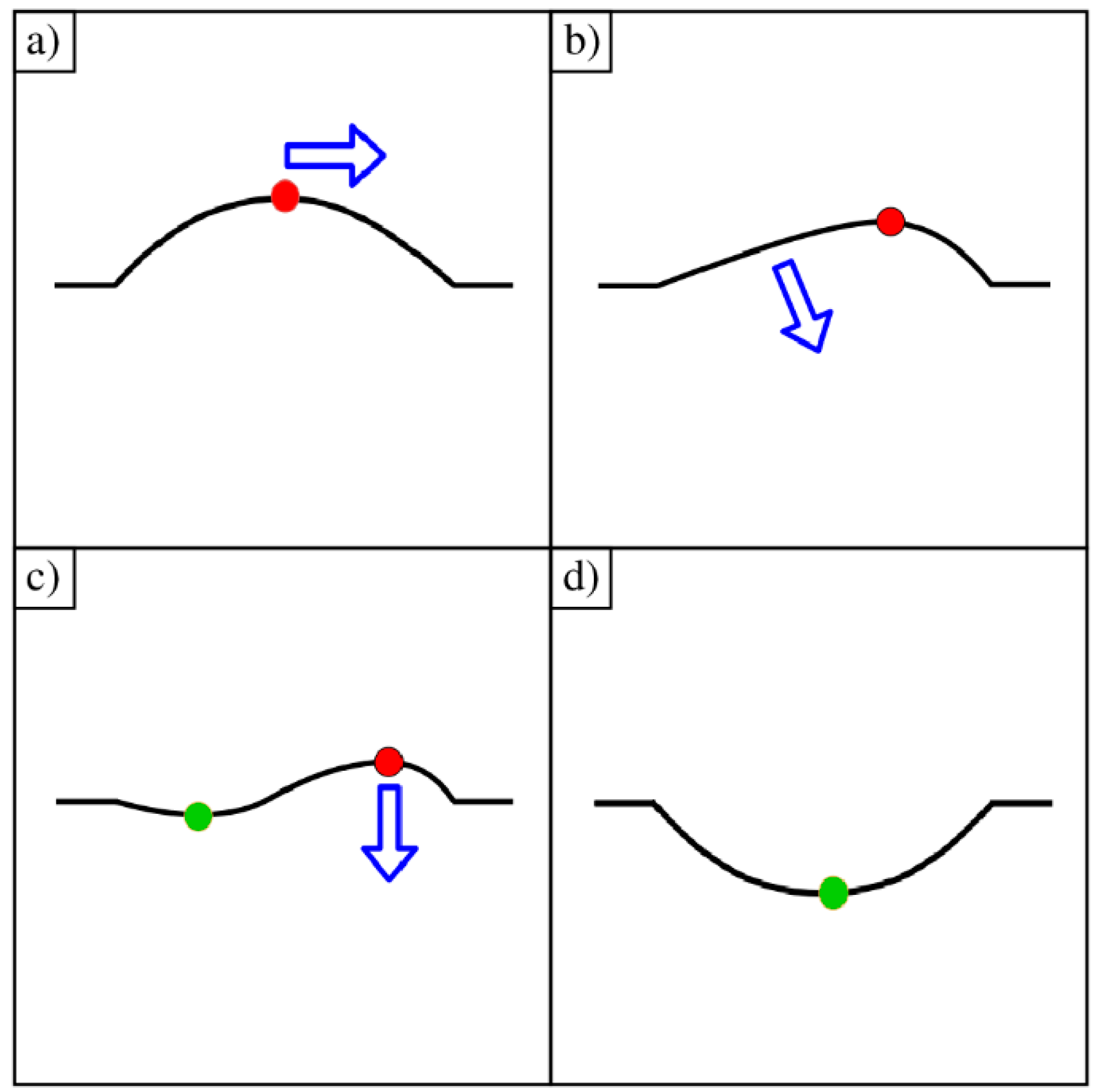
3.3. C. Physical Transformation during Ripple Inversion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hanson, S.; Seok, M.; Lin, Y.-S.; Foo, Z.; Kim, D.; Lee, Y.; Liu, N.; Sylvester, D.; Blaauw, D. A Low-Voltage Processor for Sensing Applications with Picowatt Standby Mode. IEEE J. Solid-State Circuits 2009, 44, 1145–1155. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Wang, L. Vibration Energy Harvesting by Magnetostrictive Material for Powering Wireless Sensors. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2008. [Google Scholar]
- Tong, C. Introduction to Materials for Advanced Energy Systems; Springer International Publishing AG: Cham, Switzerland, 2019. [Google Scholar]
- Lopez-Suarez, M.; Rurali, R.; Gammaitoni, L.; Abadal, G. Nanostructured graphene for energy harvesting. Phys. Rev. B 2011, 84, 161401. [Google Scholar] [CrossRef]
- El Mahboubi, F.; Bafleur, M.; Boitier, V.; Dilhac, J.-M. Energy-harvesting powered variable storage topology for battery-free wireless sensors. Technologies 2018, 6, 106. [Google Scholar] [CrossRef] [Green Version]
- Torres, E.O.; Rincon-Mora, G.A. Electrostatic Energy Harvester and Li-Ion Charger Circuit for Micro-Scale Applications. In Proceedings of the 2006 49th IEEE International Midwest Symposium on Circuits and Systems, San Juan, PR, USA, 6–9 August 2006; pp. 65–69. [Google Scholar]
- Wang, Z.L.; Wu, W. Nanotechnology Enabled Energy Harvesting for Self Powered Micro/Nanosystems. Angew. Chem. Int. Ed. 2012, 51, 11700–11721. [Google Scholar] [CrossRef]
- Abdelghany, M.; Ledwosinska, E.; Szkopek, T. Theory of the suspended graphene varactor. Appl. Phys. Lett. 2012, 101, 153102. [Google Scholar] [CrossRef]
- AbdelGhany, M.; Mahvash, F.; Mukhopadhyay, M.; Favron, A.; Martel, R.; Siaj, M.; Szkopek, T. Suspended graphene variable capacitor. 2D Mater. 2016, 3, 041005. [Google Scholar] [CrossRef] [Green Version]
- Philp, S.F. Vacuum-Insulated, Varying-Capacitance Machine. IEEE Trans. Electr. Insul. 1977, 12, 130–136. [Google Scholar] [CrossRef]
- Harerimana, F.; Peng, H.; Otobo, M.; Luo, F.; Gikunda, M.N.; Mangum, J.M.; Labella, V.P.; Thibado, P.M. Efficient circuit design for low power energy harvesting. AIP Adv. 2020, 10, 105006. [Google Scholar] [CrossRef]
- Thibado, P.M.; Kumar, P.; Singh, S.; Ruiz-Garcia, M.; Lasanta, A.; Bonilla, L.L. Fluctuation-induced current from freestanding graphene. Phys. Rev. E 2020, 102, 042101. [Google Scholar] [CrossRef] [PubMed]
- Littman, W. Properties of the Euler-Bernoulli beam equation and the Kirchoff plate equation related to controllability. In Proceedings of the 28th IEEE Conference on Decision and Control, Tampa, FL, USA, 13–15 December 1989; Volume 2283, p. 2286. [Google Scholar]
- Bunch, J.S.; van der Zande, A.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [Green Version]
- Fasolino, A.; Los, J.H.; Katsnelson, M.I.; Fasolino, A.; Los, J.H.; Katsnelson, M.I. Intrinsic ripples in graphene. Nat. Mater. 2007, 6, 858–861. [Google Scholar] [CrossRef] [Green Version]
- Breitwieser, R.; Hu, Y.C.; Chao, Y.C.; Tzeng, Y.R.; Liou, S.C.; Lin, K.C.; Chen, C.W.; Pai, W.W. Investigating ultraflexible freestanding graphene by scanning tunneling microscopy and spectroscopy. Phys. Rev. B 2017, 96, 085433. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hanggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Dutta, P.; Horn, P.M. Low-Frequency Fluctuations in Solids-1-F Noise. Rev. Mod. Phys. 1981, 53, 497–516. [Google Scholar] [CrossRef] [Green Version]
- Yamaletdinov, R.D.; Ivakhnenko, O.; Sedelnikova, O.V.; Shevchenko, S.N.; Pershin, Y.V. Snap-through transition of buckled graphene membranes for memcapacitor applications. Sci. Rep. 2018, 8, 3566. [Google Scholar] [CrossRef] [PubMed]
- Lindahl, N.; Midtvedt, D.; Svensson, J.; Nerushev, O.A.; Lindvall, N.; Isacsson, A.; Campbell, E.E.B. Determination of the Bending Rigidity of Graphene via Electrostatic Actuation of Buckled Membranes. Nano Lett. 2012, 12, 3526–3531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scharfenberg, S.; Mansukhani, N.; Chialvo, C.; Weaver, R.L.; Mason, N. Observation of a snap-through instability in graphene. Appl. Phys. Lett. 2012, 100, 21910. [Google Scholar] [CrossRef] [Green Version]
- Baumgarten, L.; Kierfeld, J. Shallow shell theory of the buckling energy barrier: From the Pogorelov state to softening and imperfection sensitivity close to the buckling pressure. Phys. Rev. E 2019, 99, 022803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef]
- Zan, R.; Muryn, C.; Bangert, U.; Mattocks, P.; Wincott, P.; Vaughan, D.; Li, X.; Colombo, L.; Ruoff, R.S.; Hamilton, B.; et al. Scanning tunnelling microscopy of suspended graphene. Nanoscale 2012, 4, 3065–3068. [Google Scholar] [CrossRef]
- Klimov, N.N.; Jung, S.; Zhu, S.; Li, T.; Wright, C.A.; Solares, S.D.; Newell, D.B.; Zhitenev, N.; Stroscio, J.A. Electromechanical Properties of Graphene Drumheads. Science 2012, 336, 1557–1561. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Yang, Y.; Barber, S.D.; Ackerman, M.L.; Schoelz, J.K.; Qi, D.; Kornev, I.; Dong, L.; Bellaiche, L.; Barraza-Lopez, S.; et al. Thibado, Atomic control of strain in freestanding graphene. Phys. Rev. B 2012, 85, 121406. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Zhai, X.; Zhao, A.; Wang, B.; Hou, J.G. Fabrication and scanning tunneling microscopy characterization of suspended monolayer graphene on periodic Si nanopillars. Appl. Phys. Lett. 2013, 102, 201602. [Google Scholar] [CrossRef]
- Illing, B.; Fritschi, S.; Kaiser, H.; Klix, C.L.; Maret, G.; Keim, P. Mermin–Wagner fluctuations in 2D amorphous solids. Proc. Natl. Acad. Sci. USA 2017, 114, 1856–1861. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abedpour, N.; Neek-Amal, M.; Asgari, R.; Shahbazi, F.; Nafari, N.; Tabar, M.R.R. Roughness of undoped graphene and its short-range induced gauge field. Phys. Rev. B 2007, 76, 195407. [Google Scholar] [CrossRef] [Green Version]
- Gazit, D. Correlation between charge inhomogeneities and structure in graphene and other electronic crystalline membranes. Phys. Rev. B 2009, 80, 161406. [Google Scholar] [CrossRef] [Green Version]
- San-Jose, P.; González, J.; Guinea, F. Electron-Induced Rippling in Graphene. Phys. Rev. Lett. 2011, 106, 045502. [Google Scholar] [CrossRef] [Green Version]
- Guinea, F.; le Doussal, P.; Wiese, K.J. Collective excitations in a large-d model for graphene. Phys. Rev. B 2014, 89, 125428. [Google Scholar] [CrossRef] [Green Version]
- Bonilla, L.L.; Ruiz-Garcia, M. Critical radius and temperature for buckling in graphene. Phys. Rev. B 2016, 93, 115407. [Google Scholar] [CrossRef] [Green Version]
- Bonilla, L.; Carpio, A. Ripples in a graphene membrane coupled to Glauber spins. J. Stat. Mech. Theory Exp. 2012, 2012, P09015. [Google Scholar] [CrossRef]
- Ruiz-Garcia, M.; Bonilla, L.; Prados, A. Ripples in hexagonal lattices of atoms coupled to Glauber spins. J. Stat. Mech. Theory Exp. 2015, 2015, P05015. [Google Scholar] [CrossRef] [Green Version]
- Lundeberg, M.B.; Folk, J. Rippled Graphene in an In-Plane Magnetic Field: Effects of a Random Vector Potential. Phys. Rev. Lett. 2010, 105, 146804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishigami, M.; Chen, J.H.; Cullen, W.G.; Fuhrer, M.S.; Williams, E.D. Atomic Structure of Graphene on SiO2. Nano Lett. 2007, 7, 1643–1648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geringer, V.; Liebmann, M.; Echtermeyer, T.; Runte, S.; Schmidt, M.; Rückamp, R.; Lemme, M.C.; Morgenstern, M. Intrinsic and extrinsic corrugation of monolayer graphene deposited on SiO2. Phys. Rev. Lett. 2009, 102, 076102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Available online: http://lammps.sandia.gov (accessed on 15 February 2018).
- Dhaliwal, G.; Nair, P.B.; Singh, C.V. Uncertainty analysis and estimation of robust AIREBO parameters for graphene. Carbon 2019, 142, 300–310. [Google Scholar] [CrossRef]
- Bao, W.; Miao, F.; Chen, Z.; Zhang, H.; Jang, W.; Dames, C.; Lau, C.N. Controlled ripple texturing of suspended graphene and ultrathin graphite membranes. Nat. Nanotechnol. 2009, 4, 562–566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ackerman, M.L.; Kumar, P.; Neek-Amal, M.; Thibado, P.M.; Peeters, F.M.; Singh, S. Anomalous Dynamical Behavior of Freestanding Graphene Membranes. Phys. Rev. Lett. 2016, 117, 126801. [Google Scholar] [CrossRef]
- Deng, S.; Berry, V. Wrinkled, rippled and crumpled graphene: An overview of formation mechanism, electronic properties, and applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Kramers, H.A. Brownian motion in field of force and diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Davini, C.; Favata, A.; Paroni, R. A new material property of graphene: The bending Poisson coefficient. EPL 2017, 118, 26001. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Wang, B.; Wu, J.; Yang, R.; Dunn, M. Bending Rigidity and Gaussian Bending Stiffness of Single-Layered Graphene. Nano Lett. 2013, 13, 26–30. [Google Scholar] [CrossRef] [Green Version]
- Koskinen, P.; Kit, O.O. Approximate modeling of spherical membranes. Phys. Rev. B 2010, 82, 235420. [Google Scholar] [CrossRef] [Green Version]
- Neek-Amal, M.; Xu, P.; Schoelz, J.; Ackerman, M.; Barber, S.; Thibado, P.; Sadeghi, A.; Peeters, F. Thermal mirror buckling in freestanding graphene locally controlled by scanning tunneling microscopy. Nat. Commun. 2014, 5, 4962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, K.; Batra, R.C. Pull-in and snap-through instabilities in transient deformations of microelectromechanical systems. J. Micromech. Microeng. 2009, 19, 035008. [Google Scholar] [CrossRef]
- Overvelde, J.; Kloek, T.; D’Haen, J.J.A.; Bertoldi, K. Amplifying the response of soft actuators by harnessing snap-through instabilities. Proc. Natl. Acad. Sci. USA 2015, 112, 10863–10868. [Google Scholar] [CrossRef] [Green Version]
- Harne, R.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Ramlan, R.; Brennan, M.J.; Mace, B.R.; Kovacic, I. Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 2010, 59, 545–558. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangum, J.M.; Harerimana, F.; Gikunda, M.N.; Thibado, P.M. Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations. Membranes 2021, 11, 516. https://doi.org/10.3390/membranes11070516
Mangum JM, Harerimana F, Gikunda MN, Thibado PM. Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations. Membranes. 2021; 11(7):516. https://doi.org/10.3390/membranes11070516
Chicago/Turabian StyleMangum, James M., Ferdinand Harerimana, Millicent N. Gikunda, and Paul M. Thibado. 2021. "Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations" Membranes 11, no. 7: 516. https://doi.org/10.3390/membranes11070516
APA StyleMangum, J. M., Harerimana, F., Gikunda, M. N., & Thibado, P. M. (2021). Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations. Membranes, 11(7), 516. https://doi.org/10.3390/membranes11070516





