Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling
Abstract
:1. Introduction
2. Theoretical Part—Modeling of Transport Phenomena in Haemofilters
2.1. Complete Modeling/Characterization of the Flow Field
2.2. Modeling Mass Transfer in Haemofilters
3. Experimental Part
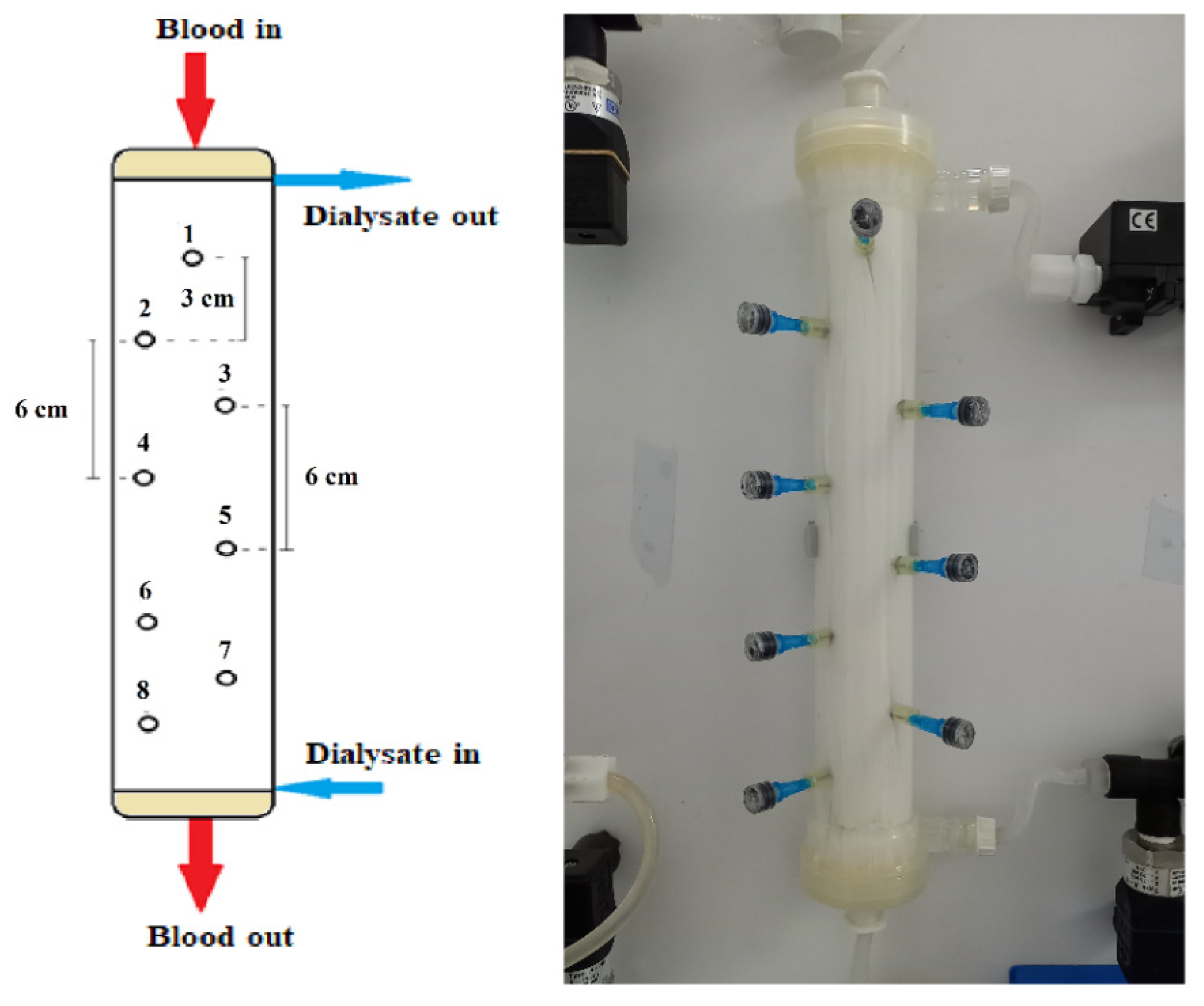
3.1. Materials Used—Instrumented Module/Haemofilter
3.2. Experimental Set up—Operating Modes
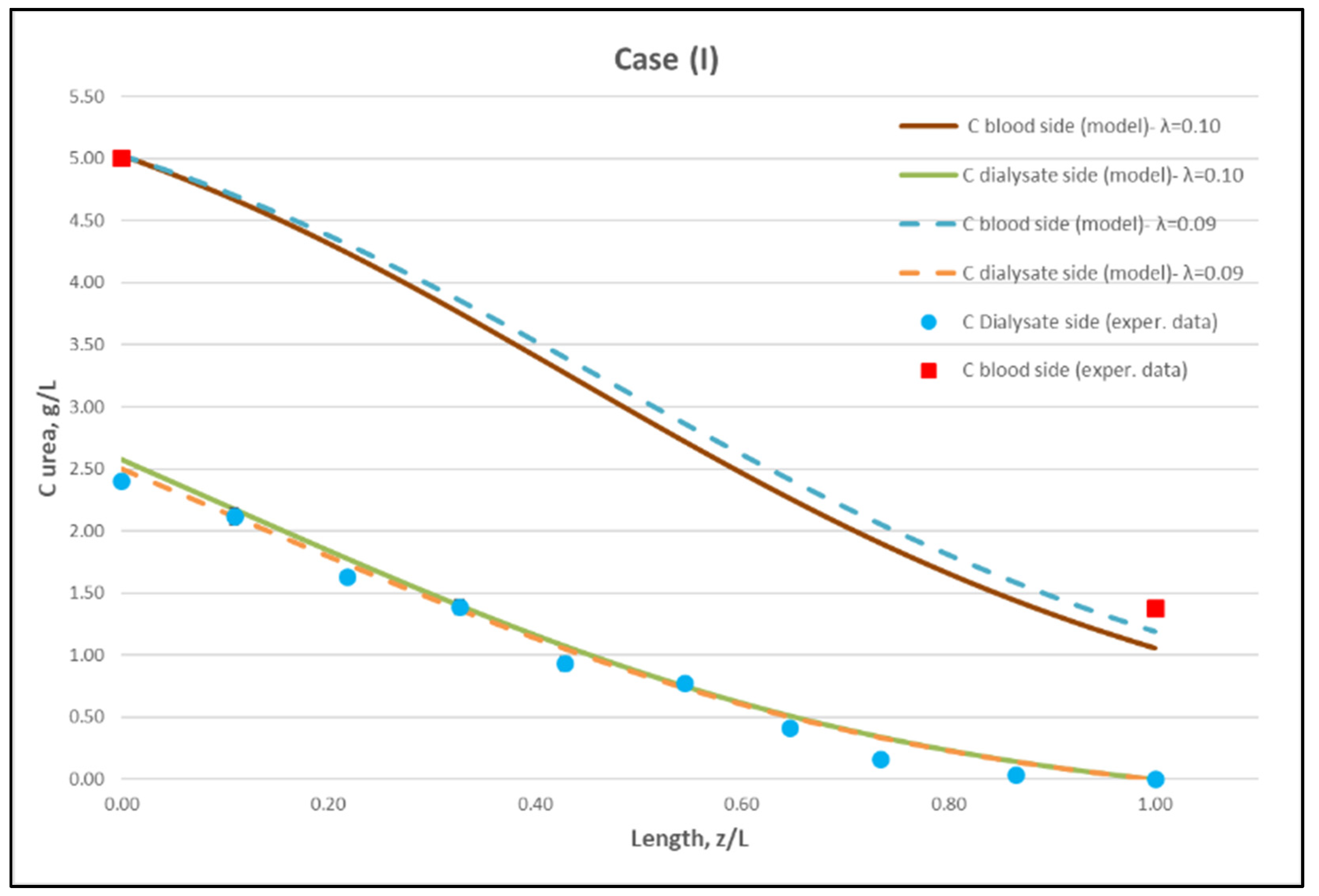
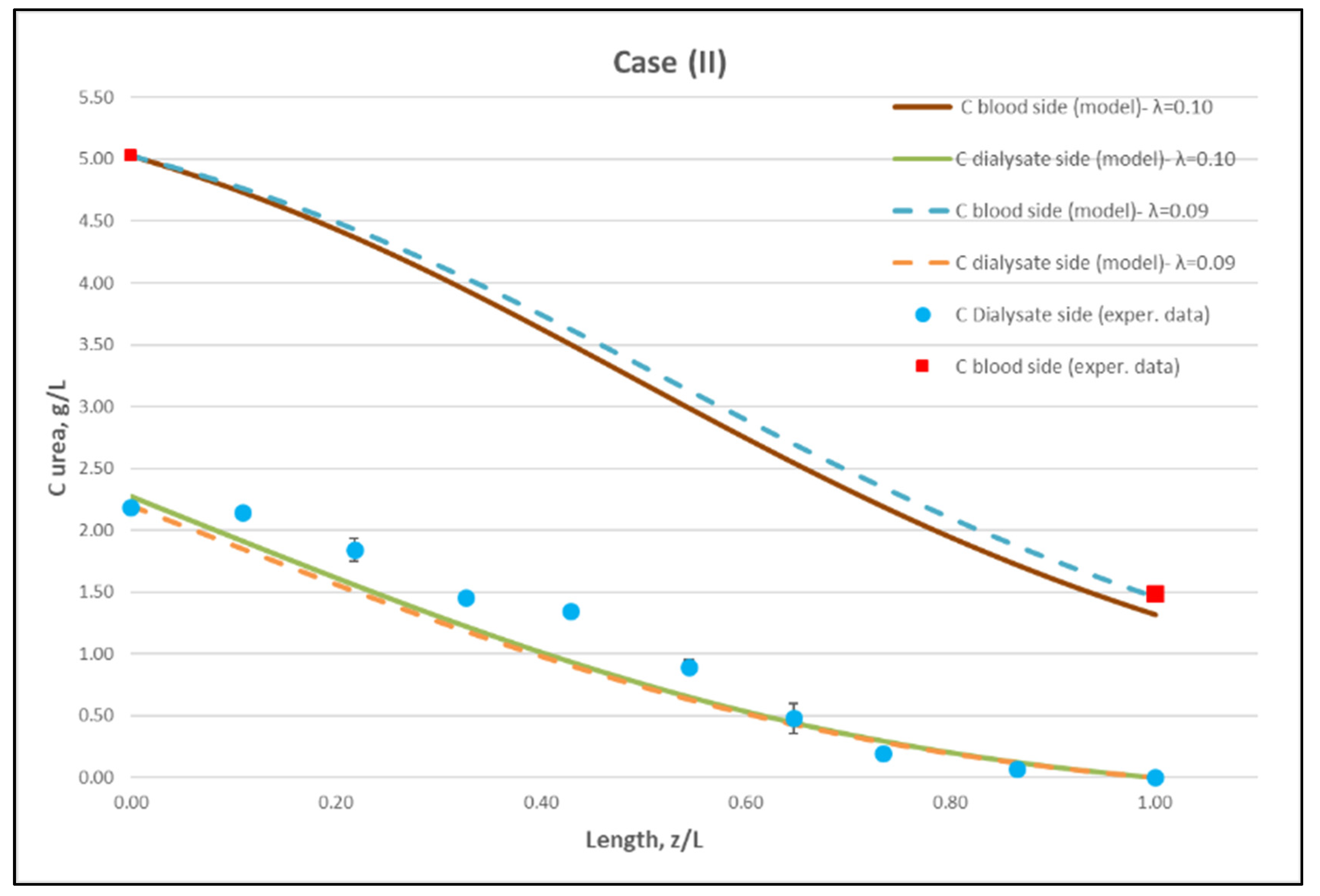
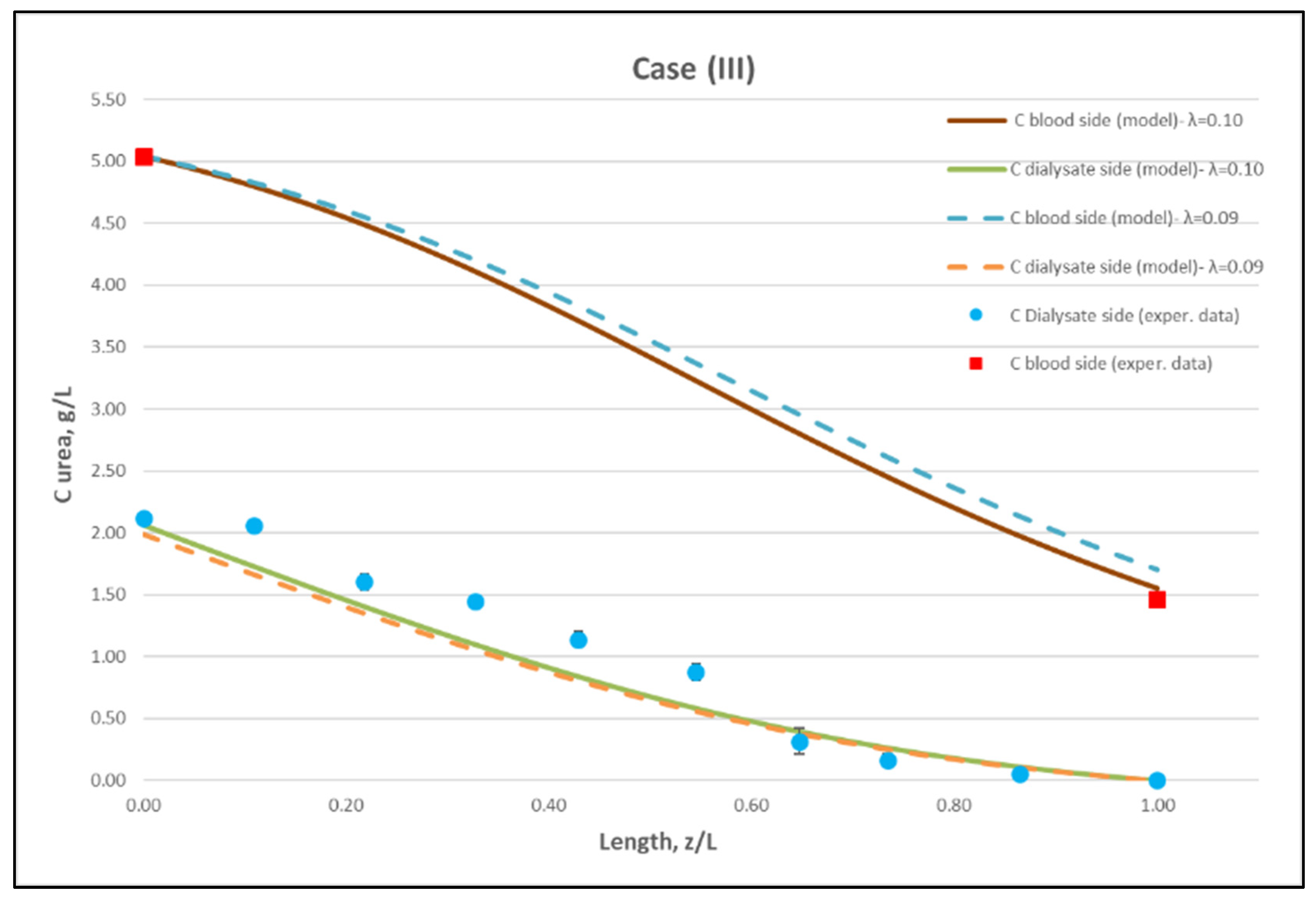
4. Experimental Results—Comparison with Model Prediction
4.1. Fluid Mechanical Module Characteristics
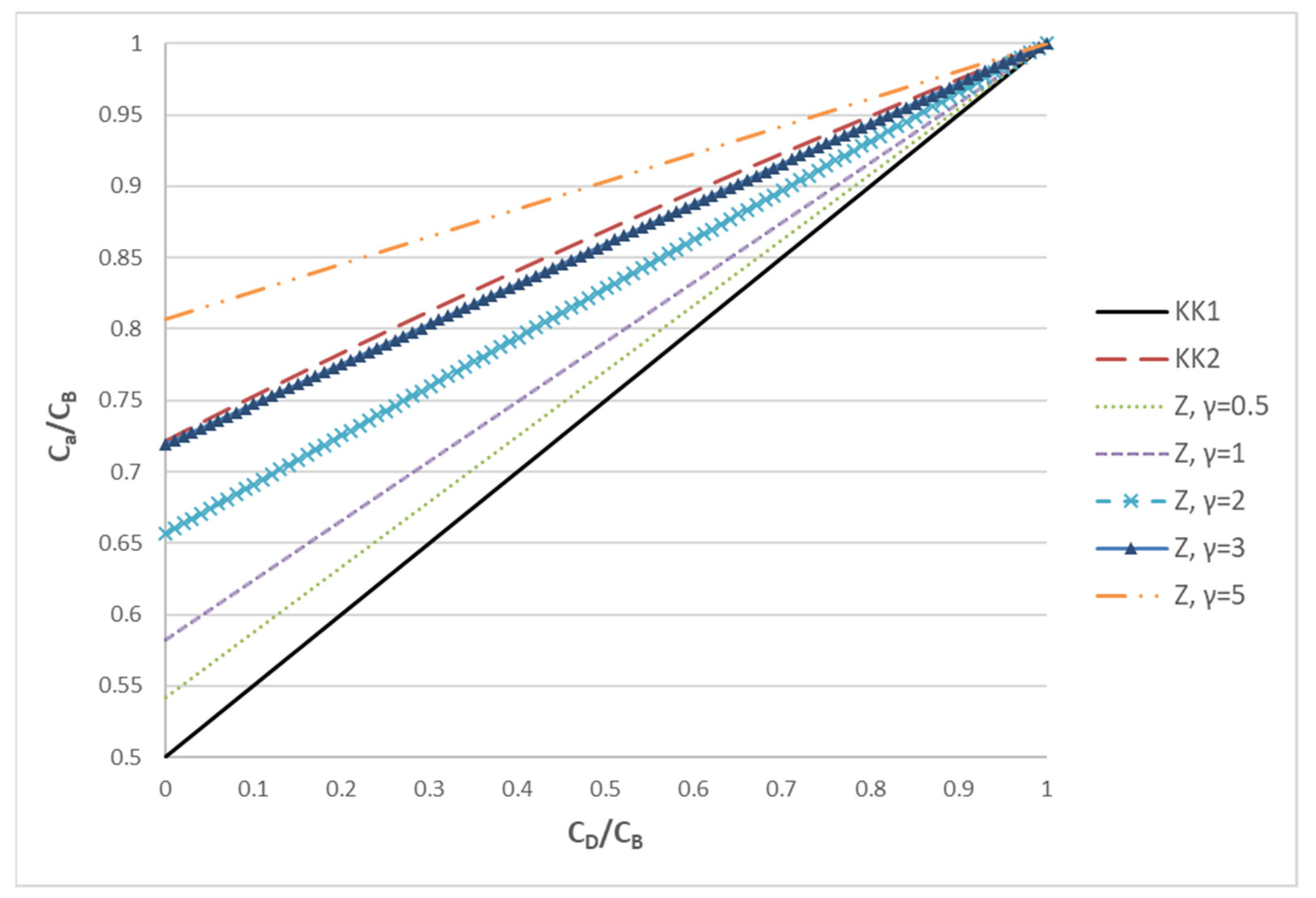
4.2. Mass Transfer Module Performance/Characteristics—Method Validation
4.2.1. Experimental Results
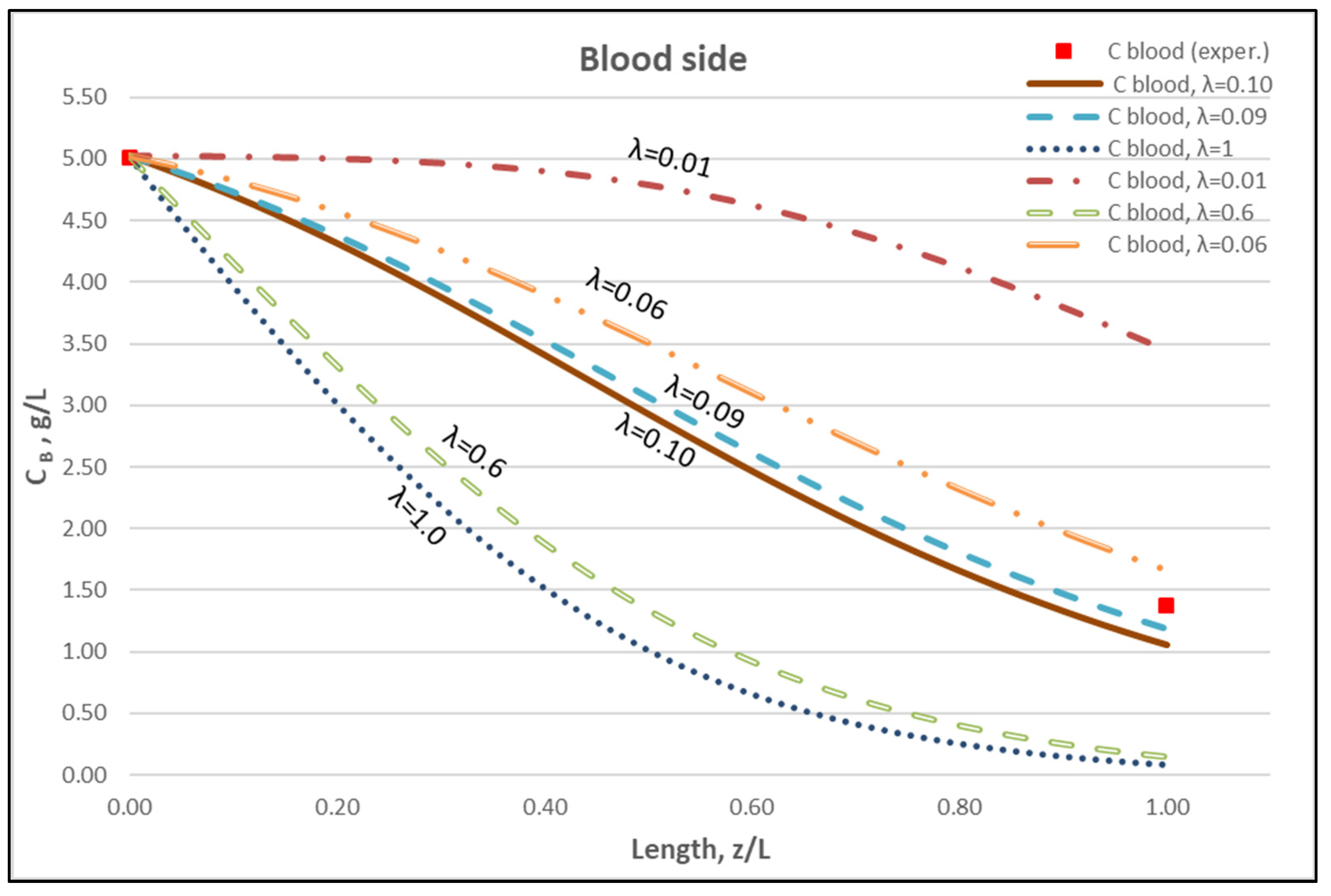
4.2.2. Data Interpretation/Assessment—Model Validation
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Af, As | normalized lumen side and shell side friction factors |
| A = (Af + As)0.5 | normalized total friction factor |
| c1, c2, c3, c4, c5, c6 | auxiliary problem solution constants |
| Ca | characteristic concentration, g/L |
| CB, CBlood | solute concentration blood-side, g/L |
| CD, CDialysate | solute concentration shell-side, g/L |
| CL | fractional solute clearance; Equation (18) |
| D | diffusion coefficient of the solute, m2/s |
| De | effective diffusion coefficient of the solute in the membrane, m2/s |
| ff | lumen-side friction coefficient, (Pa∙s)/m4 |
| fs | shell-side friction coefficient, (Pa∙s)/m4 |
| G | solute mass transferred through membrane, kg/m/s |
| hin | inner (cylindrical) channel mass transfer coefficient, m2/s |
| hout | outer (annular) channel mass transfer coefficient, m2/s |
| K | membrane permeance, m2/Pa/s |
| KD | effective mass transfer coefficient, m2/s |
| KCL | solute clearance, mL/min; Equation (19) |
| KUF | ultrafiltration coefficient, mL/h/mmHg |
| L | active module length, m |
| N | total number of fibers in module |
| NGr | local Graetz number |
| P1, P2, P3, P4 | external pressures, psi or Pa |
| QBlood, Qf | blood-side (lumen) flow rate, m3/s |
| QDialysate, Qs | dialysate-side (shell) flow rate, m3/s |
| Q | local transmembrane flow rate per unit length, m2/s |
| QUF | ultrafiltration rate, m3/s |
| Ro | inner fiber radius, m |
| R1 | outer fiber radius and inner radius of annular unit cell, m |
| Rc | outer radius of the annular unit cell on the dialysate/shell side, m |
| Rew | wall Reynolds number, |
| U | velocity on the lumen-side, m/s |
| Uc | velocity on the shell-side, m/s |
| vw | wall flux, m/s |
| v | kinematic viscosity, m2/s |
| z | axial coordinate along membrane module, m |
| z′ | location of transmembrane flow reversal, m |
| Greek letters | |
| β | ratio of dialysate to blood inlet flow rates |
| γ | relative strength of convection to diffusion (γ = Q/KD) |
| ΔP | pressure difference, psi or Pa |
| ε | void fraction on the shell-side |
| ζi | parameters, related to pressure-drop in headers, Pa/m6/s2 |
| λ | diffusion hindering factor |
| τ | membrane tortuosity |
| φ | membrane porosity |
Appendix A
| Experiment | QBlood (mL/min) | QDialysate (mL/min) | QUF (mL/min) | P1 psi (kPa) | P2 psi (kPa) | P3 psi (kPa) | P4 psi (kPa) | CBlood in (g/L) | CBlood out (g/L) | CDialysate in (g/L) | CDialysate out (g/L) | Clearance CL (%) | Clearance KCL (mL/min) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
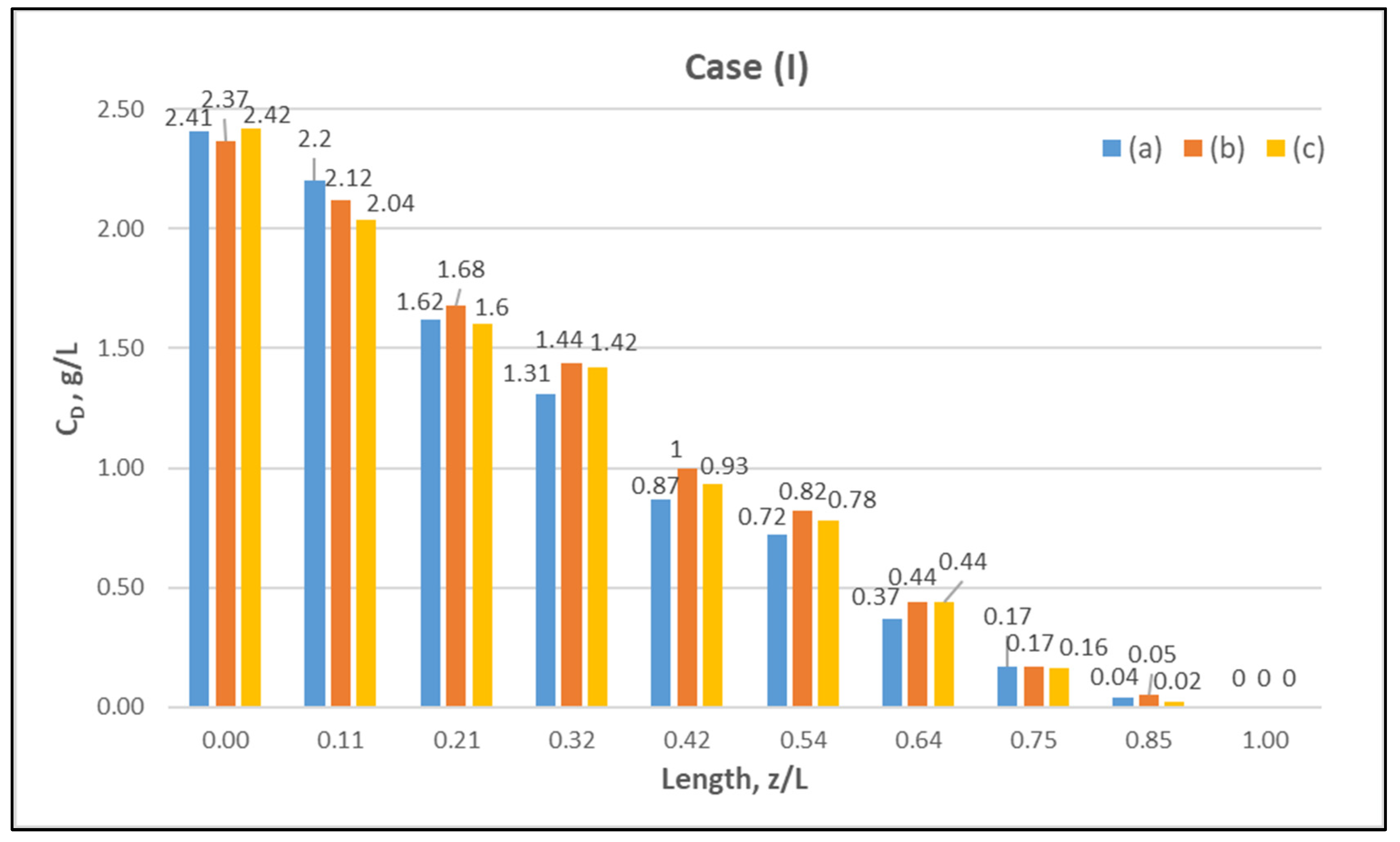
| CASE (I): Nominal flow rates: QBlood = 200 mL/min, QDialysate = 300 mL/min | |||||||||||||
| (a) | 204 | 299 | 14.00 | 1.47 (10.13) | 0.68 (4.69) | 1.32 (9.10) | 0.50 (3.45) | 5.00 | 1.39 ± 0.02 | 0.0 | 2.41 ± 0.01 | 73.96 | 151 |
| (b) | 199 | 301 | 14.00 | 1.54 (10.62) | 0.69 (4.69) | 1.35 (9.31) | 0.58 (4.00) | 5.01 | 1.38 ± 0.02 | 0.0 | 2.37 ± 0.02 | 73.39 | 148 |
| (c) | 200 | 298 | 14.07 | 1.51 (10.41) | 0.69 (4.69) | 1.37 (9.45) | 0.55 (3.79) | 5.02 | 1.36 ± 0.03 | 0.0 | 2.42 ± 0.05 | 74.17 | 149 |
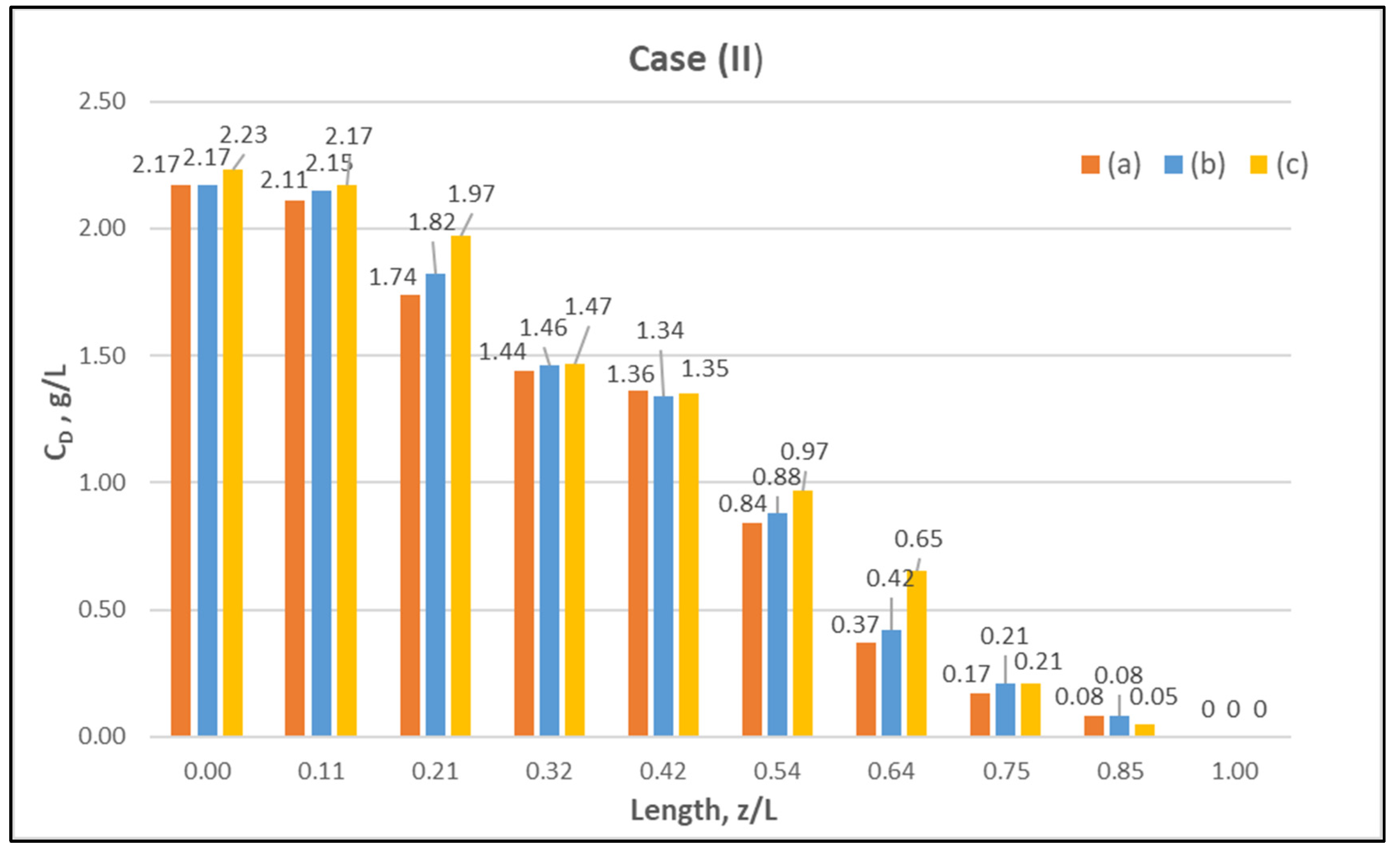
| CASE (II): Nominal flow rates: QBlood = 250 mL/min, QDialysate = 400 mL/min | |||||||||||||
| (a) | 249 | 400 | 16.00 | 2.57 (17.72) | 1.44 (9.93) | 2.51 (17.31) | 1.19 (8.20) | 5.02 | 1.49 ± 0.02 | 0.0 | 2.17 ± 0.01 | 72.28 | 180 |
| (b) | 252 | 401 | 17.00 | 2.60 (17.93) | 1.44 (9.93) | 2.46 (16.96) | 1.19 (8.20) | 5.01 | 1.52 ± 0.01 | 0.0 | 2.17 ± 0.01 | 71.75 | 181 |
| (c) | 250 | 399 | 17.87 | 2.71 (18.68) | 1.50 (10.34) | 2.52 (17.37) | 1.24 (8.55) | 5.07 | 1.46 ± 0.05 | 0.0 | 2.23 ± 0.02 | 73.34 | 183 |
| CASE (III): Nominal flow rates: QBlood = 300 mL/min, QDialysate = 500 mL/min | |||||||||||||
| (a) | 304 | 502 | 26.00 | 3.78 (26.06) | 2.35 (16.20) | 3.79 (26.13) | 2.00 (13.79) | 5.05 | 1.47 ± 0.03 | 0.0 | 2.13 ± 0.01 | 72.51 | 223 |
| (b) | 297 | 498 | 25.00 | 3.75 (25.85) | 2.30 (15.86) | 3.74 (25.79) | 1.94(13.38) | 5.04 | 1.48 ± 0.02 | 0.0 | 2.09 ± 0.01 | 73.15 | 217 |
| (c) | 300 | 503 | 26.50 | 3.80 (26.20) | 2.35 (16.20) | 3.81 (26.27) | 1.97 (13.58) | 5.02 | 1.43 ± 0.04 | 0.0 | 2.14 ± 0.02 | 73.42 | 222 |
References
- Lorenzin, A.; Neri, M.; Clark, W.R.; Garzotto, F.; Brendolan, A.; Nalesso, F.; Marchionna, N.; Zanella, M.; Sartori, M.; Fiore, G.B.; et al. Modeling of Internal Filtration in Theranova Hemodialyzers. Contrib. Nephrol. 2017, 191, 127–141. [Google Scholar] [CrossRef]
- Yamamoto, K.-I.; Hiwatari, M.; Kohori, F.; Sakai, K.; Fukuda, M.; Hiyoshi, T. Membrane fouling and dialysate flow pattern in an internal filtration-enhancing dialyzer. J. Artif. Organs 2005, 8, 198–205. [Google Scholar] [CrossRef]
- Ronco, C.; Clark, W.R. Haemodialysis membranes. Nat. Rev. Nephrol. 2018, 14, 394–410. [Google Scholar] [CrossRef]
- Chapdelaine, I.; Zuijdewijn, C.L.D.R.V.; Mostovaya, I.M.; Lévesque, R.; Davenport, A.; Blankestijn, P.J.; Wanner, C.; Nubé, M.J.; Grooteman, M.P.; on behalf of the EUDIAL Group; et al. Optimization of the convection volume in online post-dilution haemodiafiltration: Practical and technical issues. Clin. Kidney J. 2015, 8, 191–198. [Google Scholar] [CrossRef] [Green Version]
- Ronco, C.; Marchionna, N.; Brendolan, A.; Neri, M.; Lorenzin, A.; Rueda, A.J.M. Expanded haemodialysis: From operational mechanism to clinical results. Nephrol. Dial. Transplant. 2018, 33, iii41–iii47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, W.R.; Gao, D.; Neri, M.; Ronco, C. Solute Transport in Hemodialysis: Advances and Limitations of Current Membrane Technology. Expand. Hemodial.—Innov. Clin. Approach Dial. 2017, 191, 84–99. [Google Scholar]
- Ficheux, A.; Ronco, C.; Brunet, P.; Argilés, À. The ultrafiltration coefficient: This old ‘grand inconnu’ in dialysis. Nephrol. Dial. Transplant. 2015, 30, 204–208. [Google Scholar] [CrossRef] [Green Version]
- Hulko, M.; Haug, U.; Gauss, J.; Boschetti-De-Fierro, A.; Beck, W.; Krause, B. Requirements and Pitfalls of Dialyzer Sieving Coefficients Comparisons. Artif. Organs 2018, 42, 1164–1173. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. Reliable fluid-mechanical characterization of haemofilters—Addressing the deficiencies of current standards and practices. Artif. Organs 2021, 5, 1348–1359. [Google Scholar] [CrossRef]
- Donato, D.; Storr, M.; Krause, B. Design optimization of hollow fiber dialyzers to enhance internal filtration based on a mathematical model. J. Membr. Sci. 2020, 598, 117690. [Google Scholar] [CrossRef]
- Hirano, A.; Yamamoto, K.-I.; Matsuda, M.; Yakushiji, T.; Miyasaka, T.; Ogawa, T.; Sakai, K. Evaluation of Dialyzer Jacket Structure and Hollow-Fiber Dialysis Membranes to Achieve High Dialysis Performance. Ther. Apher. Dial. 2010, 15, 66–74. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Kostoglou, M.; Moschona, A.; Sioutopoulos, D.C. Method development for experimental determination οf key fluid-mechanical parameters of haemo-catharsis modules. J. Membr. Sci. 2020, 611, 118353. [Google Scholar] [CrossRef]
- Kostoglou, M.; Moschona, A.; Karabelas, A.J.; Sioutopoulos, D.C. Implementation and validation of an innovative method for fluid mechanical characterization of haemo-catharsis modules. J. Membr. Sci. 2021, 624, 119117. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.; He, L.; Liu, J.; Sun, S.; Huang, Z.; Liang, X.M.; Gao, D.; Ding, W. Simulation and experimental study on the effect of channeling flows on the transport of toxins in hemodialyzers. J. Membr. Sci. 2016, 501, 123–133. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Martinus Nijhoff Publishers: The Hague, The Netherlands, 1981. [Google Scholar]
- Legallais, C. A theoretical model to predict the in vitro performance of hemodiafilters. J. Membr. Sci. 2000, 168, 3–15. [Google Scholar] [CrossRef]
- Raithby, G. Laminar heat transfer in the thermal entrance region of circular tubes and two-dimensional rectangular ducts with wall suction and injection. Int. J. Heat Mass Transf. 1971, 14, 223–243. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A. On the structure of the single-phase flow field in hollow fiber membrane modules during filtration. J. Membr. Sci. 2008, 322, 128–138. [Google Scholar] [CrossRef]
- Donato, D.; Boschetti-De-Fierro, A.; Zweigart, C.; Kolb, M.; Eloot, S.; Storr, M.; Krause, B.; Leypoldt, K.; Segers, P. Optimization of dialyzer design to maximize solute removal with a two-dimensional transport model. J. Membr. Sci. 2017, 541, 519–528. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim. et Biophys. Acta 1958, 27, 229–246. [Google Scholar] [CrossRef]
- Ding, W.; Li, W.; Sun, S.; Zhou, X.; Hardy, P.A.; Ahmad, S.; Gao, D. Three-Dimensional Simulation of Mass Transfer in Artificial Kidneys. Artif. Organs 2015, 39, E79–E89. [Google Scholar] [CrossRef]
- Zydney, A.L. Bulk Mass Transport Limitations during High-Flux Hemodialysis. Artif. Organs 2008, 17, 919–924. [Google Scholar] [CrossRef] [PubMed]
- Langsdorf, L.J.; Zydney, A.L. Diffusive and convective solute transport through hemodialysis membranes: A hydrodynamic analysis. J. Biomed. Mater. Res. 1994, 28, 573–582. [Google Scholar] [CrossRef] [PubMed]
- Mu, T.; Zhang, Y.; Shi, W.; Chen, G.; Liu, Y.; Huang, M. A novel UiO-66/PSF-composite membrane for the rejection of multiple antibiotics: Numerical simulation and experiment verification. Chemosphere 2021, 269, 128686. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Qin, H. A Mathematical Modeling of the Reverse Osmosis Concentration Process of a Glucose Solution. Process. 2019, 7, 271. [Google Scholar] [CrossRef] [Green Version]
- Kostoglou, M.; Bissett, E.J.; Konstandopoulos, A.G. Improved Transfer Coefficients for Wall-Flow Monolithic Catalytic Reactors: Energy and Momentum Transport. Ind. Eng. Chem. Res. 2012, 51, 13062–13072. [Google Scholar] [CrossRef]
- Churchill, S.W.; Usagi, R. A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 1972, 18, 1121–1128. [Google Scholar] [CrossRef]
- Deen, W.M. Analysis of Transport Phenomena; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- ISO 8637-1:2017(E). Extracorporeal Systems for Blood Purification—Part 1: Haemodialysers, Haemodiafilters, Haemofilters and Haemoconcentrators. International Standard. 2017. Available online: https://www.iso.org/standard/69843.html (accessed on 24 January 2020).
- Elisio™. 2018. Available online: https://www.nipro-group.com/en-en/products/elisiotm (accessed on 4 March 2020).
- Sakai, K.; Takesawa, S.; Mimura, R.; Ohashi, H. Determination of pore radius of hollow-fiber dialysis membranes using tritium-labeled water. J. Chem. Eng. Jpn. 1988, 21, 207–210. [Google Scholar] [CrossRef] [Green Version]
- Longsworth, L.G. Temperature Dependence of Diffusion in Aqueous Solutions. J. Phys. Chem. 1954, 58, 770–773. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, C.; Ma, P.; Yu, K.T. Studies on the Diffusion Coefficients of Amino Acids in Aqueous Solutions. J. Chem. Eng. Data 2005, 50, 1192–1196. [Google Scholar] [CrossRef]




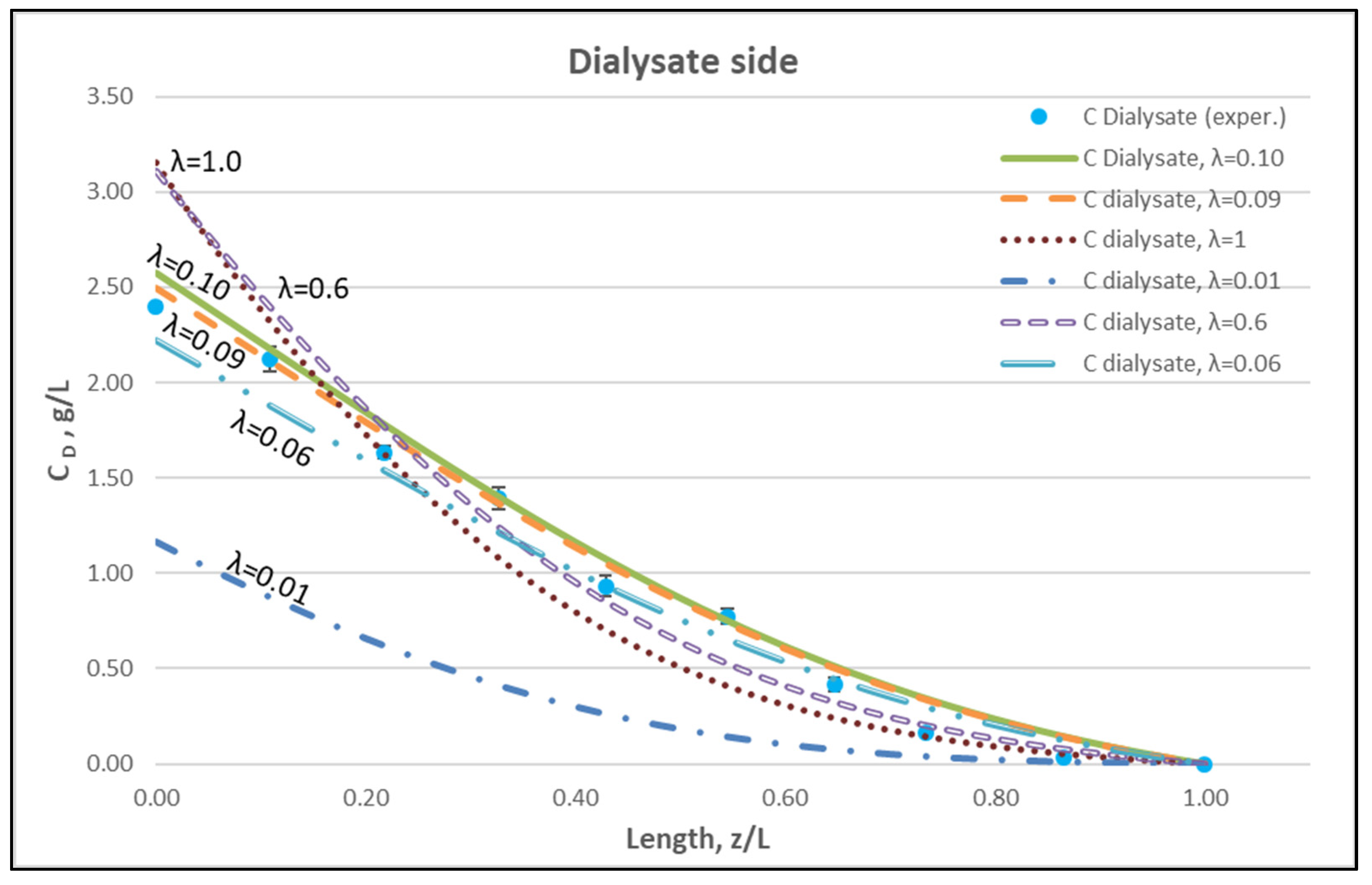
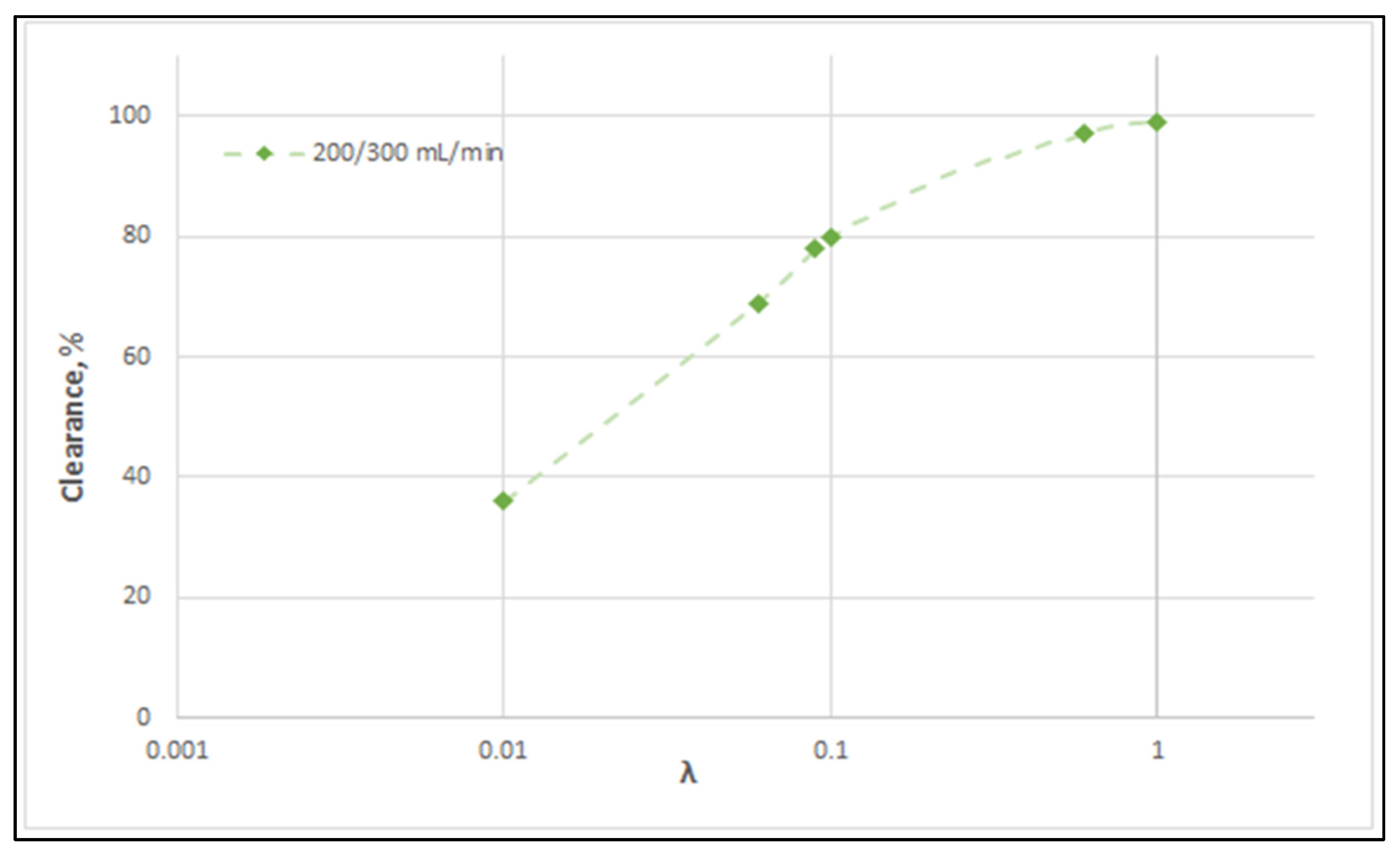
| Parameter | Units | Value |
|---|---|---|
| K | mL/(h∙m∙mmHg) m2/Pa/s | 2.21 × 103 4.60 × 10−9 |
| ff | (Pa∙s)/m4 | 5.68 × 109 |
| fs | (Pa∙s)/m4 | 0.90 × 109 |
| ζ1 | Pa/(m6/s2) | 10.25 × 1013 |
| ζ2 | Pa/(m6/s2) | 6.95 × 1013 |
| ζ3 | Pa/(m6/s2) | 5.46 × 1013 |
| ζ4 | Pa/(m6/s2) | 6.88 × 1013 |
| Parameter | Symbol, Units | Value |
|---|---|---|
| Inner fiber radius | Ro, m | 1.0 × 10−4 |
| Outer fiber radius | R1, m | 1.4 × 10−4 |
| Void fraction, shell-side | ε | 0.51 |
| Length of active section | L, m | 0.28 |
| Number of fibers | N | 10,760 |
| Membrane permeance | K, m2/Pa∙s | 4.6 × 10−9 |
| Lumen-side friction coefficient | ff, (Pa∙s)/m4 | 5.68 × 109 |
| Shell-side friction coefficient | fs, (Pa∙s)/m4 | 8.98 × 108 |
| Diffusion coefficient of urea, at 25 °C | D, m2/s | 1.34 × 10−9 |
| Diffusion hindering factor * | λ | ~0.095 * |
| λ | Clearance CL % (Prediction) | Clearance CL % (Experimental) | Clearance KCL mL/min (Predict.) | Clearance KCL mL/min (Exper.) |
|---|---|---|---|---|
| CASE (I): QBlood = 200 mL/min, QDialysate = 300 mL/min | ||||
| 0.09 | 78 | 74.17 ± 0.18 | 156 | 149.3 |
| 0.10 | 80 | 161 | ||
| CASE (II): QBlood = 250 mL/min, QDialysate = 400 mL/min | ||||
| 0.09 | 73 | 72.46 ± 0.66 | 182.4 | 181.3 |
| 0.10 | 76 | 189 | ||
| CASE (III): QBlood = 300 mL/min, QDialysate = 500 mL/min | ||||
| 0.09 | 69 | 73.03 ± 0.38 | 207 | 220.7 |
| 0.10 | 72 | 216 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschona, A.; Kostoglou, M.; Karabelas, A.J. Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling. Membranes 2022, 12, 62. https://doi.org/10.3390/membranes12010062
Moschona A, Kostoglou M, Karabelas AJ. Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling. Membranes. 2022; 12(1):62. https://doi.org/10.3390/membranes12010062
Chicago/Turabian StyleMoschona, Alexandra, Margaritis Kostoglou, and Anastasios J. Karabelas. 2022. "Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling" Membranes 12, no. 1: 62. https://doi.org/10.3390/membranes12010062
APA StyleMoschona, A., Kostoglou, M., & Karabelas, A. J. (2022). Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling. Membranes, 12(1), 62. https://doi.org/10.3390/membranes12010062






