Lévy Flights Diffusion with Drift in Heterogeneous Membranes
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Model Membranes
2.2. Simulations of Gauss and Cauchy Flights
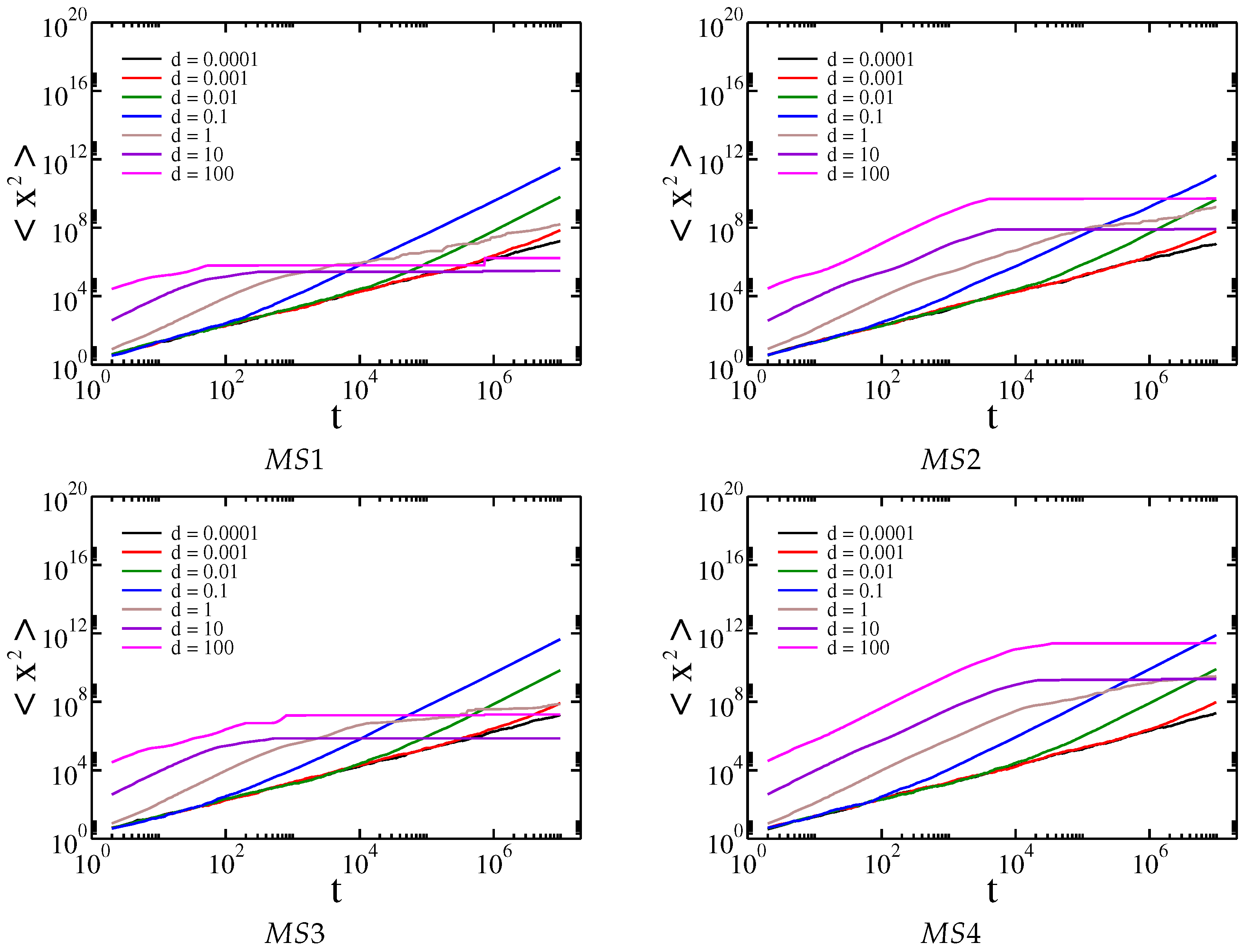
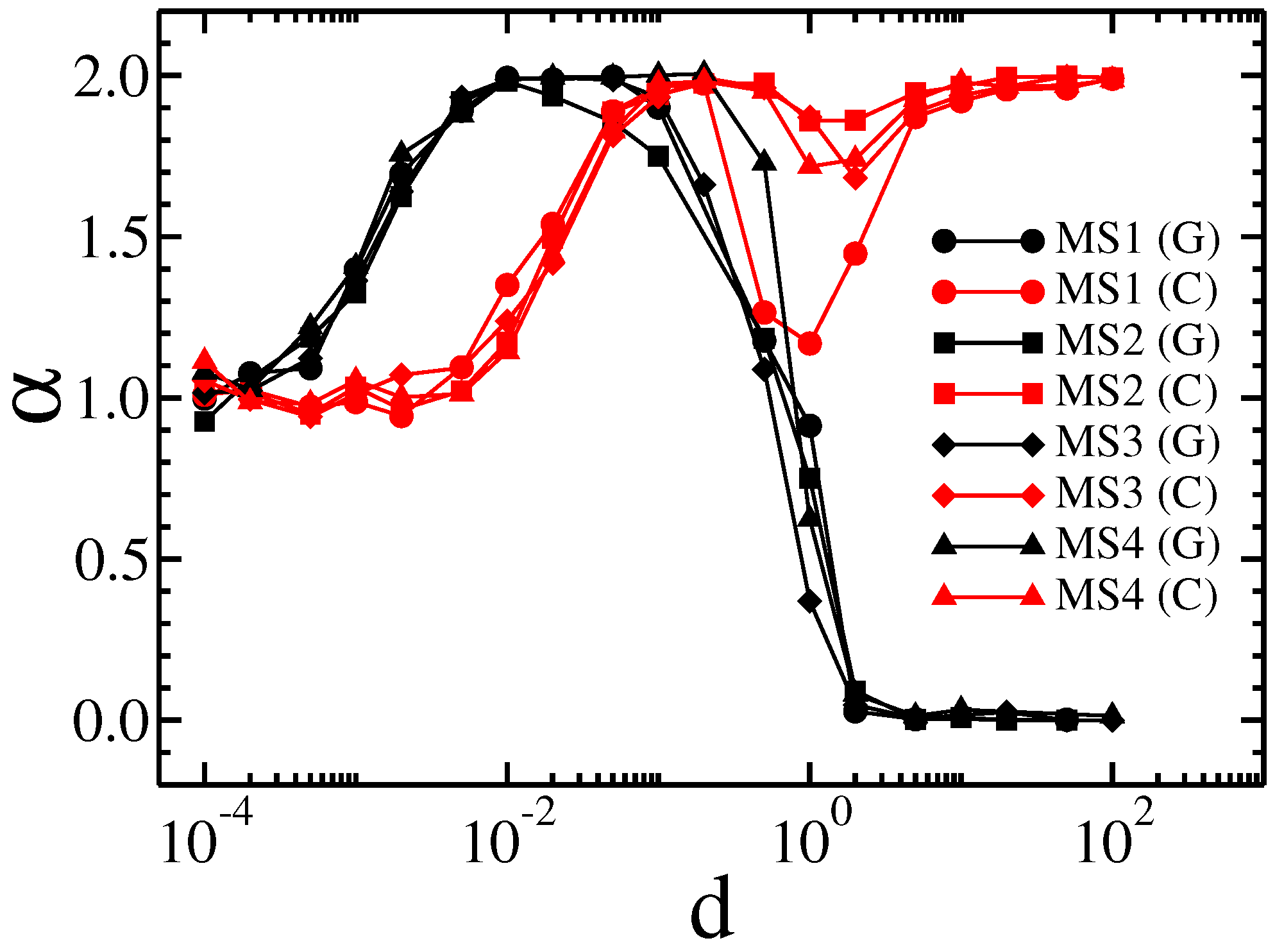
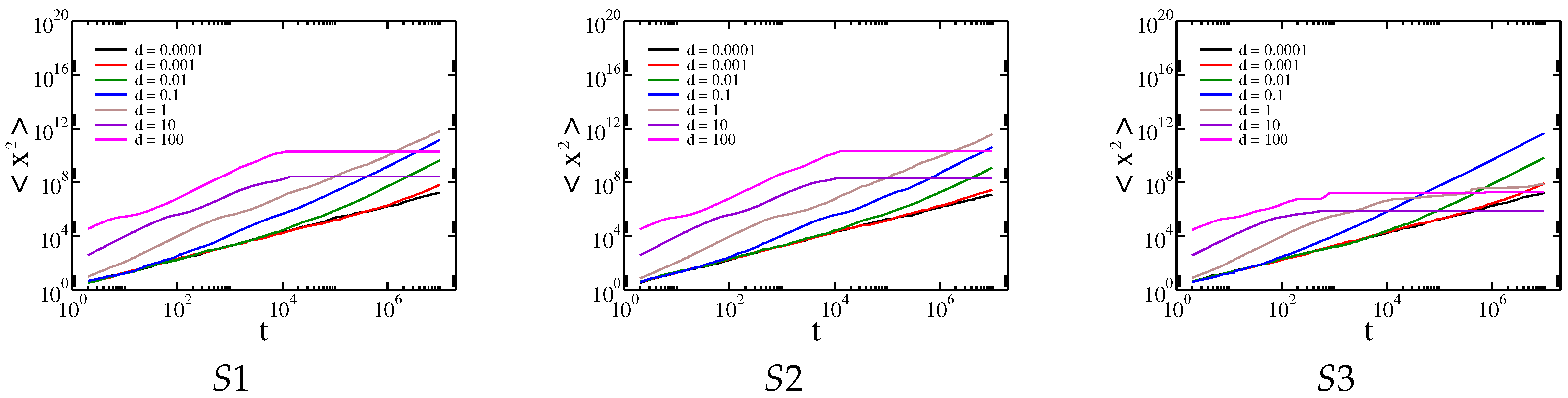
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Effective diffusion exponent | |
| d | Drift |
| Fractal dimension of polymer matrix | |
| Degree of multifractality | |
| MSD | Mean square displacement |
| Amount of polymer matrix | |
| Width of the Cauchy distribution/standard deviation of the Gaussian distribution |
References
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter. 2012, 8, 9043. [Google Scholar] [CrossRef]
- Barrer, R.M.; Petropoulos, J.H. Diffusion in heterogeneous media: Lattices of parallelepipeds in a continuous phase. Br. J. Appl. Phys. 1961, 12, 691. [Google Scholar] [CrossRef]
- Kabbej, M.; Guillard, V.; Angellier-Coussy, H.; Wolf, C.; Gontard, N.; Gaucel, S. 3D Modelling of Mass Transfer into Bio-Composite. Polymers 2021, 13, 2257. [Google Scholar] [CrossRef]
- Kosztołowicz, T.; Dworecki, K.; Lewandowska, K.D. Subdiffusion in a system with thin membranes. Phys. Rev. E 2012, 86, 021123. [Google Scholar] [CrossRef] [PubMed]
- Kosztołowicz, T.; Piwnik, M.; Lewandowska, K.D.; Klinkosz, T. The solution to subdiffusion-reaction equation for system with one mobile and one static raeactant. Acta Phys. Pol. B 2013, 44, 967–975. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.K.; Cherstvy, A.G.; Grebenkov, D.S.; Metzler, R. Anomalous, non-Gaussian tracer diffusion in crowded two-dimensional environments. New J. Phys. 2016, 18, 013027. [Google Scholar] [CrossRef]
- Santamaria-Holek, I.; Rubi, J.M.; Gadomski, A. Thermokinetic Approach of Single Particles and Clusters Involving Anomalous Diffusion under Viscoelastic Response. J. Phys. Chem. B 2007, 111, 2293–2298. [Google Scholar] [CrossRef] [Green Version]
- Sokolov, I.M.; Klafter, J. From diffusion to anomalous diffusion: A century after Einstein’s Brownian motion. Chaos 2005, 15, 026103. [Google Scholar] [CrossRef] [Green Version]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks. From Tools to Applications; Oxford University Press: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Oliveira, F.A.; Ferreira, R.M.S.; Lapas, L.C.; Vainstein, M.H. Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Vainstein, M.H.; Costa, I.V.L.; Oliveira, F.A. Mixing, Ergodicity and the Fluctuation-Dissipation Theorem in Complex Systems. In Jamming, Yielding, and Irreversible Deformation in Condensed Matter; Miguel, M.C., Rubi, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 159–188. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Blackburn, G.; Lomholt, M.A.; Watkins, N.W.; Metzler, R.; Klages, R.; Chechkin, A.V. First passage and first hitting times of Lévy flights and Lévy walks. New J. Phys. 2019, 21, 103028. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Kuśmierz, Ł.; Chechkin, A.; Gudowska-Nowak, E.; Bier, M. Breaking microscopic reversibility with Lévy flights. EPL 2016, 114, 60009. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E. Discriminating between normal and anomalous random walks. Phys. Rev. E 2009, 80, 061122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montroll, E.W.; Weiss, G.H. Random Walks on Lattices. II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Mai, J.; Blumen, A. Paradoxal Diffusion in Chemical Space for Nearest-Neighbor Walks over Polymer Chains. Phys. Rev. Lett. 1997, 79, 857. [Google Scholar] [CrossRef]
- Sokolov, I.M. Lévy flights from a continuous-time process. Phys. Rev. E 2000, 63, 011104. [Google Scholar] [CrossRef] [Green Version]
- Klafter, J.; Shlesinger, M.F.; Zumofen, G. Beyond Brownian Motion. Phys. Today 1996, 49, 33. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef] [Green Version]
- Shlesinger, M.F.; Zaslavsky, G.M.; Frisch, J. (Eds.) Lévy Flights and Related Topics in Physics; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar] [CrossRef]
- Metzler, R.; Chechkin, A.V.; Gonchar, V.Y.; Klafter, J. Some fundamental aspects of Lévy flights. Chaos Soliton. Fract. 2007, 34, 129. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E 2017, 95, 052102. [Google Scholar] [CrossRef] [Green Version]
- Krasowska, M.; Strzelewicz, A.; Dudek, G.; Cieśla, M. Structure-diffusion relationship of polymer membranes with different texture. Phys. Rev. E 2017, 95, 012155. [Google Scholar] [CrossRef] [PubMed]
- Strzelewicz, A.; Krasowska, M.; Dudek, G.; Cieśla, M. Optimal hybrid membrane structure based on experimental results and simulation analysis of diffusion process. J. Mater. Sci. 2022, 57, 11491. [Google Scholar] [CrossRef]
- Krasowska, M.; Strzelewicz, A.; Dudek, G.; Cieśla, M. Numerical Study of Drift Influence on Diffusion Transport through the Hybrid Membrane. Membranes 2022, 12, 788. [Google Scholar] [CrossRef]
- Cieśla, M.; Dybiec, B.; Sokolov, I.; Gudowska-Nowak, E. Taming Lévy flights in confined crowded geometries. J. Chem. Phys. 2015, 142, 164904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kubala, P.; Cieśla, M.; Dybiec, B. Diffusion in crowded environments: Trapped by the drift. Phys. Rev. E 2021, 104, 044127. [Google Scholar] [CrossRef]
- Strzelewicz, A.; Krasowska, M.; Dudek, G.; Cieśla, M. Design of polymer membrane morphology with prescribed structure and diffusion properties. Chem. Phys. 2020, 531, 110662. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A note on the generation of random normal deviates. Ann. Math. Stat. 1958, 29, 610. [Google Scholar] [CrossRef]
- Cieśla, M.; Capała, K.; Dybiec, B. Multimodal stationary states under Cauchy noise. Phys. Rev. E 2019, 99, 052118. [Google Scholar] [CrossRef] [Green Version]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strzelewicz, A.; Krasowska, M.; Cieśla, M. Lévy Flights Diffusion with Drift in Heterogeneous Membranes. Membranes 2023, 13, 417. https://doi.org/10.3390/membranes13040417
Strzelewicz A, Krasowska M, Cieśla M. Lévy Flights Diffusion with Drift in Heterogeneous Membranes. Membranes. 2023; 13(4):417. https://doi.org/10.3390/membranes13040417
Chicago/Turabian StyleStrzelewicz, Anna, Monika Krasowska, and Michał Cieśla. 2023. "Lévy Flights Diffusion with Drift in Heterogeneous Membranes" Membranes 13, no. 4: 417. https://doi.org/10.3390/membranes13040417
APA StyleStrzelewicz, A., Krasowska, M., & Cieśla, M. (2023). Lévy Flights Diffusion with Drift in Heterogeneous Membranes. Membranes, 13(4), 417. https://doi.org/10.3390/membranes13040417






