Dynamics Management of Intermediate Water Storage in an Air-Breathing Single-Cell Membrane Electrode Assembly
Abstract
:1. Introduction
2. Materials and Methods
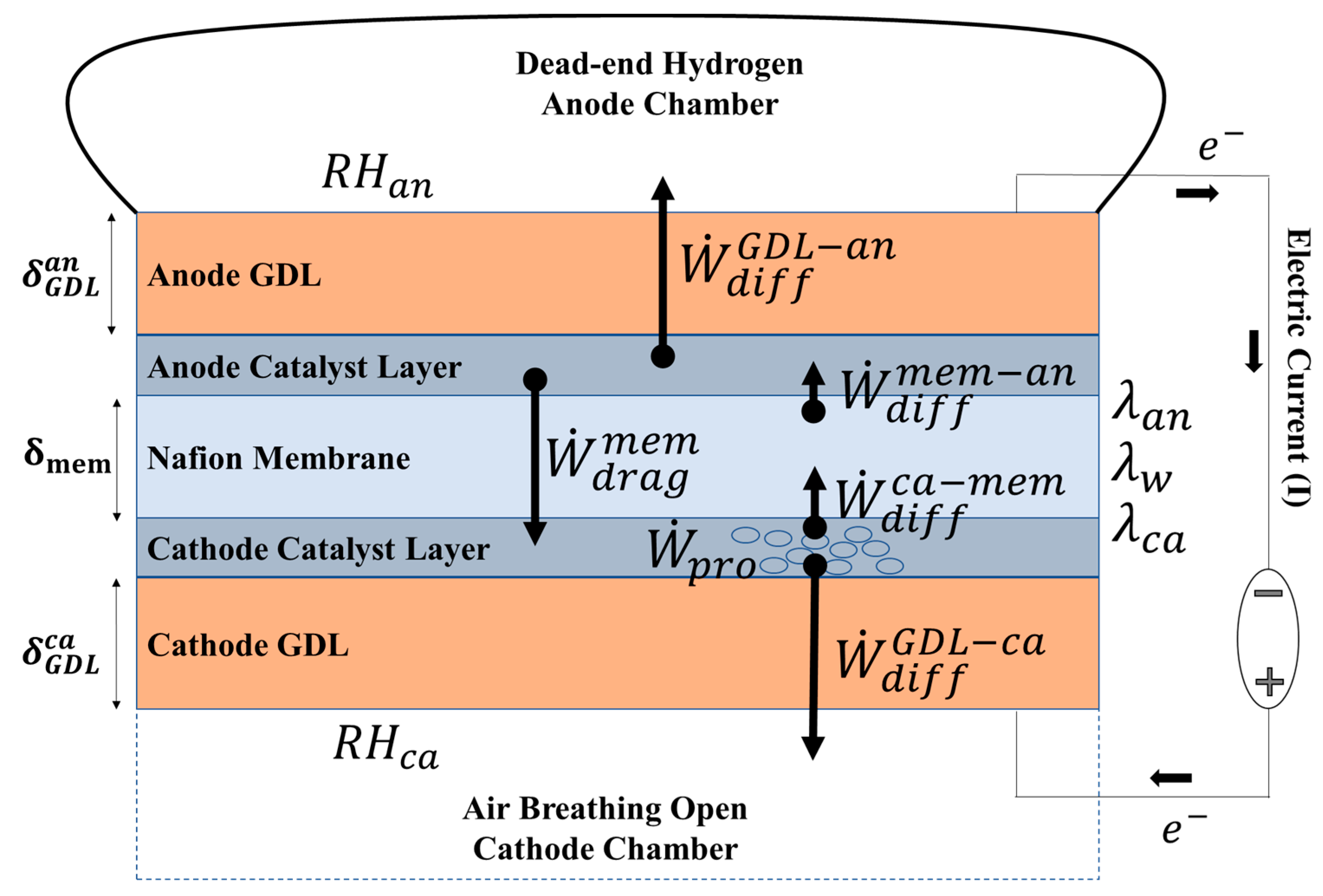
2.1. Transient Water Balance Model of the Membrane Electrode Assembly (MEA)
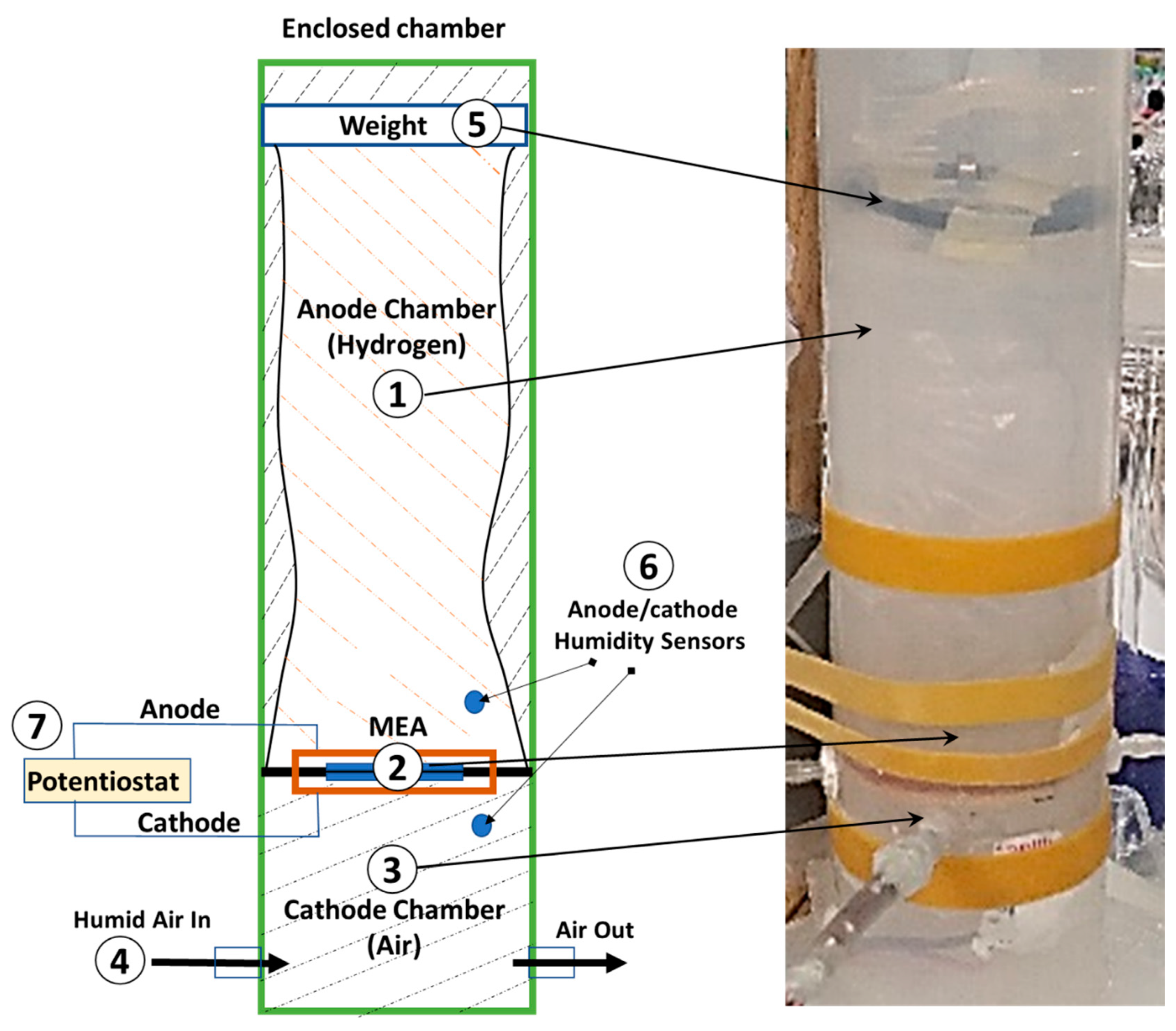
2.2. Experimental Setup for Model Validation
3. Results
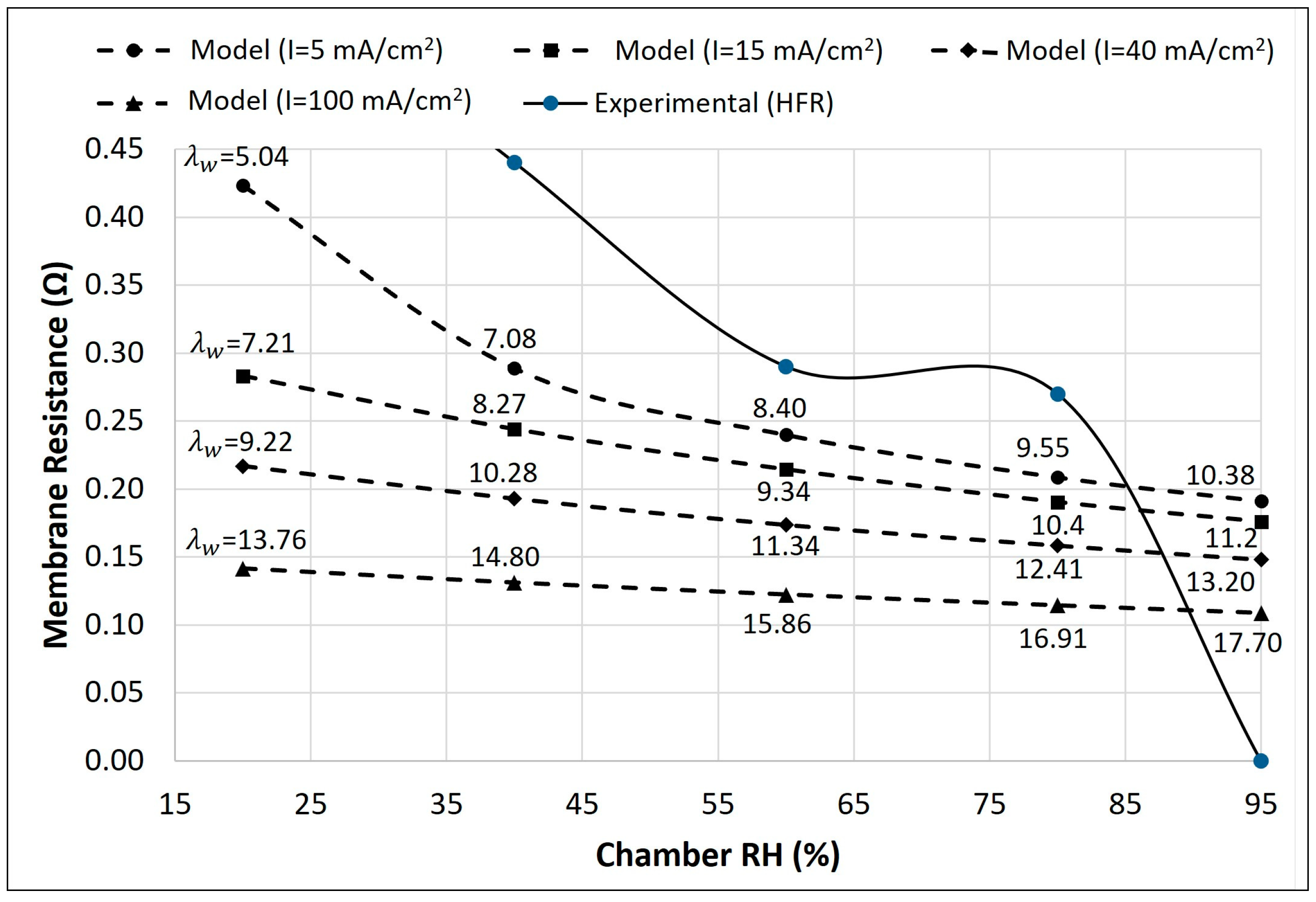
3.1. Steady-State Characteristics of the MEA
- Step 1: At the onset of each experiment, the cathode and anode chambers were purged with a flow of dry nitrogen for 30 min to eliminate trapped humidity and air inside the anode chamber.
- Step 2: Then, the anode and cathode chambers were maintained at the same selected constant humidity ( = 20–95%) by continuously flowing humid air and hydrogen into the chambers for 30 min.
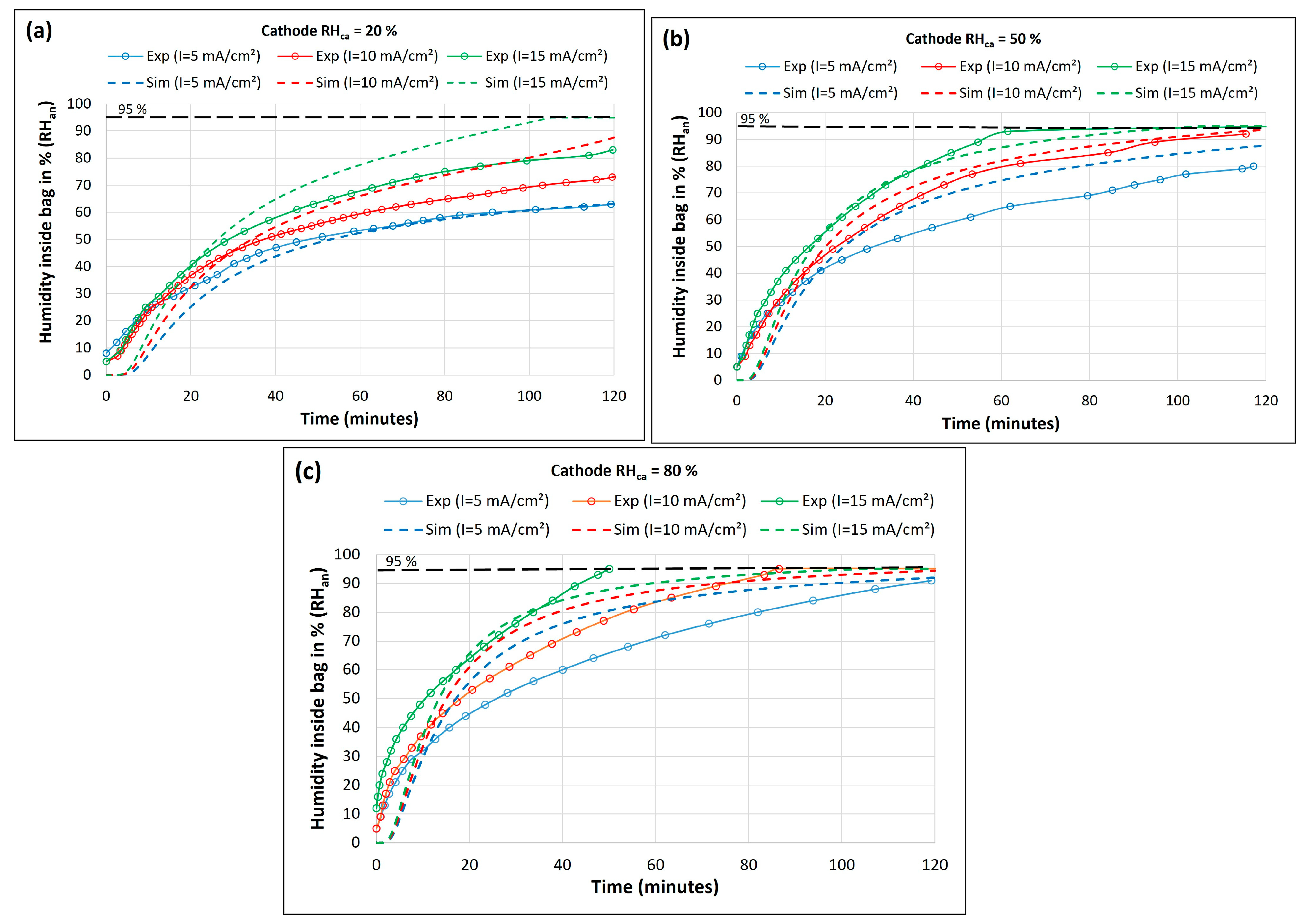
3.2. Transient Dynamics of MEA Hydration over Time
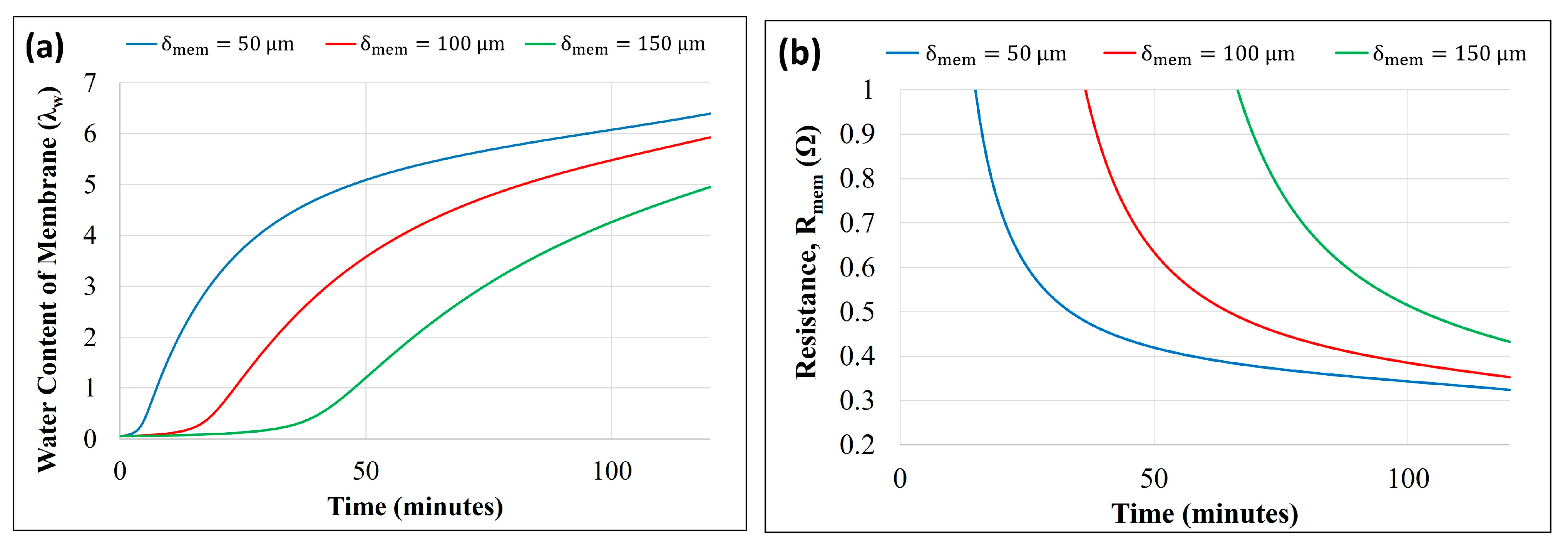
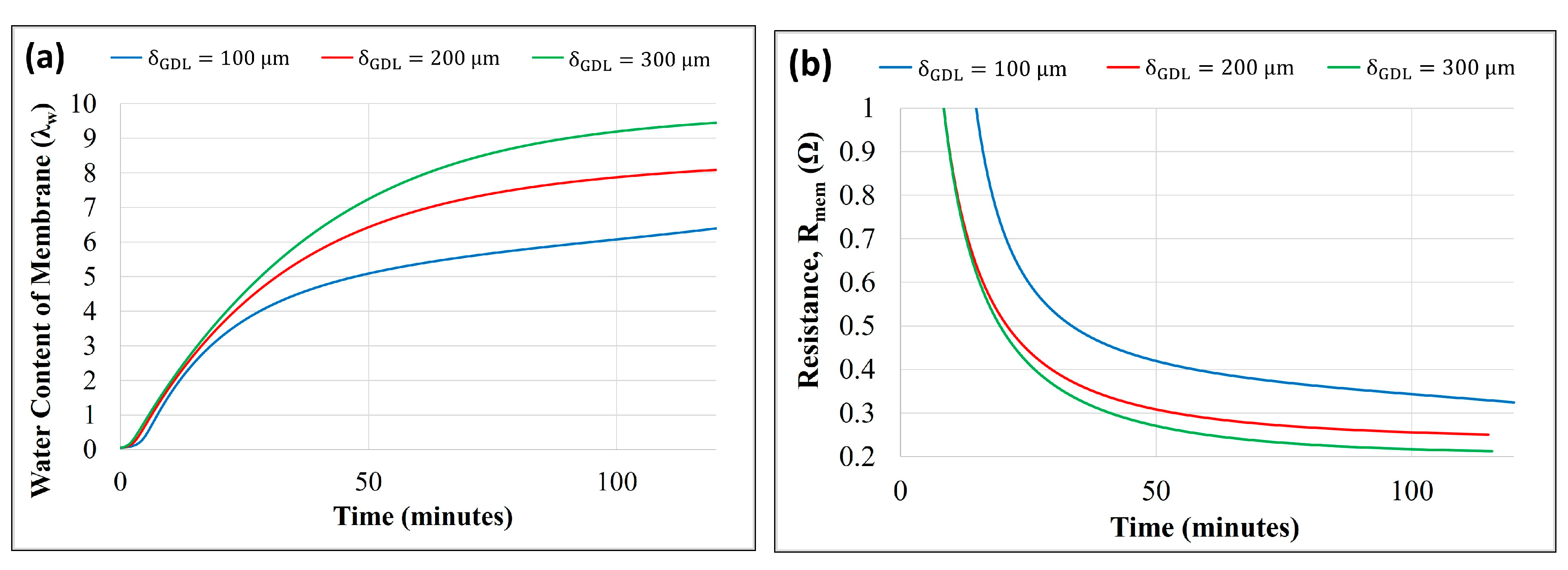
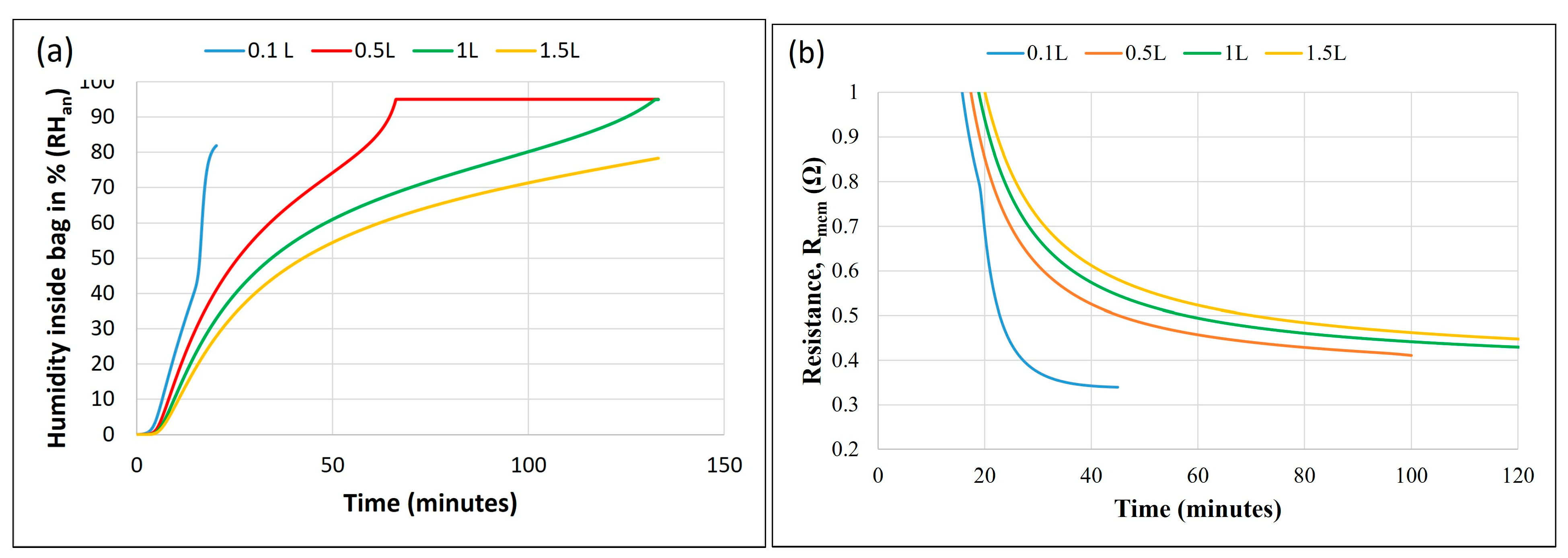
3.3. Effect of MEA and Storage Configurations
4. Discussion
Limitations
5. Conclusions
- A lightweight, inflatable hydrogen-filled bag around the anode is proposed to trap and store the produced water for self-humidification of the anode.
- As demonstrated with an experimentally validated numerical model, the water transport of FC-produced water from the cathode to the anode increases with current density and cathode humidity.
- The power output almost doubles, and membrane resistance is reduced by 2–3 times when a fully hydrated membrane is used compared to a dry membrane.
- The model under equilibrium predicts an increase in membrane resistance by about three-fold with an increase in membrane thickness (50–150 µm) and a decrease of approximately three times with an increase in GDL thickness (100–300 µm).
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sharaf, O.Z.; Orhan, M.F. An overview of fuel cell technology: Fundamentals and applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Safari, A. Comparative study of different fuel cell technologies. Renew. Sustain. Energy Rev. 2012, 16, 981–989. [Google Scholar] [CrossRef]
- Calili-Cankir, F.; Ismail, M.S.; Ingham, D.B.; Hughes, K.J.; Ma, L.; Pourkashanian, M. Air-breathing polymer electrolyte fuel cells: A review. Renew. Energy 2023, 213, 86–108. [Google Scholar] [CrossRef]
- Seo, Y.H.; Kim, H.J.; Jang, W.K.; Kim, B.H. Development of active breathing micro PEM fuel cell. Int. J. Precis. Eng. Manuf. Technol. 2014, 1, 101–106. [Google Scholar] [CrossRef]
- Felseghi, R.-A.; Carcadea, E.; Raboaca, M.S.; Trufin, C.N.; Filote, C. Hydrogen Fuel Cell Technology for the Sustainable Future of Stationary Applications. Energies 2019, 12, 4593. [Google Scholar] [CrossRef]
- Fan, L.; Shi, J.; Xi, Y. PVDF-Modified Nafion Membrane for Improved Performance of MFC. Membranes 2020, 10, 185. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.-Y.; Li, Y.-C.; Liu, J.; He, J.; Wang, L.-Y.; Lei, J.-D. Recent developments in high-performance Nafion membranes for hydrogen fuel cells applications. Pet. Sci. 2022, 19, 1371–1381. [Google Scholar] [CrossRef]
- Mathur, V.K.; Crawford, J. Fundamentals of gas diffusion layers in PEM fuel cells. In Recent Trends in Fuel Cell Science and Technology; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Martín-Alcántara, A.; González-Morán, L.; Pino, J.; Guerra, J.; Iranzo, A. Effect of the Gas Diffusion Layer Design on the Water Management and Cell Performance of a PEM Fuel Cell. Processes 2022, 10, 1395. [Google Scholar] [CrossRef]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Fu, H.; Shen, J.; Sun, L.; Lee, K.Y. Fuel cell humidity modeling and control using cathode internal water content. Int. J. Hydrogen Energy 2021, 46, 9905–9917. [Google Scholar] [CrossRef]
- Chen, F.; Jiao, J.; Hou, Z.; Cheng, W.; Cai, J.; Xia, Z.; Chen, J. Robust polymer electrolyte membrane fuel cell temperature tracking control based on cascade internal model control. J. Power Sources 2020, 479, 229008. [Google Scholar] [CrossRef]
- Headley, A.; Yu, V.; Borduin, R.; Chen, D.; Li, W. Development and Experimental Validation of a Physics-Based PEM Fuel Cell Model for Cathode Humidity Control Design. IEEE/ASME Trans. Mechatron. 2016, 21, 1775–1782. [Google Scholar] [CrossRef]
- Hong, P.; Xu, L.; Li, J.; Ouyang, M. Modeling of membrane electrode assembly of PEM fuel cell to analyze voltage losses inside. Energy 2017, 139, 277–288. [Google Scholar] [CrossRef]
- Chen, D.; Peng, H. Modeling and simulation of a PEM fuel cell humidification system. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar] [CrossRef]
- Hao, Y.; Nakajima, H.; Yoshizumi, H.; Inada, A.; Sasaki, K.; Ito, K. Characterization of an electrochemical hydrogen pump with internal humidifier and dead-end anode channel. Int. J. Hydrogen Energy 2016, 41, 13879–13887. [Google Scholar] [CrossRef]
- Vasu, G.; Tangirala, A.; Viswanathan, B.; Dhathathreyan, K. Continuous bubble humidification and control of relative humidity of H2 for a PEMFC system. Int. J. Hydrogen Energy 2008, 33, 4640–4648. [Google Scholar] [CrossRef]
- Kong, I.M.; Jung, A.; Kim, M.S. Investigations on the double gas diffusion backing layer for performance improvement of self-humidified proton exchange membrane fuel cells. Appl. Energy 2016, 176, 149–156. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, L.; Fang, C.; Jiang, H.; Li, J.; Ouyang, M. Study on voltage clamping and self-humidification effects of pem fuel cell system with dual recirculation based on orthogonal test method. Int. J. Hydrogen Energy 2018, 43, 16268–16278. [Google Scholar] [CrossRef]
- Hamel, S.; Fréchette, L.G. Critical importance of humidification of the anode in miniature air-breathing polymer electrolyte membrane fuel cells. J. Power Sources 2011, 196, 6242–6248. [Google Scholar] [CrossRef]
- Fabian, T.; O’hayre, R.; Litster, S.; Prinz, F.; Santiago, J. Active water management at the cathode of a planar air-breathing polymer electrolyte membrane fuel cell using an electroosmotic pump. J. Power Sources 2010, 195, 3640–3644. [Google Scholar] [CrossRef]
- Uchida, H.; Ueno, Y.; Hagihara, H.; Watanabe, M. Self-Humidifying Electrolyte Membranes for Fuel Cells. Preparation of highly dispersed TiO2 particles in Nafion 112. J. Electrochem. Soc. 2003, 150, A57–A62. [Google Scholar] [CrossRef]
- Hagihara, H.; Uchida, H.; Watanabe, M. Preparation of highly dispersed SiO2 and Pt particles in Nafion®112 for self-humidifying electrolyte membranes in fuel cells. Electrochim. Acta 2006, 51, 3979–3985. [Google Scholar] [CrossRef]
- Yang, H.; Lee, D.; Park, S.; Kim, W. Preparation of Nafion/various Pt-containing SiO2 composite membranes sulfonated via different sources of sulfonic group and their application in self-humidifying PEMFC. J. Membr. Sci. 2013, 443, 210–218. [Google Scholar] [CrossRef]
- Jung, U.H.; Park, K.T.; Park, E.H.; Kim, S.H. Improvement of low-humidity performance of PEMFC by addition of hydrophilic SiO2 particles to catalyst layer. J. Power Sources 2006, 159, 529–532. [Google Scholar] [CrossRef]
- Chao, W.-K.; Lee, C.-M.; Tsai, D.-C.; Chou, C.-C.; Hsueh, K.-L.; Shieu, F.-S. Improvement of the proton exchange membrane fuel cell (PEMFC) performance at low-humidity conditions by adding hygroscopic γ-Al2O3 particles into the catalyst layer. J. Power Sources 2008, 185, 136–142. [Google Scholar] [CrossRef]
- Su, H.; Xu, L.; Zhu, H.; Wu, Y.; Yang, L.; Liao, S.; Song, H.; Liang, Z.; Birss, V. Self-humidification of a PEM fuel cell using a novel Pt/SiO2/C anode catalyst. Int. J. Hydrogen Energy 2010, 35, 7874–7880. [Google Scholar] [CrossRef]
- Inoue, N.; Uchida, M.; Watanabe, M.; Uchida, H. SiO2-containing catalyst layers for PEFCs operating under low humidity. Electrochem. Commun. 2012, 16, 100–102. [Google Scholar] [CrossRef]
- Fernández-Moreno, J.; Guelbenzu, G.; Martín, A.; Folgado, M.; Ferreira-Aparicio, P.; Chaparro, A. A portable system powered with hydrogen and one single air-breathing PEM fuel cell. Appl. Energy 2013, 109, 60–66. [Google Scholar] [CrossRef]
- González-Espasandín, Ó.; Leo, T.J.; Navarro-Arévalo, E. Fuel Cells: A Real Option for Unmanned Aerial Vehicles Propulsion. Sci. World J. 2014, 2014, 497642. [Google Scholar] [CrossRef]
- Khanafari, A.; Alasty, A.; Kermani, M.J.; Asghari, S. Flooding and dehydration diagnosis in a polymer electrolyte membrane fuel cell stack using an experimental adaptive neuro-fuzzy inference system. Int. J. Hydrogen Energy 2022, 47, 34628–34639. [Google Scholar] [CrossRef]
- Ji, M.; Wei, Z. A Review of Water Management in Polymer Electrolyte Membrane Fuel Cells. Energies 2009, 2, 1057–1106. [Google Scholar] [CrossRef]
- Raguman, A.; Vedagiri, P. A review on recent approaches in thermal and water management of polymer electrolyte membrane fuel cells. Mater. Today Proc. 2022, 68, 1975–1979. [Google Scholar] [CrossRef]
- Ge, N.; Banerjee, R.; Muirhead, D.; Lee, J.; Liu, H.; Shrestha, P.; Wong, A.; Jankovic, J.; Tam, M.; Susac, D.; et al. Membrane dehydration with increasing current density at high inlet gas relative humidity in polymer electrolyte membrane fuel cells. J. Power Sources 2019, 422, 163–174. [Google Scholar] [CrossRef]
- Stauffer, D.B.; Hirschenhofer, J.H.; Klett, M.G.; Engleman, R.R.; Hirschenhofer, R.R.; Stauffer, J.H.; Engleman, D.B. Fuel Cell Handbook, Fourth Edition. 1998. Available online: https://www.osti.gov/biblio/14997 (accessed on 31 October 2023).
- Pourcelly, G.; Oikonomou, A.; Gavach, C.; Hurwitz, H. Influence of the water content on the kinetics of counter-ion transport in perfluorosulphonic membranes. J. Electroanal. Chem. Interfacial Electrochem. 1990, 287, 43–59. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Davey, J.; Valerio, J.; Gottesfeld, S. The water content dependence of electro-osmotic drag in proton-conducting polymer electrolytes. Electrochim. Acta 1995, 40, 297–302. [Google Scholar] [CrossRef]
- Nishiyama, H.; Iiyama, A.; Inukai, J. The distribution and diffusion coefficient of water inside a Nafion® membrane in a running fuel cell under transient conditions analyzed by operando time-resolved CARS spectroscopy. J. Power Sources Adv. 2022, 13, 10-1016. [Google Scholar] [CrossRef]
- Janssen, G.; Overvelde, M. Water transport in the proton-exchange-membrane fuel cell: Measurements of the effective drag coefficient. J. Power Sources 2001, 101, 117–125. [Google Scholar] [CrossRef]
- Yusaf, T.; Mahamude, A.S.F.; Kadirgama, K.; Ramasamy, D.; Farhana, K.; Dhahad, H.A.; Abu Talib, A.R. Sustainable hydrogen energy in aviation—A narrative review. Int. J. Hydrog. Energy 2023, 52, 1026–1045. [Google Scholar] [CrossRef]
- Molinero, A.; Oller, J.C.; Barcala, J.M.; Duque, L.; Folgado, M.A.; Chaparro, A.M. Assembly and Testing of a Hydrogen Fuel Cell System to Power an Airship. ECS Meet. Abstr. 2022, 242, 1475. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Springer, T.E.; Davey, J.; Jestel, R.; Lopez, C.; Valerio, J.; Gottesfeld, S. A Comparative Study of Water Uptake By and Transport Through Ionomeric Fuel Cell Membranes. J. Electrochem. Soc. 1993, 140, 1981–1985. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Derouin, C.; Radzinski, S.; Sherman, R.J.; Smith, V.T.; Springer, T.E.; Gottesfeld, S. Water Uptake by and Transport Through Nafion® 117 Membranes. J. Electrochem. Soc. 1993, 140, 1041–1047. [Google Scholar] [CrossRef]
- O’hayre, R.; Fabian, T.; Litster, S.; Prinz, F.B.; Santiago, J.G. Engineering model of a passive planar air breathing fuel cell cathode. J. Power Sources 2007, 167, 118–129. [Google Scholar] [CrossRef]
- Calili-Cankir, F.; Ismail, M.S.; Ingham, D.B.; Hughes, K.J.; Ma, L.; Pourkashanian, M. Air-breathing versus conventional polymer electrolyte fuel cells: A parametric numerical study. Energy 2022, 250, 123827. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Miao, D.; Chen, W.; Zhao, W.; Demsas, T. Parameter estimation of PEM fuel cells employing the hybrid grey wolf optimization method. Energy 2020, 193, 116616. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Sellin, R.; Mozet, K.; Ménage, A.; Dillet, J.; Didierjean, S.; Maranzana, G. Measuring electro-osmotic drag coefficients in PFSA membranes without any diffusion assumption. Int. J. Hydrogen Energy 2019, 44, 24905–24912. [Google Scholar] [CrossRef]
- Rahbari, A.; Hartkamp, R.; Moultos, O.A.; Bos, A.; Van Den Broeke, L.J.; Ramdin, M.; Dubbeldam, D.; Lyulin, A.V.; Vlugt, T.J.H. Electro-osmotic Drag and Thermodynamic Properties of Water in Hydrated Nafion Membranes from Molecular Dynamics. J. Phys. Chem. C 2022, 126, 8121–8133. [Google Scholar] [CrossRef]
- Buchi, F.N.; Scherer, G.G. Investigation of the Transversal Water Profile in Nafion Membranes in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2001, 148, A183–A188. [Google Scholar] [CrossRef]
- Meng, H.; Wang, C.-Y. Electron Transport in PEFCs. J. Electrochem. Soc. 2004, 151, A358–A367. [Google Scholar] [CrossRef]
- Seddiq, M.; Khaleghi, H.; Mirzaei, M. Numerical analysis of gas cross-over through the membrane in a proton exchange membrane fuel cell. J. Power Sources 2006, 161, 371–379. [Google Scholar] [CrossRef]
- Wang, L.; Husar, A.; Zhou, T.; Liu, H. A parametric study of PEM fuel cell performances. Int. J. Hydrogen Energy 2003, 28, 1263–1272. [Google Scholar] [CrossRef]
- Gebru, M.G.; Yadav, R.S.; Teller, H.; Kornweitz, H.; Subramanian, P.; Schechter, A. Harnessing dimethyl ether and methyl formate fuels for direct electrochemical energy conversion. J. Energy Chem. 2023, 83, 454–464. [Google Scholar] [CrossRef]
- Kashyap, D.; Teller, H.; Subramanian, P.; Bělský, P.; Gebru, M.G.; Pitussi, I.; Yadav, R.S.; Kornweitz, H.; Schechter, A. Sn-based atokite alloy nanocatalyst for high-power dimethyl ether fueled low-temperature polymer electrolyte fuel cell. J. Power Sources 2022, 544, 231882. [Google Scholar] [CrossRef]
- Modak, A.; Velayudham, P.; Bendikov, T.; Mohan, R.; Schechter, A. A trifunctional N-doped activated carbon–ceria shell, derived from covalent porphyrin polymers for promoting Pt activity in fuel cell cathode performance. Catal. Sci. Technol. 2023, 13, 1180–1195. [Google Scholar] [CrossRef]
- Ge, S.; Wang, C.-Y. Characteristics of subzero startup and water/ice formation on the catalyst layer in a polymer electrolyte fuel cell. Electrochim. Acta 2007, 52, 4825–4835. [Google Scholar] [CrossRef]
- Yang, X.; Sun, J.; Jiang, G.; Sun, S.; Shao, Z.; Yu, H.; Duan, F.; Yang, Y. Experimental Study on Critical Membrane Water Content of Proton Exchange Membrane Fuel Cells for Cold Storage at −50 °C. Energies 2021, 14, 4520. [Google Scholar] [CrossRef]
- Tajiri, K.; Wang, C.-Y.; Tabuchi, Y. Water removal from a PEFC during gas purge. Electrochim. Acta 2008, 53, 6337–6343. [Google Scholar] [CrossRef]
- Nara, H.; Momma, T.; Osaka, T. Impedance analysis of the effect of flooding in the cathode catalyst layer of the polymer electrolyte fuel cell. Electrochim. Acta 2013, 113, 720–729. [Google Scholar] [CrossRef]
- Lin, T.; Hu, L.; Wisely, W.; Gu, X.; Cai, J.; Litster, S.; Kara, L.B. Prediction of high frequency resistance in polymer electrolyte membrane fuel cells using long short term memory based model. Energy AI 2021, 3, 100045. [Google Scholar] [CrossRef]
- Edwards, R.L.; Demuren, A. Interface model of PEM fuel cell membrane steady-state behavior. Int. J. Energy Environ. Eng. 2019, 10, 85–106. [Google Scholar] [CrossRef]
- Van Nguyen, T.; Ahosseini, A.; Wang, X.; Yarlagadda, V.; Kwong, A.; Weber, A.Z.; Deevanhxay, P.; Tsushima, S.; Hirai, S. Hydrophobic Gas-Diffusion Media for Polymer-Electrolyte Fuel Cells by Direct Fluorination. J. Electrochem. Soc. 2015, 162, F1451–F1460. [Google Scholar] [CrossRef]
- Watanabe, M.; Uchida, H.; Seki, Y.; Emori, M.; Stonehart, P. Self-Humidifying Polymer Electrolyte Membranes for Fuel Cells. J. Electrochem. Soc. 1996, 143, 3847–3852. [Google Scholar] [CrossRef]
- Büchi, F.N.; Srinivasan, S. Operating Proton Exchange Membrane Fuel Cells without External Humidification of the Reactant Gases: Fundamental Aspects. J. Electrochem. Soc. 1997, 144, 2767–2772. [Google Scholar] [CrossRef]
- Eckl, R.; Zehtner, W.; Leu, C.; Wagner, U. Experimental analysis of water management in a self-humidifying polymer electrolyte fuel cell stack. J. Power Sources 2004, 138, 137–144. [Google Scholar] [CrossRef]
- Jang, J.-H.; Chiu, H.-C.; Yan, W.-M.; Sun, W.-L. Effects of operating conditions on the performances of individual cell and stack of PEM fuel cell. J. Power Sources 2008, 180, 476–483. [Google Scholar] [CrossRef]
- Andreasen, S.J.; Jespersen, J.L.; Schaltz, E.; Kær, S.K. Characterisation and Modelling of a High Temperature PEM Fuel Cell Stack using Electrochemical Impedance Spectroscopy. Fuel Cells 2009, 9, 463–473. [Google Scholar] [CrossRef]
- Yan, Q.; Toghiani, H.; Causey, H. Steady state and dynamic performance of proton exchange membrane fuel cells (PEMFCs) under various operating conditions and load changes. J. Power Sources 2006, 161, 492–502. [Google Scholar] [CrossRef]
- Yuan, X.; Sun, J.C.; Blanco, M.; Wang, H.; Zhang, J.; Wilkinson, D.P. AC impedance diagnosis of a 500W PEM fuel cell stack: Part I: Stack impedance. J. Power Sources 2006, 161, 920–928. [Google Scholar] [CrossRef]
- Chu, D.; Jiang, R. Performance of polymer electrolyte membrane fuel cell (PEMFC) stacks: Part I. Evaluation and simulation of an air-breathing PEMFC stack. J. Power Sources 1999, 83, 128–133. [Google Scholar] [CrossRef]
- Pérez-Page, M.; Pérez-Herranz, V. Effect of the Operation and Humidification Temperatures on the Performance of a PEM Fuel Cell Stack. ECS Meet. Abstr. 2009, MA2009-02, 905. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Chen, S.; Huang, L.; Shao, Z. Modeling and Control of Cathode Air Humidity for PEM Fuel Cell Systems. IFAC-PapersOnLine 2017, 50, 4751–4756. [Google Scholar] [CrossRef]
- Urbani, F.; Barbera, O.; Giacoppo, G.; Squadrito, G.; Passalacqua, E. Effect of operative conditions on a PEFC stack performance. Int. J. Hydrogen Energy 2008, 33, 3137–3141. [Google Scholar] [CrossRef]
- Jung, G.-B.; Lo, K.-F.; Su, A.; Weng, F.-B.; Tu, C.-H.; Yang, T.-F.; Chan, S.-H. Experimental evaluation of an ambient forced-feed air-supply PEM fuel cell. Int. J. Hydrogen Energy 2008, 33, 2980–2985. [Google Scholar] [CrossRef]
- Bonnet, C.; Didierjean, S.; Guillet, N.; Besse, S.; Colinart, T.; Carré, P. Design of an 80kWe PEM fuel cell system: Scale up effect investigation. J. Power Sources 2008, 182, 441–448. [Google Scholar] [CrossRef]
- Wahdame, B.; Candusso, D.; François, X.; Harel, F.; Péra, M.-C.; Hissel, D.; Kauffmann, J.-M. Comparison between two PEM fuel cell durability tests performed at constant current and under solicitations linked to transport mission profile. Int. J. Hydrogen Energy 2007, 32, 4523–4536. [Google Scholar] [CrossRef]
- Corbo, P.; Migliardini, F.; Veneri, O. Experimental analysis and management issues of a hydrogen fuel cell system for stationary and mobile application. Energy Convers. Manag. 2007, 48, 2365–2374. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Lu, Z. Thermal management issues in a PEMFC stack—A brief review of current status. Appl. Therm. Eng. 2009, 29, 1276–1280. [Google Scholar] [CrossRef]
- Aber, J.; Marzolff, I.; Ries, J.; Aber, S. Small-Format Aerial Photography and UAS Imagery: Principles, Techniques and Geoscience Applications; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Burtis, M.F. The Performance Assessment of a Small Lighter-Than-Air Vehicle for Earth Science Remote Sensing Missions (2022). 2022. Available online: https://digitalcommons.library.umaine.edu/honors/728 (accessed on 31 October 2023).
- Rana, M.; Islam, M.S. Designing Approach of Blimp for a Hybrid VTOL Aerial Robot. In Proceedings of the International Conference on Mechanical, Industrial and Energy Engineering, Khulna, Bangladesh, 23–24 December 2018. [Google Scholar]
- Ning, F.; He, X.; Shen, Y.; Jin, H.; Li, Q.; Li, D.; Li, S.; Zhan, Y.; Du, Y.; Jiang, J.; et al. Flexible and Lightweight Fuel Cell with High Specific Power Density. ACS Nano 2017, 11, 5982–5991. [Google Scholar] [CrossRef]
- Thangavelautham, J.; Strawser, D.; Cheung, M.Y.; Dubowsky, S. Lithium hydride powered PEM fuel cells for long-duration small mobile robotic missions. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2012; pp. 415–422. [Google Scholar] [CrossRef]
- Strawser, D.; Thangavelautham, J.; Dubowsky, S. A passive lithium hydride based hydrogen generator for low power fuel cells for long-duration sensor networks. Int. J. Hydrogen Energy 2014, 39, 10216–10229. [Google Scholar] [CrossRef]
- Eickhoff, S.; Zhang, C.; Cui, T. Micro fuel cell utilizing fuel cell water recovery and pneumatic valve. J. Power Sources 2013, 240, 1–7. [Google Scholar] [CrossRef]
- Balakrishnan, A.; Mueller, C.; Reinecke, H. A Millimeter Scale Reactor Integrated PEM Fuel Cell Energy System with an On-Board Hydrogen Production, Storage and Regulation Unit for Autonomous Small Scale Applications. In Proceedings of the 6th Forum on New Materials—Part A, Montecatini Terme, Italy, 8–13 June 2014. [Google Scholar] [CrossRef]
- Thangavelautham, J.; Strawser, D.D.; Dubowsky, S. The design of long-life, high-efficiency PEM fuel cell power supplies for low power sensor networks. Int. J. Hydrogen Energy 2017, 42, 20277–20296. [Google Scholar] [CrossRef]

| S. No. | Parameter | Name | Value |
|---|---|---|---|
| 1 | Area of MEA | 4 × 10−4 m2 | |
| 2 | Thickness of membrane | ||
| 3 | Thickness of cathode GDL | ||
| 4 | Thickness of anode GDL | ||
| 5 | I | Current density | 5 mA/cm2 |
| 5 | Cathode chamber humidity | 0.2 | |
| 6 | V0 | Bag initial volume | 1 L |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Schechter, A.; Avrahami, I. Dynamics Management of Intermediate Water Storage in an Air-Breathing Single-Cell Membrane Electrode Assembly. Membranes 2024, 14, 4. https://doi.org/10.3390/membranes14010004
Kumar A, Schechter A, Avrahami I. Dynamics Management of Intermediate Water Storage in an Air-Breathing Single-Cell Membrane Electrode Assembly. Membranes. 2024; 14(1):4. https://doi.org/10.3390/membranes14010004
Chicago/Turabian StyleKumar, Avinash, Alex Schechter, and Idit Avrahami. 2024. "Dynamics Management of Intermediate Water Storage in an Air-Breathing Single-Cell Membrane Electrode Assembly" Membranes 14, no. 1: 4. https://doi.org/10.3390/membranes14010004
APA StyleKumar, A., Schechter, A., & Avrahami, I. (2024). Dynamics Management of Intermediate Water Storage in an Air-Breathing Single-Cell Membrane Electrode Assembly. Membranes, 14(1), 4. https://doi.org/10.3390/membranes14010004






