1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode
Abstract
:1. Introduction
2. Mathematical Models
- (1)
- The “primary” model, which differs from potentiostatic models by the boundary condition: The potential gradient determined by the current density is given instead of the potential drop. Only a numerical solution is obtained for this model.
- (2)
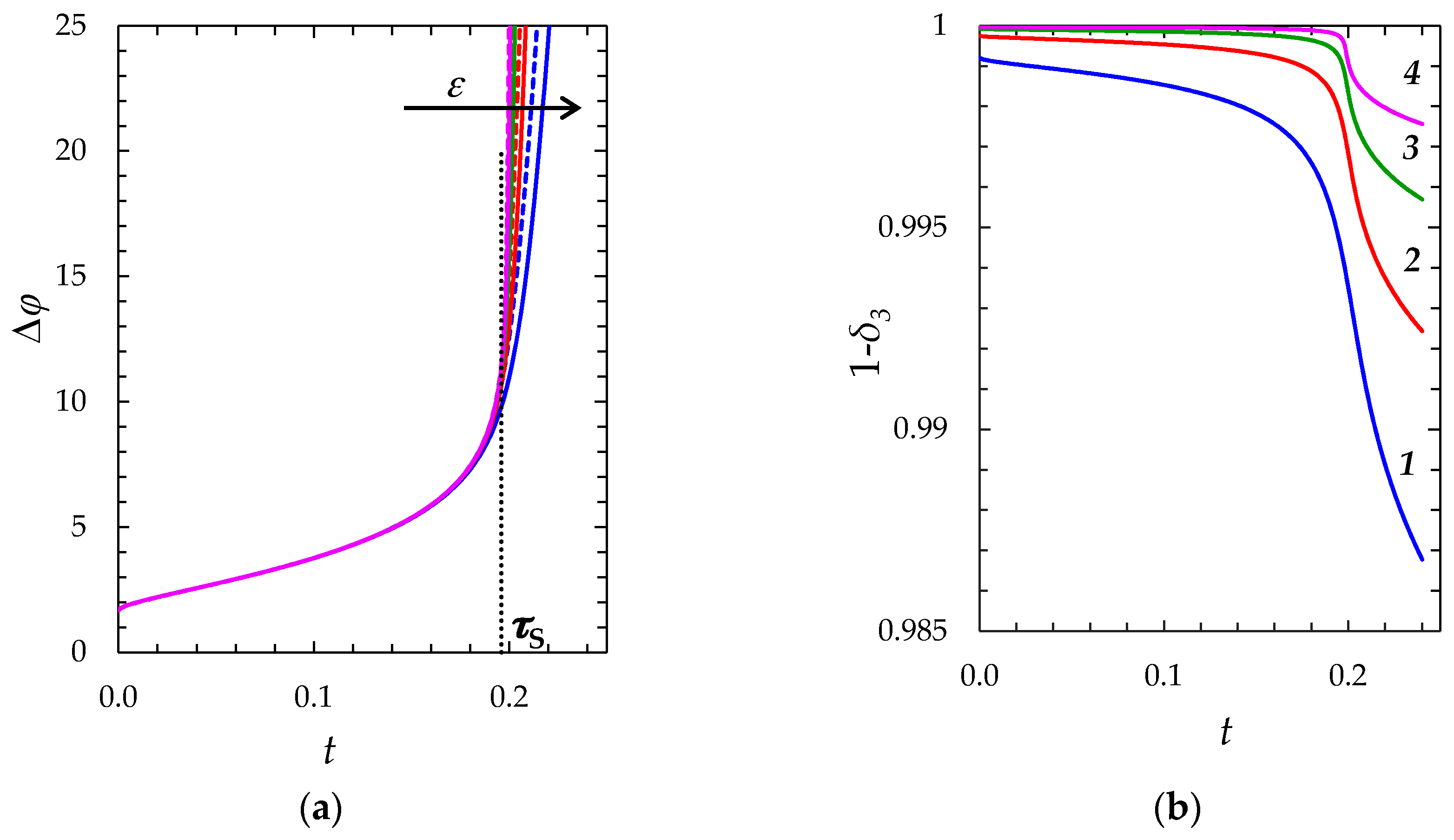
- The “zonal” numerical-analytical model, in which the diffusion layer is split into two zones, where the solution is determined separately. The first zone includes the electroneutral region δ1 and the extended SCR δ2, the second zone is the equilibrium part of EDL δ3 (Figure 1). The model considers the change in the thickness of both zones with time, when concentration polarization develops under an applied current density i.
- (3)
- The “simplified” model, in which the thickness of the equilibrium part of EDL is assumed equal to zero: δ3 = 0. Since the sum of the thicknesses of all zones is given (equal to δ), in this simplification the thickness of the first zone is overestimated. It is shown, that at relatively large values of the inlet concentration of the electrolyte solution, this overestimation can be neglected, and the calculations are considerably simplified.
2.1. The “Primary” Galvanostatic Model
2.1.1. The System of Equations and the Boundary Conditions
2.1.2. Numerical Solution
2.1.3. Parameters Used in Computations
2.1.4. Choice of the Boundary Conditions to Set the Current Density
2.1.5. Results
Concentration Profiles, Distribution of Space Charge and Current Density
Chronopotentiograms
2.2. The “Zonal” Model
2.2.1. Decomposition of the Problem
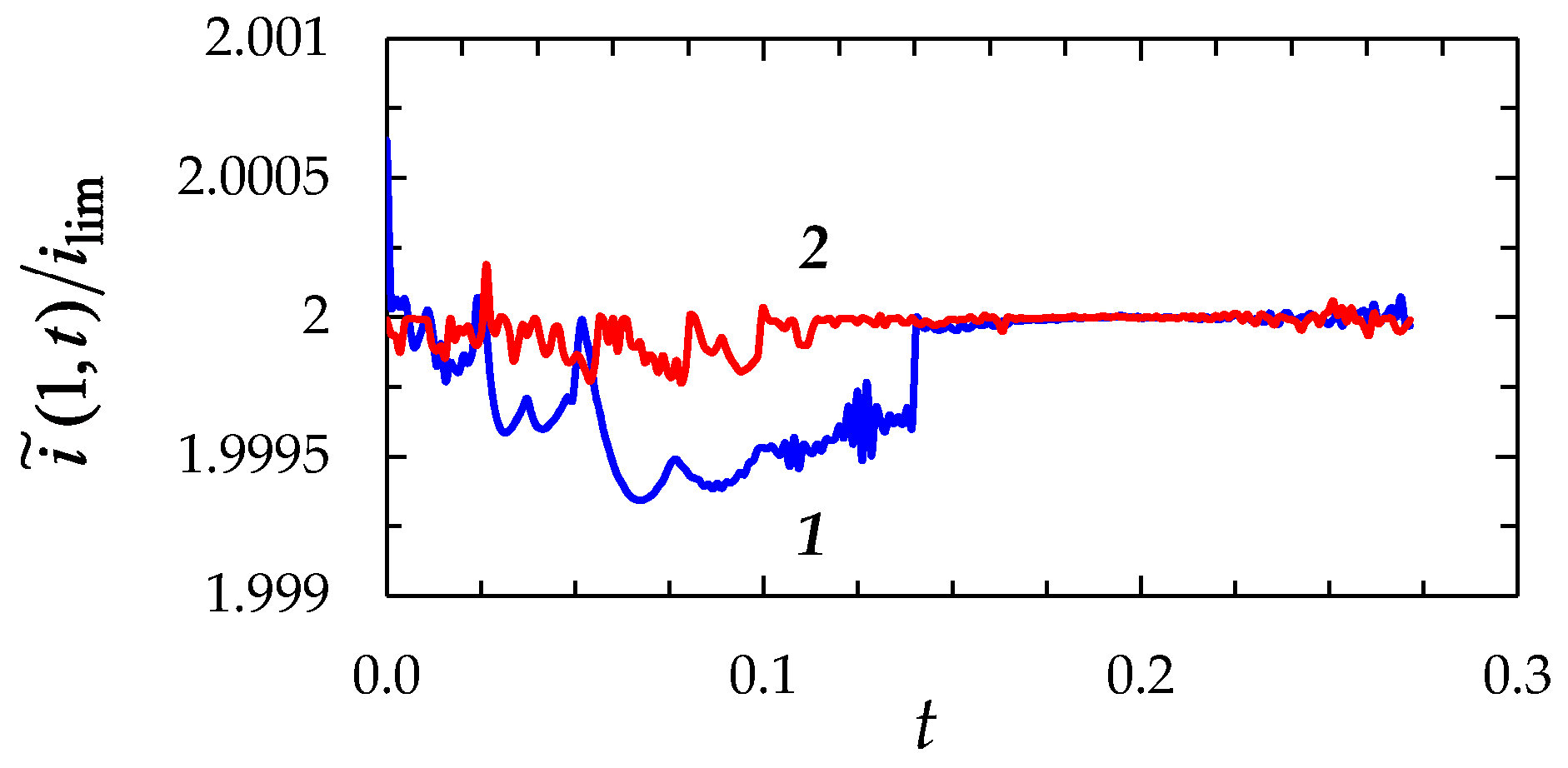
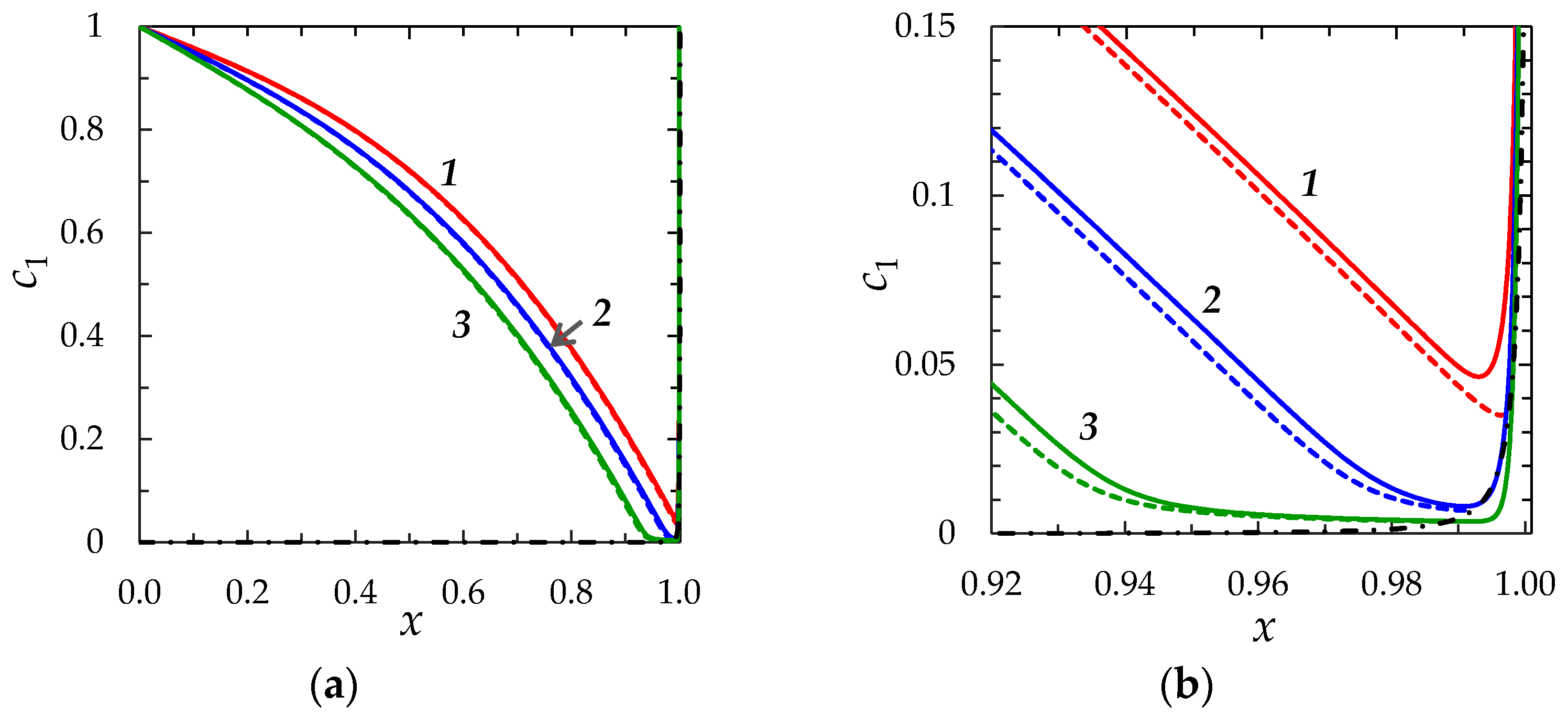
2.2.2. Comparison of the “Primary” and “Zonal” Models
2.3. The “Simplified” Model
Idea and Limits of Applicability of the “Simplified” Model
2.4. Effect of Setting Condition for the Current Density at the Left-Hand Boundary
3. Comparison with the Experiment
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Boundary Condition | tst, s | |
|---|---|---|
| Left-Hand Boundary | Right-Hand Boundary | |
| Equation (11) | 1866 | 8005 |
| Equation (13) | 2491 | 30,200 |
Appendix B
Appendix C
Appendix D
| Model | Relative Error, γ | Number of Mesh Elements, K | The Computation Time, the Case of t’ = 0.239, s |
|---|---|---|---|
| “Primary” | 0.14% | 75,000 | 563 |
| “Zonal” | 0.14% | 1000 | 16 |
| “Simplified” | 0.14% | 1000 | 10 |
References
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons, Inc.: Honoken, NJ, USA, 2004; 647p, ISBN 0-471-47756-7. [Google Scholar]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Pham, S.V.; Li, Z.; Lim, K.M.; White, J.K.; Han, J. Direct numerical simulation of electroconvective instability and hysteretic current-voltage response of a permselective membrane. Phys. Rev. E 2012, 86, 046310. [Google Scholar] [CrossRef] [PubMed]
- Demekhin, E.A.; Shelistov, V.S.; Polyanskikh, S.V. Linear and nonlinear evolution and diffusion layer selection in electrokinetic instability. Phys. Rev. E 2011, 84, 036318. [Google Scholar] [CrossRef] [PubMed]
- Ganchenko, G.S.; Kalaydin, E.N.; Schiffbauer, J.; Demekhin, E.A. Modes of electrokinetic instability for imperfect electric membranes. Phys. Rev. E 2016, 94, 063106. [Google Scholar] [CrossRef] [PubMed]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190–202. [Google Scholar] [CrossRef]
- Karatay, E.; Druzgalski, C.L.; Mani, A. Simulation of Chaotic Electrokinetic Transport: Performance of Commercial Software versus Custom-built Direct Numerical Simulation Codes. J. Colloid Interface Sci. 2015, 446, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Druzgalski, C.; Mani, A. Statistical analysis of electroconvection near an ion-selective membrane in the highly chaotic regime. Phys. Rev. Fluids 2016, 1, 073601. [Google Scholar] [CrossRef]
- Davidson, S.M.; Wessling, M.; Mani, A. On the Dynamical Regimes of Pattern-Accelerated Electroconvection. Sci. Rep. 2016, 6, 22505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Druzgalski, C.L.; Andersen, M.B.; Mani, A. Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 2013, 25, 110804. [Google Scholar] [CrossRef]
- Pham, S.V.; Kwon, H.; Kim, B.; White, J.K.; Lim, G.; Han, J. Helical vortex formation in three-dimensional electrochemical systems with ion-selective membranes. Phys. Rev. E 2016, 93, 033114. [Google Scholar] [CrossRef] [PubMed]
- Andersen, M.; Wang, K.; Schiffbauer, J.; Mani, A. Confinement effects on electroconvective instability. Electrophoresis 2017, 38, 702–711. [Google Scholar] [CrossRef] [PubMed]
- Femmer, R.; Mani, A.; Wessling, M. Ion transport through electrolyte/polyelectrolyte multi-layers. Sci. Rep. 2015, 5, 11583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moya, A.A. Electrochemical Impedance of Ion-Exchange Membranes with Interfacial Charge Transfer Resistances. J. Phys. Chem. C 2016, 120, 6543–6552. [Google Scholar] [CrossRef]
- Kodým, R.; Fíla, V.; Šnita, D.; Bouzek, K. Poisson-Nernst-Planck model of multiple ion transport across an ion-selective membrane under conditions close to chlor-alkali electrolysis. J. Appl. Electrochem. 2016, 46, 679–694. [Google Scholar] [CrossRef]
- Suzuki, Y.; Seki, K. Possible influence of the Kuramoto length in a photo-catalytic water splitting reaction revealed by Poisson–Nernst–Planck equations involving ionization in a weak electrolyte. Chem. Phys. 2018, 502, 39–49. [Google Scholar] [CrossRef]
- Sistat, P.; Pourcelly, G. Chronopotentiometric response of an ion exchanges membrane in the underlimiting current range. Transport phenomena within the diffusion layers. J. Membr. Sci. 1997, 123, 121–131. [Google Scholar] [CrossRef]
- Krol, J.J.; Wessling, M.; Strathmann, H. Chronopotentiometry and overlimiting ion transport through monopolar ion exchange membranes. J. Membr. Sci. 1999, 162, 155–164. [Google Scholar] [CrossRef]
- Choi, J.-H.; Moon, S.-H. Pore size characterization of cation-exchange membranes by chronopotentiometry using homologous amine ions. J. Membr. Sci. 2001, 191, 225–236. [Google Scholar] [CrossRef]
- Lerman, I.; Rubinstein, I.; Zaltzman, B. Absence of bulk electroconvective instability in concentration polarization. Phys. Rev. E 2005, 71, 011506. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I.; Zaltzman, T.; Zaltzman, B. Electroconvection in a layer and in a loop. Phys. Fluids 1995, 7, 1467–1482. [Google Scholar] [CrossRef]
- Larchet, C.; Nouri, S.; Auclair, B.; Dammak, L.; Nikonenko, V. Application of chronopotentiometry to determine the thickness of diffusion layer adjacent to an ion-exchange membrane under natural convection. Adv. Colloid Interface Sci. 2008, 139, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Pismensky, A.V.; Urtenov, M.K.; Nikonenko, V.V.; Sistat, P.; Pismenskaya, N.D.; Kovalenko, A.V. Model and Experimental Studies of Gravitational Convection in an Electromembrane Cell. Russ. J. Electrochem. 2012, 48, 756–766. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nichka, V.S.; Butylskii, D.Y.; Urtenov, M.K.; Pismenskaya, N.D.; Apel, P.Y.; Nikonenko, V.V. Chronopotentiometric Response of Electrically Heterogeneous Permselective Surface: 3D Modeling of Transition Time and Experiment. J. Phys. Chem. C 2016, 120, 13113–13119. [Google Scholar] [CrossRef]
- Mareev, S.A.; Butylskii, D.Y.; Pismenskaya, N.D.; Nikonenko, V.V. Chronopotentiometry of ion-exchange membranes in the overlimiting current range. Transition time for a finite-length diffusion layer: Modeling and experiment. J. Membr. Sci. 2016, 500, 171–179. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Murphy, W.D.; Mafe, S.; Reiss, H. Numerical Simulation of the Nonequilibrium Diffuse Double Layer in Ion-Exchange Membranes. J. Phys. Chem. 1993, 97, 8524–8530. [Google Scholar] [CrossRef]
- Zaltzman, B.; Rubinstein, I. Electro-osmotic slip and Electroconvective instability. J. Fluid Mech. 2007, 579, 173–226. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium Electro-Convective Instability. Phys. Rev. Lett. 2015, 114, 114502. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Zabolotsky, V.I.; Gnusin, N.P. Electromigration of ions through a diffusion layer with broken electroneutrality. Sov. J. Electrochem. (Transl. Elektrokhimiya) 1989, 25, 301–305. [Google Scholar]
- Brumleve, T.R.; Buck, R.P. Numerical solution of the Nernst-Planck and Poisson equation system with applications to membrane electrochemistry and solid state physics. J. Electroanal. Chem. 1978, 90, 1–31. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.D.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef] [PubMed]
- Someda, C.G. Electromagnetic Waves; CRC Press: Boca Raton, FL, USA, 2017; p. 275. ISBN 9780849395895. [Google Scholar]
- Vasil’eva, A.B.; Butuzov, V.F. Asymptotic Expansions of Solutions of Singularly Perturbed Equations; Nauka: Moscow, Russia, 1973; 272p. [Google Scholar]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of Electroconvection and Its Use in Intensifying the Mass Transfer in Electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Gil, V.V.; Andreeva, M.A.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Dammak, L. Effect of counterion hydration numbers on the development of Electroconvection at the surface of heterogeneous cation-exchange membrane modified with an MF-4SK film. Pet. Chem. 2016, 56, 440–449. [Google Scholar] [CrossRef]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst-Planck and Poisson equations, Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 11151, 14208–14222. [Google Scholar] [CrossRef] [PubMed]
- Sand, H.J.S. On the concentration at the electrodes in a solution, with special reference to the liberation of hydrogen by electrolysis of a mixture of copper sulphate and sulphuric acid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 1, 45–79. [Google Scholar] [CrossRef]
- Pismenskaya, N.; Sistat, P.; Huguet, P.; Nikonenko, V.; Pourcelly, G. Chronopotentiometry applied to the study of ion transfer through anion exchange membranes. J. Membr. Sci. 2004, 228, 65–76. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Mishchuk, N.A. Unlimited current growth through the ion exchanger granule. Sov. Colloid J. (Transl. Kolloidn. Zhurnal) 1988, 49, 1047. [Google Scholar]
- Dukhin, S.S. Electrokinetic phenomena of second kind and their applications. Adv. Colloid Interface Sci. 1991, 35, 173–196. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef] [PubMed]
- Soestbergen, M.; Biesheuvel, P.M.; Bazant, M.Z. Diffuse-charge effects on the transient response of electrochemical cells. Phys. Rev. E 2010, 81, 021503. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I.; Zaltzman, B.; Futerman, A.; Gitis, V.; Nikonenko, V. Reexamination of electrodiffusion time scales. Phys. Rev. E 2009, 79, 021506. [Google Scholar] [CrossRef] [PubMed]
- Abu-Rjal, R.; Prigozhin, L.; Rubinstein, I.; Zaltzman, B. Equilibrium Electro-Convective Instability in Concentration Polarization: The Effect of Non-Equal Ionic Diffusivities and Longitudinal Flow. Russ. J. Electrochem. 2017, 53, 903–918. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.S.; Lim, K.M.; Han, J. Shear Flow of an Electrically Charged Fluid by Ion Concentration Polarization: Scaling Laws for Electroconvective Vortices. Phys. Rev. Lett. 2013, 110, 114501. [Google Scholar] [CrossRef] [PubMed]
- Demekhin, E.A.; Nikitin, N.V.; Shelistov, V.S. Direct numerical simulation of electrokinetic instability and transition to chaotic motion. Phys. Fluids 2013, 25, 122001. [Google Scholar] [CrossRef] [Green Version]
- Abu-Rjal, R.; Rubinstein, I.; Zaltzman, B. Driving factors of electro-convective instability in concentration polarization. Phys. Rev. Fluids 2016, 1, 023601. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B.; Pundik, T. Ion-Exchange Funneling in Thin-Film Coating Modification of Heterogeneous Electrodialysis Membranes. Phys. Rev. E 2002, 65, 041507. [Google Scholar] [CrossRef] [PubMed]








| ε | c0, mol/m3 | |||
|---|---|---|---|---|
| 0.01 | 0.214 | 0.208 | 2.7 | |
| 0.1 | 0.204 | 0.202 | 1.3 | |
| 1 | 0.200 | 0.199 | 0.7 | |
| 10 | 0.199 | 0.198 | 0.4 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. https://doi.org/10.3390/membranes8030084
Uzdenova A, Kovalenko A, Urtenov M, Nikonenko V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes. 2018; 8(3):84. https://doi.org/10.3390/membranes8030084
Chicago/Turabian StyleUzdenova, Aminat, Anna Kovalenko, Makhamet Urtenov, and Victor Nikonenko. 2018. "1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode" Membranes 8, no. 3: 84. https://doi.org/10.3390/membranes8030084
APA StyleUzdenova, A., Kovalenko, A., Urtenov, M., & Nikonenko, V. (2018). 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes, 8(3), 84. https://doi.org/10.3390/membranes8030084








