Hybrid E/M Phenotype(s) and Stemness: A Mechanistic Connection Embedded in Network Topology
Abstract
:1. Introduction
2. Results
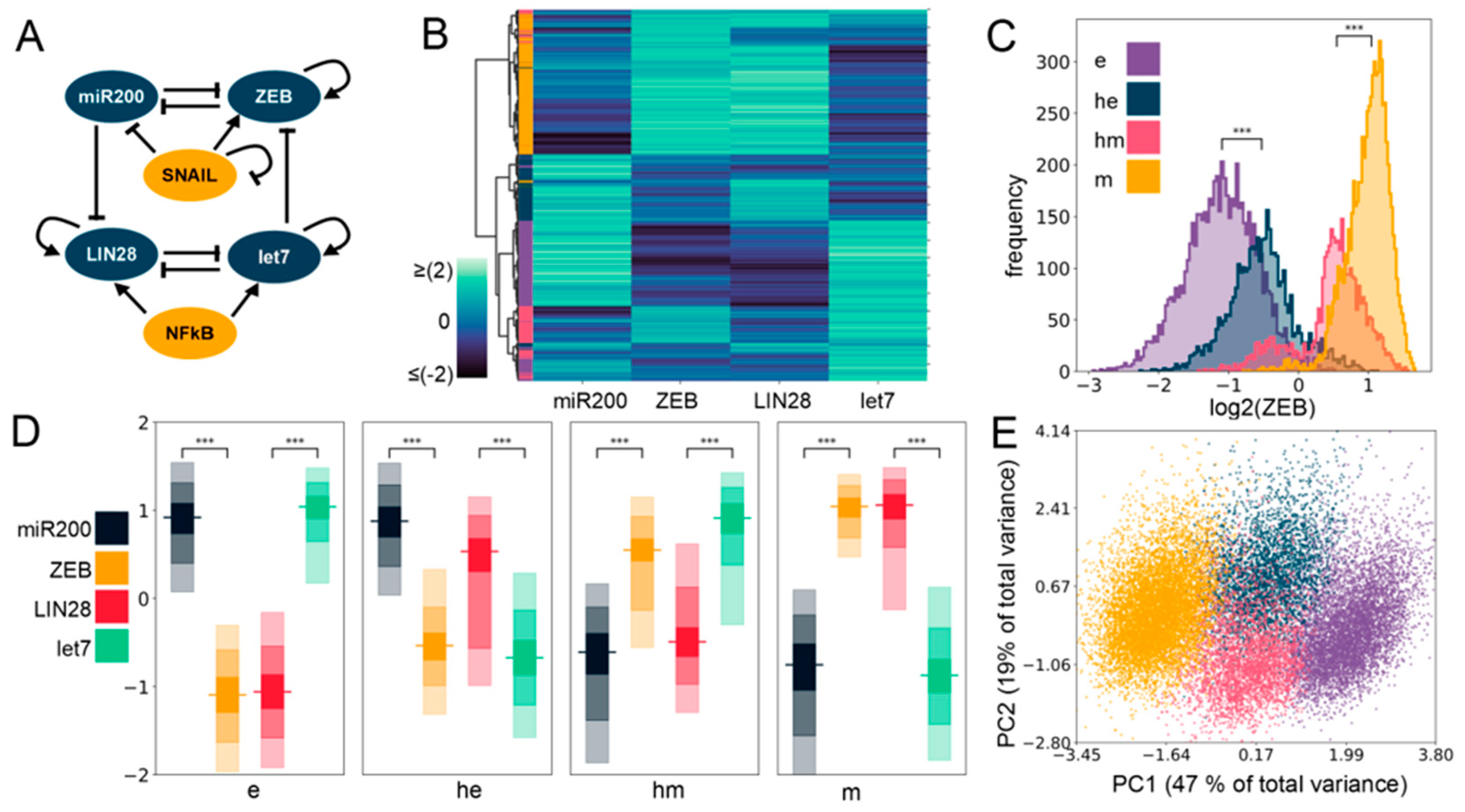
2.1. Gene Regulatory Network Underlying E/M Plasticity and Stemness Enables the Existence of Four E/M Phenotypes
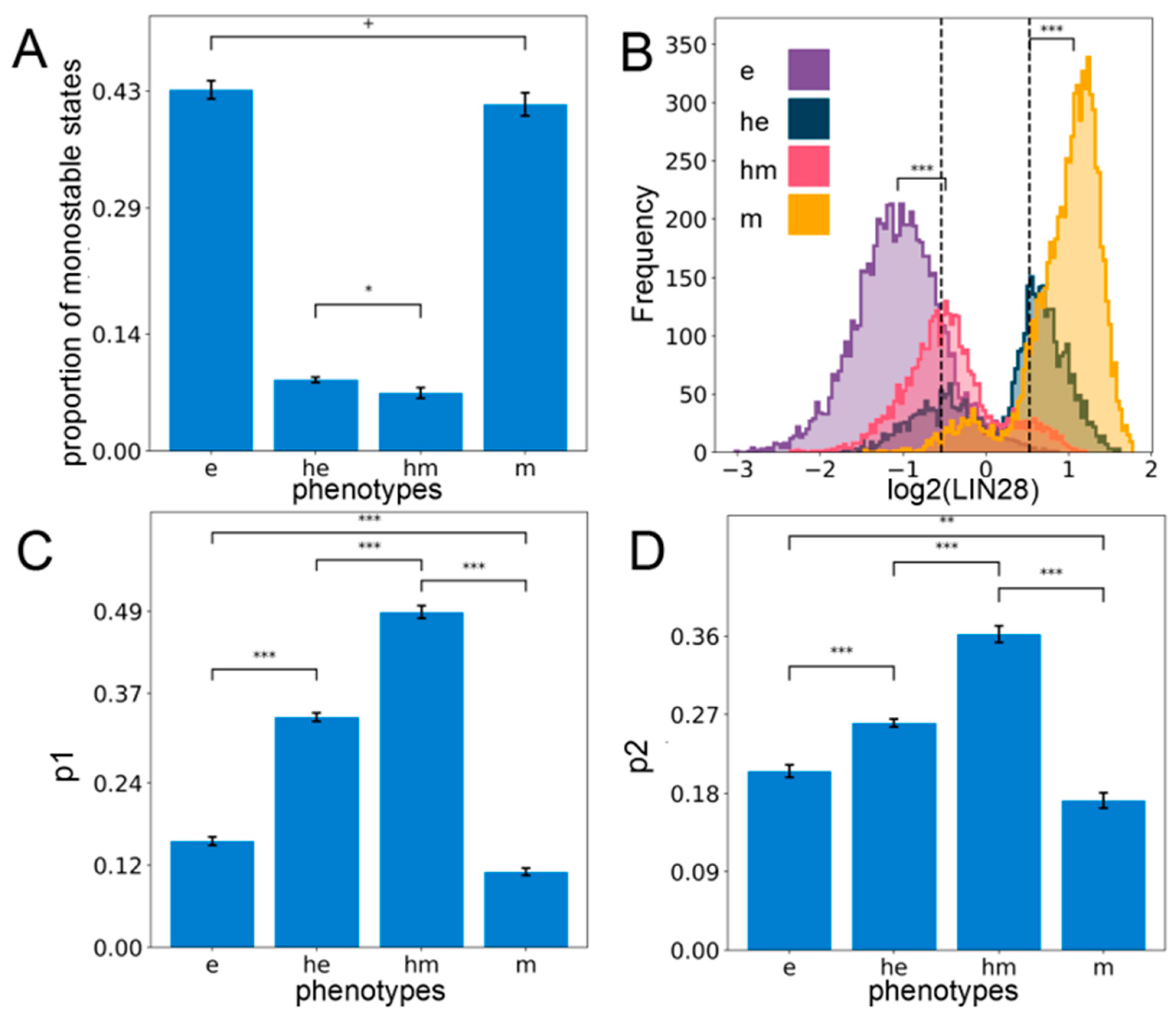
2.2. Stemness Characteristics are Enriched for in the Hybrid E/M Phenotypes
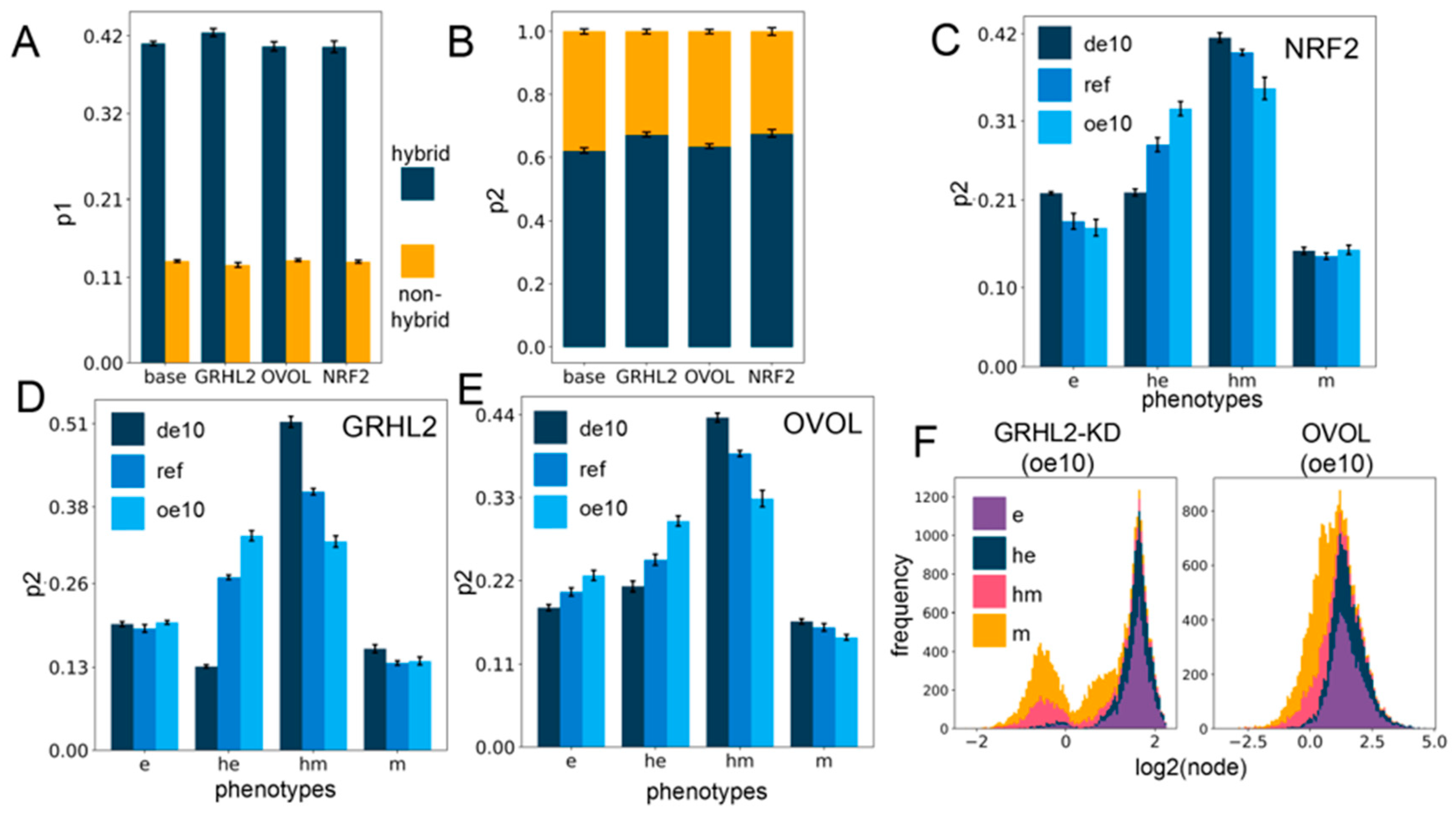
2.3. The Effect of Phenotypic Stability Factors (PSFs) on the Phenotypic Landscape of EMP
2.4. Networks Incorporating Phenotype Stability Factors (PSFs) Preserve the Association of the Hybrid E/M States with Stemness
3. Discussion
4. Methods
4.1. Random Circuit Perturbation (RACIPE)
4.2. Parameter Sampling
4.3. Simulation
4.4. Link Strength Metrics
4.5. Calculation of p1 and p2 Values
4.6. Clustering
4.7. Significance Testing
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lambert, A.W.; Pattabiraman, D.R.; Weinberg, R.A. Emerging Biological Principles of Metastasis. Cell 2017, 168, 670–691. [Google Scholar] [CrossRef] [Green Version]
- Fidler, I.J. Metastasis: Quantitative Analysis of Distribution and Fate of Tumor Emboli Labeled. J. Natl. Cancer Inst. 1970, 45, 773–782. [Google Scholar] [PubMed]
- Celià-Terrassa, T.; Jolly, M.K. Cancer Stem Cells and Epithelial-to-Mesenchymal Transition in Cancer Metastasis. Cold Spring Harb. Perspect. Med. 2020, 10, a036905. [Google Scholar] [CrossRef] [PubMed]
- Celià-Terrassa, T.; Kang, Y. Distinctive properties of metastasis-initiating cells. Genes Dev. 2016, 30, 892–908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, D.; Li, X.; Bocci, F.; Tripathi, S.; Deng, Y.; Jolly, M.K.; Onuchic, J.N.; Levine, H. Quantifying Cancer Epithelial-Mesenchymal Plasticity and its Association with Stemness and Immune Response. J. Clin. Med. 2019, 8, 725. [Google Scholar] [CrossRef] [Green Version]
- Hari, K.; Sabuwala, B.; Subramani, B.V.; La Porta, C.; Zapperi, S.; Font-Clos, F.; Jolly, M.K. Identifying inhibitors of epithelial-mesenchymal plasticity using a network topology based approach. NPJ Syst. Biol. Appl. 2020, 6, 15. [Google Scholar] [CrossRef]
- Williams, E.D.; Gao, D.; Redfern, A.; Thompson, E.W. Controversies around epithelial–mesenchymal plasticity in cancer metastasis. Nat. Rev. Cancer 2019, 19, 716–732. [Google Scholar] [CrossRef] [Green Version]
- Mani, S.A.; Guo, W.; Liao, M.-J.; Eaton, E.N.; Ayyanan, A.; Zhou, A.Y.; Brooks, M.; Reinhard, F.; Zhang, C.C.; Shipitsin, M.; et al. The epithelial-mesenchymal transition generates cells with properties of stem cells. Cell 2008, 133, 704–715. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.-P.; Lièvre, M.; Thomas, C.; Hinkal, G.; Ansieau, S.; Puisieux, A. Generation of breast cancer stem cells through epithelial-mesenchymal transition. PLoS ONE 2008, 3, e2888. [Google Scholar] [CrossRef]
- Celià-Terrassa, T.; Meca-Cortés, Ó.; Mateo, F.; De Paz, A.M.; Rubio, N.; Arnal-Estapé, A.; Ell, B.J.; Bermudo, R.; Díaz, A.; Guerra-Rebollo, M.; et al. Epithelial-mesenchymal transition can suppress major attributes of human epithelial tumor-initiating cells. J. Clin. Investig. 2012, 122, 1849–1868. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Cong, Y.; Wang, D.; Sun, Y.; Deng, L.; Liu, Y.; Martin-Trevino, R.; Shang, L.; McDermott, S.P.; Landis, M.D.; et al. Breast cancer stem cells transition between epithelial and mesenchymal states reflective of their normal counterparts. Stem Cell Rep. 2014, 2, 78–91. [Google Scholar] [CrossRef] [PubMed]
- Grosse-Wilde, A.; Fouquier d’ Herouei, A.; McIntosh, E.; Ertaylan, G.; Skupin, A.; Kuestner, R.E.; del Sol, A.; Walters, K.-A.; Huang, S. Stemness of the hybrid epithelial/mesenchymal state in breast cancer and its association with poor survival. PLoS ONE 2015, 10, e0126522. [Google Scholar] [CrossRef]
- Kröger, C.; Afeyan, A.; Mraz, J.; Ng, E.; Reinhardt, F.; Khodor, Y.L. Acquisition of a hybrid E / M state is essential for tumorigenicity of basal breast cancer cells. Proc. Natl. Acad. Sci. USA 2019, 116, 7353–7362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bierie, B.; Pierce, S.E.; Kroeger, C.; Stover, D.G.; Pattabiraman, D.R.; Thiru, P.; Liu Donaher, J.; Reinhardt, F.; Chaffer, C.L.; Keckesova, Z.; et al. Integrin-β4 identifies cancer stem cell-enriched populations of partially mesenchymal carcinoma cells. Proc. Natl. Acad. Sci. USA 2017, 114, E2337–E2346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jolly, M.K.; Huang, B.; Lu, M.; Mani, S.A.; Levine, H.; Ben-Jacob, E. Towards elucidating the connection between epithelial-mesenchymal transitions and stemness. J. R. Soc. Interface 2014, 11, 20140962. [Google Scholar] [CrossRef] [PubMed]
- Pastushenko, I.; Brisebarre, A.; Sifrim, A.; Fioramonti, M.; Revenco, T.; Boumahdi, S.; Van Keymeulen, A.; Brown, D.; Moers, V.; Lemaire, S.; et al. Identification of the tumour transition states occurring during EMT. Nature 2018, 556, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Ombrato, L.; Malanchi, I. The EMT Universe: Space between Cancer Cell Dissemination and Metastasis Initiation. Crit. Rev. Oncog. 2014, 19, 349–361. [Google Scholar] [CrossRef]
- Quan, Q.; Wang, X.; Lu, C.; Ma, W.; Wang, Y.; Xia, G.; Wang, C.; Yang, G. Cancer stem-like cells with hybrid epithelial/mesenchymal phenotype leading the collective invasion. Cancer Sci. 2020, 111, 467–476. [Google Scholar] [CrossRef]
- Ruscetti, M.; Dadashian, E.L.; Guo, W.; Quach, B.; Mulholland, D.J.; Park, J.W.; Tran, L.M.; Kobayashi, N.; Bianchi-Frias, D.; Xing, Y.; et al. HDAC inhibition impedes epithelial-mesenchymal plasticity and suppresses metastatic, castration-resistant prostate cancer. Oncogene 2016, 35, 3781–3795. [Google Scholar] [CrossRef] [Green Version]
- Tripathi, S.; Chakraborty, P.; Levine, H.; Jolly, M.K. A mechanism for epithelial-mesenchymal heterogeneity in a population of cancer cells. PLoS Comput. Biol. 2020, 16, e1007619. [Google Scholar] [CrossRef] [Green Version]
- Jolly, M.K.; Somarelli, J.A.; Sheth, M.; Biddle, A.; Tripathi, S.C.C.; Armstrong, A.J.J.; Hanash, S.M.M.; Bapat, S.A.A.; Rangarajan, A.; Levine, H. Hybrid epithelial/mesenchymal phenotypes promote metastasis and therapy resistance across carcinomas. Pharmacol. Ther. 2019, 194, 161–184. [Google Scholar] [CrossRef] [PubMed]
- Jolly, M.K.; Jia, D.; Boareto, M.; Mani, S.A.; Pienta, K.J.; Ben-Jacob, E.; Levine, H. Coupling the modules of EMT and stemness: A tunable “stemness window” model. Oncotarget 2015, 6, 25161–25174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bocci, F.; Jolly, M.K.; George, J.T.; Levine, H.; Onuchic, J.N. A mechanism-based computational model to capture the interconnections among epithelial-mesenchymal transition, cancer stem cells and Notch-Jagged signaling. Oncotarget 2018, 9, 29906–29920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bracken, C.P.; Gregory, P.A.; Kolesnikoff, N.; Bert, A.G.; Wang, J.; Shannon, M.F.; Goodall, G.J. A double-negative feedback loop between ZEB1-SIP1 and the microRNA-200 family regulates epithelial-mesenchymal transition. Cancer Res. 2008, 68, 7846–7854. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-M.M.; Gaur, A.B.; Lengyel, E.; Peter, M.E. The miR-200 family determines the epithelial phenotype of cancer cells by targeting the E-cadherin repressors ZEB1 and ZEB2. Genes Dev. 2008, 22, 894–907. [Google Scholar] [CrossRef] [Green Version]
- Preca, B.-T.; Bajdak, K.; Mock, K.; Lehmann, W.; Sundararajan, V.; Bronsert, P.; Matzge-Ogi, A.; Orian-Rousseau, V.; Brabletz, S.; Brabletz, T.; et al. A novel ZEB1/HAS2 positive feedback loop promotes EMT in breast cancer. Oncotarget 2017, 8, 11530–11543. [Google Scholar] [CrossRef] [Green Version]
- Jolly, M.K.; Preca, B.-T.; Tripathi, S.C.; Jia, D.; George, J.T.; Hanash, S.M.; Brabletz, T.; Stemmler, M.P.; Maurer, J.; Levine, H. Interconnected feedback loops among ESRP1, HAS2, and CD44 regulate epithelial-mesenchymal plasticity in cancer. APL Bioeng. 2018, 2, 031908. [Google Scholar] [CrossRef]
- Preca, B.-T.; Bajdak, K.; Mock, K.; Sundararajan, V.; Pfannstiel, J.; Maurer, J.; Wellner, U.; Hopt, U.T.; Brummer, T.; Brabletz, S.; et al. A self-reinforcing CD44s/ZEB1 feedback loop maintains EMT and stemness properties in cancer cells. Int. J. Cancer 2015, 137, 2566–2577. [Google Scholar] [CrossRef]
- Lu, M.; Jolly, M.K.; Levine, H.; Onuchic, J.N.; Ben-Jacob, E. MicroRNA-based regulation of epithelial-hybrid-mesenchymal fate determination. Proc. Natl. Acad. Sci. USA 2013, 110, 18144–18149. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Lin, X.; Zhong, X.; Kaur, S.; Li, N.; Liang, S.; Lassus, H.; Wang, L.; Katsaros, D.; Montone, K.; et al. Double-negative feedback loop between reprogramming factor LIN28 and microRNA let-7 regulates aldehyde dehydrogenase 1-positive cancer stem cells. Cancer Res. 2010, 70, 9463–9472. [Google Scholar] [CrossRef] [Green Version]
- Hafner, M.; Max, K.E.A.; Bandaru, P.; Morozov, P.; Gerstberger, S.; Brown, M.; Molina, H.; Tuschl, T. Identification of mRNAs bound and regulated by human LIN28 proteins and molecular requirements for RNA recognition. RNA 2013, 19, 613–626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilbert, M.L.; Huelga, S.C.; Kapeli, K.; Stark, T.J.; Liang, T.Y.; Chen, S.X.; Yan, B.Y.; Nathanson, J.L.; Hutt, K.R.; Lovci, M.T.; et al. LIN28 binds messenger RNAs at GGAGA motifs and regulates splicing factor abundance. Mol. Cell 2012, 48, 195–206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zisoulis, D.G.; Kai, Z.S.; Chang, R.K.; Pasquinelli, A.E. Autoregulation of microRNA biogenesis by let-7 and Argonaute. Nature 2012, 486, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.; Ma, Y.; Wang, J.; Peng, S.; Huang, Y. Lin28-mediated post-transcriptional regulation of Oct4 expression in human embryonic stem cells. Nucleic Acids Res. 2010, 38, 1240–1248. [Google Scholar] [CrossRef] [Green Version]
- Niwa, H.; Miyazaki, J.; Smith, A.G. Quantitative expression of Oct-3/4 defines differentiation, dedifferentiation or self-renewal of ES cells. Nat. Genet. 2000, 24, 372–376. [Google Scholar] [CrossRef]
- Karwacki-Neisius, V.; Göke, J.; Osorno, R.; Halbritter, F.; Ng, J.H.; Weiße, A.Y.; Wong, F.C.K.; Gagliardi, A.; Mullin, N.P.; Festuccia, N.; et al. Reduced Oct4 expression directs a robust pluripotent state with distinct signaling activity and increased enhancer occupancy by Oct4 and Nanog. Cell Stem Cell 2013, 12, 531–545. [Google Scholar] [CrossRef] [Green Version]
- Theunissen, T.W.; Van Oosten, A.L.; Castelo-Branco, G.; Hall, J.; Smith, A.; Silva, J.C.R. Nanog overcomes reprogramming barriers and induces pluripotency in minimal conditions. Curr. Biol. 2011, 21, 65–71. [Google Scholar] [CrossRef] [Green Version]
- Sato, H.; Shien, K.; Tomida, S.; Okayasu, K.; Suzawa, K.; Hashida, S.; Torigoe, H.; Watanabe, M.; Yamamoto, H.; Soh, J.; et al. Targeting the miR-200c/LIN28B axis in acquired EGFR-TKI resistance non-small cell lung cancer cells harboring EMT features. Sci. Rep. 2017, 7, 40847. [Google Scholar] [CrossRef]
- Kong, D.; Banerjee, S.; Ahmad, A.; Li, Y.; Wang, Z.; Sethi, S.; Sarkar, F.H. Epithelial to mesenchymal transition is mechanistically linked with stem cell signatures in prostate cancer cells. PLoS ONE 2010, 5, e12445. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Feng, J.; Cui, X.; Huang, W.; Li, Y.; Su, F.; Liu, Q.; Zhu, J.; Lv, X.; et al. Lin28 induces epithelial-to-mesenchymal transition and stemness via downregulation of let-7a in breast cancer cells. PLoS ONE 2013, 8, e83083. [Google Scholar] [CrossRef] [Green Version]
- Brabletz, S.; Brabletz, T. The ZEB/miR-200 feedback loop—A motor of cellular plasticity in development and cancer? EMBO Rep. 2010, 11, 670–677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, P.; Karaayvaz, M.; Jia, N.; Kaneuchi, M.; Hamada, J.; Watari, H.; Sudo, S.; Ju, J.; Sakuragi, N. Mutant p53 gain-of-function induces epithelial-mesenchymal transition through modulation of the miR-130b-ZEB1 axis. Oncogene 2013, 32, 3286–3295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, B.; Lu, M.; Jia, D.; Ben-Jacob, E.; Levine, H.; Onuchic, J.N. Interrogating the topological robustness of gene regulatory circuits by randomization. PLoS Comput. Biol. 2017, 13, e1005456. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Font-Clos, F.; Zapperi, S.; Porta, C.A.M. La Topography of epithelial–mesenchymal plasticity. Proc. Natl. Acad. Sci. USA 2018, 115, 5902–5907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinway, S.N.; Zañudo, J.G.T.; Michel, P.J.; Feith, D.J.; Loughran, T.P.; Albert, R. Combinatorial interventions inhibit TGFβ-driven epithelial-to-mesenchymal transition and support hybrid cellular phenotypes. NPJ Syst. Biol. Appl. 2015, 1, 15014. [Google Scholar] [CrossRef] [Green Version]
- Jolly, M.K.; Tripathi, S.C.; Jia, D.; Mooney, S.M.; Celiktas, M.; Hanash, S.M.; Mani, S.A.; Pienta, K.J.; Ben-Jacob, E.; Levine, H. Stability of the hybrid epithelial/mesenchymal phenotype. Oncotarget 2016, 7, 27067–27084. [Google Scholar] [CrossRef] [Green Version]
- Hong, T.; Watanabe, K.; Ta, C.H.; Villarreal-Ponce, A.; Nie, Q.; Dai, X. An Ovol2-Zeb1 Mutual Inhibitory Circuit Governs Bidirectional and Multi-step Transition between Epithelial and Mesenchymal States. PLoS Comput. Biol. 2015, 11, e1004569. [Google Scholar] [CrossRef]
- Bocci, F.; Tripathi, S.C.; Vilchez, M.S.A.; George, J.T.; Casabar, J.; Wong, P.; Hanash, S.; Levine, H.; Onuchic, J.; Jolly, M. NRF2 activates a partial Epithelial-Mesenchymal Transition and is maximally present in a hybrid Epithelial/Mesenchymal phenotype. Integr. Biol. 2019, 11, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, K.; Villarreal-Ponce, A.; Sun, P.; Salmans, M.L.; Fallahi, M.; Andersen, B.; Dai, X. Mammary morphogenesis and regeneration require the inhibition of EMT at terminal end buds by Ovol2 transcriptional repressor. Dev. Cell 2014, 29, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Somarelli, J.A.; Shetler, S.; Jolly, M.K.; Wang, X.; Bartholf Dewitt, S.; Hish, A.J.; Gilja, S.; Eward, W.C.; Ware, K.E.; Levine, H.; et al. Mesenchymal-epithelial transition in sarcomas is controlled by the combinatorial expression of microRNA 200s and GRHL2. Mol. Cell. Biol. 2016, 36, 2503–2513. [Google Scholar] [CrossRef] [Green Version]
- Cieply, B.; Riley, P., IV; Pifer, P.M.; Widmeyer, J.; Addison, J.B.; Ivanov, A.V.; Denvir, J.; Frisch, S.M. Suppression of the epithelial-mesenchymal transition by grainyhead-like-2. Cancer Res. 2012, 72, 2440–2453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, V.Y.; Tan, T.Z.; Tan, M.; Wong, M.K.; Kuay, K.T.; Yang, Z.; Ye, J.; Muller, J.; Koh, C.M.; Guccione, E.; et al. GRHL2-miR-200-ZEB1 maintains the epithelial status of ovarian cancer through transcriptional regulation and histone modification. Sci. Rep. 2016, 6, 19943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saxena, K.; Srikrishnan, S.; Celia-Terrassa, T.; Jolly, M.K. OVOL1/2: Drivers of epithelial differentiation in development, disease and reprogramming. Cells Tissues Organs 2020, in press. [Google Scholar]
- Chung, V.Y.; Tan, T.Z.; Ye, J.; Huang, R.-L.; Lai, H.-C.; Kappei, D.; Wollmann, H.; Guccione, E.; Huang, R.Y.-J. The role of GRHL2 and epigenetic remodeling in epithelial–mesenchymal plasticity in ovarian cancer cells. Commun. Biol. 2019, 2, 272. [Google Scholar] [CrossRef] [Green Version]
- Farris, J.C.; Pifer, P.M.; Zheng, L.; Gottlieb, E.; Denvir, J.; Frisch, S.M. Grainyhead-like 2 reverses the metabolic changes induced by the oncogenic epithelial-mesenchymal transition: Effects on anoikis. Mol. Cancer Res. 2016, 14, 528–538. [Google Scholar] [CrossRef] [Green Version]
- MacFawn, I.; Wilson, H.; Selth, L.A.; Leighton, I.; Serebriiskii, I.; Bleackley, R.C.; Elzamzamy, O.; Farris, J.; Pifer, P.M.; Richer, J.; et al. Grainyhead-like-2 confers NK-sensitivity through interactions with epigenetic modifiers. Mol. Immunol. 2019, 105, 137–149. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. The Hallmarks of Cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Welch, D.R.; Hurst, D.R. Defining the Hallmarks of Metastasis. Cancer Res. 2019, 79, 3011–3027. [Google Scholar] [CrossRef]
- Pisco, A.O.; Brock, A.; Zhou, J.; Moor, A.; Mojtahedi, M.; Jackson, D.; Huang, S. Non-Darwinian dynamics in therapy-induced cancer drug resistance. Nat. Commun. 2013, 4, 2467. [Google Scholar] [CrossRef] [Green Version]
- Salgia, R.; Kulkarni, P. The genetic/non-genetic duality of drug “resistance.”. Trends Cancer 2018. [Google Scholar] [CrossRef]
- Jolly, M.K.; Kulkarni, P.; Weninger, K.; Orban, J.; Levine, H. Phenotypic plasticity, bet-hedging, and androgen independence in prostate cancer: Role of non-genetic heterogeneity. Front. Oncol. 2018, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- Robles-Espinoza, C.D. Beating tumour drug resistance: “Lamarckian” induction in the spotlight. Pigment Cell Melanoma Res. 2019, 32, 6–8. [Google Scholar] [CrossRef] [PubMed]
- Marine, J.-C.; Dawson, S.-J.; Dawson, M.A. Non-genetic mechanisms of therapeutic resistance in cancer. Nat. Rev. Cancer 2020, in press. [Google Scholar] [CrossRef] [PubMed]
- Godin, L.; Balsat, C.; Van Eycke, Y.; Allard, J.; Royer, C.; Remmelink, M.; Pastushenko, I.; Haene, N.D.; Blanpain, C.; Salmon, I.; et al. A Novel Approach for Quantifying Cancer Cells Showing Hybrid Epithelial / Mesenchymal States in Large Series of Tissue Samples: Towards a New Prognostic Marker. Cancers 2020, 12, 906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vega, S.; Morales, A.V.; Ocaña, O.H.; Valdés, F.; Fabregat, I.; Nieto, M.A. Snail blocks the cell cycle and confers resistance to cell death. Genes Dev. 2004, 18, 1131–1143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Comaills, V.; Kabeche, L.; Morris, R.; Zou, L.; Daniel, A.; Yu, M.; Madden, M.W.; Licausi, J.A.; Boukhali, M.; Tajima, K.; et al. Genomic Instability Is Induced by Persistent Proliferation of Cells Undergoing Epithelial-to- Mesenchymal Transition. Cell Rep. 2016, 17, 2632–2647. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, T.; Ibaragi, S.; Shima, K.; Hu, M.G.; Katsurano, M.; Sasaki, A.; Hu, G.F. Epithelial-mesenchymal transition induced by growth suppressor p12 CDK2-AP1 promotes tumor cell local invasion but suppresses distant colony growth. Cancer Res. 2008, 68, 10377–10386. [Google Scholar] [CrossRef] [Green Version]
- Colacino, J.A.; Azizi, E.; Brooks, M.D.; Harouaka, R.; Fouladdel, S.; McDermott, S.P.; Lee, M.; Hill, D.; Madde, J.; Boerner, J.; et al. Heterogeneity of human breast stem and progenitor cells as revelaed by transcriptional profiling. Stem Cell Rep. 2018, 10, 1596–1609. [Google Scholar] [CrossRef] [Green Version]
- Tong, T.; Wang, Y.; Brooks, M.D.; Lee, C.; Scott, C.; Balzano, L.; Wicha, M.S.; Colacino, J.A. Hybrid stem cell states: Insights into the relationship between mammary development and breast cancer using single-cell transcriptomics. Front. Cell Dev. Biol. 2020, in press. [Google Scholar] [CrossRef]
- Galoczova, M.; Nenutil, R.; Pokorna, Z.; Vojtesek, B.; Coates, P. TAp63 and ΔNp63 (p40) in prostate adenocarcinomas: ΔNp63 associates with a basal-like cancer stem cell population but not with metastasis. Virchows Arch. 2020, in press. [Google Scholar] [CrossRef]
- He, Y.; Xiao, M.; Fu, H.; Chen, L.; Qi, L.; Liu, D.; Guo, P.; Chen, L.; Luo, Y.; Xiao, H.; et al. cPLA2α reversibly regulates different subsets of cancer stem cells transformation in cervical cancer. Stem Cells 2020, 38, 487–503. [Google Scholar] [CrossRef] [PubMed]
- Biddle, A.; Liang, X.; Gammon, L.; Fazil, B.; Harper, L.J.; Emich, H.; Costea, D.E.; Mackenzie, I.C. Cancer stem cells in squamous cell carcinoma switch between two distinct phenotypes that are preferentially migratory or proliferative. Cancer Res. 2011, 71, 5317–5326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amôr, N.G.; Buzo, R.F.; Ortiz, R.C.; Lopes, N.M.; Saito, L.M.; Mackenzie, I.C.; Rodini, C.O. In vitro and in vivo characterization of cancer stem cell subpopulations in oral squamous cell carcinoma. J. Oral Pathol. Med. 2020, in press. [Google Scholar]
- Bocci, F.; Gearhart-Serna, L.; Boareto, M.; Ribeiro, M.; Ben-Jacob, E.; Devi, G.R.; Levine, H.; Onuchic, J.N.; Jolly, M.K. Toward understanding cancer stem cell heterogeneity in the tumor microenvironment. Proc. Natl. Acad. Sci. USA 2019, 116, 148–157. [Google Scholar] [CrossRef] [Green Version]
- Roylance, R.; Endesfelder, D.; Gorman, P.; Burrell, R.A.; Sander, J.; Tomlinson, I.; Hanby, A.M.; Speirs, V.; Richardson, A.L.; Birkbak, N.J.; et al. Relationship of extreme chromosomal instability with long-term survival in a retrospective analysis of primary breast cancer. Cancer Epidemiol. Biomark. Prev. 2011, 20, 2183–2194. [Google Scholar] [CrossRef] [Green Version]
- Birkbak, N.J.; Eklund, A.C.; Li, Q.; McClelland, S.E.; Endesfelder, D.; Tan, P.; Tan, I.B.; Richardson, A.L.; Szallasi, Z.; Swanton, C. Paradoxical relationship between chromosomal instability and survival outcome in cancer. Cancer Res. 2011, 71, 3447–3452. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Yi, J.K.; Shimane, T.; Mehrazarin, S.; Lin, Y.L.; Shin, K.H.; Kim, R.H.; Park, N.H.; Kang, M.K. Grainyhead-like 2 regulates epithelial plasticity and stemness in oral cancer cells. Carcinogenesis 2016, 37, 500–510. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Choi, B.; Ryoo, I.; Kwak, M.-K. High NRF2 level mediates cancer stem cell-like properties of aldehyde dehydrogenase (ALDH)-high ovarian cancer cells: Inhibitory role of all-trans retinoic acid in ALDH/NRF2 signaling. Cell Death Dis. 2018, 9, 896. [Google Scholar] [CrossRef]
- Jia, W.; Tripathi, S.; Chakraborty, P.; Chedere, A.; Rangarajan, A.; Levine, H.; Jolly, M.K. Epigenetic feedback and stochastic partitioning during cell division can drive resistance to EMT. Oncotarget 2020, 11, 2611–2624. [Google Scholar] [CrossRef]
- Subbalakshmi, A.R.; Sahoo, S.; Biswas, K.; Jolly, M.K. A computational systems biology approach identifies SLUG as a mediator of partial Epithelial-Mesenchymal Transition (EMT). bioRxiv 2020. [Google Scholar] [CrossRef]
- Jolly, M.K.; Ware, K.E.; Gilja, S.; Somarelli, J.A.; Levine, H. EMT and MET: Necessary or permissive for metastasis? Mol. Oncol. 2017, 11, 755–769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jolly, M.K.; Levine, H. Computational systems biology of epithelial-hybrid-mesenchymal transitions. Curr. Opin. Syst. Biol. 2017, 3, 1–6. [Google Scholar] [CrossRef]
- Devaraj, V.; Bose, B. Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition. J. Clin. Med. 2019, 8, 911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xin, Y.; Cummins, B.; Gedeon, T. Multistability in the epithelial-mesenchymal transition network. BMC Bioinform. 2020, 21, 71. [Google Scholar] [CrossRef] [Green Version]
- Shomar, A.; Barak, O.; Brenner, N. Local and global features of genetic networks supporting a phenotypic switch. PLoS ONE 2020, 15, e0238433. [Google Scholar] [CrossRef]
- Sha, Y.; Wang, S.; Zhou, P.; Nie, Q. Inference and multiscale model of epithelial-to-mesenchymal transition via single-cell transcriptomic data. Nucleic Acids Res. 2020, 48, 9505–9520. [Google Scholar] [CrossRef]
- Jia, D.; Lu, M.; Jung, K.H.; Park, J.H.; Yu, L.; Onuchic, J.N.; Kaipparettu, B.A.; Levine, H. Elucidating cancer metabolic plasticity by coupling gene regulation with metabolic pathways. Proc. Natl. Acad. Sci. USA 2019, 116, 3909–3918. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Ware, K.; Ding, Y.; Kim, S.; Sheth, M.; Rao, S.; Chan, W.; Armstrong, A.; Eward, W.; Jolly, M.; et al. An Integrative Systems Biology and Experimental Approach Identifies Convergence of Epithelial Plasticity, Metabolism, and Autophagy to Promote Chemoresistance. J. Clin. Med. 2019, 8, 205. [Google Scholar] [CrossRef] [Green Version]
- Tavassoly, I.; Parmar, J.; Shajahan-Haq, A.N.; Clarke, R.; Baumann, W.T.; Tyson, J.J. Dynamic modeling of the interaction between autophagy and apoptosis in mammalian cells. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 263–272. [Google Scholar] [CrossRef]
- Gómez Tejeda Zañudo, J.; Scaltriti, M.; Albert, R. A network modeling approach to elucidate drug resistance mechanisms and predict combinatorial drug treatments in breast cancer. Cancer Converg. 2017, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Goldman, A.; Majumder, B.; Dhawan, A.; Ravi, S.; Goldman, D.; Kohandel, M.; Majumder, P.K.; Sengupta, S. Temporally sequenced anticancer drugs overcome adaptive resistance by targeting a vulnerable chemotherapy-induced phenotypic transition. Nat. Commun. 2015, 6, 6139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tripathi, S.C.; Peters, H.L.; Taguchi, A.; Katayama, H.; Wang, H.; Momin, A.; Jolly, M.K.; Celiktas, M.; Rodriguez-Canales, J.; Liu, H.; et al. Immunoproteasome deficiency is a feature of non-small cell lung cancer with a mesenchymal phenotype and is associated with a poor outcome. Proc. Natl. Acad. Sci. USA 2016, 113, E1555–E1564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Celià-Terrassa, T.; Bastian, C.; Liu, D.D.; Ell, B.; Aiello, N.M.; Wei, Y.; Zamalloa, J.; Blanco, A.M.; Hang, X.; Kunisky, D.; et al. Hysteresis control of epithelial-mesenchymal transition dynamics conveys a distinct program with enhanced metastatic ability. Nat. Commun. 2018, 9, 5005. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Jorgensen, P.; Moran, U.; Weber, G.; Springer, M. BioNumbers—The database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010, 38, D750–D753. [Google Scholar] [CrossRef] [Green Version]
- Duddu, A.S.; Sahoo, S.; Hati, S.; Jhunjhunwala, S.; Jolly, M.K. Multistability in cellular differentiation enabled by a network of three mutually repressing master regulators. J. R. Soc. Interface 2020, 17, 20200631. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Hardy, A. On the number of clusters. Comput. Stat. Data Anal. 1996, 23, 83–96. [Google Scholar] [CrossRef]
- Caliñski, T.; Harabasz, J. A Dendrite Method for Cluster Analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Welch, B.L. The Generalization of Student’s Problem when Several Different Population Variances are Involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasani, S.; Sahoo, S.; Jolly, M.K. Hybrid E/M Phenotype(s) and Stemness: A Mechanistic Connection Embedded in Network Topology. J. Clin. Med. 2021, 10, 60. https://doi.org/10.3390/jcm10010060
Pasani S, Sahoo S, Jolly MK. Hybrid E/M Phenotype(s) and Stemness: A Mechanistic Connection Embedded in Network Topology. Journal of Clinical Medicine. 2021; 10(1):60. https://doi.org/10.3390/jcm10010060
Chicago/Turabian StylePasani, Satwik, Sarthak Sahoo, and Mohit Kumar Jolly. 2021. "Hybrid E/M Phenotype(s) and Stemness: A Mechanistic Connection Embedded in Network Topology" Journal of Clinical Medicine 10, no. 1: 60. https://doi.org/10.3390/jcm10010060
APA StylePasani, S., Sahoo, S., & Jolly, M. K. (2021). Hybrid E/M Phenotype(s) and Stemness: A Mechanistic Connection Embedded in Network Topology. Journal of Clinical Medicine, 10(1), 60. https://doi.org/10.3390/jcm10010060




