Using Minimum Redundancy Maximum Relevance Algorithm to Select Minimal Sets of Heart Rate Variability Parameters for Atrial Fibrillation Detection
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Used in the Study
2.2. Software Tools
2.3. Splitting Data into the Training Set and Test Set
2.4. Data Preprocessing
2.5. Feature Extraction
- pRR50 (percentage of successive differences between RR intervals greater or equal to 50 ms)—it is an example of counting statistics in which the rate of a specific event (in this case, the difference between two consecutive RR intervals of at least 50 ms) is counted;
- SD1 (standard deviation of points in the Poincare plot across the identity line)—it reflects the short-term RR variability from the Poincare plot;
- SD2 (standard deviation of points in the Poincare plot along the identity line)—it shows the long-term RR variability from the Poincare plot;
- SDRR (standard deviation of RR intervals)—it reflects the total HRV;
- RRdif = mean(|RRn+1 − RRn|) (mean of absolute differences between successive RR) − it summarizes the averaged range of differences between two consecutive RR intervals.
- CV = SDRR/(mean RR) (coefficient of variance)—it reflects the dispersion of the total variance around the mean;
- SD2/SD1 [57]—describes how much the long-term variance changes with the short-term variance. Another interpretation is how much the dispersions of points along and across the identity line change when compared to another. If SD2/SD1 is over 1, then the long-term HRV is larger than the short-term HRV, and vice versa;
- relRRdif = RRdif/(mean RR) (relative RRdif)—it shows the average rate of the absolute differences between successive RR normalized to the mean of all RR intervals.
- meanSuccRat = mean(RRn+1/RRn) (mean ratio of successive RR), the interpretation of this parameter is as follows: what is the average relative change between two consecutive RR intervals in a specific ECG segment;
- SDSuccRat = SD (RRn+1/RRn) (standard deviation of ratios of successive RR), the interpretation of this parameter is as follows: what is the variability of the relative changes between two consecutive RR intervals in a specific ECG segment.
- mean RR (mean of RR intervals);
- RRrange = max(RR) − min(RR).
- relRRrange = RRrange/(mean RR) (relative RRrange), the interpretation of this parameter is as follows: how much the range between the shortest and the longest RR interval in a specific ECG segment is larger than the mean of all RR intervals in the same ECG segment.
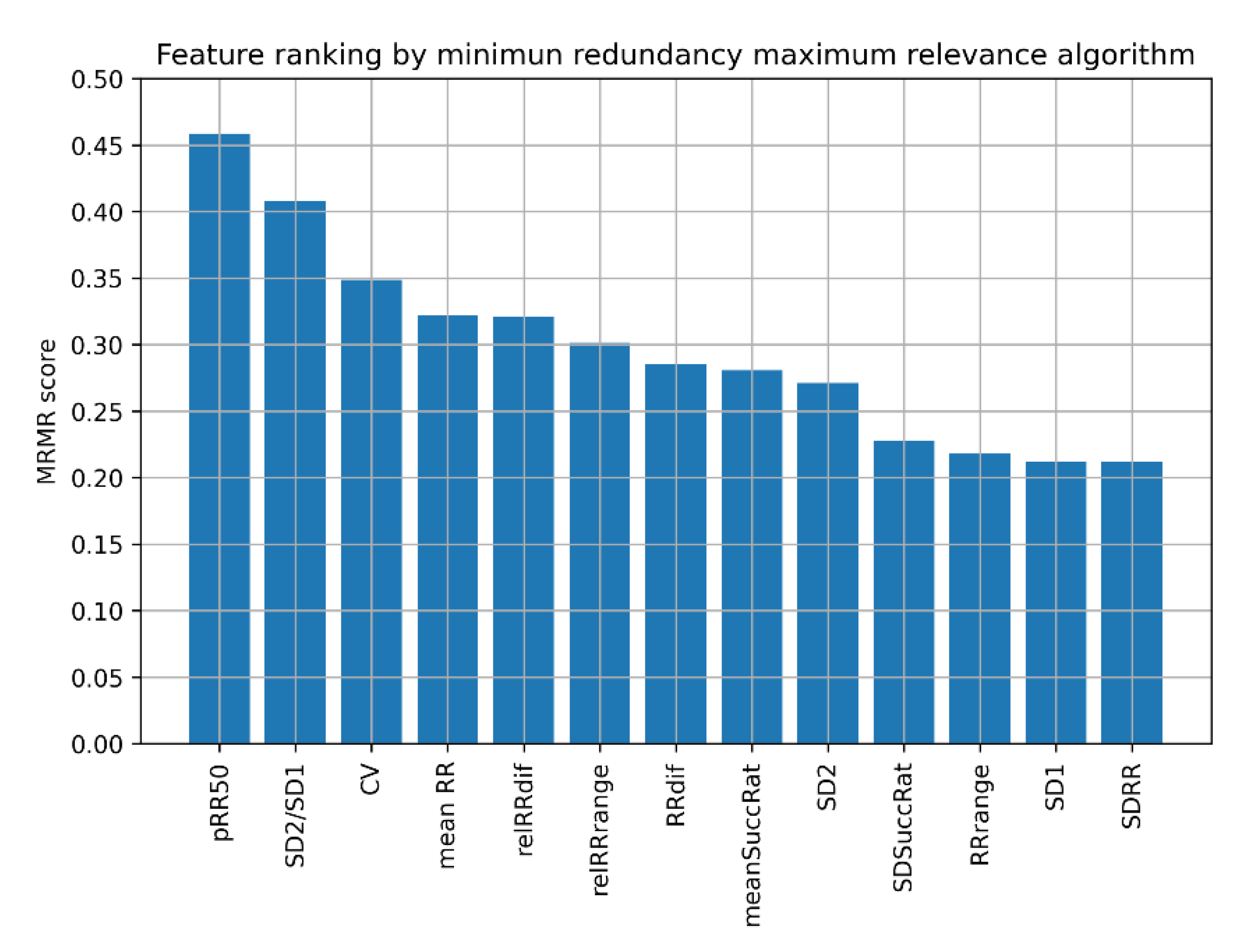
2.6. Feature Selection
2.7. Classification Algorithms
- Decision Tree (DT),
- K Nearest Neighbors (KNN),
- Support Vector Machine with the linear kernel (SVM linear),
- Support Vector Machine with radial basis function kernel (SVM RBF),
- Ada Boost (ADA),
- Random Forest (RF),
- Artificial Neural Network (ANN).
3. Results
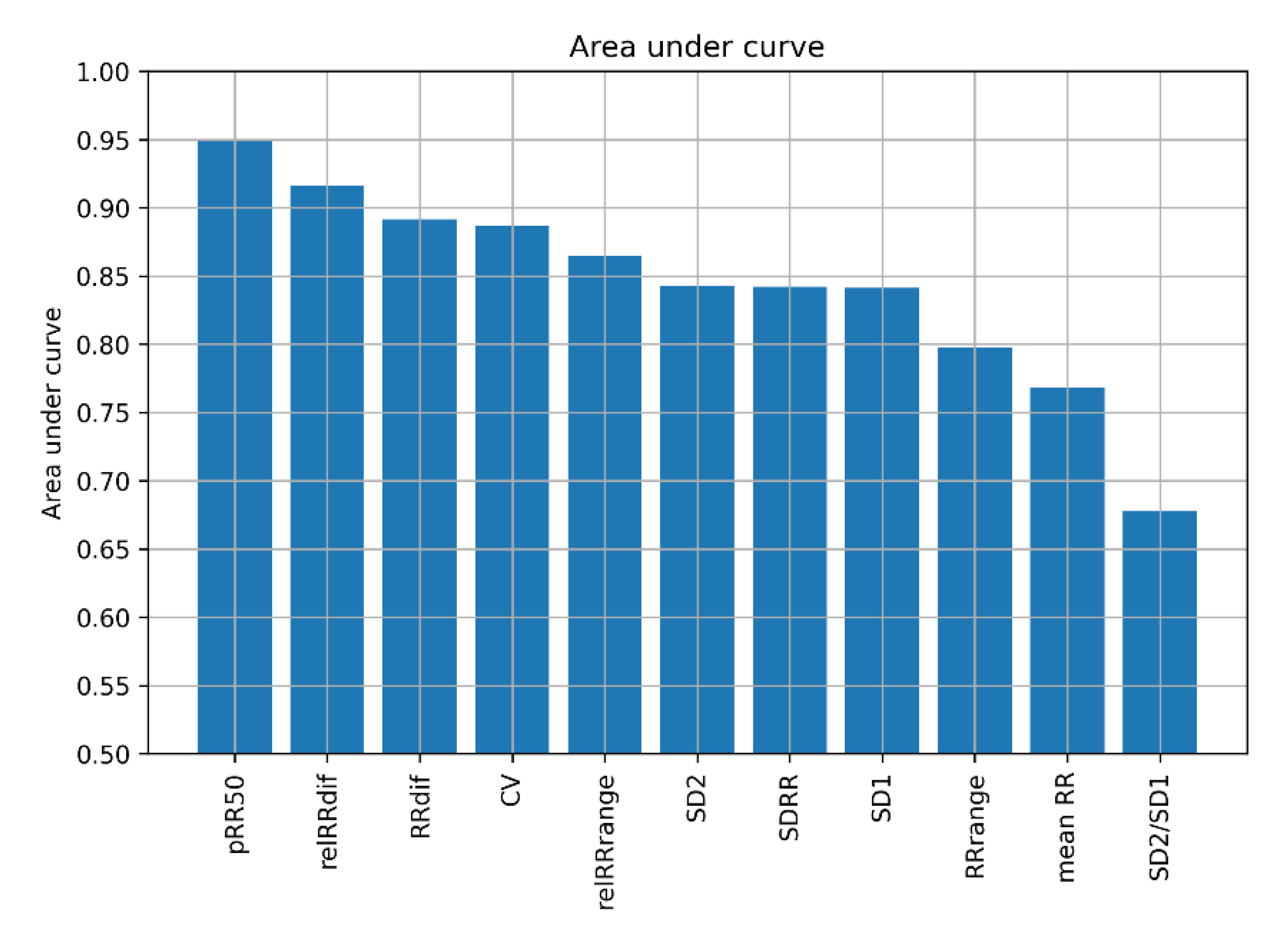
3.1. Feature Sets with pRR50
3.2. Feature Sets without pRR50
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kirchhoff, P.; Benussi, S.; Kotecha, D.; Ahlsson, A.; Atar, D.; Casadei, B. 2016 ESC Guidelines for the Management of Atrial Fibrillation Developed in Collaboration with EACTS. Eur. J. Cardio-Thorac. Surg. 2016, 50, e1–e88. [Google Scholar] [CrossRef] [PubMed]
- Hindricks, G.; Potpara, T.; Dagres, N.; Arbelo, E.; Bax, J.J.; Blomström-Lundqvist, C.; Boriani, G.; Castella, M.; Dan, G.A.; Dilaveris, P.E.; et al. 2020 ESC Guidelines for the Diagnosis and Management of Atrial Fibrillation Developed in Collaboration with the European Association for Cardio-Thoracic Surgery (EACTS) The Task Force for the Diagnosis and Management of Atrial Fibrillation of the European Society of Cardiology (ESC) Developed with the Special Contribution of the European Heart Rhythm Association (EHRA) of the ESC. Eur. Heart J. 2021, 42, 373–498. [Google Scholar] [CrossRef] [PubMed]
- Tonko, J.B.; Wright, M.J. Review of the 2020 ESC Guidelines for the Diagnosis and Management of Atrial Fibrillation—What Has Changed and How Does This Affect Daily Practice. J. Clin. Med. 2021, 10, 3922. [Google Scholar] [CrossRef] [PubMed]
- Magnussen, C.; Niiranen, T.J.; Ojeda, F.M.; Gianfagna, F.; Blankenberg, S.; Njølstad, I.; Vartiainen, E.; Sans, S.; Pasterkamp, G.; Hughes, M. Sex Differences and Similarities in Atrial Fibrillation Epidemiology, Risk Factors, and Mortality in Community Cohorts: Results from the BiomarCaRE Consortium (Biomarker for Cardiovascular Risk Assessment in Europe). Circulation 2017, 136, 1588–1597. [Google Scholar] [CrossRef] [Green Version]
- Sagnard, A.; Guenancia, C.; Mouhat, B.; Maza, M.; Fichot, M.; Moreau, D.; Garnier, F.; Lorgis, L.; Cottin, Y.; Zeller, M. Involvement of Autonomic Nervous System in New-Onset Atrial Fibrillation during Acute Myocardial Infarction. J. Clin. Med. 2020, 9, 1481. [Google Scholar] [CrossRef]
- Ble, M.; Benito, B.; Cuadrado-Godia, E.; Pérez-Fernández, S.; Gómez, M.; Mas-Stachurska, A.; Tizón-Marcos, H.; Molina, L.; Martí-Almor, J.; Cladellas, M. Left Atrium Assessment by Speckle Tracking Echocardiography in Cryptogenic Stroke: Seeking Silent Atrial Fibrillation. J. Clin. Med. 2021, 10, 3501. [Google Scholar] [CrossRef]
- Sörnmo, L.; Stridh, M.; Husser, D.; Bollmann, A.; Olsson, S.B. Analysis of Atrial Fibrillation: From Electrocardiogram Signal Processing to Clinical Management. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 235–253. [Google Scholar] [CrossRef] [Green Version]
- Langley, P.; Bourke, J.P.; Murray, A. Frequency Analysis of Atrial Fibrillation. In Proceedings of the Computers in Cardiology 2000 (Cat. 00CH37163), Cambridge, MA, USA, 24–27 September 2000; Volume 27, pp. 65–68. [Google Scholar] [CrossRef]
- Rieta, J.J.; Castells, F.; Sánchez, C.; Zarzoso, V.; Millet, J. Atrial Activity Extraction for Atrial Fibrillation Analysis Using Blind Source Separation. IEEE Trans. Biomed. Eng. 2004, 51, 1176–1186. [Google Scholar] [CrossRef] [Green Version]
- Alcaraz, R.; Rieta, J.J. Adaptive Singular Value Cancelation of Ventricular Activity in Single-Lead Atrial Fibrillation Electrocardiograms. Physiol. Meas. 2008, 29, 1351–1369. [Google Scholar] [CrossRef]
- Buś, S.; Jędrzejewski, K. Two Stage SVD-Based Method for QRST Waves Cancellation in Atrial Fibrillation Detection. In Proceedings of the 2019 Signal Processing Symposium (SPSympo), Krakow, Poland, 17–19 September 2019; pp. 24–28. [Google Scholar] [CrossRef]
- Heart Rate Variability: Standards of Measurement, Physiological Interpretation and Clinical Use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996, 93, 1043–1065. [CrossRef] [Green Version]
- Bauer, A.; Camm, A.J.; Cerutti, S.; Guzik, P.; Huikuri, H.; Lombardi, F.; Malik, M.; Peng, C.-K.; Porta, A.; Sassi, R. Reference Values of Heart Rate Variability. Heart Rhythm 2017, 14, 302–303. [Google Scholar] [CrossRef]
- Guzik, P.; Piskorski, J.; Barthel, P.; Bauer, A.; Müller, A.; Junk, N.; Ulm, K.; Malik, M.; Schmidt, G. Heart Rate Deceleration Runs for Postinfarction Risk Prediction. J. Electrocardiol. 2012, 45, 70–76. [Google Scholar] [CrossRef]
- Guzik, P.; Piekos, C.; Pierog, O.; Fenech, N.; Krauze, T.; Piskorski, J.; Wykretowicz, A. Classic Electrocardiogram-Based and Mobile Technology Derived Approaches to Heart Rate Variability Are Not Equivalent. Int. J. Cardiol. 2018, 258, 154–156. [Google Scholar] [CrossRef]
- Michel, P.; Ngo, N.; Pons, J.-F.; Delliaux, S.; Giorgi, R. A Filter Approach for Feature Selection in Classification: Application to Automatic Atrial Fibrillation Detection in Electrocardiogram Recordings. BMC Med. Inform. Decis. Mak. 2021, 21, 130. [Google Scholar] [CrossRef]
- Buś, S.; Jędrzejewski, K.; Guzik, P. A Study on Selection of HRV-based Features for Different Classifiers in Atrial Fibrillation Detection. In Proceedings of the 2021 Signal Processing Symposium (SPSympo), Lodz, Poland, 20–23 September 2021; pp. 31–34. [Google Scholar] [CrossRef]
- Boon, K.H.; Khalil-Hani, M.; Malarvili, M.B.; Sia, C.W. Paroxysmal Atrial Fibrillation Prediction Method with Shorter HRV Sequences. Comput. Methods Programs Biomed. 2016, 134, 187–196. [Google Scholar] [CrossRef]
- Mustaqeem, A.; Anwar, S.M.; Majid, M.; Khan, A.R. Wrapper Method for Feature Selection to Classify Cardiac Arrhythmia. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; pp. 3656–3659. [Google Scholar] [CrossRef]
- de Chazal, P.; Heneghan, C. Automated Assessment of Atrial Fibrillation. In Proceedings of the Computers in Cardiology 2001 (Cat. No.01CH37287), Rotterdam, The Netherlands, 23–26 September 2001; Volume 28, pp. 117–120. [Google Scholar] [CrossRef]
- Clifford, G.D.; Liu, C.; Moody, B.; Li-wei, H.L.; Silva, I.; Li, Q.; Johnson, A.E.; Mark, R.G. AF Classification from a Short Single Lead ECG Recording: The PhysioNet/Computing in Cardiology Challenge 2017. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Datta, S.; Puri, C.; Mukherjee, A.; Banerjee, R.; Dutta Choudhury, A.; Singh, R.; Ukil, A.; Bandyopadhyay, S.; Pal, A.; Khandelwal, S. Identifying Normal, AF and Other Abnormal ECG Rhythms Using a Cascaded Binary Classifier. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017. [Google Scholar]
- Jiménez Serrano, S.; Yagüe Mayans, J.; Simarro-Mondéjar, E.; Calvo, C.; Castells Ramon, F.; Roig, J. Atrial Fibrillation Detection Using Feedforward Neural Networks and Automatically Extracted Signal Features. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Zabihi, M.; Rad, A.B.; Katsaggelos, A.K.; Kiranyaz, S.; Narkilahti, S.; Gabbouj, M. Detection of Atrial Fibrillation in ECG Hand-Held Devices Using a Random Forest Classifier. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Krasteva, V.; Christov, I.; Naydenov, S.; Stoyanov, T.; Jekova, I. Application of Dense Neural Networks for Detection of Atrial Fibrillation and Ranking of Augmented ECG Feature Set. Sensors 2021, 21, 6848. [Google Scholar] [CrossRef]
- Christov, I.; Krasteva, V.; Simova, I.; Neycheva, T.; Schmid, R. Ranking of the Most Reliable Beat Morphology and Heart Rate Variability Features for the Detection of Atrial Fibrillation in Short Single-Lead ECG. Physiol. Meas. 2018, 39, 094005. [Google Scholar] [CrossRef]
- Shao, M.; Zhou, Z.; Bin, G.; Bai, Y.; Wu, S. A Wearable Electrocardiogram Telemonitoring System for Atrial Fibrillation Detection. Sensors 2020, 20, 606. [Google Scholar] [CrossRef] [Green Version]
- Parsi, A.; Glavin, M.; Jones, E.; Byrne, D. Prediction of Paroxysmal Atrial Fibrillation Using New Heart Rate Variability Features. Comput. Biol. Med. 2021, 133, 104367. [Google Scholar] [CrossRef]
- Biton, S.; Gendelman, S.; Ribeiro, A.H.; Miana, G.; Moreira, C.; Ribeiro, A.L.P.; Behar, J.A. Atrial Fibrillation Risk Prediction from the 12-Lead Electrocardiogram Using Digital Biomarkers and Deep Representation Learning. Eur. Heart J.-Digit. Health 2021, 2, 576–585. [Google Scholar] [CrossRef]
- Zhu, J.; Pu, Y.; Huang, H.; Wang, Y.; Li, X.; Yan, T. A Feature Selection-Based Algorithm for Detection of Atrial Fibrillation Using Short-Term ECG. J. Mech. Med. Biol. 2021, 21, 2140013. [Google Scholar] [CrossRef]
- Kotynia, M.M. Application for Atrial Fibrillation Classification Based on ECG Recordings. Bachelor’s Thesis, Warsaw University of Technology, Warsaw, Poland, 2021. [Google Scholar]
- Jiang, F.; Xu, B.; Zhu, Z.; Zhang, B. Topological Data Analysis Approach to Extract the Persistent Homology Features of Ballistocardiogram Signal in Unobstructive Atrial Fibrillation Detection. IEEE Sens. J. 2022, 22, 6920–6930. [Google Scholar] [CrossRef]
- Parsi, A.; Byrne, D.; Glavin, M.; Jones, E. Heart Rate Variability Feature Selection Method for Automated Prediction of Sudden Cardiac Death. Biomed. Signal Process. Control 2021, 65, 102310. [Google Scholar] [CrossRef]
- Oster, J.; Behar, J.; Colloca, R.; Li, Q.; Li, Q.; Clifford, G.D. Open Source Java-Based ECG Analysis Software and Android App for Atrial Fibrillation Screening. In Proceedings of the Computing in Cardiology 2013, Zaragoza, Spain, 22–25 September 2013; pp. 731–734. [Google Scholar]
- Mohebbi, M.; Ghassemian, H. Detection of Atrial Fibrillation Episodes Using SVM. IEEE Eng. Med. Biol. Soc. 2008, 2008, 177–180. [Google Scholar] [CrossRef]
- Sepulveda-Suescun, J.P.; Murillo-Escobar, J.; Urda-Benitez, R.D.; Orrego-Metaute, D.A.; Orozco-Duque, A. Atrial Fibrillation Detection through Heart Rate Variability Using a Machine Learning Approach and Poincare Plot Features. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Colombia, 26–28 October 2016; pp. 565–568. [Google Scholar] [CrossRef]
- Nguyen, A.; Ansari, S.; Hooshmand, M.; Lin, K.; Ghanbari, H.; Gryak, J.; Najarian, K. Comparative Study on Heart Rate Variability Analysis for Atrial Fibrillation Detection in Short Single-Lead ECG Recordings. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 526–529. [Google Scholar] [CrossRef]
- Mei, Z.; Gu, X.; Chen, H.; Chen, W. Automatic Atrial Fibrillation Detection Based on Heart Rate Variability and Spectral Features. IEEE Access 2018, 6, 53566–53575. [Google Scholar] [CrossRef]
- Kara, S.; Okandan, M. Atrial Fibrillation Classification with Artificial Neural Networks. Pattern Recognit. 2007, 40, 2967–2973. [Google Scholar] [CrossRef]
- Pourbabaee, B.; Roshtkhari, M.J.; Khorasani, K. Deep Convolutional Neural Networks and Learning ECG Features for Screening Paroxysmal Atrial Fibrillation Patients. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2095–2104. [Google Scholar] [CrossRef]
- Faust, O.; Shenfield, A.; Kareem, M.; San, T.R.; Fujita, H.; Acharya, U.R. Automated Detection of Atrial Fibrillation Using Long Short-Term Memory Network with RR Interval Signals. Comput. Biol. Med. 2018, 102, 327–335. [Google Scholar] [CrossRef] [Green Version]
- Malakhov, A.I.; Schookin, S.I.; Ivancov, V.I.; Tikhomirov, A.N. A Combined Algorithm for Identification and Differentiation of Atrial Flutter and Atrial Fibrillation Based on ECG Analysis. Biomed. Eng. 2013, 47, 14–17. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, J.; Liang, W.; Xue, J. Automated Classification of Atrial Fibrillation Using Artificial Neural Network for Wearable Devices. Math. Probl. Eng. 2020, 2020, 9159158. [Google Scholar] [CrossRef] [Green Version]
- Marsili, I.A.; Mase, M.; Pisetta, V.; Ricciardi, E.; Andrighetti, A.O.; Ravelli, F.; Nollo, G. Optimized Algorithms for Atrial Fibrillation Detection by Wearable Tele-Holter Devices. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Erdenebayar, U.; Kim, H.; Park, J.-U.; Kang, D.; Lee, K.-J. Automatic Prediction of Atrial Fibrillation Based on Convolutional Neural Network Using a Short-Term Normal Electrocardiogram Signal. J. Korean Med. Sci. 2019, 34, e64. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.; Afghah, F.; Acharya, U.R. HAN-ECG: An Interpretable Atrial Fibrillation Detection Model Using Hierarchical Attention Networks. Comput. Biol. Med. 2020, 127, 104057. [Google Scholar] [CrossRef] [PubMed]
- Faust, O.; Kareem, M.; Shenfield, A.; Ali, A.; Acharya, U.R.; Sheffield, B. Validating the Robustness of an Internet of Things Based Atrial Fibrillation Detection System. Pattern Recognit. Lett. 2020, 133, 55–61. [Google Scholar] [CrossRef]
- Peng, H.C.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Moody, G. A New Method for Detecting Atrial Fibrillation Using RR Intervals. Comput. Cardiol. 1983, 10, 227–230. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [Green Version]
- Petrutiu, S.; Sahakian, A.V.; Swiryn, S. Abrupt Changes in Fibrillatory Wave Characteristics at the Termination of Paroxysmal Atrial Fibrillation in Humans. Europace 2007, 9, 466–470. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2017; ISBN 978–0–387–84858–7. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine Learning Algorithm Validation with a Limited Sample Size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Walsh, I.; Pollastri, G.; Tosatto, S. Correct Machine Learning on Protein Sequences: A Peer-Reviewing Perspective. Brief. Bioinform. 2015, 17, 831–840. [Google Scholar] [CrossRef] [Green Version]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [Green Version]
- Guzik, P.; Piskorski, J.; Krauze, T.; Schneider, R.; Wesseling, K.H.; Wykretowicz, A.; Wysocki, H. Correlations between the Poincaré plot and conventional heart rate variability parameters assessed during paced breathing. J. Physiol. Sci. 2007, 57, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Kleiger, R.E.; Stein, P.K.; Bigger, J.T., Jr. Heart Rate Variability: Measurement and Clinical Utility. Ann. Noninvasive Electrocardiol. 2005, 10, 88–101. [Google Scholar] [CrossRef]
- Rizwan, A.; Zoha, A.; Mabrouk, I.B.; Sabbour, H.M.; Al-Sumaiti, A.S.; Alomainy, A.; Imran, M.A.; Abbasi, Q.H. A Review on the State of the Art in Atrial Fibrillation Detection Enabled by Machine Learning. IEEE Rev. Biomed. Eng. 2020, 14, 219–239. [Google Scholar] [CrossRef] [Green Version]
- Bolon-Candedo, V.; Alonso-Betanzos, A. Recent Advances in Ensembles for Feature Selection; Springer: Heidelberg, Germany, 2018. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Glas, A.S.; Lijmer, J.G.; Prins, M.H.; Bonsel, G.J.; Bossuyt, P.M.M. The Diagnostic Odds Ratio: A Single Indicator of Test Performance. J. Clin. Epidemiol. 2003, 56, 1129–1135. [Google Scholar] [CrossRef]
- Mitrega, K.; Lip, G.Y.; Sredniawa, B.; Sokal, A.; Streb, W.; Przyludzki, K.; Zdrojewski, T.; Wierucki, L.; Rutkowski, M.; Bandosz, P. Predicting Silent Atrial Fibrillation in the Elderly: A Report from the NOMED-AF Cross-Sectional Study. J. Clin. Med. 2021, 10, 2321. [Google Scholar] [CrossRef]
- Boriani, G.; Palmisano, P.; Malavasi, V.L.; Fantecchi, E.; Vitolo, M.; Bonini, N.; Imberti, J.F.; Valenti, A.C.; Schnabel, R.B.; Freedman, B. Clinical Factors Associated with Atrial Fibrillation Detection on Single-Time Point Screening Using a Hand-Held Single-Lead ECG Device. J. Clin. Med. 2021, 10, 729. [Google Scholar] [CrossRef]
- Guzik, P.; Malik, M. ECG by Mobile Technologies. J. Electrocardiol. 2016, 49, 894–901. [Google Scholar] [CrossRef] [PubMed]
- Roten, L.; Goulouti, E.; Lam, A.; Elchinova, E.; Nozica, N.; Spirito, A.; Wittmer, S.; Branca, M.; Servatius, H.; Noti, F. Age and Sex Specific Prevalence of Clinical and Screen-Detected Atrial Fibrillation in Hospitalized Patients. J. Clin. Med. 2021, 10, 4871. [Google Scholar] [CrossRef]
- Jin, H.; Abu-Raya, Y.S.; Haick, H. Advanced Materials for Health Monitoring with Skin-Based Wearable Devices. Adv. Healthc. Mater. 2017, 6, 1700024. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, M.; Prymas, P.; Konobrodzka, A.; Filberek, P.; Sibrecht, G.; Sierocki, W.; Osinska, Z.; Wykretowicz, A.; Lobodzinski, S.; Guzik, P. Clinical Stage of Acquired Immunodeficiency Syndrome in HIV-Positive Patients Impacts the Quality of the Touch ECG Recordings. J. Electrocardiol. 2019, 55, 87–90. [Google Scholar] [CrossRef]
- Tsukada, S.; Nakashima, H.; Torimitsu, K. Conductive Polymer Combined Silk Fiber Bundle for Bioelectrical Signal Recording. PLoS ONE 2012, 7, e33689. [Google Scholar] [CrossRef] [Green Version]
- Yapici, M.K.; Alkhidir, T.E. Intelligent Medical Garments with Graphene-Functionalized Smart-Cloth ECG Sensors. Sensors 2017, 17, 875. [Google Scholar] [CrossRef] [Green Version]
- Cvach, M.M.; Biggs, M.; Rothwell, K.J.; Charles-Hudson, C. Daily Electrode Change and Effect on Cardiac Monitor Alarms: An Evidence-Based Practice Approach. J. Nurs. Care Qual. 2013, 28, 265–271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, Y.; Wang, M.; Li, Y.; Sun, Z.; Liu, Z.; He, L.; Liu, R. High-Adhesive Flexible Electrodes and Their Manufacture: A Review. Micromachines 2021, 12, 1505. [Google Scholar] [CrossRef] [PubMed]
- Attia, Z.I.; Noseworthy, P.A.; Lopez-Jimenez, F.; Asirvatham, S.J.; Deshmukh, A.J.; Gersh, B.J.; Carter, R.E.; Yao, X.; Rabinstein, A.A.; Erickson, B.J. An Artificial Intelligence-Enabled ECG Algorithm for the Identification of Patients with Atrial Fibrillation during Sinus Rhythm: A Retrospective Analysis of Outcome Prediction. Lancet 2019, 394, 861–867. [Google Scholar] [PubMed]
- Khurshid, S.; Friedman, S.; Reeder, C.; Di Achille, P.; Diamant, N.; Singh, P.; Harrington, L.X.; Wang, X.; Al-Alusi, M.A.; Sarma, G. ECG-Based Deep Learning and Clinical Risk Factors to Predict Atrial Fibrillation. Circulation 2022, 145, 122–133. [Google Scholar] [CrossRef]
- Attia, Z.I.; Harmon, D.M.; Behr, E.R.; Friedman, P.A. Application of Artificial Intelligence to the Electrocardiogram. Eur. Heart J. 2021, 42, 4717–4730. [Google Scholar] [CrossRef]
- Bauer, A.; Malik, M.; Schmidt, G.; Barthel, P.; Bonnemeier, H.; Cygankiewicz, I.; Guzik, P.; Lombardi, F.; Müller, A.; Oto, A. Heart Rate Turbulence: Standards of Measurement, Physiological Interpretation, and Clinical Use: International Society for Holter and Noninvasive Electrophysiology Consensus. J. Am. Coll. Cardiol. 2008, 52, 1353–1365. [Google Scholar] [CrossRef] [Green Version]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.-K.; Schmidt, G.; Yamamoto, Y.; Reviewers, D.; Gorenek, B. Advances in Heart Rate Variability Signal Analysis: Joint Position Statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association Co-Endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef]
- Cygankiewicz, I.; Zareba, W.; Vazquez, R.; Bayes-Genis, A.; Pascual, D.; Macaya, C.; Almendral, J.; Fiol, M.; Bardaji, A.; Gonzalez-Juanatey, J.R. Risk Stratification of Mortality in Patients with Heart Failure and Left Ventricular Ejection Fraction > 35%. Am. J. Cardiol. 2009, 103, 1003–1010. [Google Scholar] [CrossRef]










| Reference | Dataset | Accuracy [%] | Sensitivity [%] | Specificity [%] | Classifier | Notes |
|---|---|---|---|---|---|---|
| Parsi et al., 2021 [28] | Physionet Atrial Fibrillation Prediction Database | 97.7 | 98.8 | 96.7 | SVM (also MLP, RF, KNN) | 5 min ECG segments, established and new HRV parameters, the distinction between SR and rhythm just before the onset of AF. 10-fold cross-validation (by the patient). |
| Biton et al., 2021 [29] | Telehealth Network of Minas Gerais (TNMG) database | - | 59.6 | 95.3 | RF | DNN features from a raw 12-lead ECG (7–10 s), morphology, HRV, EMR metadata. Prediction of developing AF within 5 years. |
| Zhu et al., 2021 [30] | 13,354 short-term ECG segments | 90.46 | 94.04 | 86.74 | ANN | 10 s ECG, seven classes (rhythms). Feature selection: correlation with label, MRMR, Fisher criterion. |
| Jiang et al., 2022 [32] | Own BCG database | 94.50 | 96.70 | 92.62 | SVM (also KNB, LR, RF, BT) | 24 s BCG signal, MRMR feature selection, 10-fold CV |
| Oster et al., 2013 [34] | AFDB | - | 92.7 | 94.2 | RR entropy threshold | Length: 12 RR intervals, features: coefficient of sample entropy. |
| Mohebbi et al., 2008 [35] | MIT-BIH Arrhythmia Database | - | 99.07 | 100 | SVM | HRV from 32 RR, feature selection with LDA |
| Sepulveda-Suescun et al., 2017 [36] | AFDB | 97.8 | 97.9 | 97.8 | SVM | Poincare plot-based HRV. Only 226 AF and 264 SR segments. |
| Nguyen et al., 2018 [37] | 2017 PhysioNet/Computers in Cardiology Challenge Database | 95.15 | - | - | SVM | 30–60 s recordings, HRV |
| Mei et al., 2018 [38] | 2017 PhysioNet/Computers in Cardiology Challenge Database | 96.6 | 83.2 | 98.6 | BT | 30–60 s recordings, HRV, and frequency analysis |
| Pourbabaee et al., 2018 [40] | Physionet PAF prediction challenge database | 91 | - | - | KNN (and other classifiers) | Neural network-extracted features. |
| Faust et al., 2018 [41] | AFDB | 99.77 | 99.87 | 99.61 | RNN | Sequence of 100 RR intervals |
| Ma et al., 2020 [43] | MIT-BIH Arrhythmia Database | 98.3 | 97.4 | 99.3 | Shallow ANN | RR interval series as features, not specified how long. |
| Marsili et al., 2016 [44] | AFDB | 98.44 | 97.33 | 98.67 | Symbolic dynamics, threshold | Beat-by-beat classification based on RR intervals (symbolic dynamics). |
| Erdenebayar et al., 2019 [45] | AFDB, MIT-BIH Normal Sinus Rhythm Database | 98.7 | 98.7 | 98.6 | CNN | 30 s segments, CNN features from raw ECG, training/test division not specified. |
| Mousavi et al., 2020 [46] | AFDB | 82.41 | 90.53 | 79.54 | Bidirectional RNN | 5 s RR interval sequence |
| Faust el al., 2020 [47] | AFDB, LTAFDB | 94 | RNN | 100 RR sequence, blindfold validation on LTAFDB |
| Dataset | AF Total | AF Filtered | SR Total | SR Filtered |
|---|---|---|---|---|
| Training | 27,630 | 26,464 | 27,823 | 27,311 |
| Test | 11,191 | 11,167 | 25,461 | 14,294 |
| No. of Features | Feature Set |
|---|---|
| 1 | pRR50 |
| 2 | pRR50, SD2/SD1, |
| 3 | pRR50, SD2/SD1, CV |
| 4 | pRR50, SD2/SD1, CV, mean RR |
| 5 | pRR50, SD2/SD1, CV, mean RR, relRRdif |
| 6 | pRR50, SD2/SD1, CV, mean RR, relRRdif, relRRrange |
| Features | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Classifier | |||||||
| DT | 92.29 (0.27) | 94.06 (0.27) | 95.15 (0.15) | 96.65 (0.13) | 96.84 (0.10) | 97.16 (0.09) | |
| KNN | 92.00 (0.38) | 94.20 (0.32) | 95.32 (0.19) | 97.18 (0.13) | 97.53 (0.14) | 97.90 (0.12) | |
| SVM linear | 91.91 (0.35) | 91.93 (0.34) | 91.92 (0.31) | 95.00 (0.16) | 95.04 (0.16) | 95.08 (0.16) | |
| SVM RBF | 91.99 (0.34) | 94.26 (0.31) | 95.45 (0.11) | 97.25 (0.07) | 97.87 (0.13) | 98.06 (0.10) | |
| ADA | 92.01 (0.35) | 93.28 (0.40) | 93.18 (0.37) | 95.21 (0.23) | 95.24 (0.26) | 95.19 (0.23) | |
| RF | 92.40 (0.32) | 94.26 (0.26) | 95.42 (0.13) | 97.24 (0.15) | 97.57 (0.09) | 97.88 (0.13) | |
| ANN | 91.89 (0.30) | 94.32 (0.36) | 95.20 (0.11) | 96.79 (0.21) | 97.16 (0.29) | 97.48 (0.23) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buś, S.; Jędrzejewski, K.; Guzik, P. Using Minimum Redundancy Maximum Relevance Algorithm to Select Minimal Sets of Heart Rate Variability Parameters for Atrial Fibrillation Detection. J. Clin. Med. 2022, 11, 4004. https://doi.org/10.3390/jcm11144004
Buś S, Jędrzejewski K, Guzik P. Using Minimum Redundancy Maximum Relevance Algorithm to Select Minimal Sets of Heart Rate Variability Parameters for Atrial Fibrillation Detection. Journal of Clinical Medicine. 2022; 11(14):4004. https://doi.org/10.3390/jcm11144004
Chicago/Turabian StyleBuś, Szymon, Konrad Jędrzejewski, and Przemysław Guzik. 2022. "Using Minimum Redundancy Maximum Relevance Algorithm to Select Minimal Sets of Heart Rate Variability Parameters for Atrial Fibrillation Detection" Journal of Clinical Medicine 11, no. 14: 4004. https://doi.org/10.3390/jcm11144004
APA StyleBuś, S., Jędrzejewski, K., & Guzik, P. (2022). Using Minimum Redundancy Maximum Relevance Algorithm to Select Minimal Sets of Heart Rate Variability Parameters for Atrial Fibrillation Detection. Journal of Clinical Medicine, 11(14), 4004. https://doi.org/10.3390/jcm11144004







