Comparison of In-Vivo and Ex-Vivo Ascending Aorta Elastic Properties through Automatic Deep Learning Segmentation of Cine-MRI and Biomechanical Testing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Related Work
2.2. Clinical Background
2.2.1. Aortic Compliance
2.2.2. Young’s Modulus and Strain
2.3. Data
2.3.1. In-Vivo Data: Magnetic Resonance Imaging (MRI)
2.3.2. Ex-Vivo Data
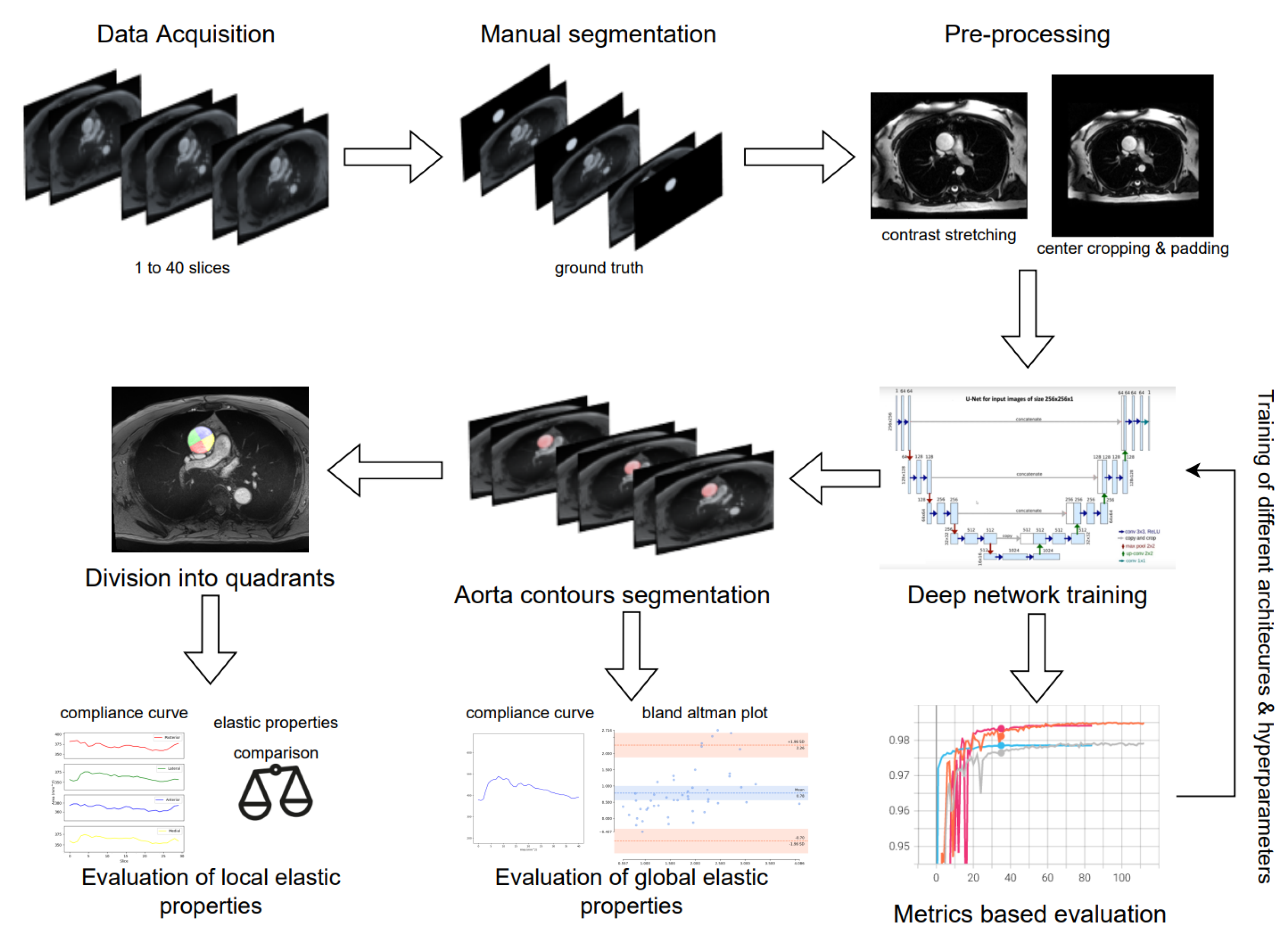
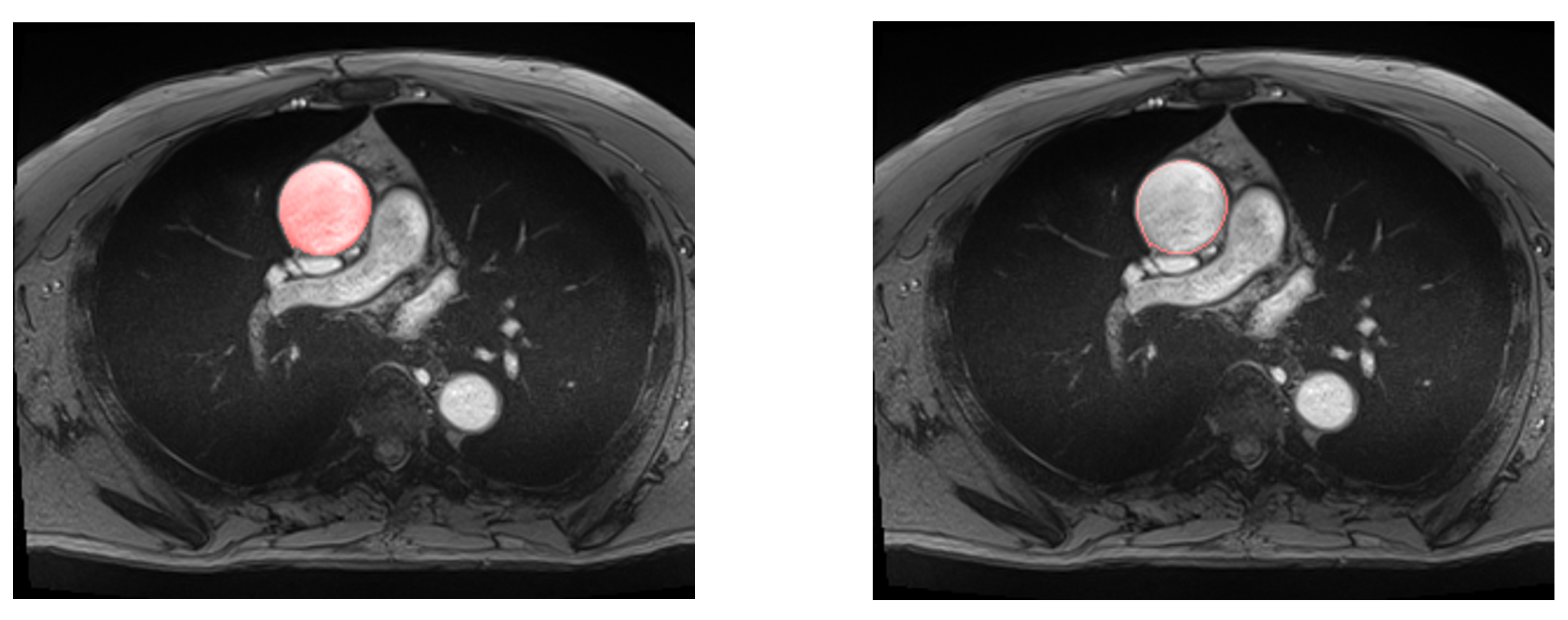
2.4. Deep Learning Segmentation and In-Vivo Elasticity Assessment
2.4.1. Preprocessing
2.4.2. Data Augmentation
2.4.3. Fully Convolutional Networks and U-Net
2.4.4. Training
3. Results
3.1. Evaluation of Deep Learning Models
3.2. Global Elastic Properties’ Evaluation
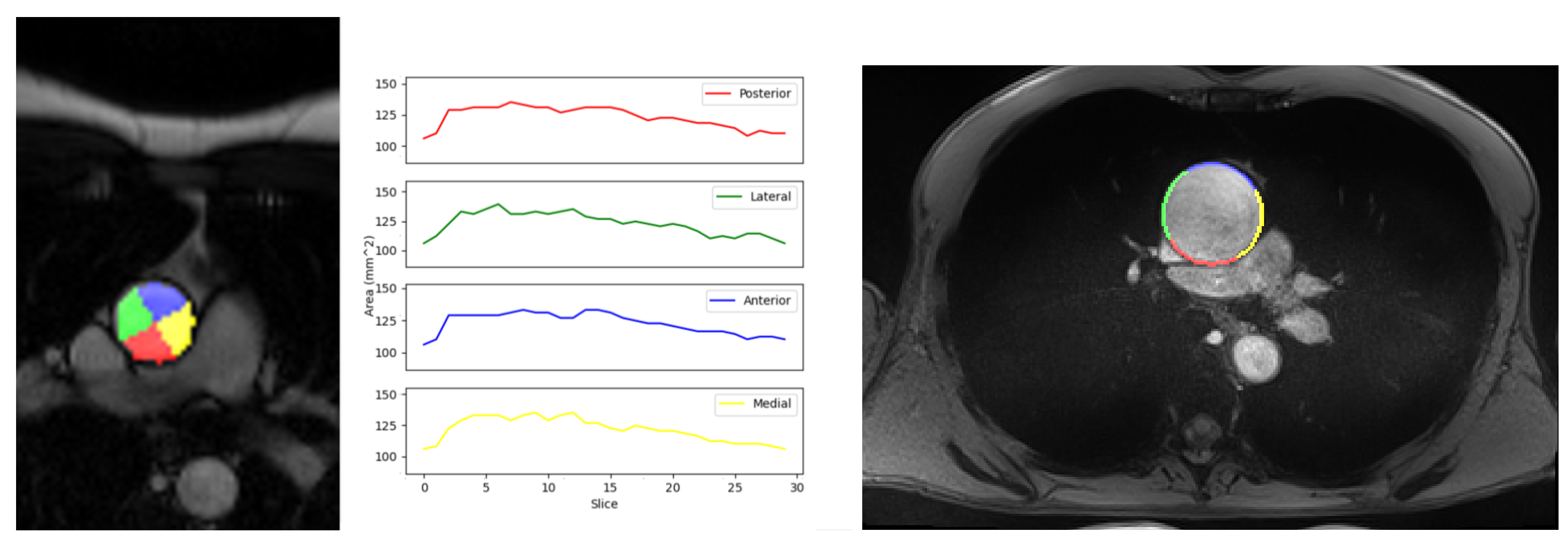
3.3. Local Elastic Properties’ Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRI | Magnetic Resonance Imaging |
| CMRI | Cardiac Magnetic Resonance Imaging |
| 2D | Two Dimensional |
| DL | Deep Learning |
| IoU | Intersection over Union |
| SSFP | Steady State Free Precession |
| GRAPPA | GeneRalized Auto-calibrating Partially Parallel Acquisitions |
| RNN | Recurrent Neural Networks |
| ReLu | Rectified Linear Unit |
| ADAM | Adaptive Moment Estimation |
| TP | True Positive |
| FP | False Positive |
| FN | False Negative |
References
- Xodo, A.; Gallo, A.; Magagna, P.; D’Oria, M. Acute Aortic Syndromes and Thoracic Aortic Aneurysms: From Diagnosis to Treatment. In Primary Management in General, Vascular and Thoracic Surgery: A Practical Approach; Bissacco, D., Settembrini, A.M., Mazzari, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 81–95. [Google Scholar] [CrossRef]
- Hagan, P.G.; Nienaber, C.A.; Isselbacher, E.M.; Bruckman, D.; Karavite, D.J.; Russman, P.L.; Evangelista, A.; Fattori, R.; Suzuki, T.; Oh, J.K.; et al. The International Registry of Acute Aortic Dissection (IRAD). New Insights Into an Old Disease. JAMA 2000, 283, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Umebayashi, R.; Uchida, H.A.; Wada, J. Abdominal aortic aneurysm in aged population. Aging 2018, 10, 3650–3651. [Google Scholar] [CrossRef] [PubMed]
- Isselbacher, E.M. Thoracic and Abdominal Aortic Aneurysms. Circulation 2005, 111, 816–828. [Google Scholar] [CrossRef] [Green Version]
- Daily, P.O.; Trueblood, H.W.; Stinson, E.B.; Wuerflein, R.D.; Shumway, N.E. Management of Acute Aortic Dissections. Ann. Thorac. Surg. 1970, 10, 237–247. [Google Scholar] [CrossRef]
- Erbel, R.; Aboyans, V.; Boileau, C.; Bossone, E.; Bartolomeo, R.D.; Eggebrecht, H.; Evangelista, A.; Falk, V.; Frank, H.; Gaemperli, O.; et al. 2014 ESC Guidelines on the diagnosis and treatment of aortic diseases: Document covering acute and chronic aortic diseases of the thoracic and abdominal aorta of the adult The Task Force for the Diagnosis and Treatment of Aortic Diseases of the European Society of Cardiology ESC. Eur. Heart J. 2014, 35, 2873–2926. [Google Scholar]
- Kim, E.K.; Choi, S.H.; Sung, K.; Kim, W.S.; Choe, Y.H.; Oh, J.K.; Kim, D.K. Aortic diameter predicts acute type A aortic dissection in patients with Marfan syndrome but not in patients without Marfan syndrome. J. Thorac. Cardiovasc. Surg. 2014, 147, 1505–1510. [Google Scholar] [CrossRef] [Green Version]
- Pape, L.A.; Tsai, T.T.; Isselbacher, E.M.; Oh, J.K.; O’Gara, P.T.; Evangelista, A.; Fattori, R.; Meinhardt, G.; Trimarchi, S.; Bossone, E.; et al. Aortic diameter ≥ 5.5 cm is not a good predictor of type A aortic dissection: Observations from the International Registry of Acute Aortic Dissection (IRAD). Circulation 2007, 116, 1120–1127. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Morgant, M.C.; Marín-Castrillón, D.M.; Walker, P.M.; Glélé, L.S.A.; Boucher, A.; Presles, B.; Bouchot, O.; Lalande, A. Aortic local biomechanical properties in ascending aortic aneurysms. Acta Biomater. 2022, 149, 40–50. [Google Scholar] [CrossRef]
- Bulychev, S.; Alekhin, V.; Shorshorov, M.K.; Ternovskij, A.; Shnyrev, G. Determination of Young modulus by the hardness indentation diagram. Zavod. Lab. 1975, 41, 1137–1140. [Google Scholar]
- O’Rourke, M.F.; Staessen, J.A.; Vlachopoulos, C.; Duprez, D.; Plante, G.E. Clinical applications of arterial stiffness; definitions and reference values. Am. J. Hypertens. 2002, 15, 426–444. [Google Scholar] [CrossRef]
- Morgant, M.C.; Lin, S.; Marin-Castrillon, D.; Bernard, C.; Laubriet, A.; Cochet, A.; Lalande, A.; Bouchot, O. Comparison of two techniques (in vivo and ex-vivo) for evaluating the elastic properties of the ascending aorta: Prospective cohort study. PLoS ONE 2021, 16, e0256278. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, M.P.; Biederman, R.W. Cardiac MRI. Med. Clin. N. Am. 2015, 99, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, E.D. Clinical value of aortic pulse-wave velocity measurement. Lancet 1999, 354, 528–529. [Google Scholar] [CrossRef]
- Belz, G.G. Elastic properties and Windkessel function of the human aorta. Cardiovasc. Drugs Ther. 1995, 9, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Lalande, A.; van Kien, P.K.; Salve, N.; SALEM, D.B.; Legrand, L.; Walker, P.M.; Wolf, J.E.; Brunotte, F. Automatic determination of aortic compliance with cine-magnetic resonance imaging: An application of fuzzy logic theory. Investig. Radiol. 2002, 37, 685–691. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.L.; Lalande, A.; Bouchot, O.; Bourennane, E.B.; Walker, P.M.; Ugolini, P.; Revol-Muller, C.; Cartier, R.; Brunotte, F. Influence of age and sex on aortic distensibility assessed by MRI in healthy subjects. Magn. Reson. Imaging 2010, 28, 255–263. [Google Scholar] [CrossRef]
- Rose, J.L.; Lalande, A.; Bourennane, E.B.; Walker, P.M.; Bouchot, O.; Steinmetz, E.; Legrand, L.; Voisin, Y.; Wolf, Y.; Brunotte, F. Automatic detection of vessel wall contours from cine-MRI for aortic compliance determination. In Proceedings of the Computers in Cardiology, Lyon, France, 25–28 September 2005; pp. 411–414. [Google Scholar]
- Krug, R.; Boese, J.M.; Schad, L.R. Determination of aortic compliance from magnetic resonance images using an automatic active contour model. Phys. Med. Biol. 2003, 48, 2391. [Google Scholar] [CrossRef]
- Mitéran, J.; Bouchot, O.; Cochet, A.; Lalande, A. Automatic determination of aortic compliance based on MRI and adapted curvilinear detector. Biomed. Signal Process. Control 2018, 40, 295–311. [Google Scholar] [CrossRef]
- Fung, Y.C. What are the residual stresses doing in our blood vessels? Ann. Biomed. Eng. 1991, 19, 237–249. [Google Scholar] [CrossRef]
- Agache, P.G.; Monneur, C.; Leveque, J.L.; Rigal, J.D. Mechanical properties and Young’s modulus of human skin in vivo. Arch. Dermatol. Res. 1980, 269, 221–232. [Google Scholar] [CrossRef]
- Sjontoft, E.; Edmund, C. Determination of young’s modulus for the human cornea. Bull. Math. Biol. 1987, 49, 217–232. [Google Scholar] [CrossRef] [PubMed]
- Kinney, J.; Balooch, M.; Marshall, S.; Marshall, G.; Weihs, T. Hardness and young’s modulus of human peritubular and intertubular dentine. Arch. Oral Biol. 1996, 41, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Harris, E.H.; Walker, L.B.; Bass, B.R. Stress-strain studies in cadaveric human tendon and an anomaly in the young’s modulus thereof. Med. Biolog. Eng. 1966, 4, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Duprey, A.; Khanafer, K.; Schlicht, M.; Avril, S.; Williams, D.; Berguer, R. In Vitro Characterisation of Physiological and Maximum Elastic Modulus of Ascending Thoracic Aortic Aneurysms Using Uniaxial Tensile Testing. Eur. J. Vasc. Endovasc. Surg. 2010, 39, 700–707. [Google Scholar] [CrossRef] [Green Version]
- Iliopoulos, D.C.; Deveja, R.P.; Kritharis, E.P.; Perrea, D.; Sionis, G.D.; Toutouzas, K.; Stefanadis, C.; Sokolis, D.P. Regional and directional variations in the mechanical properties of ascending thoracic aortic aneurysms. Med. Eng. Phys. 2009, 31, 1–9. [Google Scholar] [CrossRef]
- Xuan, Y.; Wisneski, A.D.; Wang, Z.; Lum, M.; Kumar, S.; Pallone, J.; Flores, N.; Inman, J.; Lai, L.; Lin, J.; et al. Regional biomechanical and failure properties of healthy human ascending aorta and root. J. Mech. Behav. Biomed. Mater. 2021, 123, 104705. [Google Scholar] [CrossRef]
- Chung, J.C.Y.; Wong, E.; Tang, M.; Eliathamby, D.; Forbes, T.L.; Butany, J.; Simmons, C.A.; Ouzounian, M. Biomechanics of Aortic Dissection: A Comparison of Aortas Associated With Bicuspid and Tricuspid Aortic Valves. J. Am. Heart Assoc. 2020, 9, e016715. [Google Scholar] [CrossRef] [PubMed]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: New York, NY, USA, 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef] [Green Version]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.C.H.; Heinrich, M.P.; Misawa, K.; Mori, K.; McDonagh, S.G.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Chen, X.; Yao, L.; Zhang, Y. Residual Attention U-Net for Automated Multi-Class Segmentation of COVID-19 Chest CT Images. arXiv 2020, arXiv:2004.05645. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Alom, M.Z.; Hasan, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Recurrent Residual Convolutional Neural Network based on U-Net (R2U-Net) for Medical Image Segmentation. arXiv 2018, arXiv:1802.06955. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Squizzato, F.; Antonello, M.; Forcella, E.; Coppadoro, S.; Colacchio, C.; Xodo, A.; Grego, F.; Piazza, M. Geometrical determinants of target vessel instability in fenestrated endovascular aortic repair. J. Vasc. Sur. 2022, 76, 335–343.e2. [Google Scholar] [CrossRef] [PubMed]

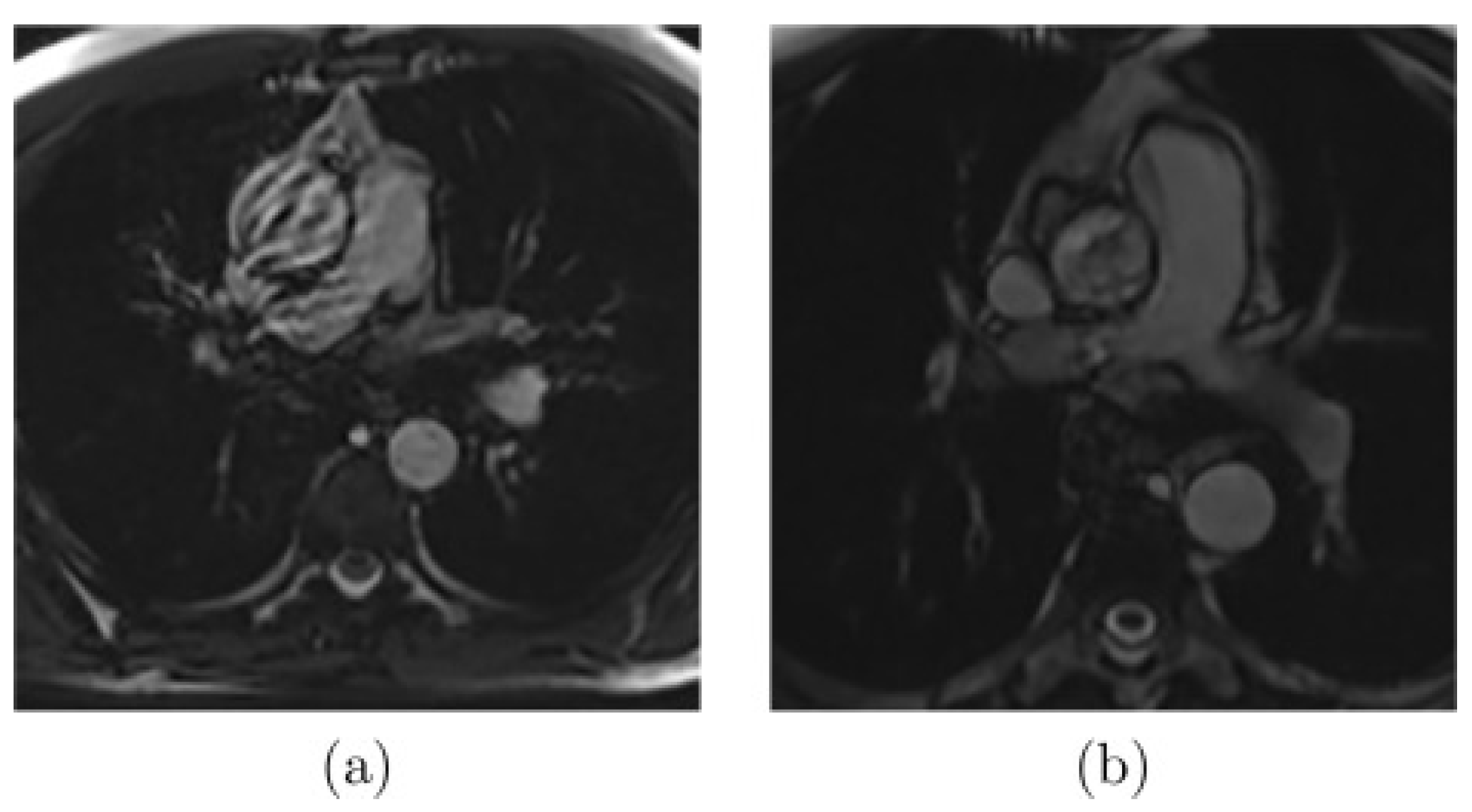
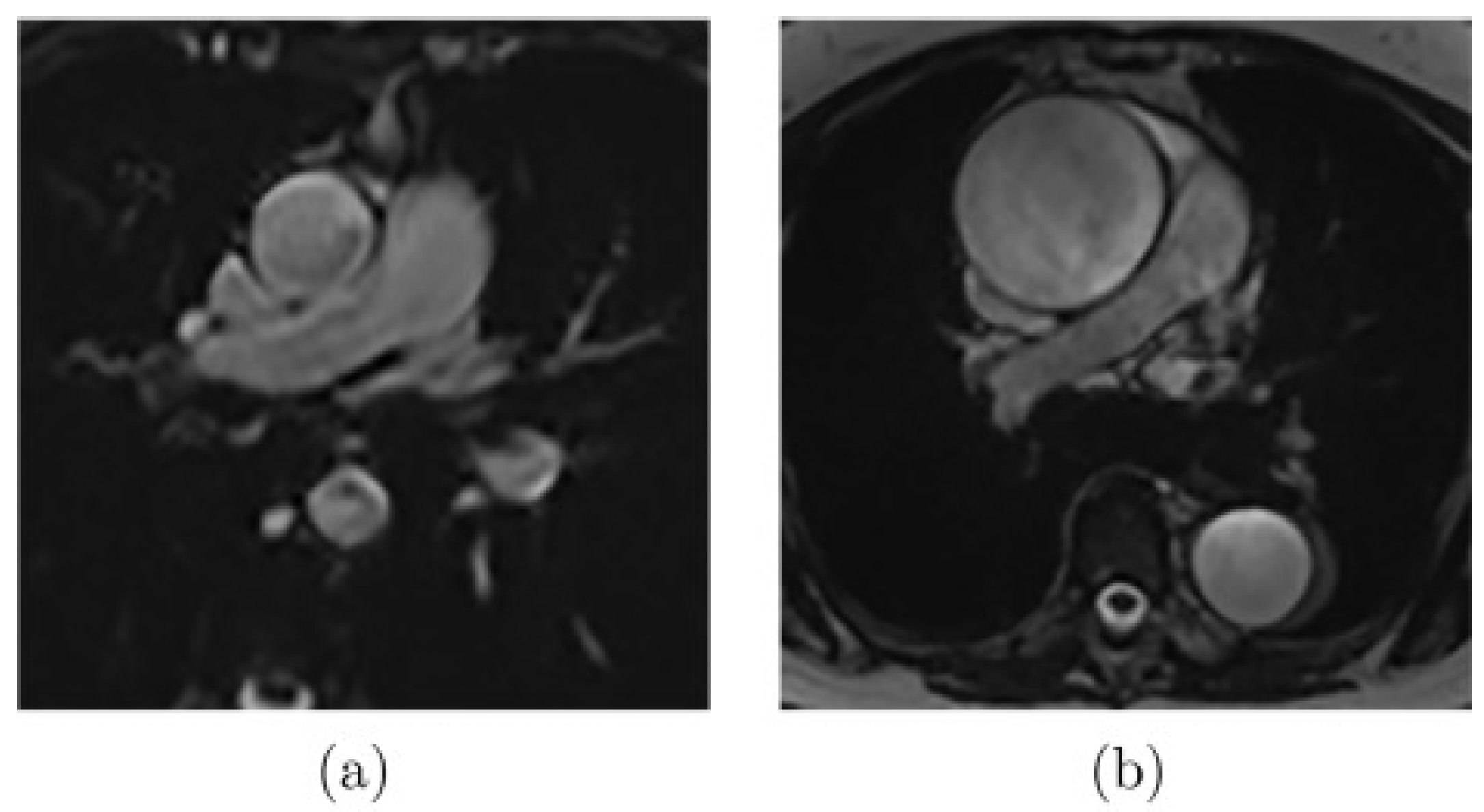


| Early stopping patience | 1 | 2 | 4 | 8 | 16 |
| Starting learning rate | 0.1 | 0.01 | 0.001 | 0.0001 | |
| Loss function | Dice Loss | Focal Loss | Tversky Loss | ||
| Layer Normalization | Batch | Instance | Group |
| Model | Dice Coeff Mean ± Std. Dev. | IoU Mean ± Std. Dev. | Hausdorff Mean ± Std. Dev. (mm) | Precision Mean ± Std. Dev. | Recall Mean ± Std. Dev. |
|---|---|---|---|---|---|
| U-Net | 98.09% (±0.96%) | 96.27% (±1.83%) | 4.88 (±1.70) | 98.47% (±1.45%) | 97.80% (±1.74%) |
| Res-U-Net | 98.09% (±0.88%) | 96.26% (±1.68%) | 4.91 (±1.74) | 98.28% (±1.53%) | 97.99% (±1.54%) |
| Att-U-Net | 97.64% (±1.61%) | 95.43% (±2.85%) | 5.66 (±2.01) | 98.62% (±1.15%) | 96.83% (±3.01%) |
| Att-Res-U-Net | 98.03% (±0.78%) | 96.14% (±1.47%) | 5.24 (±1.72) | 98.14% (±1.27%) | 97.99% (±1.64%) |
| Correlation (p-Value) | Mean Difference ± Std. Dev. | |
|---|---|---|
| Minimum area | 0.99 (<0.05) | 36.85 mm (±52.38) |
| Maximum area | 0.99 (<0.05) | 63.13 mm (±50.22) |
| Compliance | 0.79 (<0.05) | 0.48 mm/mmHg (±0.54) |
| Quadrants | Medial | Anterior | Lateral | Posterior |
|---|---|---|---|---|
| Compliance Mean ± Std. Dev. (mm/mmHg) | 0.511 (±0.25) | 0.462 (±0.19) | 0.534 (±0.21) | 0.491 (±0.18) |
| In-vivo Strain Mean ± Std. Dev. | 0.086 (±0.03) | 0.072 (±0.02) | 0.097 (±0.03) | 0.095 (±0.04) |
| Maximum Young’s Modulus Mean ± Std. Dev. (MPa) [9] | 0.622 (±0.19) | 0.768 (±0.24) | 1.208 (±0.47) | 0.993 (±0.31) |
| Physiological Young’s Modulus Mean ± Std. Dev. (MPa) | 0.354 (±0.13) | 0.362 (±0.15) | 0.411 (±0.13) | 0.419 (±0.15) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markodimitrakis, E.; Lin, S.; Koutoulakis, E.; Marín-Castrillón, D.M.; Tovar Sáez, F.A.; Leclerc, S.; Bernard, C.; Boucher, A.; Presles, B.; Bouchot, O.; et al. Comparison of In-Vivo and Ex-Vivo Ascending Aorta Elastic Properties through Automatic Deep Learning Segmentation of Cine-MRI and Biomechanical Testing. J. Clin. Med. 2023, 12, 402. https://doi.org/10.3390/jcm12020402
Markodimitrakis E, Lin S, Koutoulakis E, Marín-Castrillón DM, Tovar Sáez FA, Leclerc S, Bernard C, Boucher A, Presles B, Bouchot O, et al. Comparison of In-Vivo and Ex-Vivo Ascending Aorta Elastic Properties through Automatic Deep Learning Segmentation of Cine-MRI and Biomechanical Testing. Journal of Clinical Medicine. 2023; 12(2):402. https://doi.org/10.3390/jcm12020402
Chicago/Turabian StyleMarkodimitrakis, Emmanouil, Siyu Lin, Emmanouil Koutoulakis, Diana Marcela Marín-Castrillón, Francisco Aarón Tovar Sáez, Sarah Leclerc, Chloé Bernard, Arnaud Boucher, Benoit Presles, Olivier Bouchot, and et al. 2023. "Comparison of In-Vivo and Ex-Vivo Ascending Aorta Elastic Properties through Automatic Deep Learning Segmentation of Cine-MRI and Biomechanical Testing" Journal of Clinical Medicine 12, no. 2: 402. https://doi.org/10.3390/jcm12020402
APA StyleMarkodimitrakis, E., Lin, S., Koutoulakis, E., Marín-Castrillón, D. M., Tovar Sáez, F. A., Leclerc, S., Bernard, C., Boucher, A., Presles, B., Bouchot, O., Decourselle, T., Morgant, M.-C., & Lalande, A. (2023). Comparison of In-Vivo and Ex-Vivo Ascending Aorta Elastic Properties through Automatic Deep Learning Segmentation of Cine-MRI and Biomechanical Testing. Journal of Clinical Medicine, 12(2), 402. https://doi.org/10.3390/jcm12020402








