Decision Support for the Optimization of Provider Staffing for Hospital Emergency Departments with a Queue-Based Approach
Abstract
1. Introduction
1.1. Background
1.2. Contribution Profile
2. Related Work
3. The Proposed Model of Medical Emergency Services
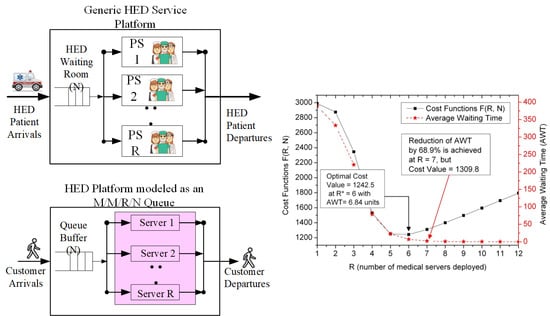
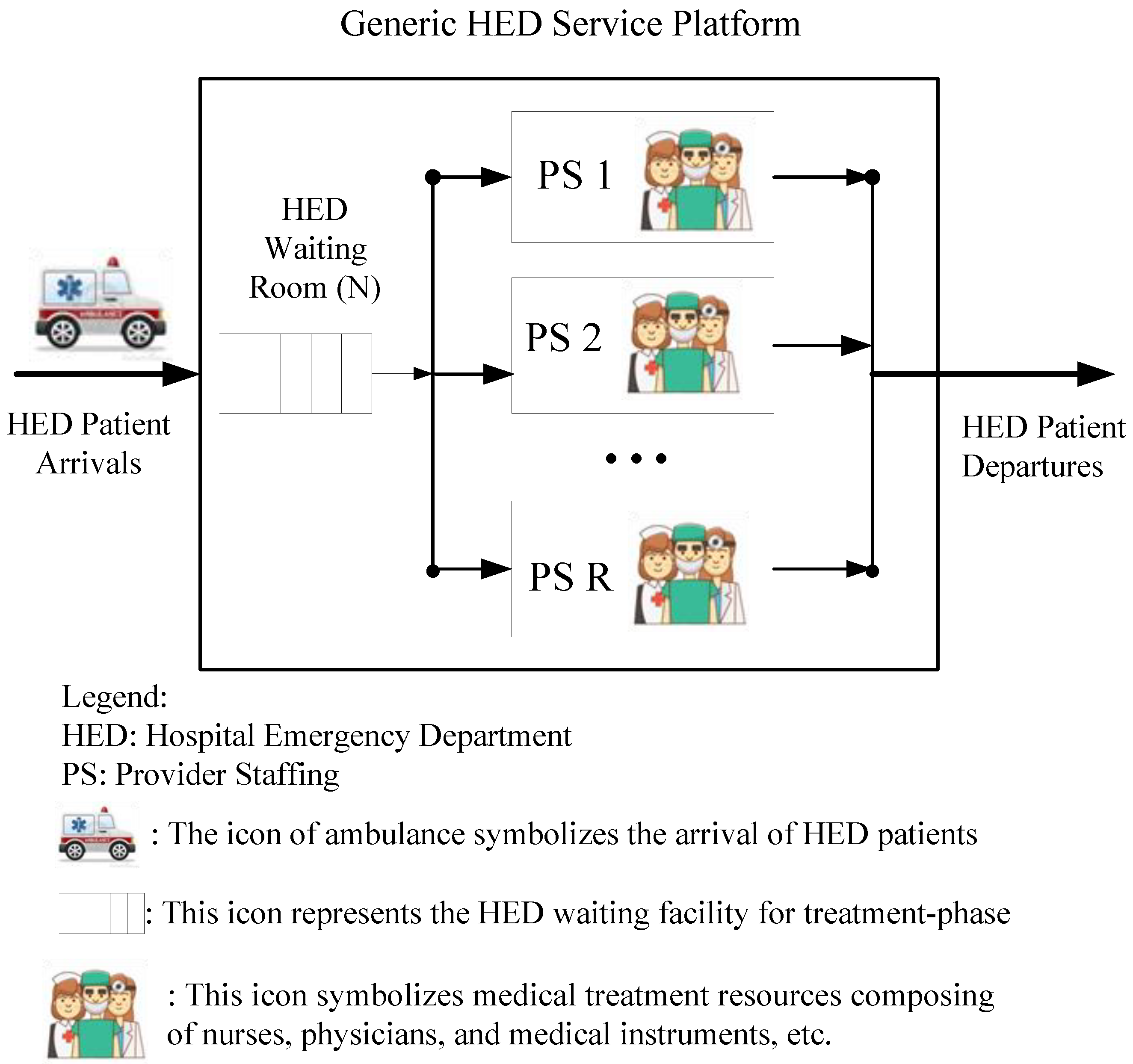
3.1. The Generic Platform of Medical Emergency Services
3.2. Mapping Profile between the HED Service Platform and the M/M/R/N Queuing System
4. Quantitative Modeling and System Measures for the HED Platform
4.1. Theoretical Analysis
- (A)
- Segment (1): 1 ≤ n ≤ R
- (B)
- Segment (2): (R+1) ≤ n ≤ N,
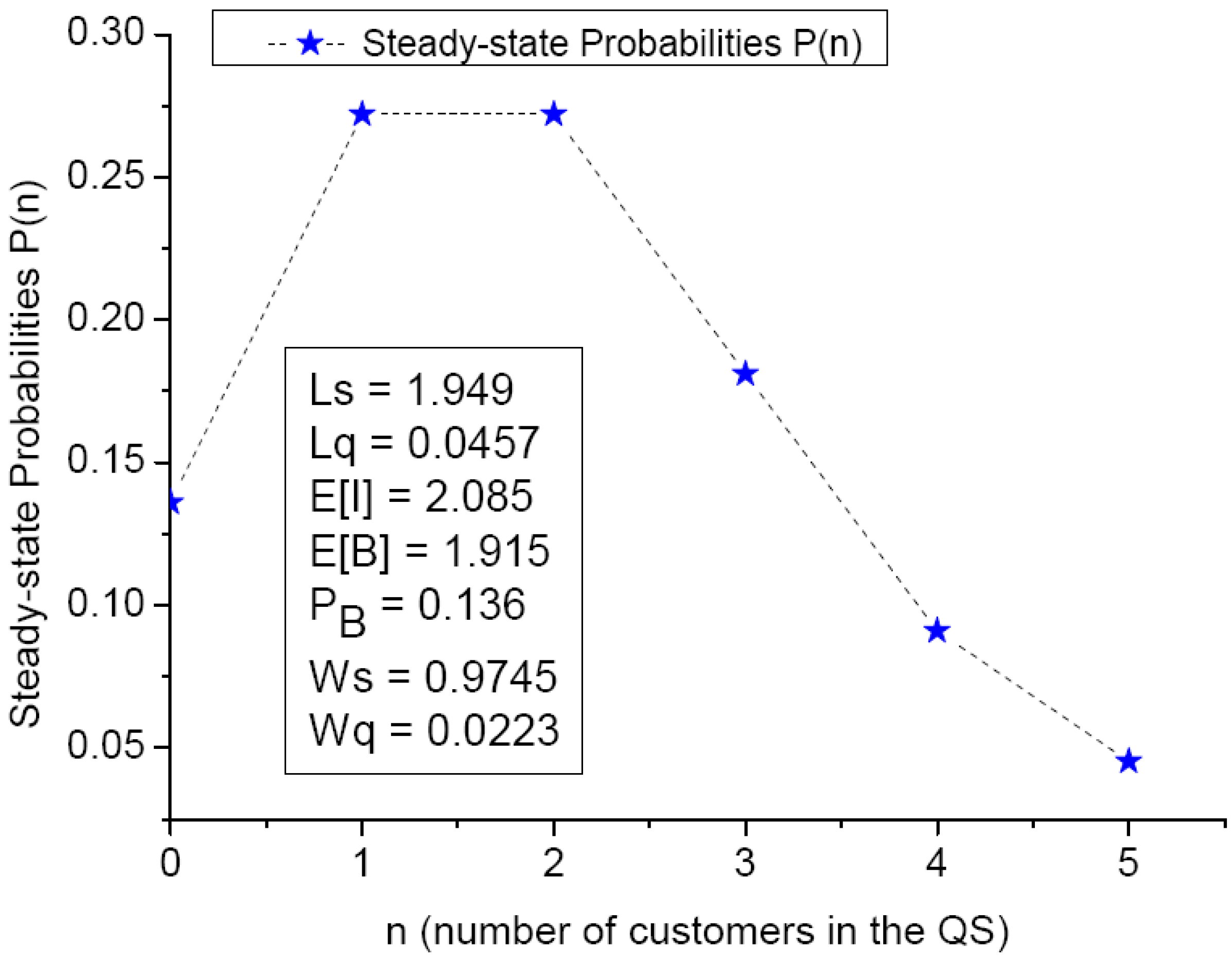
4.2. System Performance Measures
- Ls = expected number of customers in the system,
- Lq = expected number of customers in the queue buffer,
- E[I] = expected number of idle servers,
- E[B] = expected number of busy servers,
- PB = Probability that all servers are busy,
- Ws = average waiting times in the system,
- Wq = average waiting times in the queue buffer.
4.3. An Illustrative Example with Computation Details
- (1)
- 0 ≤ n ≤ (R–1) = 3,
- (2)
- R ≤ n ≤ N, i.e., For 4 ≤ n ≤ 5,⇒[P(1), P(2), P(3), P(4), P(5)] = = [2, 2, 1.333, 0.667, 0.333] P(0).
5. Issue on Decision Support for HED Management
5.1. Evaluation Formulation on Cost
- Cq = cost per unit time when one customer is waiting for service,
- Cs = cost per unit time when one customer joins the system and is served,
- (CB, CI) = cost per unit time when one server is (busy, idle).
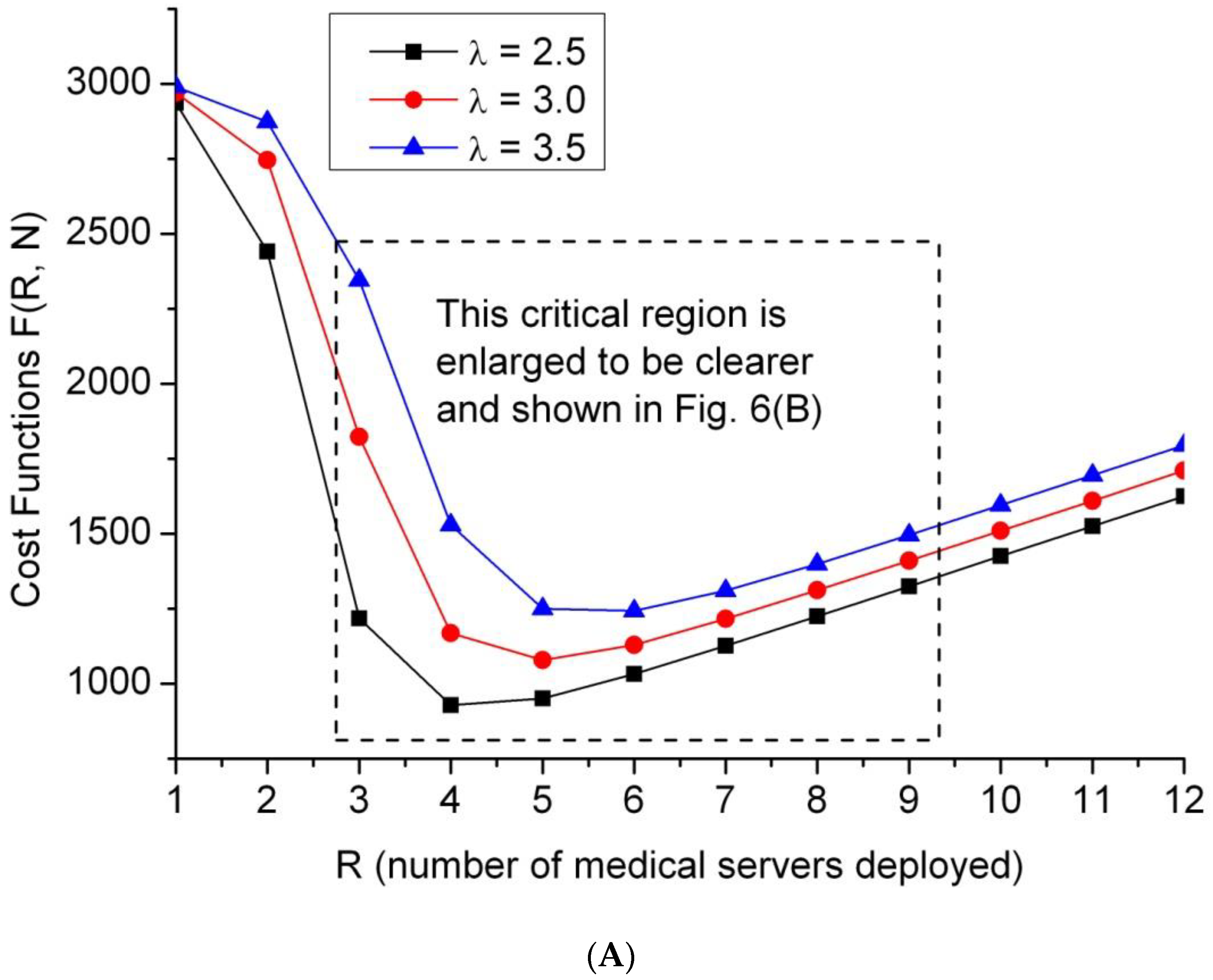
5.2. Evaluation of Cost Optimization
- (a)
- Average arrival rate of patients (λ) = 2.5, 3.0, and 3.5,
- (b)
- Average service rate of a server (µ) = 1,
- (c)
- Cost rate: (Cq, Cs, CB, CI,) = (200, 150, 120, 100),
- (d)
- N = 15 for emergency departments of small and medium size.
5.3. Issues on Cost Profile under the Constraint of Average Waiting Time
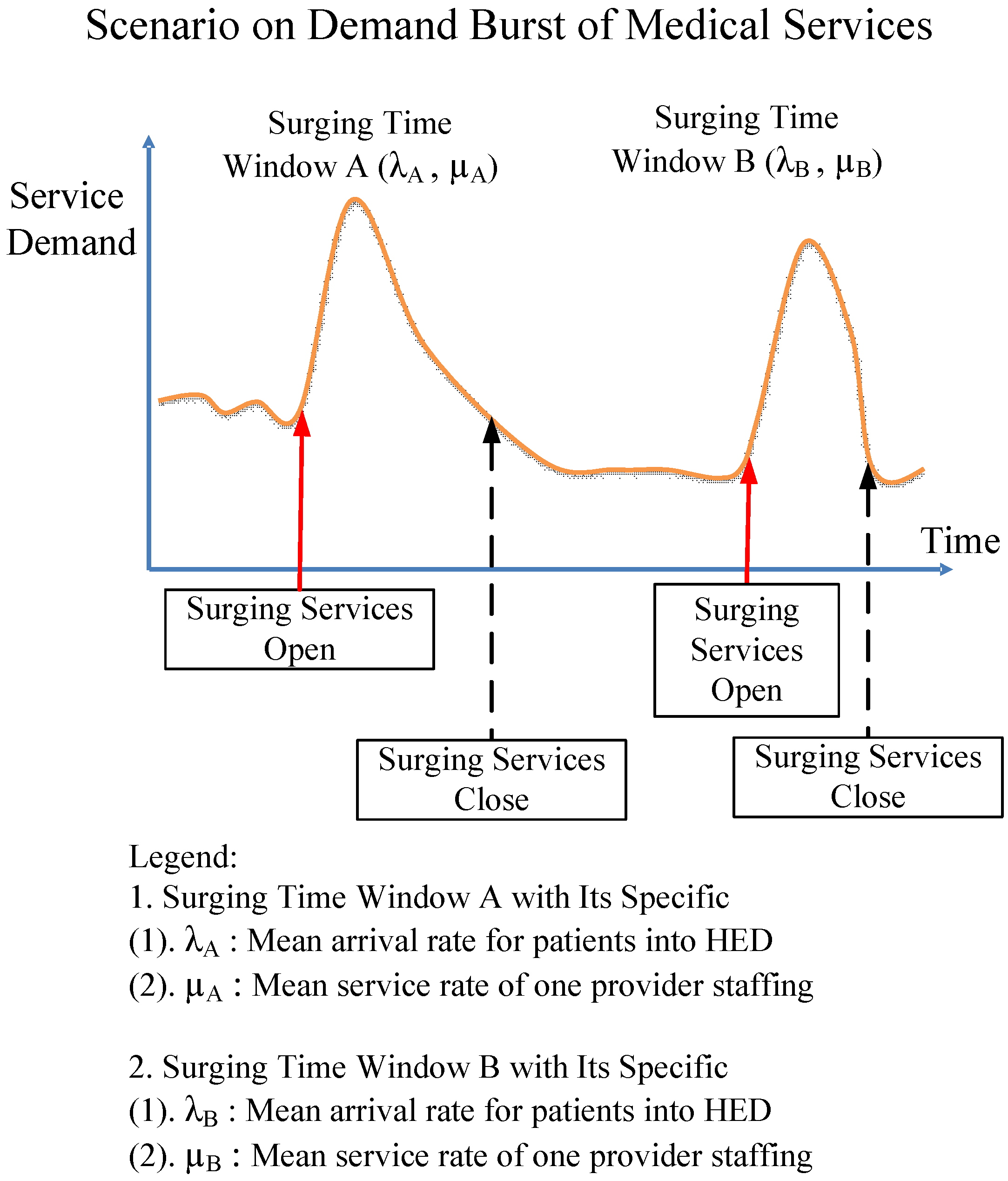
5.4. Application Profile in a Window-by-Window Way
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zengin, S.; Guzel, R.; Al, B.; Kartal, S.; Sarcan, E.; Yildirim, C. Cost analysis of a university hospital’s adult emergency service. J. Acad. Emerg. Med. 2013, 12, 71–75. [Google Scholar] [CrossRef]
- Simonet, D. Cost reduction strategies for emergency services: Insurance role, practice changes and patients accountability. Health Care Anal. 2009, 17, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Cremonesi, P.; Di Bella, E.; Montefiori, M. Cost analysis of emergency department. J. Prev. Med. Hyg. 2010, 51, 157–163. [Google Scholar] [PubMed]
- Cooper, R.B. Introduction to Queuing Theory, 2nd ed.; Elsevier Science Publishing Co., Inc.: New York, NY, USA, 1990. [Google Scholar]
- Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C. Fundamentals of Queuing Theory, 4th ed.; John Wiley &Sons, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Finamore, S.R.; Sheila, S.A. Shorting the wait: A strategy to reduce waiting times in the emergency department. J. Emerg. Nurs. 2009, 35, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Green, L.V.; Soares, J.; Giglio, J.F.; Green, R.A. Using queuing theory to increase the effectiveness of emergency department provider staffing. Acad. Emerg. Med. 2006, 13, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Derlet, R.W.; Richards, J.R.; Kravitz, R.L. Frequent overcrowding in U.S. emergency departments. Acad. Emerg. Med. 2001, 8, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Rhodes, K.; Walls, C.A.; Asplin, B.R. Access to emergency care: Restricted by long waiting times and cost and coverage concerns. Ann. Emerg. Med. 2004, 43, 567–573. [Google Scholar] [CrossRef] [PubMed]
- Hoot, N.R.; Aronsky, D. Systematic review of emergency department crowding: Causes, effects, and solutions. Ann. Emerg. Med. 2008, 52, 126–136. [Google Scholar] [CrossRef] [PubMed]
- Ding, R.; Zeger, S.L.; McCarthy, M.L.; Pines, J.M. Comparison of methods for measuring crowding and its effects on length of stay in the emergency department. Acad. Emerg. Med. 2011, 18, 1269–1277. [Google Scholar]
- Kaushal, A.; Zhao, Y.; Peng, Q.; Strome, T.; Weldon, E.; Zhang, M.; Chochinov, A. Evaluation of fast track strategies using agent-based simulation modeling to reduce waiting time in a hospital emergency department. Socio Econ. Plan. Sci. 2015, 50, 18–31. [Google Scholar] [CrossRef]
- Vass, H.; Szabo, Z.K. Application of queuing model to patient flow in emergency department. Case study. Procedia Econ. Financ. 2015, 32, 479–487. [Google Scholar] [CrossRef][Green Version]
- Taichung Veterans General Hospital (TVGH): Departments of Medical Services. Available online: http://www.vghtc.org.tw/ (accessed on 5 December 2019).
- Fletcher, A.; Worthington, D. What is a ‘generic’ hospital model?—A comparison of ‘generic’ and ‘specific’ hospital models of emergency patient flows. Health Care Manag. Sci. 2009, 12, 374–391. [Google Scholar] [CrossRef]
- Hoot, N.R.; Leblanc, L.J.; Jones, I.; Levin, S.R.; Zhou, C.; Gadd, C.S.; Aronsky, D. Forecasting emergency department crowding: A discrete event simulation. Ann. Emerg. Med. 2008, 52, 116–125. [Google Scholar] [CrossRef]
- Cochran, J.K.; Roche, K.T. A multi-class queuing network analysis methodology for improving hospital emergency department performance. Comput. Oper. Res. 2009, 36, 1497–1512. [Google Scholar] [CrossRef]
- McManus, M.L.; Long, M.C.; Cooper, A.; Litvak, E. Queuing theory accurately models the need for critical care resources. Anesthesiology 2004, 100, 1271–1276. [Google Scholar] [CrossRef]
- Marmor, Y.N.; Wasserkrug, S.; Zeltyn, S.; Mesika, Y.; Greenshpan, O.; Carmeli, B.; Shtub, A.; Mandelbaum, A. Toward simulation-based real-time decision-support systems for emergency departments. In Proceedings of the 2009 Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009. [Google Scholar]
- Oh, C.; Novotny, A.M.; Carter, P.L.; Ready, R.K.; Campbell, D.D.; Leckie, M.C. Use of a simulation-based decision support tool to improve emergency department throughput. Oper. Res. Health Care 2016, 9, 29–39. [Google Scholar] [CrossRef]





| R | Cost Values | AWT | R | Cost Values | AWT |
|---|---|---|---|---|---|
| 1 | 2990.0 | 388.57 | 7 | 1309.9 | 2.13 |
| 2 | 2873.9 | 333.42 | 8 | 1399.5 | 0.65 |
| 3 | 2345.8 | 220.77 | 9 | 1496.3 | 0.19 |
| 4 | 1530.2 | 78.57 | 10 | 1595.4 | 0.05 |
| 5 | 1250.7 | 22.51 | 11 | 1695.1 | 0.01 |
| 6 | 1242.5 | 6.84 | 12 | 1795.0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.-C.; Shih, C.-M.; Wang, Y.-M.; Yang, C.-T.; Chiang, Y.-J.; Lee, C.-H. Decision Support for the Optimization of Provider Staffing for Hospital Emergency Departments with a Queue-Based Approach. J. Clin. Med. 2019, 8, 2154. https://doi.org/10.3390/jcm8122154
Jiang F-C, Shih C-M, Wang Y-M, Yang C-T, Chiang Y-J, Lee C-H. Decision Support for the Optimization of Provider Staffing for Hospital Emergency Departments with a Queue-Based Approach. Journal of Clinical Medicine. 2019; 8(12):2154. https://doi.org/10.3390/jcm8122154
Chicago/Turabian StyleJiang, Fuu-Cheng, Cheng-Min Shih, Yun-Ming Wang, Chao-Tung Yang, Yi-Ju Chiang, and Cheng-Hung Lee. 2019. "Decision Support for the Optimization of Provider Staffing for Hospital Emergency Departments with a Queue-Based Approach" Journal of Clinical Medicine 8, no. 12: 2154. https://doi.org/10.3390/jcm8122154
APA StyleJiang, F.-C., Shih, C.-M., Wang, Y.-M., Yang, C.-T., Chiang, Y.-J., & Lee, C.-H. (2019). Decision Support for the Optimization of Provider Staffing for Hospital Emergency Departments with a Queue-Based Approach. Journal of Clinical Medicine, 8(12), 2154. https://doi.org/10.3390/jcm8122154