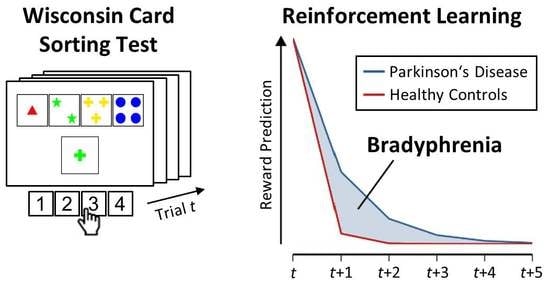
Computational Modeling for Neuropsychological Assessment of Bradyphrenia in Parkinson’s Disease
Abstract
:1. Introduction
2. Materials and Methods
2.1. Procedure
2.2. Participants
2.3. Computerized Wisconsin Card Sorting Test
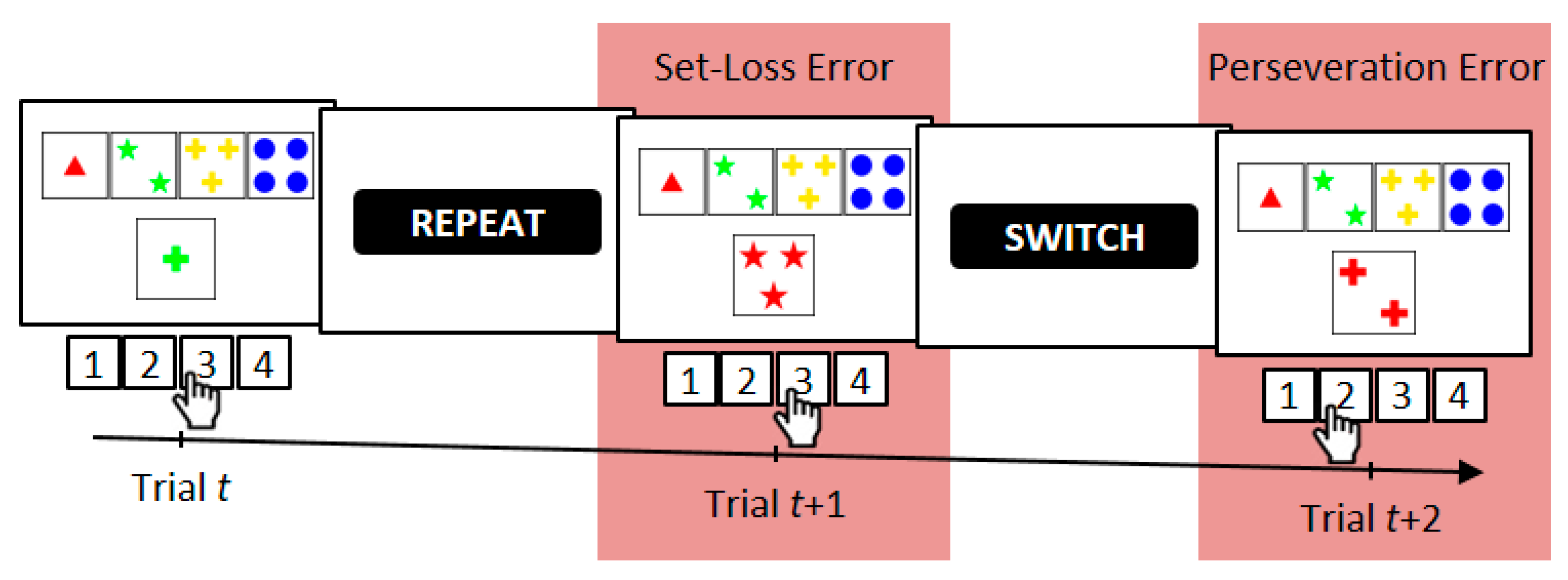
2.4. Error Analysis
2.5. Computational Modeling
3. Results
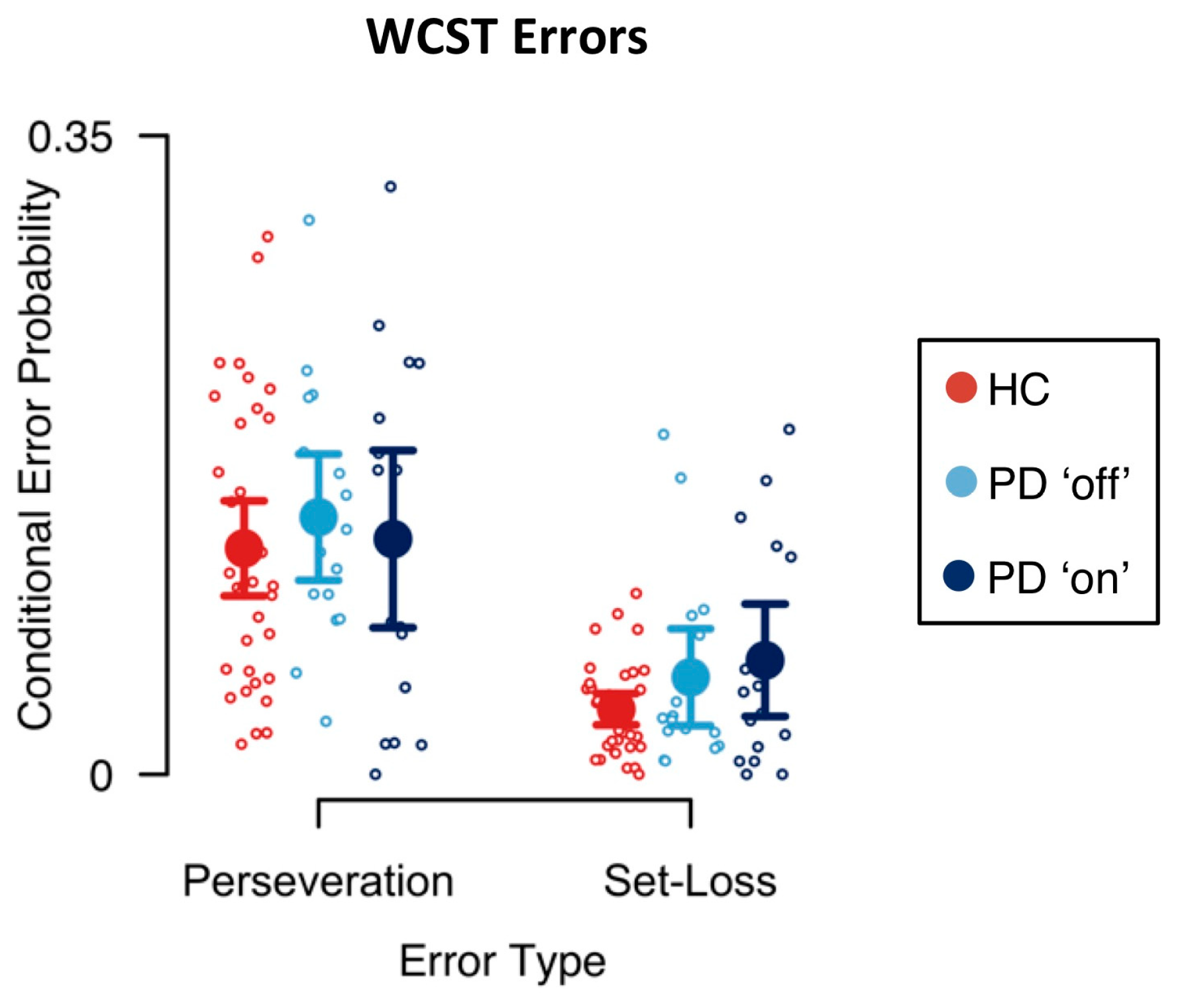
3.1. Error Analysis
3.2. Computational Modeling
4. Discussion
4.1. Implications for Neuropsychological Sequelae of PD
4.2. Implications for Neuropsychological Sequelae of DA Replacement Therapy
4.3. Implications for Brain–Behavior Relationships
4.4. Implications for Neuropsychological Assessment
4.5. Study Limitations and Directions for Future Research
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Healthy Control Participants (N = 34) | Parkinson’s Disease Patients (N = 16) | |||||
|---|---|---|---|---|---|---|
| Mean | SD | n | Mean | SD | n | |
| Age (years) | 63.18 | 9.71 | 34 | 59.94 | 8.84 | 16 |
| Education (years) | 13.49 | 4.09 | 34 | 14.40 | 2.88 | 15 |
| Disease duration (years) | - | - | - | 6.75 | 4.04 | 16 |
| UPDRS III ‘on’ | - | - | - | 17.75 | 8.05 | 16 |
| UPDRS III ‘off’ | - | - | - | 27.92 | 12.68 | 13 |
| LEDD | - | - | - | 932.63 | 437.86 | 16 |
| MoCA (cognitive status) | 28.35 | 1.97 | 34 | 27.47 | 1.08 | 16 |
| WST (premorbid intelligence) | 30.71 | 3.79 | 34 | 23.00 | 32.71 | 16 |
| AES (apathy) | 10.77 | 6.81 | 34 | 15.31 | 8.85 | 16 |
| BDI-II (depression) | 6.59 | 8.28 | 34 | 6.56 | 4.43 | 16 |
| BSI-18 (psychiatric status) | 6.16 | 7.99 | 33 | 7.07 | 4.89 | 14 |
| Anxiety | 1.82 | 2.31 | 33 | 2.79 | 1.37 | 14 |
| Depression | 1.91 | 3.14 | 33 | 1.29 | 1.33 | 14 |
| Somatization | 2.44 | 3.26 | 33 | 3.00 | 2.96 | 14 |
| SF-36 (health status) | 74.21 | 20.12 | 33 | 59.07 | 16.66 | 14 |
| Physical functioning | 79.55 | 22.65 | 33 | 56.79 | 24.15 | 14 |
| Physical role functioning | 71.97 | 40.87 | 33 | 35.71 | 41.27 | 14 |
| Bodily pain | 71.58 | 26.20 | 33 | 61.71 | 26.67 | 14 |
| General health perception | 60.33 | 18.35 | 33 | 51.29 | 20.08 | 14 |
| Vitality | 63.79 | 19.61 | 33 | 54.29 | 17.85 | 14 |
| Social role functioning | 88.26 | 16.52 | 33 | 65.18 | 24.60 | 14 |
| Emotional role functioning | 84.91 | 30.11 | 33 | 83.36 | 36.39 | 14 |
| Mental health | 77.58 | 15.84 | 33 | 67.71 | 12.10 | 14 |
| BIS-brief (impulsiveness) | 15.45 | 4.17 | 34 | 14.84 | 3.74 | 16 |
| DII (impulsivity) | ||||||
| Functional | 5.85 | 2.95 | 34 | 6.00 | 2.45 | 16 |
| Dysfunctional | 2.38 | 2.59 | 34 | 3.31 | 3.95 | 16 |
| QUIP-RS (impulse control) | 0.61 | 1.42 | 28 | 6.00 | 9.78 | 15 |
| SPQ (schizotypal traits) | 4.46 | 3.67 | 33 | 4.57 | 3.67 | 14 |
| Interpersonal | 2.52 | 2.41 | 33 | 2.36 | 1.91 | 14 |
| Cognitive-perceptual | 1.15 | 1.18 | 33 | 1.07 | 1.39 | 14 |
| Disorganized | 0.79 | 1.11 | 33 | 1.14 | 1.51 | 14 |
| Patient Number | Medication (mg) | LEDD |
|---|---|---|
| 1 | Pramipexole 3.15 | 450 |
| 2 | Pramipexole 0.52, Rasagiline 1 | 175 |
| 3 | Pramipexole 3.15, L-Dopa 300, C-L-Dopa 100 | 825 |
| 4 | L-Dopa 400, Amantadine 200, Rasagiline 1, Rotigotine 12 | 1060 |
| 5 | L-Dopa 1000, Entecapone 1000, Pramipexole 1.75, Oral Selegiline 10 | 1680 |
| 6 | L-Dopa 400 | 400 |
| 7 | L-Dopa 600, Entecapone 600, Pramipexole 1.04 | 948 |
| 8 | L-Dopa 350, C-L-Dopa 500, Pramipexole 2.1 | 1025 |
| 9 | L-Dopa 400, Rotigotine 2 | 460 |
| 10 | L-Dopa 550, Rotigotine 16, Rasagiline 1, Amantadine 200 | 1330 |
| 11 | L-Dopa 600, Amantadine 200, Rotigotine 6, Cabergoline 6 | 1380 |
| 12 | L-Dopa 600, C-L-Dopa 100, Entecapone 1200, Pramipexole 1.57 | 1098 |
| 13 | L-Dopa 600, C-L-Dopa 300, Entecapone 800, Cabergoline 6 | 1497 |
| 14 | L-Dopa 700, C-L-Dopa 100, Entecapone 600, Rotigotine 8 | 1246 |
| 15 | L-Dopa 500, Piribidil 50 | 550 |
| 16 | L-Dopa 600, Entecapone 800 | 798 |
Appendix B
| Error Type | Session | |
|---|---|---|
| First | Second | |
| Perseveration Error | 0.145 (0.121, 0.169) | 0.110 (0.086, 0.133) |
| Set-Loss Error | 0.052 (0.039, 0.064) | 0.034 (0.023, 0.044) |
| Effects | p(Inclusion) | p(Inclusion|Data) | BFinclusion |
|---|---|---|---|
| Error Type | 0.600 | >0.999 | >1000 *** |
| Session | 0.600 | 0.998 | 319.214 *** |
| Error Type x Session | 0.200 | 0.329 | 1.962 |
Appendix C
Appendix D
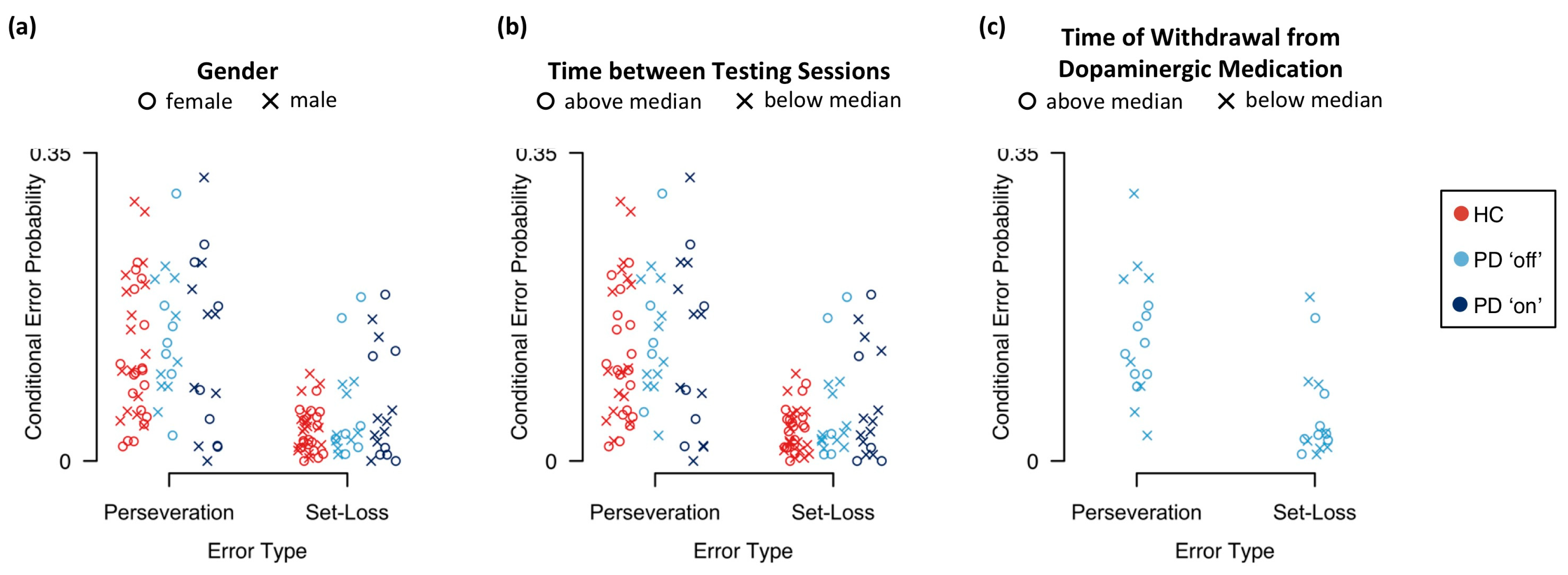

Appendix E
| Parameter | Session | |
|---|---|---|
| First | Second | |
| 0.517 (0.477, 0.558) | 0.612 (0.573, 0.652) | |
| 0.219 (0.191, 0.249) | 0.342 (0.307, 0.378) | |
| 0.121 (0.096, 0.148) | 0.188 (0.154, 0.225) | |
| 0.004 (0.002, 0.009) | <0.001 (<0.001, 0.001) | |
| 0.054 (0.046, 0.065) | 0.031 (0.024, 0.039) | |
| 0.345 (0.274, 0.406) | 0.401 (0.307, 0.480) | |
| 0.149 (0.139, 0.158) | 0.157 (0.148, 0.167) | |
| Parameter | Bayes Factor |
|---|---|
| 15.854 ** | |
| 1499.000 *** | |
| 47.387 ** | |
| 0.046 ** | |
| 0.016 ** | |
| 2.282 | |
| 2.676 |
Appendix F
| Healthy Control Participants | Parkinson’s Disease Patients | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Perseveration errors | −0.55 ** | −0.92 *** | −0.66 *** | −0.32 | 0.34 | 0.08 | 0.52 ** | −0.63 * | −0.91 *** | −0.44 | 0.34 | 0.54 | 0.30 | 0.63 * |
| Set-loss Errors | −0.94 *** | −0.70 *** | −0.61 *** | −0.21 | 0.07 | −0.04 | 0.80 *** | −0.96 *** | −0.69 ** | −0.57 * | 0.67 * | 0.22 | 0.30 | 0.88 *** |
| Age (years) | −0.40 * | −0.30 | −0.35 | −0.06 | −0.06 | 0.15 | 0.42 * | −0.50 | −0.42 | −0.46 | 0.39 | −0.02 | 0.32 | 0.42 |
| Education (years) | 0.16 | 0.07 | −0.03 | −0.05 | 0.10 | −0.21 | −0.05 | 0.62 * | 0.34 | 0.40 | −0.54 | −0.18 | −0.05 | −0.55 |
| Disease duration (years) | −0.47 | −0.10 | −0.05 | 0.51 | −0.03 | 0.09 | 0.33 | |||||||
| UPDRS III ‘on’ | −0.18 | 0.20 | 0.02 | 0.14 | −0.41 | −0.20 | 0.24 | |||||||
| UPDRS III ‘off’ | −0.20 | 0.47 | 0.32 | 0.14 | −0.14 | −0.06 | 0.19 | |||||||
| LEDD | −0.29 | −0.01 | 0.06 | 0.23 | −0.23 | −0.24 | 0.19 | |||||||
| MoCA (cognitive status) | 0.42 * | 0.34 | 0.23 | −0.21 | 0.17 | 0.12 | −0.39 | 0.03 | 0.45 | 0.16 | 0.00 | −0.05 | −0.11 | −0.16 |
| WST (premorbid intelligence) | 0.33 | 0.28 | 0.21 | 0.07 | 0.01 | −0.08 | −0.40 | 0.36 | 0.31 | 0.15 | 0.02 | 0.15 | 0.09 | −0.43 |
| AES (apathy) | −0.14 | −0.14 | −0.03 | −0.21 | 0.04 | 0.10 | 0.02 | −0.50 | 0.08 | 0.05 | 0.10 | −0.32 | −0.02 | 0.48 |
| BDI-II (depression) | −0.14 | −0.21 | −0.21 | −0.04 | 0.18 | −0.05 | 0.09 | −0.02 | 0.41 | 0.19 | −0.37 | −0.38 | −0.17 | 0.04 |
| BSI-18 (psychiatric status) | −0.23 | −0.22 | −0.26 | −0.13 | 0.07 | −0.02 | 0.16 | −0.38 | −0.11 | −0.25 | 0.20 | 0.15 | 0.52 | 0.27 |
| Anxiety | −0.24 | −0.17 | −0.23 | −0.15 | 0.11 | 0.11 | 0.18 | −0.02 | 0.05 | −0.14 | −0.14 | 0.08 | 0.35 | −0.07 |
| Depression | −0.18 | −0.22 | −0.23 | −0.09 | 0.05 | −0.20 | 0.08 | −0.50 | −0.20 | −0.32 | 0.03 | 0.03 | 0.23 | 0.40 |
| Somatization | −0.21 | −0.20 | −0.25 | −0.11 | 0.06 | 0.07 | 0.17 | −0.39 | −0.11 | −0.20 | 0.39 | 0.19 | 0.60 * | 0.29 |
| SF-36 (health status) | 0.23 | 0.31 | 0.26 | 0.06 | −0.04 | −0.03 | −0.26 | 0.28 | −0.11 | 0.22 | −0.13 | 0.24 | −0.41 | −0.19 |
| Physical functioning | 0.21 | 0.20 | 0.16 | 0.19 | 0.02 | 0.01 | −0.22 | 0.14 | −0.32 | −0.03 | −0.31 | 0.00 | −0.48 | −0.06 |
| Physical role functioning | 0.23 | 0.41 * | 0.29 | 0.11 | −0.07 | −0.03 | −0.29 | −0.02 | −0.40 | −0.02 | −0.11 | 0.45 | −0.28 | 0.07 |
| Bodily pain | 0.25 | 0.29 | 0.23 | 0.26 | −0.17 | −0.20 | −0.23 | 0.27 | 0.15 | 0.47 | −0.29 | −0.12 | −0.44 | −0.13 |
| General health perception | 0.24 | 0.30 | 0.27 | 0.16 | −0.10 | −0.21 | −0.31 | 0.23 | −0.05 | 0.15 | −0.23 | 0.18 | −0.58 | −0.20 |
| Vitality | 0.03 | 0.00 | 0.03 | −0.06 | −0.04 | 0.01 | −0.06 | 0.18 | −0.24 | −0.03 | −0.02 | 0.30 | −0.30 | −0.18 |
| Social role functioning | 0.29 | 0.31 | 0.18 | 0.04 | −0.05 | 0.00 | −0.24 | 0.22 | −0.18 | −0.22 | 0.27 | 0.47 | 0.25 | −0.25 |
| Emotional role functioning | 0.10 | 0.22 | 0.21 | −0.14 | 0.05 | 0.07 | −0.10 | 0.35 | 0.25 | 0.34 | 0.19 | 0.01 | 0.14 | −0.32 |
| Mental health | 0.14 | 0.17 | 0.21 | −0.15 | 0.07 | 0.05 | −0.16 | 0.19 | 0.12 | 0.25 | 0.17 | 0.27 | −0.13 | −0.12 |
| BIS-brief (impulsiveness) | −0.17 | −0.17 | −0.07 | −0.17 | 0.06 | 0.22 | 0.08 | −0.12 | 0.45 | −0.02 | −0.05 | −0.24 | −0.03 | −0.01 |
| DII (impulsivity) | ||||||||||||||
| Functional | 0.03 | 0.06 | 0.09 | 0.04 | −0.07 | 0.06 | 0.13 | −0.06 | −0.31 | −0.26 | 0.18 | 0.06 | −0.21 | 0.04 |
| Dysfunctional | −0.23 | −0.11 | −0.01 | 0.06 | −0.19 | −0.04 | 0.30 | −0.19 | 0.28 | −0.03 | −0.22 | −0.27 | −0.32 | 0.10 |
| QUIP-RS (impulse control) | −0.03 | 0.23 | 0.27 | 0.02 | −0.14 | −0.23 | −0.04 | 0.13 | 0.45 | 0.37 | −0.11 | −0.08 | 0.07 | −0.17 |
| SPQ (schizotypal traits) | −0.12 | −0.27 | −0.12 | −0.33 | 0.30 | −0.04 | 0.03 | −0.28 | 0.04 | 0.00 | −0.26 | 0.01 | −0.21 | 0.26 |
| Interpersonal | −0.14 | −0.33 | −0.15 | −0.25 | 0.16 | 0.00 | 0.09 | −0.31 | 0.07 | 0.10 | −0.11 | 0.11 | 0.16 | 0.29 |
| Cognitive-perceptual | 0.10 | 0.17 | 0.12 | −0.15 | 0.49 ** | 0.00 | −0.24 | 0.05 | 0.11 | 0.09 | −0.33 | 0.10 | −0.49 | −0.05 |
| Disorganized | −0.19 | −0.35 | −0.20 | −0.38 | 0.11 | −0.13 | 0.13 | −0.34 | −0.10 | −0.21 | −0.19 | −0.19 | −0.27 | 0.33 |
References
- Seer, C.; Lange, F.; Georgiev, D.; Jahanshahi, M.; Kopp, B. Event-related potentials and cognition in Parkinson’s disease: An integrative review. Neurosci. Biobehav. Rev. 2016, 71, 691–714. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, C.H.; Del Tredici, K.; Braak, H. A timeline for Parkinson’s disease. Parkinsonism Relat. Disord. 2010, 16, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Braak, H.; Del Tredici, K. Nervous system pathology in sporadic Parkinson disease. Neurology 2008, 70, 1916–1925. [Google Scholar] [CrossRef]
- Braak, H.; Tredici, K.D.; Rüb, U.; de Vos, R.A.I.; Jansen Steur, E.N.H.; Braak, E. Staging of brain pathology related to sporadic Parkinson’s disease. Neurobiol. Aging 2003, 24, 197–211. [Google Scholar] [CrossRef]
- Dirnberger, G.; Jahanshahi, M. Executive dysfunction in Parkinson’s disease: A review. J. Neuropsychol. 2013, 7, 193–224. [Google Scholar] [CrossRef]
- Kudlicka, A.; Clare, L.; Hindle, J.V. Executive functions in Parkinson’s disease: Systematic review and meta-analysis. Mov. Disord. 2011, 26, 2305–2315. [Google Scholar] [CrossRef]
- Cools, R. Dopaminergic modulation of cognitive function-implications for L-DOPA treatment in Parkinson’s disease. Neurosci. Biobehav. Rev. 2006, 30, 1–23. [Google Scholar] [CrossRef]
- Gotham, A.M.; Brown, R.G.; Marsden, C.D. ‘Frontal’ cognitive function in patients with Parkinson’s disease “on” and “off” Levodopa. Brain 1988, 111, 299–321. [Google Scholar] [CrossRef]
- Thurm, F.; Schuck, N.W.; Fauser, M.; Doeller, C.F.; Stankevich, Y.; Evens, R.; Riedel, O.; Storch, A.; Lueken, U.; Li, S.-C. Dopamine modulation of spatial navigation memory in Parkinson’s disease. Neurobiol. Aging 2016, 38, 93–103. [Google Scholar] [CrossRef]
- Vaillancourt, D.E.; Schonfeld, D.; Kwak, Y.; Bohnen, N.I.; Seidler, R. Dopamine overdose hypothesis: Evidence and clinical implications. Mov. Disord. 2013, 28, 1920–1929. [Google Scholar] [CrossRef] [Green Version]
- Cools, R.; D’Esposito, M. Inverted-U–shaped dopamine actions on human working memory and cognitive control. Biol. Psychiatry 2011, 69, 113–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.-C.; Lindenberger, U.; Bäckman, L. Dopaminergic modulation of cognition across the life span. Neurosci. Biobehav. Rev. 2010, 34, 625–630. [Google Scholar] [CrossRef] [PubMed]
- Postuma, R.B.; Berg, D.; Stern, M.; Poewe, W.; Olanow, C.W.; Oertel, W.; Obeso, J.; Marek, K.; Litvan, I.; Lang, A.E.; et al. MDS clinical diagnostic criteria for Parkinson’s disease. Mov. Disord. 2015, 30, 1591–1601. [Google Scholar] [CrossRef] [PubMed]
- Bologna, M.; Paparella, G.; Fasano, A.; Hallett, M.; Berardelli, A. Evolving concepts on bradykinesia. Brain 2020, 143, 727–750. [Google Scholar] [CrossRef]
- Peavy, G.M. Mild cognitive deficits in Parkinson disease: Where there is bradykinesia, there is bradyphrenia. Neurology 2010, 75, 1038–1039. [Google Scholar] [CrossRef]
- Pate, D.S.; Margolin, D.I. Cognitive slowing in Parkinson’s and Alzheimer’s patients: Distinguishing bradyphrenia from dementia. Neurology 1994, 44, 669. [Google Scholar] [CrossRef]
- Weiss, H.D.; Pontone, G.M. “Pseudo-syndromes” associated with Parkinson disease, dementia, apathy, anxiety, and depression. Neurol. Clin. Pract. 2019, 9, 354–359. [Google Scholar] [CrossRef]
- Low, K.A.; Miller, J.; Vierck, E. Response slowing in Parkinson’s disease: A psychophysiological analysis of premotor and motor processes. Brain 2002, 125, 1980–1994. [Google Scholar] [CrossRef] [Green Version]
- Rogers, D.; Lees, A.J.; Smith, E.; Trimble, M.; Stern, G.M. Bradyphrenia in Parkinson’s disease and psychomotor retardation in depressive illness: An experimental study. Brain 1987, 110, 761–776. [Google Scholar] [CrossRef]
- Vlagsma, T.T.; Koerts, J.; Tucha, O.; Dijkstra, H.T.; Duits, A.A.; van Laar, T.; Spikman, J.M. Mental slowness in patients with Parkinson’s disease: Associations with cognitive functions? J. Clin. Exp. Neuropsychol. 2016, 38, 844–852. [Google Scholar] [CrossRef] [Green Version]
- Revonsuo, A.; Portin, R.; Koivikko, L.; Rinne, J.O.; Rinne, U.K. Slowing of information processing in Parkinson’s disease. Brain Cogn. 1993, 21, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Kehagia, A.A.; Barker, R.A.; Robbins, T.W. Neuropsychological and clinical heterogeneity of cognitive impairment and dementia in patients with Parkinson’s disease. Lancet Neurol. 2010, 9, 1200–1213. [Google Scholar] [CrossRef]
- Rogers, D. Bradyphrenia in parkinsonism: A historical review. Psychol. Med. 1986, 16, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Rustamov, N.; Rodriguez-Raecke, R.; Timm, L.; Agrawal, D.; Dressler, D.; Schrader, C.; Tacik, P.; Wegner, F.; Dengler, R.; Wittfoth, M.; et al. Absence of congruency sequence effects reveals neurocognitive inflexibility in Parkinson’s disease. Neuropsychologia 2013, 51, 2976–2987. [Google Scholar] [CrossRef] [PubMed]
- Rustamov, N.; Rodriguez-Raecke, R.; Timm, L.; Agrawal, D.; Dressler, D.; Schrader, C.; Tacik, P.; Wegner, F.; Dengler, R.; Wittfoth, M.; et al. Attention shifting in Parkinson’s disease: An analysis of behavioral and cortical responses. Neuropsychology 2014, 28, 929–944. [Google Scholar] [CrossRef] [PubMed]
- Aarsland, D.; Bronnick, K.; Williams-Gray, C.; Weintraub, D.; Marder, K.; Kulisevsky, J.; Burn, D.; Barone, P.; Pagonabarraga, J.; Allcock, L.; et al. Mild cognitive impairment in Parkinson disease: A multicenter pooled analysis. Neurology 2010, 75, 1062–1069. [Google Scholar] [CrossRef]
- Lange, F.; Seer, C.; Kopp, B. Cognitive flexibility in neurological disorders: Cognitive components and event-related potentials. Neurosci. Biobehav. Rev. 2017, 83, 496–507. [Google Scholar] [CrossRef]
- Lange, F.; Brückner, C.; Knebel, A.; Seer, C.; Kopp, B. Executive dysfunction in Parkinson’s disease: A meta-analysis on the Wisconsin Card Sorting Test literature. Neurosci. Biobehav. Rev. 2018, 93, 38–56. [Google Scholar] [CrossRef]
- Beeldman, E.; Raaphorst, J.; Twennaar, M.; de Visser, M.; Schmand, B.A.; de Haan, R.J. The cognitive profile of ALS: A systematic review and meta-analysis update. J. Neurol. Neurosurg. Psychiatry 2016, 87, 611–619. [Google Scholar] [CrossRef] [Green Version]
- Demakis, G.J. A meta-analytic review of the sensitivity of the Wisconsin Card Sorting Test to frontal and lateralized frontal brain damage. Neuropsychology 2003, 17, 255–264. [Google Scholar] [CrossRef]
- Lange, F.; Seer, C.; Müller-Vahl, K.; Kopp, B. Cognitive flexibility and its electrophysiological correlates in Gilles de la Tourette syndrome. Dev. Cogn. Neurosci. 2017, 27, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Lange, F.; Seer, C.; Salchow, C.; Dengler, R.; Dressler, D.; Kopp, B. Meta-analytical and electrophysiological evidence for executive dysfunction in primary dystonia. Cortex 2016, 82, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Lange, F.; Vogts, M.-B.; Seer, C.; Fürkötter, S.; Abdulla, S.; Dengler, R.; Kopp, B.; Petri, S. Impaired set-shifting in amyotrophic lateral sclerosis: An event-related potential study of executive function. Neuropsychology 2016, 30, 120–134. [Google Scholar] [CrossRef] [PubMed]
- Nyhus, E.; Barceló, F. The Wisconsin Card Sorting Test and the cognitive assessment of prefrontal executive functions: A critical update. Brain Cogn. 2009, 71, 437–451. [Google Scholar] [CrossRef]
- Roberts, M.E.; Tchanturia, K.; Stahl, D.; Southgate, L.; Treasure, J. A systematic review and meta-analysis of set-shifting ability in eating disorders. Psychol. Med. 2007, 37, 1075–1084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romine, C. Wisconsin Card Sorting Test with children: A meta-analytic study of sensitivity and specificity. Arch. Clin. Neuropsychol. 2004, 19, 1027–1041. [Google Scholar] [CrossRef]
- Shin, N.Y.; Lee, T.Y.; Kim, E.; Kwon, J.S. Cognitive functioning in obsessive-compulsive disorder: A meta-analysis. Psychol. Med. 2014, 44, 1121–1130. [Google Scholar] [CrossRef]
- Snyder, H.R. Major depressive disorder is associated with broad impairments on neuropsychological measures of executive function: A meta-analysis and review. Psychol. Bull. 2013, 139, 81–132. [Google Scholar] [CrossRef] [Green Version]
- Grant, D.A.; Berg, E.A. A behavioral analysis of degree of reinforcement and ease of shifting to new responses in a Weigl-type card-sorting problem. J. Exp. Psychol. 1948, 38, 404–411. [Google Scholar] [CrossRef]
- Berg, E.A. A simple objective technique for measuring flexibility in thinking. J. Gen. Psychol. 1948, 39, 15–22. [Google Scholar] [CrossRef]
- Heaton, R.K.; Chelune, G.J.; Talley, J.L.; Kay, G.G.; Curtiss, G. Wisconsin Card Sorting Test Manual: Revised and Expanded; Psychological Assessment Resources Inc.: Odessa, FL, USA, 1993. [Google Scholar]
- Bishara, A.J.; Kruschke, J.K.; Stout, J.C.; Bechara, A.; McCabe, D.P.; Busemeyer, J.R. Sequential learning models for the Wisconsin card sort task: Assessing processes in substance dependent individuals. J. Math. Psychol. 2010, 54, 5–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kopp, B.; Steinke, A.; Bertram, M.; Skripuletz, T.; Lange, F. Multiple levels of control processes for Wisconsin Card Sorts: An observational study. Brain Sci. 2019, 9, 141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinke, A.; Lange, F.; Kopp, B. Parallel model-based and model-free reinforcement learning for card sorting performance. 2020. manuscript submitted for publication. [Google Scholar]
- Barceló, F. The Madrid card sorting test (MCST): A task switching paradigm to study executive attention with event-related potentials. Brain Res. Protoc. 2003, 11, 27–37. [Google Scholar] [CrossRef]
- Lange, F.; Dewitte, S. Cognitive flexibility and pro-environmental behaviour: A multimethod approach. Eur. J. Pers. 2019, 56, 46–54. [Google Scholar] [CrossRef]
- Lange, F.; Kröger, B.; Steinke, A.; Seer, C.; Dengler, R.; Kopp, B. Decomposing card-sorting performance: Effects of working memory load and age-related changes. Neuropsychology 2016, 30, 579–590. [Google Scholar] [CrossRef]
- Steinke, A.; Lange, F.; Seer, C.; Kopp, B. Toward a computational cognitive neuropsychology of Wisconsin card sorts: A showcase study in Parkinson’s disease. Comput. Brain Behav. 2018, 1, 137–150. [Google Scholar] [CrossRef]
- Gläscher, J.; Adolphs, R.; Tranel, D. Model-based lesion mapping of cognitive control using the Wisconsin Card Sorting Test. Nat. Commun. 2019, 10, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Beste, C.; Adelhöfer, N.; Gohil, K.; Passow, S.; Roessner, V.; Li, S.-C. Dopamine modulates the efficiency of sensory evidence accumulation during perceptual decision making. Int. J. Neuropsychopharmacol. 2018, 21, 649–655. [Google Scholar] [CrossRef]
- Caso, A.; Cooper, R.P. A neurally plausible schema-theoretic approach to modelling cognitive dysfunction and neurophysiological markers in Parkinson’s disease. Neuropsychologia 2020, 140, 107359. [Google Scholar] [CrossRef]
- Browning, M.; Carter, C.; Chatham, C.H.; Ouden, H.D.; Gillan, C.; Baker, J.T.; Paulus, M.P. Realizing the clinical potential of computational psychiatry: Report from the Banbury Center Meeting, February 2019. 2019. Available online: https://www.doi.org/10.31234/osf.io/5qbxp (accessed on 1 March 2020).
- McCoy, B.; Jahfari, S.; Engels, G.; Knapen, T.; Theeuwes, J. Dopaminergic medication reduces striatal sensitivity to negative outcomes in Parkinson’s disease. Brain 2019, 142, 3605–3620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Niv, Y. Reinforcement learning in the brain. J. Math. Psychol. 2009, 53, 139–154. [Google Scholar] [CrossRef] [Green Version]
- Silvetti, M.; Verguts, T. Reinforcement learning, high-level cognition, and the human brain. In Neuroimaging—Cognitive and Clinical Neuroscience; Bright, P., Ed.; InTech: Rijeka, Croatia, 2012; pp. 283–296. [Google Scholar]
- Gerraty, R.T.; Davidow, J.Y.; Foerde, K.; Galvan, A.; Bassett, D.S.; Shohamy, D. Dynamic flexibility in striatal-cortical circuits supports reinforcement learning. J. Neurosci. 2018, 38, 2442–2453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fontanesi, L.; Gluth, S.; Spektor, M.S.; Rieskamp, J. A reinforcement learning diffusion decision model for value-based decisions. Psychon. Bull. Rev. 2019, 26, 1099–1121. [Google Scholar] [CrossRef]
- Fontanesi, L.; Palminteri, S.; Lebreton, M. Decomposing the effects of context valence and feedback information on speed and accuracy during reinforcement learning: A meta-analytical approach using diffusion decision modeling. Cogn. Affect. Behav. Neurosci. 2019, 19, 490–502. [Google Scholar] [CrossRef]
- Caligiore, D.; Arbib, M.A.; Miall, R.C.; Baldassarre, G. The super-learning hypothesis: Integrating learning processes across cortex, cerebellum and basal ganglia. Neurosci. Biobehav. Rev. 2019, 100, 19–34. [Google Scholar] [CrossRef]
- Frank, M.J.; Seeberger, L.C.; O’Reilly, R.C. By carrot or by stick: Cognitive reinforcement learning in Parkinsonism. Science 2004, 306, 1940–1943. [Google Scholar] [CrossRef] [Green Version]
- Schultz, W.; Dayan, P.; Montague, P.R. A neural substrate of prediction and reward. Science 1997, 275, 1593–1599. [Google Scholar] [CrossRef] [Green Version]
- Schultz, W. Reward prediction error. Curr. Biol. 2017, 27, 369–371. [Google Scholar] [CrossRef] [Green Version]
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Steingroever, H.; Wetzels, R.; Wagenmakers, E.J. Validating the PVL-Delta model for the Iowa gambling task. Front. Psychol. 2013, 4, 1–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lange, F.; Seer, C.; Loens, S.; Wegner, F.; Schrader, C.; Dressler, D.; Dengler, R.; Kopp, B. Neural mechanisms underlying cognitive inflexibility in Parkinson’s disease. Neuropsychologia 2016, 93, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Nasreddine, Z.S.; Phillips, N.A.; Bédirian, V.; Charbonneau, S.; Whitehead, V.; Collin, I.; Cummings, J.L.; Chertkow, H. The Montreal Cognitive Assessment, MoCA: A brief screening tool for mild cognitive impairment. J. Am. Geriatr. Soc. 2005, 53, 695–699. [Google Scholar] [CrossRef] [PubMed]
- Kopp, B.; Lange, F. Electrophysiological indicators of surprise and entropy in dynamic task-switching environments. Front. Hum. Neurosci. 2013, 7, 300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altmann, E.M. Advance preparation in task switching. Psychol. Sci. 2004, 15, 616–622. [Google Scholar] [CrossRef] [PubMed]
- JASP Team. JASP, Version 0.11.1. 2019. Available online: https://www.jasp-stats.org (accessed on 7 January 2020).
- Van den Bergh, D.; van Doorn, J.; Marsman, M.; Draws, T.; van Kesteren, E.-J.; Derks, K.; Dablander, F.; Gronau, Q.F.; Kucharský, Š.; Raj, A.; et al. A Tutorial on Conducting and Interpreting a Bayesian ANOVA in JASP. 2019. Available online: https://www.psyarxiv.com/spreb (accessed on 1 February 2020).
- Daw, N.D.; Gershman, S.J.; Seymour, B.; Dayan, P.; Dolan, R.J. Model-based influences on humans’ choices and striatal prediction errors. Neuron 2011, 69, 1204–1215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frank, M.J.; Moustafa, A.A.; Haughey, H.M.; Curran, T.; Hutchison, K.E. Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc. Natl. Acad. Sci. USA 2007, 104, 16311–16316. [Google Scholar] [CrossRef] [Green Version]
- Ahn, W.-Y.; Haines, N.; Zhang, L. Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hBayesDM package. Comput. Psychiatry 2017, 1, 24–57. [Google Scholar] [CrossRef]
- Palminteri, S.; Lebreton, M.; Worbe, Y.; Grabli, D.; Hartmann, A.; Pessiglione, M. Pharmacological modulation of subliminal learning in Parkinson’s and Tourette’s syndromes. Proc. Natl. Acad. Sci. USA 2009, 106, 19179–19184. [Google Scholar] [CrossRef] [Green Version]
- Haines, N.; Vassileva, J.; Ahn, W.-Y. The Outcome-Representation Learning model: A novel reinforcement learning model of the Iowa Gambling Task. Cogn. Sci. 2018, 42, 2534–2561. [Google Scholar] [CrossRef] [Green Version]
- Steingroever, H.; Wetzels, R.; Wagenmakers, E.J. Absolute performance of reinforcement-learning models for the Iowa Gambling Task. Decision 2014, 1, 161–183. [Google Scholar] [CrossRef]
- Pedersen, M.L.; Frank, M.J.; Biele, G. The drift diffusion model as the choice rule in reinforcement learning. Psychon. Bull. Rev. 2017, 24, 1234–1251. [Google Scholar] [CrossRef] [PubMed]
- Wagenmakers, E.-J.; Wetzels, R.; Borsboom, D.; van der Maas, H.L.J. Why psychologists must change the way they analyze their data: The case of psi: Comment on Bem (2011). J. Pers. Soc. Psychol. 2011, 100, 426–432. [Google Scholar] [CrossRef] [PubMed]
- Willemssen, R.; Falkenstein, M.; Schwarz, M.; Müller, T.; Beste, C. Effects of aging, Parkinson’s disease, and dopaminergic medication on response selection and control. Neurobiol. Aging 2011, 32, 327–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knowlton, B.J.; Mangels, J.A.; Squire, L.R. A neostriatal habit learning system in humans. Science 1996, 273, 1399–1402. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.H.; Knowlton, B.J. The role of the basal ganglia in habit formation. Nat. Rev. Neurosci. 2006, 7, 464–476. [Google Scholar] [CrossRef]
- Shohamy, D.; Myers, C.E.; Kalanithi, J.; Gluck, M.A. Basal ganglia and dopamine contributions to probabilistic category learning. Neurosci. Biobehav. Rev. 2008, 32, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Floresco, S.B.; Magyar, O. Mesocortical dopamine modulation of executive functions: Beyond working memory. Psychopharmacology 2006, 188, 567–585. [Google Scholar] [CrossRef]
- Müller, J.; Dreisbach, G.; Goschke, T.; Hensch, T.; Lesch, K.-P.; Brocke, B. Dopamine and cognitive control: The prospect of monetary gains influences the balance between flexibility and stability in a set-shifting paradigm. Eur. J. Neurosci. 2007, 26, 3661–3668. [Google Scholar] [CrossRef]
- Goschke, T.; Bolte, A. Emotional modulation of control dilemmas: The role of positive affect, reward, and dopamine in cognitive stability and flexibility. Neuropsychologia 2014, 62, 403–423. [Google Scholar] [CrossRef]
- Shohamy, D.; Adcock, R.A. Dopamine and adaptive memory. Trends Cogn. Sci. 2010, 14, 464–472. [Google Scholar] [CrossRef] [PubMed]
- Aarts, E.; Nusselein, A.A.M.; Smittenaar, P.; Helmich, R.C.; Bloem, B.R.; Cools, R. Greater striatal responses to medication in Parkinson׳s disease are associated with better task-switching but worse reward performance. Neuropsychologia 2014, 62, 390–397. [Google Scholar] [CrossRef] [PubMed]
- Beste, C.; Willemssen, R.; Saft, C.; Falkenstein, M. Response inhibition subprocesses and dopaminergic pathways: Basal ganglia disease effects. Neuropsychologia 2010, 48, 366–373. [Google Scholar] [CrossRef] [PubMed]
- Barceló, F.; Knight, R.T. Both random and perseverative errors underlie WCST deficits in prefrontal patients. Neuropsychologia 2002, 40, 349–356. [Google Scholar] [CrossRef]
- Albin, R.L.; Leventhal, D.K. The missing, the short, and the long: Levodopa responses and dopamine actions. Ann. Neurol. 2017, 82, 4–19. [Google Scholar] [CrossRef]
- Beste, C.; Stock, A.-K.; Epplen, J.T.; Arning, L. Dissociable electrophysiological subprocesses during response inhibition are differentially modulated by dopamine D1 and D2 receptors. Eur. Neuropsychopharmacol. 2016, 26, 1029–1036. [Google Scholar] [CrossRef]
- Eisenegger, C.; Naef, M.; Linssen, A.; Clark, L.; Gandamaneni, P.K.; Müller, U.; Robbins, T.W. Role of dopamine D2 receptors in human reinforcement learning. Neuropsychopharmacology 2014, 39, 2366–2375. [Google Scholar] [CrossRef]
- Bensmann, W.; Zink, N.; Arning, L.; Beste, C.; Stock, A.-K. Dopamine D1, but not D2, signaling protects mental representations from distracting bottom-up influences. Neuroimage 2020, 204, 116243. [Google Scholar] [CrossRef]
- Freitas, S.; Simões, M.R.; Alves, L.; Santana, I. Montreal Cognitive Assessment: Validation study for Mild Cognitive Impairment and Alzheimer Disease. Alzheimer Dis. Assoc. Disord. 2013, 27, 37–43. [Google Scholar] [CrossRef]
- Litvan, I.; Goldman, J.G.; Tröster, A.I.; Schmand, B.A.; Weintraub, D.; Petersen, R.C.; Mollenhauer, B.; Adler, C.H.; Marder, K.; Williams-Gray, C.H.; et al. Diagnostic criteria for mild cognitive impairment in Parkinson’s disease: Movement Disorder Society Task Force guidelines. Mov. Disord. 2012, 27, 349–356. [Google Scholar] [CrossRef] [Green Version]
- Palminteri, S.; Wyart, V.; Koechlin, E. The importance of falsification in computational cognitive modeling. Trends Cogn. Sci. 2017, 21, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Schretlen, D.J. Modified Wisconsin Card Sorting Test (M-WCST): Professional Manual; Psychological Assessment Resources Inc.: Lutz, FL, USA, 2010. [Google Scholar]
- Kongs, S.K.; Thompson, L.L.; Iverson, G.L.; Heaton, R.K. WCST-64: Wisconsin Card Sorting Test-64 Card Version: Professional Manual; Psychological Assessment Resources Inc.: Lutz, FL, USA, 2000. [Google Scholar]
- Nelson, H.E. A modified card sorting test sensitive to frontal lobe defects. Cortex 1976, 12, 313–324. [Google Scholar] [CrossRef]
- Kruschke, J.K. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Tomlinson, C.L.; Stowe, R.; Patel, S.; Rick, C.; Gray, R.; Clarke, C.E. Systematic review of levodopa dose equivalency reporting in Parkinson’s disease. Mov. Disord. 2010, 25, 2649–2653. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, K.-H.; Metzler, P. Wortschatztest: WST.; Beltz Test: Göttingen, Germany, 1992. [Google Scholar]
- Marin, R.S.; Biedrzycki, R.C.; Firinciogullari, S. Reliability and validity of the apathy evaluation scale. Psychiatry Res. 1991, 38, 143–162. [Google Scholar] [CrossRef]
- Beck, A.T.; Steer, R.A.; Ball, R.; Ranieri, W.F. Comparison of Beck Depression Inventories-IA and-II in psychiatric outpatients. J. Pers. Assess. 1996, 67, 588–597. [Google Scholar] [CrossRef]
- Derogatis, L.R. Brief Symptom Inventory 18: Administration, Scoring and Procedures Manual; NCS Pearson Inc.: Minneapolis, MN, USA, 2001. [Google Scholar]
- Ware, J.E.; Sherbourne, C.D. The MOS 36-item short-form health survey (SF-36). I. Conceptual framework and item selection. Med. Care 1992, 30, 473–483. [Google Scholar] [CrossRef]
- Steinberg, L.; Sharp, C.; Stanford, M.S.; Tharp, A.T. New tricks for an old measure: The development of the Barratt Impulsiveness Scale–Brief (BIS-Brief). Psychol. Assess. 2013, 25, 216–226. [Google Scholar] [CrossRef]
- Dickman, S.J. Functional and dysfunctional impulsivity: Personality and cognitive correlates. J. Pers. Soc. Psychol. 1990, 58, 95–102. [Google Scholar] [CrossRef]
- Weintraub, D.; Mamikonyan, E.; Papay, K.; Shea, J.A.; Xie, S.X.; Siderowf, A. Questionnaire for impulsive-compulsive disorders in Parkinson’s Disease-Rating Scale. Mov. Disord. 2012, 27, 242–247. [Google Scholar] [CrossRef] [Green Version]
- Raine, A.; Benishay, D. The SPQ-B: A brief screening instrument for schizotypal personality disorder. J. Pers. Disord. 1995, 9, 346–355. [Google Scholar] [CrossRef]
- Ahn, W.-Y.; Krawitz, A.; Kim, W.; Busemeyer, J.R.; Brown, J.W. A model-based fMRI analysis with hierarchical Bayesian parameter estimation. J. Neurosci. Psychol. Econ. 2011, 4, 95–110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, M.D. How cognitive modeling can benefit from hierarchical Bayesian models. J. Math. Psychol. 2011, 55, 1–7. [Google Scholar] [CrossRef]
- Lee, M.D.; Wagenmakers, E.-J. Bayesian Cognitive Modeling: A Practical Course; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rouder, J.N.; Lu, J. An introduction to Bayesian hierarchical models with an application in the theory of signal detection. Psychon. Bull. Rev. 2005, 12, 573–604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shiffrin, R.; Lee, M.D.; Kim, W.; Wagenmakers, E.-J. A survey of model evaluation approaches with a tutorial on hierarchical Bayesian methods. Cogn. Sci. 2008, 32, 1248–1284. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R interface to Stan 2018. Available online: https://www.mc-stan.org (accessed on 1 November 2019).
- Betancourt, M.J.; Girolami, M. Hamiltonian Monte Carlo for hierarchical models. In Current Trends in Bayesian Methodology with Applications; Upadhyay, S.K., Umesh, S., Dey, D.K., Loganathan, A., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 79–97. [Google Scholar]
- Sharp, M.E.; Foerde, K.; Daw, N.D.; Shohamy, D. Dopamine selectively remediates “model-based” reward learning: A computational approach. Brain 2016, 139, 355–364. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Marsman, M.; Wagenmakers, E.-J. Three insights from a Bayesian interpretation of the one-sided P value. Educ. Psychol. Meas. 2017, 77, 529–539. [Google Scholar] [CrossRef]

| Effects | p(Inclusion) | p(Inclusion|Data) | BFinclusion |
|---|---|---|---|
| Error Type | 0.600 | >0.999 | >1000 *** |
| Disease | 0.600 | 0.404 | 0.452 |
| Error Type x Disease | 0.200 | 0.104 | 0.465 |
| Effects | p(Inclusion) | p(Iinclusion|Data) | BFinclusion |
|---|---|---|---|
| Error Type | 0.600 | >0.999 | >1000 *** |
| Medication | 0.600 | 0.270 | 0.247 |
| Error Type x Medication | 0.200 | 0.081 | 0.351 |
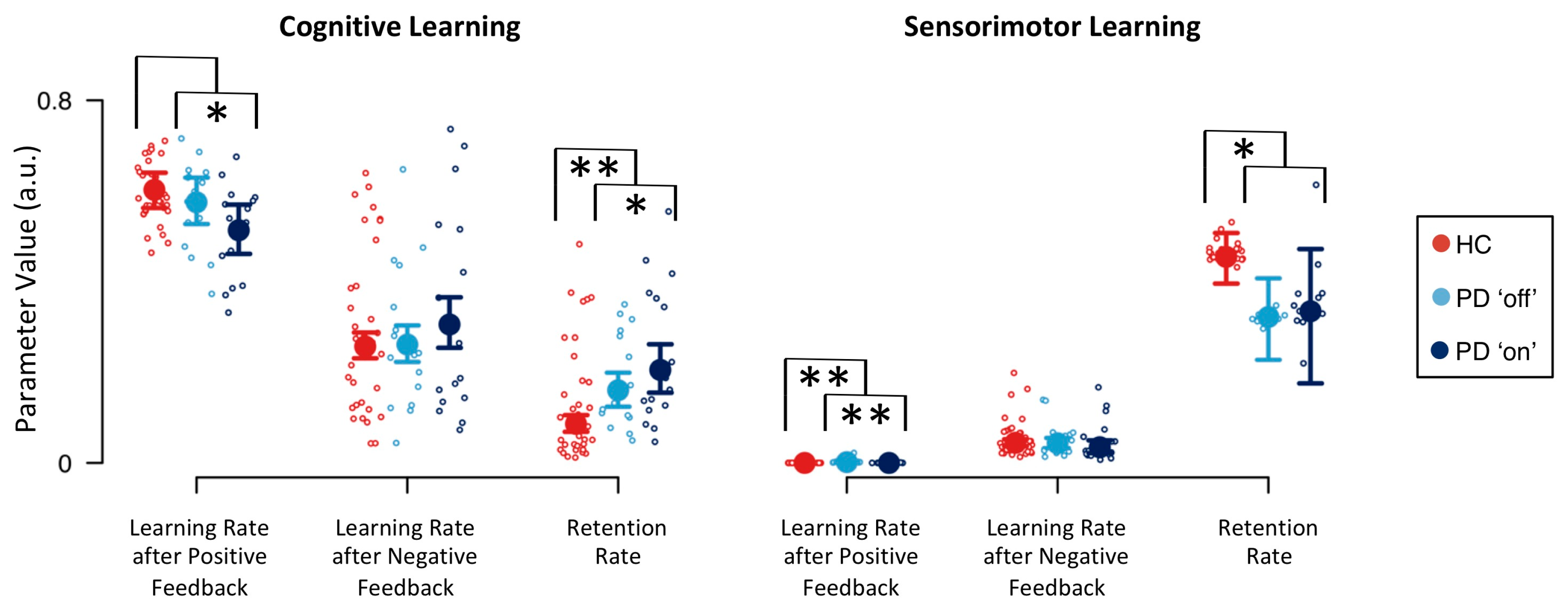
| Parameter | Definition | Effect | |
|---|---|---|---|
| Disease | Medication | ||
| cognitive learning rate following positive feedback | 1.519 | 0.282 * | |
| cognitive learning rate following negative feedback | 0.940 | 2.676 | |
| cognitive retention rate | 0.095 ** | 3.323 * | |
| sensorimotor learning rate following positive feedback | 0.073 ** | 0.077 ** | |
| sensorimotor learning rate following negative feedback | 1.137 | 0.521 | |
| sensorimotor retention rate | 4.725 * | 1.075 | |
| inverse temperature parameter | 0.551 | 0.720 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinke, A.; Lange, F.; Seer, C.; Hendel, M.K.; Kopp, B. Computational Modeling for Neuropsychological Assessment of Bradyphrenia in Parkinson’s Disease. J. Clin. Med. 2020, 9, 1158. https://doi.org/10.3390/jcm9041158
Steinke A, Lange F, Seer C, Hendel MK, Kopp B. Computational Modeling for Neuropsychological Assessment of Bradyphrenia in Parkinson’s Disease. Journal of Clinical Medicine. 2020; 9(4):1158. https://doi.org/10.3390/jcm9041158
Chicago/Turabian StyleSteinke, Alexander, Florian Lange, Caroline Seer, Merle K. Hendel, and Bruno Kopp. 2020. "Computational Modeling for Neuropsychological Assessment of Bradyphrenia in Parkinson’s Disease" Journal of Clinical Medicine 9, no. 4: 1158. https://doi.org/10.3390/jcm9041158
APA StyleSteinke, A., Lange, F., Seer, C., Hendel, M. K., & Kopp, B. (2020). Computational Modeling for Neuropsychological Assessment of Bradyphrenia in Parkinson’s Disease. Journal of Clinical Medicine, 9(4), 1158. https://doi.org/10.3390/jcm9041158