Quantifying the Landscape and Transition Paths for Proliferation–Quiescence Fate Decisions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling
2.2. Self Consistent Mean Field Approximation
2.3. Transition Paths
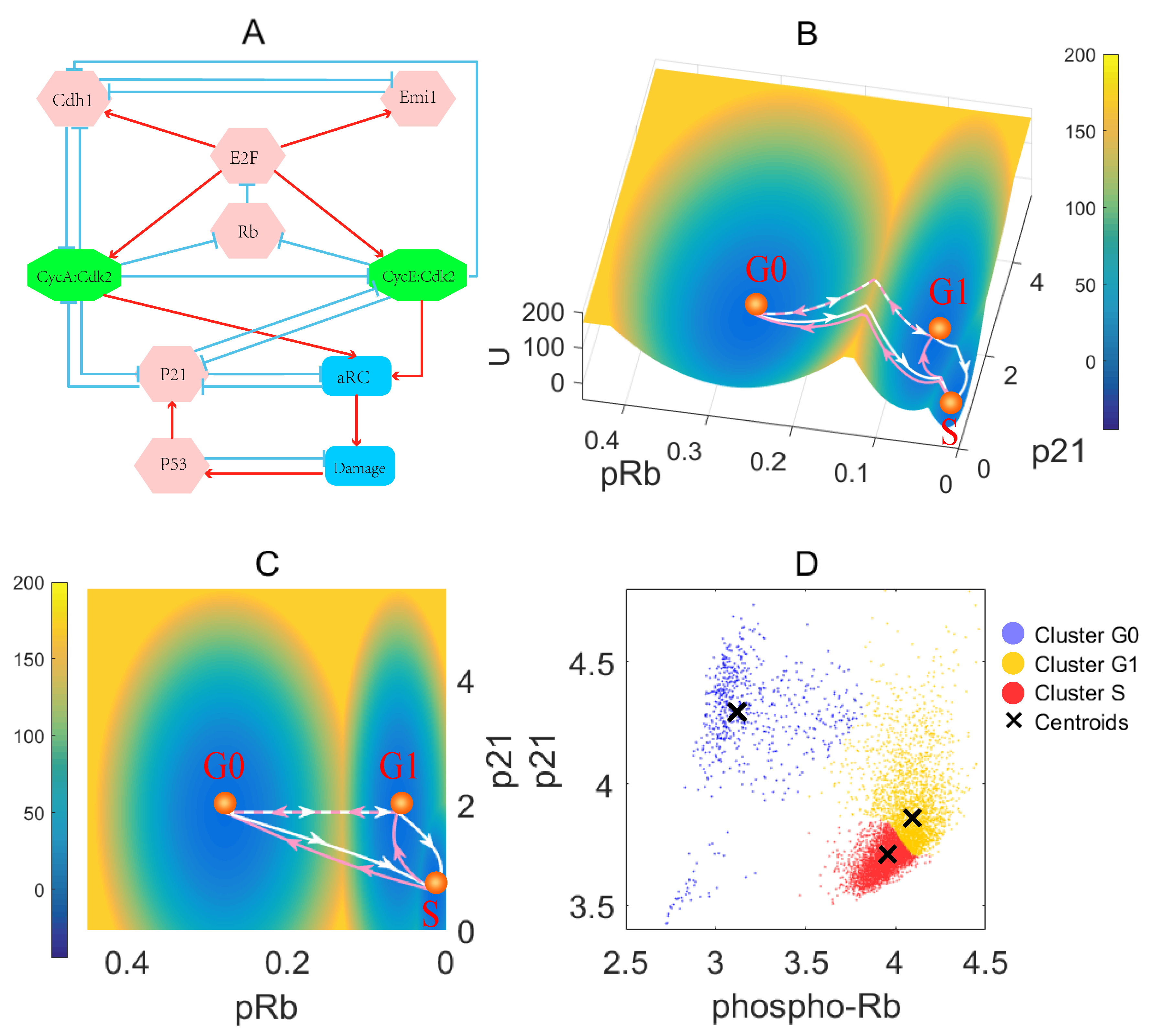
2.4. Processing Single-Cell Data with a K-Means Algorithm
3. Results
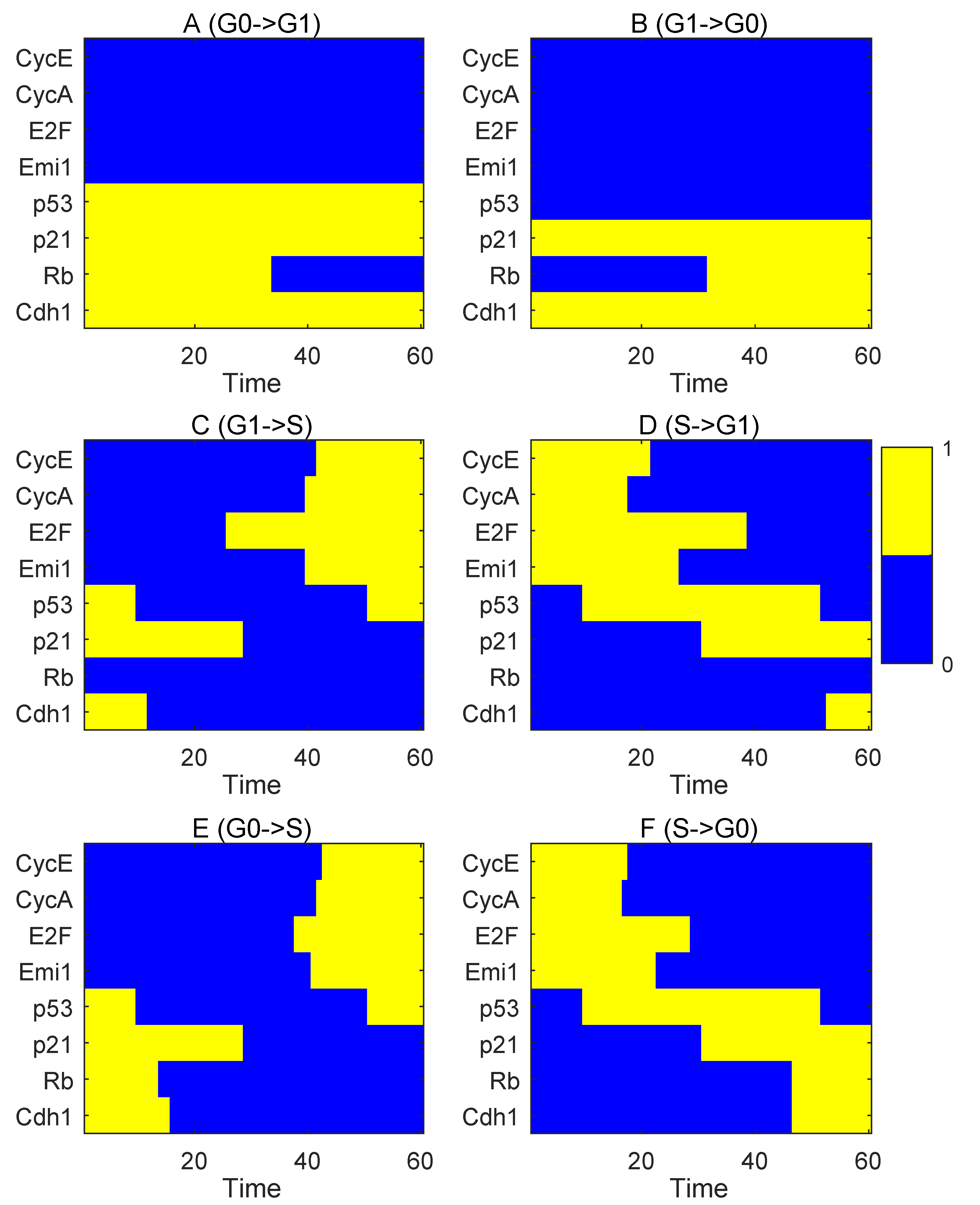
3.1. Landscape and Path for the Proliferation–Quiescence Decision
3.2. Rb Controls RP and P21 Governs the G1/S Checkpoint
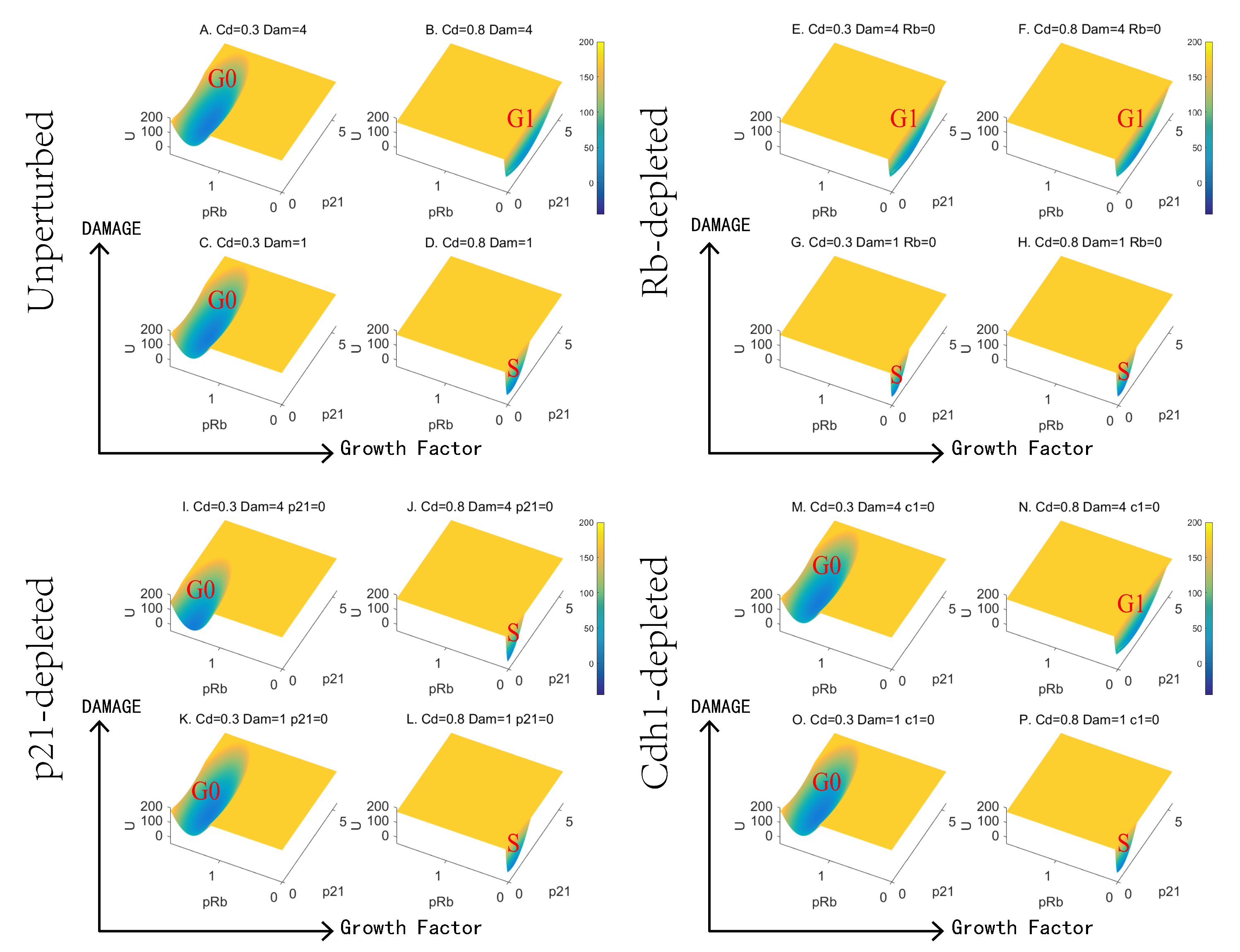
3.3. Landscape Quantifies the Effects of Growth Factor and DNA Damage
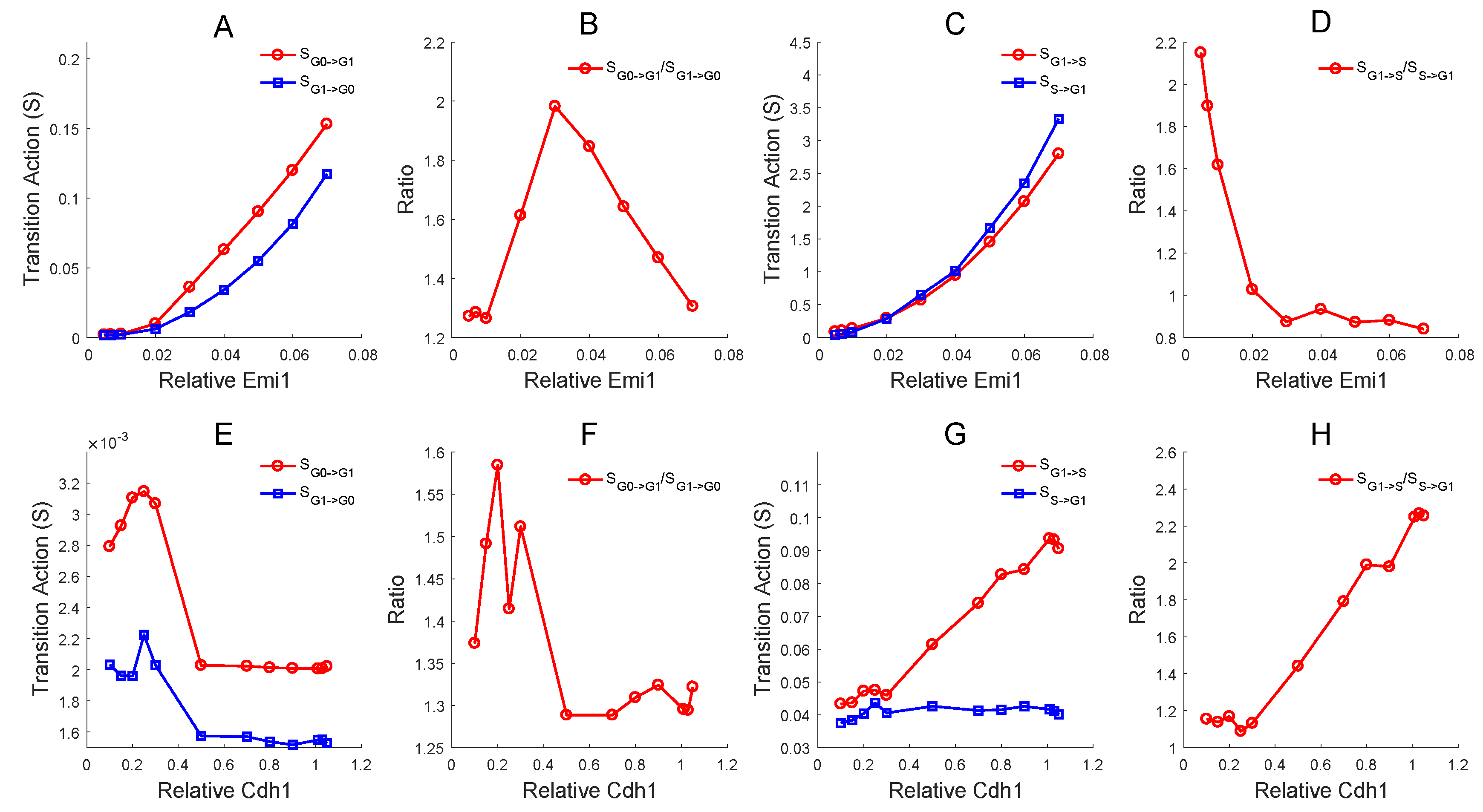
3.4. The Disparate Roles of Emi1 and Cdh1 in G0 to G1 and G1 to S Transitions
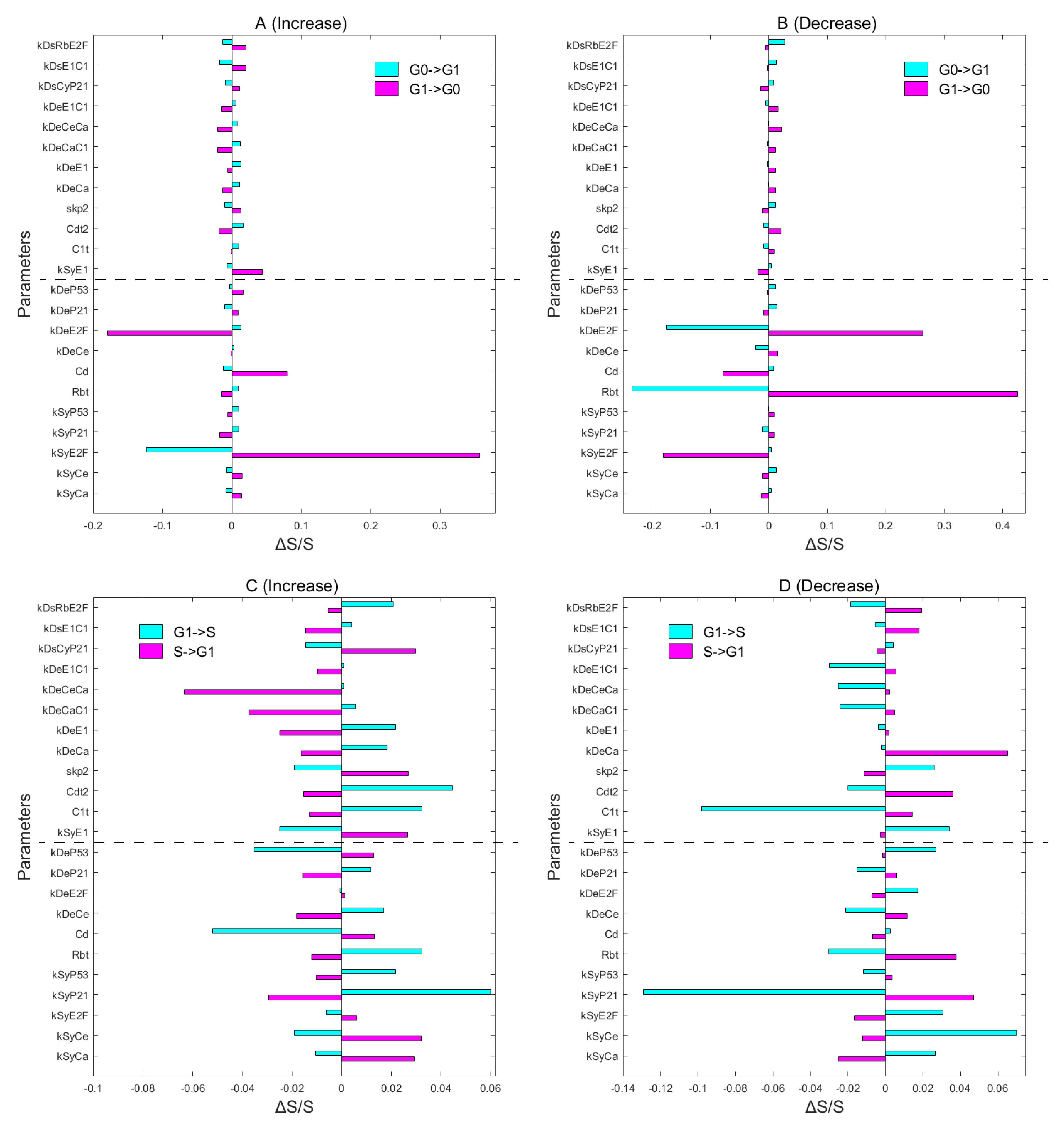
3.5. Global Sensitivity Analysis on Key Regulations and Network Structure
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Modeling
Appendix A.1. Restriction Point and G1/S Checkpoint
Appendix A.2. Synthesis and Degradation of Cyclin and the Inhibition of Emi1 to APC/C Cdh1
Appendix A.3. Activity of P21 and the Inhibition on Cdk2
Appendix A.4. Activation of DNA Replication, DNA Damage and Repair
Appendix B. Model Parameters
| Value | Value | ||||
|---|---|---|---|---|---|
| Parameter | Description | Used in | from | Unit | Reference |
| This Work | Ref. [12] | ||||
| kSyCa | constitutive CycA synthesis | 0.008 | 0.02 | 1/min | estimated |
| kSyCe | constitutive CycE synthesis | 0.004 | 0.01 | 1/min | estimated |
| kSyE2F | constitutive E2F synthesis | 0.0642 | 0.03 | AU/min | estimated |
| kSyE1 | constitutive Emi1 synthesis | 0.005 | 0.005 | 1/min | [12] |
| kSyP21 | constitutive p21 synthesis | 0.002 | 0.002 | AU/min | [12] |
| kSyP53 | constitutive p53 synthesis | 0.05 | 0.05 | AU/min | [12] |
| C1t | total level | 1 | 1 | AU | [12] |
| Rbt | total Rb level | 5.58 | 5 | AU | estimated |
| Cd | relative CycD:Cdk4/6 level | 0.65 | 0.65 | AU | [12] |
| Cdt2 | relative level | 1 | 1 | -/min | [12] |
| skp2 | relative level | 1 | 1 | -/min | [12] |
| kDeCa | constitutive CycA degradation | 0.015 | 0.01 | 1/min | estimated |
| kDeCe | constitutive CycE degradation | 0.006 | 0.004 | 1/min | estimated |
| kDeE2F | constitutive E2F degradation | 0.05 | 0.05 | 1/min | [12] |
| kDeE1 | constitutive Emi1 degradation | 0.0025 | 0.0005 | 1/min | estimated |
| kDeP21 | constitutive p21 degradation | 0.0025 | 0.0025 | 1/min | [12] |
| kDeP53 | constitutive p53 degradation | 0.05 | 0.05 | AU/min | [12] |
| kDeCaC1 | -mediated CycA degradation | 3 | 2 | 1/(AU·min) | estimated |
| kDeCeCa | CycA:Cdk2-mediated CycE degradation | 0.03 | 0.015 | 1/(AU·min) | estimated |
| kDeE1C1 | -mediated Emi1 degradation | 0.005 | 0.005 | 1/min | [12] |
| kDsCyP21 | dissociation of cyclin:Cdk2:p21 complexes | 0.05 | 0.05 | 1/min | [12] |
| kDsE1C1 | dissociation of Emi1: complexes | 0.01 | 0.01 | 1/min | [12] |
| kDsRbE2F | dissociation of Rb:E2F complexes | 0.005 | 0.005 | 1/min | [12] |
| kPhRbCa | CycA:Cdk2-mediated Rb phosphorylation | 0.18 | 0.3 | 1/(AU·min) | estimated |
| kPhRbCd | CycD:Cdk4/6-mediated Rb phosphorylation | 0.2 | 0.2 | 1/(AU·min) | [12] |
| kPhRbCe | CycE:Cdk2-mediated Rb phosphorylation | 0.18 | 0.3 | 1/(AU·min) | estimated |
| kAsRbE2F | association of Rb and E2F | 18 | 5 | 1/(AU·min) | estimated |
| kAsE1C1 | association of Emi1 and | 10 | 10 | 1/(AU·min) | [12] |
| kPhC1 | Constitutive phosphorylation | 0.01 | 0 | 1/min | estimated |
| kPhC1Ca | CycA:Cdk2-mediated phosphorylation | 1 | 1 | 1/(AU·min) | [12] |
| kPhC1Ce | CycE:Cdk2-mediated phosphorylation | 0.01 | 0.01 | 1/(AU·min) | [12] |
| kAsCyP21 | association of p21 and cyclin:Cdk2 | 10 | 10 | 1/(AU·min) | [12] |
| kSyE2FE2F | E2F-dependent E2F synthesis | 0.06 | 0.04 | AU/min | estimated |
| kDeP21Cy | cyclin:Cdk2-mediated p21 degradation | 0.01 | 0.007 | 1/(AU·min) | estimated |
| kDeP21RCa | -mediated p21 degradation | 1 | 0.01 | 1/(AU·min) | [12] |
| kDpC1 | dephosphorylation of | 0.05 | 0.05 | 1/min | [12] |
| kDpRb | dephosphorylation of Rb | 0.06 | 0.05 | 1/min | estimated |
| kDpRc | dephosphorylation of primed RCs | 0.05 | 0.05 | 1/min | [12] |
| kPhRc | cyclin:Cdk2-mediated priming of RCs | 0.1 | 0.1 | 1/min | [12] |
| kSyP21P53 | p53-dependent p21 synthesis | 0.008 | 0.008 | 1/min | [12] |
| kSyDNA | DNA synthesis by active RCs | 0.0093 | 0.0093 | 1/min | [12] |
| kGeDam | replication-independent DNA damage | 0.001 | 0.001 | AU/min | [12] |
| kGeDamRCa | replication-dependent DNA damage | 0.012 | 0.012 | 1/min | [12] |
| kReDam | P53-independent DNA damage repair | 0.001 | 0.001 | 1/min | [12] |
| kReDamP53 | P53-dependent DNA damage repair | 0.005 | 0.005 | 1/min | [12] |
| jCy | Cdk2 threshold for RC priming | 1.8 | 1.8 | AU | [12] |
| jDam | DNA damage threshold for repair | 0.5 | 0.5 | AU | [12] |
| jP53 | inhibition constant of p53 degradation | 0.01 | 0.01 | AU | [12] |
| jSyE2F | Michealis-Menten constant for E2F synthesis | 0.2 | 0.2 | AU | [12] |
| kAsPcP21 | association of PCNA and p21 | 100 | 100 | 1/(AU·min) | [12] |
| kAsRcPc | association of primed RCs and PCNA | 0.01 | 0.01 | 1/(AU·min) | [12] |
| kDsPcP21 | dissociation of PCNA:p21 complexes | 0.01 | 0.01 | 1/min | [12] |
| kDsRcPc | dissociation of :PCNA complexes | 0.001 | 0.001 | 1/min | [12] |
| kExPc | PCNA export from the nucleus | 0.006 | 0.006 | 1/min | [12] |
| kImPc | PCNA import into the nucleus | 0.003 | 0.003 | AU/min | [12] |
| n | hill coefficient for priming of RCs | 6 | 6 | 0.29 | [12] |
References
- Murray, A.W. Recycling the cell cycle: Cyclins revisited. Cell 2004, 116, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Pardee, A.B. A Restriction Point for Control of Normal Animal Cell Proliferation. Proc. Natl. Acad. Sci. USA 1974, 71, 1286–1290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zetterberg, A.; Larsson, O.; Wiman, K.G. What is the restriction point? Curr. Opin. Cell Biol. 1995, 7, 835–842. [Google Scholar] [CrossRef]
- Blagosklonny, M.V.; Pardee, A.B. The restriction point of the cell cycle. Cell Cycle 2002, 1, 103–110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adhikary, S.; Eilers, M. Transcriptional regulation and transformation by Myc proteins. Nat. Rev. Mol. Cell Biol. 2005, 6, 635–645. [Google Scholar] [CrossRef] [PubMed]
- Diehl, J.A.; Cheng, M. Glycogen synthase kinase-3β regulates cyclin D1 proteolysis and subcellular localization. Genes Dev. 1998, 12, 3499–3511. [Google Scholar] [CrossRef] [Green Version]
- Levens, D. Disentangling the MYC web. Proc. Natl. Acad. Sci. USA 2002, 99, 5757–5759. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Hunter, T. Ubiquitylation and proteasomal degradation of the p21Cip1, p27Kip1 and p57Kip2 CDK inhibitors. Cell Cycle 2010, 9, 2342–2352. [Google Scholar] [CrossRef] [Green Version]
- Strausfeld, U.P.; Howell, M.; Descombes, P. Both cyclin A and cyclin E have S-phase promoting (SPF) activity in Xenopus egg extracts. J. Cell Sci. 1996, 109, 1555–1563. [Google Scholar]
- Gérard, C.; Goldbeter, A. Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle. Proc. Natl. Acad. Sci. USA 2009, 106, 21643–21648. [Google Scholar] [CrossRef] [Green Version]
- Gérard, C.; Goldbeter, A. A skeleton model for the network of cyclin-dependent kinases driving the mammalian cell cycle. Interface Focus 2011, 1, 24–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heldt, F.S.; Barr, A.R. A comprehensive model for the proliferation–quiescence decision in response to endogenous DNA damage in human cells. Proc. Natl. Acad. Sci. USA 2018, 115, 2532–2537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pines, J. Cyclins, CDKs and cancer. Semin. Cancer Biol. 1995, 6, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Ezhevsky, S.A.; Nagahara, H. Hypo-phosphorylation of the retinoblastoma protein (pRb) by cyclin D:Cdk4/6 complexes results in active pRb. Proc. Natl. Acad. Sci. USA 1997, 94, 10699–10704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Q.; Liu, X. Overexpression of DOC-1R inhibits cell cycle G1/S transition by repressing CDK2 expression and activation. Int. J. Biol. Sci. 2013, 9, 541–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, L.; Harlow, E.; Meyerson, M. Isolation of the human cdk2 gene that encodes the cyclin A- and adenovirus E1A-associated p33 kinase. Nature 1991, 353, 174–177. [Google Scholar] [CrossRef]
- Duliac, V.; Kaufmann, W.K. p53-dependent inhibition of cyclin-dependent kinase activities in human fibroblasts during radiation-induced G1 arrest. Cell 1994, 76, 1013–1023. [Google Scholar] [CrossRef]
- Cayrol, C.; Knibiehler, M.; Ducommun, B. p21 binding to PCNA causes G1 and G2 cell cycle arrest in p53-deficient cells. Oncogene 1998, 16, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, R.A. The Retinoblastoma Protein and Cell Cycle Control. Cell 1995, 81, 323–330. [Google Scholar] [CrossRef] [Green Version]
- Varija, N.B.; Erin, D.W.; Christina, S.M. Regulation of E2F1 by APC/CCdh1 via K11 linkage-specific ubiquitin chain formation. Cell Cycle 2012, 11, 2030–2038. [Google Scholar]
- Johnson, D.G.; Ohtani, K.; Nevins, J.R. Autoregulatory control of E2F1 expression in response to positive and negative regulators of cell cycle progression. Genes Dev. 1994, 8, 1514–1525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reimann, J.D.; Freed, E. Emi1 Is a Mitotic Regulator that Interacts with Cdc20 and Inhibits the Anaphase Promoting Complex. Cell 2001, 105, 645–655. [Google Scholar] [CrossRef] [Green Version]
- Waddington, C.H. The Strategy of the Genes: A Discussion of Some Aspects of Theoretical Biology; Allen and Unwin: London, UK, 1957; p. 290. [Google Scholar]
- Wolynes, P.G.; Frauenfelder, H. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar]
- Wang, J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 2015, 64, 1–137. [Google Scholar]
- Lv, C.; Li, X. Energy Landscape Reveals That the Budding Yeast Cell Cycle Is a Robust and Adaptive Multi-stageProcess. PLoS Comput. Biol. 2015, 11, e1004156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Wang, J. Landscape and flux reveal a new global view and physical quantification of mammalian cell cycle. Proc. Natl. Acad. Sci. USA 2014, 111, 14130–14135. [Google Scholar] [CrossRef] [Green Version]
- Ge, H.; Qian, H. Mesoscopic kinetic basis of macroscopic chemical thermodynamics: A mathematical theory. Phys. Rev. E 2016, 94, 052150. [Google Scholar] [CrossRef] [Green Version]
- Ao, P. Emerging of Stochastic Dynamical Equalities and Steady State Thermodynamics from Darwinian Dynamics. Commun. Theor. Phys. 2008, 49, 1073. [Google Scholar] [CrossRef] [Green Version]
- Gookin, S.; Min, M. A map of protein dynamics during cell-cycle progression and cell-cycle exit. PLoS Biol. 2017, 15, 1–25. [Google Scholar]
- Li, C.; Wang, J. Quantifying Cell Fate Decisions for Differentiation and Reprogramming of a Human Stem Cell Network: Landscape and Biological Paths. PLoS Comput. Biol. 2013, 9, e1003165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C. Identifying the optimal anticancer targets from the landscape of a cancer–immunity interaction network. Phys. Chem. Chem. Phys. 2017, 19, 7642–7651. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, K.; Xu, L.; Wang, E.K. Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Natl. Acad. Sci. USA 2011, 108, 8257–8262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cappell, S.D.; Mark, K.G. EMI1 switches from being a substrate to an inhibitor of APC/CCDH1 to start the cell cycle. Nature 2018, 558, 313–317. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Mao, Y.L. Robustness of cell cycle control and flexible orders of signaling events. Sci. Rep. 2015, 5, 1–13. [Google Scholar]
- Novak, B.; Tyson, J.J.; Gyorffy, B. Irreversible cell-cycle transitions are due to systems level feedback. Nat. Cell Biol. 2007, 9, 724–728. [Google Scholar] [CrossRef]
- Sasai, M.; Wolynes, P.G. Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. USA 2003, 100, 2374–2379. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Wolynes, P.G. Stem cell differentiation as a many-body problem. Proc. Natl. Acad. Sci. USA 2014, 111, 10185–10190. [Google Scholar] [CrossRef] [Green Version]
- Wolynes, P.G.; Walczak, A.M. Self-Consistent Proteomic Field Theory of Stochastic Gene Switches. Biophys. J. 2005, 88, 828–850. [Google Scholar]
- Kampen, N.G.V. Stochastic Processes in Chemistry and Physics, 1st ed.; North Holland: Amsterdam, The Netherlands, 1992; pp. 120–127. [Google Scholar]
- Hu, G. Stochastic Forces and Nonlinear Systems; Shanghai Scientific and Technological Education Press: Shanghai, China, 1994; pp. 68–74. [Google Scholar]
- Wang, J.; Xu, L. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 2008, 105, 12271–12276. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Baumann, W.; Xing, J.; Xu, L.; Clarke, R.; Tyson, J. Mathematical models of the transitions between endocrine therapy responsive and resistant states in breast cancer. J. R Soc. Interface 2014, 11, 20140206. [Google Scholar] [CrossRef]
- Ren, W.; Eric, V.E. Minimum action method for the study of rare events. Commun. Pure Appl. Math. 2004, 57, 637–656. [Google Scholar]
- Zhou, X.; Ren, W. Adaptive minimum action method for the study of rare events. J. Chem. Phys. 2008, 128, 104111. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, M.; Weber, M. Random perturbations of dynamical systems and diffusion processes with conservation laws. Probab. Theory Relat. Fields 2004, 128, 441–466. [Google Scholar] [CrossRef]
- Tibshirani, R.; Walther, G. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2002, 63, 411–423. [Google Scholar] [CrossRef]
- Li, C.; Hong, T.; Nie, Q. Quantifying the landscape and kinetic paths for epithelial-mesenchymal transition from a core circuit. Phys. Chem. Chem. Phys. 2016, 18, 17949–17956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bahmani, B.; Moseley, B. Scalable K-Means++. Comput. Sci. 2012, 5, 622–633. [Google Scholar] [CrossRef]
- Heldt, F.S.; Barr, A.R. A Dynamical Framework for the All-or-None G1/S Transition. Cell Syst. 2016, 27, 27–37. [Google Scholar]
- Ertel, A.; Dean, J.L. RB-pathway disruption in breast cancer. Cell Cycle 2010, 9, 4153–4163. [Google Scholar] [CrossRef]
- Dick, F.; Goodrich, D.; Sage, J. Non-canonical functions of the RB protein in cancer. Nat. Rev. Cancer 2018, 18, 442–451. [Google Scholar] [CrossRef]
- Frolov, M.V.; Dyson, N.J. Molecular mechanisms of E2F-dependent activation and pRB-mediated repression. Cell Sci. 2004, 117, 2173–2181. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Lee, T.J. A bistable Rb-E2F switch underlies the restriction point. Nat. Cell Biol. 2008, 10, 476–482. [Google Scholar] [CrossRef]
- Privado, I.M.; Martinez, M.R.; Rebollo, P. E2F1 expression is deregulated and plays an oncogenic role in sporadic Burkitt’ s lymphoma. Cancer Res. 2009, 69, 4052–4058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zielke, N.; Kim, K.J. Control of Drosophila endocycles by E2F and CRL4Cdt2. Nature 2012, 480, 123–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Balazsi, G. A landscape view on the interplay between EMT and cancer metastasis. NPJ Syst. Biol. Appl. 2018, 4, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.Z.; Leone, G.; Tsai, S. Emerging roles of E2Fs in cancer: An exit from cell cycle control. Nat. Rev. Cancer 2009, 9, 785–797. [Google Scholar] [CrossRef] [Green Version]
- Heldt, F.S.; Barr, A.R. DNA damage during S-phase mediates the proliferation-quiescence decision in the subsequent G1 via p21 expression. Nat. Commun. 2017, 8, 14728. [Google Scholar]
- Tamara, A.P.; John, R.D.; Bradley, D.P. The reversibility of mitotic exit in vertebrate cells. Nature 2006, 440, 954–958. [Google Scholar]
- Overton, K.W.; Spencer, S.L. Basal p21 controls population heterogeneity in cycling and quiescent cell cycle states. Proc. Natl. Acad. Sci. USA 2014, 111, E4386–E4393. [Google Scholar] [CrossRef] [Green Version]
- Lafranchi, L.; Harmen, R.D.B. APC/CCdh1 controls CtIP stability during the cell cycle and in response to DNA damage. EMBO J. 2014, 33, 2860–2879. [Google Scholar] [CrossRef] [Green Version]
- Machida, Y.J.; Dutta, A. The APC/C inhibitor, Emi1, is essential for prevention of rereplication. Genes Dev. 2007, 558, 313–317. [Google Scholar] [CrossRef] [Green Version]
- Sorensen, C.S.; Lukas, C. Nonperiodic Activity of the Human Anaphase-Promoting Complex-Cdh1 Ubiquitin Ligase Results in Continuous DNA Synthesis Uncoupled from Mitosis. Mol. Cell Biol. 2000, 20, 7613–7623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duijf, P.; Cato, K.; Tang, L. In vivo overexpression of Emi1 promotes chromosome instability and tumorigenesis. Oncogene 2016, 35, 5446–5455. [Google Scholar] [CrossRef]
- Steven, D.; Cappell, M.C. Irreversible APCCdh1 Inactivation Underlies the Point of No Return for Cell-Cycle Entry. Cell 1974, 71, 1286–1290. [Google Scholar]
- Marti, A.; Wirbelauer, C. Interaction between ubiquitin-protein ligase SCFSKP2 and E2F-1 underlies the regulation of E2F-1 degradation. Nat. Cell Biol. 1999, 1, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Starostina, N.G.; Kipreos, E.T. Regulation of CIP/KIP CKIs by ubiquitin-mediated proteolysis. Trends Cell Biol. 2012, 22, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Sheng, C.; Mendler, I.H.; Rieke, S. PCNA-Mediated Degradation of p21 Coordinates the DNA Damage Response and Cell Cycle Regulation in Individual Cells. Cell Rep. 2019, 27, 48–58. [Google Scholar] [CrossRef] [Green Version]
- Assoian, R.K.; Yung, Y. A reciprocal relationship between Rb and Skp2: Implications for restriction point control, signal transduction to the cell cycle, and cancer. Cell Cycle 2008, 7, 24–27. [Google Scholar] [CrossRef] [Green Version]
- Shibutani, S.T. Intrinsic Negative Cell Cycle Regulation Provided by PIP Box- and Cul4Cdt2-Mediated Destruction of E2F1 during S Phase. Dev. Cell 2008, 15, 890–900. [Google Scholar] [CrossRef] [Green Version]
- Chung, M.; Liu, C.; Yang, H.W. Transient Hysteresis in CDK4/6 Activity Underlies Passage of the Restriction Point in G1. Mol. Cell 2019, 76, 1–12. [Google Scholar] [CrossRef]
- Liu, L.; Liu, K. Two Transcripts of FBXO5 Promote Migration and Osteogenic Differentiation of Human Periodontal Ligament Mesenchymal Stem Cells. Biomed. Res. Int. 2018, 2018, 7849294. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Trusina, A. Defining Network Topologies that Can Achieve Biochemical Adaptation. Cell 2009, 138, 760–773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hari, K.; Sabuwala, B. Identifying Inhibitors of Epithelial-Mesenchymal Plasticity Using a Network Topology-Based Approach. NPJ Syst. Biol. Appl. 2020, 6, 15. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Li, C. Quantifying the Landscape and Transition Paths for Proliferation–Quiescence Fate Decisions. J. Clin. Med. 2020, 9, 2582. https://doi.org/10.3390/jcm9082582
Chen Z, Li C. Quantifying the Landscape and Transition Paths for Proliferation–Quiescence Fate Decisions. Journal of Clinical Medicine. 2020; 9(8):2582. https://doi.org/10.3390/jcm9082582
Chicago/Turabian StyleChen, Zihao, and Chunhe Li. 2020. "Quantifying the Landscape and Transition Paths for Proliferation–Quiescence Fate Decisions" Journal of Clinical Medicine 9, no. 8: 2582. https://doi.org/10.3390/jcm9082582
APA StyleChen, Z., & Li, C. (2020). Quantifying the Landscape and Transition Paths for Proliferation–Quiescence Fate Decisions. Journal of Clinical Medicine, 9(8), 2582. https://doi.org/10.3390/jcm9082582




