Fusion of Feature Selection Methods and Regression Algorithms for Predicting the Canopy Water Content of Rice Based on Hyperspectral Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Hyperspectral Images Acquisition
2.3. Image Preprocessing
2.4. Canopy Water Content Computation
2.5. Dataset and Data Analysis Software
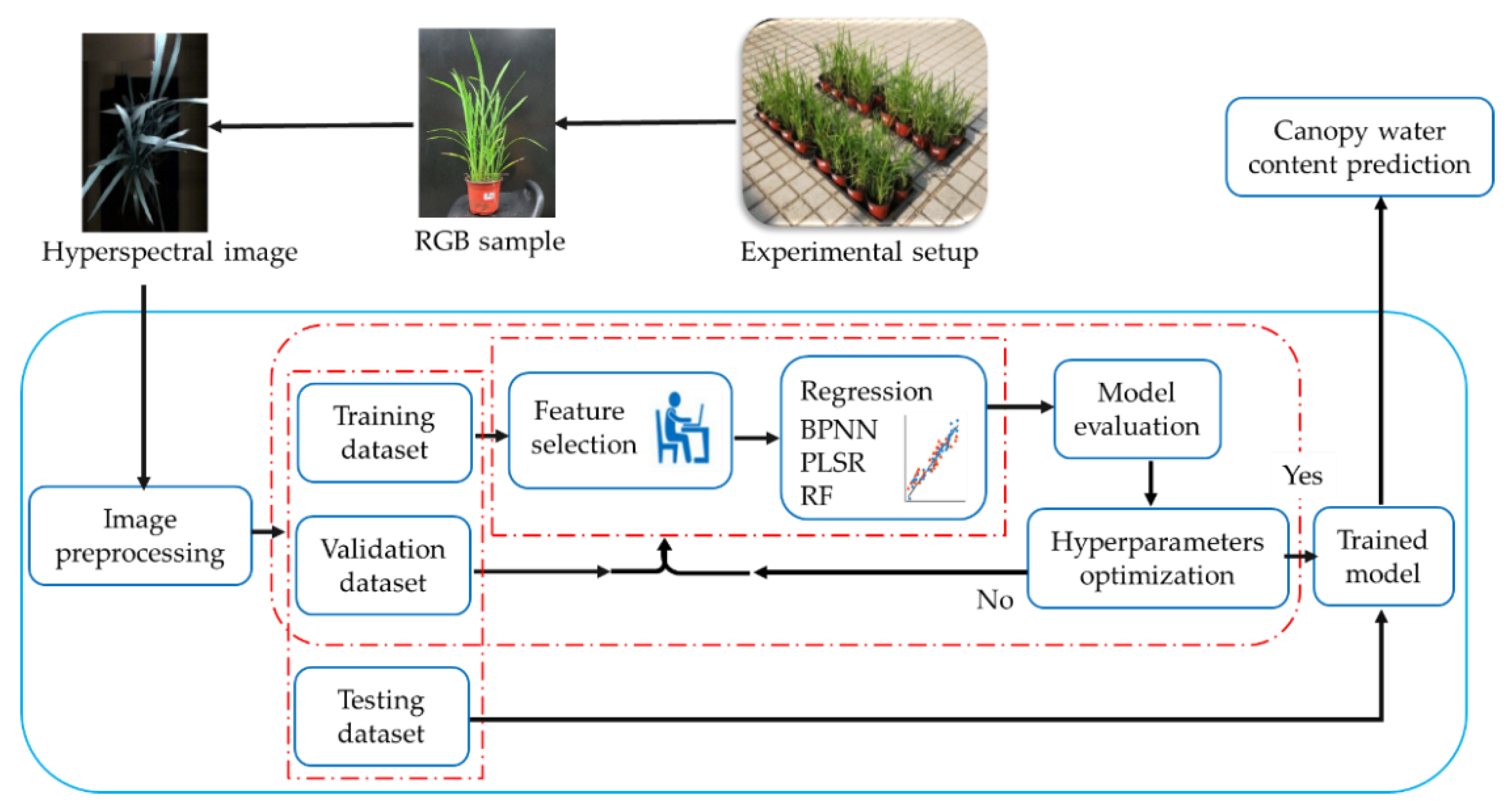
2.6. Overview of the Proposed Methods
2.7. The Spectral Features
2.7.1. Vegetation Indices
2.7.2. Spectral Bands
2.7.3. Feature Extracted from PCA
2.8. Training Models Based on MF and Feature Selection
2.8.1. Partial Least Square Regression (PLSR)
2.8.2. Random Forest (RF)
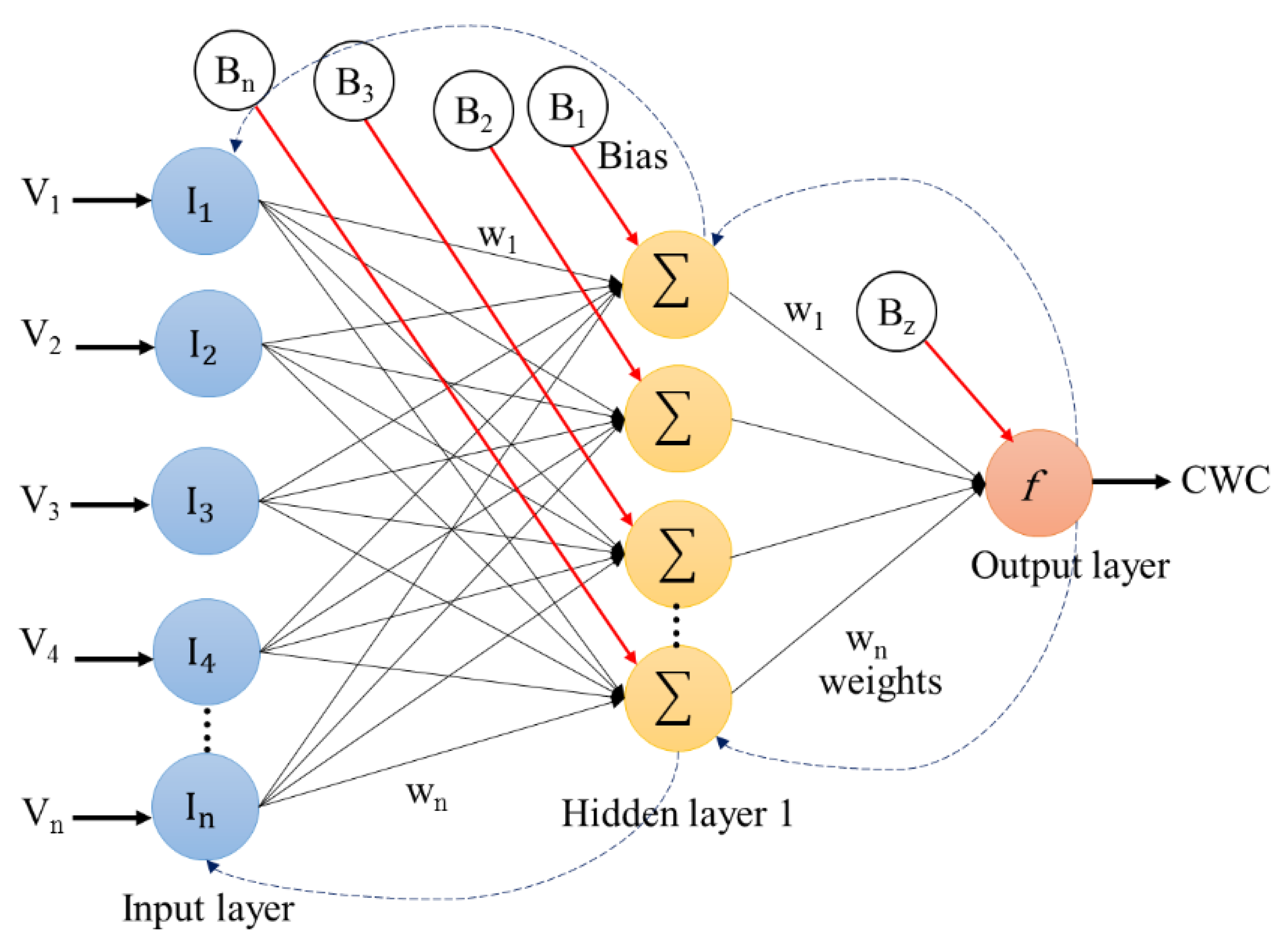
2.8.3. Back-Propagation Neural Network (BPNN)
2.9. Model Evaluation
3. Results and Discussion
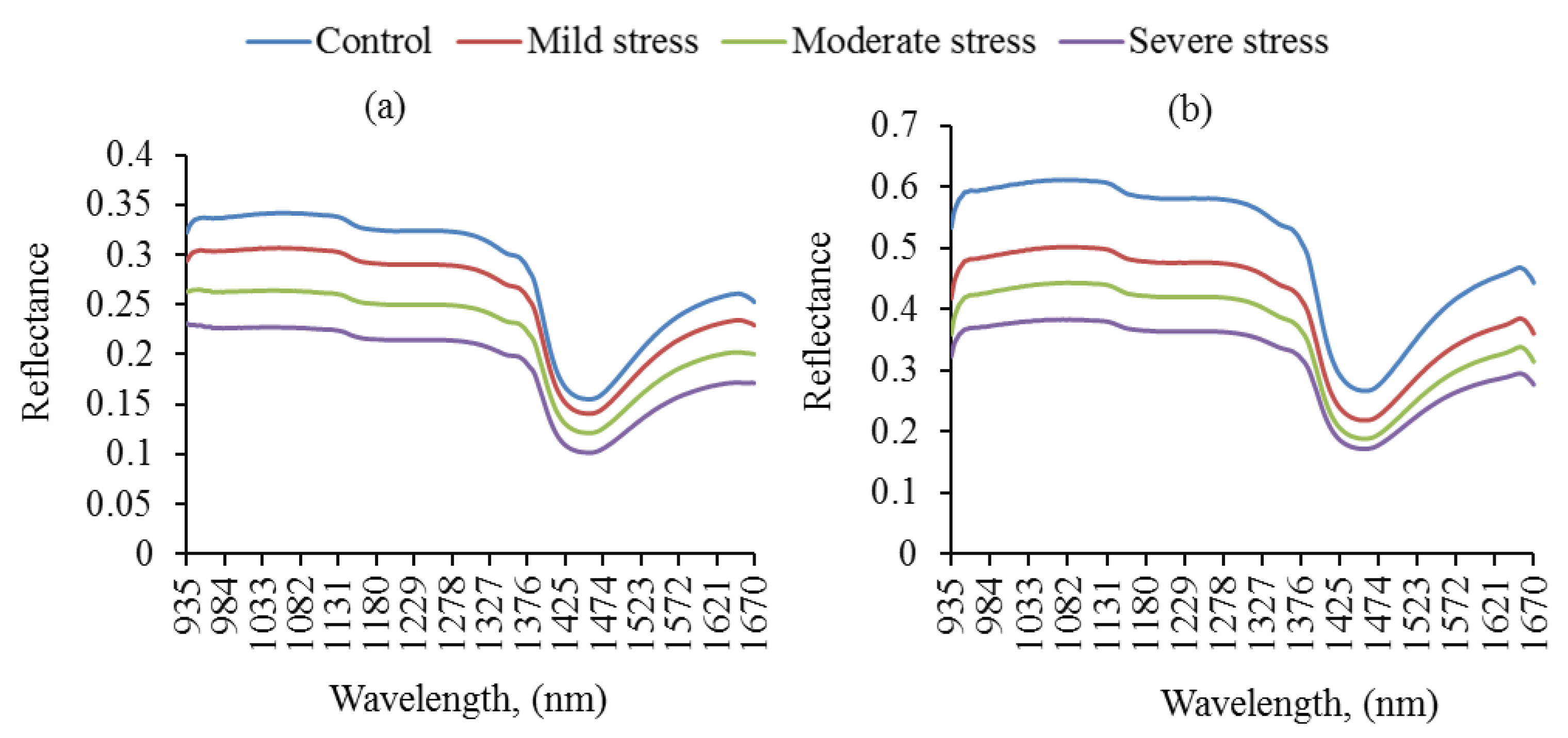
3.1. Effects of Water Deficit Stress on Spectral Reflectance Pattern
3.2. The Features
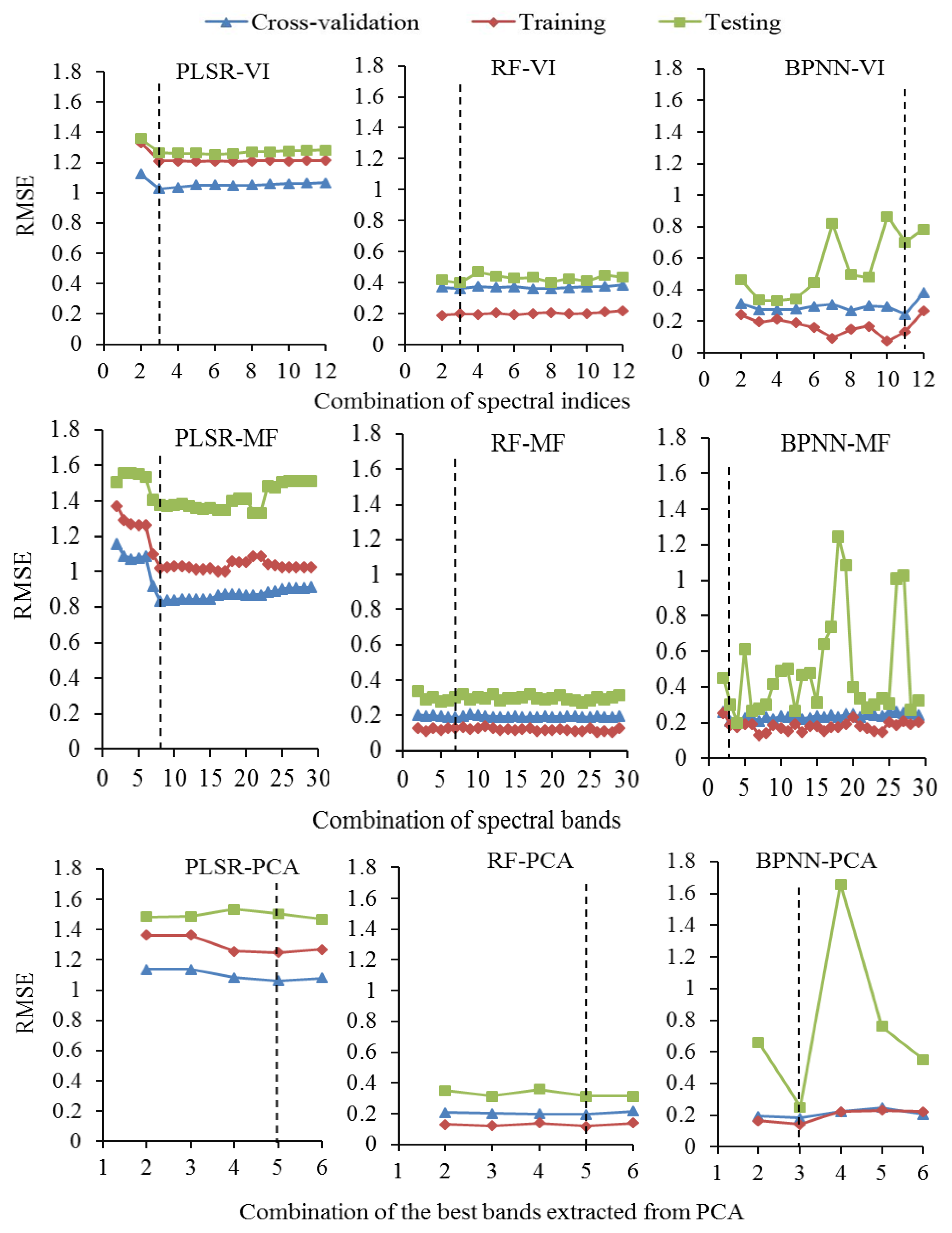
3.2.1. Vegetation Indices (VI)
3.2.2. Model-Based Features (MF)
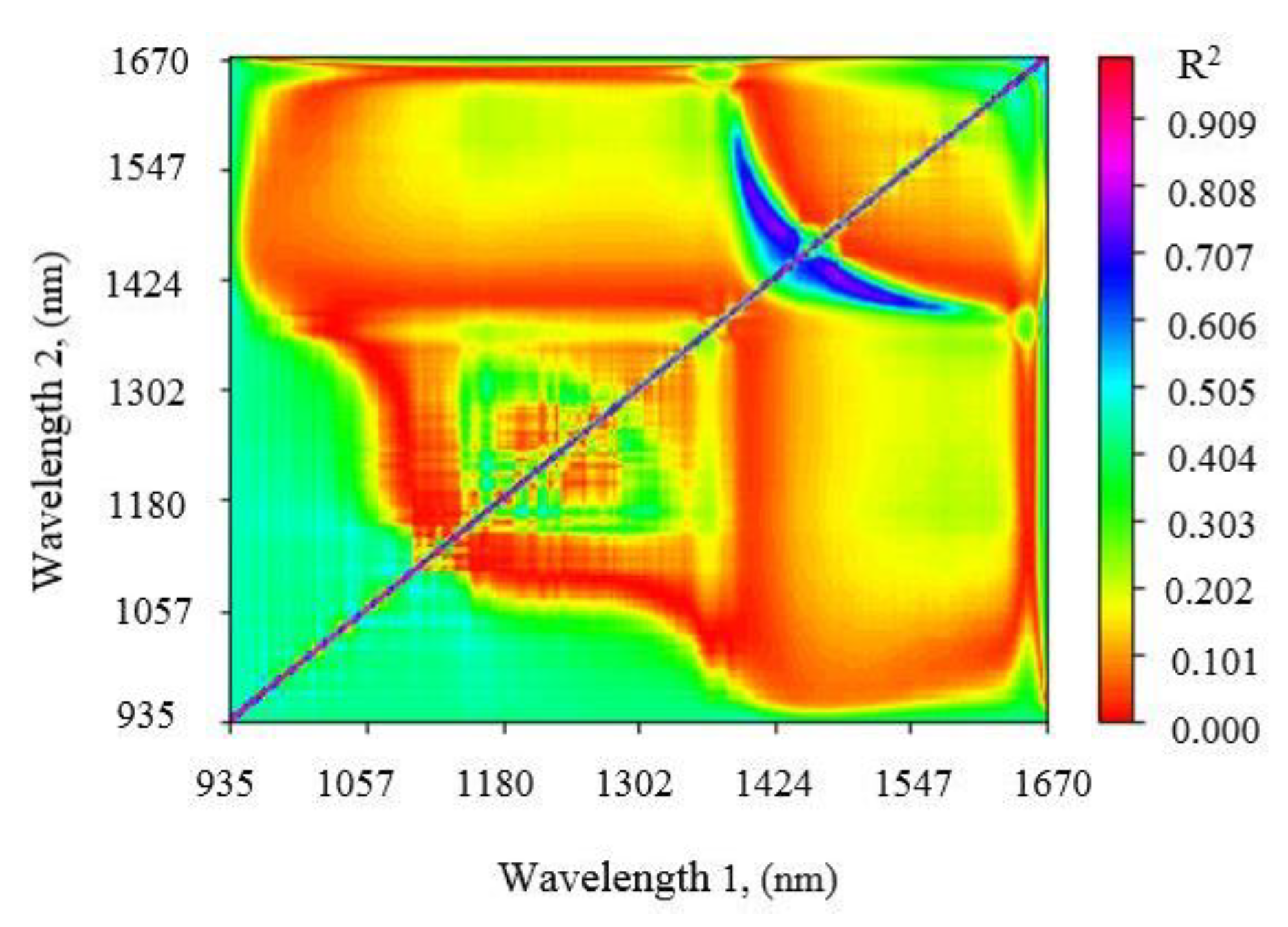
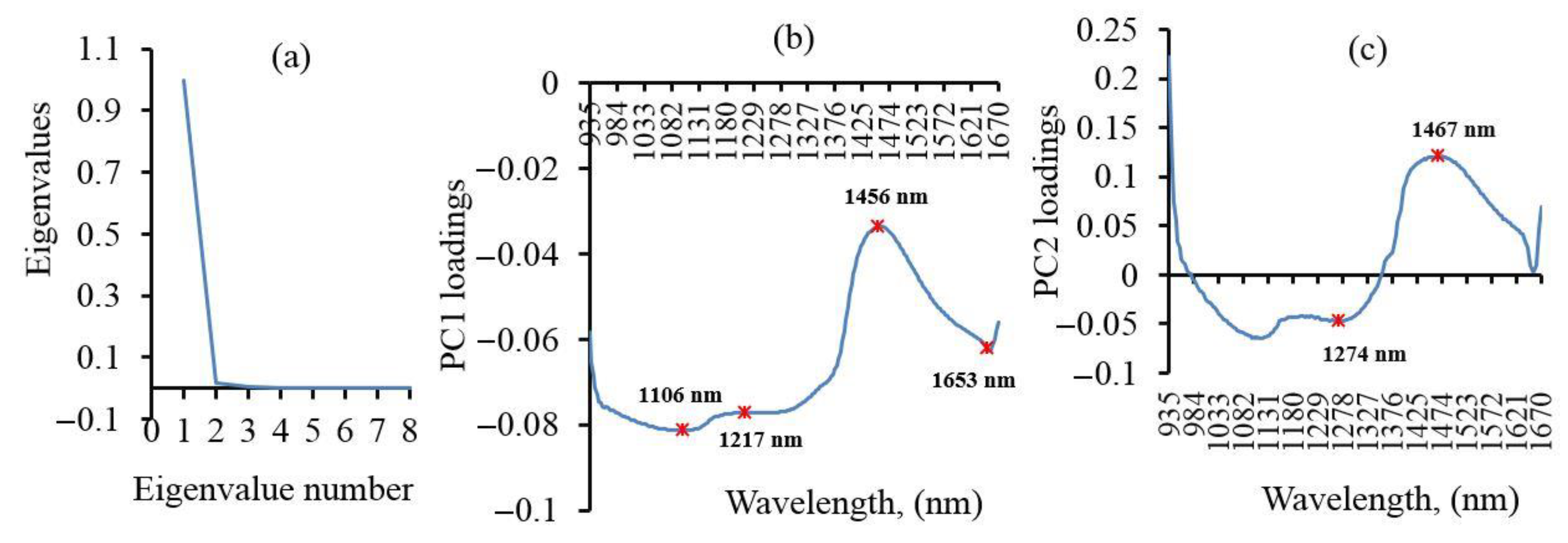
3.2.3. The Best Bands Extracted from PCA
3.3. Assessment of Regression Models
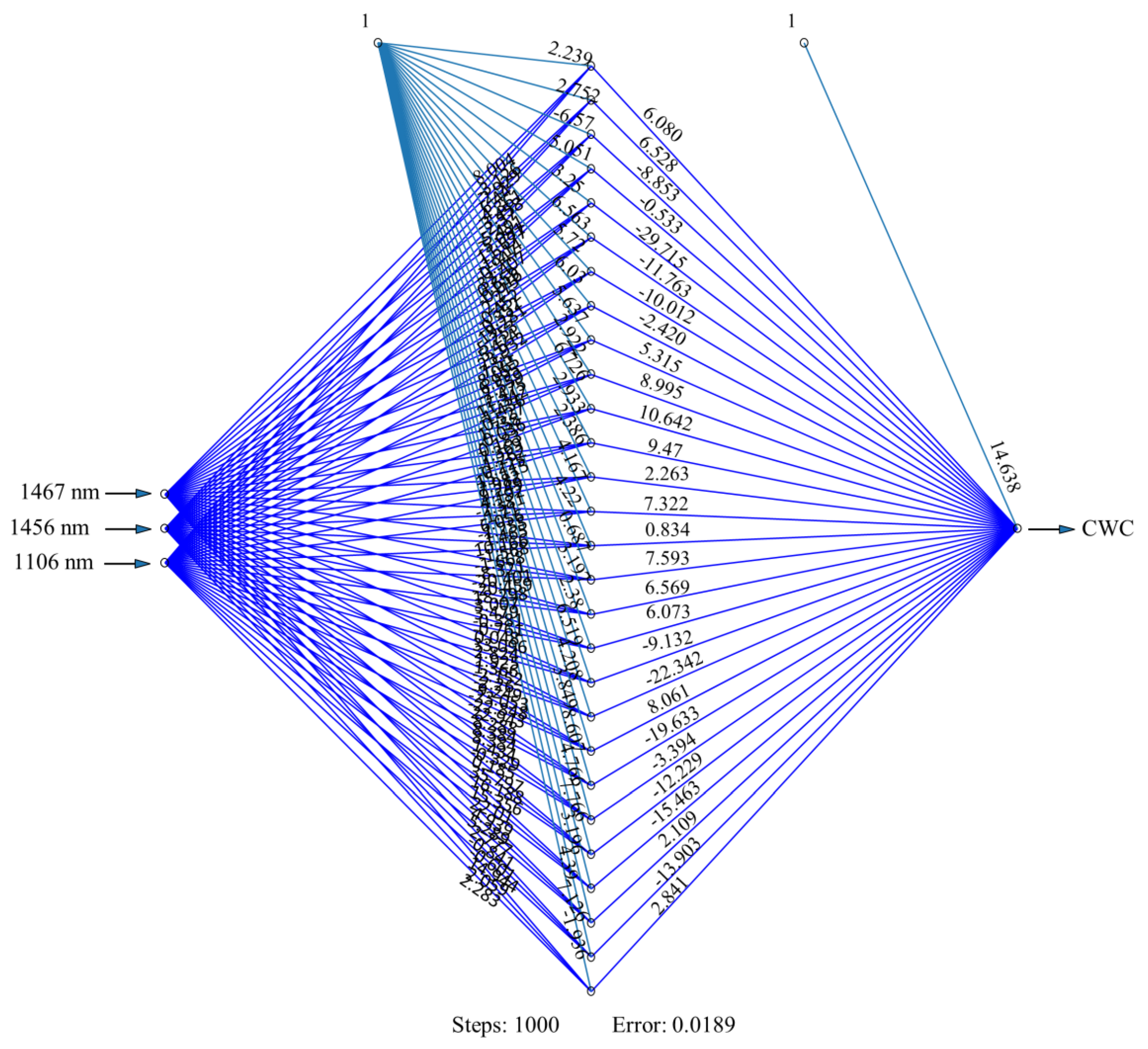
3.4. Neural Network Topology with Higher Variants
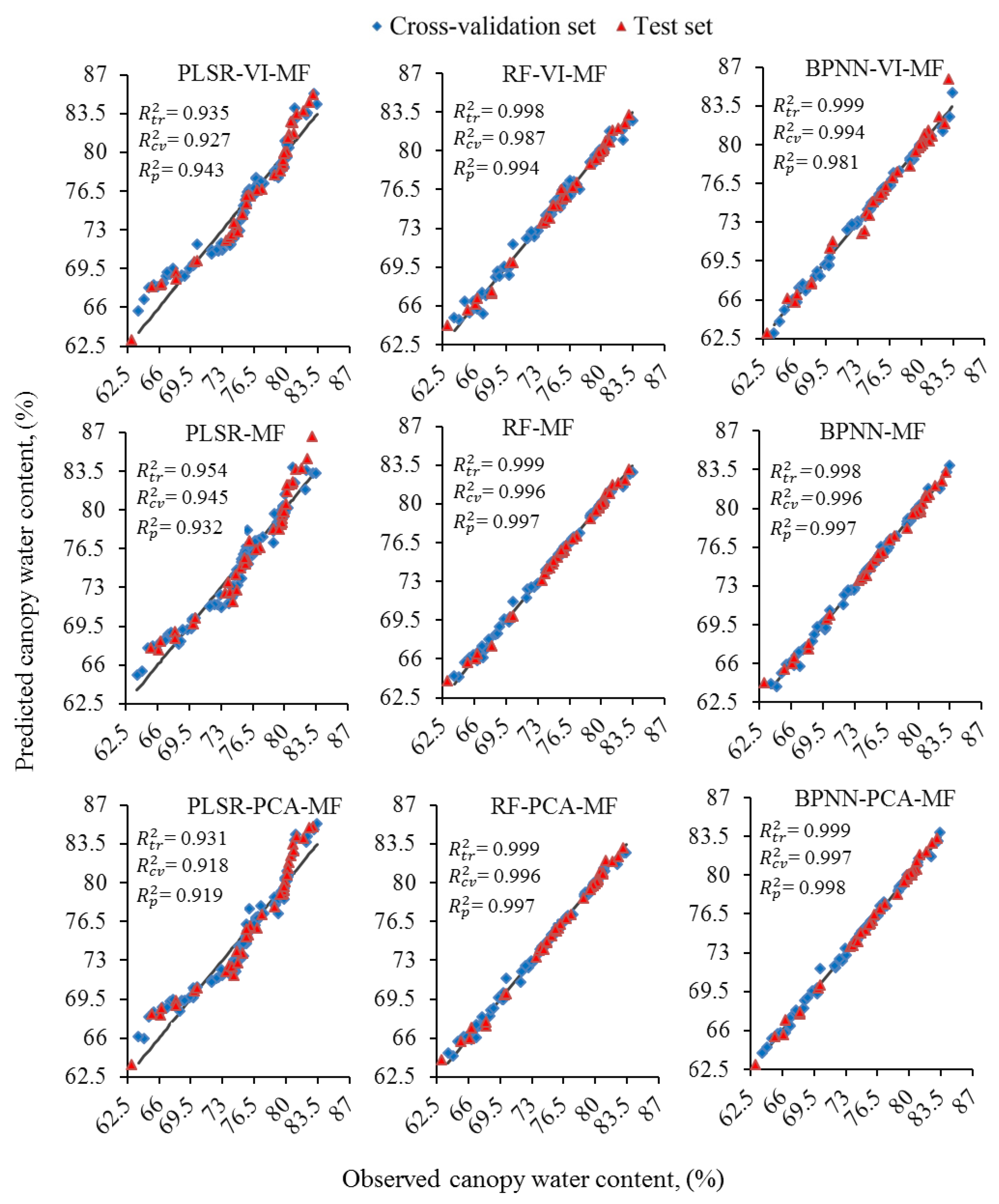
3.5. Canopy Water Content Prediction and Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gilbert, N. Water under pressure. Nature 2012, 483, 256–257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Hendawy, S.; Al-Suhaibani, N.; Salem, A.; Ur Rehman, S.; Schmidhalter, U. Spectral reflectance indices as a rapid nondestructive phenotyping tool forestimating different morphophysiological traits of contrasting spring wheatgermplasms under arid conditions. Turk. J. Agric. For. 2015, 39, 572–587. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Peñuelas, J.; Piñol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index WI (R900/R970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth. Obs. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Serrano, L.; Save, R. Cell wall elasticity and water index (r970nm/r900nm) in wheat under different nitrogen availabilities. Int. J. Remote Sens. 1996, 17, 373–382. [Google Scholar] [CrossRef]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2018, 40, 515–551. [Google Scholar] [CrossRef] [Green Version]
- Danson, F.M.; Steven, M.D.; Malthus, T.J.; Clark, J.A. High-spectral resolution data for determining leaf water content. Int. J Remote Sens. 1992, 13, 461–470. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Using spectral information from the NIR water absorption features for the retrieval of canopy water content. Int. J. Appl. Earth Obs. 2008, 10, 388–397. [Google Scholar] [CrossRef]
- Scholander, P.F.; Hammel, H.; Bradstreet, E.D.; Hemmingsen, E. Sap pressure in vascular plants. Science 1965, 148, 339–346. [Google Scholar] [CrossRef]
- Singh, A.K.; Madramootoo, C.A.; Smith, D.L. Water balance and corn yield under different water table management scenarios in Southern Quebec. In Proceedings of the 9th International Drainage Symposium Held Jointly with CIGR and CSBE/SCGAB, Quebec City, QC, Canada, 13–16 June 2010. [Google Scholar]
- Agam, N.; Cohen, Y.; Berni, J.; Alchanatis, V.; Kool, D.; Dag, A.; Yermiyahu, U.; Ben-Gal, A. An insight to the performance of crop water stress index for olive trees. Agric. Water Manag. 2013, 118, 79–86. [Google Scholar] [CrossRef]
- Huntjr, E.; Rock, B. Detection of changes in leaf water content using near and middle-infrared reflectance. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty Five Years of Remote Sensing in Precision Agriculture: Key Advances and Remaining Knowledge Gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Jain, N.; Ray, S.S.; Singh, J.P.; Panigrahy, S. Use of hyperspectral data to assess the effects of different nitrogen applications on a potato crop. Precis. Agric. 2007, 8, 225–239. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Rueda, C.A.; Ustin, S.L. Water content estimation in vegetation with MODIS reflectance data and model inversion methods. Remote Sens. Environ. 2003, 85, 109–124. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Sensitivity of spectral vegetation indices for monitoring water stress in tomato plants. Comput. Electron. Agric. 2019, 163, 104860. [Google Scholar] [CrossRef]
- Li, W.; Sun, Z.; Lu, S.; Omasa, K. Estimation of the leaf chlorophyll content using multiangular spectral reflectance factor. Plant Cell Environ. 2019, 42, 3152–3165. [Google Scholar] [CrossRef]
- Wang, J.-J.; Li, Z.; Jin, X.; Liang, G.; Struik, P.C.; Gu, J.; Zhou, Y. Phenotyping flag leaf nitrogen content in rice using a three-band spectral index. Comput. Electron. Agric. 2019, 162, 475–481. [Google Scholar] [CrossRef]
- Lu, J.; Ehsani, R.; Shi, Y.; de Castro, A.I.; Wang, S. Detection of multi-tomato leaf diseases (late blight, target and bacterial spots) in different stages by using a spectral-based sensor. Sci. Rep.-UK 2018, 8, 2793. [Google Scholar] [CrossRef] [Green Version]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 1994, 15, 697–704. [Google Scholar] [CrossRef]
- Ullah, S.; Skidmore, A.K.; Ramoelo, A.; Groen, T.A.; Naeem, M.; Ali, A. Retrieval of leaf water content spanning the visible to thermal infrared spectra. ISPRS J. Photogramm. 2014, 93, 56–64. [Google Scholar] [CrossRef]
- Imanishi, J.; Sugimoto, K.; Morimoto, Y. Detecting drought status and LAI of two Quercus species canopies using derivative spectra. Comput. Electron. Agric. 2004, 43, 109–129. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Peñuelas, J. Deriving water content of chaparral vegetation from AVIRIS data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Pu, R.; Ge, S.; Kelly, N.M.; Gong, P. Spectral absorption features as indicators of water status in coast live oak (Quercus agrifolia) leaves. Int. J. Remote Sens. 2003, 24, 1799–1810. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Yi, Q.; Bao, A.; Wang, Q.; Zhao, J. Estimation of leaf water content in cotton by means of hyperspectral indices. Comput. Electron. Agric. 2013, 90, 144–151. [Google Scholar] [CrossRef]
- Beltrán, N.H.; Duarte-Mermoud, M.A.; Salah, S.A.; Bustos, M.A.; Peña-Neira, A.I.; Loyola, E.A.; Jalocha, J.W. Feature selection algorithms using Chilean wine chromatograms as examples. J. Food Eng. 2005, 67, 483–490. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Schuize, F.H.; Wolf, H.; Jansen, H.; Vander, V.P. Applications of artificial neural networks in integrated water management: Fiction or future? Water Sci. Technol. 2005, 52, 21–31. [Google Scholar] [CrossRef]
- EIMasry, G.; Sun, D.W.; Allen, P. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef. J. Food Eng. 2012, 110, 127–140. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glorfeld, L.W. A methodology for simplification and interpretation of backpropagation-based neural network models. Expert Syst. Appl. 1996, 10, 37–54. [Google Scholar] [CrossRef]
- Moreira, R.C.; Galvão, L.S. Variation in spectral shape of urban materials. Remote Sens. Lett. 2010, 1, 149–158. [Google Scholar] [CrossRef]
- Ferwerda, J.G.; Skidmore, A.K.; Mutanga, O. Nitrogen detection with hyperspectral normalized ratio indices across multiple plant species. Int. J. Remote Sens. 2005, 26, 4083–4095. [Google Scholar] [CrossRef]
- Ecarnot, M.; Compan, F.; Roumet, P. Assessing leaf nitrogen content and leaf mass per unit area of wheat in the field throughout plant cycle with a portable spectrometer. Field Crop Res. 2013, 140, 44–50. [Google Scholar] [CrossRef]
- Vaiphasa, C.; Ongsomwang, S.; Vaiphasa, T.; Skidmore, A.K. Tropical mangrove species discrimination using hyperspectral data: A laboratory study. Estuar. Coast. Shelf Sci. 2005, 65, 371–379. [Google Scholar] [CrossRef]
- Dawson, T.P.; Curran, P.J.; Plummer, S.E. LIBERTY—Modelling the effects of leaf biochemical concentration on reflectance spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. ISPRS J. Photogramm. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Cao, L.; Pan, J.; Li, R.; Li, J.; Li, Z. Integrating airborne LiDAR and optical data to estimate forest aboveground biomass in arid and semi-arid regions of China. Remote Sens. 2018, 10, 532. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, G.; Liu, F.; Lu, Y.; Yang, F.; Yang, F.; Yang, M.; Zhao, Y.; Li, D. Comparison of boosted regression tree and random forest models for mapping topsoil organic carbon concentration in an alpine ecosystem. Ecol. Indic. 2016, 60, 870–878. [Google Scholar] [CrossRef]
- Melis, G.; Dyer, C.; Blunsom, P. On the state of the art of evaluation in neural language models. arXiv 2017, arXiv:1707.05589. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning (ICML 2013), Atlanta, Gerorgia, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Abtew, W.; Melesse, A. Evaporation and Evapotranspiration: Measurements and Estimations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 53, p. 62. [Google Scholar]
- Zhu, H.; Chu, B.; Fan, Y.; Tao, X.; Yin, W.; He, Y. Hyperspectral Imaging for Predicting the Internal Quality of Kiwifruits Based on Variable Selection Algorithms and Chemometric Models. Sci. Rep.-UK 2017, 7, 7845. [Google Scholar] [CrossRef] [Green Version]
- Elmasry, G.; Kamruzzaman, M.; Sun, D.W.; Allen, P. Principles and applications of hyperspectral imaging in quality evaluation of agro-food products: A review. Crit. Rev. Food Sci. 2012, 52, 999–1023. [Google Scholar] [CrossRef]
- Smith, S.W. The Scientist and Engineer’s Guide to Digital Signal Processing, 2nd ed.; California Technical Publishing: San Diego, CA, USA, 1999; ISBN 0-9660176-7-6. [Google Scholar]
- Wang, C.; Nie, S.; Xi, X.H.; Luo, S.Z.; Sun, X.F. Estimating the biomass of maize with hyperspectral and LiDAR data. Remote Sen. 2017, 9, 11. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Huang, Z.H.; Sun, H.; Wang, G.X. Mapping forest ecosystem biomass density for Xiangjiang river basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef] [Green Version]
- Ye, X.; Sakai, K.; Okamoto, H.; Garciano, L.O. A ground-based hyperspectral imaging system for characterizing vegetation spectral features. Comput. Electron. Agric. 2008, 63, 13–21. [Google Scholar] [CrossRef]
- Carol, L.J.; Paul, R.W.; Niels, O.M.; Marvin, L.S.; Roshani, J. Estimating Water Stress in Plants Using Hyperspectral Sensing. In Proceedings of the ASAE/CSAE Annual International Meeting, Ottawa, ON, Canada, 4–11 August 2004. [Google Scholar]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.M. Detecting vegetation water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Galvão, L.S.; Formaggio, A.R.; Tisot, D.A. Discrimination of sugarcane varieties in Southeastern Brazil with EO-1 Hyperion data. Remote Sens. Environ. 2005, 94, 523–534. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef] [Green Version]
- Jolliffe, I. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Pierna, J.A.F.; Abbas, O.; Baeten, V.; Dardenne, P. A Backward Variable Selection method for PLS regression (BVSPLS). Anal. Chim. Acta 2009, 642, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kisi, O.; Demir, V. Evapotranspiration estimation using six different multi-layer perceptron algorithms. Irrig. Drain. Syst. Eng. 2016, 5, 991–1000. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Jensen, J.L.; Kendall, W.S. Networks and Chaos: Statistical and Probabilistic Aspects; Chapman and Hall: London, UK, 1993; Volume 50, p. 48. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Li, J.; Yoder, R.; Odhiambo, L.O.; Zhang, J. Simulation of nitrate distribution under drip irrigation using artificial neural networks. Irrig. Sci. 2004, 23, 29–37. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. Siam J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Malone, B.P.; Styc, Q.; Minasny, B.; McBratney, A.B. Digital soil mapping of soil carbon at the farm scale: A spatial downscaling approach in consideration of measured and uncertain data. Geoderma 2017, 290, 91–99. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Carter, G.A. Primary and secondary effects of water content on the spectral reflectance of leaves. Am. J. Bot. 1991, 78, 916–924. [Google Scholar] [CrossRef]
- Carter, G.A. Responses of leaf spectral reflectance to plant stress. Am. J. Bot. 1993, 80, 239–243. [Google Scholar] [CrossRef]
- Wang, D.; Shannon, M.C. Canopy reflectance, temperature, and leaf chlorophyll content of soybean plants under salinity stress and different irrigation methods. Remote Sens. Environ. 1999, 57, 287–296. [Google Scholar]
- Sun, H.; Feng, M.; Xiao, L.; Yang, W.; Wang, C.; Jia, X.; Zhao, Y.; Zhao, C.; Muhammad, S.K.; Li, D. Assessment of plant water status in winter wheat (Triticum aestivum L.) based on canopy spectral indices. PLoS ONE 2019, 14, e0216890. [Google Scholar] [CrossRef] [PubMed]
- Eitel, J.U.H.; Gessler, P.E.; Smith, A.M.S.; Robberecht, R. Suitability of existing and novel spectral indices to remotely detect water stress in Populus spp. For. Ecol. Manag. 2006, 229, 170–182. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using spectral information at the NIR water absorption features to estimate canopy water content and biomass. In Proceedings of the ISPRS Mid-Term Symposium Remote Sensing: From Pixels to Processes, Enschede, The Netherlands, 8–11 May 2006; p. 6. [Google Scholar]
- Al Iqbal, R. Using Feature Weights to Improve Performance of Neural Networks. arXiv 2011, arXiv:1101.4918. [Google Scholar]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Bajpai, V.; Patra, H.; Kumar, S.; Dandapani, R.; Gupta, V.K.; Viswanathan, C.; Ahmad, T.; et al. Comparison of various modelling approaches for water deficit stress monitoring in rice crop through hyperspectral remote sensing. Agric. Water Manag. 2019, 213, 231–244. [Google Scholar] [CrossRef]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef] [Green Version]
- Pandey, P.; Ge, Y.; Stoerger, V.; Schnable, J.C. High throughput in vivo analysis of plant leaf chemical properties using hyperspectral imaging. Front. Plant Sci. 2017, 8, 1348. [Google Scholar] [CrossRef] [Green Version]
- Saha, B.N.; Ray, N.; Zhang, H. Snake Validation: A PCA-Based Outlier Detection Method. IEEE Signal Proc. Lett. 2009, 16, 549–552. [Google Scholar] [CrossRef]
- Krishna, G.; Sahoo, R.N.; Pargal, S.; Gupta, V.K.; Sinha, P.; Bhagat, S.; Saharan, M.S.; Singh, R.; Chattopadhyay, C. Assessing wheat yellow rust disease through hyperspectral remote sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 1413–1416. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.R.; Li, X.; Yu, K.Q.; Cheng, F.; He, Y. Hyperspectral imaging for determining pigment contents in cucumber leaves in response to angular leaf spot disease. Sci. Rep.-UK 2016, 6, 27790. [Google Scholar] [CrossRef] [PubMed]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ. 2008, 112, 1820–1834. [Google Scholar] [CrossRef]



| Date | Temperature (°C) | Relative Humidity (%) | VPD (Kpa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Avg. | Std. | Min. | Max. | Avg. | Std. | ||
| 10 July to 12 August | 24 | 38 | 31 | 5.29 | 41 | 95 | 68 | 20.10 | 1.44 |
| 13 August to 30 August | 23 | 34 | 28.5 | 4.10 | 44 | 97 | 70.5 | 16.97 | 1.15 |
| Spectral Indices | Formula | Developer |
|---|---|---|
| SB-1 | [54] | |
| SB-2 | [55] | |
| WBI-1 | [25] | |
| WBI-2 | [25] | |
| NDVI-1 | [56] | |
| NDVI-2 | [56] | |
| TBR | [26] | |
| SRI-1 | [57] | |
| SRI-2 | [28] |
| Models | The Best Selected Features |
|---|---|
| PLSR-MF | 935, 945, 1666, 1416, 1369, 1025, 1022, 938, 1035, 1015, 995, 1032, 1056, 1029, 962, 1052, 1046, 1426, 1177, 1072, 1049, 1187, 992, 1099, 1214, 1069, 1670, 1423, 1200 nm |
| RF-MF | 1126, 965, 1244, 1002, 1670, 1160, 948, 985, 1663, 1639, 1396, 1029, 1473, 1595, 1237, 1565, 1062, 975, 1133, 1130, 1140, 1575, 1609, 1504, 1649, 1298, 1359, 1440, 1156 nm |
| BPNN-MF | 935, 938, 941, 1670, 1663, 945, 1666, 948, 1653, 1656, 952, 1413, 1409, 1423, 1402, 1659, 1416, 958, 1406, 955, 1426, 1429, 1419, 1433, 1399, 972, 968, 1446, 1440 nm |
| Model | FSM | Optimum Features | Rank |
|---|---|---|---|
| PLSR | VI-MF-3 | NDVI-1, WBI-1, SB-1 | 8 |
| MF-8 | R1426, R1406, R1187, R1035, R1032, R1177, R962, R1022 | 7 | |
| PCA-MF-5 | R1653, R1467, R1274, R1106, R1217 | 9 | |
| RF | VI-MF-3 | SRI#3, SB-1, SB-2 | 6 |
| MF-7 | R1359, R985, R1565, R1649, R1062, R1140, R1244 | 2 | |
| PCA-MF-5 | R1467, R1653, R1106, R1217, R1274 | 3 | |
| BPNN | VI-MF-11 | NDVI-2, WBI-1, SRI-1, SRI#2, TBR, SRI#1, NDVI-1, SRI#3, WBI-2, SB-1, SB-2 | 5 |
| MF-3 | R938, R1663, R1656 | 4 | |
| PCA-MF-3 | R1467, R1456, R1106 | 1 |
| Model | FSM | n | Optimum Parameters | Training | Cross Validation | Test | Acc | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAPE | R2 | RMSE | MAPE | R2 | RMSE | MAPE | R2 | |||||
| All suggested features | |||||||||||||
| PLSR | VI | 12 | LVs = 5 | 1.215 | 1.319 | 0.934 | 1.067 | 1.455 | 0.909 | 1.285 | 1.392 | 0.941 | 0.986 |
| MF | 219 | LVs = 6 | 1.026 | 1.095 | 0.953 | 0.914 | 1.240 | 0.914 | 1.508 | 1.570 | 0.918 | 0.984 | |
| PCA | 6 | LVs = 4 | 1.272 | 1.378 | 0.928 | 1.079 | 1.471 | 0.917 | 1.469 | 1.609 | 0.922 | 0.984 | |
| RF | VI | 12 | ntree = 50, mtry = 8 | 0.221 | 0.216 | 0.998 | 0.387 | 0.529 | 0.986 | 0.435 | 0.432 | 0.993 | 0.995 |
| MF | 219 | ntree = 40, mtry = 38 | 0.134 | 0.117 | 0.999 | 0.212 | 0.291 | 0.996 | 0.311 | 0.289 | 0.996 | 0.997 | |
| PCA | 6 | ntree = 20, mtry = 6 | 0.141 | 0.121 | 0.999 | 0.217 | 0.297 | 0.995 | 0.314 | 0.282 | 0.996 | 0.997 | |
| BPNN | VI | 12 | nr = 24, f = Tanh | 0.265 | 0.264 | 0.997 | 0.379 | 0.502 | 0.989 | 0.783 | 0.818 | 0.978 | 0.992 |
| MF | 219 | nr = 28, f = logistic | 0.183 | 0.192 | 0.998 | 0.329 | 0.444 | 0.978 | 1.836 | 0.708 | 0.879 | 0.978 | |
| PCA | 6 | nr = 26, f = logistic | 0.222 | 0.215 | 0.998 | 0.207 | 0.283 | 0.996 | 0.552 | 0.373 | 0.989 | 0.996 | |
| High-level features | |||||||||||||
| PLSR | VI-MF | 3 | LVs = 3 | 1.212 | 1.325 | 0.935 | 1.026 | 1.398 | 0.927 | 1.265 | 1.349 | 0.943 | 0.986 |
| MF | 8 | LVs = 5 | 1.020 | 1.063 | 0.954 | 0.833 | 1.138 | 0.945 | 1.376 | 1.440 | 0.932 | 0.986 | |
| PCA-MF | 5 | LVs = 5 | 1.250 | 1.341 | 0.931 | 1.063 | 1.448 | 0.918 | 1.504 | 1.634 | 0.919 | 0.983 | |
| RF | VI-MF | 3 | ntree = 40, mtry = 3 | 0.201 | 0.184 | 0.998 | 0.361 | 0.495 | 0.987 | 0.401 | 0.388 | 0.994 | 0.996 |
| MF | 7 | ntree = 20, mtry = 3 | 0.126 | 0.113 | 0.999 | 0.189 | 0.261 | 0.996 | 0.299 | 0.259 | 0.997 | 0.997 | |
| PCA-MF | 5 | ntree = 50, mtry = 2 | 0.118 | 0.103 | 0.999 | 0.197 | 0.269 | 0.996 | 0.312 | 0.275 | 0.997 | 0.997 | |
| BPNN | VI-MF | 11 | nr = 10, f = logistic | 0.146 | 0.160 | 0.999 | 0.256 | 0.347 | 0.994 | 0.736 | 0.610 | 0.981 | 0.994 |
| MF | 3 | nr = 20, f = logistic | 0.189 | 0.191 | 0.998 | 0.207 | 0.338 | 0.996 | 0.304 | 0.279 | 0.997 | 0.997 | |
| PCA-MF * | 3 | nr = 28, f = logistic | 0.143 | 0.148 | 0.999 | 0.183 | 0.249 | 0.997 | 0.252 | 0.259 | 0.998 | 0.998 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsherbiny, O.; Fan, Y.; Zhou, L.; Qiu, Z. Fusion of Feature Selection Methods and Regression Algorithms for Predicting the Canopy Water Content of Rice Based on Hyperspectral Data. Agriculture 2021, 11, 51. https://doi.org/10.3390/agriculture11010051
Elsherbiny O, Fan Y, Zhou L, Qiu Z. Fusion of Feature Selection Methods and Regression Algorithms for Predicting the Canopy Water Content of Rice Based on Hyperspectral Data. Agriculture. 2021; 11(1):51. https://doi.org/10.3390/agriculture11010051
Chicago/Turabian StyleElsherbiny, Osama, Yangyang Fan, Lei Zhou, and Zhengjun Qiu. 2021. "Fusion of Feature Selection Methods and Regression Algorithms for Predicting the Canopy Water Content of Rice Based on Hyperspectral Data" Agriculture 11, no. 1: 51. https://doi.org/10.3390/agriculture11010051
APA StyleElsherbiny, O., Fan, Y., Zhou, L., & Qiu, Z. (2021). Fusion of Feature Selection Methods and Regression Algorithms for Predicting the Canopy Water Content of Rice Based on Hyperspectral Data. Agriculture, 11(1), 51. https://doi.org/10.3390/agriculture11010051








