Research on the Physical Characteristic Parameters of Banana Bunches for the Design and Development of Postharvesting Machinery and Equipment
Abstract
1. Introduction
2. Materials and Methods
2.1. Cultivation and Morphological Characteristics of the Banana Plant
2.2. Measurement of the Physical Characteristics Parameters of Banana Crop
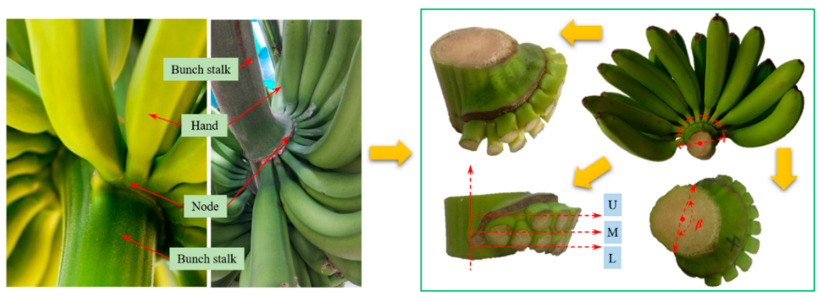
2.2.1. The Diameter of the Bunch Stalk
2.2.2. The Thickness of Bunch Stalk Rind
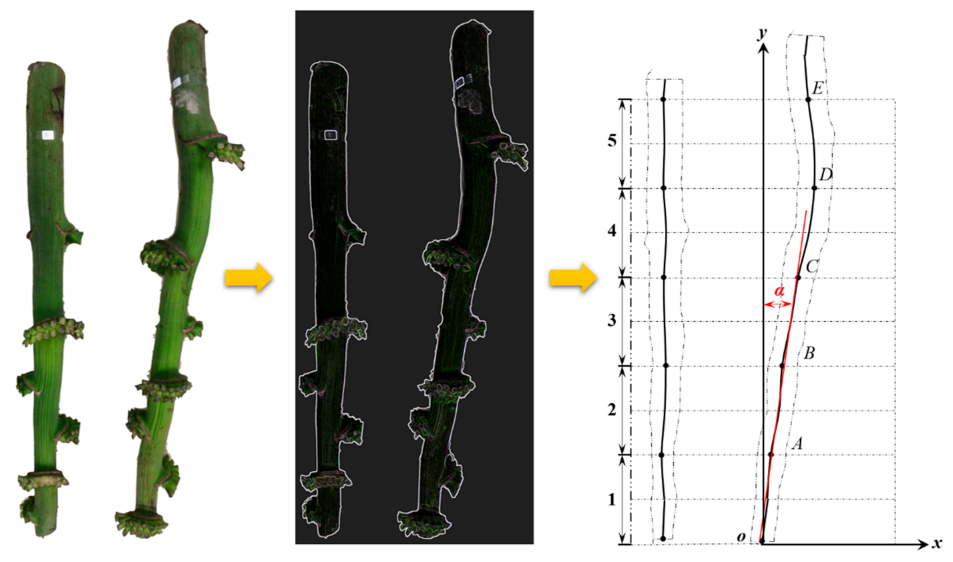
2.2.3. The Curvature of the Bunch Stalk
2.2.4. The Density of the Bunch Stalk
2.2.5. The Moisture Content of the Bunch Stalk
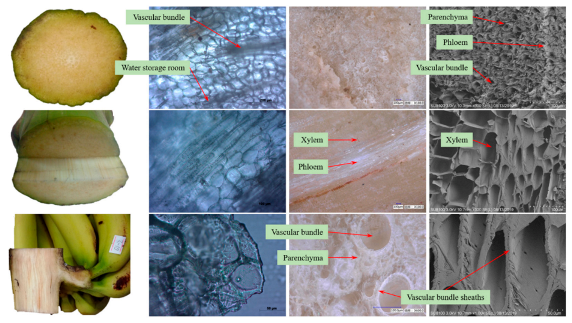
2.2.6. The Diameter of the Vascular Bundle
2.2.7. The Weight of the Bunch
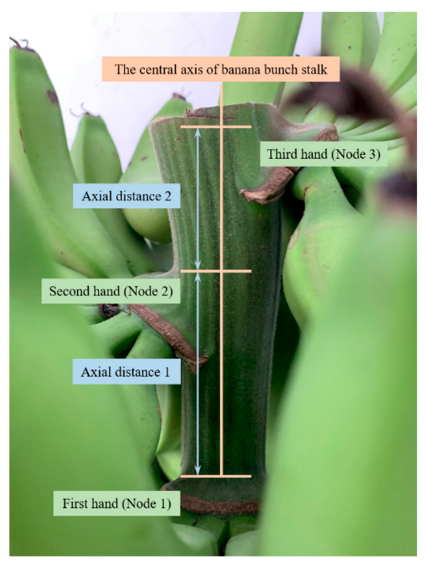
2.2.8. The Axial Distance of Banana Hands
2.2.9. The Circumferential Angle of Banana Hands
3. Results and Discussion
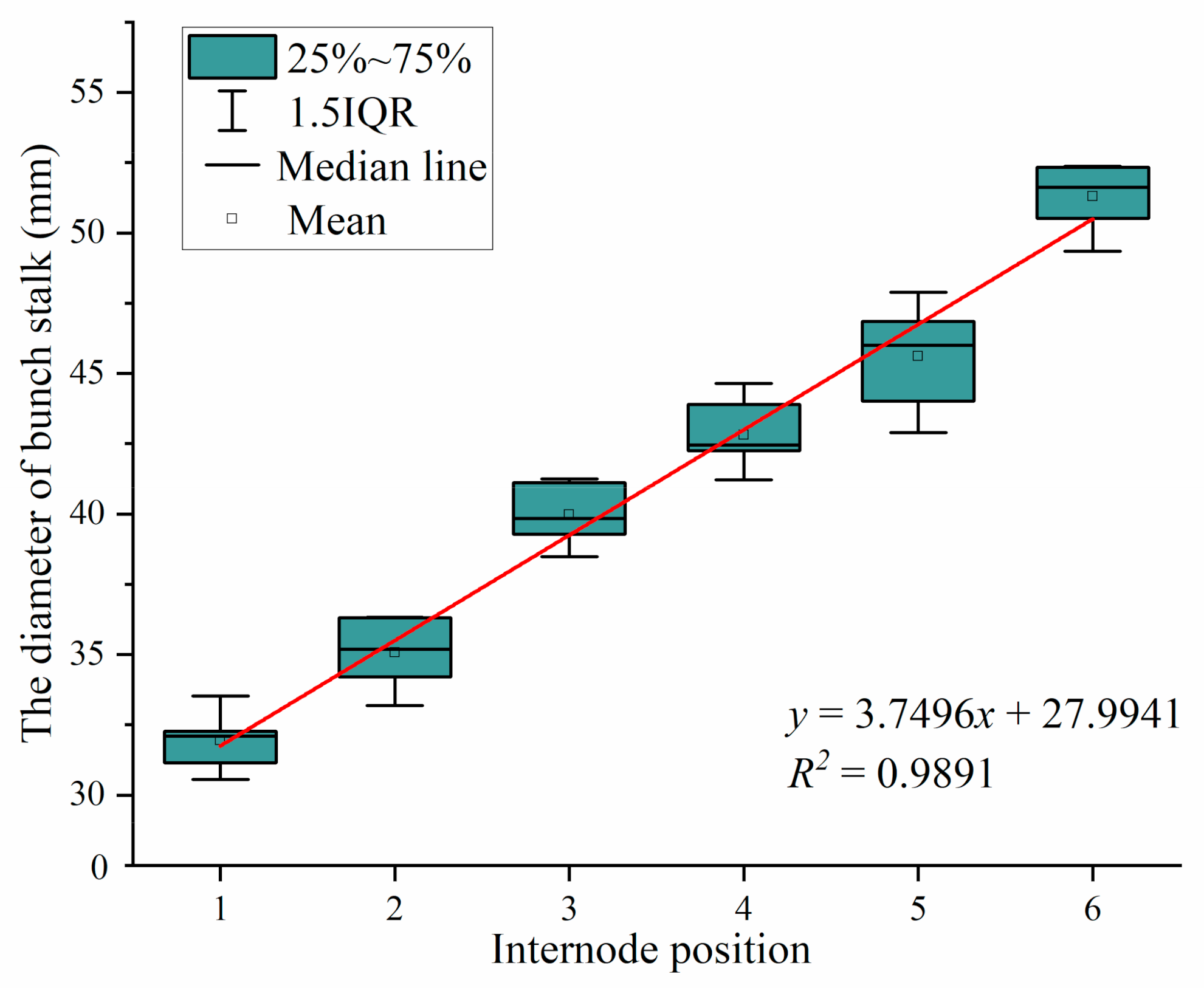
3.1. Statistical Analysis of the Diameter of Bunch Stalk
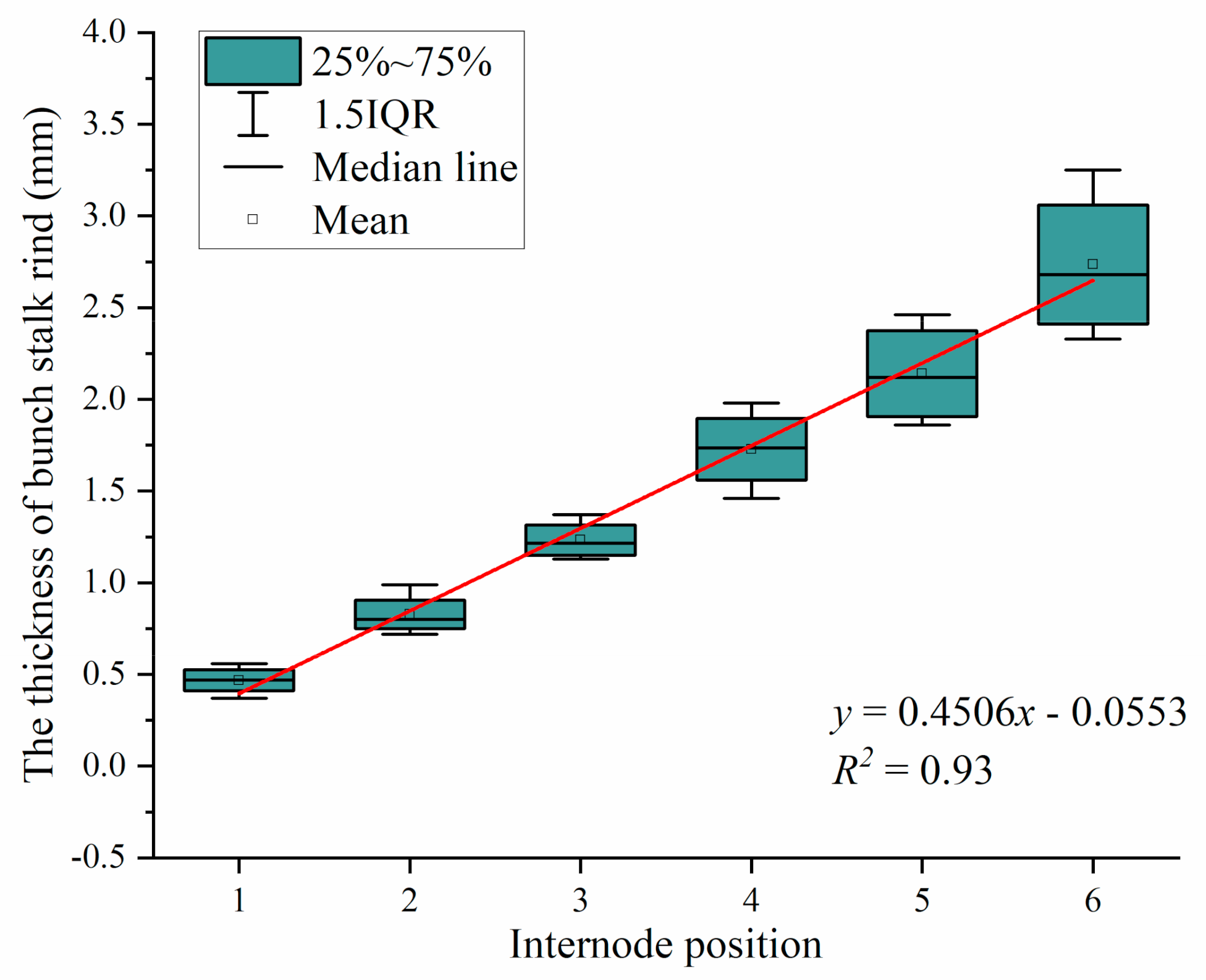
3.2. Statistical Analysis of the Thickness of Bunch Stalk Rind
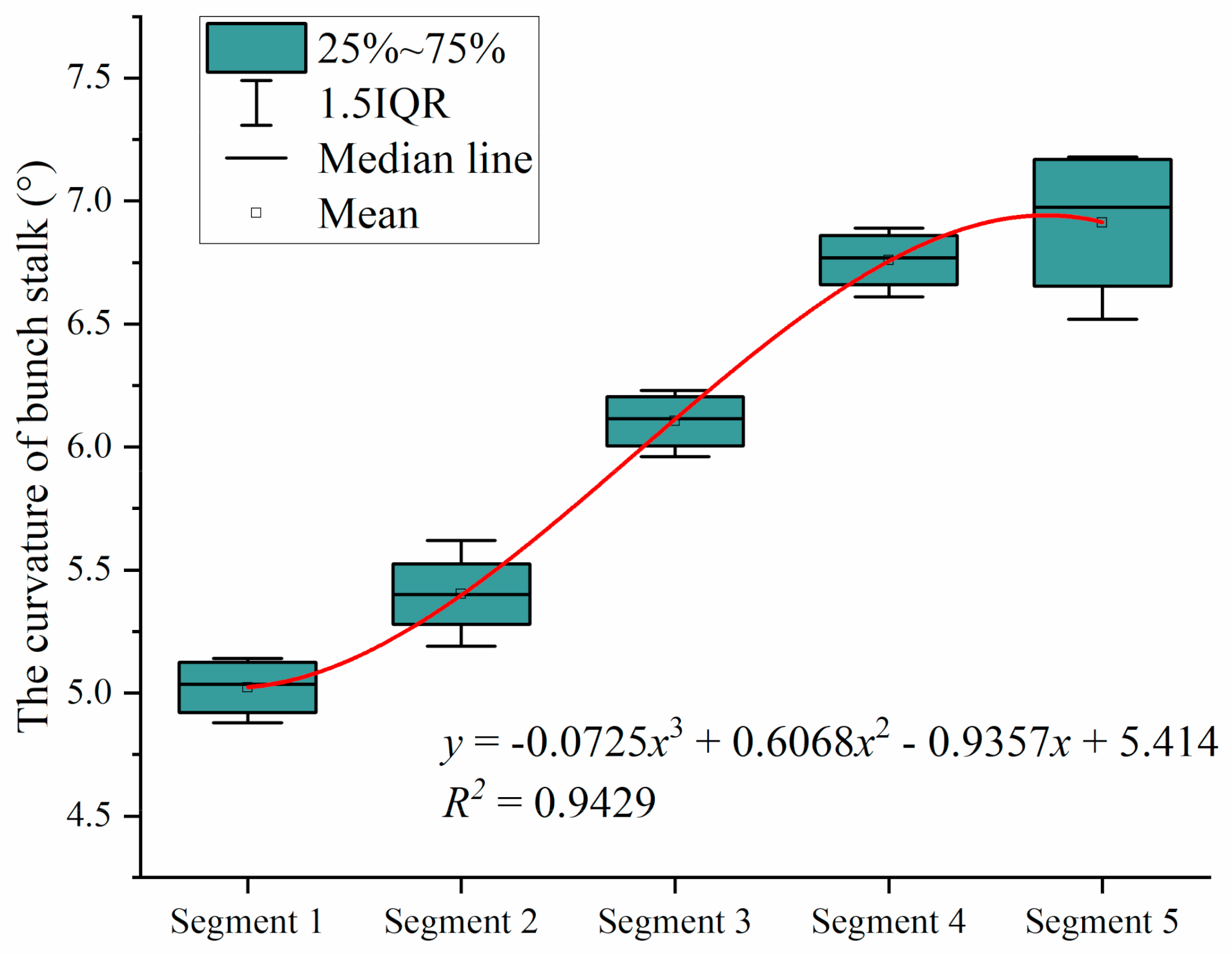
3.3. Statistical Analysis of the Curvature of Bunch Stalks
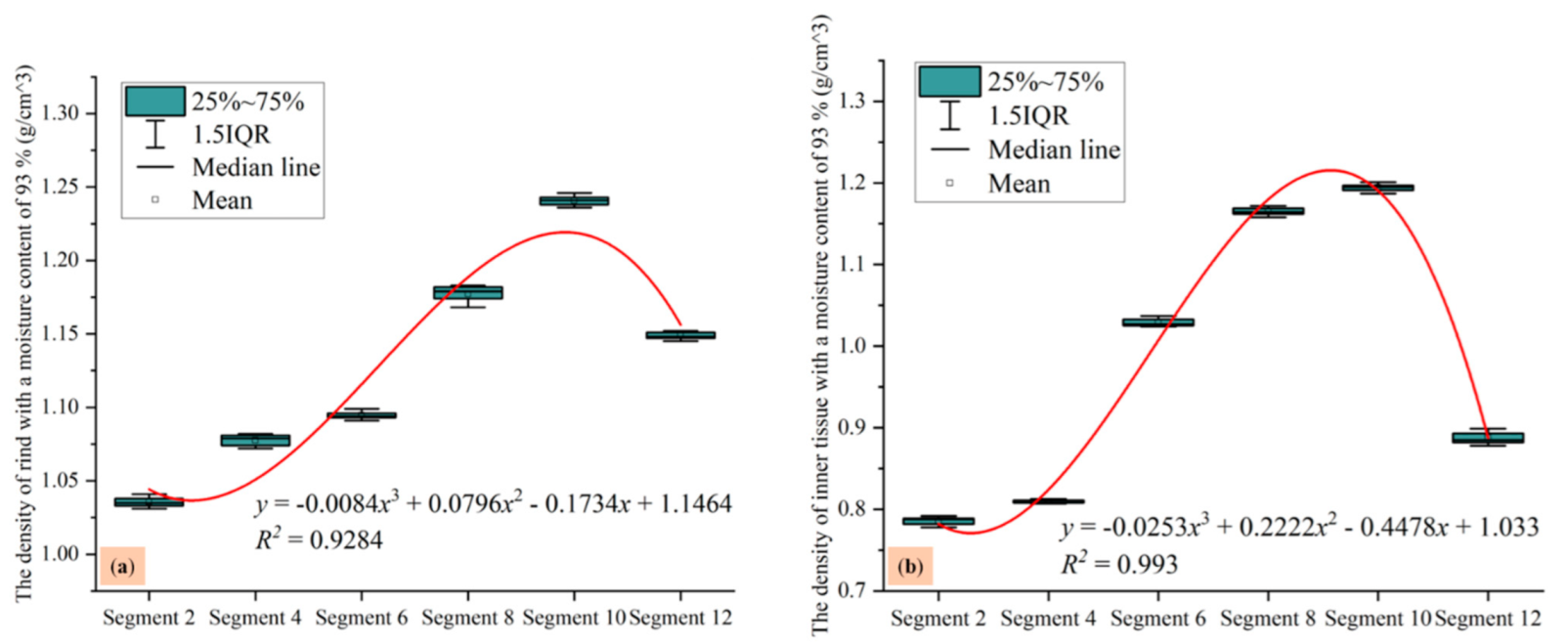
3.4. Statistical Analysis of the Density of Bunch Stalks
3.5. Statistical Analysis of the Moisture Content of Bunch Stalks
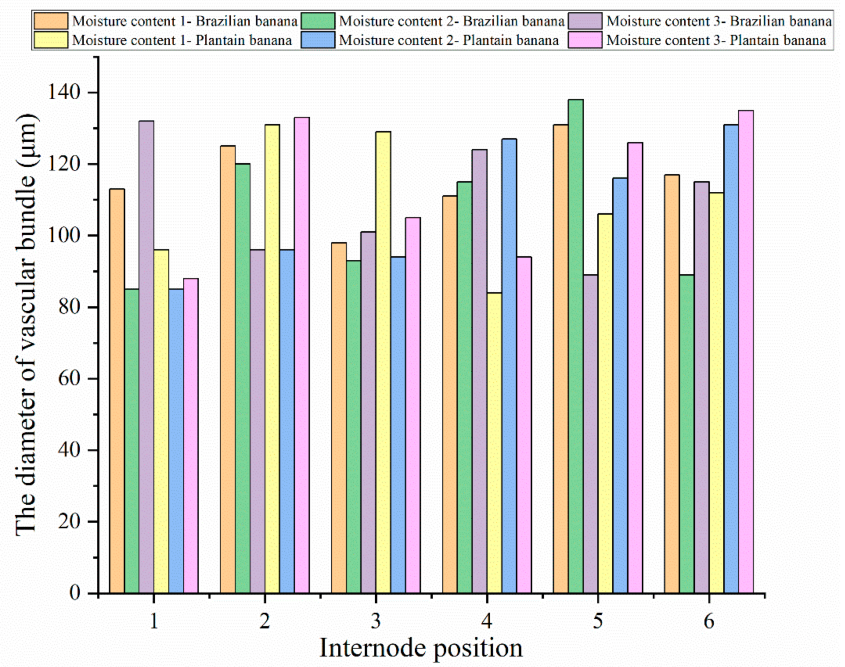
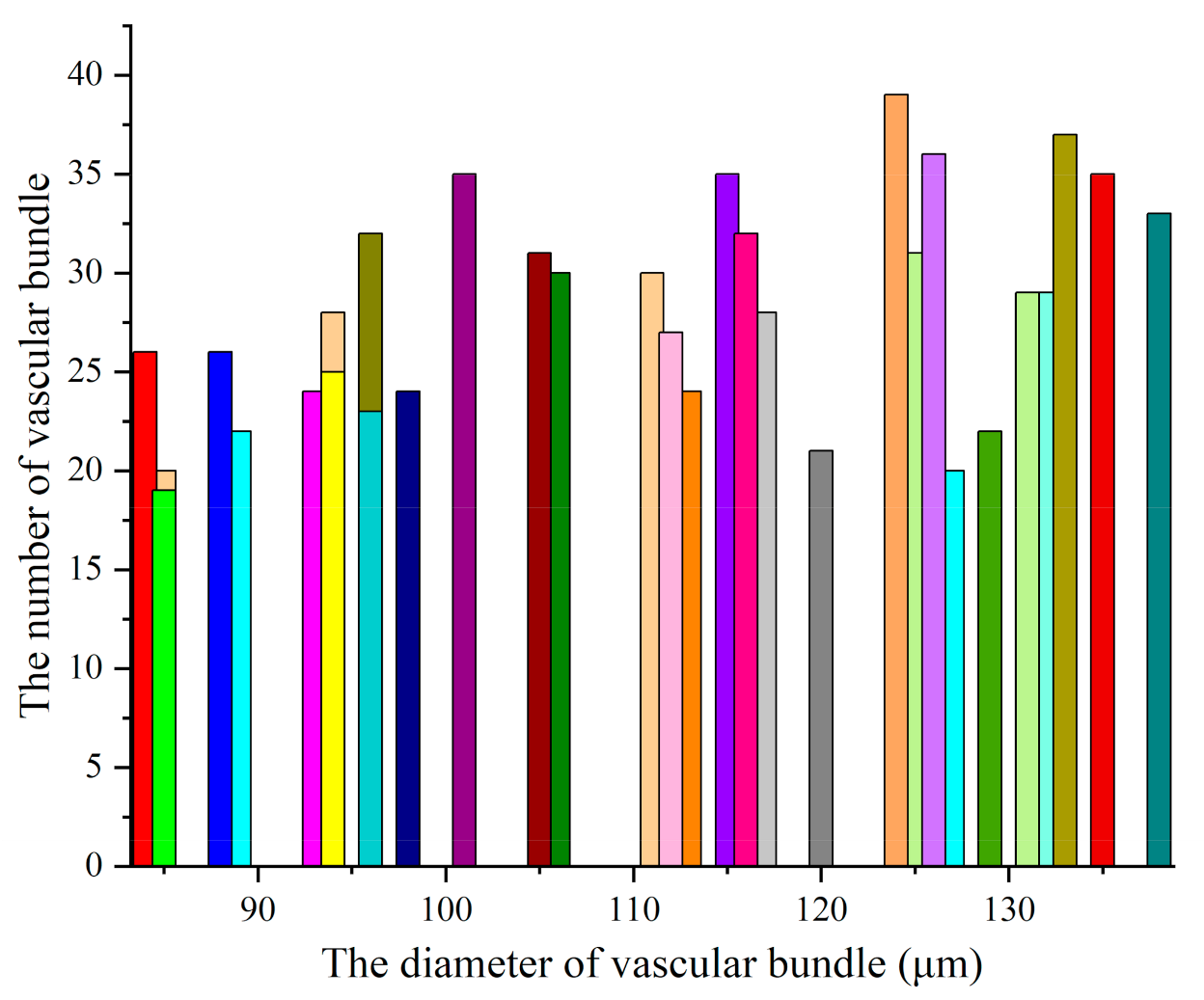
3.6. Statistical Analysis of the Diameter of the Vascular Bundle
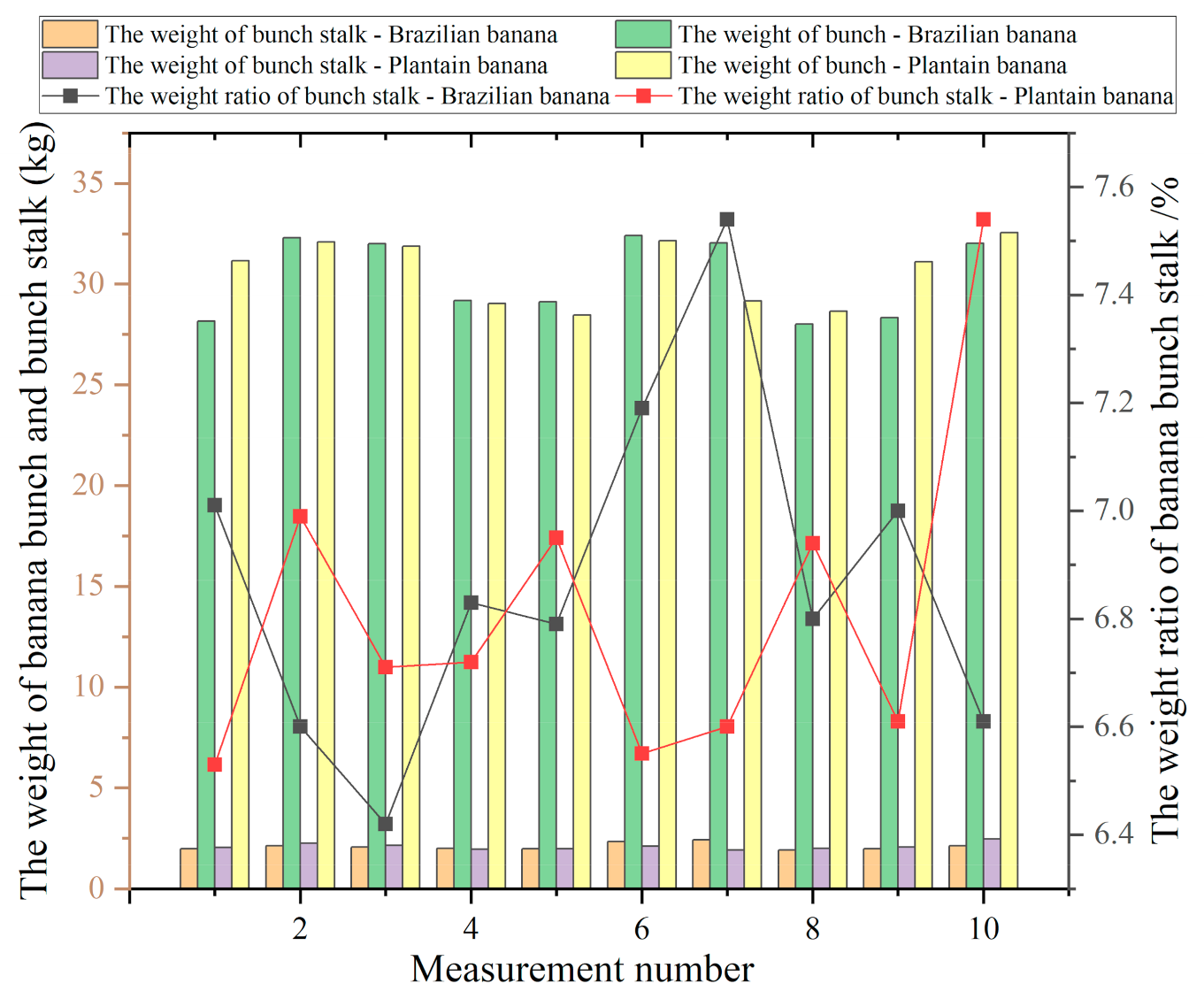
3.7. Statistical Analysis of the Weight of Bunch
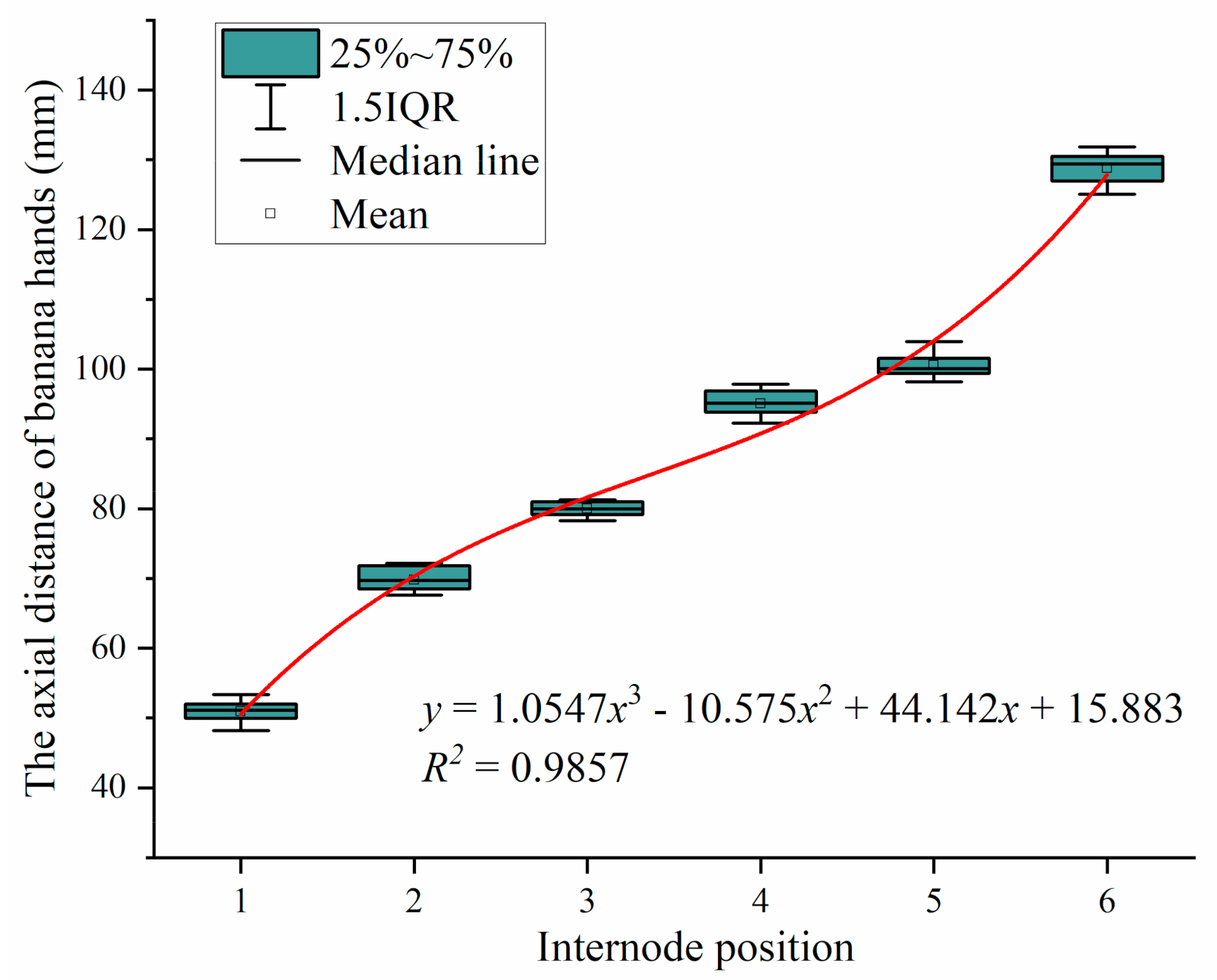
3.8. Statistical Analysis of the Axial Distance of Banana Hands
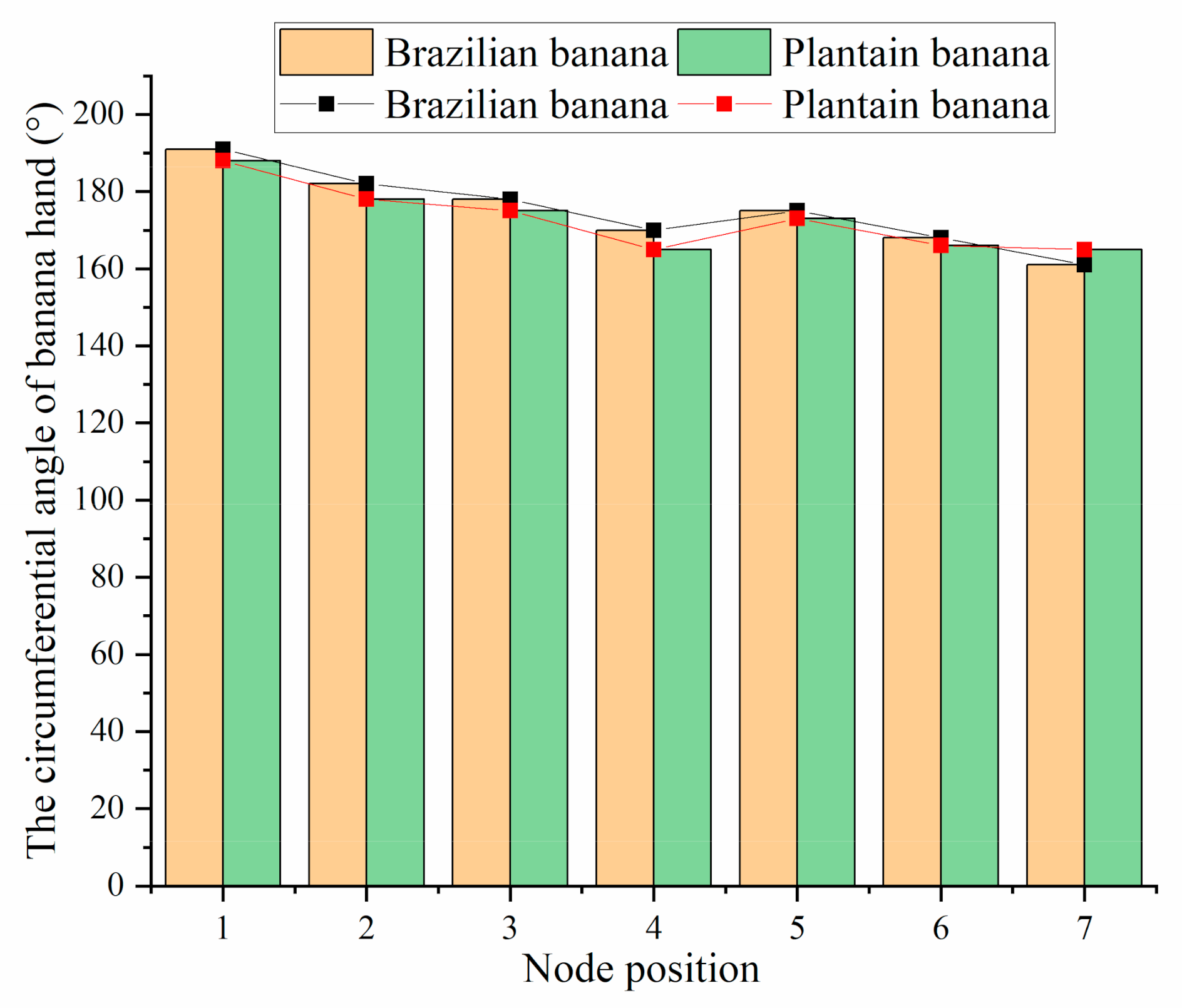
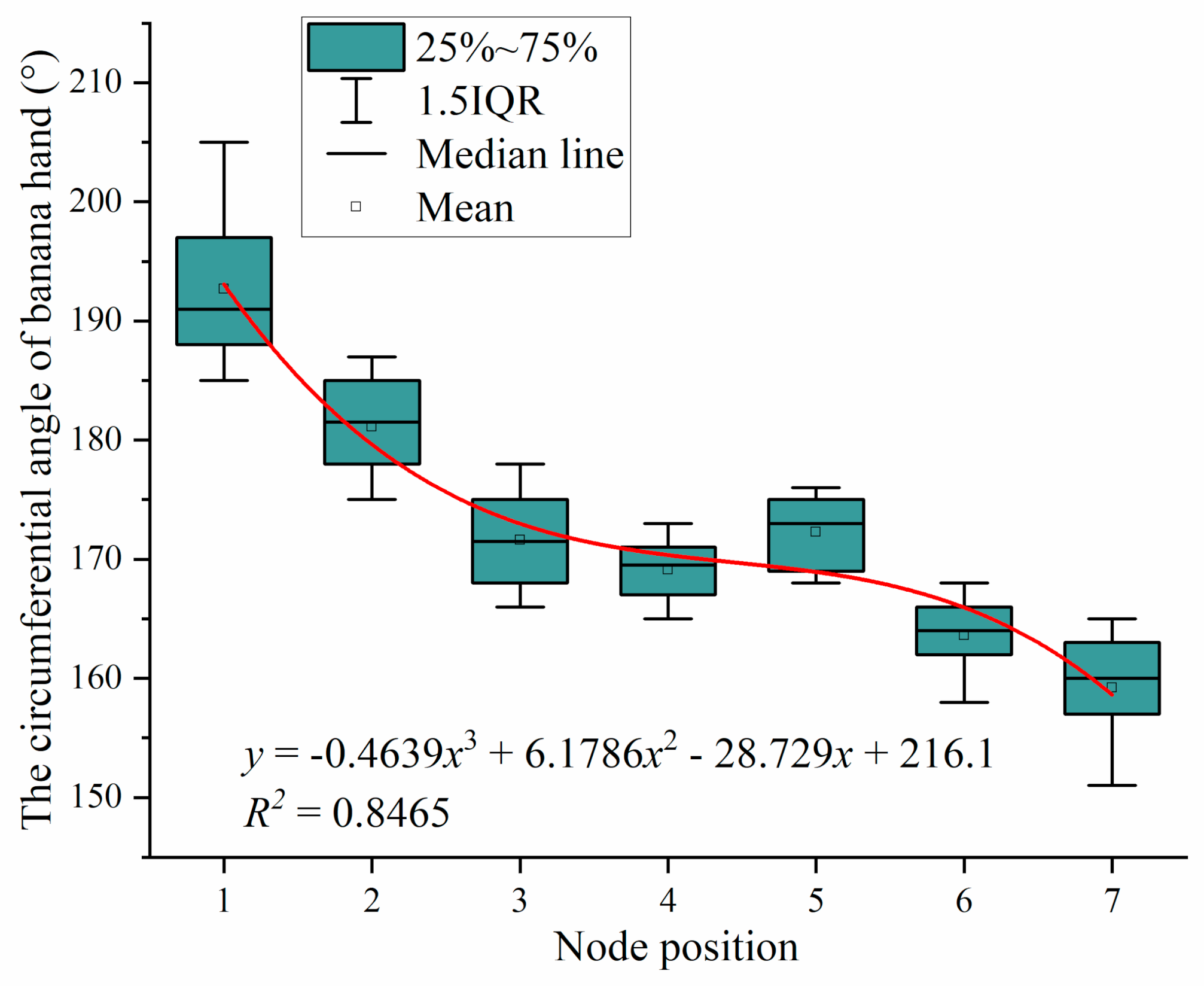
3.9. Statistical Analysis of the Circumferential Angle of Banana Hands
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ke, Y.; Guo, J.; Fang, J.; Ma, C.; Zhang, H. Analysis on the development trend of world banana production and trade. World Agric. 2008, 4, 38–39. [Google Scholar]
- Production/Yield Quantities of Bananas in the World. Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/faostat/zh/#data/QC/visualize (accessed on 29 December 2020).
- Xie, J. Fruit scientific research in New China in the past 70 years: Banana. J. Fruit Sci. 2019, 36, 1429–1440. [Google Scholar]
- Guo, J.; Duan, J.; Li, J.; Yang, Z. Mechanized technology research and equipment application of banana post-harvesting: A review. Agronomy 2020, 10, 374. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Wang, L.; Wang, W. Research and application for mechanization of banana production. J. Anhui Agric. Sci. 2011, 39, 1836–1838. [Google Scholar]
- Merino, G.; da Silva, L.; Mattos, D.; Guimarães, B.; Merino, E. Ergonomic evaluation of the musculoskeletal risks in a banana harvesting activity through qualitative and quantitative measures, with emphasis on motion capture (Xsens) and EMG. Int. J. Ind. Ergon. 2019, 69, 80–89. [Google Scholar] [CrossRef]
- Guo, J.; Jin, M.; Duan, J.; Li, J.; Fu, H.; Zhao, L.; Xu, Z.; Ding, Y.; Jiang, Y.; Yang, Z. Design and experiment of banana de-handing device based on symmetrical shape deployable mechanism. Symmetry 2020, 12, 415. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Z.; Duan, J.; Jin, M.; Mo, J.; Zhao, L.; Guo, J.; Yao, H. Design and experiment of symmetrical shape deployable arc profiling mechanism based on composite multi-cam structure. Symmetry 2019, 11, 958. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, J.; Jin, M.; Duan, J.; Fu, H.; Xu, Z. Design and analysis of self-adaptability in banana crown-cutting device based on constant-force mechanism. Trans. Chin. Soc. Agric. Mach. 2019, 50, 148–155. [Google Scholar]
- Xiong, Y.; Cui, Y. Research status of banana fiber and its prospect of development and application. J. Text. Res. 2007, 28, 122–124. [Google Scholar]
- Tian, Y.; Liu, J.; Sun, L.; He, Q.; Xu, Y.; Wang, L.; Han, X.; Zu, B. Research progress on banana fiber. Dyest. Color. 2019, 56, 44–46. [Google Scholar]
- Muralikrishna, M.V.V.; Surya Kumari, T.S.A.; Gopi, R.; Loganathan, G.B. Development of mechanical properties in banana fiber composite. Mater. Today Proc. 2020, 22, 541–545. [Google Scholar] [CrossRef]
- Pothan, A.L.; Thomas, S.; Oommen, Z. Dynamic mechanical analysis of banana fiber reinforced polyester composites. Compos. Sci. Technol. 2003, 63, 283–293. [Google Scholar] [CrossRef]
- Rao, D.N.; Mukesh, G.; Ramesh, A.; Anjaneyulu, T. Investigations on the mechanical properties of hybrid goat hair and banana fiber reinforced polymer composites. Mater. Today Proc. 2020, 27, 1703–1707. [Google Scholar]
- Boopalan, M.; Niranjanaa, M.; Umapathy, M.J. Study on the mechanical properties and thermal properties of jute and banana fiber reinforced epoxy hybrid composites. Compos. Part B Eng. 2013, 51, 54–57. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Li, B.; Zhang, J. Utilization status and outlook of banana stalk and leaves residues in China. Chin. J. Trop. Agric. 2015, 10, 69–74. [Google Scholar]
- Wang, C. The utilisation of vanana by-product in the livestock. Feed Res. 2020, 43, 144–146. [Google Scholar]
- Huang, W.; Qin, H.; Lu, Y.; Li, B.; Tang, X.; Wang, C.; Yang, Y.; Ou, J. Effects of banana stem and its biochar application on soil aggregate characteristics in the Pearl River Delta. Chin. J. Eco-Agric. 2020, 28, 413–420. [Google Scholar]
- Luo, X.; Liao, J.; Hu, L.; Zang, Y.; Zhou, Z. Improving agricultural mechanization level to promote agricultural sustainable development. Trans. Chin. Soc. Agric. Eng. 2016, 32, 1–11. [Google Scholar]
- Zhang, X.; Wang, C.; Liang, D.; Li, Y. Experiment of parameter optimization of fiber roller-scraping device for banana stalk. Trans. Chin. Soc. Agric. Eng. 2016, 32, 55–62. [Google Scholar]
- Zhang, X.; Wang, Z.; Li, Y.; Liang, D. Design and experiment of sliding-cutting and anti-twining returning device for banana straw. Trans. Chin. Soc. Agric. Eng. 2018, 34, 26–34. [Google Scholar]
- Cheng, S.; Fan, X. Effects of nursey stock age on the timing of harvest, yield and fruit quality in banana. J. Fruit Sci. 2014, 31, 879–884. [Google Scholar]
- Robinson, J.C.; Zhuang, Y.; Wang, R. Effects of banana planting period, bud suction selection, planting density on yield and harvest period. Agron. Abroad Fruit Tree 1987, 2, 24–26. [Google Scholar]
- Hu, H.; Zhao, Q. Extraction optimization, stability and antioxidant activity of yellow pigment from the banana pulp of Xiangfen No.1. Food Sci. Technol. 2019, 44, 251–260. [Google Scholar]
- Yan, S.; Qi, C.; Wei, Y. Observation on the growth and growth period of banana test-tube seedlings after planting. Trop. Crop Res. 1997, 2, 21–24. [Google Scholar]
- Gao, G.; Yi, G.; Wei, Y. Banana cultivation and management technologies research. Chin. Agric. Sci. Bull. 2010, 26, 337–342. [Google Scholar]
- Yao, M.; Lai, C. Variety characteristics and planting prospects of red apple awn. Guangxi Trop. Agric. 2006, 5, 19. [Google Scholar]
- Li, E. Banana bunch thinning and strong fruit technology. China Trop. Agric. 2009, 2, 64. [Google Scholar] [CrossRef]
- Hu, H.; Xie, J. Color Illustration of Banana Cultivation with High Quality and High Yield; Guangdong Science Technology Press: Guangzhou, China, 2019; pp. 1–134. [Google Scholar]
- Li, W. Relationship between Soil Nutrients and Water Spatial and Temporal Variation and Growth and Yield of Banana. Master’s Thesis, Hainan University, Haikou, China, 2011. [Google Scholar]
- Li, S.; Liang, D.; Zhang, X.; Li, Y. Improved design of banana stalk fiber extraction blade. Food Mach. 2019, 35, 130–135. [Google Scholar]
- Mi, H.; Wei, Y.; Pan, S.; Li, Z. Research progress on resource utilization of banana stems and leaves. Guangxi Sci. 2018, 25, 279–289. [Google Scholar]
- Wei, S.; Duan, S.; Song, C.; Fu, Z.; Hu, R.; Shi, W.; Cheng, X.; Xiao, R.; Ling, P.; Tian, B. Moisture migration characteristics of tobacco leaves with stalks in different ways during curing. J. Northwest Univ. Nat. Sci. Ed. 2019, 47, 28–37. [Google Scholar]
- Gao, D.; Wang, D. Water loss of alfalfa stem affected by flattening coefficient. J. China Agric. Univ. 2016, 21, 89–95. [Google Scholar]
- Zhou, H. Study on Sensing Mechanism and In-Situ Detection of Plant Water Relations. Ph.D. Thesis, China Agricultural University, Beijing, China, 2018. [Google Scholar]
- Xu, S.; Tan, W.; Zhang, Y. Process of degumming by chemical for banana pseudo-stem fibers and characterization of degummed fibers. Trans. Chin. Soc. Agric. Eng. 2015, 31, 301–308. [Google Scholar]
- Wang, Q. Research on the Production of the Banana Stalk Biological Feed. Master’s Thesis, Hainan University, Haikou, China, 2013. [Google Scholar]
- Zheng, L.; Han, B.; Sheng, Z.; Chen, J.; Li, Y.; Zhao, L. Effect of pretreatment by steam explosion on degradation of the banana stalk component. Chin. J. Trop. Agric. 2014, 34, 84–88. [Google Scholar]
- Li, R. Method of shape feature extraction and recognition of packaging materials. Packag. Eng. 2020, 41, 209–213. [Google Scholar]
- Cheng, M.; Wang, J. Research on the in-site measurement of spur gears based on machine vision. J. Mach. Des. 2020, 37, 19–22. [Google Scholar]
- Ge, J. Analysis on the development trend of computer image processing technology. Comput. Prod. Circ. 2019, 5, 6. [Google Scholar]
- Zhang, H. Computer image processing technology and its application in agricultural engineering. Telecom World 2019, 26, 65–66. [Google Scholar]
- Duan, J.; Lu, H.; Wang, W.; Wang, L.; Zhao, L. Present situation and development of the fruit harvesting machinery. Guangdong Agric. Sci. 2012, 39, 189–192. [Google Scholar]
- Zhao, L.; Yang, H.; Xie, H.; Duan, J.; Jin, M.; Fu, H.; Guo, J.; Xu, Z.; Jiang, T.; Yang, Z. Effects of morphological and anatomical characteristics of banana crown vascular bundles on cutting mechanical properties using multiple imaging methods. Agronomy 2020, 10, 1199. [Google Scholar] [CrossRef]





| Model | Unstandardized Coefficients | R2 | F | Sig. (Significance) | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF (Variance Inflation Factor) | ||||
| (Constant) | 17.090 | 4.453 | 0.973 | 385.956 | 0.001 | ||
| Variety | −1.276 | 0.380 | 0.002 | 1.000 | 1.000 | ||
| Moisture content | 0.143 | 0.049 | 0.006 | 1.000 | 1.000 | ||
| Internode position | 3.750 | 0.111 | 0.000 | 1.000 | 1.000 | ||
| Model | Unstandardized Coefficients | R2 | F | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF | ||||
| (Constant) | −2.905 | 0.586 | 0.973 | 241.159 | 0.000 | ||
| Variety | −0.122 | 0.059 | 0.051 | 1.000 | 1.000 | ||
| Moisture content | 0.034 | 0.007 | 0.000 | 1.000 | 1.000 | ||
| Internode position | 0.451 | 0.017 | 0.000 | 1.000 | 1.000 | ||
| Segments | 93% Moisture Content | 84% Moisture Content | Total Density (g/cm3) | Node (Yes/No)? | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Density-Rind (g/cm3) | Density-Inner Tissue (g/cm3) | Density-Rind (g/cm3) | Density-Inner Tissue (g/cm3) | ||||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | ||
| 1 | 1.071 | 0.45 | 0.792 | 0.27 | 1.045 | 0.33 | 0.767 | 0.21 | 0.885 | 0.05 | Yes |
| 2 | 1.035 | 0.23 | 0.788 | 0.06 | 1.007 | 0.15 | 0.751 | 0.05 | 0.891 | 0.02 | No |
| 3 | 1.084 | 0.55 | 0.935 | 0.31 | 1.052 | 0.41 | 0.902 | 0.28 | 0.946 | 0.03 | Yes |
| 4 | 1.079 | 0.51 | 0.811 | 0.33 | 1.046 | 0.46 | 0.784 | 0.25 | 0.873 | 0.03 | No |
| 5 | 1.165 | 0.36 | 1.143 | 0.18 | 1.131 | 0.22 | 1.119 | 0.14 | 1.151 | 0.07 | Yes |
| 6 | 1.096 | 0.54 | 1.027 | 0.29 | 1.064 | 0.38 | 0.993 | 0.09 | 1.046 | 0.05 | No |
| 7 | 1.243 | 0.29 | 1.203 | 0.04 | 1.217 | 0.15 | 1.176 | 0.04 | 1.225 | 0.01 | Yes |
| 8 | 1.179 | 0.44 | 1.169 | 0.16 | 1.143 | 0.32 | 1.133 | 0.12 | 1.173 | 0.03 | No |
| 9 | 1.287 | 0.57 | 1.279 | 0.38 | 1.256 | 0.41 | 1.241 | 0.25 | 1.281 | 0.08 | Yes |
| 10 | 1.243 | 0.19 | 1.195 | 0.01 | 1.211 | 0.06 | 1.168 | 0.01 | 1.226 | 0.06 | No |
| 11 | 1.199 | 0.48 | 0.931 | 0.22 | 1.162 | 0.27 | 0.909 | 0.19 | 1.006 | 0.05 | Yes |
| 12 | 1.148 | 0.53 | 0.882 | 0.37 | 1.118 | 0.42 | 0.853 | 0.23 | 0.998 | 0.07 | No |
| 13 | 1.153 | 0.25 | 0.947 | 0.07 | 1.121 | 0.18 | 0.915 | 0.02 | 0.965 | 0.01 | Yes |
| Model | Unstandardized Coefficients | R2 | F | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF | ||||
| (Constant) | 104.411 | 0.424 | 0.996 | 2927.345 | 0.000 | ||
| Variety | −0.022 | 0.189 | 0.909 | 1.000 | 1.000 | ||
| State | −10.832 | 0.116 | 0.000 | 1.000 | 1.000 | ||
| Internode position | 0.165 | 0.055 | 0.005 | 1.000 | 1.000 | ||
| Model | Unstandardized Coefficients | R2 | F | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF | ||||
| (Constant) | 1.396 | 0.229 | 0.970 | 176.589 | 0.000 | ||
| Variety | 0.024 | 0.122 | 0.850 | 1.000 | 1.000 | ||
| Node position | 0.575 | 0.031 | 0.000 | 1.000 | 1.000 | ||
| Model | Unstandardized Coefficients | R2 | F | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF | ||||
| (Constant) | 36.580 | 5.720 | 0.966 | 128.944 | 0.000 | ||
| Variety | 0.602 | 3.036 | 0.847 | 1.000 | 1.000 | ||
| Internode position | 14.271 | 0.889 | 0.000 | 1.000 | 1.000 | ||
| Model | Unstandardized Coefficients | R2 | F | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| Beta | Standard Error | Tolerance | VIF | ||||
| (Constant) | 192.571 | 4.064 | 0.824 | 25.703 | 0.000 | ||
| Variety | −2.143 | 2.173 | 0.345 | 1.000 | 1.000 | ||
| Node position | −3.857 | 0.543 | 0.000 | 1.000 | 1.000 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Fu, H.; Yang, Z.; Li, J.; Jiang, Y.; Jiang, T.; Liu, E.; Duan, J. Research on the Physical Characteristic Parameters of Banana Bunches for the Design and Development of Postharvesting Machinery and Equipment. Agriculture 2021, 11, 362. https://doi.org/10.3390/agriculture11040362
Guo J, Fu H, Yang Z, Li J, Jiang Y, Jiang T, Liu E, Duan J. Research on the Physical Characteristic Parameters of Banana Bunches for the Design and Development of Postharvesting Machinery and Equipment. Agriculture. 2021; 11(4):362. https://doi.org/10.3390/agriculture11040362
Chicago/Turabian StyleGuo, Jie, Han Fu, Zhou Yang, Jun Li, Yinlong Jiang, Tingting Jiang, Enxiu Liu, and Jieli Duan. 2021. "Research on the Physical Characteristic Parameters of Banana Bunches for the Design and Development of Postharvesting Machinery and Equipment" Agriculture 11, no. 4: 362. https://doi.org/10.3390/agriculture11040362
APA StyleGuo, J., Fu, H., Yang, Z., Li, J., Jiang, Y., Jiang, T., Liu, E., & Duan, J. (2021). Research on the Physical Characteristic Parameters of Banana Bunches for the Design and Development of Postharvesting Machinery and Equipment. Agriculture, 11(4), 362. https://doi.org/10.3390/agriculture11040362









