A Novel Approach for the Simulation of Reference Evapotranspiration and Its Partitioning
Abstract
:1. Introduction
2. Materials and Methods
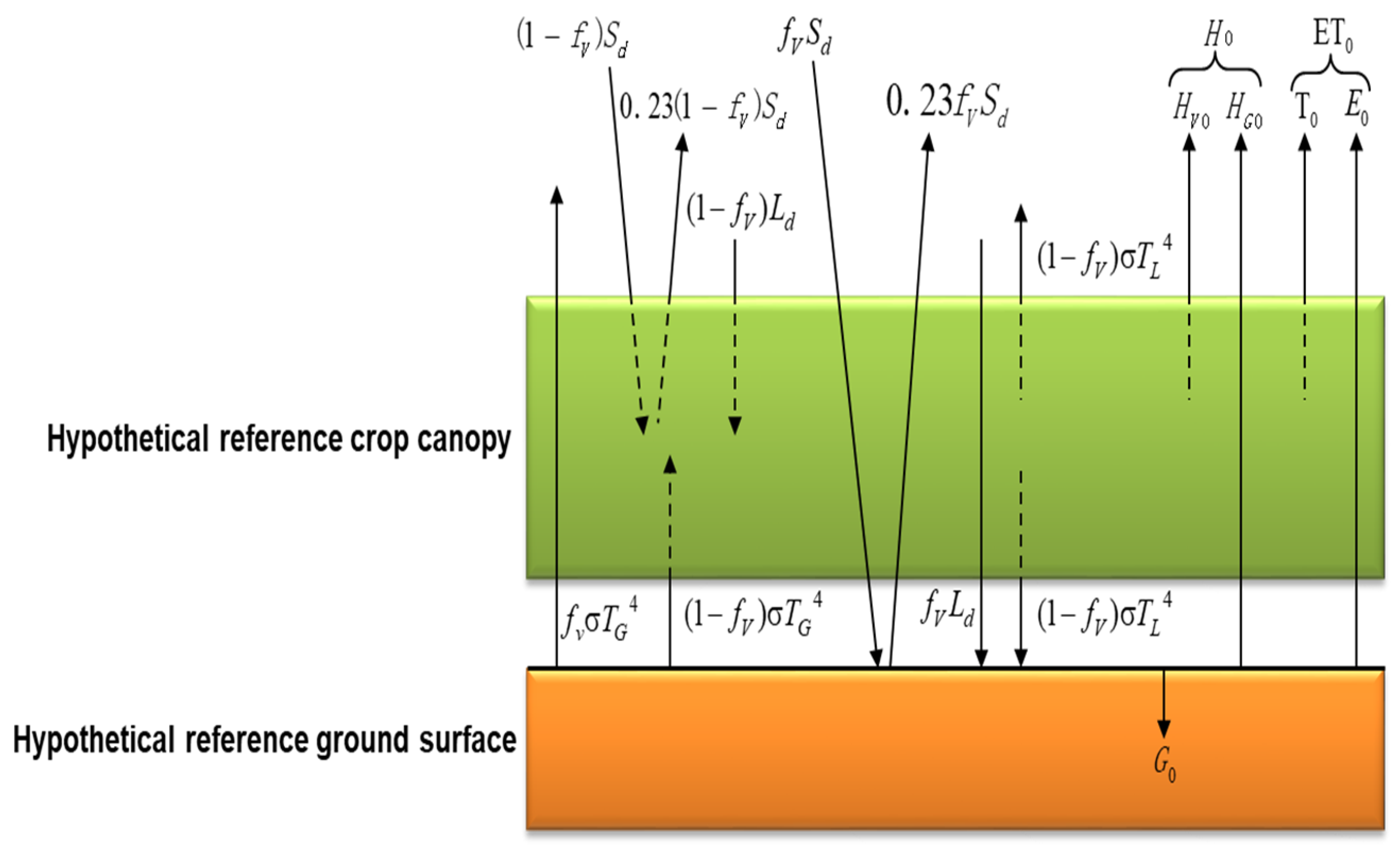
2.1. An Updated Reference-SPAC (R-SPAC) Model for ET0
2.2. Numerical Solution for ET0 by the R-SPAC Model
2.3. The FAO-PM Model for Estimating ET0
2.4. An Analysis of the Sensitivity of the R-SPAC Model
2.5. Model Validation Dataset
3. Results
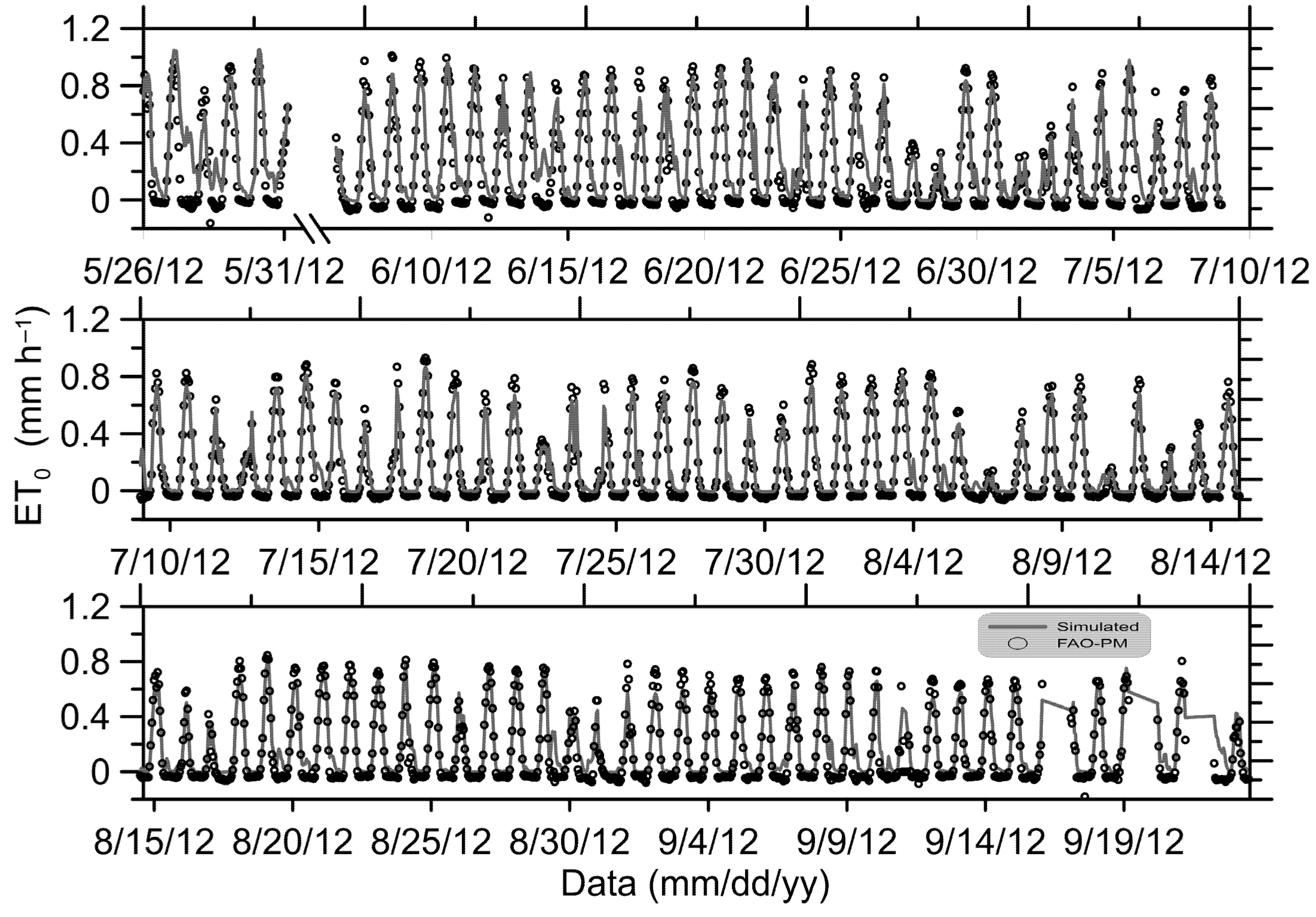
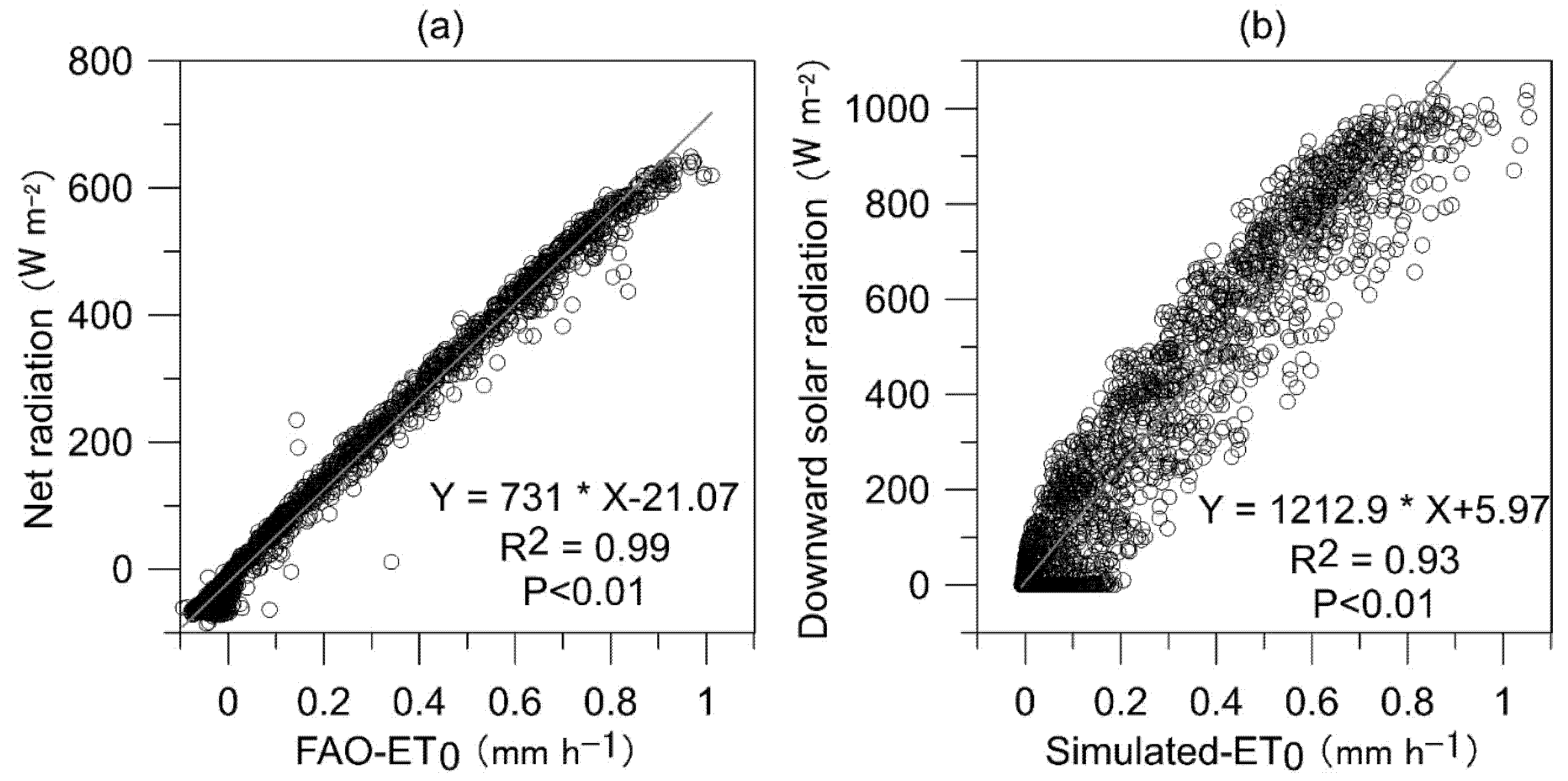
3.1. R-SPAC Model Performance in Simulating ET0
3.2. Seasonal Variations in ETo
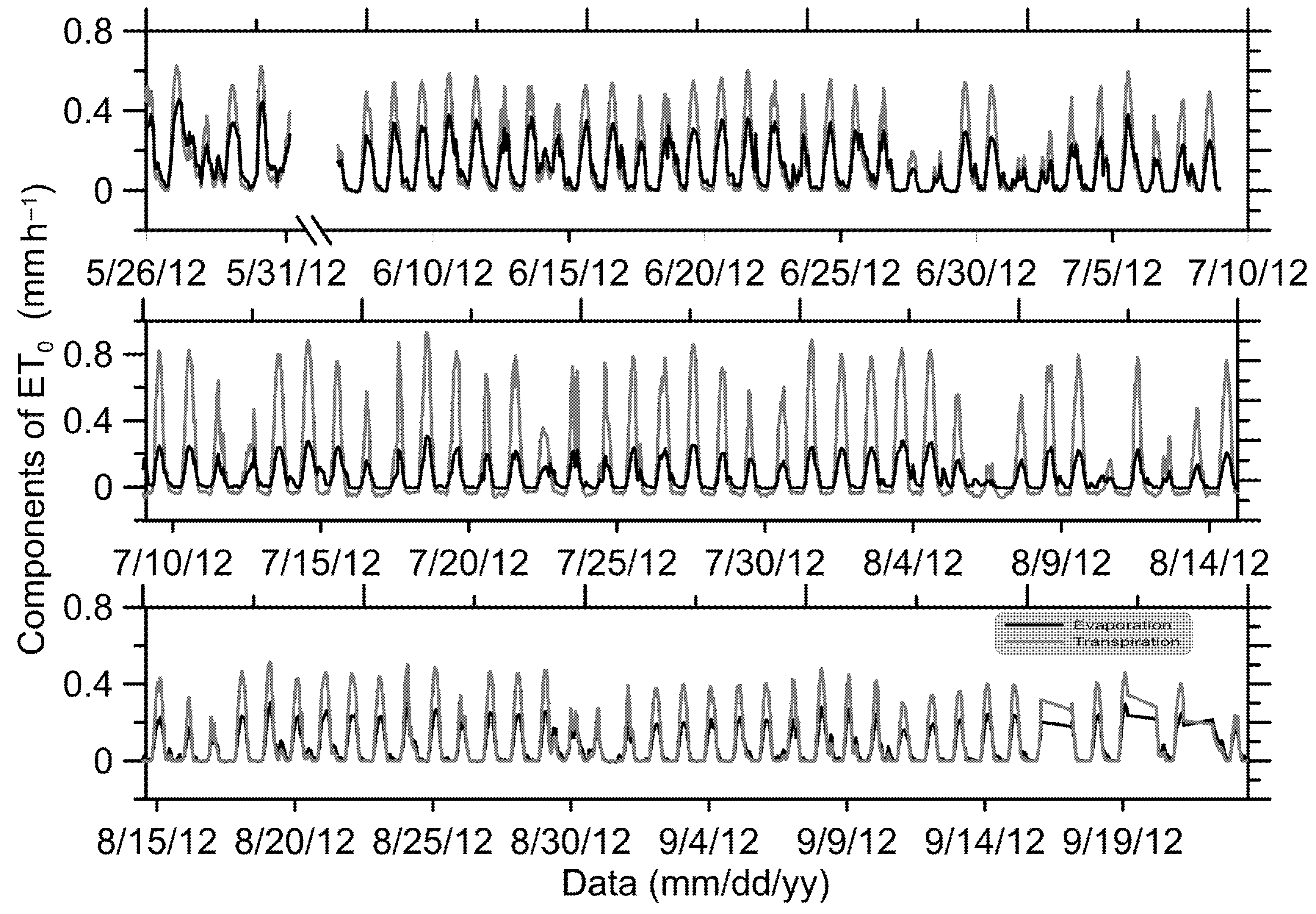
3.3. Partitioning of ET0
3.4. Results of Sensitivity Analysis
4. Discussion
4.1. Modeling Advantages and Limitations
4.2. Controls of ET0
4.3. Implications and Prospective Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Wang, T.; Melton, F.S.; Pas, I.; Johnson, L.F.; Thao, T.; Post, K.; Florence, C.S. Evaluation of crop coefficient and evapotranspiration data for sugar beets from landsat surface reflectances using micrometeorological measurements and weighing lysimetry. Agric. Water Manag. 2021, 244, 106533. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Turc, L. Estimation des besoins en eau d’irrigation, evapotranspiration potentielle, formule climatique simplifiee etmise a jour. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- Monteith, J.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Burt, C.M.; Mutziger, A.J.; Allen, R.G.; Howell, T.A. Evaporation research: Review and interpretation. J. Irrig. Drain. Eng. 2005, 131, 37–58. [Google Scholar] [CrossRef] [Green Version]
- Guan, H.; Wilson, J.L. A hybrid dual-source model for potential evaporation and transpiration partitioning. J. Hydrol. 2009, 377, 405–416. [Google Scholar] [CrossRef]
- McVicar, T.R.; Van Niel, T.G.; Li, L.-T.; Hutchinson, M.F.; Mu, X.-M.; Liu, Z.-H. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007, 338, 196–220. [Google Scholar] [CrossRef]
- Pˆoças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficientes: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Pereira, L.; Paredes, P.; Melton, F.; Johnson, L.; Wang, T.; L’opez-Urrea, R.; Cancela, J.; Allen, R. Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agric. Water Manag. 2020, 241, 106197. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Paredes, P.; Cunha, M.; Pereira, L.S. Estimation of actual crop coefficients using remotely sensed vegetation indices and soil water balance modelled data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef] [Green Version]
- Harbeck, E. A practical and field technique for measuring reservoir evaporation utilizing mass-transfer theory. Geol. Surv. Prof. Pap. Wash. 1962, 272, 100–105. [Google Scholar]
- Mohammad, J.; Hamidreza, K.; Ali, K.; Akbar, M. Estimation of evapotranspiration and crop coefficient of drip-irrigated orange trees under a semi-arid climate. Agric. Water Manag. 2021, 248, 106769. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate: The Geographical Review; Taylor & Francis Ltd.: New York, NY, USA, 1948; Volume 38, pp. 55–94. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrol. Process. 2001, 15, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of radiation based methods for calculating evaporation. Hydrol. Process. 2000, 14, 339–349. [Google Scholar] [CrossRef]
- Sumner, D.M.; Jacobs, J.M. Utility of Penman–Monteith, Priestley–Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture evapotranspiration. J. Hydrol. 2005, 308, 81–104. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops—An energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source approach for estimating turbulent fluxes using multiple angle thermal infrared observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
- Wang, P.; Deng, Y.J.; Li, X.Y.; Wei, Z.; Hu, X.; Tian, F.; Wu, X.; Huang, Y.; Ma, Y.J.; Zhang, C.; et al. Dynamical effects of plastic mulch on evapotranspiration partition in a mulched agriculture ecosystem: Measurement with numerical modeling. Agric. For. Meteorol. 2019, 268, 98–108. [Google Scholar] [CrossRef]
- Wang, P.; Li, X.Y.; Wang, L.X.; Wu, X.C.; Hu, X.; Fan, Y.; Tong, Y.Q. Divergent evapotranspiration partition dynamics between shrubs and grasses in a shrub-encroached steppe ecosystem. New Phytol. 2018, 219, 1325–1337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norman, J.M.; Anderson, M.C.; Kustas, W.P.; French, A.N.; Mecikalski, J.; Torn, R.; Diak, G.R.; Schmugge, T.J.; Tanner, B.C.W. Remote sensing of surface energy fluxes at 101-m pixel resolutions. Water Resour. Res. 2003, 39, 1221. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Tong, Y.; Wang, P.; Li, X.Y.; Wang, L.; Wu, X.; Shi, F.; Bai, Y.; Li, E.; Wang, J.; Wang, Y. Seasonality of the transpiration fraction and its controls across typical ecosystems within the Heihe River Basin. J. Geophys. Res. Atmos. 2019, 124, 1277–1291. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- Peng, L.; Zeng, Z.; Wei, Z.; Chen, A.; Wood, E.F.; Sheffield, J. Determinants of the ratio of actual to potential evapotranspiration. Glob. Chang. Biol. 2019, 25, 1326–1343. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Yamanaka, T. Application of a two-source model for partitioning evapotranspiration and assessing its controls in temperate grasslands in central Japan. Ecohydrology 2014, 7, 345–353. [Google Scholar] [CrossRef]
- Cui, J.; Tian, L.; Wei, Z.; Huntingford, C.; Wang, P.; Cai, Z.; Ma, N.; Wang, L. Quantifying the controls on evapotranspiration partitioning in the highest alpine meadow ecosystem. Water Resour. Res. 2020, 55, 1–22. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation in the Atmosphere. Theory, History, and Applications; Reidel Dordrecht: Boston, MA, USA; London, UK, 1982. [Google Scholar]
- Paniconi, C.; Putti, M. A comparison of Picard and Newton iteration in the numerical solution of multidimensional variably saturated flow problems. Water Resour. Res. 1994, 30, 3357–3374. [Google Scholar] [CrossRef]
- Yamanaka, T.; Takeda, A.; Sugita, F. A modified surface-resistance approach for representing bare-soil evaporation: Wind-tunnel experiments under various atmospheric conditions. Water Resour. Res. 1997, 33, 2117–2128. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 571, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230, 97–113. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Water use efficiency and evapotranspiration partitioning for three typical ecosystems in the Heihe river basin, northwestern china. Agric. For. Meteorol. 2018, 253, 261–273. [Google Scholar] [CrossRef]
- Ahmed, E.; Jinsong, D.; Ke, W.; Anurag, M.; Saman, M. Modeling long-term dynamics of crop evapotranspiration using deep learning in a semi-arid environment. Agric. Water Manag. 2020, 241, 106334. [Google Scholar] [CrossRef]
- Evett, S.R.; Schwartz, R.C.; Howell, T.A.; Louis Baumhardt, R.; Copeland, K.S. Can weighing lysimeter ET represent surrounding field ET well enough to test flux station measurements of daily and sub-daily ET? Adv. Water Resour. 2012, 50, 79–90. [Google Scholar] [CrossRef]
- Kaiser, D.P.; Qian, Y. Decreasing trends in sunshine duration over China for 1954–1998: Indication of increased haze pollution? Geophys. Res. Lett. 2002, 29, 2042. [Google Scholar] [CrossRef]
- Liepert, B.G.; Feichter, J.; Lohmann, U.; Roeckner, E. Can aerosols spin down the water cycle in a warmer and moister world? Geophys. Res. Lett. 2004, 31, L06207. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Tenberth, K.E.; Karl, T.R. Effects of clouds, soil moisture, precipitation and water vapor on diurnal Temperature range. J. Clim. 1999, 12, 2451–2473. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2009, 101, 19–28. [Google Scholar] [CrossRef]
- Wang, P.; Yamanaka, T.; Qiu, G.Y. Causes of decreased reference evapotranspiration and pan evaporation in the Jinghe River catchment, northern China. Environmentalist 2012, 32, 1–10. [Google Scholar] [CrossRef]
- Liu, C.; Sun, G.; McNulty, S.G.; Noormets, A.; Fang, Y. Environmental controls on seasonal ecosystem evapotranspiration/potential evapotranspiration ratio as determined by the global eddy flux measurements. Hydrol. Earth Syst. Sci. 2017, 21, 311–322. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Lee, X.; Wen, X.; Xiao, W. Evapotranspiration partitioning for three agro-ecosystems with contrasting moisture conditions: A comparison of an isotope method and a two-source model calculation. Agric. For. Meteorol. 2018, 252, 296–310. [Google Scholar] [CrossRef]

| Variables | Dataset | Unit | 2 RMSD | I index | R2 | n |
|---|---|---|---|---|---|---|
| Reference Evapotranspiration, ET0 | All dataset | mm h−1 | 0.05 | 0.98 | 0.96 | 2813 |
| 1 Daily time | mm h−1 | 0.05 | 0.99 | 0.96 | 1046 | |
| Actual Evapotranspiration, ETa | All dataset | W m−2 | 47.90 | 0.96 | 0.87 | 1464 |
| 3 Actual Transpiration, T | All dataset | mm h−1 | 0.11 | 0.82 | 0.80 | 335 |
| 1 8:00am–16:00pm. 2 root mean square difference. 3 Hourly mean T dataset was obtained from Zhou et al., 2018 [35]. | ||||||
| Variables | Mean (s.d.) | ||
|---|---|---|---|
| T0 | E0 | ET0 | |
| Sd | 0.98 (0.30) | 0.64 (0.23) | 0.89 (0.29) |
| Ld | 0.80 (0.47) | 0.49 (0.31) | 0.67 (0.39) |
| u | 0.22 (0.14) | 0.27 (0.11) | 0.25 (0.12) |
| Ta | 0.56 (0.13) | 0.28 (0.25) | 0.44 (0.13) |
| ha | −0.12 (0.20) | −0.42 (0.35) | −0.23 (0.25) |
| P | 0.08 (0.11) | 0.00 (0.10) | 0.05 (0.10) |
| Tss | 0.05 (0.06) | 0.38 (0.24) | 0.18 (0.15) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Ma, J.; Ma, J.; Sun, H.; Chen, Q. A Novel Approach for the Simulation of Reference Evapotranspiration and Its Partitioning. Agriculture 2021, 11, 385. https://doi.org/10.3390/agriculture11050385
Wang P, Ma J, Ma J, Sun H, Chen Q. A Novel Approach for the Simulation of Reference Evapotranspiration and Its Partitioning. Agriculture. 2021; 11(5):385. https://doi.org/10.3390/agriculture11050385
Chicago/Turabian StyleWang, Pei, Jingjing Ma, Juanjuan Ma, Haitao Sun, and Qi Chen. 2021. "A Novel Approach for the Simulation of Reference Evapotranspiration and Its Partitioning" Agriculture 11, no. 5: 385. https://doi.org/10.3390/agriculture11050385







