Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soil Sampling
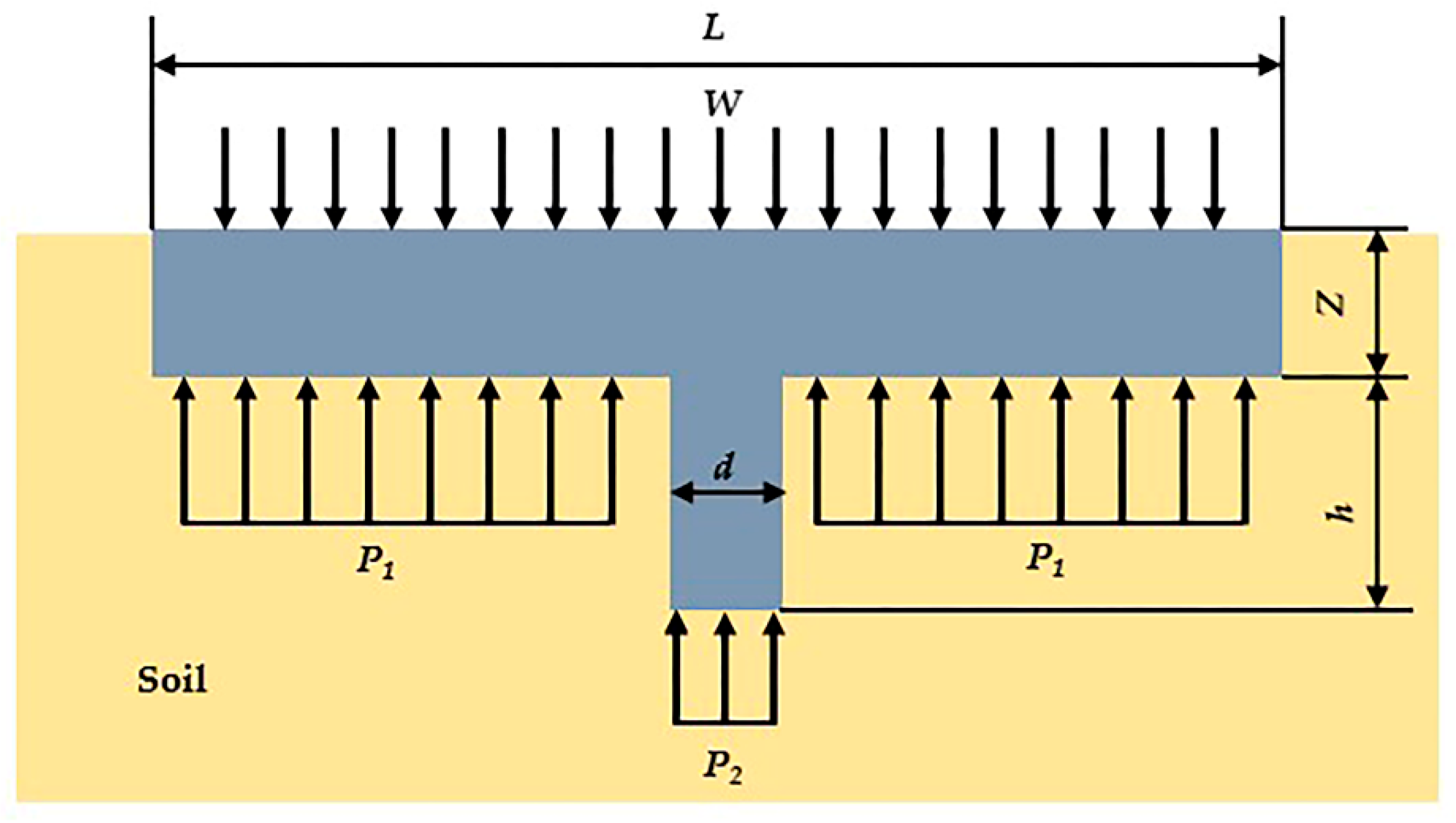
2.2. Vertical Stress Analysis of the Grouser Shoes
2.3. Experimental Equipment
2.4. Experiment Scheme
2.5. Data Analysis
3. Results and Discussion
3.1. ANOVA Analysis
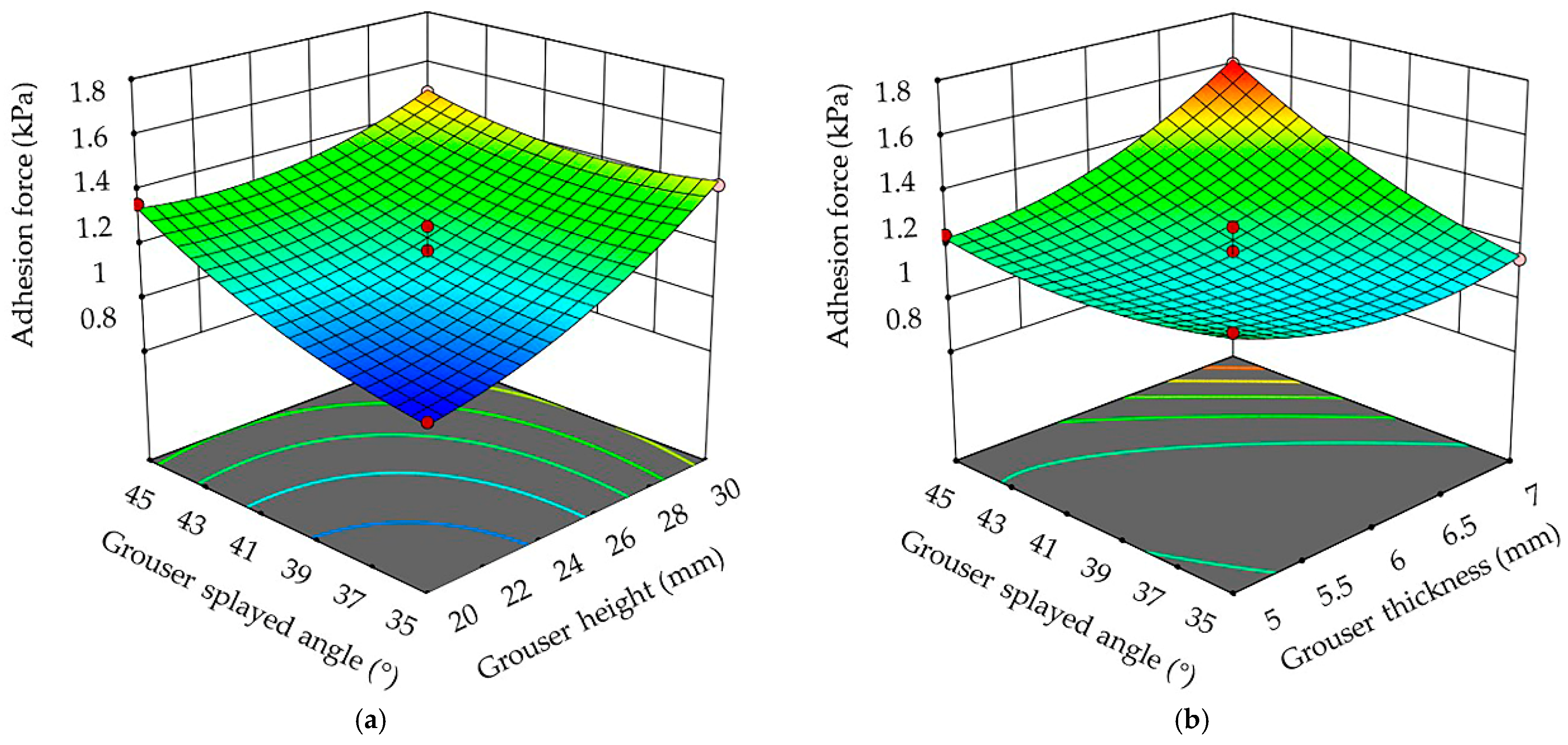
3.2. Analysis of Interactive Factors
3.2.1. Analysis of Interactive Factors on Adhesion Force
3.2.2. Analysis of Interactive Factors on Adhesive Soil Mass
3.3. Multi-Objective Optimization Model
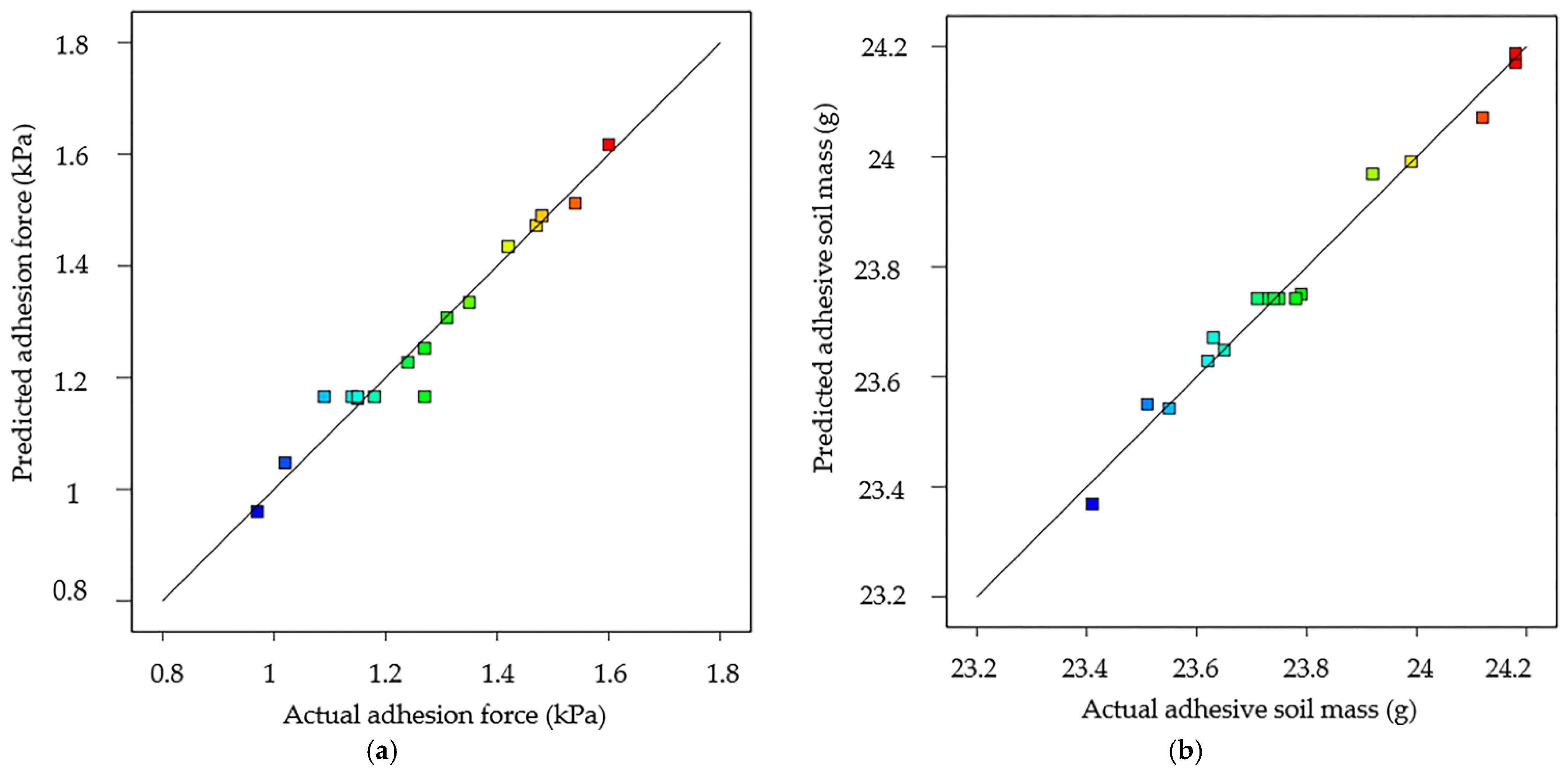
3.4. Verification Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Wu, Y.; Liu, B.; Zheng, Q.; Yin, J. Characteristics and factors controlling the development of ephemeral gullies in cultivated catchments of black soil region, Northeast China. Soil Tillage Res. 2007, 96, 28–41. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Z.; Zhang, B.; Song, K.; Duan, H. Spatial distribution of soil organic carbon and analysis of related factors in croplands of the black soil region, Northeast China. Agric. Ecosyst. Environ. 2006, 113, 73–81. [Google Scholar] [CrossRef]
- Li, J.; Tong, J.; Hu, B. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China. Trans. Chin. Soc. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
- Jiang, Q.; Cao, M.; Wang, Y. Quantification of the soil stiffness constants using physical properties of paddy soils in Yangtze Delta Plain, China. Biosyst. Eng. 2020, 200, 89–100. [Google Scholar] [CrossRef]
- Jia, X.; Ren, L. Theoretical Analysis of Adhesion Force of Soil to Solid Materials. Trans. Chin. Soc. Agric. Eng. 1995, 87, 489–493. [Google Scholar] [CrossRef]
- Ren, L.; Tong, J.; Li, J.; Chen, B.C. Soil Adhesion and Biomimetics of Soil-engaging Components: A Review. J. Agric. Eng. Res. 2001, 79, 239–263. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.H.; Shin, G.B.; Lee, S.H. Evaluation of the Slip Sinkage and its Effect on the Compaction Resistance of an Off-Road Tracked Vehicle. Appl. Sci. 2020, 10, 3175. [Google Scholar] [CrossRef]
- Massah, J.; Fard, M.R.; Aghel, H. An optimized bionic electro-osmotic soil-engaging implement for soil adhesion reduction. J. Terramechanics 2021, 95, 1–6. [Google Scholar] [CrossRef]
- Barzegar, M.; Karimi, R.; Hashemi, S.J.; Nazokdast, H. Evaluating the draft force and soil-tool adhesion of a UHMW-PE coated furrower. Soil Tillage Res. 2016, 163, 160–167. [Google Scholar] [CrossRef]
- Marani, S.M.; Shahgholi, G.; Moinfar, A. Effect of nano coating materials on reduction of soil adhesion and external friction. Soil Tillage Res. 2019, 193, 42–49. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Zenkov, S.A. Application of thermal effect as a means to combat ground-and-machine part adhesion. Mater. Sci. Eng. 2020, 862, 32–60. [Google Scholar] [CrossRef]
- Zenkov, S.A.; Lkhanag, D. Use of repair-recovery compositions for reducing the adhesion of soils to working bodies of machines. Mater. Sci. Eng. 2020, 971, 52–55. [Google Scholar]
- Ren, L.; Han, Z.; Li, J. Experimental investigation of bionic rough curved soil cutting blade surface to reduce soil adhesion and friction. Soil Tillage Res. 2006, 85, 1–12. [Google Scholar] [CrossRef]
- Ren, L.; Deng, S.Q.; Wang, J.C. Design Principles of the Non-smooth Surface of Bionic Plow Moldboard. J. Bionic Eng. 2004, 1, 9–19. [Google Scholar] [CrossRef]
- Ren, L. Progress in the bionic study on anti-adhesion and resistance reduction of terrain machines. Sci. China 2009, 52, 273–284. [Google Scholar] [CrossRef]
- Tong, J.; Sun, J.; Chen, D. Geometrical features and wettability of dung beetles and potential biomimetic engineering appli cations in tillage implements. Soil Tillage Res. 2005, 80, 1–12. [Google Scholar] [CrossRef]
- Wang, X. Study on use of vibration to reduce soil adhesion. J. Terramech. 1998, 35, 87–101. [Google Scholar] [CrossRef]
- Jia, H.; Wang, W. Application of anti-adhesion structure based on earthworm motion characteristics. Soil Tillage Res. 2018, 178, 159–166. [Google Scholar] [CrossRef]
- Sun, J.; Chen, H.; Wang, Z. Study on plowing performance of EDEM low-resistance animal bionic device based on red soil. Soil Tillage Res. 2020, 196, 104336. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, H.; Sun, J. Review of application of biomimetics for designing soil-engaging tillage implements in Northeast China. Int. J. Agric. Biol. Eng. 2016, 9, 12–21. [Google Scholar]
- Sun, J.; Wang, Y.; Zhang, S. The mechanism of resistance-reducing/anti-adhesion and its application on biomimetic disc furrow opener. Math. Biosci. Eng. 2020, 17, 4657–4677. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, S.A.; Li, Y.; Zheng, M. Effect of grouser height on the tractive performance of single grouser shoe under different soil moisture contents in clay loam terrain. Sustainability 2021, 13, 1156. [Google Scholar] [CrossRef]
- Ge, J.; Wang, X.; Kito, K. Comparing tractive performance of steel and rubber single grouser shoe under different soil moisture contents. Int. J. Agric. Biol. Eng. 2016, 9, 11–20. [Google Scholar]
- Grisso, R.; Perumpral, J.; Zoz, F. An empirical model for tractive performance of rubber-tracks in agricultural soils. J. Terramechanics 2006, 43, 225–236. [Google Scholar] [CrossRef]
- Park, W.; Chang, Y.; Lee, S.S. Prediction of the tractive performance of a flexible tracked vehicle. J. Terramech. 2008, 45, 13–23. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Y.; Ren, L.; Tang, Z. Distribution uniformity of soil stress under compaction of tracked undercarriage. Trans. Chin. Soc. Agric. Eng. 2020, 36, 52–58. [Google Scholar]
- Bekker, M. Introduction of Terrain Vehicle Systems; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Wong, J. Theory of Ground Vehicles, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Ren, L. Soil Adhesion Mechanics, 1st ed.; Machinery Industry Press: Beijing, China, 2011; pp. 4–7, 214–215. [Google Scholar]
- Zhang, L.; Yang, Z.; Xu, S. Application of electronic universal testing machine in soil adhesion testing. Test. Technol. Test. Mach. 2005, 45, 27–29. (In Chinese) [Google Scholar]
- Mosayebi, A. Methanol steam reforming over Co-Cu-Zn/γ-Al2O3 catalyst: Kinetic and RSM-BBD modeling approaches. Int. J. Energy Res. 2021, 45, 3288–3304. [Google Scholar] [CrossRef]
- Alipour, M.; Vosoughi, M.; Mokhtari, S.A. Optimizing the basic violet 16 adsorption from aqueous solutions by magnetic graphene oxide using the response surface model based on the Box–Behnken design. Int. J. Environ. Anal. Chem. 2019, 101, 758–777. [Google Scholar] [CrossRef]
- Fu, J.; Yuan, H.; Zhang, D. Multi-Objective Optimization of Process Parameters of Longitudinal Axial Threshing Cylinder for Frozen Corn Using RSM and NSGA-II. Appl. Sci. 2020, 10, 1646. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Jia, H.; Zhang, S. Optimization of cold pressing process parameters of chopped corn straws for fuel. Energies 2020, 13, 652. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, R.A.; Eperjesi, F.; Gilmartin, B. The application of analysis of variance (ANOVA) to different experimental designs in optometry. Ophthalmic Physiol. Opt. 2002, 22, 248–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagelkerke, N. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]


| Sample Depth (mm) | Bulk Density (kg·m−3) | Hardness (kPa) | Moisture Content (%) |
|---|---|---|---|
| 0–100 | 1130 | 42 | 24.31 |
| 100–200 | 1352 | 972 | 21.28 |
| 200–300 | 1326 | 1165 | 19.87 |
| Coded Levels | Grouser Height (mm) | Grouser Thickness (mm) | Grouser Splayed Angle (°) |
|---|---|---|---|
| −1 | 20 | 5 | 35 |
| 0 | 25 | 6 | 40 |
| 1 | 30 | 7 | 45 |
| Factors | Evaluation Indexes | ||||
|---|---|---|---|---|---|
| Numbers | Grouser Height (mm) | Grouser Thickness (mm) | Grouser Splayed Angle (°) | Adhesion Force (kPa) | Adhesive Soil Mass (g) |
| 1 | 1 | 0 | 1 | 1.48 | 23.55 |
| 2 | 1 | 1 | 0 | 1.54 | 23.62 |
| 3 | −1 | 0 | −1 | 0.97 | 24.18 |
| 4 | −1 | 1 | 0 | 1.31 | 23.63 |
| 5 | 1 | −1 | 0 | 1.47 | 23.41 |
| 6 | −1 | 0 | 1 | 1.35 | 23.79 |
| 7 | 0 | 1 | −1 | 1.15 | 24.12 |
| 8 | 0 | 1 | 1 | 1.60 | 23.65 |
| 9 | −1 | −1 | 0 | 1.02 | 24.18 |
| 10 | 0 | −1 | 1 | 1.24 | 23.92 |
| 11 | 0 | −1 | −1 | 1.27 | 23.99 |
| 12 | 1 | 0 | −1 | 1.42 | 23.51 |
| 13 | 0 | 0 | 0 | 1.27 | 23.71 |
| 14 | 0 | 0 | 0 | 1.09 | 23.74 |
| 15 | 0 | 0 | 0 | 1.18 | 23.78 |
| 16 | 0 | 0 | 0 | 1.15 | 23.75 |
| 17 | 0 | 0 | 0 | 1.14 | 23.73 |
| Source | Adhesion Force (kPa) | Adhesive Soil Mass (g) | ||||||
|---|---|---|---|---|---|---|---|---|
| Sum of Squares | Degrees of Freedom | F-Value | p Value | Sum of Squares | Degrees of Freedom | F-Value | p-Value | |
| Model | 0.5150 | 9 | 19.24 | 0.0004 *** | 0.8227 | 9 | 44.73 | <0.0001 *** |
| h | 0.1985 | 1 | 66.72 | <0.0001 *** | 0.3570 | 1 | 174.70 | <0.0001 *** |
| d | 0.0450 | 1 | 15.13 | 0.0060 ** | 0.0288 | 1 | 14.09 | 0.0071 * |
| α | 0.0925 | 1 | 31.08 | 0.0008 *** | 0.0990 | 1 | 48.45 | 0.0002 *** |
| h-d | 0.0121 | 1 | 4.07 | 0.0835 | 0.1444 | 1 | 70.66 | <0.0001 *** |
| h-α | 0.0256 | 1 | 8.61 | 0.0219 * | 0.0462 | 1 | 22.62 | 0.0021 ** |
| d-α | 0.0576 | 1 | 19.37 | 0.0032 ** | 0.0400 | 1 | 19.57 | 0.0031 ** |
| h2 | 0.0266 | 1 | 8.95 | 0.0202 * | 0.0398 | 1 | 19.49 | 0.0031 * |
| d2 | 0.0337 | 1 | 11.34 | 0.0120 * | 0.0179 | 1 | 8.77 | 0.0211 * |
| α2 | 0.0149 | 1 | 5.01 | 0.0602 | 0.0535 | 1 | 26.19 | 0.0014 ** |
| Residual | 0.0208 | 7 | 0.0143 | 7 | ||||
| Lack of Fit | 0.0031 | 3 | 0.2333 | 0.8692 | 0.0116 | 3 | 5.78 | 0.0615 |
| Pure Error | 0.0177 | 4 | 0.0027 | 4 | ||||
| Cor Total | 0.5358 | 16 | 0.8370 | 16 | ||||
| Response Indicators | R2 | Adjusted R2 | Predicted R2 | Predicted Precision |
|---|---|---|---|---|
| Adhesion force (kPa) | 0.96 | 0.91 | 0.86 | 15.72 |
| Adhesive soil mass (g) | 0.98 | 0.96 | 0.77 | 23.61 |
| Indicators | Adhesion Force (kPa) | Adhesive Soil Mass (g) |
|---|---|---|
| Predicted value | 1.16 | 23.76 |
| Measured value | 1.11 | 22.68 |
| Relative error value | 0.045 | 0.0476 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Li, J.; Tang, X.; Wang, R.; Chen, Z. Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil. Agriculture 2021, 11, 795. https://doi.org/10.3390/agriculture11080795
Fu J, Li J, Tang X, Wang R, Chen Z. Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil. Agriculture. 2021; 11(8):795. https://doi.org/10.3390/agriculture11080795
Chicago/Turabian StyleFu, Jun, Jian Li, Xinlong Tang, Ruixue Wang, and Zhi Chen. 2021. "Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil" Agriculture 11, no. 8: 795. https://doi.org/10.3390/agriculture11080795
APA StyleFu, J., Li, J., Tang, X., Wang, R., & Chen, Z. (2021). Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil. Agriculture, 11(8), 795. https://doi.org/10.3390/agriculture11080795






