Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay
Abstract
:1. Introduction
2. Grain Truck Controller Strategy
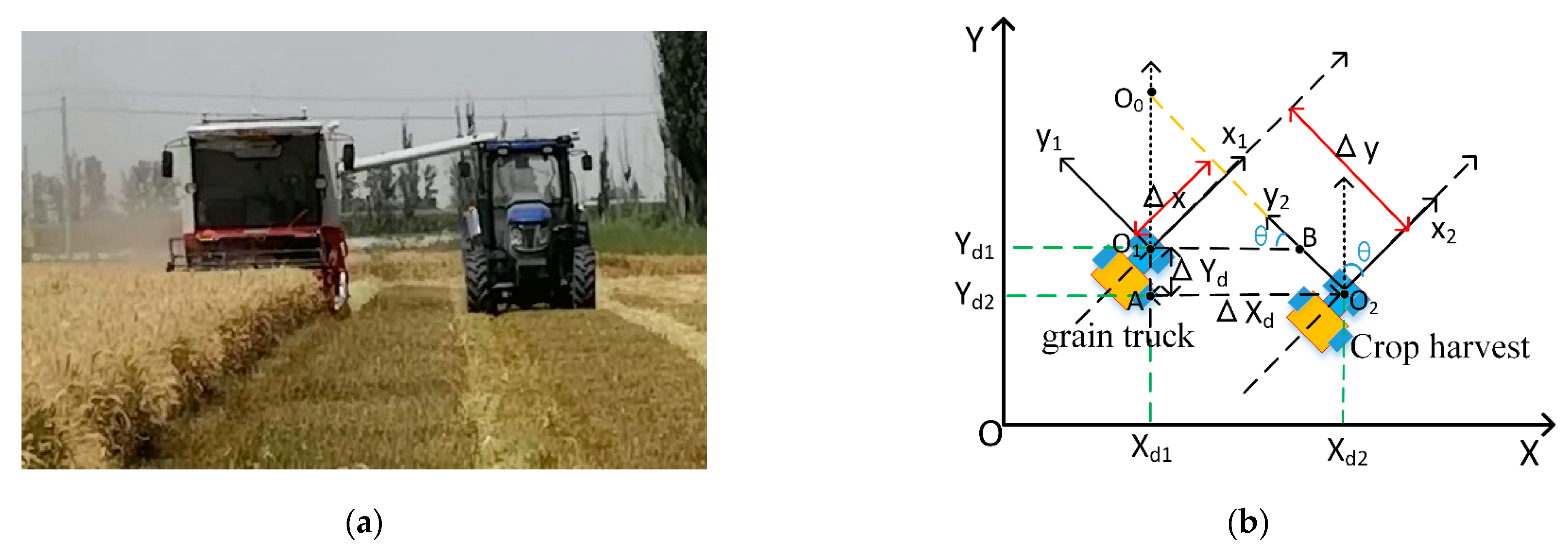
2.1. Crop Harvester and Grain Truck Follow-up Operation Model
2.2. Grain Truck Following Strategy
3. Design of Follower Controller for Grain Truck
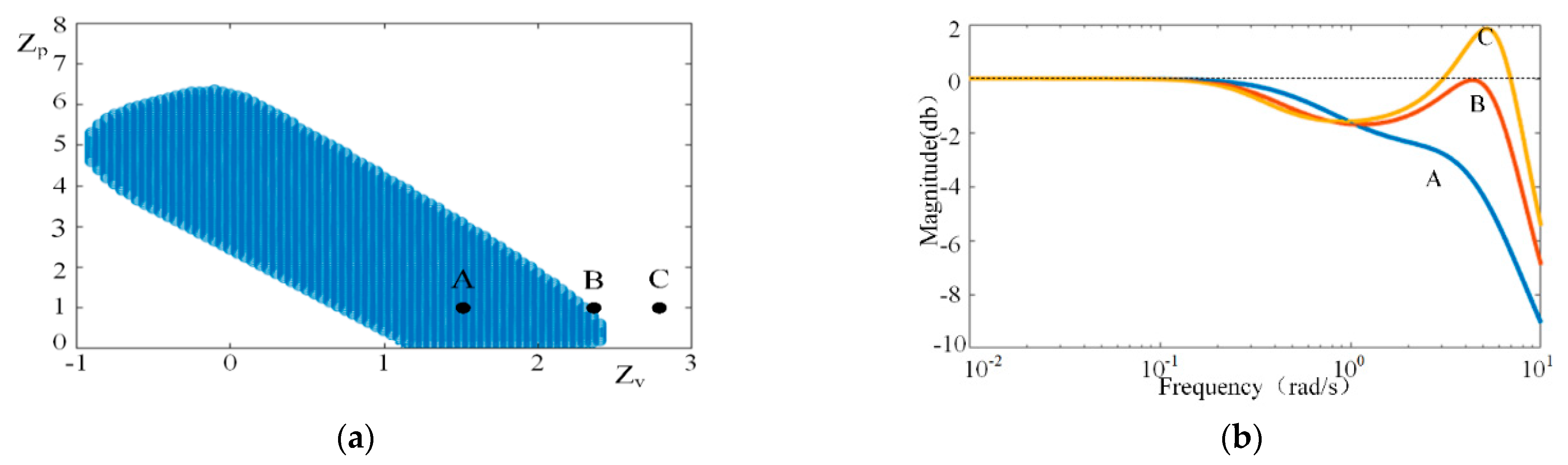
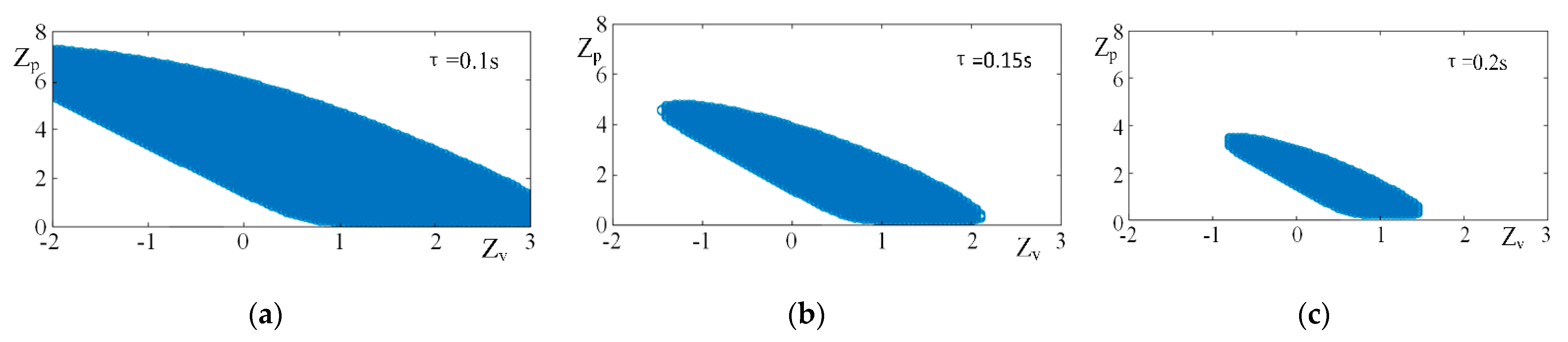
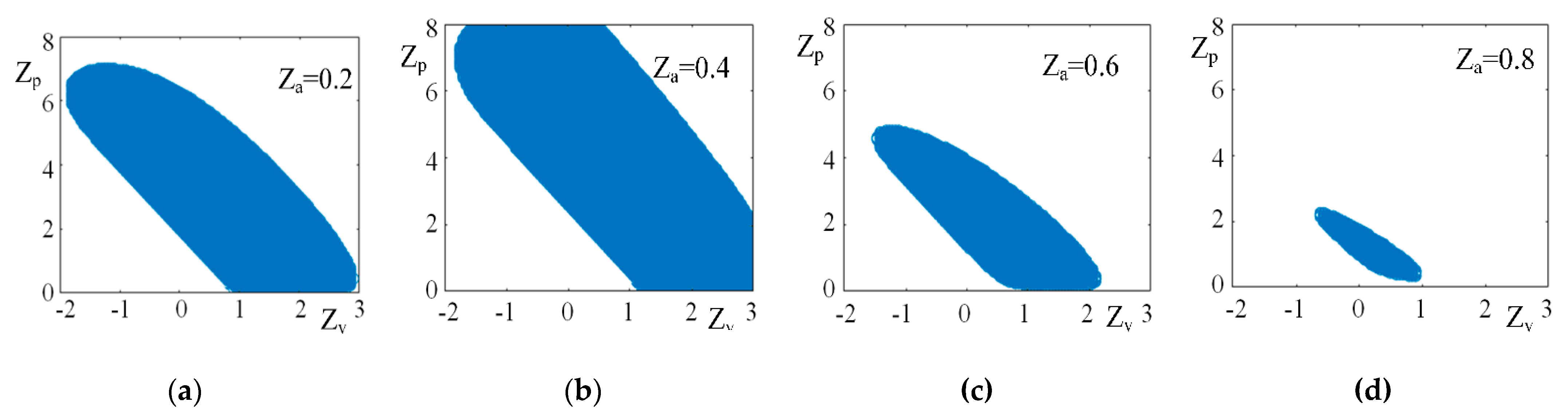
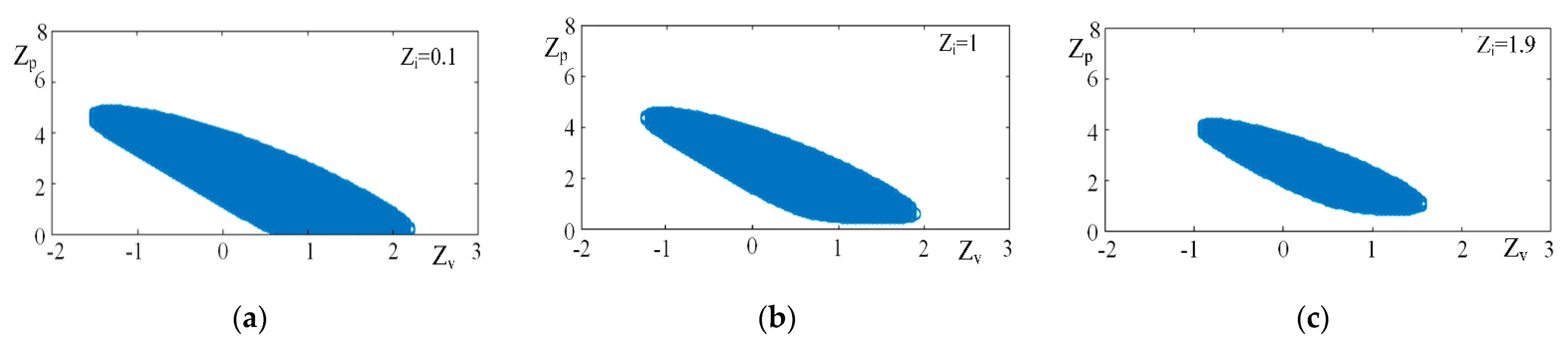
4. Stability Analysis of Following System for Grain Truck and Crop Harvester
5. Simulation and Vehicle Testing
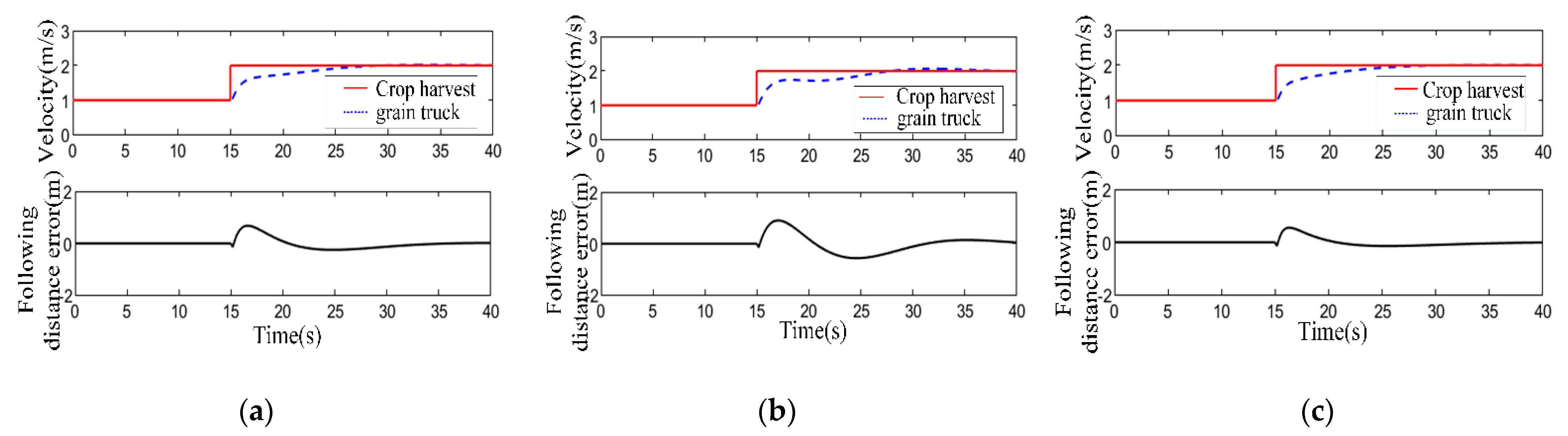
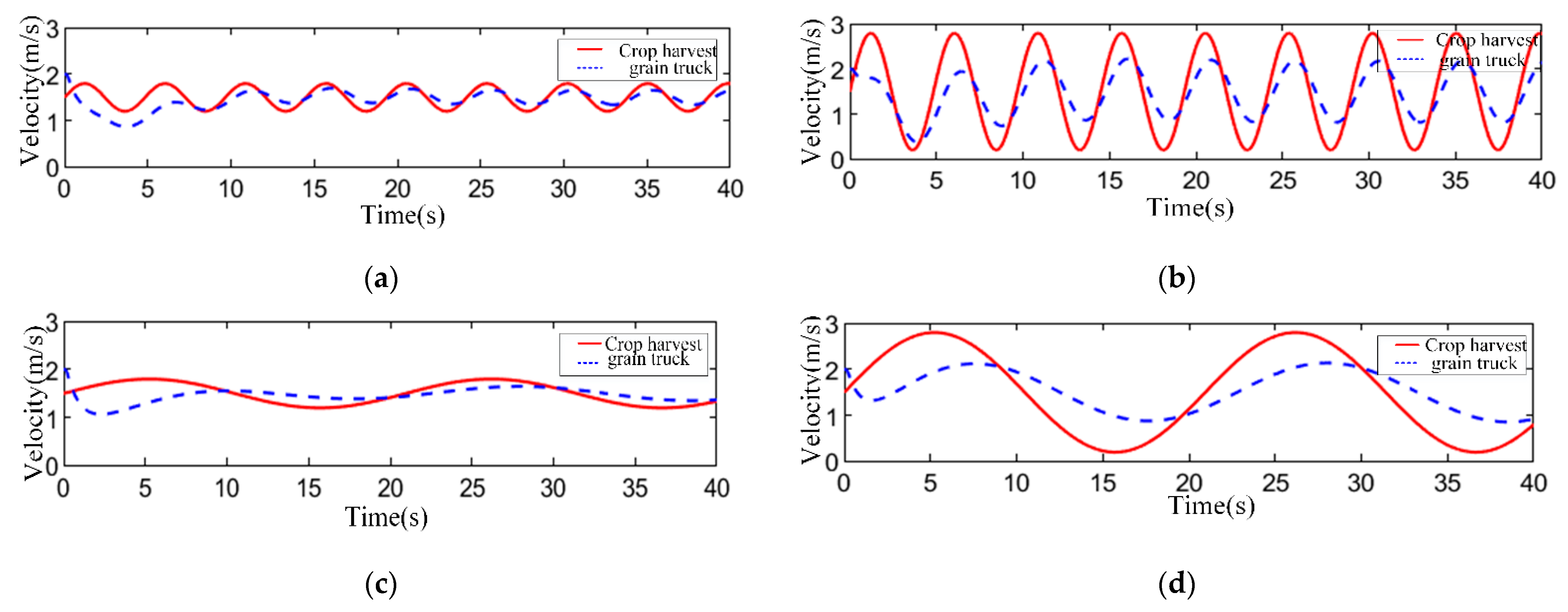
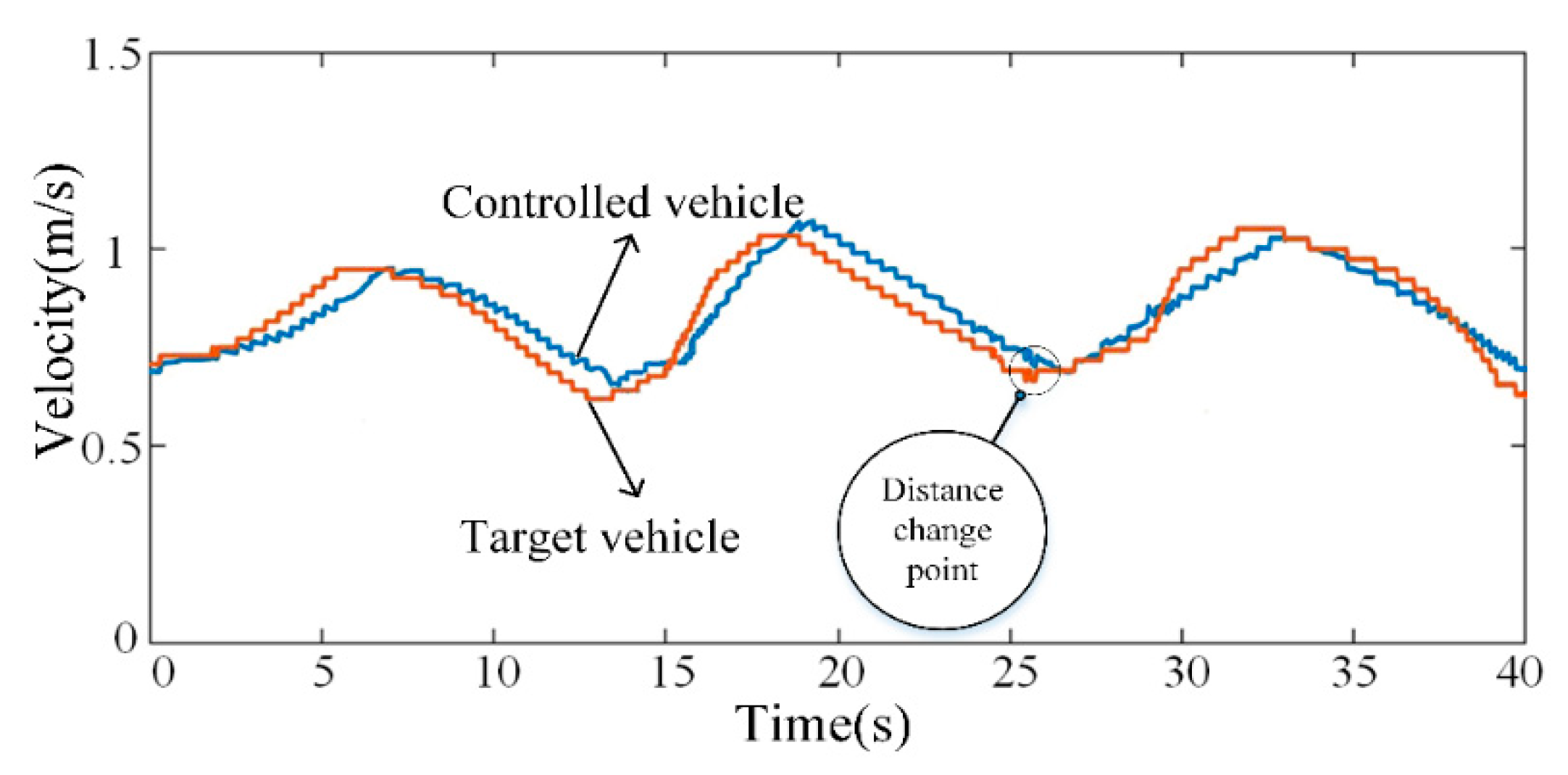
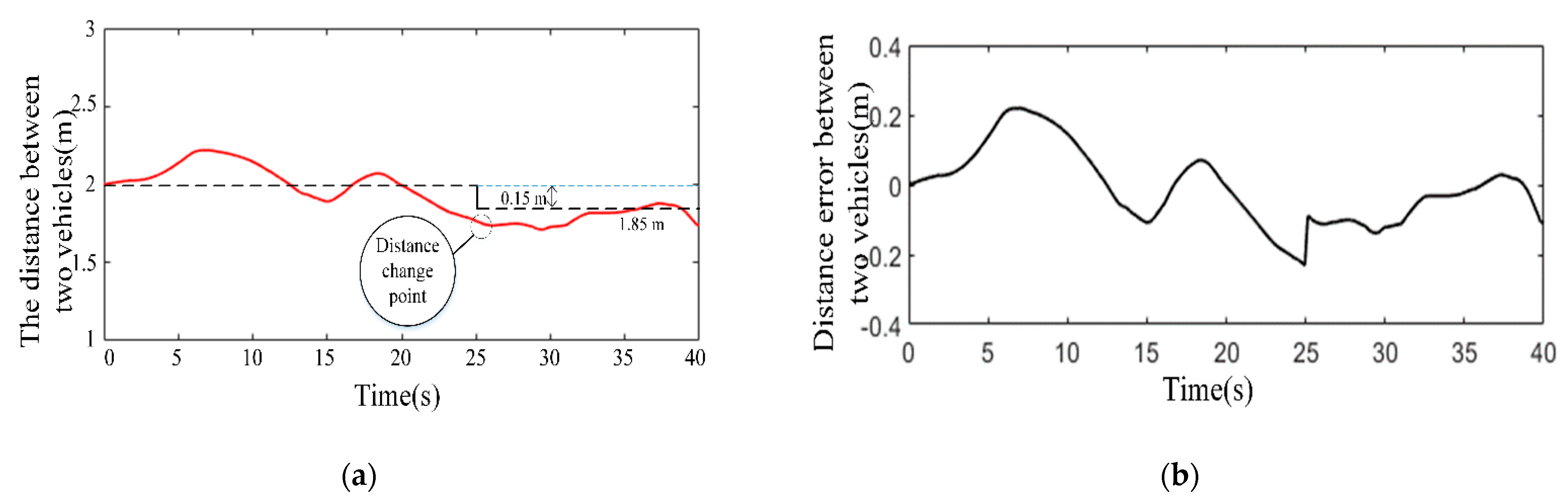
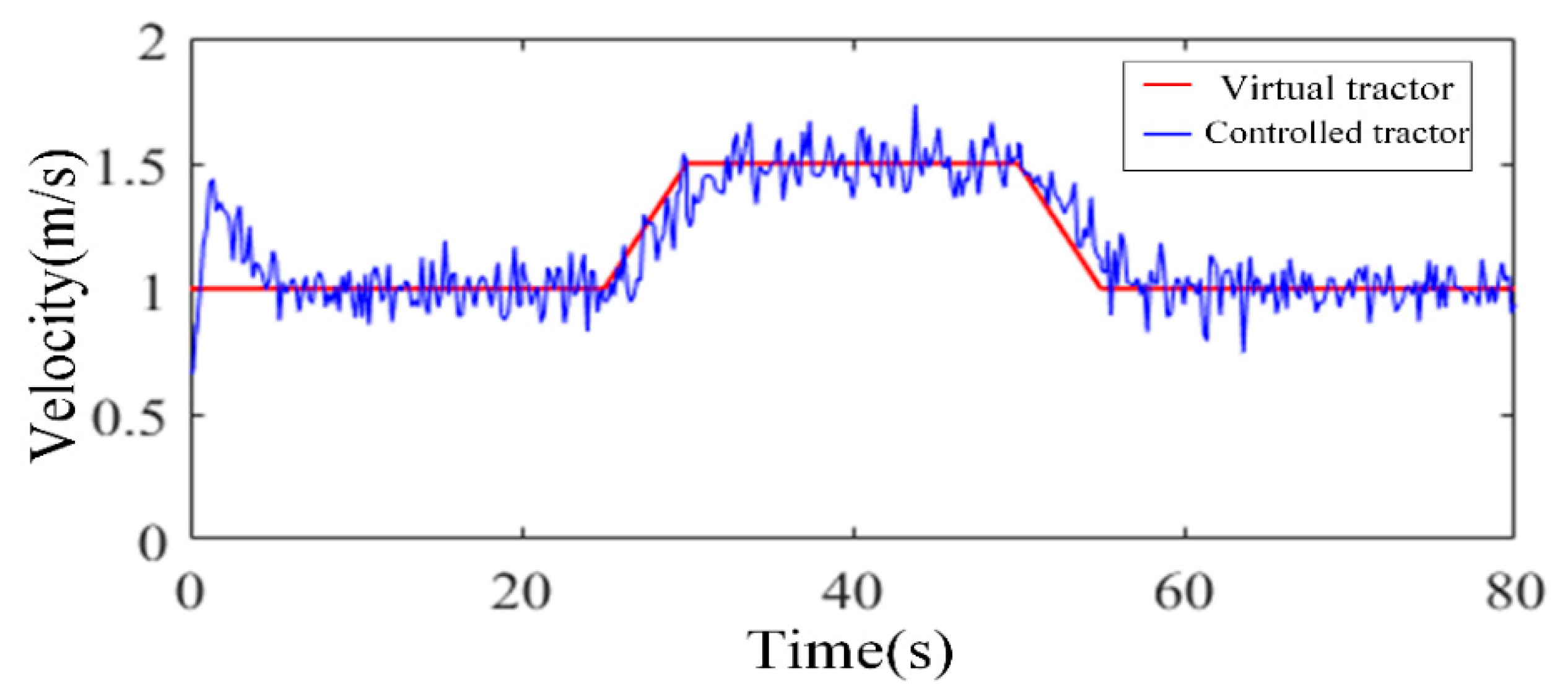
5.1. Simulation Analysis
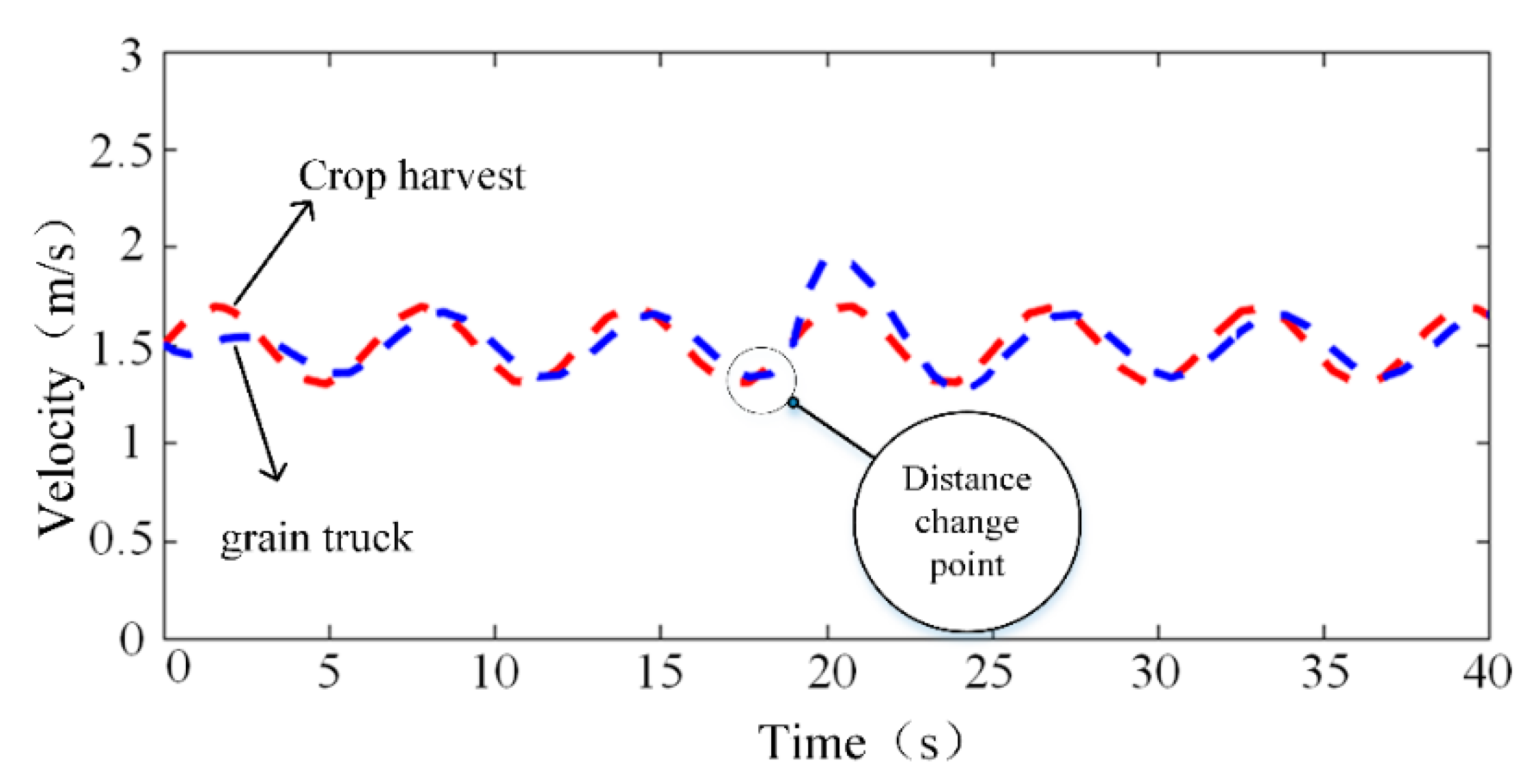
5.2. Real-Vehicle Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Backman, J.; Oksanen, T.; Visala, A. Navigation system for agricultural machines: Nonlinear model predictive path tracking. Comput. Electron. Agric. 2012, 82, 32–43. [Google Scholar] [CrossRef]
- Subramanian, V.; Burks, T.F.; Arroyo, A.A. Development of machine vision and laser radar based autonomous vehicle guidance systems for citrus grove navigation. Comput. Electron. Agric. 2006, 53, 130–143. [Google Scholar] [CrossRef]
- Kayacan, E.; Kayacan, E.; Ramon, H.; Saeys, W. Towards agrobots: Identification of the yaw dynamics and trajectory tracking of an autonomous tractor. Comput. Electron. Agric. 2015, 115, 78–87. [Google Scholar] [CrossRef]
- Oksanen, T. Laser scanner based collision prevention system for autonomous agricultural tractor. Agron. Res. 2015, 13, 167–172. [Google Scholar]
- Li, S.; Xu, H.; Ji, Y.; Cao, R.; Zhang, M.; Li, H. Development of a following agricultural machinery automatic navigation system. Comput. Electron. Agric. 2019, 158, 335–344. [Google Scholar] [CrossRef]
- Hu, J.; Gao, L.; Bai, X.; Li, T.; Liu, X. Review of research on automatic guidance of agricultural vehicles. Trans. Chin. Soc. Agric. Eng. 2015, 31, 1–10. [Google Scholar]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model predictive multi-objective vehicular adaptive cruise control. IEEE Trans. Control Syst. Technol. 2010, 19, 556–566. [Google Scholar] [CrossRef]
- Cheng, T.M.; Savkin, A.V.; Javed, F. Decentralized control of a group of mobile robots for deployment in sweep coverage. Robot. Auton. Syst. 2011, 59, 497–507. [Google Scholar] [CrossRef]
- Iida, M.; Kudou, M.; Ono, K.; Umeda, M. Automatic following control for agricultural vehicle. In Proceedings of the 6th International Workshop on Advanced Motion Control, Nagoya, Japan, 30 March–1 April 2000. [Google Scholar]
- Noguchi, N.; Will, J.; Reid, J.; Zhang, Q. Development of a master–slave robot system for farm operations. Comput. Electron. Agric. 2004, 44, 1–19. [Google Scholar] [CrossRef]
- Zhang, M.; Ji, Y.; Li, S. Research progress of agricultural machinery navigation technology. Trans. Chin. Soc. Agric. Mach. 2020, 51, 1–18. [Google Scholar]
- Zhang, C.; Noguchi, N.; Yang, L. Leader–follower system using two robot tractors to improve work efficiency. Comput. Electron. Agric. 2016, 121, 269–281. [Google Scholar] [CrossRef]
- Zhang, X.; Geimer, M.; Noack, P.O.; Grandl, L. Development of an intelligent master-slave system between agricultural vehicles. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 250–255. [Google Scholar]
- Bai, X.; Wang, Z.; Hu, J.; Gao, L.; Xiong, F. Harvester group corporative navigation method based on leader-follower structure. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2017, 48, 14–21. [Google Scholar]
- Bai, X.; Hu, J.; Wang, Z. Slave positioning method for cooperative navigation of combine harvester group based on visual servo. Trans. Chin. Soc. Agric. Eng. 2016, 32, 59–68. [Google Scholar]
- Xu, G.; Chen, M.; Miao, H.; Yao, W.; Diao, P.; Wang, W. Following Operation Control Method of Farmer Machinery Based on Model Predictive Control. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2020, 51, 11–20. [Google Scholar]
- Lee, K.H.; Ehsani, R.; Schueller, J.K. Forward movement synchronization of two vehicles in parallel using a laser scanner. Appl. Eng. Agric. 2007, 23, 827–834. [Google Scholar] [CrossRef]
- Luo, C.; Mohsenimanesh, A.; Laguë, C. Synchronous Tracking Control for Agricultural Wide-Span Implement Carrier (WSIC). Trans. ASABE 2018, 61, 873–883. [Google Scholar] [CrossRef]
- Zhu, Z.; Takeda, J.; Xie, B.; Song, Z.; Torisu, R.; Mao, E. Tractor platooning system on sloping terrain at low speed. Trans. ASABE 2009, 52, 1385–1393. [Google Scholar] [CrossRef]
- Vougioukas, S.G. A distributed control framework for motion coordination of teams of autonomous agricultural vehicles. Biosyst. Eng. 2012, 113, 284–297. [Google Scholar] [CrossRef]
- Hao, Y.; Laxton, B.; Benson, E.R.; Agrawal, S.K. Differential flatness-based formation following of a simulated autonomous small grainharvesting system. Trans. ASAE 2004, 47, 933. [Google Scholar] [CrossRef]
- Jensen, M.A.F.; Bochtis, D.; Sørensen, C.G.; Blas, M.R.; Lykkegaard, K.L. In-field and inter-field path planning for agricultural transport units. Comput. Ind. Eng. 2012, 63, 1054–1061. [Google Scholar] [CrossRef]
- Li, D.; Li, Z. System Analysis and Development Prospect of Unmanned Farming. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2020, 51, 1–12. [Google Scholar]
- Shafi, U.; Mumtaz, R.; García-Nieto, J.; Hassan, S.A.; Zaidi, S.A.R.; Iqbal, N. Precision agriculture techniques and practices: From considerations to applications. Sensors 2019, 19, 3796. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhang, W.; Luo, X.; Zhang, Z.; Lu, Y.; Wang, B. Developing an IoT-Enabled Cloud Management Platform for Agricultural Machinery Equipped with Automatic Navigation Systems. Agriculture 2022, 12, 310. [Google Scholar] [CrossRef]
- Amiri-Zarandi, M.; Hazrati Fard, M.; Yousefinaghani, S.; Kaviani, M.; Dara, R. A Platform Approach to Smart Farm Information Processing. Agriculture 2022, 12, 838. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, L.; Chen, S.; Wang, W.; Miao, Z.; Liu, C. Autonomous identification and positioning of trucks during collaborative forage harvesting. Sensors 2021, 21, 1166. [Google Scholar] [CrossRef] [PubMed]
- Shearer, S.A.; Pitla, S.K.; Luck, J.D. Trends in the automation of agricultural field machinery. In Proceedings of the 21st Annual Meeting of the Club of Bologna, Bologna, Italy, 13–14 November 2010. [Google Scholar]
- Chehardoli, H.; Ghasemi, A. Adaptive centralized/decentralized control and identification of 1-D heterogeneous vehicular platoons based on constant time headway policy. IEEE Trans. Intell. Transp. 2018, 19, 3376–3386. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Chong, K.; Ma, S.; Fu, W.; Yin, Y.; Yu, H.; Zhao, C. Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay. Agriculture 2022, 12, 1545. https://doi.org/10.3390/agriculture12101545
Ma Z, Chong K, Ma S, Fu W, Yin Y, Yu H, Zhao C. Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay. Agriculture. 2022; 12(10):1545. https://doi.org/10.3390/agriculture12101545
Chicago/Turabian StyleMa, Zhikai, Kun Chong, Shiwei Ma, Weiqiang Fu, Yanxin Yin, Helong Yu, and Chunjiang Zhao. 2022. "Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay" Agriculture 12, no. 10: 1545. https://doi.org/10.3390/agriculture12101545
APA StyleMa, Z., Chong, K., Ma, S., Fu, W., Yin, Y., Yu, H., & Zhao, C. (2022). Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay. Agriculture, 12(10), 1545. https://doi.org/10.3390/agriculture12101545





