Double-Arm Cooperation and Implementing for Harvesting Kiwifruit
Abstract
:1. Introduction
2. Materials and Methods
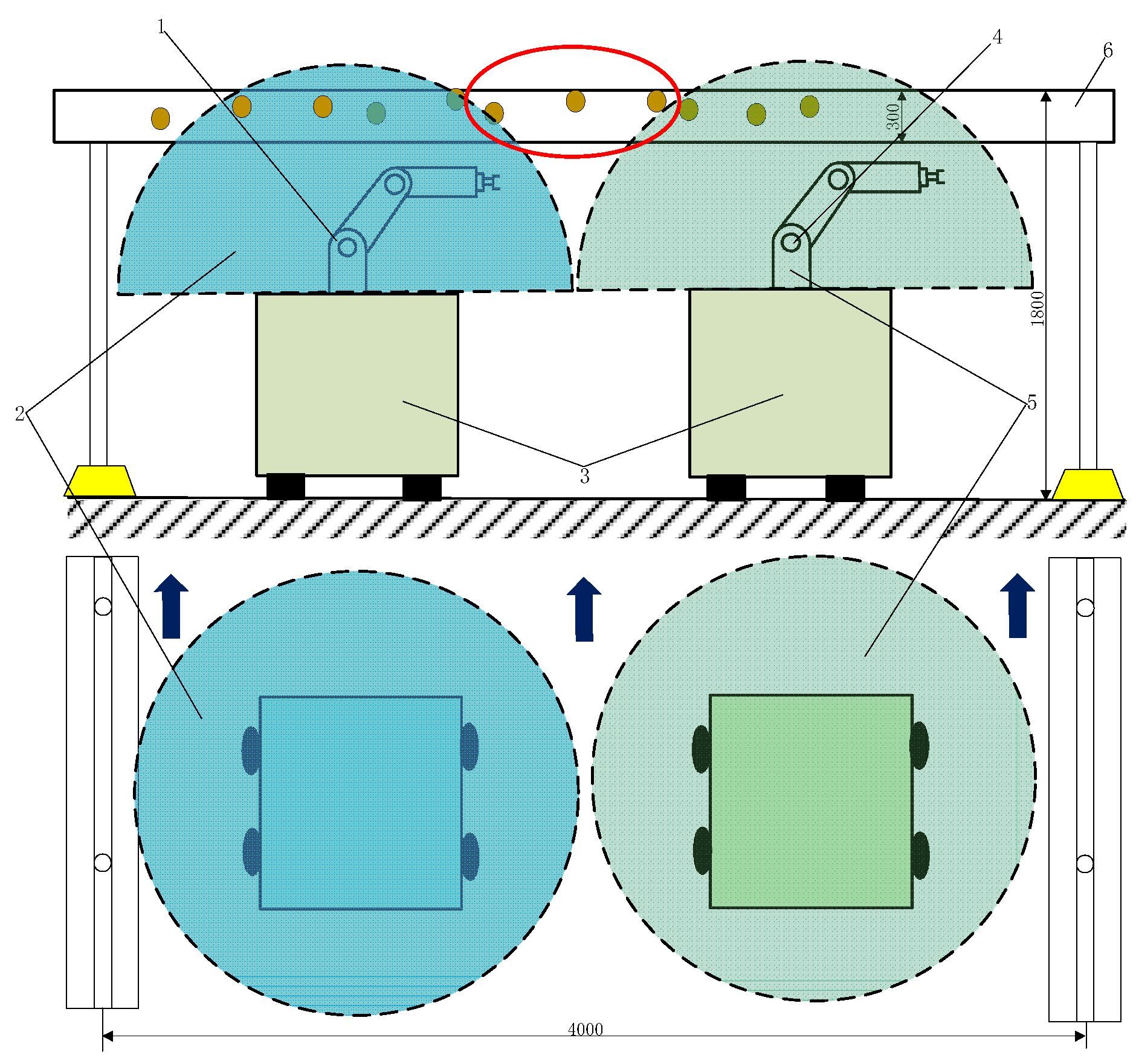
2.1. Kiwifruit Trellis Cultivation Structure
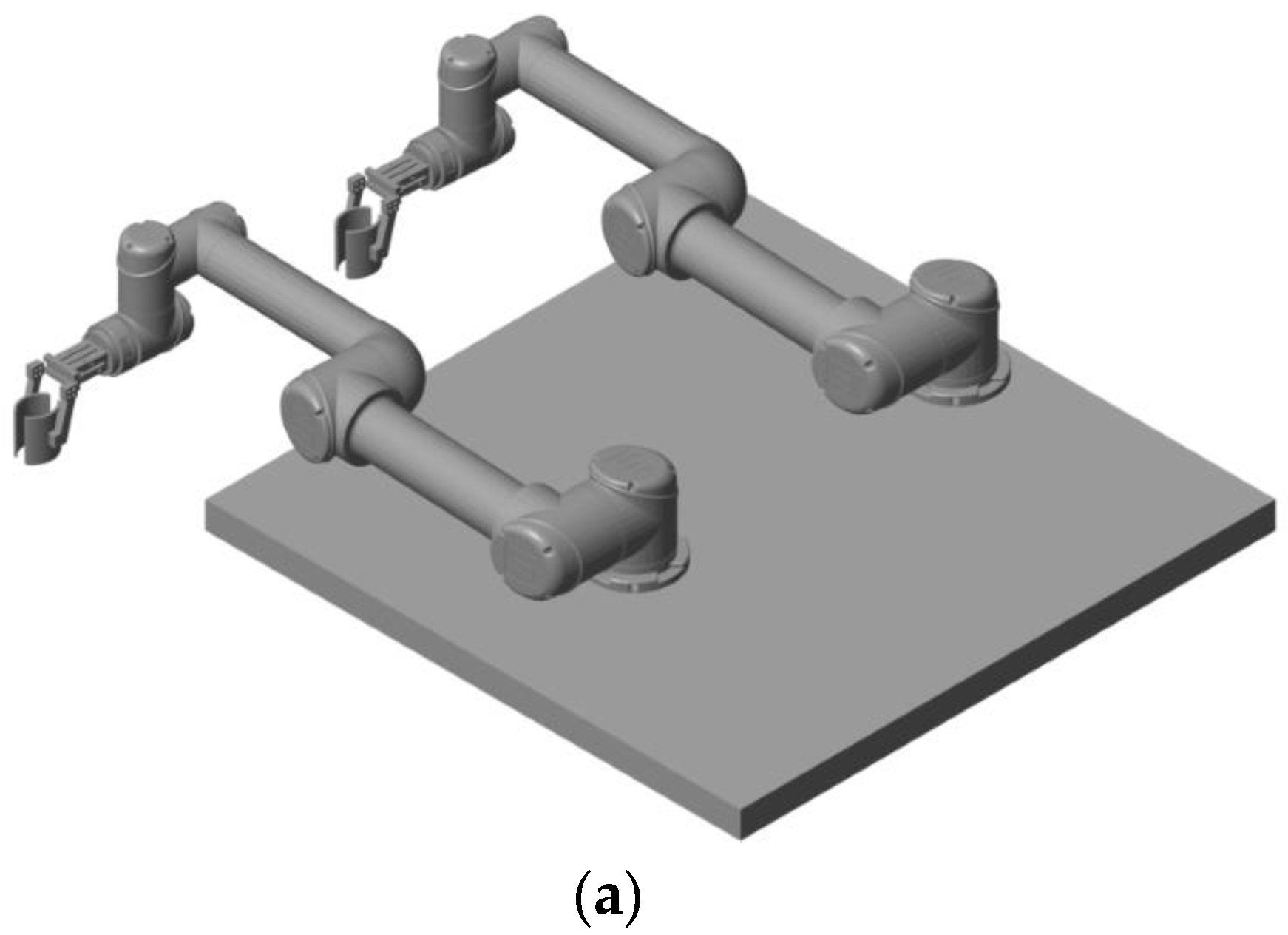
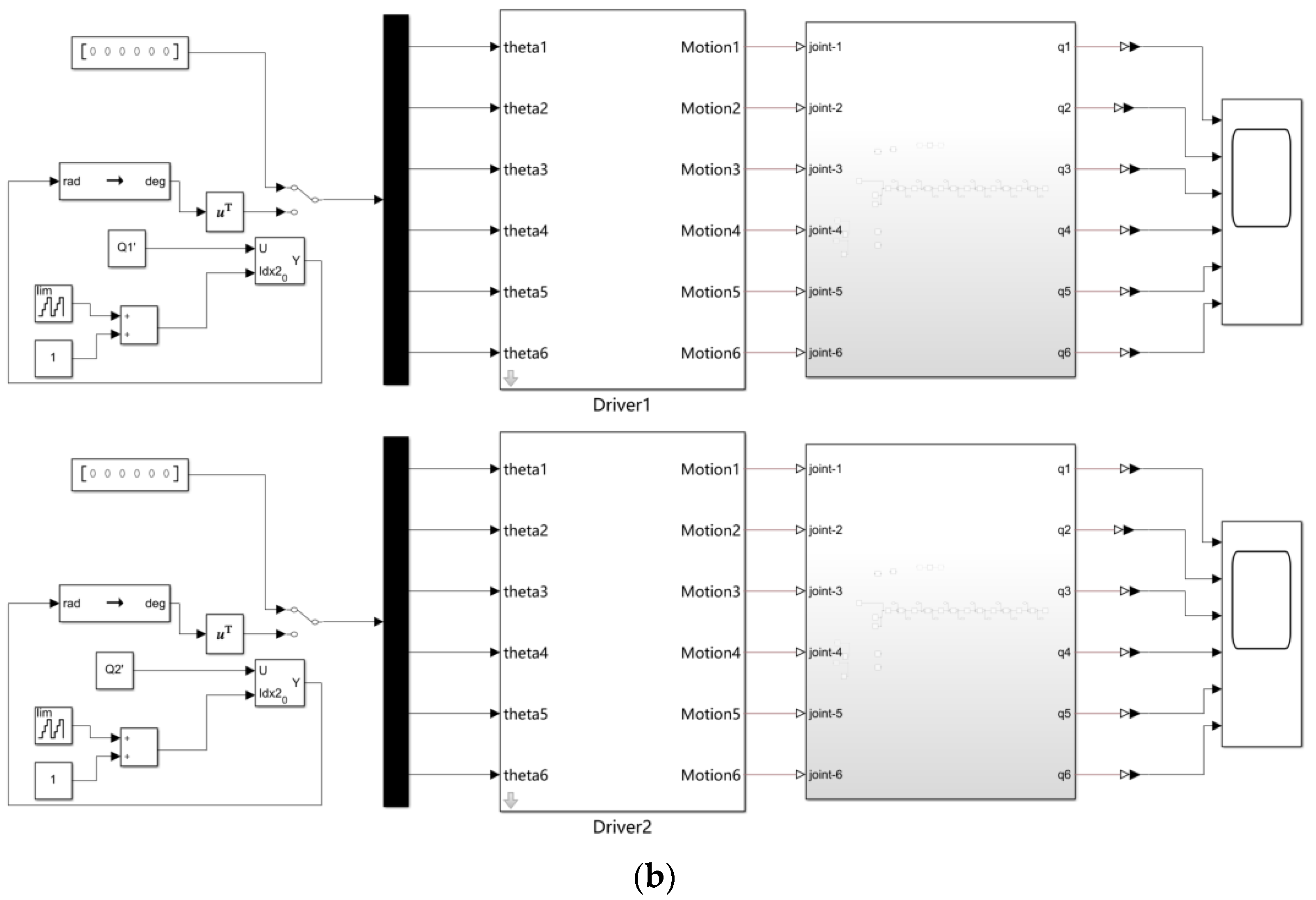
2.2. System Overview
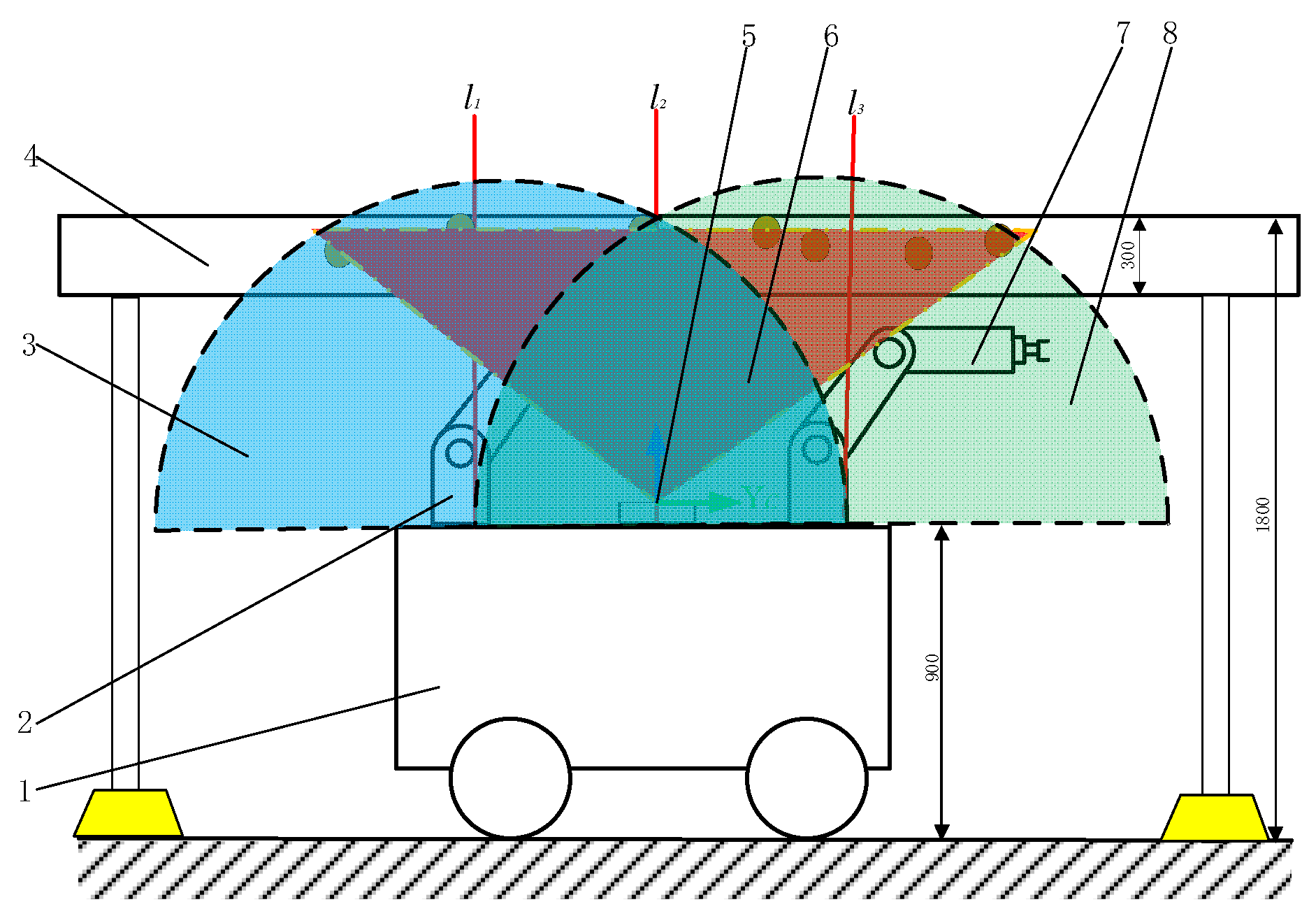
2.3. Collaborative Operation Method of Kiwifruit Picking Robots
- After determining the picking position, the picking area for each robotic arm is divided into a pickable subarea and a collision-prone subarea based on the robot arm’s installation position and work space. Based on this division, the picking order in the pickable subarea is set, and the solution is optimized by BSO in combination with the growth characteristics of the kiwifruits distributed in clusters.
- Collision is detected between robotic arms in the collision-prone subarea, while the joint position and the kinematic solution of the robotic arms are figured out. After determining the collision situation between robotic arms, a delayed picking strategy is adopted wherever a collision is detected.
- An integrated “grab-pick-unload-reset” continuous kiwifruit picking cycle is developed, and the next task is planned when both arms have finished the current picking task. In addition, the kiwifruit was harvested without damage when the pressure between the end-effector and the fruit was less than 18.8 kpa [24].
2.4. Kiwifruit Picking Area Planning
2.4.1. Clustering
2.4.2. Variation and Crossover
2.4.3. Generation of New Individuals
2.4.4. Selection
2.5. Double-Arm Picking Robot Collision Detection
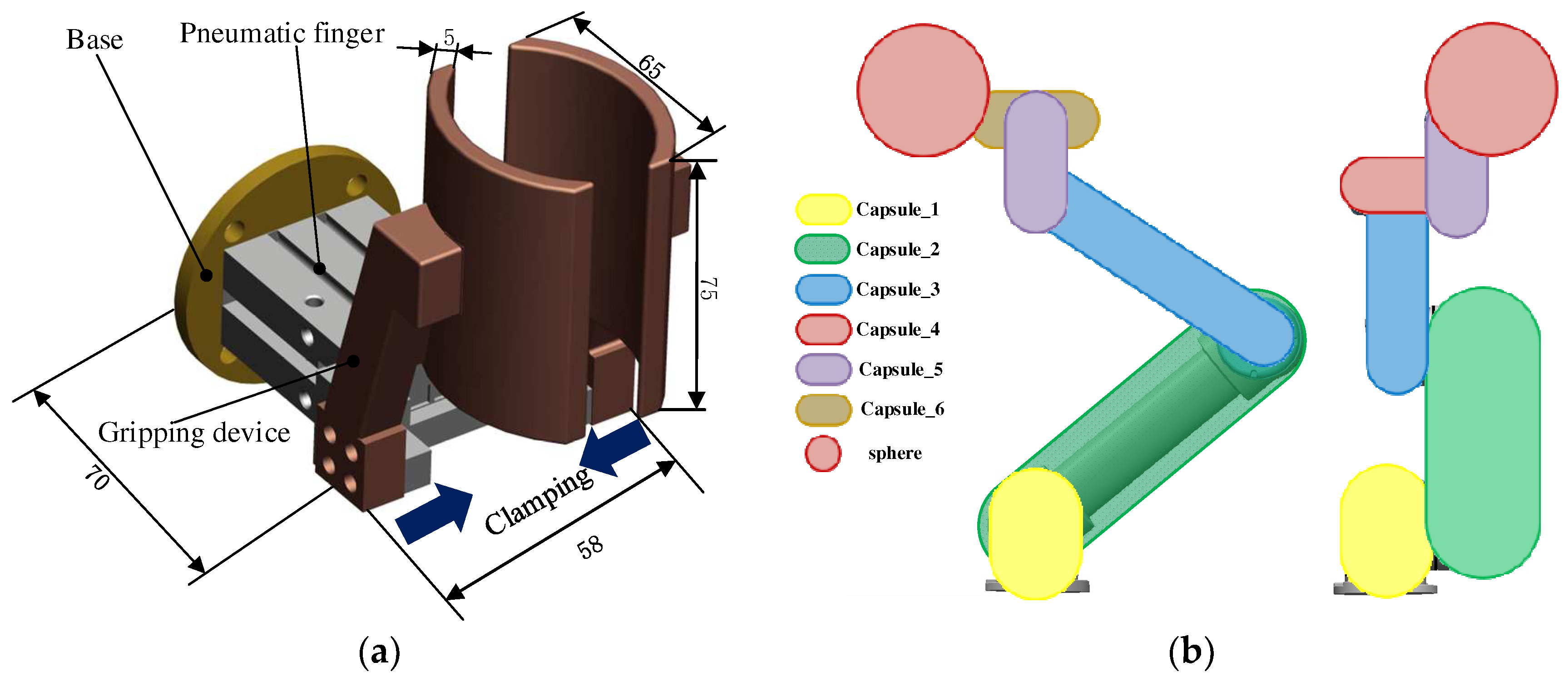
2.5.1. Simplified Model of Robotic Arms
2.5.2. Collision Detection Methods
3. Result and Discussion
3.1. Evaluation of the Picking Area Planning Algorithm
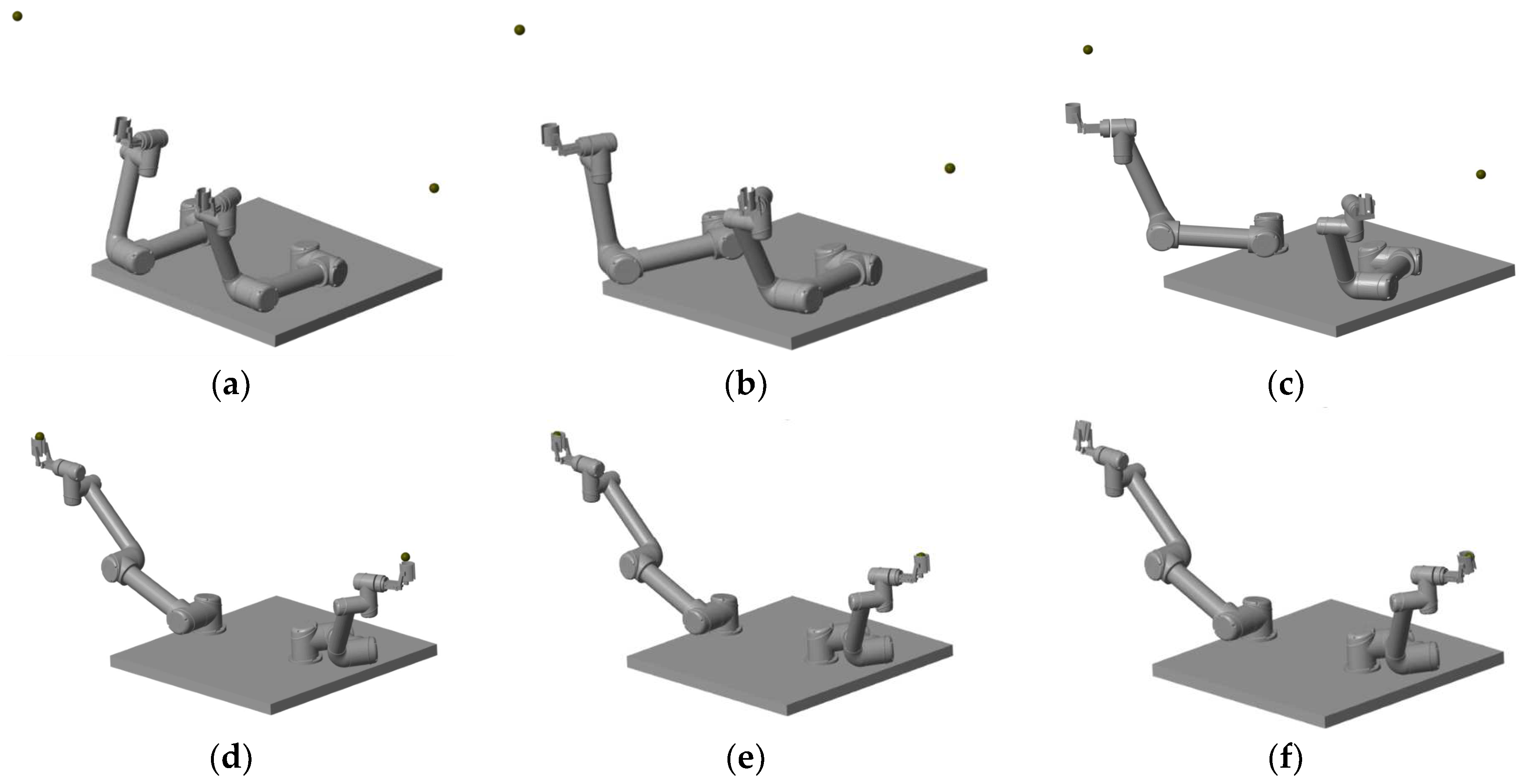
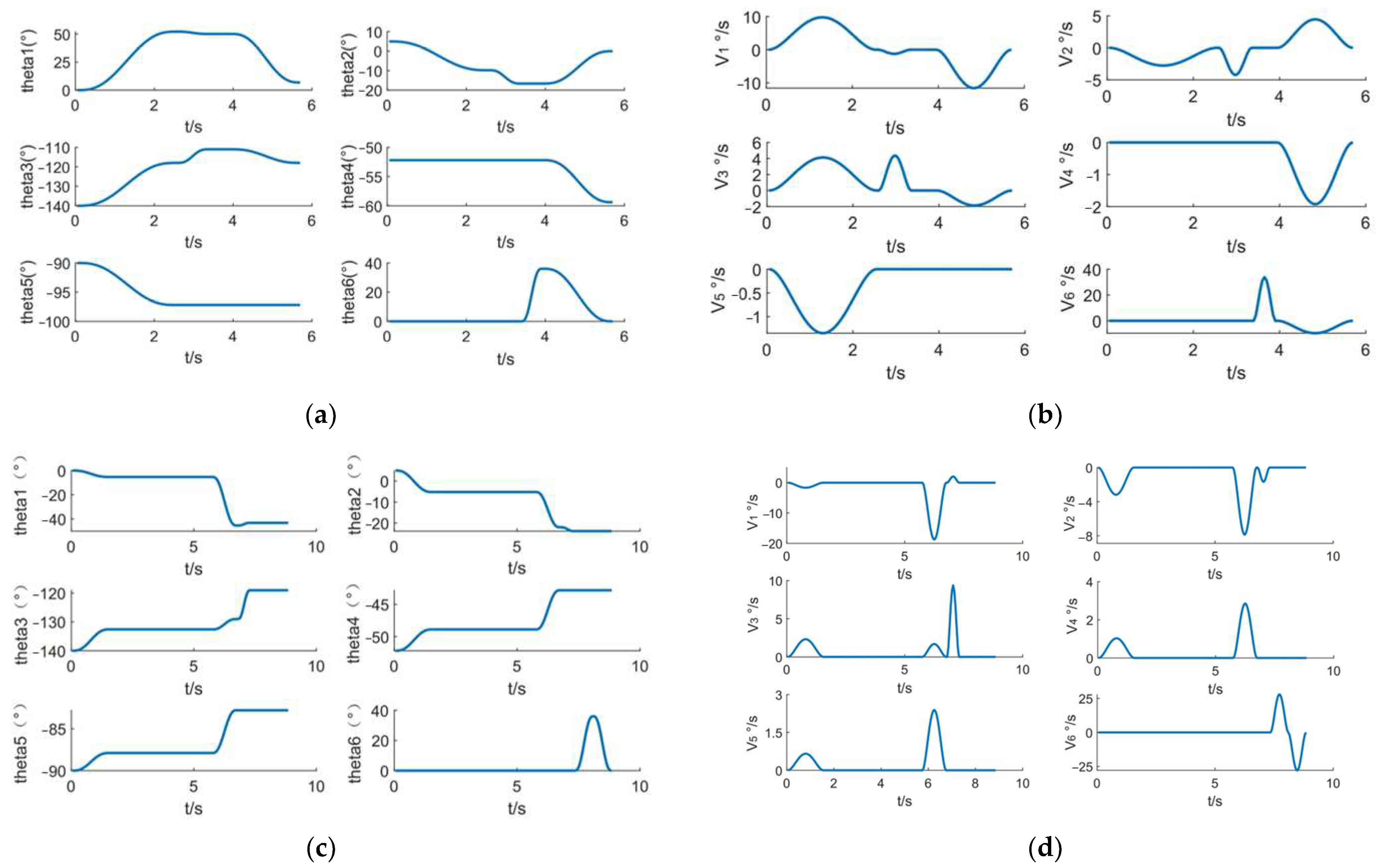
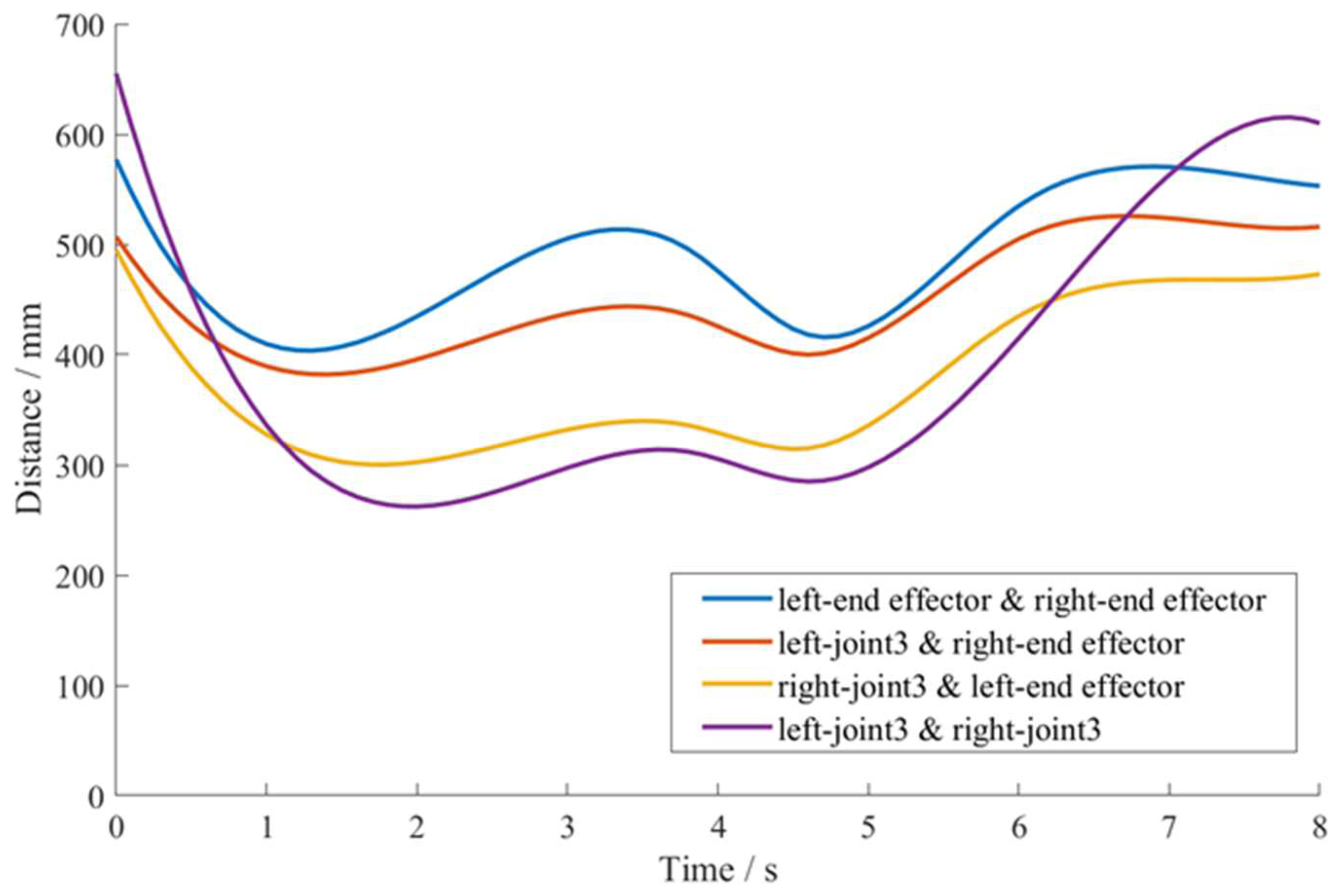
3.2. Simulation on Collision Detection of the Double-Arm Picking Robot
3.3. Experimental Verification
3.3.1. Picking Test Platform
3.3.2. Experiment on the Double-Arm Picking Robot
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leontowicz, M.; Jesion, I.; Leontowicz, H.; Park, Y.S.; Namiesnik, J.; Rombolaì, A.D.; Weisz, M.; Gorinstein, S. Health-promoting effects of ethylene-treated kiwifruit “Hayward” from conventional and organic crops in rats fed an atherogenic diet. J. Agric. Food Chem. 2013, 61, 3661–3668. [Google Scholar] [CrossRef] [PubMed]
- Fazayeli, A.; Kamgar, S.; Mehdi, S.; Fazayeli, H.; Guardia, M. Dielectric spectroscopy as a potential technique for prediction of kiwifruit quality indices during storage. Inf. Process. Agric. 2019, 6, 479–486. [Google Scholar] [CrossRef]
- Yuan, J. Research progress analysis of robotics selective harvesting technologies. Trans. Chin. Soc. Agric. Mach. 2020, 51, 1–17. [Google Scholar]
- UN Food & Agriculture Organization. Production of Kiwi (Fruit) by Countries. Retrieved 2020-06-25; UN Food & Agriculture Organization: Rome, Italy, 2020. [Google Scholar]
- Zhao, C.J. Current situations and prospects of smart agriculture. J. S. Chin. Agric. Univ. 2021, 42, 1–7. [Google Scholar]
- Wang, Y.; Yang, Y.; Yang, C.; Zhao, H.; Chen, G.; Zhang, Z.; Fu, S.; Zhang, M.; Xu, H. End-effector with a bite mode for harvesting citrus fruit in random stalk orientation environment. Comput. Electron. Agric. 2019, 157, 454–470. [Google Scholar] [CrossRef]
- Bu, L.; Chen, C.; Hu, G.; Zhou, J.; Sugirbay, A.; Chen, J. Investigating the dynamic behavior of an apple branch-stem-fruit model using experimental and simulation analysis. Comput. Electron. Agric. 2021, 186, 106224. [Google Scholar] [CrossRef]
- Liu, J.Z.; Peng, Y.; Faheem, M. Experimental and theoretical analysis of fruit plucking pat-terns for robotic tomato harvesting. Comput. Electron. Agric. 2020, 173, 105330. [Google Scholar] [CrossRef]
- Fu, L.; Tola, E.; Al-Mallahi, A.; Li, R.; Cui, Y. A novel image processing algorithm to separate linearly clustered kiwifruits. Biosyst. Eng. 2019, 183, 184–195. [Google Scholar] [CrossRef]
- Wan, H.; Fan, Z.; Yu, X.; Kang, M.; Wang, P.; Zeng, X. A real-time branch detection and reconstruction mechanism for harvesting robot via convolutional neural network and image segmentation. Comput. Electron. Agric. 2022, 192, 106609. [Google Scholar] [CrossRef]
- Cao, X.; Zou, X.; Jia, C.; Chen, M.; Zeng, Z. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, Y.; Zhang, B.; Fu, W.; Shen, C. Path planning of the fruit tree pruning manipulator based on improved RRT-Connect algorithm. Int. J. Agric. Biol. Eng. 2022, 15, 177–188. [Google Scholar] [CrossRef]
- Mu, L.; Cui, G.; Liu, Y.; Cui, Y.; Fu, L.; Gejima, Y. Design and simulation of an integrated end-effector for picking kiwifruit by robot. Inf. Process. Agric. 2020, 7, 58–71. [Google Scholar] [CrossRef]
- Williams, H.; Nejati, M.; Hussein, S.; Penhall, N.; Lim, J.Y.; Jones, M.H.; Bell, J.; Ahn, H.S.; Bradley, S.; Schaare, P.; et al. Autonomous pollination of individual kiwifruit flowers: Toward a robotic kiwifruit pollinator. J. Field Robot. 2020, 37, 246–262. [Google Scholar] [CrossRef]
- Ling, X.; Zhao, Y.; Gong, L.; Liu, C.; Wang, T. Dual-arm cooperation and implementing for robotic harvesting tomato using binocular vision. Robot. Auton. Syst. 2019, 114, 134–143. [Google Scholar] [CrossRef]
- Li, T.; Qiu, Q.; Zhao, C.J.; Xie, F. Task planning of multi-arm harvesting robots for high-density dwarf orchards. Trans. Chin. Soc. Agric. Mach. 2021, 37, 1–10. [Google Scholar]
- Kahani, A. Multi-Robot Crop Harvesting Machine. U.S. Patent 9475189B2, 2 October 2022. [Google Scholar]
- Suo, R.; Gao, F.; Zhou, Z.; Fu, L.; Song, Z.; Dhupia, J.; Li, R.; Cui, Y. Improved mul-ti-classes kiwifruit detection in orchard to avoid collisions during robotic picking. Comput. Electron. Agric. 2021, 182, 106052. [Google Scholar] [CrossRef]
- Qi, R.; Wang, T. An obstacle avoidance trajectory planning scheme for space manipulators based on genetic algorithm. Robot 2014, 36, 263–270. [Google Scholar]
- Williams, H.; Jones, M.H.; Nejati, M.; Seabright, M.J.; Bell, J.; Penhall, N.D.; Barnett, J.J.; Duke, M.; Scarfe, A.J.; Ahn, H.S.; et al. Robotic kiwifruit harvesting using machine vision, convolutional neural networks, and robotic arms. Biosyst. Eng. 2019, 181, 140–156. [Google Scholar] [CrossRef]
- Xiong, Y.; Ge, Y.; Grimstad, L.; From, P.J. An autonomous strawberry-harvesting robot: Design, development, integration, and field evaluation. J. Field Robot 2020, 37, 202–224. [Google Scholar] [CrossRef] [Green Version]
- Lei, M.; Wang, T.; Yao, C.; Liu, H.; Wang, Z.; Deng, Y. Real-Time Kinematics-Based Self-Collision Avoidance Algorithm for Dual-Arm Robots. Appl. Sci. 2020, 10, 5893. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, M.; Wang, X. An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. Int. J. Adv. Robot. Syst. 2018, 5, 128–135. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Zhang, F.; Gejima, Y.; Li, Z.; Wang, B.; Cui, Y. Development and experiment of end-effector for kiwifruit harvesting robot. Trans. Chin. Soc. Agric. Mach. 2015, 46, 3. [Google Scholar]
- Safeea, M.; Mendes, N.; Neto, P. Minimum distance calculation for safe human robot interaction. Procedia Manuf. 2017, 11, 99–106. [Google Scholar] [CrossRef]
- Gao, G.; Sun, G.; Na, J.; Guo, Y.; Xing, W. Structural parameter identification for 6 DOF industrial robots. Mech. Syst. Signal Process. 2018, 113, 145–155. [Google Scholar] [CrossRef]
- Mu, L.T.; Gao, Z.B.; Cui, Y.J.; Li, K.; Liu, H.Z.; Fu, L.S. Kiwifruit detection of far-view and occluded fruit based on improved AlexNet. Trans. Chin. Soc. Agric. Mach. 2019, 50, 24–34. [Google Scholar]
- Wu, C.; Fu, X. An agglomerative greedy brain storm optimization algorithm for solving the TSP. IEEE Access 2020, 8, 201606–201621. [Google Scholar] [CrossRef]
- Shi, J.; Wang, D.; Shang, F.; Zhang, H. Research advances on stochastic gradient descent algorithms. Acta Auto Sin. 2021, 9, 2103–2119. [Google Scholar]




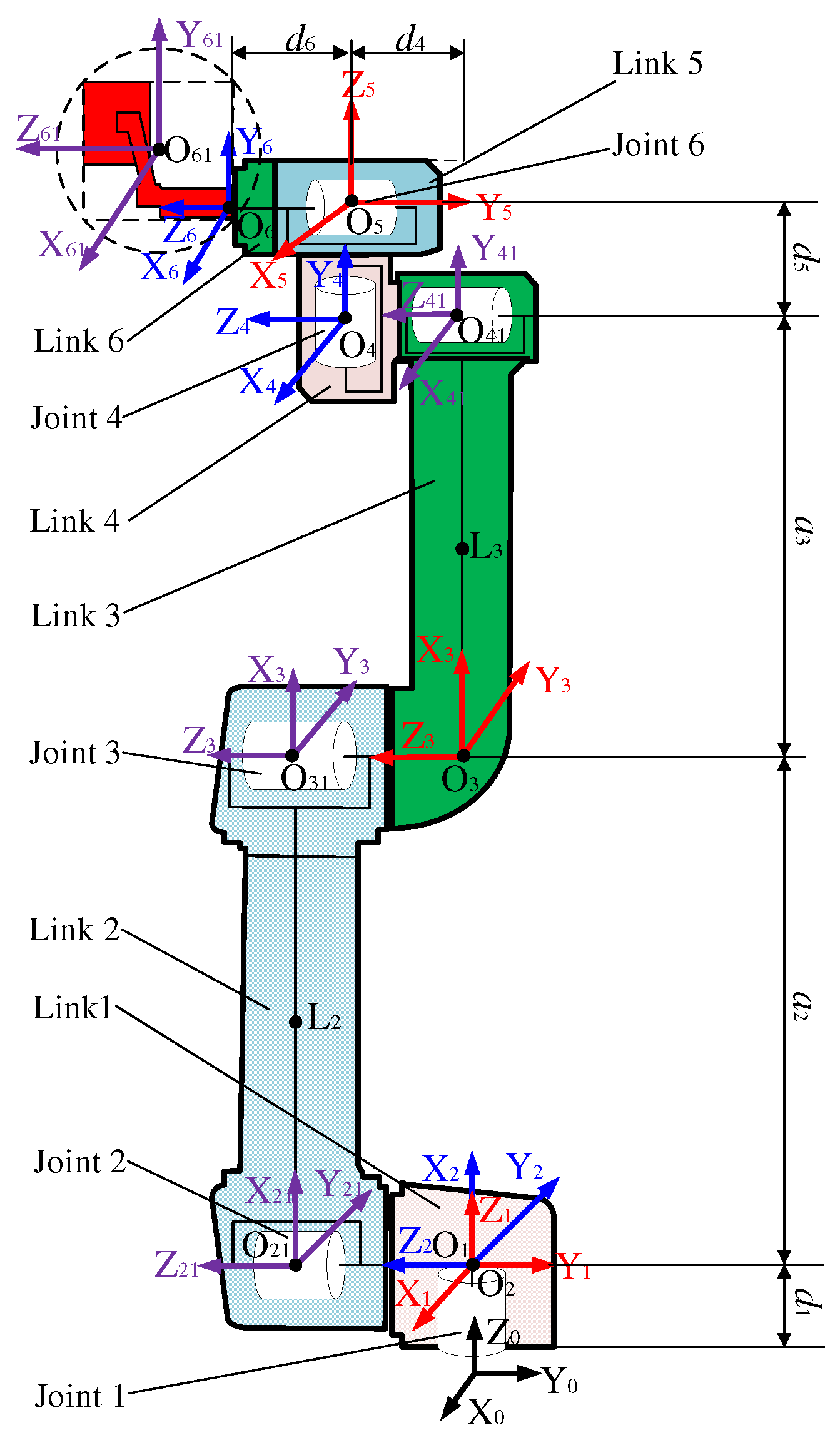
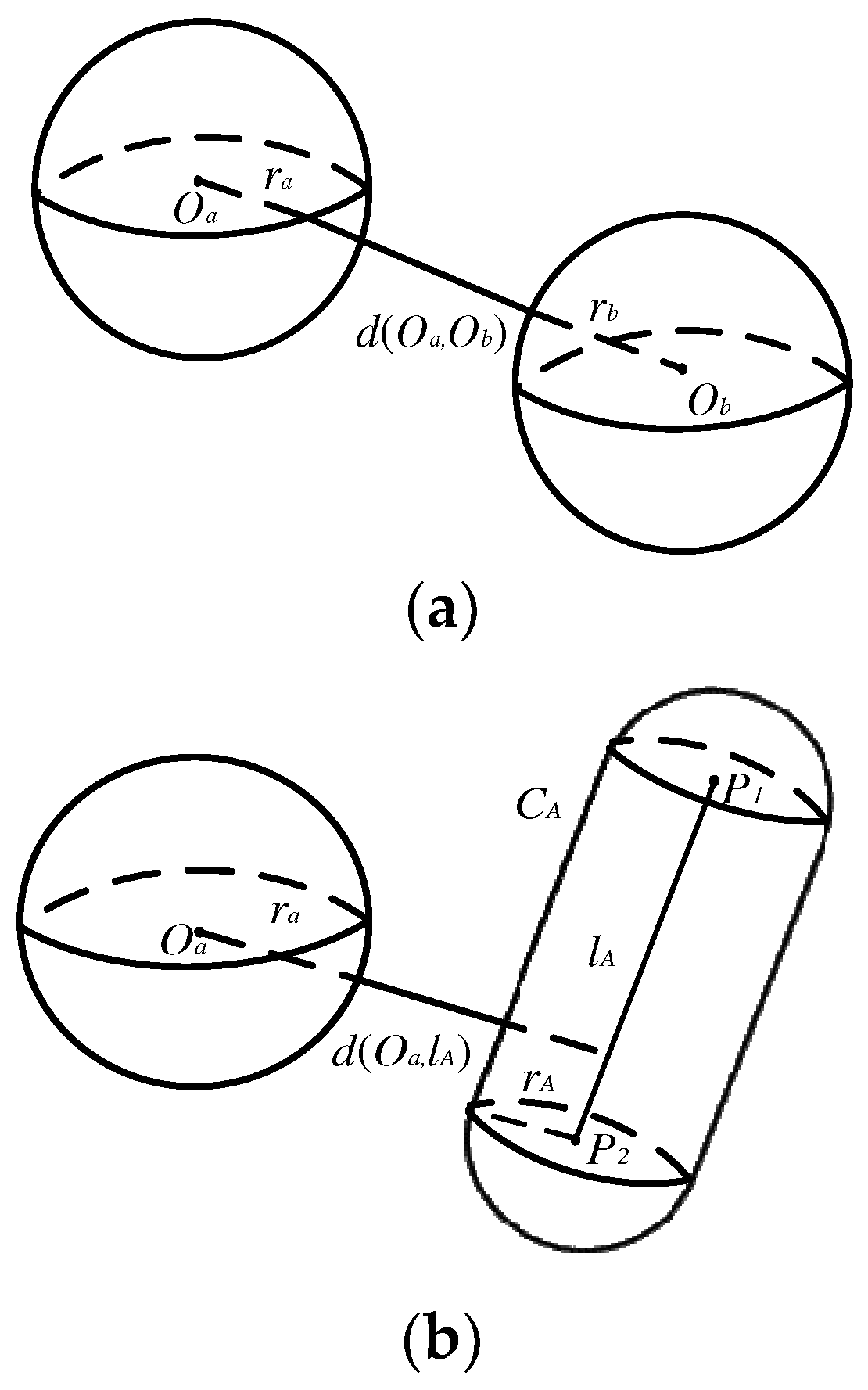
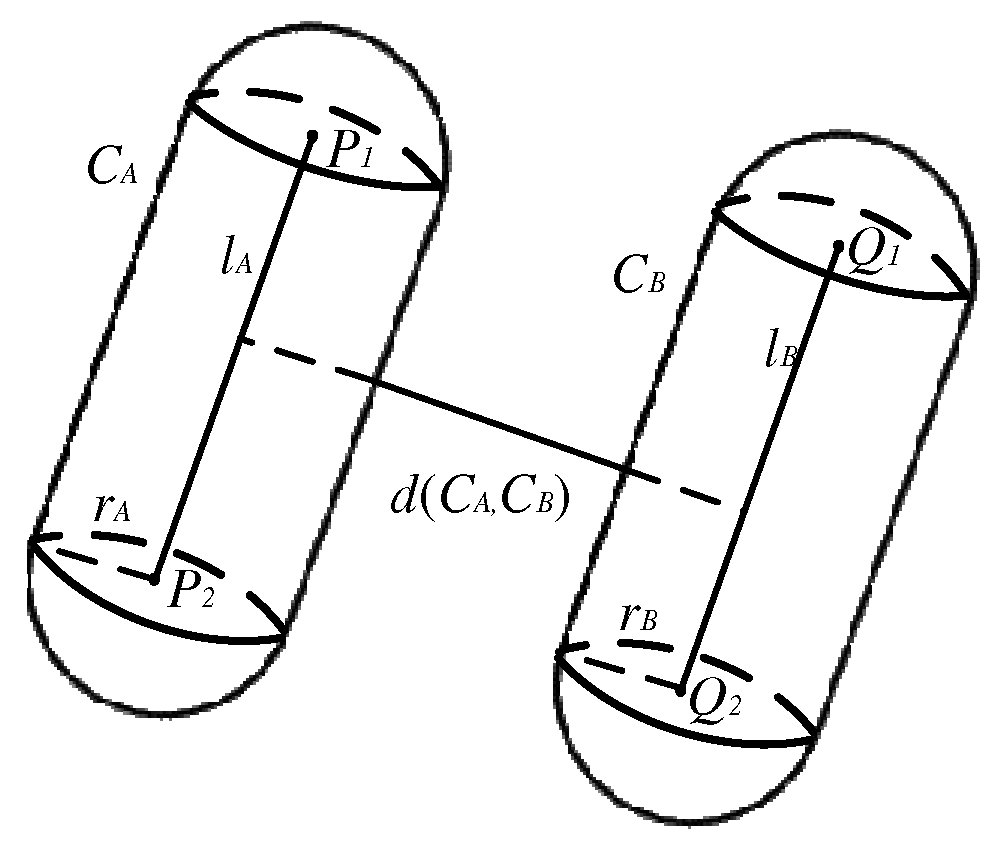









| Link | (°) | (mm) | (mm) |
|---|---|---|---|
| 1 | 0 | 0 | d1 = 89.2 |
| 2 | α2 = 90 | a2 = −425 | 0 |
| 3 | 0 | a3 = −392 | 0 |
| 4 | 0 | 0 | d4 = 109.3 |
| 5 | α5 = 90 | 0 | d5 = 94.75 |
| 6 | α6 = −90 | 0 | d6 = 82.5 |
| Number | Geometric Size | |
|---|---|---|
| Radius/mm | High/mm | |
| Capsule_1 | 110 | 140 |
| Capsule_2 | 140 | 530 |
| Capsule_3 | 110 | 410 |
| Capsule_4 | 70 | 110 |
| Capsule_5 | 70 | 110 |
| Capsule_6 | 80 | 140 |
| Sphere | 80 | / |
| Parameter | Scenario 1 | Scenario 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| GA | BSO | PSO | SA | GA | BSO | PSO | SA | |
| Quantity of populations [28] | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Quantity of fruits | 52 | 52 | 52 | 52 | 41 | 41 | 52 | 52 |
| Iteration times | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 |
| Crossover-ratio | 0.7 | / | / | / | 0.8 | / | / | / |
| Mutation-ratio | 0.3 | / | / | / | 0.2 | / | / | / |
| P1 | / | 0.8 | / | / | / | 0.8 | / | / |
| P2 | / | 0.8 | / | / | / | 0.8 | / | / |
| Test Group | Distribution of Fruits | Recognition Rate of the Fruit | Algorithm | Calculating Time/s |
|---|---|---|---|---|
| Scenario 1 | Figure 12a Left 23 Middle 21 Right 8 | 92.31% | BSO | 2.45 |
| GA | 4.62 | |||
| PSO | 4.98 | |||
| SA | 3.25 | |||
| Scenario 2 | Figure 12b Left 12 Middle 24 Right 6 | 92.16% | BSO | 2.21 |
| GA | 4.33 | |||
| PSO | 4.55 | |||
| SA | 3.78 |
| Joint 1 (°) | Joint 2 (°) | Joint 3 (°) | Joint 4 (°) | Joint 5 (°) | Joint 6 (°) | ||
|---|---|---|---|---|---|---|---|
| Left robot arm | Initial states | −7.2 | 11.8 | −108 | −86.4 | −86.4 | 0 |
| Target states | −86 | −23.6 | −20.6 | −137 | −93.6 | 40 | |
| Right robotic arm | Initial states | 0 | 0 | −64.8 | −115 | −79.2 | 0 |
| Target states | 63.8 | −8.2 | −47.2 | −130 | −43.2 | 40 | |
| Joint 1 (°) | Joint 2 (°) | Joint 3 (°) | Joint 4 (°) | Joint 5 (°) | Joint 6 (°) | ||
|---|---|---|---|---|---|---|---|
| Left robotic arm | Initial states | 0° | 5° | −140° | −52.2° | −90° | 0° |
| Target states | 6.8° | 0° | −118° | −59.4° | −97.2° | 40° | |
| Right robotic arm | Initial states | 0° | 5° | −140° | −52.2° | −90° | 0° |
| Target states | −43.2 | −23.8 | −119 | −42.8 | −82.8 | 40 | |
| Test Groups | Number of Fruit Distribution | Number of Collisions | Collision Detection Time of Single Fruit (s) | Harvested (%) |
|---|---|---|---|---|
| the first test | area I: 5 | 0 | 3.12 | 93.3% |
| area III: 5 | 2 | 4.56 | ||
| area II: 5 | 0 | 3.53 | ||
| the second test | area I: 1 | 0 | 3.2 | 86.7% |
| area III: 7 | 1 | 4.32 | ||
| area II: 7 | 0 | 3.42 | ||
| the third test | area I: 0 | 0 | 0 | 80% |
| area III: 15 | 6 | 4.78 | ||
| area II: 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Ma, L.; Wang, Y.; Wei, Y.; Ding, X.; Li, K.; Cui, Y. Double-Arm Cooperation and Implementing for Harvesting Kiwifruit. Agriculture 2022, 12, 1763. https://doi.org/10.3390/agriculture12111763
He Z, Ma L, Wang Y, Wei Y, Ding X, Li K, Cui Y. Double-Arm Cooperation and Implementing for Harvesting Kiwifruit. Agriculture. 2022; 12(11):1763. https://doi.org/10.3390/agriculture12111763
Chicago/Turabian StyleHe, Zhi, Li Ma, Yinchu Wang, Yongzhe Wei, Xinting Ding, Kai Li, and Yongjie Cui. 2022. "Double-Arm Cooperation and Implementing for Harvesting Kiwifruit" Agriculture 12, no. 11: 1763. https://doi.org/10.3390/agriculture12111763
APA StyleHe, Z., Ma, L., Wang, Y., Wei, Y., Ding, X., Li, K., & Cui, Y. (2022). Double-Arm Cooperation and Implementing for Harvesting Kiwifruit. Agriculture, 12(11), 1763. https://doi.org/10.3390/agriculture12111763








