Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%)
Abstract
:1. Introduction
2. Materials and Methods
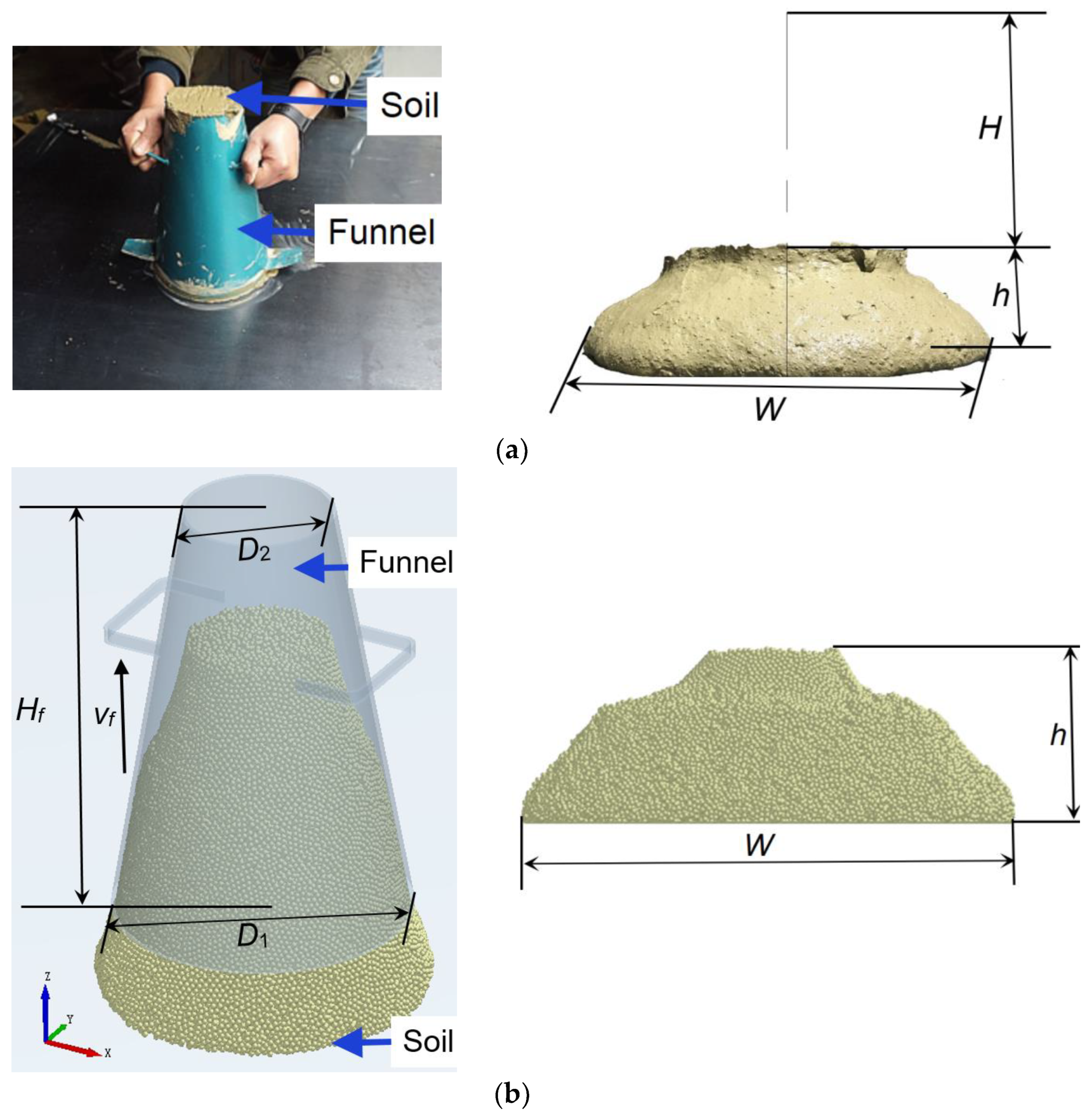
2.1. Laboratory Test
2.2. DEM Simulations
2.2.1. DEM Contact Model
2.2.2. Model Parameter Calibration
3. Results and Discussion
3.1. Laboratory Test Results
3.2. Plackett–Burman (PB) Test
3.3. Steepest Ascent (SA) Test
3.4. Central Composite Test (CCT)
3.5. Parameter Optimization and Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Aryal, J.P.; Mehrotra, M.B.; Jat, M.L.; Sidhu, S.H. Impacts of laser land leveling in rice–wheat systems of the north–western indo-gangetic plains of India. Food Secur. 2015, 7, 725–738. [Google Scholar] [CrossRef]
- Jat, M.L.; Gathala, M.K.; Ladha, J.K.; Saharawat, Y.S.; Jat, A.S.; Kumar, V.; Sharma, S.K.; Kumar, V.; Gupta, R. Evaluation of precision land leveling and double zero-till systems in the rice-wheat rotation: Water use, productivity, profitability and soil physical properties. Soil Tillage Res. 2009, 105, 112–121. [Google Scholar] [CrossRef]
- Agarwal, M.C.; Goel, A.C. Effect of field leveling quality on irrigation efficiency and crop yield. Agric. Water Manage. 1981, 4, 89–97. [Google Scholar] [CrossRef]
- Towa, J.J.; Guo, X.P. Effects of irrigation and weed-control methods on growth of weed and rice. Int. J. Agric. Biol. Eng. 2014, 7, 22–33. [Google Scholar] [CrossRef]
- Finney, C. The benefits of land leveling on irrigation schemes in Turkey and Sindh Province, Pakistan. ICID J. 1996, 45, 1523–1539. [Google Scholar]
- Onodera, T.; Tsuruta, M.; Osari, H. Leveling rice paddies using a laser land leveler when tilling. Trans. Jpn. Soc. Irrig. Drain. Reclam. Eng. Jpn. 2002, 1–8. [Google Scholar]
- Kan, Z.; Jin, H.; Hongwen, L.; Peisong, D.; Qingjie, W.; Hongbo, Z. Research on polyline soil-breaking blade subsoiler based on subsoiling soil model using discrete element method. Trans. Chin. Soc. Agric. Mach. 2016, 47, 62–72. [Google Scholar]
- Zhang, L.; Zhai, Y.; Chen, J.; Zhang, Z.; Huang, S. Optimization design and performance study of a subsoiler underlying the tea garden subsoiling mechanism based on bionics and EDEM. Soil Tillage Res. 2022, 220, 105375. [Google Scholar] [CrossRef]
- Wang, Y.; Li, N.; Ma, Y.; Tong, J.; Pfleging, W.; Sun, J. Field experiments evaluating a biomimetic shark-inspired (BioS) subsoiler for tillage resistance reduction. Soil Tillage Res. 2020, 196, 104432. [Google Scholar] [CrossRef]
- Chen, Y.; Munkholm, L.J.; Nyord, T. A discrete element model for soil-sweep interaction in three different soils. Soil Tillage Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Chen, Y.; Zhang, X.R. Modelling the interaction of a deep tillage tool with heterogeneous soil. Comput. Electron. Agric. 2017, 143, 130–138. [Google Scholar] [CrossRef]
- Wang, X.; Li, P.; He, J.; Wei, W.; Huang, Y. Discrete element simulations and experiments of soil-winged subsoiler interaction. Int. J. Agric. Biol. Eng. 2021, 14, 50–62. [Google Scholar] [CrossRef]
- Sadek, M.A.; Chen, Y.; Zeng, Z.W. Draft force prediction for a high-speed disc implement using discrete element modelling. Biosyst. Eng. 2021, 202, 133–141. [Google Scholar] [CrossRef]
- Song, W.; Jiang, X.H.; Li, L.K.; Ren, L.L.; Tong, J. Increasing the width of disturbance of plough pan with bionic inspired subsoilers. Soil Tillage Res. 2022, 220, 105356. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Yang, L.; Cui, T.; Jing, H.; Zhong, X. Modeling the interaction of soil and a vibrating subsoiler using the discrete element method. Comput. Electron. Agric. 2020, 174, 105518. [Google Scholar] [CrossRef]
- Huang, Y.; Hang, C.; Yuan, M.; Wang, B.; Zhu, R. Discrete element simulation and experiment on disturbance behavior of subsoiling. Trans. Chin. Soc. Agric. Mach. 2016, 47, 80–88. [Google Scholar] [CrossRef]
- Hang, C.; Gao, X.; Yuan, M.; Huang, Y.; Zhu, R. Discrete element simulations and experiments of soil disturbance as affected by the tine spacing of subsoiler. Biosyst. Eng. 2018, 168, 73–82. [Google Scholar] [CrossRef]
- Ding, Q.; Ren, J.; Adam, B.; Zhao, J.; Ge, S.; Li, Y. DEM analysis of subsoiling process in wet clayey paddy soil. Trans. Chin. Soc. Agric. Mach. 2017, 48, 38–48. [Google Scholar]
- Tanaka, H.; Oida, A.; Daikoku, M.; Lnooku, K.; Sumikawa, O.; Nagasaki, Y.; Miyazaki, M. DEM simulation of soil loosening process caused by a vibrating subsoiler. Agric. Eng. Int. CIGR J. 2007, 9, 1–18. [Google Scholar]
- Tamas, K.; Bernon, L. Role of particle shape and plant roots in the discrete element model of soilesweep interaction. Biosyst. Eng. 2021, 211, 71–96. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Huang, Y.; Ji, J. An efficient method for determining DEM parameters of a loose cohesive soil modelled using hysteretic spring and linear cohesion contact models. Biosyst. Eng. 2022, 215, 283–294. [Google Scholar] [CrossRef]
- Qi, L.; Chen, Y.; Sadek, M. Simulations of soil flow properties using the discrete element method (DEM). Comput. Electron. Agric. 2019, 157, 254–260. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the effect of rake angle on narrow opener performance with the discrete element method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Yang, Y.; Li, M.; Tong, J.; Ma, Y. Design and experiment of biomimetic rotary tillage blade based on multiple claws characteristics of mole rats. Trans. Chin. Soc. Agric. Eng. 2019, 35, 37–45. [Google Scholar] [CrossRef]
- Shi, L.; Zhao, W.; Sun, W. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method. Trans. CSAE 2017, 33, 181–187. [Google Scholar] [CrossRef]
- Wu, T.; Huang, W.; Chen, X.; Ma, X.; Han, Z.; Fan, T. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles. J. South China Agric. Univ. 2017, 38, 93–98. [Google Scholar] [CrossRef]
- Wang, X.; Hu, H.; Wang, Q.; Li, H.; He, J.; Chen, W. Calibration method of soil contact characteristic parameters based on DEM theory. Trans. CSAM 2017, 48, 78–85. [Google Scholar] [CrossRef]
- Xiang, W.; Wu, M.; Lü, J.; Quan, W.; Ma, L.; Liu, J. Calibration of simulation physical parameters of clay loam based on soil accumulation test. Trans. CSAE 2019, 35, 116–123. [Google Scholar] [CrossRef]
- He, Y.; Xiang, W.; Wu, M.; Quan, W.; Chen, C. Parameters calibration of loam soil for discrete element simulation based on the repose angle of particle heap. J. Hunan Agric. Univ. 2018, 44, 216–220. [Google Scholar] [CrossRef]
- Xing, J.; Zhang, R.; Wu, P.; Zhang, X.; Dong, X.; Chen, Y.; Ru, S. Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Trans. CSAE 2020, 36, 158–166. [Google Scholar] [CrossRef]

| Symbol | Parameter | Unit | Low Level (−1) | High Level (+1) |
|---|---|---|---|---|
| X1 | Poisson’s ratio of soil | - | 0.32 | 0.42 |
| X2 | Surface energy of soil | J/m2 | 0.1 | 0.9 |
| X3 | Shear modulus of soil | Mpa | 0.1 | 1 |
| X4 | Coefficients of soil–soil restitution | - | 0.01 | 0.15 |
| X5 | Coefficients of soil–soil static friction | - | 0.1 | 0.9 |
| X6 | Coefficients of soil–soil rolling friction | - | 0.01 | 0.1 |
| X7 | Coefficients of soil–steel restitution | - | 0.01 | 0.15 |
| X8 | Coefficients of soil–steel static friction | - | 0.1 | 0.9 |
| X9 | Coefficients of soil–steel rolling friction | - | 0.01 | 0.1 |
| X10, X11 | Virtual parameters | - | - | - |
| Test No. | Slumping Value (mm) | Slumping Expansion (mm) |
|---|---|---|
| 1 | 230.17 | 360.00 |
| 2 | 238.67 | 356.33 |
| 3 | 234.00 | 347.50 |
| 4 | 233.00 | 346.00 |
| 5 | 231.67 | 344.17 |
| Mean value | 233.5 | 350.8 |
| CV (%) | 1.24 | 1.77 |
| No. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | H (mm) | W (mm) | δZH (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.32 | 0.9 | 0.3 | 0.15 | 0.9 | 0.01 | 0.15 | 0.9 | 0.1 | −1 | −1 | 220.45 | 469.56 | 19.72 |
| 2 | 0.32 | 0.9 | 1 | 0.15 | 0.1 | 0.01 | 0.01 | 0.9 | 0.01 | 1 | 1 | 208.75 | 413.83 | 14.28 |
| 3 | 0.42 | 0.1 | 0.3 | 0.01 | 0.9 | 0.01 | 0.15 | 0.9 | 0.01 | 1 | 1 | 231.94 | 569.14 | 31.45 |
| 4 | 0.42 | 0.1 | 1 | 0.15 | 0.1 | 0.1 | 0.15 | 0.9 | 0.01 | −1 | −1 | 227.16 | 532.57 | 27.27 |
| 5 | 0.42 | 0.9 | 0.3 | 0.15 | 0.9 | 0.1 | 0.01 | 0.1 | 0.01 | 1 | −1 | 259.10 | 752.85 | 62.79 |
| 6 | 0.42 | 0.9 | 1 | 0.01 | 0.1 | 0.01 | 0.15 | 0.1 | 0.1 | 1 | −1 | 263.53 | 719.80 | 59.02 |
| 7 | 0.42 | 0.1 | 1 | 0.15 | 0.9 | 0.01 | 0.01 | 0.1 | 0.1 | −1 | 1 | 272.44 | 1244.42 | 135.71 |
| 8 | 0.42 | 0.9 | 0.3 | 0.01 | 0.1 | 0.1 | 0.01 | 0.9 | 0.1 | −1 | 1 | 214.03 | 373.69 | 7.43 |
| 9 | 0.32 | 0.1 | 0.3 | 0.01 | 0.1 | 0.01 | 0.01 | 0.1 | 0.01 | −1 | −1 | 274.64 | 1243.41 | 136.03 |
| 10 | 0.32 | 0.1 | 1 | 0.01 | 0.9 | 0.1 | 0.01 | 0.9 | 0.1 | 1 | −1 | 209.40 | 473.07 | 22.59 |
| 11 | 0.32 | 0.1 | 0.3 | 0.15 | 0.1 | 0.1 | 0.15 | 0.1 | 0.1 | 1 | 1 | 267.12 | 294.14 | 109.27 |
| 12 | 0.32 | 0.9 | 1 | 0.01 | 0.9 | 0.1 | 0.15 | 0.1 | 0.01 | −1 | 1 | 262.11 | 107.87 | 60.06 |
| Parameter | Effect | Sum of Squares | Contribution/% | Significance Rank |
|---|---|---|---|---|
| X1 | −127.60 | 22,905.52 | 0.52 | 7 |
| X2 | −796.73 | 122.11 | 20.16 | 2 |
| X3 | −159.20 | 4760.88 | 0.81 | 6 |
| X4 | 174.87 | 190.08 | 0.97 | 5 |
| X5 | −69.93 | 229.34 | 0.16 | 9 |
| X6 | −356.00 | 36.68 | 4.03 | 3 |
| X7 | −240.13 | 950.52 | 1.83 | 4 |
| X8 | −1467.13 | 432.48 | 68.37 | 1 |
| X9 | 72.87 | 16,143.60 | 0.17 | 8 |
| No. | X2 (J m−2) | X6 | X8 | δZH (%) |
|---|---|---|---|---|
| 1 | 0.10 | 0.01 | 0.10 | 132.70 |
| 2 | 0.35 | 0.03 | 0.35 | 21.42 |
| 3 | 0.60 | 0.05 | 0.60 | 14.31 |
| 4 | 0.85 | 0.07 | 0.85 | 9.91 |
| 5 | 1.10 | 0.09 | 1.10 | 12.28 |
| No. | X2 (J m−2) | X6 | X8 | H (mm) | δ1 (%) | W (mm) | δ2 (%) |
|---|---|---|---|---|---|---|---|
| 1 | 1.08 | 0.1 | 1.08 | 182.50 | 21.84 | 338.68 | 3.45 |
| 2 | 1.08 | 0.1 | 0.72 | 193.07 | 17.32 | 343.78 | 2.00 |
| 3 | 1.08 | 0.06 | 1.08 | 180.04 | 22.90 | 343.61 | 2.05 |
| 4 | 1.08 | 0.06 | 0.72 | 188.14 | 19.43 | 343.89 | 1.97 |
| 5 | 0.72 | 0.1 | 1.08 | 189.80 | 18.71 | 366.29 | 4.42 |
| 6 | 0.72 | 0.1 | 0.72 | 199.34 | 14.63 | 358.51 | −2.20 |
| 7 | 0.72 | 0.06 | 1.08 | 196.03 | 16.05 | 373.00 | 6.33 |
| 8 | 0.72 | 0.06 | 0.72 | 191.50 | 17.99 | 376.05 | 7.20 |
| 9 | 0.6 | 0.08 | 0.9 | 197.07 | 15.60 | 385.59 | 9.92 |
| 10 | 1.2 | 0.08 | 0.9 | 182.20 | 21.97 | 336.92 | −3.96 |
| 11 | 0.9 | 0.05 | 0.9 | 187.77 | 19.59 | 359.58 | 2.50 |
| 12 | 0.9 | 0.11 | 0.9 | 192.07 | 17.74 | 350.62 | −0.05 |
| 13 | 0.9 | 0.08 | 0.6 | 193.97 | 16.93 | 353.84 | 0.87 |
| 14 | 0.9 | 0.08 | 1.2 | 187.30 | 19.79 | 351.18 | 0.11 |
| 15 | 0.9 | 0.08 | 0.9 | 185.57 | 20.53 | 352.65 | 0.53 |
| 16 | 0.9 | 0.08 | 0.9 | 186.30 | 20.21 | 351.57 | 0.22 |
| 17 | 0.9 | 0.08 | 0.9 | 185.47 | 20.57 | 350.80 | 0.00 |
| 18 | 0.9 | 0.08 | 0.9 | 185.83 | 20.41 | 354.11 | 0.94 |
| 19 | 0.9 | 0.08 | 0.9 | 185.60 | 20.51 | 350.65 | −0.04 |
| 20 | 0.9 | 0.08 | 0.9 | 186.23 | 20.24 | 351.91 | 0.32 |
| Indicators | Source of variation | SS | f | MS | F | Significance |
|---|---|---|---|---|---|---|
| H | Regression | 491.64 | 9 | 54.63 | 25.73 | Significant |
| Residual | 21.23 | 10 | 2.12 | |||
| Sum | 512.87 | 19 | ||||
| δ1 | Regression | 90.16 | 9 | 10.02 | 25.73 | Significant |
| Residual | 3.89 | 10 | 0.39 | |||
| Sum | 94.05 | 19 | ||||
| Y2 | Regression | 2878.03 | 9 | 319.78 | 58.26 | Significant |
| Residual | 54.87 | 10 | 5.49 | |||
| Sum | 2932.91 | 19 | ||||
| δ2 | Regression | 138.16 | 9 | 15.35 | 37.50 | Significant |
| Residual | 4.09 | 10 | 0.41 | |||
| Sum | 142.26 | 19 |
| No. | X2 | X6 | X8 | H (mm) | W (mm) | δZH (%) |
|---|---|---|---|---|---|---|
| 1 | 0.808 | 0.11 | 0.6 | 199.17 | 351.09 | 7.39 |
| 2 | 200.37 | 350.85 | 7.1 | |||
| 3 | 200.62 | 352.78 | 7.32 | |||
| 4 | 200.50 | 352.17 | 7.26 | |||
| 5 | 200.32 | 352.06 | 7.29 | |||
| Average | 200.20 | 351.79 | 7.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Zhou, T.; Wang, X.; Hu, L.; Wang, S.; Luo, X.; Ji, J. Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%). Agriculture 2022, 12, 2000. https://doi.org/10.3390/agriculture12122000
Zhou H, Zhou T, Wang X, Hu L, Wang S, Luo X, Ji J. Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%). Agriculture. 2022; 12(12):2000. https://doi.org/10.3390/agriculture12122000
Chicago/Turabian StyleZhou, Hao, Tienan Zhou, Xuezhen Wang, Lian Hu, Shengsheng Wang, Xiwen Luo, and Jiangtao Ji. 2022. "Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%)" Agriculture 12, no. 12: 2000. https://doi.org/10.3390/agriculture12122000
APA StyleZhou, H., Zhou, T., Wang, X., Hu, L., Wang, S., Luo, X., & Ji, J. (2022). Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%). Agriculture, 12(12), 2000. https://doi.org/10.3390/agriculture12122000







