Experimentally Based Numerical Simulation of the Influence of the Agricultural Subsurface Drainage Pipe Geometric Structure on Drainage Flow
Abstract
:1. Introduction
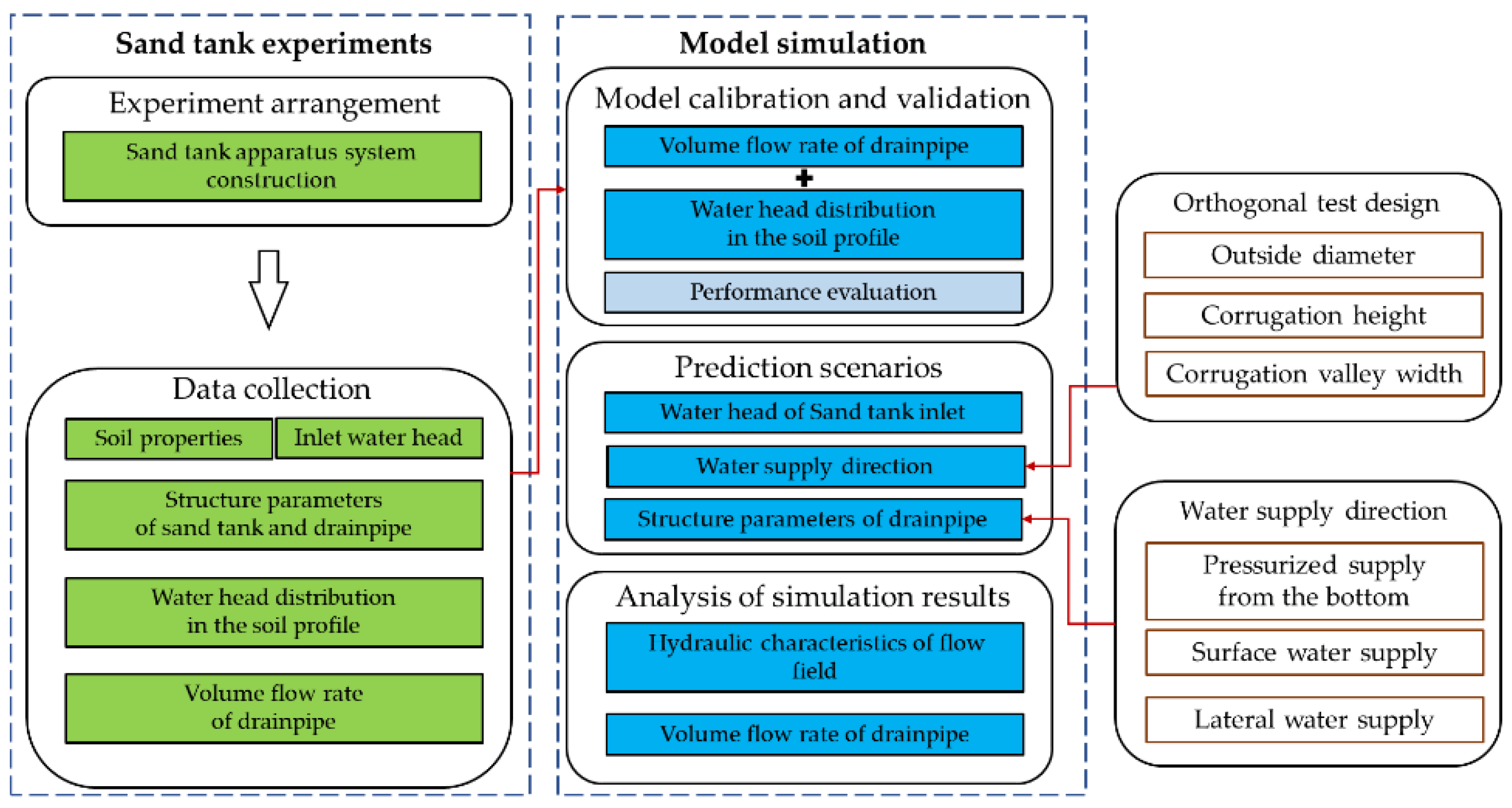
2. Materials and Methods
2.1. Sand Tank Drainage Experiment
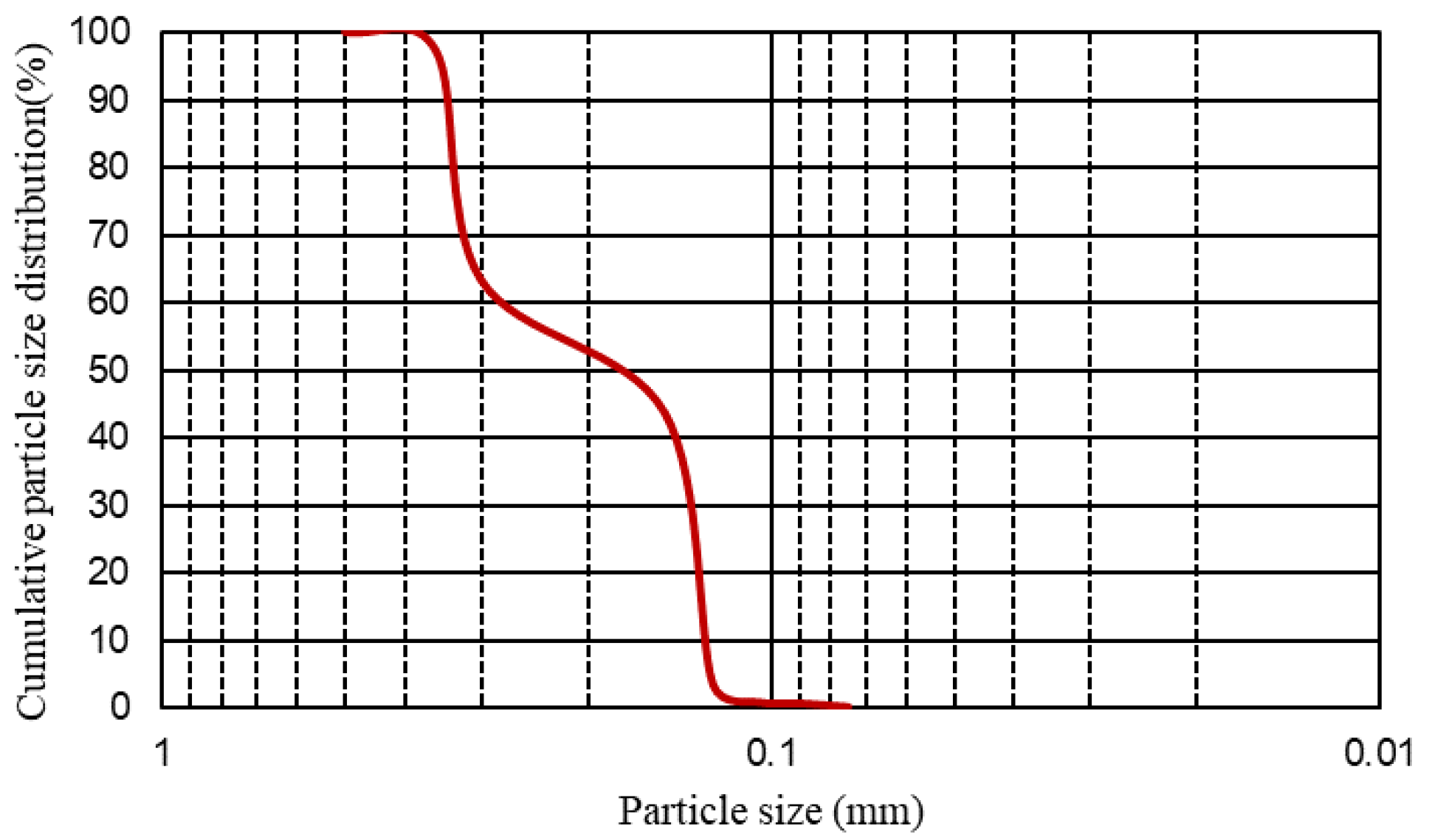
2.1.1. Experimental Design
2.1.2. Experimental Measurement
2.2. Numerical Model
2.2.1. Numerical Modeling and Boundary Conditions
2.2.2. Governing Equations
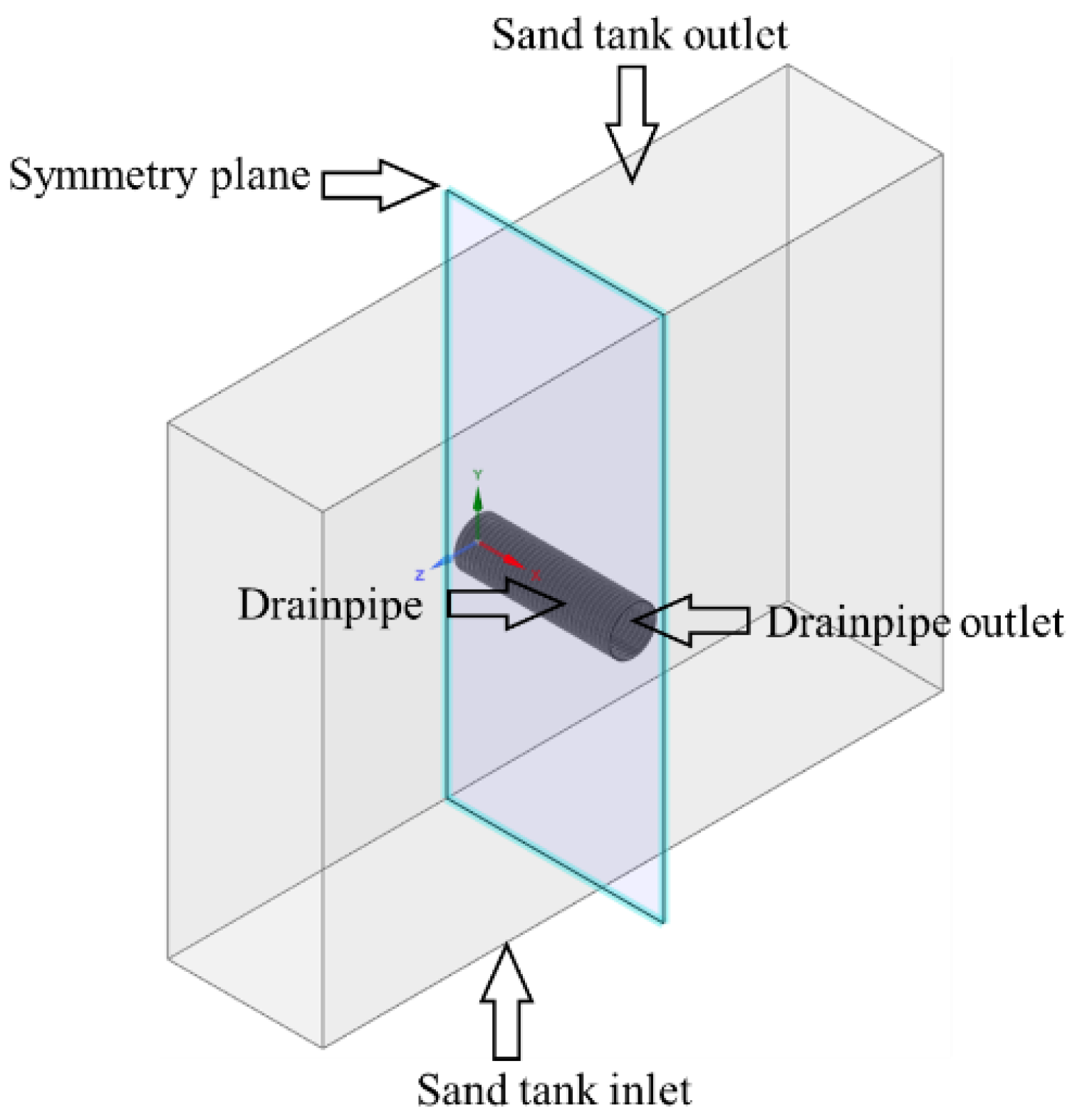
2.2.3. Computational Domain and Boundary Conditions
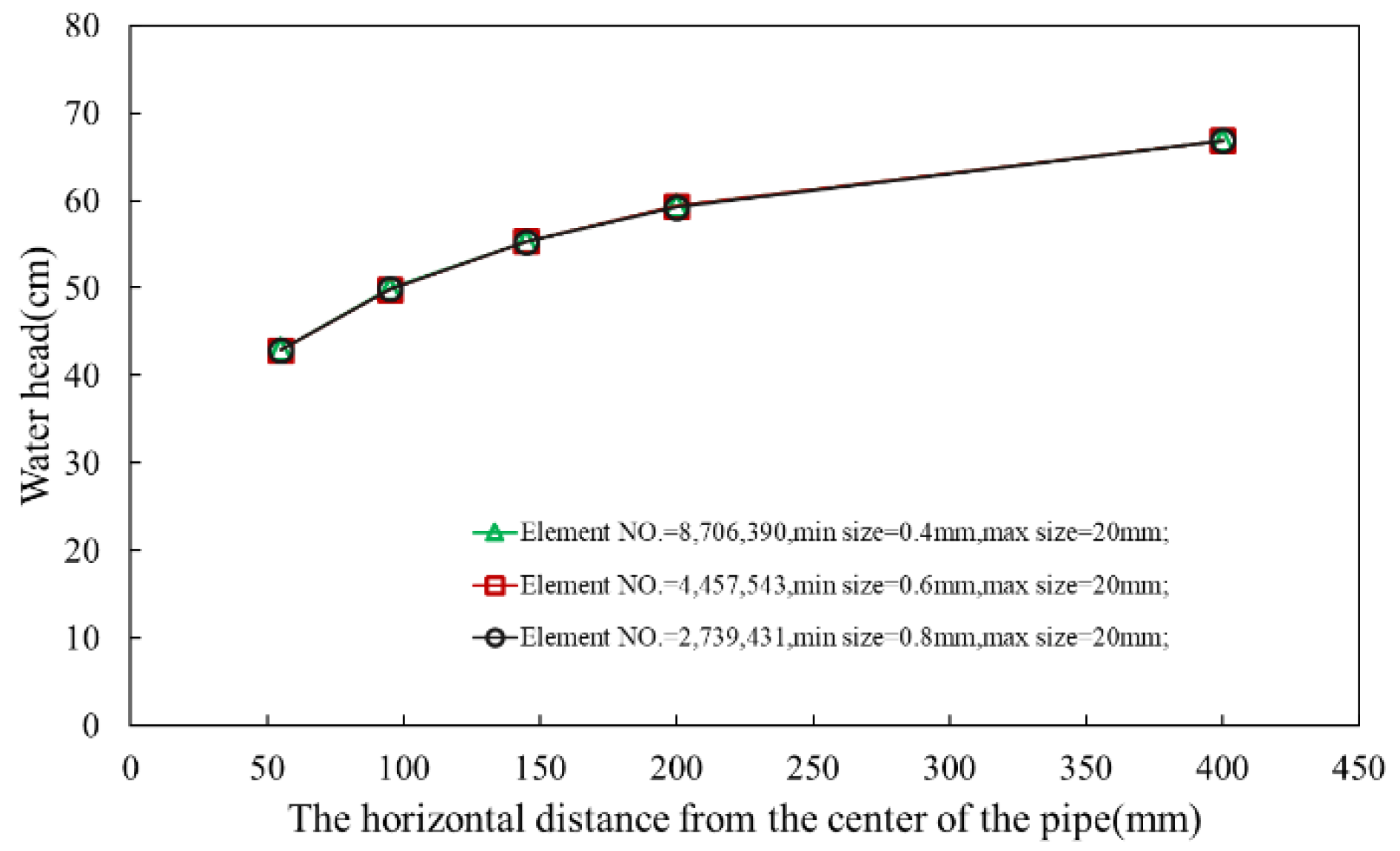
2.2.4. Grid Independent Test
2.2.5. Model Validation and Evaluation
2.3. Orthogonal Test Design
3. Results
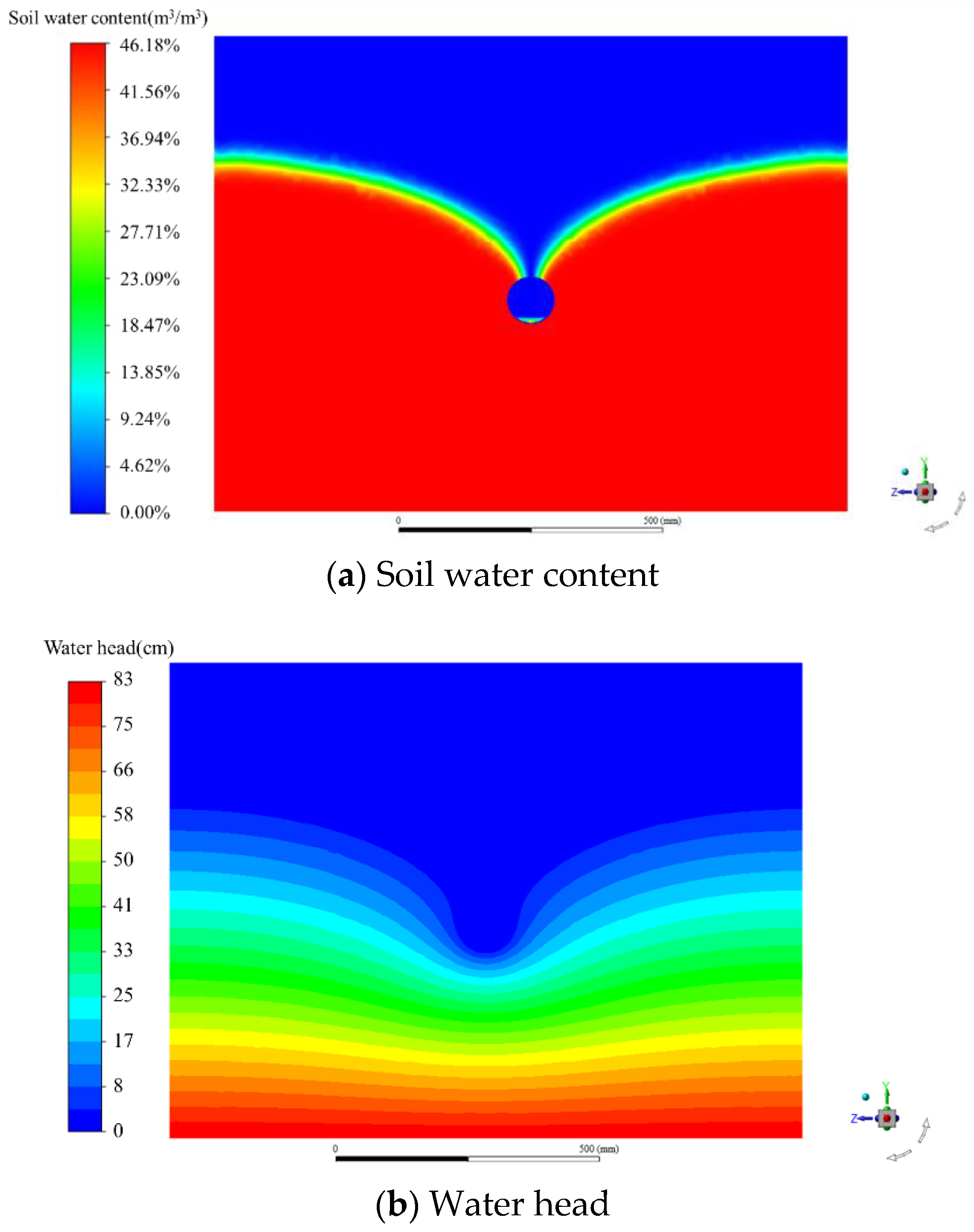
3.1. Hydraulic Properties of the Subsurface Drainage Flow Field
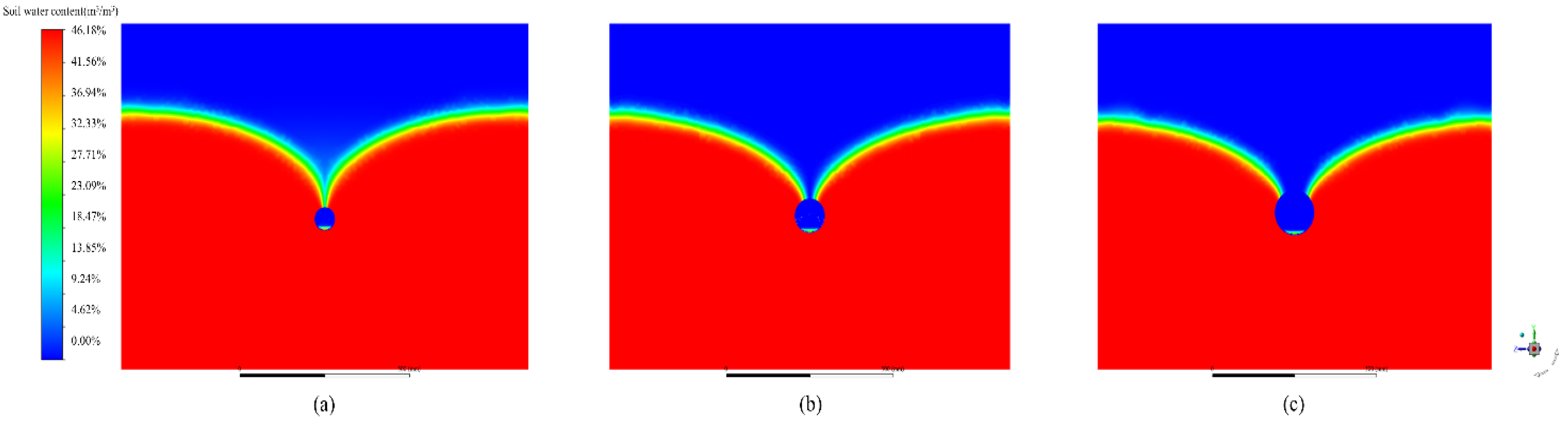
3.2. The Effect of the Geometric Parameters of the Corrugated Pipe on the Flow Field around the Pipe
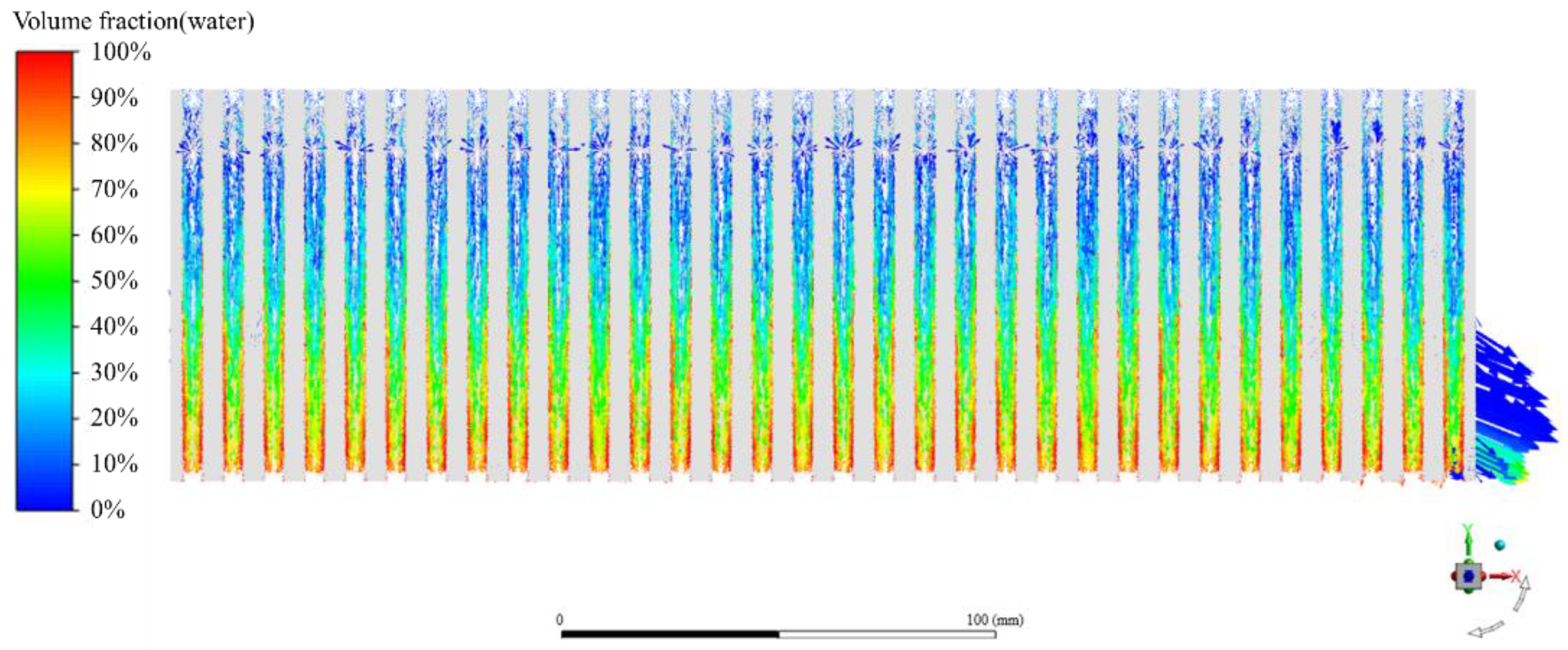
3.3. The Effect of the Geometric Structure of the Corrugated Pipe on the Drainage Rate
3.3.1. The Effect of the Corrugation Structure of the Corrugated Pipe on the Drainage Rate
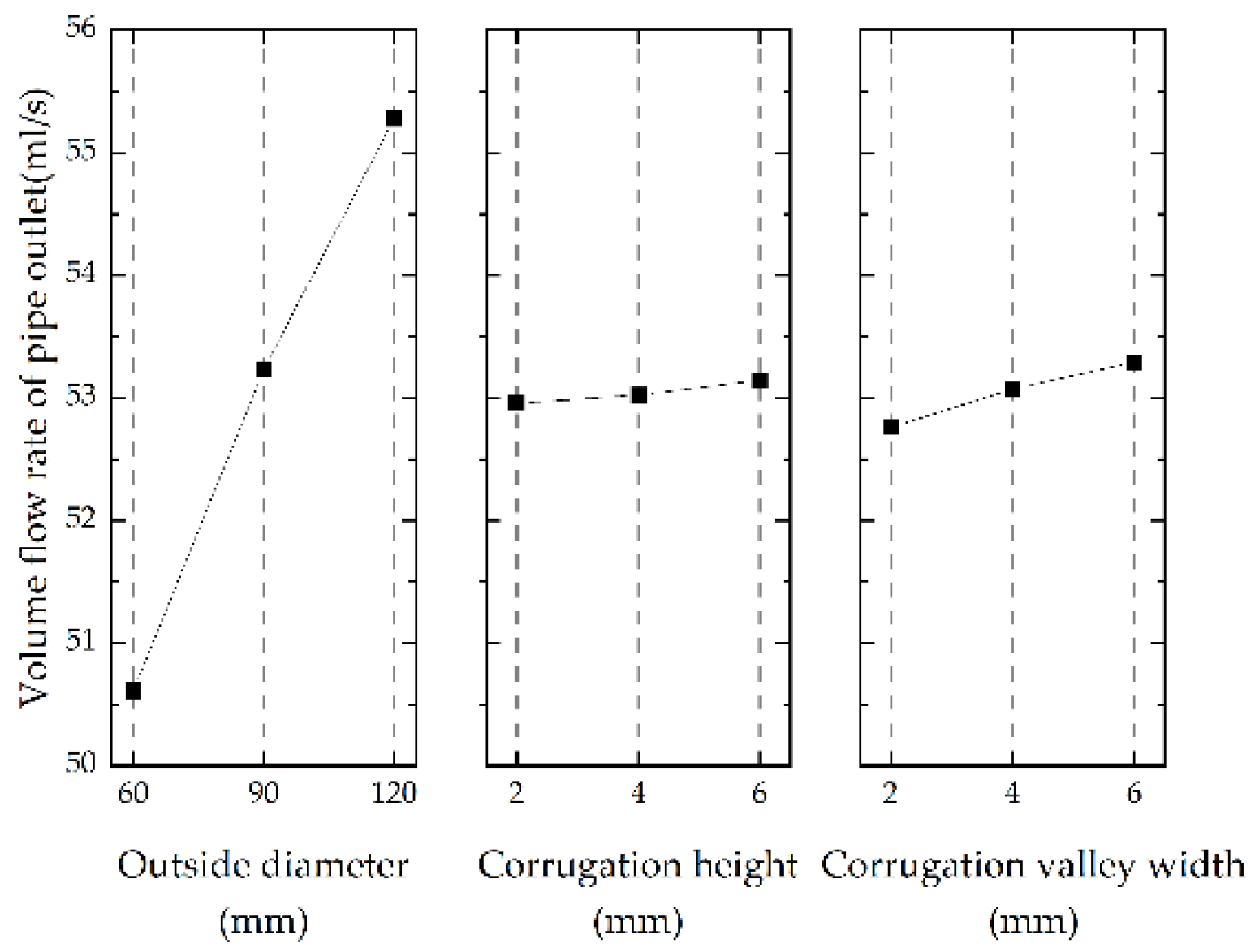
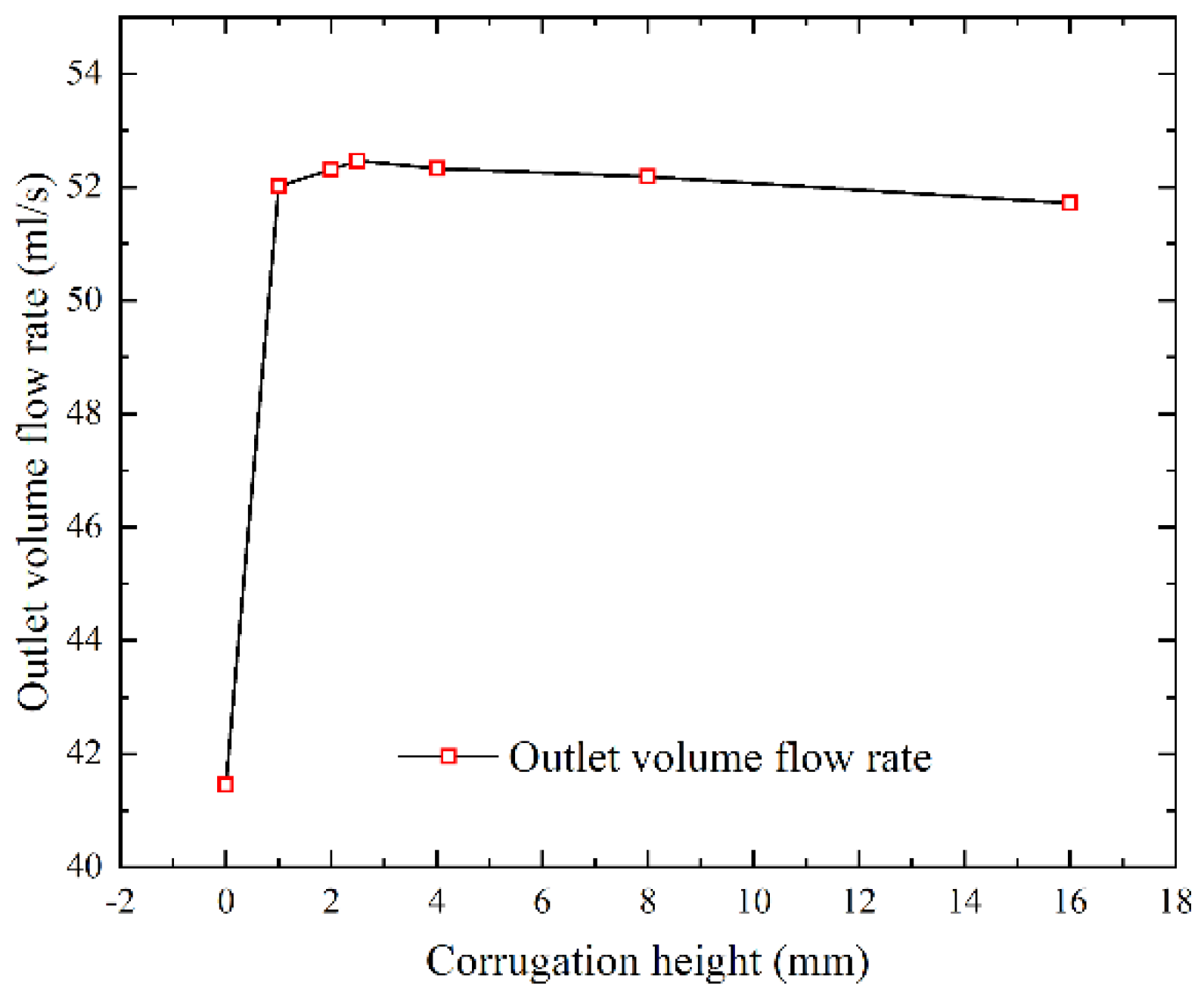
3.3.2. The Effect of Outside Diameter and Corrugation Height on Drainage Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, D.; Yang, H.; Yu, W.; Wu, X.; Wu, A.; Lu, G.; Zheng, Q. Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes. Polymers 2022, 14, 4000. [Google Scholar] [CrossRef] [PubMed]
- Yannopoulos, S.I.; Grismer, M.E.; Bali, K.M.; Angelakis, A.N. Evolution of the Materials and Methods Used for Subsurface Drainage of Agricultural Lands from Antiquity to the Present. Water 2020, 12, 1767. [Google Scholar] [CrossRef]
- Valipour, M.; Krasilnikof, J.; Yannopoulos, S.; Kumar, R.; Deng, J.; Roccaro, P.; Mays, L.; Grismer, M.E.; Angelakis, A.N. The Evolution of Agricultural Drainage from the Earliest Times to the Present. Sustainability 2020, 12, 416. [Google Scholar] [CrossRef] [Green Version]
- Stuyt, L.C.P.M.; Dierickx, W.; Beltrán, J.M. Materials for Subsurface Land Drainage Systems; Food and Agriculture Organization: Rome, Italy, 2005. [Google Scholar]
- Oyarce, P.; Gurovich, L.; Duarte, V. Experimental Evaluation of Agricultural Drains. J. Irrig. Drain. Eng. 2017, 143, 04016082. [Google Scholar] [CrossRef]
- Stuyt, L.; Dierickx, W. Design and performance of materials for subsurface drainage systems in agriculture. Agric. Water Manag. 2006, 86, 50–59. [Google Scholar] [CrossRef]
- Alavi, S.A.; Naseri, A.A.; Bazaz, A.; Ritzema, H.; Hellegers, P. Performance evaluation of the Hydroluis drainpipe-envelope system in a saline-sodic soil. Agric. Water Manag. 2020, 243, 106486. [Google Scholar] [CrossRef]
- Li, H.; Wu, Z.; Yang, H.; Wu, J.; Guo, C. Field study on the influence of subsurface drainage pipes and envelopes on discharge and salt leaching in arid areas. Irrig. Drain. 2022, 71, 697–710. [Google Scholar] [CrossRef]
- Ernst, L.F. HET Berekenen van Stationnaire Grondwaterstromingen, Welke in Een Verticaal Vlak Afgebeeld Kunnen Worden; Landbouwproefstation en Bodemkundig Instituut TNO: Groningen, The Netherlands, 1954. [Google Scholar]
- Cavelaars, J. Problems of Water Entry into Plastic and Other Drain Tubes; National College of Agricultural Engineering: Bedfordshire, UK, 1967. [Google Scholar]
- Childs, E.C.; Youngs, E.G. The nature of the drain channel as a factor in the design of a land-drainage system. Eur. J. Soil Sci. 1958, 9, 316–331. [Google Scholar] [CrossRef]
- Dierickx, W. Research and developments in selecting subsurface drainage materials. Irrig. Drain. Syst. 1993, 6, 291–310. [Google Scholar] [CrossRef]
- Smedema, L.K.; Rycroft, D.W. Land drainage. Planning and design of agricultural drainage systems. Agric. Water Manag. 1983, 10, 183–184. [Google Scholar]
- Bahçeci, I.; Nacar, A.S.; Topalhasan, L.; Tari, A.F.; Ritzema, H.P. A New Drainpipe-Envelope Concept for Subsurface Drainage Systems in Irrigated Agriculture. Irrig. Drain. 2018, 67, 40–50. [Google Scholar] [CrossRef]
- Gaj, N.; Madramootoo, C.A. Effects of Perforation Geometry on Pipe Drainage in Agricultural Lands. J. Irrig. Drain. Eng. 2020, 146, 04020015. [Google Scholar] [CrossRef]
- Wesseling, J.; Homma, F. Entrance resistance of plastic drain tubes. Neth. J. Agric. Sci. 1967, 15, 170–182. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating Two-and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Technical Manual, Version 2.0; University of California Riverside: Riverside, CA, USA, 2006. [Google Scholar]
- Skaggs, R.W.; Youssef, M.A.; Chescheir, G.M. DRAINMOD: Model Use, Calibration, and Validation. Trans. Asabe 2012, 55, 1509–1522. [Google Scholar] [CrossRef]
- Kroes, J.G.; Van Dam, J.C.; Huygen, J.; Vervoort, R.W. User’s Guide of SWAP Version 2.0; Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; Technical Document; Altera: Denver, CO, USA, 1999. [Google Scholar]
- Kroes, J.; Wesseling, J.; van Dam, J. Integrated modelling of the soil–water–atmosphere–plant system using the model SWAP 2· 0 an overview of theory and an application. Hydrol. Process. 2000, 14, 1993–2002. [Google Scholar] [CrossRef]
- Li, X.; Zuo, Q.; Shi, J.; Wang, S.; Bengal, A. Evaluation of salt discharge by subsurface pipes in the cotton field with film mulched drip irrigation in Xinjiang, China II: Application of the calibrated models and parameters. J. Hydraul. Eng. 2016, 47, 616–625. [Google Scholar]
- Shaoli, W.; Xingkui, W.; Prasher, S. Field application of DRAINMOD model to the simulation of water table, surface runoff and subsurface drainage. Trans. Chin. Soc. Agric. Eng. 2006, 22, 54–59. [Google Scholar]
- Filipović, V.; Mallmann, F.J.K.; Coquet, Y.; Šimůnek, J. Numerical simulation of water flow in tile and mole drainage systems. Agric. Water Manag. 2014, 146, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Boivin, A.; Šimůnek, J.; Schiavon, M.; Genuchten, M.T. Comparison of Pesticide Transport Processes in Three Tile-Drained Field Soils Using HYDRUS-2D. Vadose Zone J. 2006, 5, 838–849. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; Wang, S.; Xu, D.; Yuan, H.; Chen, H. Field and numerical experiment of an improved subsurface drainage system in Huaibei plain. Agric. Water Manag. 2017, 194, 24–32. [Google Scholar] [CrossRef]
- Li, X.W.; Zuo, Q.; Shi, J.C.; Alon, B.; Wang, S. Evaluation of salt discharge by subsurface pipes in the cotton field with film mulched drip irrigation in Xinjiang, China I. Calibration to models and parameters. J. Hydraul. 2016, 47, 537–544. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows. Int. J. Heat Fluid Flow 2007, 10, 371. [Google Scholar]
- Lee, I.-B.; Bitog, J.P.P.; Hong, S.-W.; Seo, I.-H.; Kwon, K.-S.; Bartzanas, T.; Kacira, M. The past, present and future of CFD for agro-environmental applications. Comput. Electron. Agric. 2013, 93, 168–183. [Google Scholar] [CrossRef]
- Afrin, T.; Khan, A.A.; Kaye, N.B.; Testik, F.Y. Numerical Model for the Hydraulic Performance of Perforated Pipe Underdrains Surrounded by Loose Aggregate. J. Hydraul. Eng. 2016, 142, 04016018. [Google Scholar] [CrossRef]
- Fu, H.; Yang, L.; Liang, H.; Wang, S.; Ling, K. Diagnosis of the single leakage in the fluid pipeline through experimental study and CFD simulation. J. Pet. Sci. Eng. 2020, 193, 107437. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics: A Practical Approach; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung Durch Boden: Zeitschrift des Vereines Deutscher Ingenieure; Eitschrift des Vereins Deutscher Ingenieure: Düsseldorf, Germany, 1901. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la ville de Dijon: Exposition et Application des Principes à Suivre et des Formules à Employer dans les Questions de Distribution D’eau: Ouvrage Terminé par un Appendice Relatif aux Fournitures D’eau de plusieurs Villes, au Filtrage des Eaux et à la Fabrication des Tuyaux de Fonte, de Plomb, de Tôle et de Bitume; Dalmont, V., Ed.; Ghent University: Ghent, Belgium, 1856; Volume 2. [Google Scholar]
- Waller, P.; Yitayew, M. Irrigation and Drainage Engineering; Springer: New York, NY, USA, 2016. [Google Scholar]
- Ritzema, H.P. Drainage Principles and Applications; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1994. [Google Scholar]
- Yuan, Y.; Na, L.; Shaoli, W. Discussion on the formula of subsurface drainage discharge considering hanging curtain section. Trans. Chin. Soc. Agric. Eng. 2021, 37, 119–126. [Google Scholar]






| Geometric Structural Parameters | Value |
|---|---|
| Outside diameter (mm) | 90 |
| Inside diameter (mm) | 82 |
| Wall thickness (mm) | 1 |
| Ridge width (mm) | 5.35 |
| Corrugation valley width (mm) | 4 |
| Corrugation height (mm) | 4 |
| Perforation length (mm) | 26.67 |
| Perforation width (mm) | 0.6 |
| Number of perforation rows | 3 |
| Perforation rate (%) | 1.99 |
| Total area of perforation per meter (cm2·m−1) | 51 |
| Inlet Water Head (cm) | Outlet Volume Water Flow Rates (mL/s) (Experimental) | Outlet Volume Water Flow Rates (mL/s) (Numerical) | Deviation (%) |
|---|---|---|---|
| 70 | 30.98 | 29.90 | −3.49 |
| 80 | 40.35 | 41.02 | 1.66 |
| 90 | 50.33 | 53.32 | 5.94 |
| Level | Factor A: Outside Diameter (mm) | Factor B: Corrugation Height (mm) | Factor C: Corrugation Valley Width (mm) | Blank |
|---|---|---|---|---|
| Level 1 | 60 | 2 | 2 | 1 |
| Level 2 | 90 | 4 | 4 | 2 |
| Level 3 | 120 | 6 | 6 | 3 |
| Treatments | Factors | Experiment Scheme | |||
|---|---|---|---|---|---|
| Factor A | Factor B | Factor C | Blank | ||
| T1 | Level 1 | Level 1 | Level 1 | Level 1 | A1B1C1 |
| T2 | Level 1 | Level 2 | Level 2 | Level 2 | A1B2C2 |
| T3 | Level 1 | Level 3 | Level 3 | Level 3 | A1B3C3 |
| T4 | Level 2 | Level 1 | Level 3 | Level 2 | A2B1C3 |
| T5 | Level 2 | Level 2 | Level 1 | Level 3 | A2B2C1 |
| T6 | Level 2 | Level 3 | Level 2 | Level 1 | A2B3C2 |
| T7 | Level 3 | Level 1 | Level 2 | Level 3 | A3B1C2 |
| T8 | Level 3 | Level 2 | Level 3 | Level 1 | A3B2C3 |
| T9 | Level 3 | Level 3 | Level 1 | Level 2 | A3B3C1 |
| Treatments | The Outer Volume Water Flow Rate (mL/s) | The Shoulder Perforation Volume Water Rate (mL/s) | The Volume Water Flow Ratio of the Shoulder Perforation to the Pipe Outlet (%) |
|---|---|---|---|
| Bottom water supply | 53.36 | 4.14 | 7.75 |
| Surface water supply | 65.24 | 7.87 | 12.07 |
| Lateral water supply | 67.96 | 4.52 | 6.65 |
| Treatments | Factors | Outer Volume Flow Rate (mL/s) | |||
|---|---|---|---|---|---|
| Factor A: Outside Diameter (mm) | Factor B: Corrugation Height (mm) | Factor C: Corrugation Valley Width (mm) | Blank | ||
| T1 | 60 | 2 | 2 | 1 | 50.31 |
| T2 | 60 | 4 | 4 | 2 | 50.62 |
| T3 | 60 | 6 | 6 | 3 | 50.91 |
| T4 | 90 | 2 | 6 | 2 | 53.39 |
| T5 | 90 | 4 | 2 | 3 | 52.88 |
| T6 | 90 | 6 | 4 | 1 | 53.43 |
| T7 | 120 | 2 | 4 | 3 | 55.17 |
| T8 | 120 | 4 | 6 | 1 | 55.57 |
| T9 | 120 | 6 | 2 | 2 | 55.09 |
| k1 | 50.61 | 52.96 | 52.76 | 53.10 | |
| k2 | 53.23 | 53.02 | 53.07 | 53.03 | |
| k3 | 55.28 | 53.14 | 53.29 | 52.99 | |
| R | 4.67 | 0.19 | 0.53 | 0.11 | |
| Factor order | A > C > B | ||||
| Optimal level combination | A3B2C3 | ||||
| Sources | Sum of Squares of Deviations | Degrees of Freedom | Mean Square | F | p-Value |
|---|---|---|---|---|---|
| Outside diameter | 32.786 | 2 | 16.393 | 1584.729 | 0.001 |
| Corrugation height | 0.054 | 2 | 0.027 | 2.595 | 0.278 |
| Corrugation valley width | 0.426 | 2 | 0.213 | 20.592 | 0.046 |
| Error | 0.021 | 2 | 0.010 | ||
| Combined errors | 33.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Guo, C.; Yang, H.; Li, H.; Wu, J. Experimentally Based Numerical Simulation of the Influence of the Agricultural Subsurface Drainage Pipe Geometric Structure on Drainage Flow. Agriculture 2022, 12, 2174. https://doi.org/10.3390/agriculture12122174
Wu Z, Guo C, Yang H, Li H, Wu J. Experimentally Based Numerical Simulation of the Influence of the Agricultural Subsurface Drainage Pipe Geometric Structure on Drainage Flow. Agriculture. 2022; 12(12):2174. https://doi.org/10.3390/agriculture12122174
Chicago/Turabian StyleWu, Zhe, Chenyao Guo, Haoyu Yang, Hang Li, and Jingwei Wu. 2022. "Experimentally Based Numerical Simulation of the Influence of the Agricultural Subsurface Drainage Pipe Geometric Structure on Drainage Flow" Agriculture 12, no. 12: 2174. https://doi.org/10.3390/agriculture12122174





