The Design and Experimentation of EVPIVS-PID Harvesters’ Header Height Control System Based on Sensor Ground Profiling Monitoring
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structural Design
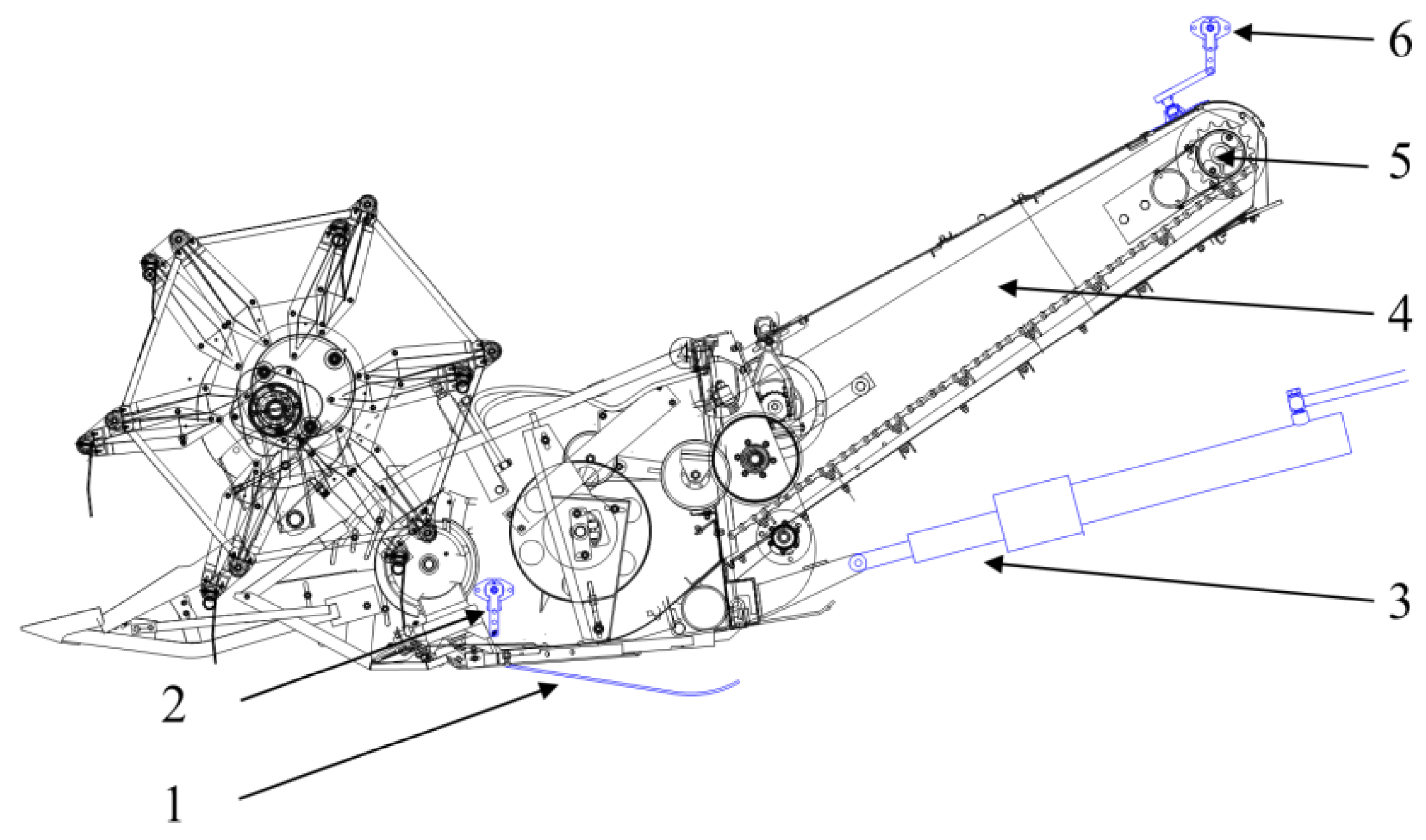
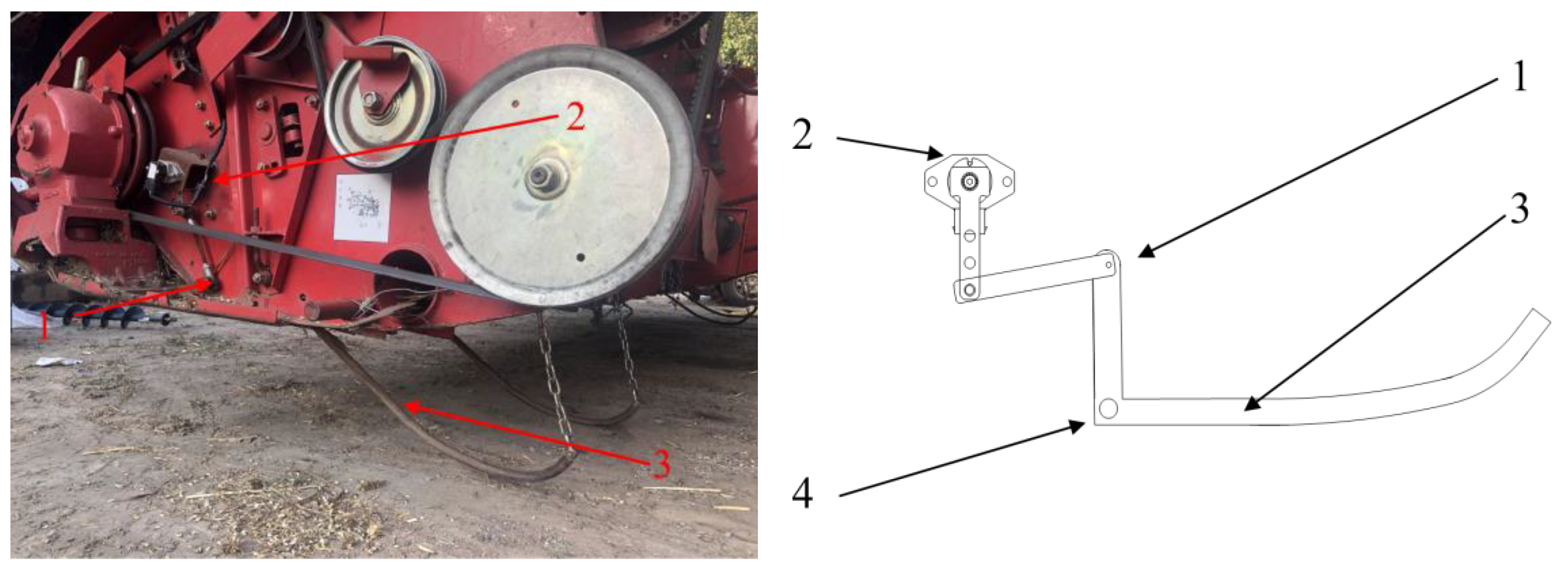
2.1.1. Design of the Ground Profiling Monitoring Mechanism Based on the Angle Sensor
2.1.2. Design of Height Feedback Mechanism of the Header Based on Angle Sensor
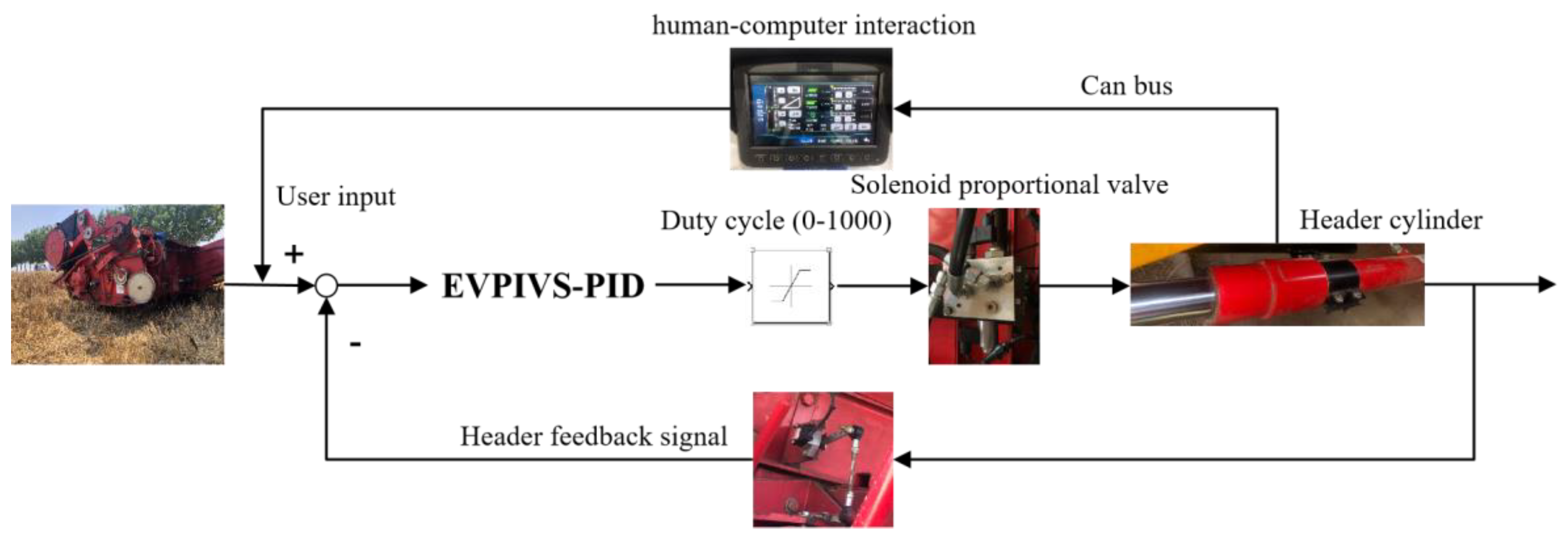
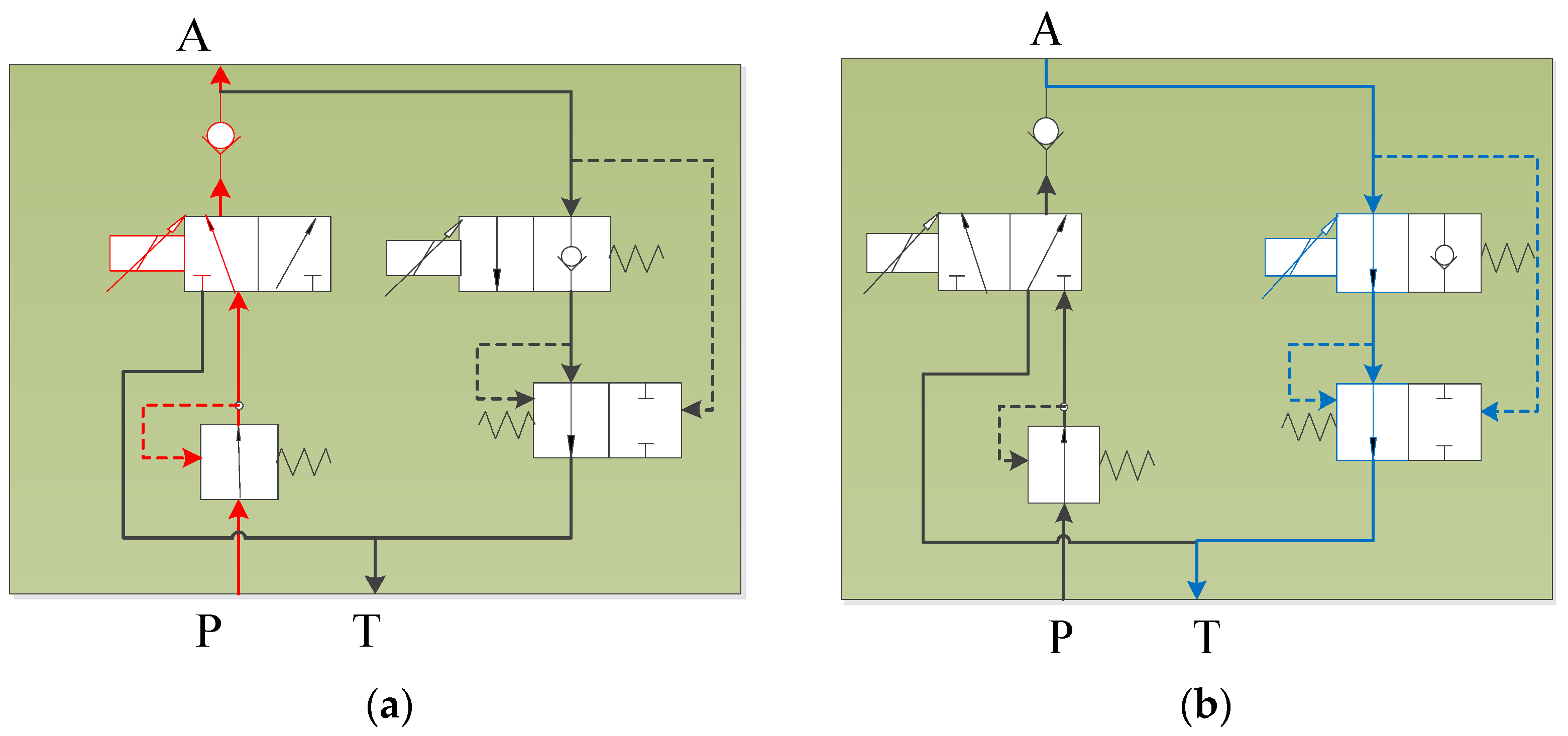
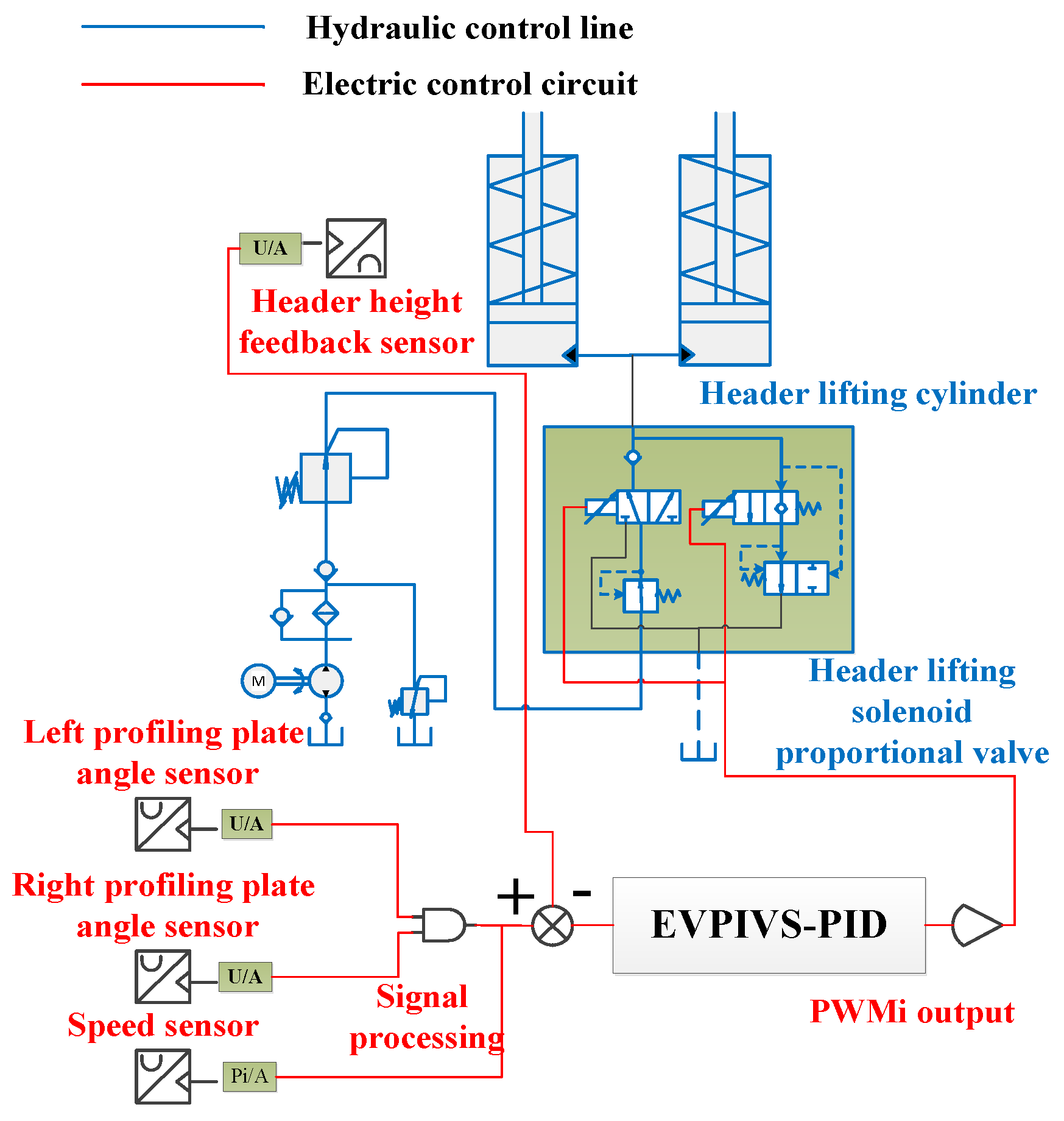
2.2. Operation Principle
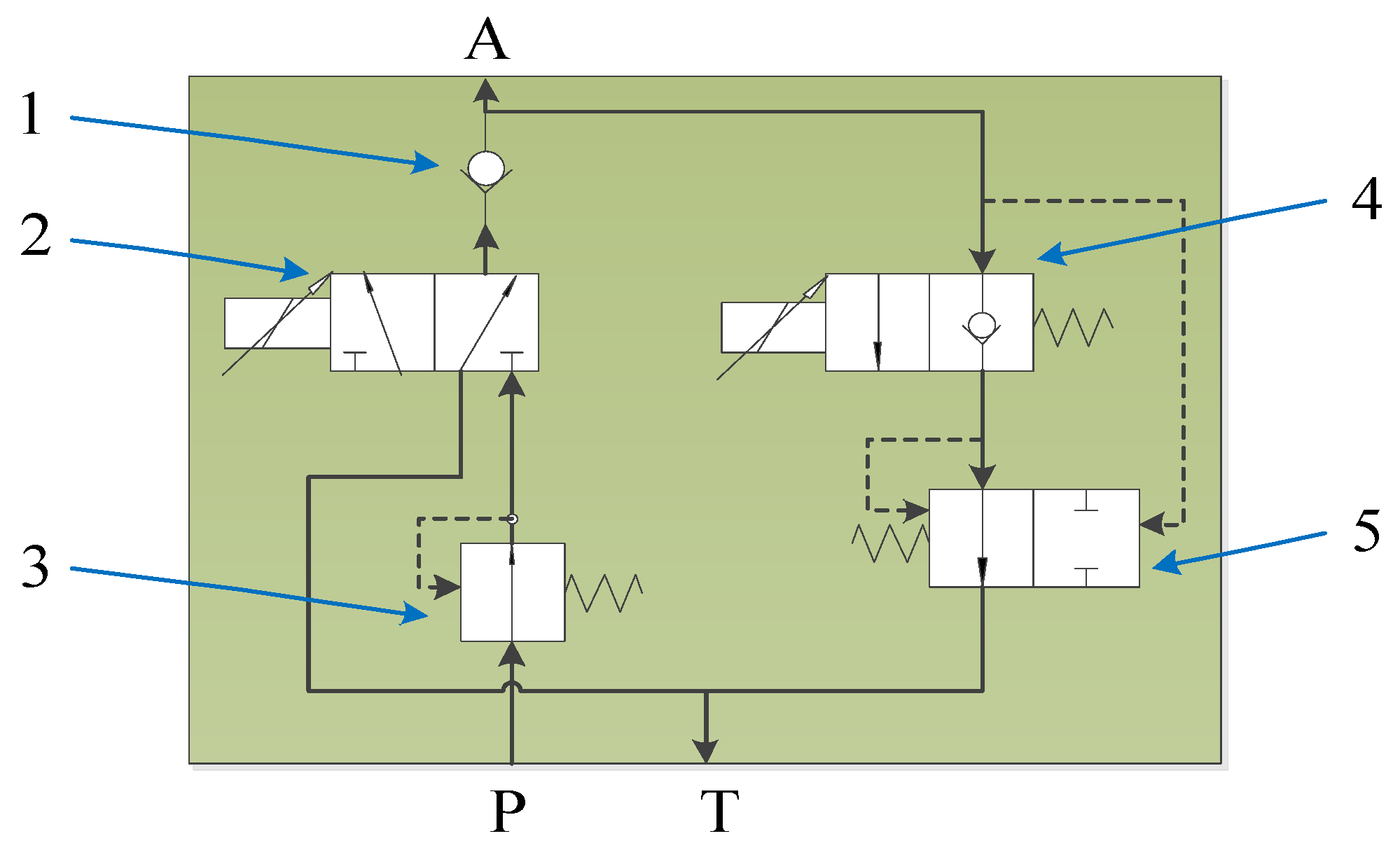
2.3. Structural Principle of Integrated Electromagnetic Proportional Valve in a Hydraulic Control System
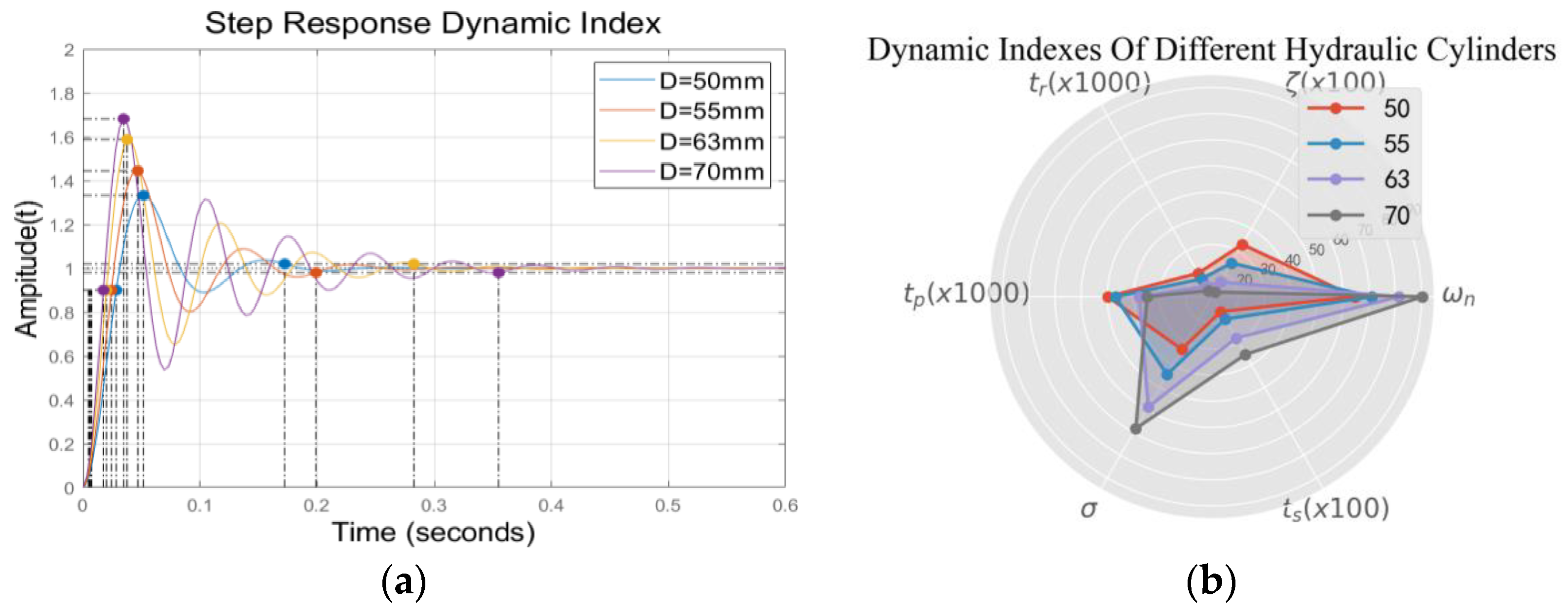
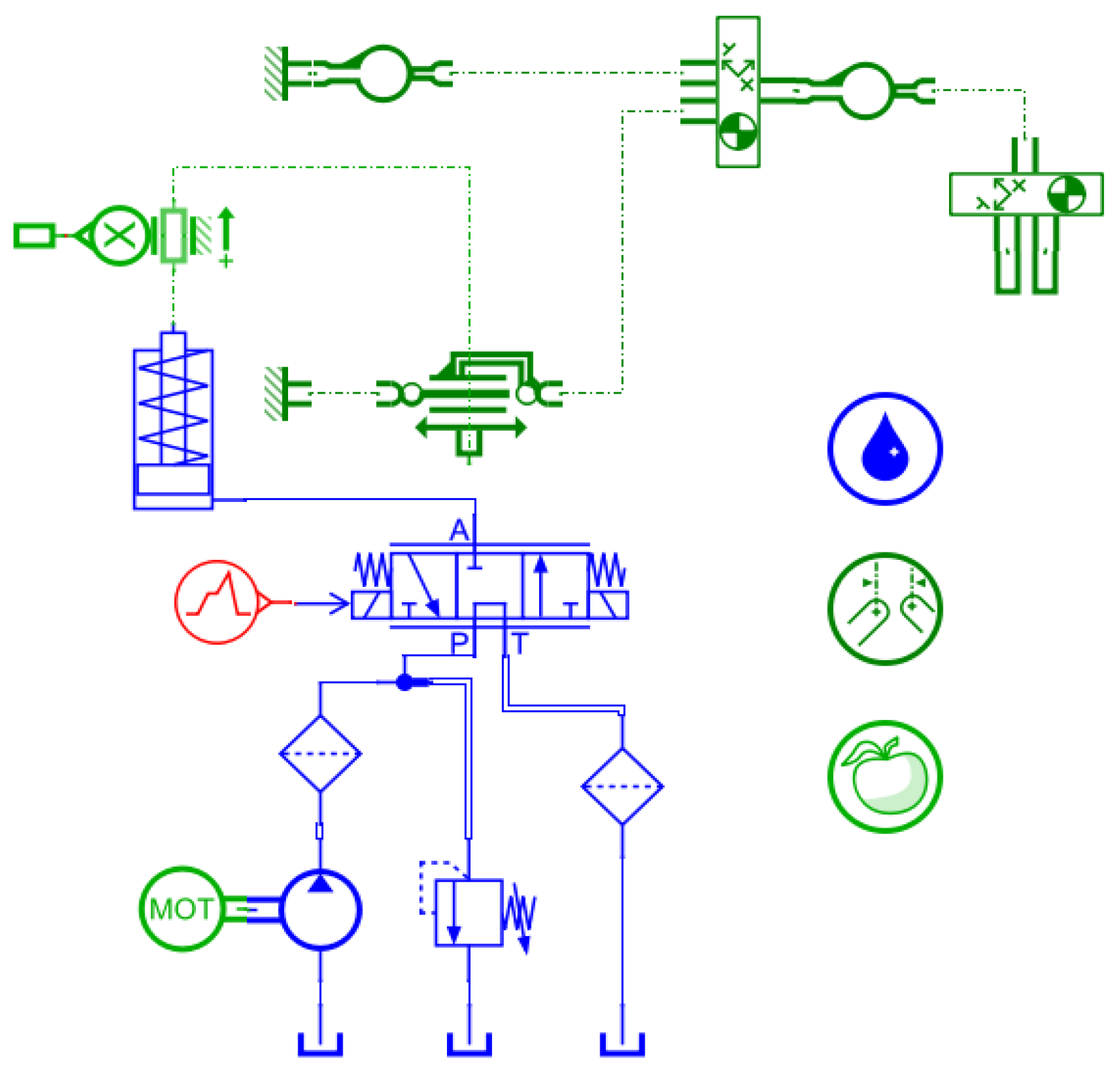
2.4. Selection of a Single-Acting Cylinder Based on Unit Step Response Analysis
2.4.1. Establishment of Transfer Function at the Single-Acting Hydraulic Cylinder
- is the load mass acting on the oil cylinder;
- is the movement distance of the load;
- is the force acting on the load;
- is the damping coefficient of the system;
- is the elastic coefficient of the system.
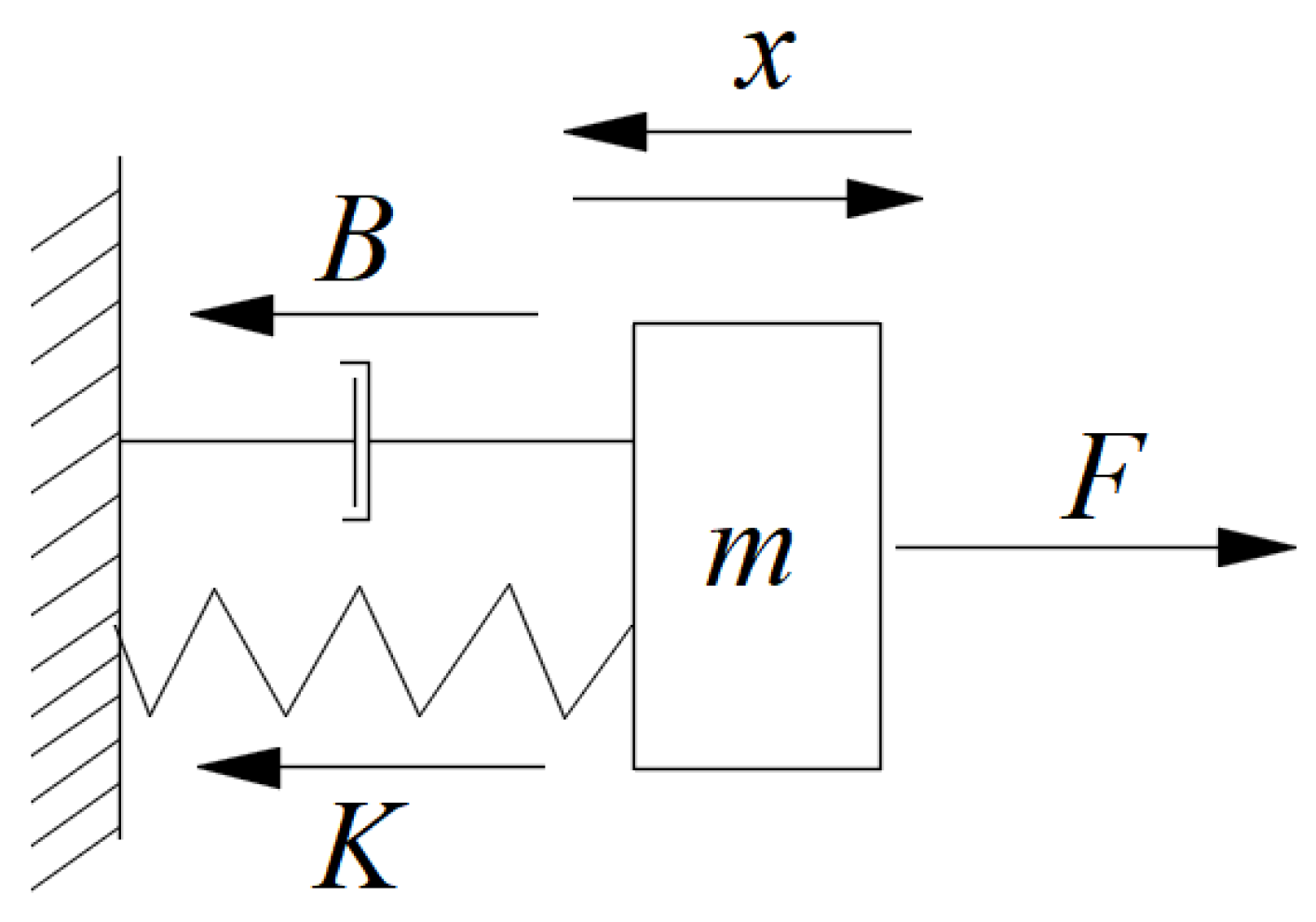
2.4.2. Parameter Selection of Hydraulic Cylinder Based on System Stability Analysis
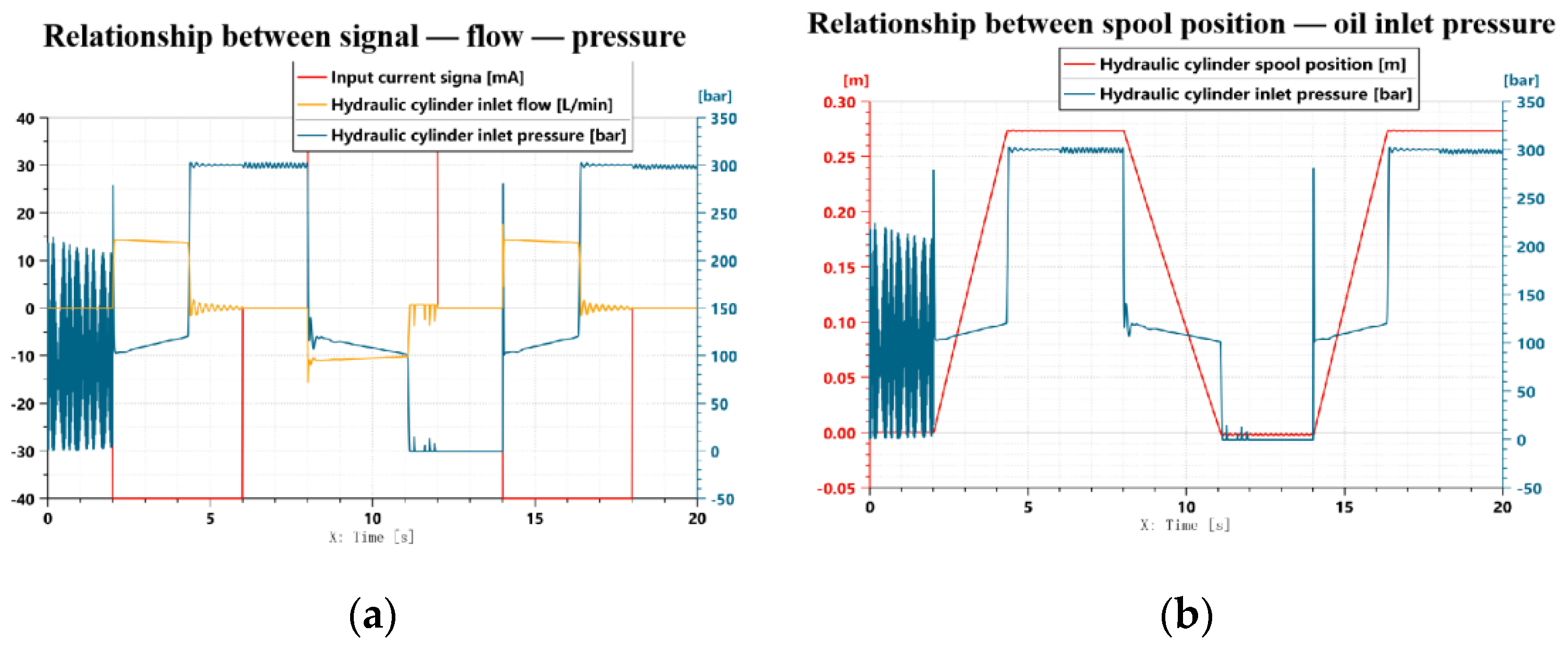
2.4.3. Performance Testing of Hydraulic Actuators
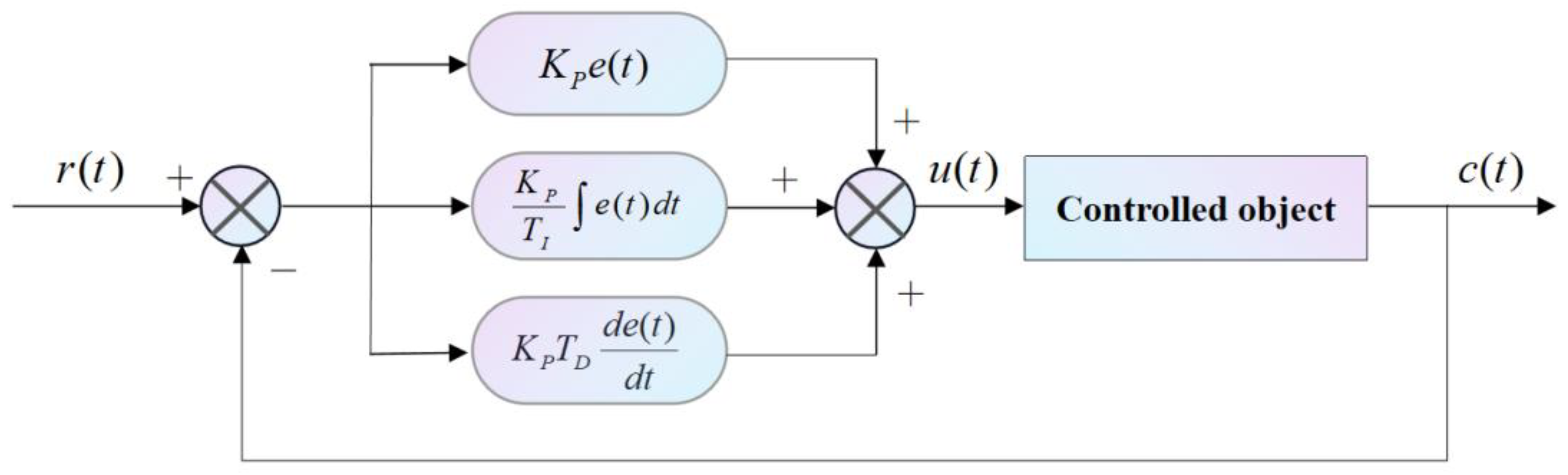
2.5. Design of EVPIVS-PID Control Strategy
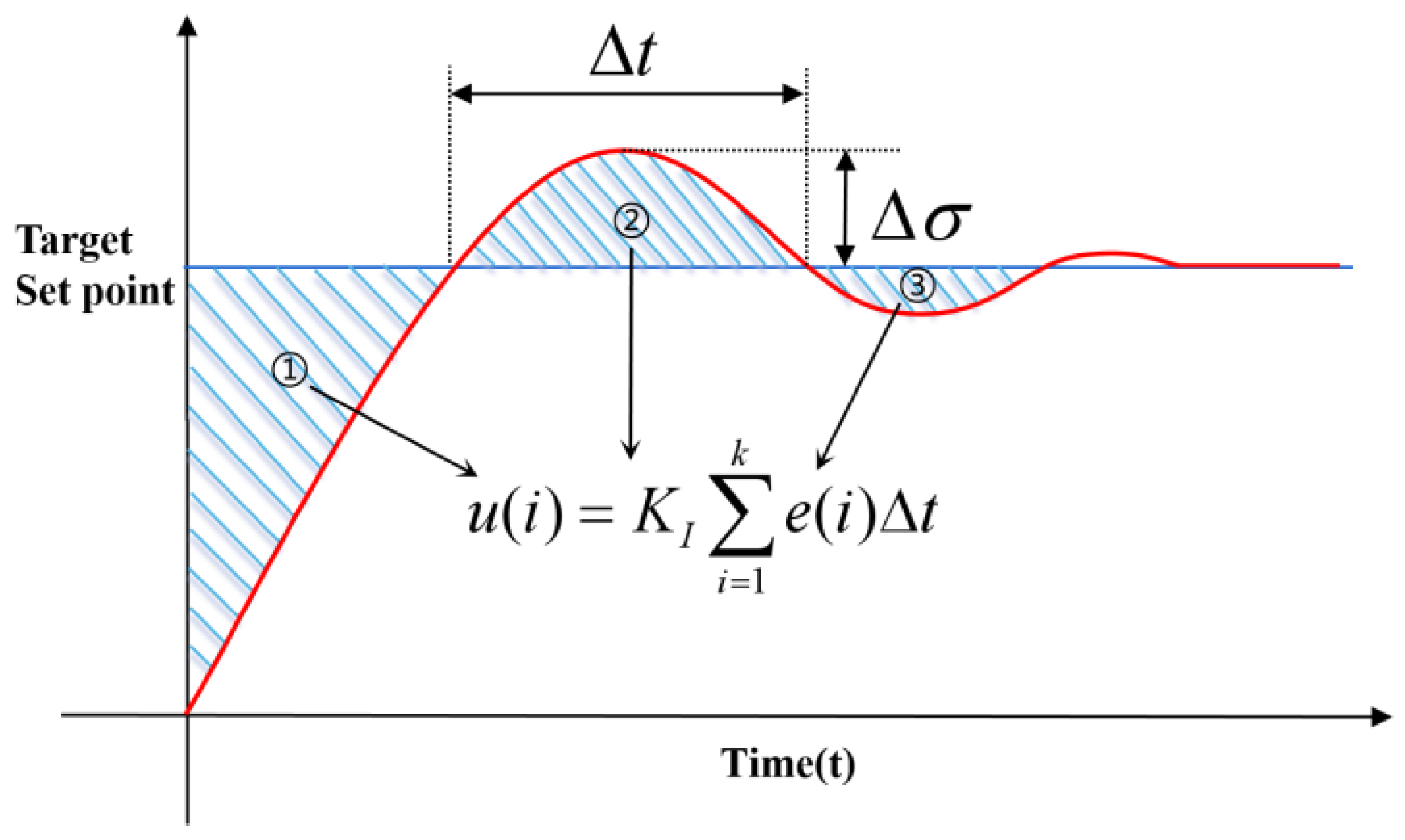
2.5.1. The Limitation of Traditional PID to Deal with Integral Saturation
2.5.2. Improved Design Based on Internal Integral Term
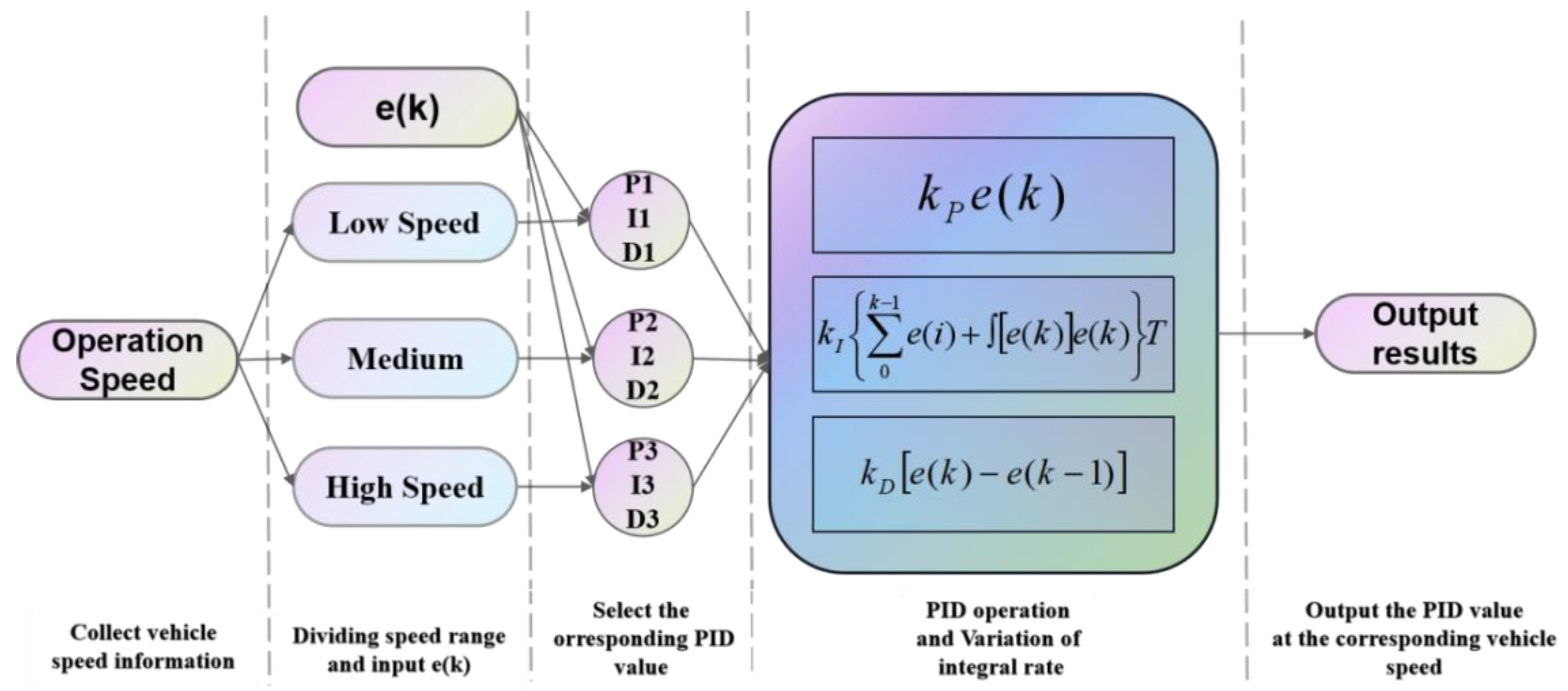
2.5.3. Design of EVPIVS-PID Based on Vehicle Speed and Error Detection
2.6. Principle of Electro-Hydraulic Hybrid Control
2.7. Methods of Amesim Simulation Tests
2.8. Header Control Accuracy Test
2.9. Correlation Test between PWM and Header Height
3. Results and Discussion
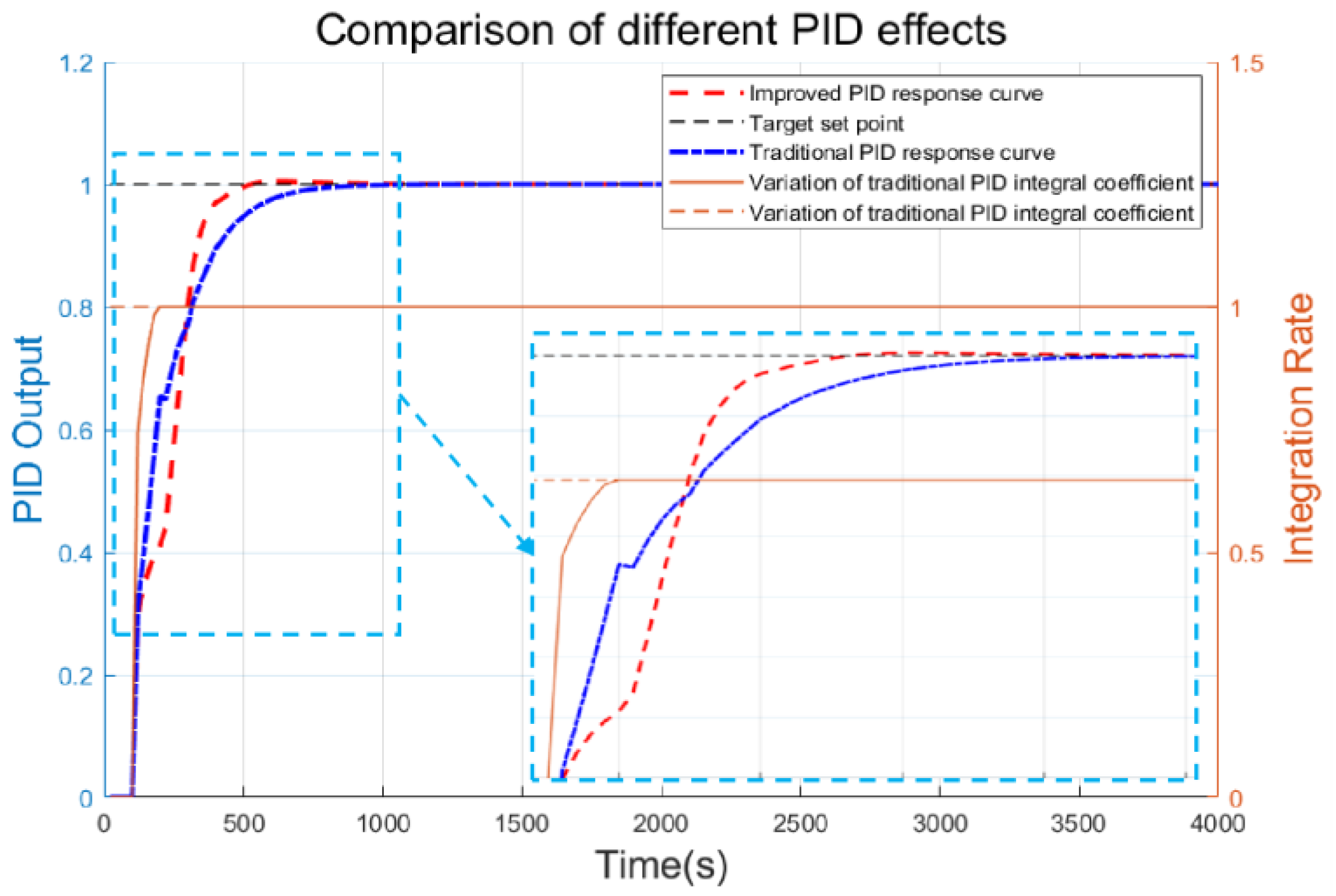
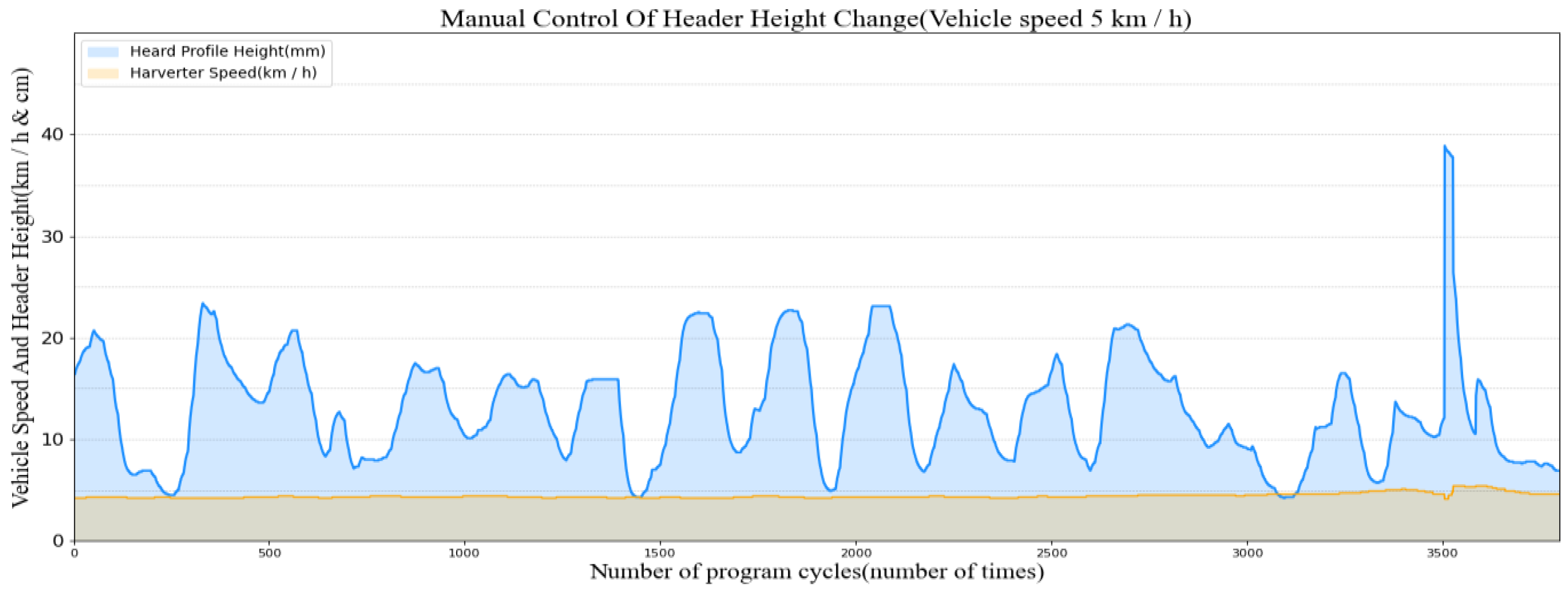
3.1. Comparison of Header Height Control Effect
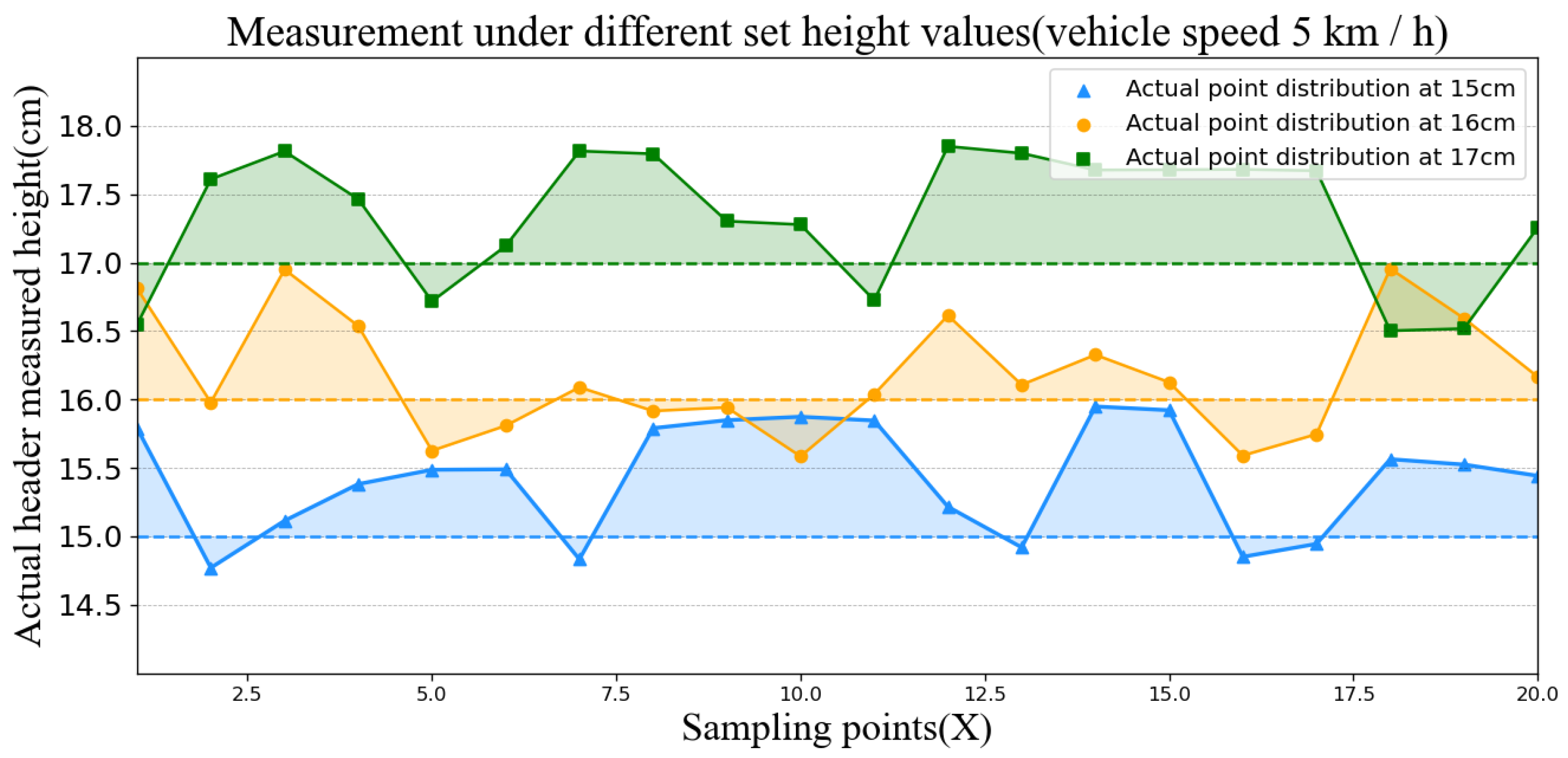
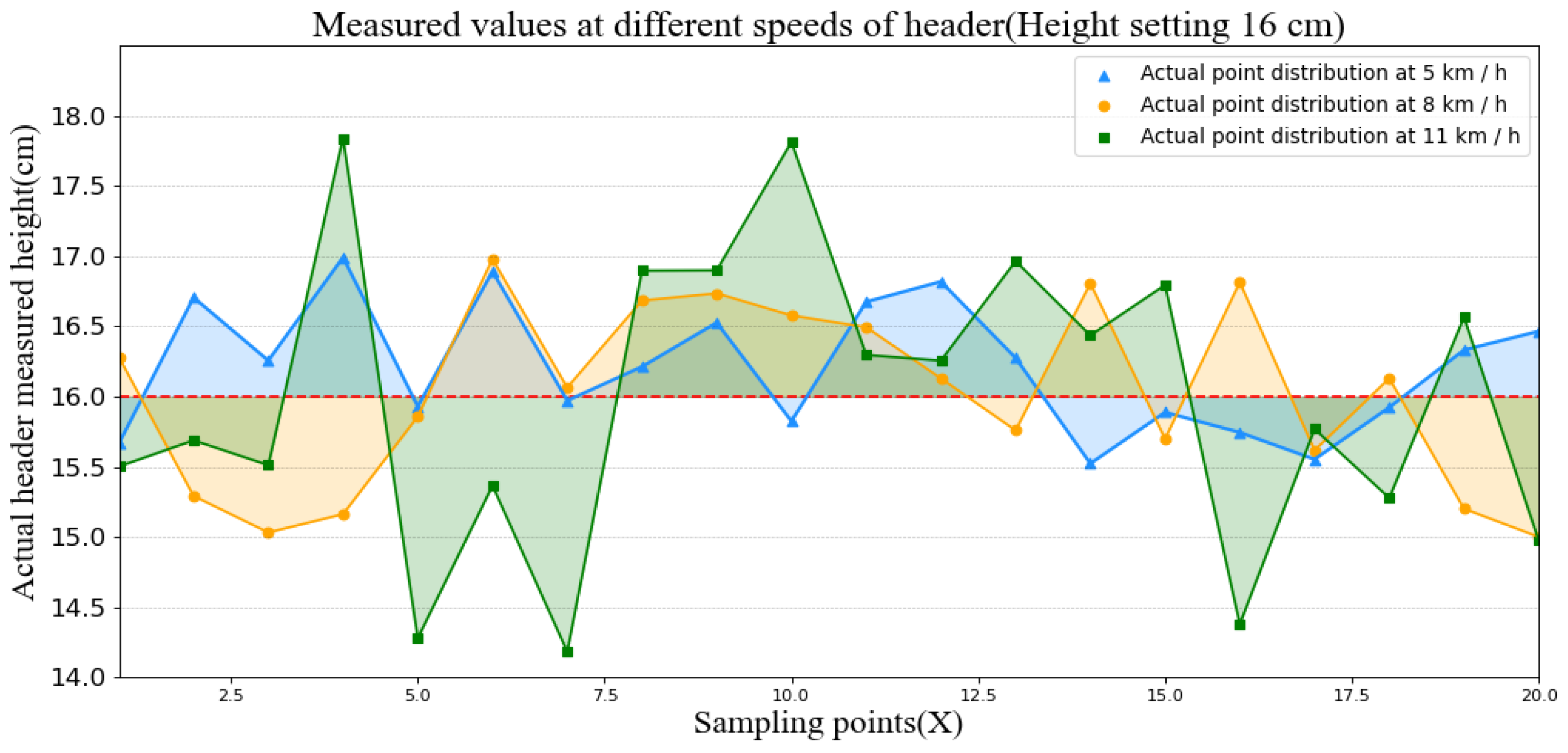
3.2. Test Results and Analysis of Header Control Accuracy
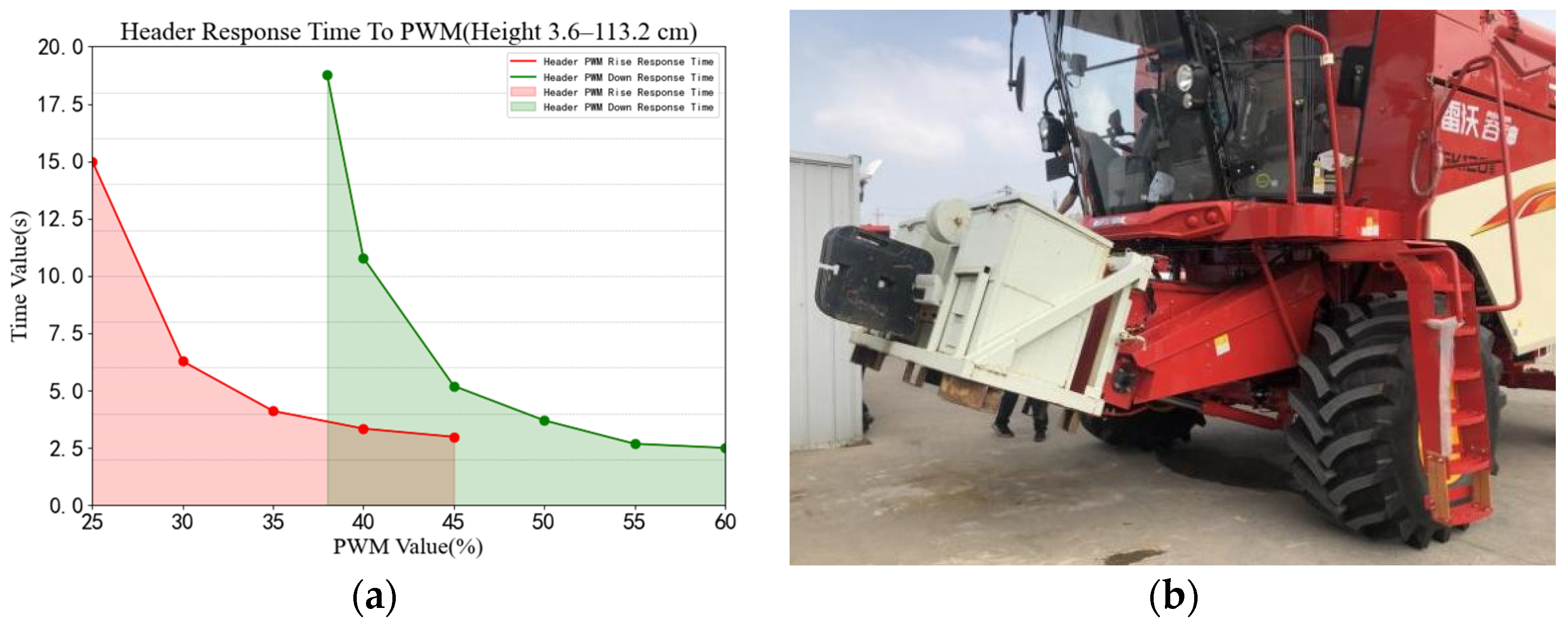
3.3. Test Results and Analysis of Correlation Test between PWM and Header Height
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glancey, J.L. Analysis of Header Loss From Pod Stripper Combines in Green Peas. Agric. Eng. Res. 1997, 68, 1–10. [Google Scholar] [CrossRef]
- Carlin, J.F. Electro-hydraulic control of combine header height and reel speed. SAE Int. 1984, 93, 252–256. [Google Scholar]
- Craessaerts, G.; De Baerdemaeker, B.J. Fuzzy control of the cleaning process on a combine harvester. Biosyst. Eng. 2010, 106, 103–111. [Google Scholar] [CrossRef]
- Lamp, B.J.; Johnson, W.H.; Harkness, K.A.; Smith, P.E. Soybean harvesting approaches to improved harvesting efficiencies. Ohio Agric. Exp. Stn. Res. Bull. 1962, 899. Available online: https://kb.osu.edu/bitstream/handle/1811/62695/1/OARDC_research_bulletin_n0899.pdf (accessed on 21 January 2022).
- Quick, G.R. Laboratory Analysis of the Combine Header. Trans ASAE 1973, 16, 0005–0012. [Google Scholar] [CrossRef]
- Dong, S.; Du, C. Development on electrical system performance test stand for combine harvester. IFAC-Pap. Online 2018, 51, 363–367. [Google Scholar] [CrossRef]
- Rehkugler, G.E. Dynamic analysis of automatic control of combine header height. Trans. ASAE 1970, 13, 225–231. [Google Scholar] [CrossRef]
- Xia, L.; Liang, X.; Wei, L.; Zhao, B. Research progress of automatic monitoring system for combine harvesters. Agric. Mach. 2013, 19, 141–144. [Google Scholar]
- Zhang, X. Design and Innovation of Combine Harvester Header Control System. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2015. [Google Scholar]
- Alleyne, A.G.; Xie, Y.; Greer, A.; Deneault, D. Fundamental limits in combine harvester header height control. J. Dyn. Syst. Meas. Control 2013, 135, 034503. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Alleyne, A.; Greer, A.; Deneault, D. Header height control of a combine harvester system. Dyn. Syst. Control Conf. 2010, 44175, 7–14. [Google Scholar] [CrossRef]
- Xie, Y.; Alleyne, A. Two degrees of freedom control for combine harvester header height control, Dynamic Systems and Control Conference. Am. Soc. Mech. Eng. 2012, 45318, 539–547. [Google Scholar] [CrossRef]
- Lopes, T.; Magalhaaes, P.S.G.; Nobrega, E.G.O. Optimal Header Height Control System for Combine Harvesters. Biosyst. Eng. 2002, 81, 261–272. [Google Scholar] [CrossRef]
- Wang, C.; Liang, Y. Analysis of the automatic control system for the height of the grain combine harvester. Grain Oil Process. Food Mach. 1989, 3, 5–8. [Google Scholar]
- Chen, J.; Zhang, S.; Li, Y. Design of automatic control system for combing table height of combine harvester. J. Agric. Mach. 2003, 6, 65–67. [Google Scholar]
- Wei, L.; Che, Y.; Wang, F.; Li, W. Design and test of ground profiling control system for combine harvester header. Agric. Mech. Res. 2017, 39, 150–154. [Google Scholar]
- Zhang, C. Research on Harvester Header Profiling and Crop Altimetry Method. Master’s Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Liu, L.; Wu, M. Least Squares Curve Fitting Based on Matlab. Fujian Comput. 2019, 8, 9–12. [Google Scholar]
- Zhang, Z. Design and Analysis of Hydraulic Lifting System for Header of Combine Harvester Cutting Table, Qingdao, China. 2019. Available online: https://portal.issn.org/resource/ISSN/1755-1315 (accessed on 21 January 2022).
- Yang, S.; Yang, Q.; Yang, Y. Design of Header Height Control System Based on Ultrasonic Sensor. Agric. Mech. Res. 2008, 3, 134–136, 156. [Google Scholar]
- Huang, C.; Shang, Q.; Yu, S.; Zhang, E. System Identification Based on Step Response Second-Order Plus Pure Lag Model. Mach. Manuf. 2010, 48, 19–21. [Google Scholar]
- Chen, B. Research on Electro-hydraulic Proportional Valve Control System Based on PID Algorithm. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2012. [Google Scholar]
- Chen, X. Design and Simulation Analysis of Hydraulic Proportional Control System at the Inlet of Continuous Press. Master’s Thesis, Northeast Forestry University, Harbin, China, 2021. [Google Scholar]
- Siddique, M.A.A.; Kim, W.-S. Effects of Temperatures and Viscosity of the Hydraulic Oils on the Proportional Valve for a Rice Transplanter Based on PID Control Algorithm. Agriculture 2020, 10, 73. [Google Scholar] [CrossRef] [Green Version]
- Shamilah, A.M.; Darius, E.P. Actual field speed of rice combine harvester and its influence on grain loss in Malaysian paddy field. J. Saudi Soc. Agric. Sci. 2020, 19, 422–425. [Google Scholar] [CrossRef]
- Cao, H.; Guo, H. Optimization of PID Parameters of Hydraulic System of Elevating Wheelchair Based on AMESim. Procedia Eng. 2011, 15, 3710–3714. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Hu, Y.; Miao, Y. Research on fuzzy control strategy of header height of harvester. Mechatronics 2018, 24, 17–22. [Google Scholar]
- Dominic, E.; Tamás, F. On relationships between the Pearson and the distance correlation coefficients. Stat. Probab. Lett. 2021, 169, 108960. [Google Scholar] [CrossRef]




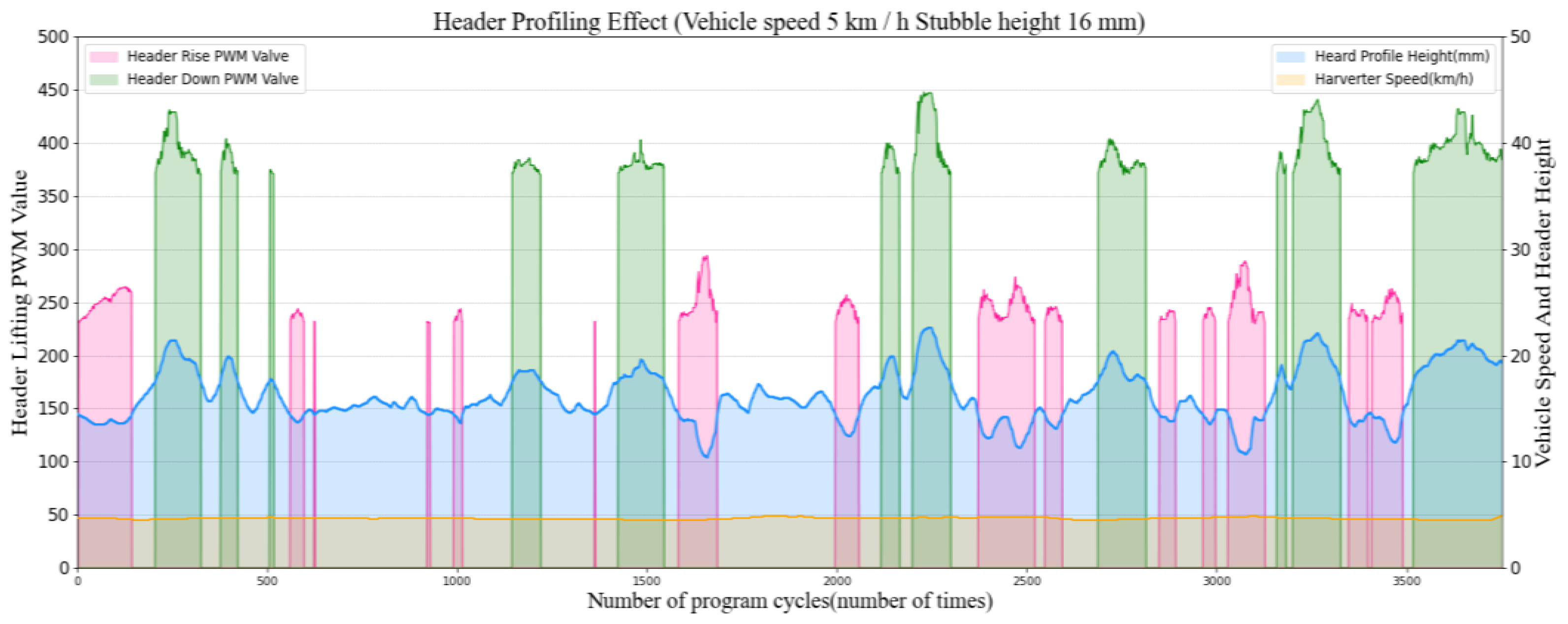
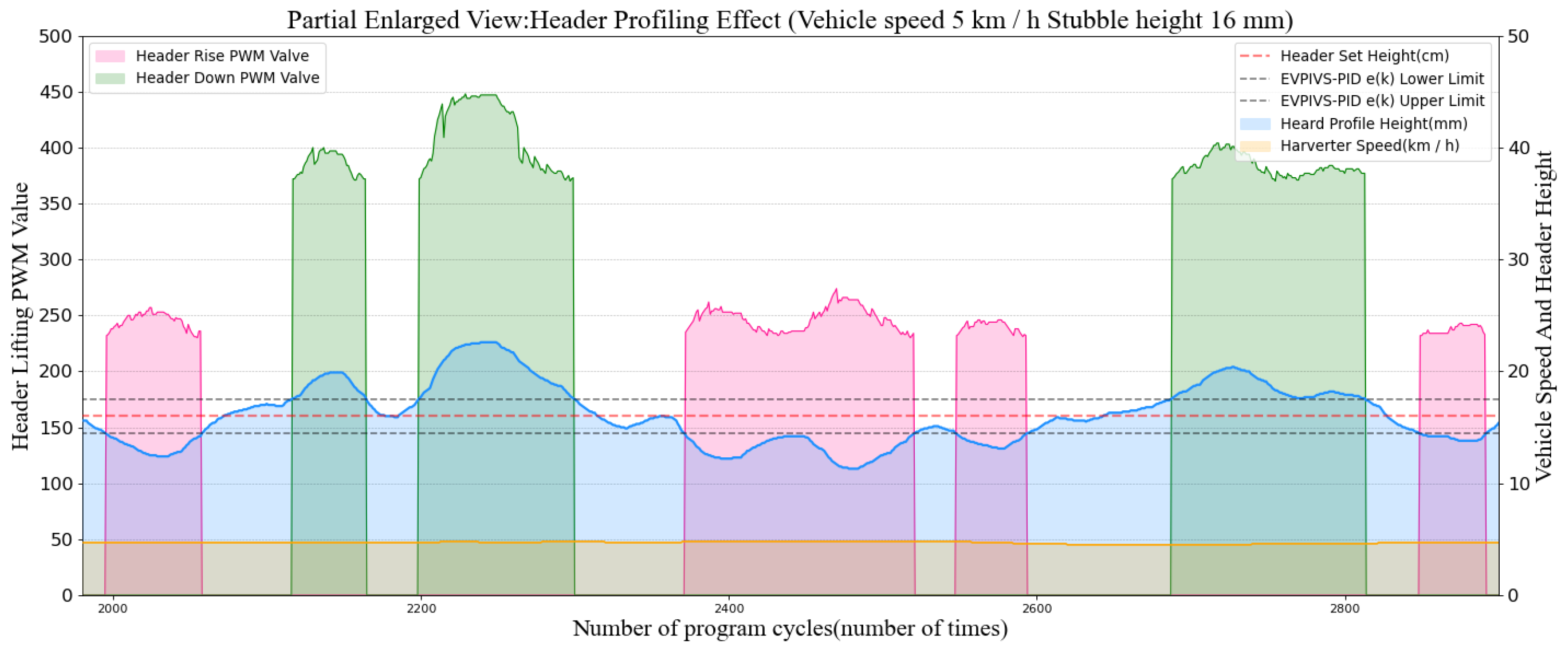


| Dynamic Indicator Type | Symbol | Calculation Formula |
|---|---|---|
| Rise Time | ||
| Peak time | ||
| System overshoot | ||
| Adjustment time |
| Piston Diameter | ||||||
|---|---|---|---|---|---|---|
| 50 | 64.52 | 0.331 | 0.0204 | 0.0498 | 33.2 | 0.166 |
| 55 | 70.97 | 0.249 | 0.0179 | 0.0469 | 44.4 | 0.199 |
| 63 | 81.29 | 0.165 | 0.0146 | 0.0378 | 58.7 | 0.283 |
| 70 | 90.32 | 0.121 | 0.0127 | 0.0348 | 68.2 | 0.355 |
| Parameter Name | Parameter | Unit |
|---|---|---|
| Hydraulic pump speed | 2100 | r/min |
| Hydraulic pump displacement | 35 | cc/rec |
| Relief valve operating pressure | 300 | bar |
| Solenoid valve operating current | 40 | mA |
| Piston diameter of hydraulic cylinder | 55 | mm |
| Stroke distance of hydraulic cylinder piston | 275 | mm |
| Single cylinder load mass | 600 | KG |
| Serial Number | Vehicle Speed 5 km/h | Height Setting 16 cm | ||||
|---|---|---|---|---|---|---|
| 15 cm | 16 cm | 17 cm | 5 km/h | 8 km/h | 11 km/h | |
| 1 | 15.79 | 16.81 | 16.55 | 15.66 | 16.28 | 15.50 |
| 2 | 14.77 | 15.98 | 17.61 | 16.71 | 15.29 | 15.69 |
| 3 | 15.11 | 16.95 | 17.81 | 16.26 | 15.03 | 15.51 |
| 4 | 15.38 | 16.54 | 17.47 | 16.99 | 15.16 | 17.84 |
| 5 | 15.49 | 15.63 | 16.72 | 15.93 | 15.86 | 14.28 |
| 6 | 15.49 | 15.81 | 17.12 | 16.89 | 16.98 | 15.37 |
| 7 | 14.83 | 16.09 | 17.82 | 15.97 | 16.06 | 14.18 |
| 8 | 15.79 | 15.92 | 17.80 | 16.21 | 16.68 | 16.90 |
| 9 | 15.85 | 15.94 | 17.30 | 16.53 | 16.74 | 16.90 |
| 10 | 15.87 | 15.58 | 17.28 | 15.82 | 16.58 | 17.82 |
| 11 | 15.85 | 16.04 | 16.73 | 16.68 | 16.49 | 16.30 |
| 12 | 15.22 | 16.61 | 17.85 | 16.82 | 16.13 | 16.26 |
| 13 | 14.92 | 16.11 | 17.80 | 16.28 | 15.76 | 16.97 |
| 14 | 15.95 | 16.33 | 17.68 | 15.52 | 16.81 | 16.44 |
| 15 | 15.92 | 16.13 | 17.68 | 15.89 | 15.70 | 16.80 |
| 16 | 14.85 | 15.59 | 17.68 | 15.74 | 16.81 | 14.38 |
| 17 | 14.94 | 15.75 | 17.67 | 15.55 | 15.62 | 15.77 |
| 18 | 15.56 | 16.96 | 16.50 | 15.92 | 16.13 | 15.28 |
| 19 | 15.52 | 16.59 | 16.52 | 16.33 | 15.20 | 16.57 |
| 20 | 15.44 | 16.17 | 17.26 | 16.47 | 15.00 | 14.97 |
| 6.79 | 4.26 | 6.85 | 4.86 | 8.08 | 22.04 | |
| Vehicle Speed (km/h) | Header Rise PWM Value | Header Down PWM Value |
|---|---|---|
| 5 | −0.865069 | 0.907017 |
| 8 | −0.894521 | 0.915443 |
| 11 | −0.931951 | 0.920679 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Wang, Z.; Shang, S.; Zhang, J.; Qing, Y.; Zha, X. The Design and Experimentation of EVPIVS-PID Harvesters’ Header Height Control System Based on Sensor Ground Profiling Monitoring. Agriculture 2022, 12, 282. https://doi.org/10.3390/agriculture12020282
Yang R, Wang Z, Shang S, Zhang J, Qing Y, Zha X. The Design and Experimentation of EVPIVS-PID Harvesters’ Header Height Control System Based on Sensor Ground Profiling Monitoring. Agriculture. 2022; 12(2):282. https://doi.org/10.3390/agriculture12020282
Chicago/Turabian StyleYang, Ranbing, Zhichao Wang, Shuqi Shang, Jian Zhang, Yiren Qing, and Xiantao Zha. 2022. "The Design and Experimentation of EVPIVS-PID Harvesters’ Header Height Control System Based on Sensor Ground Profiling Monitoring" Agriculture 12, no. 2: 282. https://doi.org/10.3390/agriculture12020282
APA StyleYang, R., Wang, Z., Shang, S., Zhang, J., Qing, Y., & Zha, X. (2022). The Design and Experimentation of EVPIVS-PID Harvesters’ Header Height Control System Based on Sensor Ground Profiling Monitoring. Agriculture, 12(2), 282. https://doi.org/10.3390/agriculture12020282






