Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico
Abstract
:1. Introduction
2. Materials and Methods
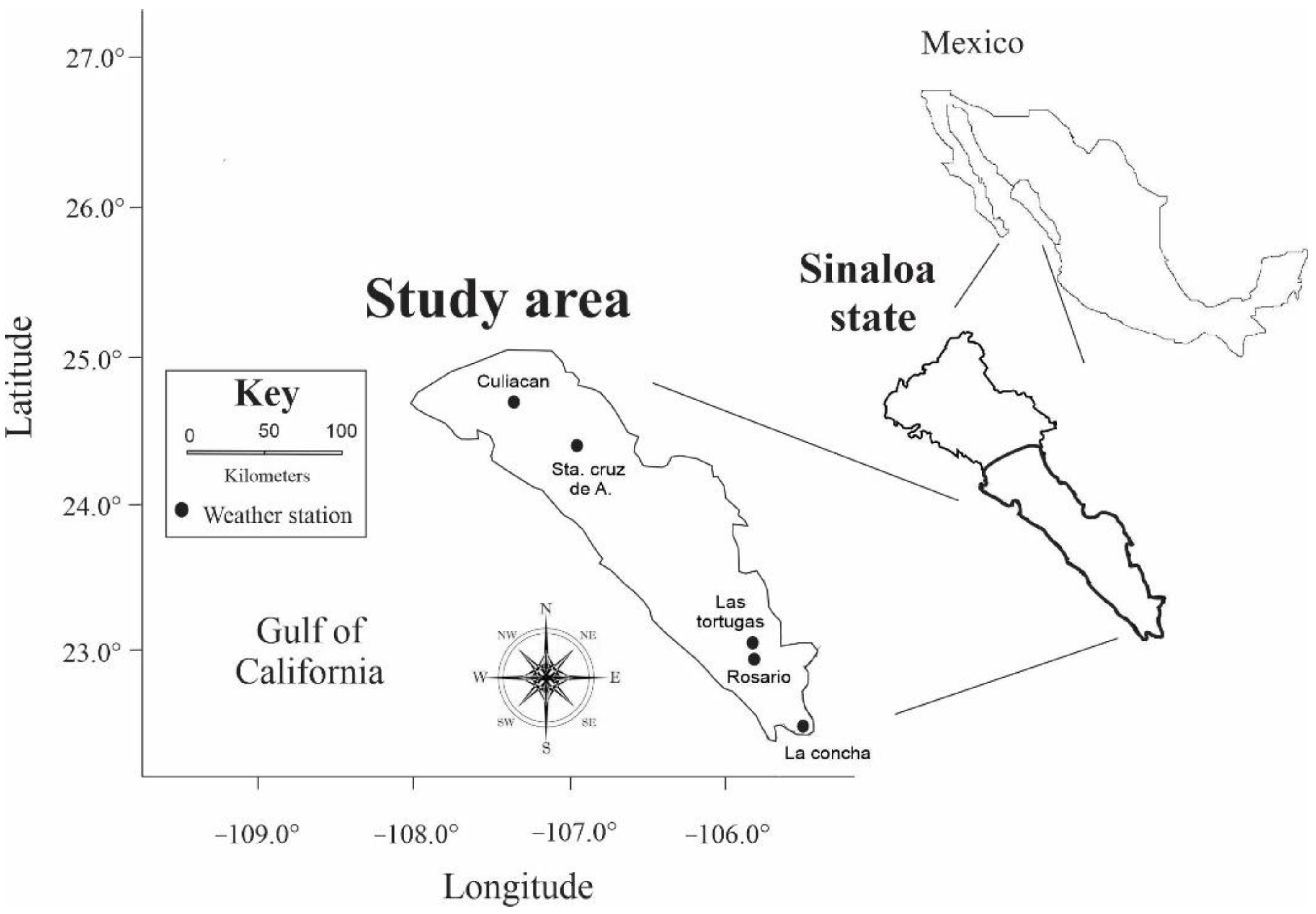
2.1. Study Area
2.2. Data
2.2.1. Precipitation (P), Maximum Temperature (Tmax) and Minimum Temperature (Tmin)
2.2.2. Observed Rainfed Corn Yield (RMYob)
2.3. Mathematical Expressions on Which the Indices of Meteorological Drought (MD) Are Based
2.3.1. Standardized Precipitation Index (SPI)
2.3.2. Agricultural Standardized Precipitation Index (aSPI)
2.3.3. Reconnaissance Drought Index (RDI)
2.3.4. Effective Reconnaissance Drought Index (eRDI)
2.4. Determination of Each of the Indices of Meteorological Drought (MD)
2.5. Z Normalization
2.6. Statistical Analysis
2.6.1. Normality, Correlation and Hypothesis Test between the SPI, aSPI, RDI, eRDI Indices and Observed Rainfed Maize Yield (RMYob)
2.6.2. Models for Predicted Rainfed Maize Yield (RMYpr)
2.6.3. Validation of the Prediction Models: Normality, Correlation and Hypothesis Testing for Observed Rainfed Maize Yield (RMYob) and Predicted Rainfed Maize Yield (RMYpr)
3. Results
3.1. Aridity Index (A.I.)
3.2. Statistical Analysis
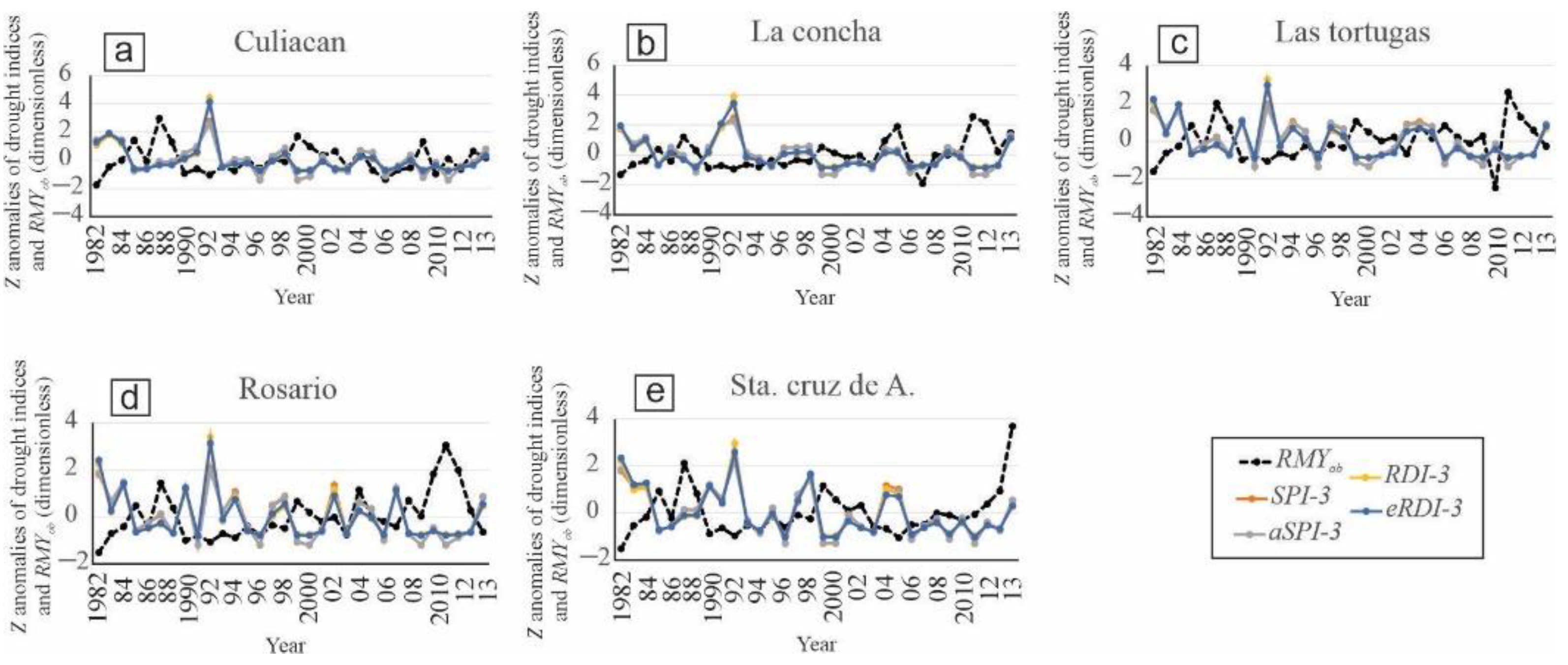
3.3. Variation of SPI-3, aSPI-3, RDI-3 and eRDI-3 Indices, and RMYob
3.4. Z Normalization
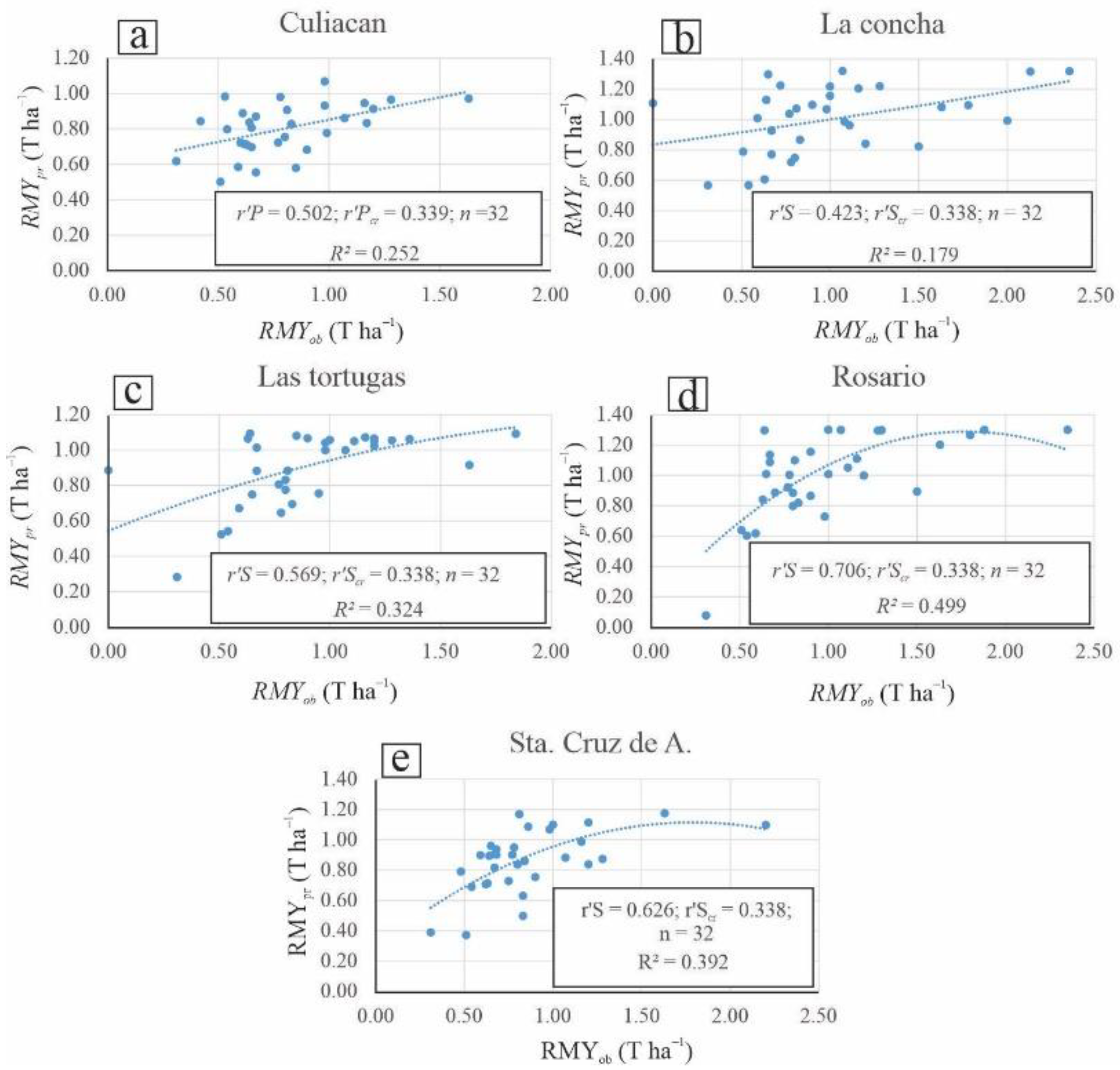
3.5. Models for Calculating Predicted Rainfed Maize Yield (RMYpr): Normality, Correlation and Hypothesis Test
4. Discussion
5. Conclusions
- The sensitivity of four indices of MD (SPI, aSPI, RDI and eRDI) is estimated to calculate RMYpr.
- The four drought indices are used with four reference periods and time steps of one month (January), two months (December–January), three months (November–January) and six months (August–January).
- The most sensitive models are for the Las Tortugas, Rosario and Sta. Cruz de A. weather stations, which include the aSPI and eRDI indices in their equations, with reference periods and time frames of one (January), two (December–January) and three months (November–January).
- In Sinaloa, it is of vital importance to calculate indices of MD in which effective P is included as the main parameter, mainly because these indices respond with greater sensitivity in arid and semi-arid conditions.
- At all five weather stations, the correlations between RMYob and RMYpr are significantly different from zero.
- It is recommended to apply these predictive models to each subregion (municipality) of southern Sinaloa, in order to have reliable early predictions, especially when it is desired to prevent severe socioeconomic damage in one of the Mexican states historically the most important for the production of rainfed maize.
- In future research, it is recommended to add more predictor variables (indices of meteorological drought or environmental variables) to try to increase the predictive capacity (R2) of the models. Some examples could be the standardized precipitation and evapotranspiration index, crop moisture index, Palmer drought severity index, minimum temperature and severe cold index.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ochieng, P.; Nyandega, I.; Wambua, B. Spatial-temporal analysis of historical and projected drought events over Isiolo County, Kenya. Theor. Appl. Climatol. 2022, 148, 531–550. [Google Scholar] [CrossRef]
- Bandak, S.; Movahedi, N.S.A.R.; Zeinali, E.; Bandak, I. Effects of superabsorbent polymer A200 on soil characteristics and rainfed winter wheat growth (Triticum aestivum L.). Arab. J. Geosci. 2021, 14, 712. [Google Scholar] [CrossRef]
- Naveen, P.S.; Anand, B.; Srivastava, S.K.; Kumar, N.R.; Sharma, S.; Bal, S.K.; Rao, K.V.; Prabhakar, M. Risk, perception and adaptation to climate change: Evidence from arid region, India. Nat. Hazards 2022, 1, 1–24. [Google Scholar] [CrossRef]
- He, H.; Wu, Z.; Li, D.; Zhang, T.; Pan, F.; Yuan, H.; Jiang, S.; Shi, Z.; Yang, S.; Wang, F. Characteristics of winter wheat evapotranspiration in Eastern China and comparative evaluation of applicability of different reference evapotranspiration models. J. Soil. Sci. Plant Nutr. 2022. [Google Scholar] [CrossRef]
- Núñez, L.J.M.; Cansino, L.B.; Sanchez, Z.X.G.; Ponce, O.J.M. Involving resilience in assessment of the water–energy–food nexus for arid and semiarid regions. Clean. Techn. Environ. Policy 2022. [Google Scholar] [CrossRef]
- Topçu, E.; Seçkin, N.; Açanal, H.N. Drought analyses of Eastern Mediterranean, Seyhan, Ceyhan, and Asi Basins by using aggregate drought index (ADI). Theor. Appl. Climatol. 2022, 147, 909–924. [Google Scholar] [CrossRef]
- Martínez, S.A.R.; Villanueva, D.J.; Correa, D.A.; Estrada, Á.J.; Trucíos, C.R.; Estrada, A.J.R.; Cardoza, M.G.F.; Garza, M.M.Á. Dendroclimatic reconstruction of precipitation and temperature for the Mayo River basin in northwestern Mexico. Trees 2022. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Wang, L.; Li, L.; Xu, B. The scenario simulations and several problems of the Sponge City construction in semi-arid loess region, Northwest China. Landscape Ecol. Eng. 2022, 18, 95–108. [Google Scholar] [CrossRef]
- Secretaría de Agricultura, Ganadería, Desarrollo Rural, Pesca y Alimentación (SAGARPA). Agenda Técnica Agrícola de Sinaloa, Segunda Edición; SAGARPA: Mexico City, Mexico, 2015; p. 242.
- Ojeda, B.W. Evaluación del impacto del cambio climático en la productividad de la agricultura de riego y temporal del estado de Sinaloa. Inf. Final. De Proy. De Investig. 2010, 45, 393. [Google Scholar]
- Tigkas, D.; Tsakiris, G. Early estimation of drought impacts on rainfed wheat yield in mediterranean climate. Environ. Process. 2015, 2, 97–114. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, A.C.C.; Neale, M.U.C.; Mekonnen, M.M.; Goncalves, Z.I.; Oliveira, G.; Álvarez, R.O.; Safa, B.; Rowe, M.C. Trends o extreme air temperature and precipitation and their impact on corn and soybean yileds in Nebraska, USA. Theor. Appl. Climatol. 2022, 147, 1379–1399. [Google Scholar] [CrossRef]
- Ozturk, A.; Erdem, E.; Aydin, M.; Murat, K.M. The effects of drought after anthesis on the grain quality of bread wheat depend on drought severity and drought resistance of the variety. Cereal Res. Commun. 2022, 50, 105–116. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. DrinC: A software for drought analysis based on drought indices. Earth. Sci. Inform. 2015, 8, 697–709. [Google Scholar] [CrossRef]
- Figueroa, S.C. Modelo de Regresión No Lineal. S.l. Bachelor’s Thesis, Instituto Politécnico Nacional, Universidad de Buenos Aires, Buenos Aires, Argentina, 2013; 51p. [Google Scholar]
- Zuluaga, G.O.A.; Patiño, Q.J.E.; Valencia, H.G.M. Modelos implementados en el análisis de series de tiempo de temperatura superficial e índices de vegetación: Una propuesta taxonómica en el contexto de cambio climático global. Rev. Geog. Nor. Gran. 2021, 78, 323–344. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Y. Cooling load prediction and optimal operation of HVAC systems using a multiple nonlinear regression model. Ener. Build. 2019, 197, 7–17. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Zhang, J.; Tan, X.; Ali, R.M.; Ma, J.; Zhu, Y.; Yang, F.; Yang, W. Assessing canopy nitrogen and carbon content in maize by canopy spectral reflectance and uninformative variable elimination. Crop. J. 2022. [Google Scholar] [CrossRef]
- Mekuria, G.; Legesse, A.; Mohammed, Y. Socioeconomic vulnerability of pastoralism under spatiotemporal patterns of drought in Eastern Africa. Arab. J. Geosci. 2021, 14, 2654. [Google Scholar] [CrossRef]
- Ilyas, A.M.; Elahi, E.; Chand, R.; Zhu, D.; Muhammad, J.; Rafique, D.M.; Majid, S.A.; Ali, K.M. Estimation of a trend of meteorological and hydrological drought over Qinhuai River Basin. Theor. Appl. Climatol. 2022, 147, 1065–1078. [Google Scholar] [CrossRef]
- McKee, T.B.; Doeskin, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–184. [Google Scholar]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought characterisation based on an agriculture-oriented standardised precipitation index. Theor. Appl. Climatol. 2019, 135, 1435–1447. [Google Scholar] [CrossRef]
- Mirakbari, M.; Ebrahimi, K.Z. Evaluation of the climate change effects on the future drought characteristics of Iranian wetlands. Arab. J. Geosci. 2021, 14, 2167. [Google Scholar] [CrossRef]
- Rassoul, Z.A.; Mehdi, M.M.; Bahrami, M. Comparison of reconnaissance drought index (RDI) and effective reconnaissance drought index (eRDI) to evaluate drought severity. Sustain. Water Resour. Manag. 2019, 5, 1345–1356. [Google Scholar] [CrossRef]
- Tsakiris, G. Meteorological Drought Assessment, Paper Prepared for the Needs of the European Research Program MEDROPLAN; Mediterranean Drought Preparedness and Mitigation Planning: Zaragoza, Spain, 2004. [Google Scholar]
- Tsakiris, G.; Loukas, A.; Pangalou, D.; Vangelis, H.; Tigkas, D.; Rossi, G.; Cancelliere, A. Drought characterization [Part 1. Components of drought planning. 1. 3. Methodological component]. In Drought Management Guidelines Technical Nnex; Iglesias, A., Moneo, M., López-Francos, A., Eds.; CIHEAM/EC MED A Water: Zaragoza, Spain, 2007; pp. 85–102. [Google Scholar]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Introducing a modified reconnaissance drought index (RDIe). Proced. Eng. 2016, 162, 332–339. [Google Scholar] [CrossRef] [Green Version]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. An enhanced effective reconnaissance drought index for the characterisation of agricultural drought. Environ. Process. 2017, 4 (Suppl. S1), S137–S148. [Google Scholar] [CrossRef]
- Ben, O.D.; Abida, H. Monitoring and mapping of drought in a semi-arid region: Case of the Merguellil watershed, central Tunisia. Environ. Monit. Assess. 2022, 194, 287. [Google Scholar] [CrossRef]
- Syed, F.S.; Adnan, S.; Zamreeq, A.; Ghulam, A. Identification of droughts over Saudi Arabia and global teleconnections. Nat. Haz. 2022. [Google Scholar] [CrossRef]
- Donovan, J.; Rutsaert, P.; Domínguez, C.; Peña, M. Capacities of local maize seed enterprises in Mexico: Implications for seed systems development. Food Sec. 2022, 1, 1–21. [Google Scholar] [CrossRef]
- Norzagaray, C.M.; Llanes, C.O.; Gaxiola, A.; González, G.G.E. Meteorological interaction between drought/oceanic indicators and rainfed maize yield in an arid agricultural zone in northwest Mexico. Arab. J. Geosci. 2020, 13, 131. [Google Scholar] [CrossRef]
- Bruno, F.C. La Paradoja de la Economía Sinaloense en la Globalización: Inseguridad Alimentaria en el Granero de México, 1994–2014. Master’s Thesis, Universidad Autónoma de Nayarit, Tepique, Mexico, 2016; p. 148. [Google Scholar]
- Morales, Z.F. El Impacto de la Biotecnología en la Formación de Redes Institucionales en el Sector Hortofrutícola de Sinaloa, México. Ph.D. Thesis, Universidad de Barcelona, Barcelona, Spain, 2007; p. 441. [Google Scholar]
- Llanes, C.O.; Norzagaray, C.M.; Gaxiola, A.; González, G.G.E. Regional precipitation teleconnected with PDO-AMO-ENSO in northern Mexico. Theor. Appl. Climatol. 2020, 140, 667–681. [Google Scholar] [CrossRef]
- Base de Datos del CLICOM. Available online: http://clicom-mex.cicese.mx/mapa.html (accessed on 31 December 2021).
- Lo Presti, R.; Barca, E.; Passarella, G. A methodology for treating missing data applied to daily rainfall data in the Candelaria River Basin (Italy). Environ. Monit. Assess. 2010, 160, 1–22. [Google Scholar] [CrossRef]
- Johnson, M. Lose Something? Ways to Find Your Missing Data. In Proceedings of the Houston Center for Quality of Care and Utilization Studies Professional Development Series, 17 September 2003. professional development seminar series. [Google Scholar]
- Aieb, A.; Madani, K.; Scarpa, M.; Bonaccorso, B.; Lefsih, K. A new approach for processing climate missing databases applied to daily rainfall data in Soummam watershed, Algeria. Heliyon 2019, 5, e01247. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Agriculture, Livestock, Rural Development, Fisheries and Food (SAGARPA) and Agri-Food and Fishing Information Service (SIAP). Available online: http://infosiap.siap.gob.mx/aagricola_siap_gb/ientidad/index.jsp (accessed on 12 December 2021).
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- UNEP (United Nations Environmental Programme). World Atlas of Desertification; United Nations: New York, NY, USA, 1992. [Google Scholar]
- Ogurinde, A.T.; Emmanuel, I.; Enaboifo, M.A.; Adedayo, A.T.; Bao, P.Q. Spatio-temporal calibration of Hargreaves–Samani model in the Northern Region of Nigeria. Theor. Appl. Climatol. 2022, 147, 1213–1228. [Google Scholar] [CrossRef]
- Bahmani, S.; Salimi, H.; Sanikhani, H. Spatiotemporal analysis of aridity indices by using the nonparametric methods (case study: Sirvan river basin, Kurdistan Province, Iran). Arab. J. Geosci. 2021, 14, 2034. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Dokou, Z.; Karatzas, G.P. Statistical Analysis and ANN modeling for predicting hydrological extremes under climate change scenarios. The example of a small mediterranean agro-watershed. J. Environ. Manag. 2015, 154, 86–101. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D. Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region. Atmosphere 2020, 11, 554. [Google Scholar] [CrossRef]
- Potopová, V.; Tűrkott, L.; Musiolková, M.; Možný, M.; Lhotka, O. The compound nature of soil temperature anomalies at various depths in the Czech Republic. Theor. Appl. Climatol. 2021, 146, 1257–1275. [Google Scholar] [CrossRef]
- Aliyar, Q.; Dhungana, S.; Shrestha, S. Spatio-temporal trend mapping of precipitation and its extremes across Afghanistan (1951–2010). Theor. Appl. Climatol. 2022, 147, 605–626. [Google Scholar] [CrossRef]
- Weathington, B.L.; Cunningham, C.J.L.; Pittenger, D.J. Understanding Business Research: Appendix B: Statistical Tables; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 435–483. [Google Scholar] [CrossRef]
- Reza, T.I.A.; Alam, N.I.; Hasanuzzaman, M.; Bozlar, R.M.; Elbeltagi, A.; Mallick, J.; Techato, K.; Chandra, P.S.; Mostafizur, R.M. Variability of climate-induced rice yields in northwest Bangladesh using multiple statistical modeling. Theor. Appl. Climatol. 2022, 147, 1263–1276. [Google Scholar] [CrossRef]
- Secretaría de Medio Ambiente y Recursos Naturales (SEMARNAT). Plan Estatal de Cambio Climático de Sinaloa (PECCSIN); SEMARNAT: Mexico City, Mexico, 2016; p. 183.
- Velasco, I.; Pimentel, E. Zonificación agroclimática de Papadakis aplicada al estado de Sinaloa, México. Investig. Geográficas. Bol. Inst. Geog. 2010, 73, 86–102. [Google Scholar]
- Wei, C.; Guo, B.; Zhang, H.; Han, B.; Li, X.; Zhao, H.; Lu, Y.; Meng, C.; Huang, X.; Zang, W.; et al. Spatial–temporal evolution pattern and prediction analysis of flood disasters in China in recent 500 years. Earth Sci. Inform. 2022, 15, 265–279. [Google Scholar] [CrossRef]
- Nemati, A.; Ghoreishi, N.S.H.; Joodaki, G.; Mousavi, N.S.S. Spatiotemporal Drought Characterization Using Gravity Recovery and Climate Experiment (GRACE) in the Central Plateau Catchment of Iran. Environ. Process. 2020, 7, 135–157. [Google Scholar] [CrossRef]
- Ramírez, B.V.H.; Jaramillo, R.Á. Relación entre el índice oceánico de el niño y la lluvia, en la región andina central de Colombia. Cenicafé 2009, 60, 161–172. [Google Scholar]
- Lavín, M.F.; Palacios, H.E.; Cabrera, C. Sea surface temperature anomalies in the Gulf of California. Geof. Int. 2003, 42, 363–375. [Google Scholar]
- Arriaga, D.A.A. Identificar Patrones de Precipitación en la CDMX en Períodos de Lluvia o Sequía, Asociados con los Índices de los Fenómenos ENSO, AMO, NAO y PDO en los años de 1951 al 2007. Bachelor’s Thesis, Instituto Politécnico Nacional, Ciudad de Mexico, Mexico, 2019; p. 150. [Google Scholar]
- Llanes, C.O.; Gaxiola, H.A.; Estrella, G.R.D.; Norzagaray, C.M.; Troyo, D.E.; Pérez, G.E.; Ruiz, G.R.; Pellegrini, C.M.J. Variabiity and factors of influence of extreme wet and dry events in northern Mexico. Atmosphere 2018, 9, 122. [Google Scholar] [CrossRef] [Green Version]


| SPI, aSPI, RDI and eRDI (Dimensionless) | Category |
|---|---|
| ≥2.00 | Extremely wet |
| 1.5 to 1.99 | Severely wet |
| 1.0 to 1.49 | Moderately wet |
| 0.0 to 0.99 | Mildly wet |
| 0.0 to −0.99 | Mild drought |
| −1.00 to −1.49 | Moderate drought |
| −1.50 to −1.99 | Severe drought |
| ≤−2.00 | Extreme drought |
| Weather Station | ||||||
|---|---|---|---|---|---|---|
| Climate Indicator | Statistical Inference | Culiacan | La Concha | Las Tortugas | Rosario | Sta. Cruz de A. |
| P (mm year−1) | Average | 681.85 | 1027.97 | 913.59 | 898.34 | 783.06 |
| Max | 1180.70 | 1623.10 | 1606.30 | 1337.30 | 1254.58 | |
| Min | 445.95 | 584.56 | 536.40 | 607.04 | 354.88 | |
| Tmax (°C year−1) | Average | 33.28 | 32.73 | 33.44 | 32.45 | 32.97 |
| Max | 35.30 | 35.18 | 35.26 | 33.41 | 34.48 | |
| Min | 31.63 | 26.44 | 31.11 | 30.54 | 31.83 | |
| Tmin (°C year−1) | Average | 18.36 | 18.76 | 16.51 | 18.74 | 17.45 |
| Max | 21.10 | 20.82 | 18.54 | 19.81 | 18.97 | |
| Min | 16.30 | 15.29 | 14.77 | 17.45 | 15.21 | |
| PET (mm year−1) | Average | 1890.59 | 1845.52 | 1965.37 | 1807.18 | 1899.39 |
| Max | 2066.29 | 1987.68 | 2075.08 | 1891.61 | 2067.52 | |
| Min | 1789.37 | 1435.05 | 1757.29 | 1595.92 | 1770.32 | |
| A.I. (dimensionless) | Average | 0.36 | 0.56 | 0.46 | 0.50 | 0.41 |
| Drought Index with Reference Period and Time Frame | Weather Station | ||||
|---|---|---|---|---|---|
| Culiacán | La Concha | Las Tortugas | Rosario | Sta. Cruz de A. | |
| SPI-1 (January) | −0.124 | −0.304 | −0.301 | −0.348 | −0.397 |
| SPI-2 (December–January) | −0.103 | −0.322 | −0.248 | −0.309 | −0.328 |
| SPI-3 (November–January) | −0.344 | −0.421 | −0.453 | −0.460 | −0.387 |
| SPI-6 (August–January) | −0.268 | 0.110 | 0.128 | 0.141 | −0.201 |
| aSPI-1 (January) | −0.124 | −0.304 | −0.301 | −0.348 | −0.397 |
| aSPI-2 (December–January) | −0.112 | −0.324 | −0.253 | −0.314 | −0.333 |
| aSPI-3 (November–January | −0.347 | −0.427 | −0.475 | −0.468 | −0.381 |
| aSPI-6 (August–January) | −0.229 | −0.238 | −0.021 | −0.199 | −0.281 |
| RDI-1 (January) | −0.134 | −0.288 | −0.305 | −0.348 | −0.395 |
| RDI-2 (December–January) | −0.103 | −0.323 | −0.270 | −0.319 | −0.329 |
| RDI-3 (November–January) | −0.311 | −0.381 | −0.480 | −0.448 | −0.385 |
| RDI-6 (August–January) | −0.257 | 0.148 | 0.097 | 0.147 | −0.273 |
| eRDI−1 (January) | −0.134 | −0.288 | −0.305 | −0.348 | −0.395 |
| eRDI-2 (December–January) | −0.112 | −0.321 | −0.270 | −0.319 | −0.331 |
| eRDI-3 (November–January) | −0.312 | −0.408 | −0.474 | −0.461 | −0.376 |
| eRDI-6 (August–January) | −0.221 | −0.191 | −0.049 | −0.166 | −0.292 |
| r’Scr = |0.338|; n = 32 | Bold = significant correlation | ||||
| r’P cr = |0.339|; n = 32 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omar, L.-C.; Mariano, N.-C.; Alberto, G.; Ernestina, P.-G.; Jorge, M.-M.; Enrique, T.-D. Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico. Agriculture 2022, 12, 525. https://doi.org/10.3390/agriculture12040525
Omar L-C, Mariano N-C, Alberto G, Ernestina P-G, Jorge M-M, Enrique T-D. Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico. Agriculture. 2022; 12(4):525. https://doi.org/10.3390/agriculture12040525
Chicago/Turabian StyleOmar, Llanes-Cárdenas, Norzagaray-Campos Mariano, Gaxiola Alberto, Pérez-González Ernestina, Montiel-Montoya Jorge, and Troyo-Diéguez Enrique. 2022. "Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico" Agriculture 12, no. 4: 525. https://doi.org/10.3390/agriculture12040525
APA StyleOmar, L.-C., Mariano, N.-C., Alberto, G., Ernestina, P.-G., Jorge, M.-M., & Enrique, T.-D. (2022). Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico. Agriculture, 12(4), 525. https://doi.org/10.3390/agriculture12040525








