RZWQM2 Simulated Drip Fertigation Management to Improve Water and Nitrogen Use Efficiency of Maize in a Solar Greenhouse
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Modeling
2.2.1. RZWQM2 Description
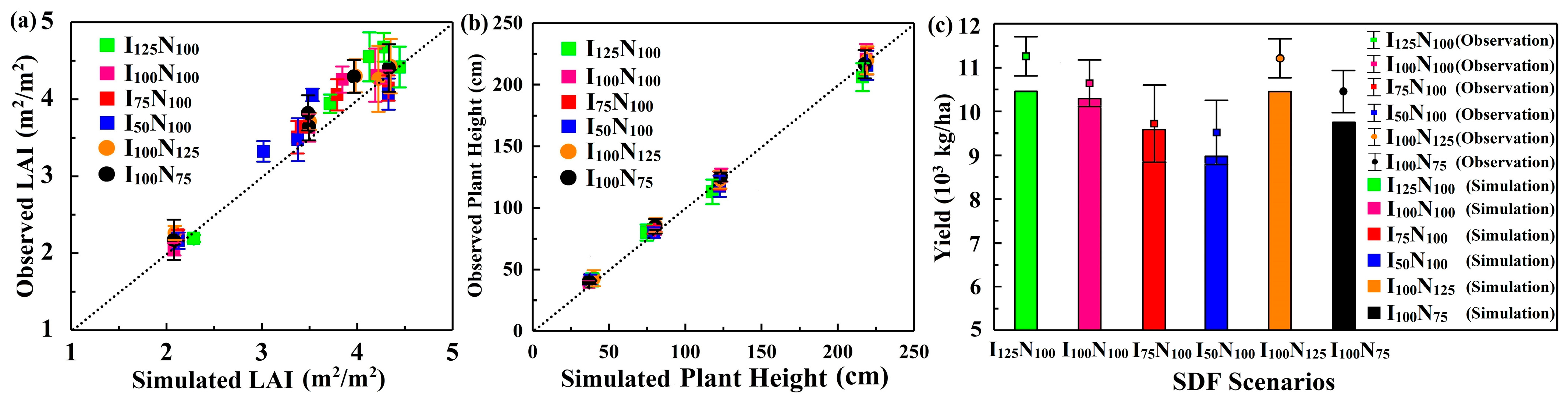
2.2.2. Model Calibration and Validation
2.2.3. Model Accuracy Statistics
2.2.4. Quantification of Surface Drip Fertigation Management Effects using RZWQM
3. Results and Discussion
3.1. Soil Volumetric Water Content and Crop Growth
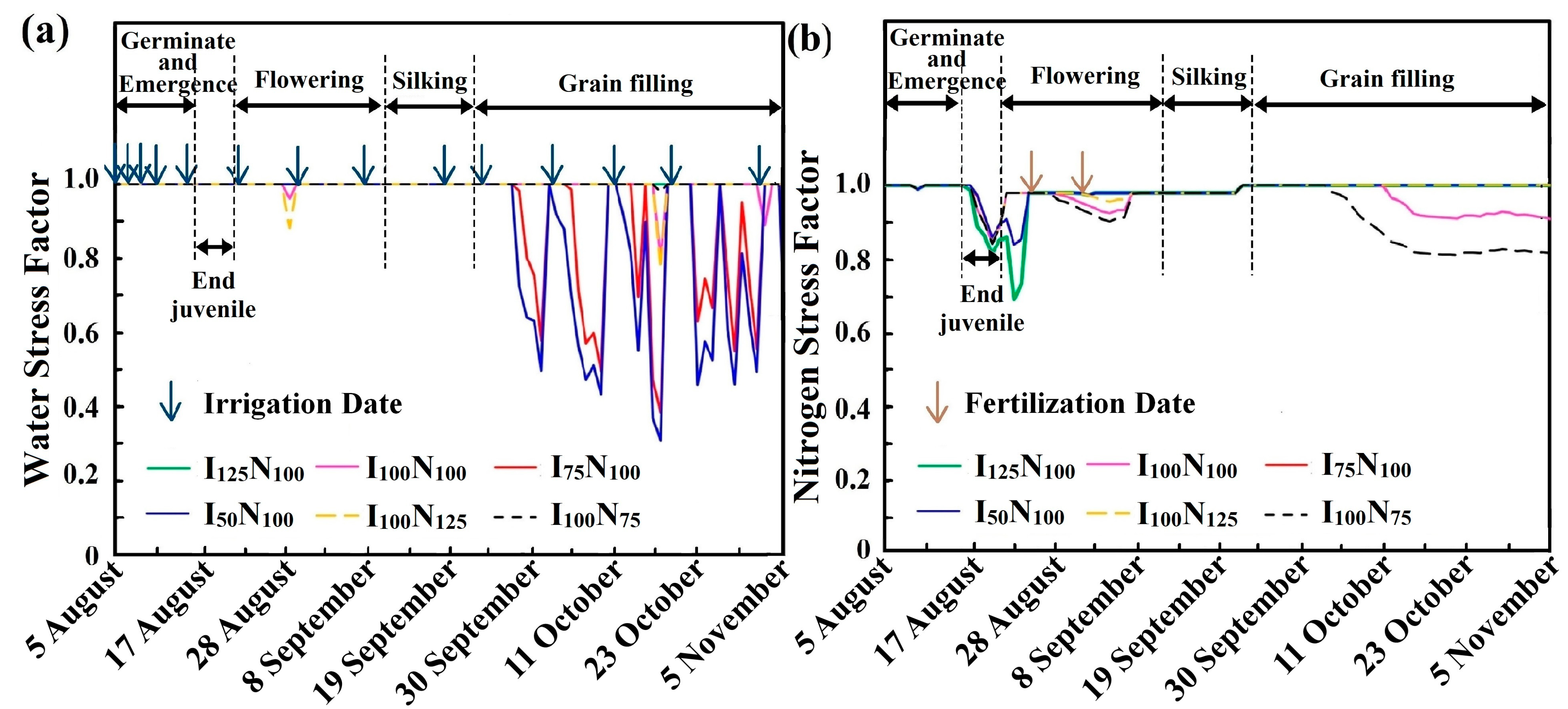
3.2. Water and N Stress Factors Simulation
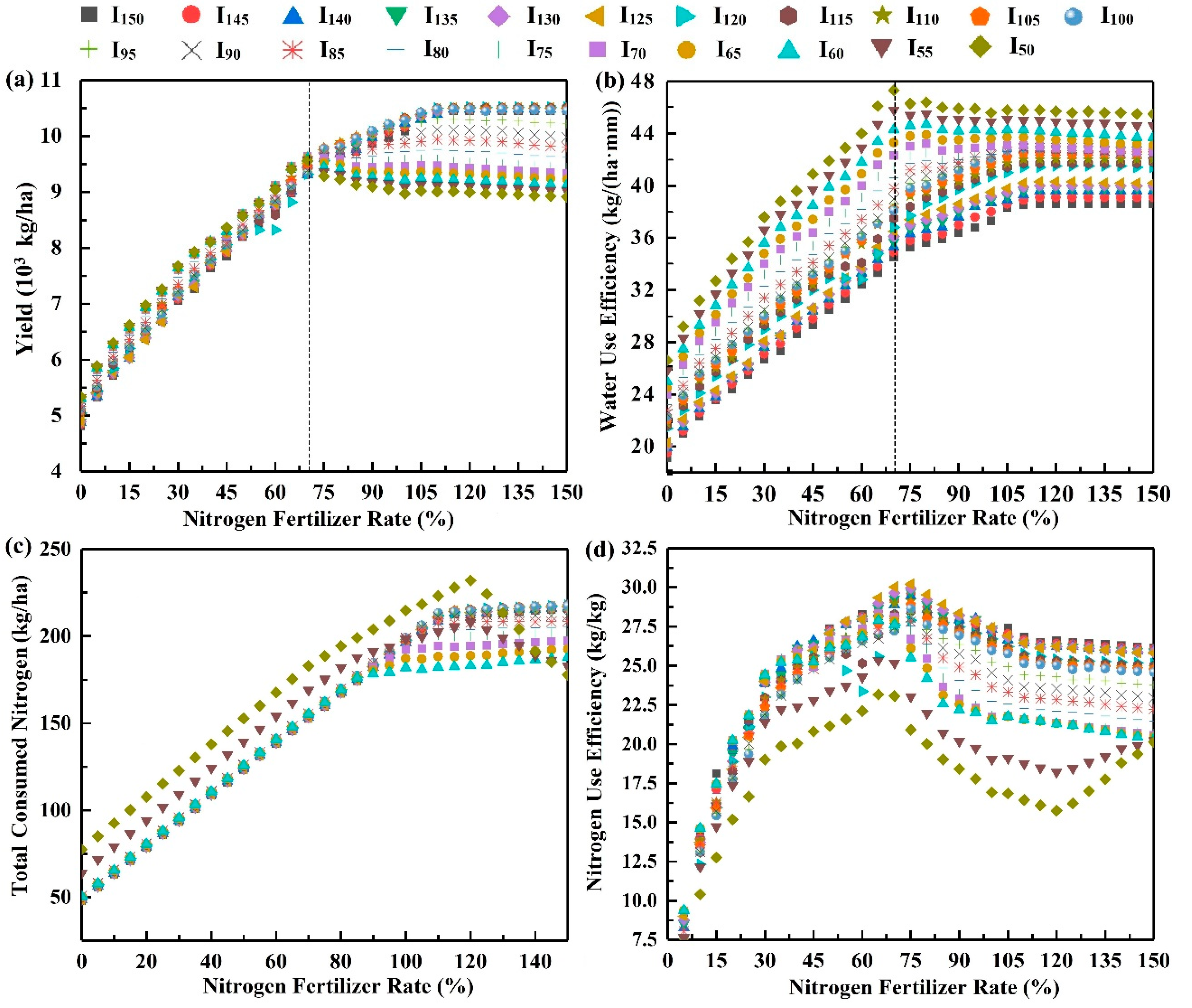
3.3. Quantification of Grain Yield, Water and Nitrogen Use Efficiency under the Influence of Surface Drip Fertigation Managements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosa, L.; Chiarelli, D.D.; Rulli, M.C.; Dell’Angelo, J.; D’Odorico, P. Global agricultural economic water scarcity. Sci. Adv. 2020, 6, eaaz6031. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Wu, J.; Wang, Q.; Lei, T.; He, B.; Li, X.; Mo, X.; Luo, H.; Zhou, H.; Lu, D. Agricultural drought hazard analysis during 1980–2008: A global perspective. Int. J. Climatol. 2016, 36, 389–399. [Google Scholar] [CrossRef]
- Giroto, A.S.; Guimarães, G.G.; Foschini, M.; Ribeiro, C. Role of slow-release nanocomposite fertilizers on nitrogen and phosphate availability in soil. Sci. Rep. 2017, 7, 46032. [Google Scholar] [CrossRef] [PubMed]
- Tarafder, C.; Daizy, M.; Alam, M.M.; Ali, M.R.; Islam, M.J.; Islam, R.; Ahommed, M.S.; Aly, M.A.S.; Khan, M.Z.H. Formulation of a hybrid nanofertilizer for slow and sustainable release of micronutrients. ACS Omega 2020, 5, 23960–23966. [Google Scholar] [CrossRef] [PubMed]
- Xin, X.; Judy, J.D.; Sumerlin, B.B.; He, Z. Nano-enabled agriculture: From nanoparticles to smart nanodelivery systems. Environ. Chem. 2020, 17, 413–425. [Google Scholar] [CrossRef]
- Ayars, J.; Phene, C.; Hutmacher, R.; Davis, K.; Schoneman, R.; Vail, S.; Mead, R.M. Subsurface drip irrigation of row crops: A review of 15 years of research at the Water Management Research Laboratory. Agric. Water Manag. 1999, 42, 1–27. [Google Scholar] [CrossRef]
- Tian, D.; Zhang, Y.; Mu, Y.; Zhou, Y.; Zhang, C.; Liu, J. The effect of drip irrigation and drip fertigation on N2O and NO emissions, water saving and grain yields in a maize field in the North China Plain. Sci. Total Environ. 2017, 575, 1034–1040. [Google Scholar] [CrossRef] [PubMed]
- Lamm, F.R. Cotton, tomato, corn, and onion production with subsurface drip irrigation: A review. Trans. ASABE 2016, 59, 263–278. [Google Scholar]
- Jensen, C.; Ørum, J.; Pedersen, S.; Andersen, M.; Plauborg, F.; Liu, F.; Jacobsen, S.E. A short overview of measures for securing water resources for irrigated crop production. J. Agron. Crop Sci. 2014, 200, 333–343. [Google Scholar] [CrossRef]
- Sandhu, O.; Gupta, R.; Thind, H.; Jat, M.; Sidhu, H. Drip irrigation and nitrogen management for improving crop yields, nitrogen use efficiency and water productivity of maize-wheat system on permanent beds in north-west India. Agric. Water Manag. 2019, 219, 19–26. [Google Scholar] [CrossRef]
- Zhou, B.; Sun, X.; Ding, Z.; Ma, W.; Zhao, M. Multisplit nitrogen application via drip irrigation improves maize grain yield and nitrogen use efficiency. Crop Sci. 2017, 57, 1687–1703. [Google Scholar] [CrossRef] [Green Version]
- Stanley, C.D.; Toor, G. Florida commercial horticultural production: Constraints limiting water and nutrient use efficiency. Horttechnology 2010, 20, 89–93. [Google Scholar] [CrossRef] [Green Version]
- Greaves, G.E.; Wang, Y.M. Effect of regulated deficit irrigation scheduling on water use of corn in southern Taiwan tropical environment. Agric. Water Manag. 2017, 188, 115–125. [Google Scholar] [CrossRef]
- Mottes, C.; Lesueur-Jannoyer, M.; Le Bail, M.; Malézieux, E. Pesticide transfer models in crop and watershed systems: A review. Agron. Sustain. Dev. 2014, 34, 229–250. [Google Scholar] [CrossRef]
- Tenreiro, T.R.; García-Vila, M.; Gómez, J.A.; Jimenez-Berni, J.A.; Fereres, E. Water modelling approaches and opportunities to simulate spatial water variations at crop field level. Agric. Water Manag. 2020, 240, 106254. [Google Scholar] [CrossRef]
- Rötter, R.; Appiah, M.; Fichtler, E.; Kersebaum, K.; Trnka, M.; Hoffmann, M. Linking modelling and experimentation to better capture crop impacts of agroclimatic extremes—A review. Field Crop Res. 2018, 221, 142–156. [Google Scholar] [CrossRef]
- Ahuja, L.; Rojas, K.; Hanson, J.D. Root Zone Water Quality Model: Modelling Management Effects on Water Quality and Crop Production; Water Resources Publications: Littleton, CO, USA, 2000; pp. 300–384. [Google Scholar]
- Qi, Z.; Ma, L.; Bausch, W.C.; Trout, T.J.; Ahuja, L.R.; Flerchinger, G.N.; Fang, Q. Simulating maize production, water and surface energy balance, canopy temperature, and water stress under full and deficit irrigation. Trans. ASABE 2016, 59, 623–633. [Google Scholar]
- Gu, Z.; Qi, Z.; Ma, L.; Gui, D.; Xu, J.; Fang, Q.; Yuan, S.; Feng, G. Development of an irrigation scheduling software based on model predicted crop water stress. Comput. Electron. Agric. 2017, 143, 208–221. [Google Scholar] [CrossRef]
- Chen, X.; Qi, Z.; Gui, D.; Gu, Z.; Ma, L.; Zeng, F.; Li, L.; Sima, M.W. A model-based real-time decision support system for irrigation scheduling to improve water productivity. Agronomy 2019, 9, 686. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.H.; Ma, L.W.; Douglas, M.K.R.; Han, M.; Trout, T.J. Modeling maize production under growth stage-based deficit irrigation management with RZWQM2. Agric. Water Manag. 2021, 248, 106767. [Google Scholar] [CrossRef]
- Fang, Q.X.; Ma, L.W.; Ahuja, L.R.; Trout, T.J.; Malone, R.; Zhang, H.H.; Gui, D.W.; Yu, Q. Long-term simulation of growth stage-based irrigation scheduling in maize under various water constraints in Colorado, USA. Front. Agric. Sci. Eng. 2017, 4, 172–184. [Google Scholar] [CrossRef]
- Chen, X.P.; Qi, Z.M.; Gui, D.W.; Sima, M.W.; Zeng, F.J.; Li, L.H.; Li, X.Y.; Gu, Z. Evaluation of a new irrigation decision support system in improving cotton yield and water productivity in an arid climate. Agric. Water Manag. 2020, 234, 106139. [Google Scholar] [CrossRef]
- Imakumbili, M.L.E.; Semu, E.; Semoka, J.M.R.; Abass, A.; Mkamilo, G. Managing cassava growth on nutrient poor soils under different water stress conditions. Heliyon 2021, 7, e07331. [Google Scholar] [CrossRef] [PubMed]
- Suman, S.; Spehia, R.; Sharma, V. Humic acid improved efficiency of fertigation and productivity of tomato. J. Plant Nutr. 2017, 40, 439–446. [Google Scholar] [CrossRef]
- Abdalhi, M.A.; Cheng, J.; Feng, S.; Yi, G. Performance of drip irrigation and nitrogen fertilizer in irrigation water saving and nitrogen use efficiency for waxy maize (Zea mays L.) and cucumber (Cucumis sativus L.) under solar greenhouse. Grassl. Sci. 2016, 62, 174–187. [Google Scholar] [CrossRef]
- Chuanyan, Z.; Zhongren, N. Estimating water needs of maize (Zea mays L.) using the dual crop coefficient method in the arid region of northwestern China. Afr. J. Agric. Res. 2007, 2, 325–333. [Google Scholar]
- Shrestha, S.; Manandhar, B. Evaluation of the Root Zone Water Quality Model (RZWQM) using field-measured data from the tropical zone, Thailand. Water Air Soil Poll. 2014, 225, 1–14. [Google Scholar] [CrossRef]
- Ahmed, I.; Rudra, R.; McKague, K.; Gharabaghi, B.; Ogilvie, J. Evaluation of the Root Zone Water Quality Model (RZWQM) for Southern Ontario: Part II. Simulating long-term effects of nitrogen management practices on crop yield and subsurface drainage water quality. Water Qual. Res. J. 2007, 42, 219–230. [Google Scholar] [CrossRef]
- Saseendran, S.A.; Trout, T.J.; Ahuja, L.R.; Ma, L.; McMaster, G.S.; Nielsen, D.C.; Andales, A.A.; Chavez, J.L.; Ham, J. Quantifying crop water stress factors from soil water measurements in a limited irrigation experiment. Agric. Syst. 2015, 137, 191–205. [Google Scholar] [CrossRef]
- Hanson, J.D.; Rojas, K.; Shaffer, M.J. Calibrating the root zone water quality model. Agron. J. 1999, 91, 171–177. [Google Scholar] [CrossRef]
- Ma, L.; Ahuja, L.; Nolan, B.; Malone, R.; Trout, T.; Qi, Z. Root zone water quality model (RZWQM2): Model use, calibration, and validation. Trans. ASABE 2012, 55, 1425–1446. [Google Scholar] [CrossRef]
- Cheng, H.; Shu, K.; Qi, Z.; Ma, L.; Jin, V.L.; Li, Y.; Schmer, M.R.; Wienhold, B.J.; Feng, S. Effects of residue removal and tillage on greenhouse gas emissions in continuous corn systems as simulated with RZWQM2. J. Environ. Manag. 2021, 285, 112097. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, H.F.E.; de Moura Campos, H.; Mesquita, M.; Machado, R.L.; Vale, L.S.R.; Siqueira, A.P.S.; Ferrarezi, R.S. Horticultural Performance of Greenhouse Cherry Tomatoes Irrigated Automatically Based on Soil Moisture Sensor Readings. Water 2021, 13, 2662. [Google Scholar] [CrossRef]
- Smagin, A.; Khakimova, G.; Khineeva, D.; Sadovnikova, N. Gravity factor of the formation of the field and capillary water capacities in soils and artificial layered soil-like bodies. Eurasian Soil Sci. 2008, 41, 1189–1197. [Google Scholar] [CrossRef]
- Krapfl, K.J.; Hatten, J.A.; Roberts, S.D.; Baldwin, B.S.; Rousseau, R.J.; Shankle, M.W. Soil Properties, Nitrogen Status, and Switchgrass Productivity in a Biochar-Amended Silty Clay Loam. Soil Sci. Soc. Am. J. 2014, 78, S136–S145. [Google Scholar] [CrossRef]
- Li, Y.; Shao, X.; Li, D.; Xiao, M.; Hu, X.; He, J. Effects of water and nitrogen coupling on growth, physiology and yield of rice. Int. J. Agric. Biol. Eng. 2019, 12, 60–66. [Google Scholar] [CrossRef] [Green Version]
- Bu, L.; Liu, J.; Zhu, L.; Luo, S.; Chen, X.; Li, S. Attainable yield achieved for plastic film-mulched maize in response to nitrogen deficit. Eur. J. Agron. 2014, 55, 53–62. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y.; Dai, C.; Fang, S.; Gong, Y.; Wu, X.; Zhu, R.; Liu, K. Remote prediction of yield based on LAI estimation in oilseed rape under different planting methods and nitrogen fertilizer applications. Agric. For. Meteorol. 2019, 271, 116–125. [Google Scholar] [CrossRef]
- Zou, Y.F.; Saddique, Q.; Dong, W.J.; Zhao, Y.; Zhang, X.; Liu, J.C.; Ding, D.Y.; Feng, H.; Wendroth, O.; Siddique, K.H.M. Quantifying the compensatory effect of increased soil temperature under plastic film mulching on crop growing degree days in a wheat–maize rotation system. Field Crop. Res. 2021, 260, 107993. [Google Scholar] [CrossRef]
- Gültaş, H.T.; Ahi, Y. Supplemental irrigation impact on yield and yield quality parameters of rapeseed. Agron. J. 2020, 112, 4207–4218. [Google Scholar] [CrossRef]
- Dogan, R.; Celik, N.; Yueruer, N. Requirement and application frequencies of nitrogen fertilizer on bread wheat variety, Arpathan-9. Asian J. Chem. 2008, 20, 3069–3078. [Google Scholar]
- Ganguly, A.; Ghosh, S. Model development and experimental validation of a floriculture greenhouse under natural ventilation. Energy Build. 2009, 41, 521–527. [Google Scholar] [CrossRef]
- Kuscu, H.; Demir, A.O. Yield and water use efficiency of maize under deficit irrigation regimes in a sub-humid climate. Philipp. Agric. Sci. 2013, 96, 32–41. [Google Scholar]
- Liu, C.; Qi, Z.; Gu, Z.; Gui, D.; Zeng, F. Optimizing irrigation rates for cotton production in an extremely arid area using RZWQM2-simulated water stress. Trans. ASABE 2017, 60, 2041–2052. [Google Scholar] [CrossRef] [Green Version]
- Celette, F.; Gary, C. Dynamics of water and nitrogen stress along the grapevine cycle as affected by cover cropping. Eur. J. Agron. 2013, 45, 142–152. [Google Scholar] [CrossRef]
- Zalud, Z.; Pokorny, E.; Stralkova, R.; Podesvova, J. Estimation of winter wheat nitrogen stress using the CERES crop model. Rostlinna Vyroba 2001, 47, 253–259. [Google Scholar]
- Kim, S.H.; Sicher, R.C.; Bae, H.; Gitz, D.C.; Baker, J.T.; Timlin, D.J.; Reddy, V.R. Canopy photosynthesis, evapotranspiration, leaf nitrogen, and transcription profiles of maize in response to CO2 enrichment. Glob. Chang. Biol. 2006, 12, 588–600. [Google Scholar] [CrossRef]
- Gholinezhad, E.; Aynaband, A.; Ghorthapeh, A.H.; Noormohamadi, G.; Bernousi, I. Study of the effect of drought stress on yield, yield components and harvest index of sunflower hybrid Iroflor at different levels of nitrogen and plant population. Not. Bot. Horti Agrobot. 2009, 37, 85–94. [Google Scholar]
- Nematpour, A.; Eshghizadeh, H.R.; Zahedi, M. Comparing the Corn, Millet and Sorghum as Silage Crops Under Different Irrigation Regime and Nitrogen Fertilizer Levels. Int. J. Plant Prod. 2021, 15, 351–361. [Google Scholar] [CrossRef]
- Xing, Y.Y.; Mi, F.Y.; Wang, X.K. Effects of different nitrogen fertilizer types and application rates on maize yield and nitrogen use efficiency in Loess Plateau of China. J. Soil. Sediments 2022, 16, 1–21. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Li, Y. Effects of drip system uniformity and nitrogen application rate on yield and nitrogen balance of spring maize in the North China Plain. Field Crop Res. 2014, 159, 10–20. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Panda, R.K.; Chakraborty, A.; Halder, D. Enhancing grain yield, biomass and nitrogen use efficiency of maize by varying sowing dates and nitrogen rate under rainfed and irrigated conditions. Field Crop Res. 2018, 221, 339–349. [Google Scholar] [CrossRef]
- El Zemrany, H.; Cortet, J.; Lutz, M.P.; Chabert, A.; Baudoin, E.; Haurat, J.; Maughan, N.; Félix, D.; Défago, G.; Bally, R. Field survival of the phytostimulator Azospirillum lipoferum CRT1 and functional impact on maize crop, biodegradation of crop residues, and soil faunal indicators in a context of decreasing nitrogen fertilisation. Soil Biol. Biochem. 2006, 38, 1712–1726. [Google Scholar] [CrossRef]
- Loussaert, D.; Clapp, J.; Mongar, N.; O’Neill, D.P.; Shen, B. Nitrate Assimilation Limits Nitrogen Use Efficiency (NUE) in Maize (Zea mays L.). Agronomy 2018, 8, 110. [Google Scholar] [CrossRef] [Green Version]


| Scenarios | Irrigation Rates | Total Irrigation Amounts (mm) | N Fertilizer Rates | Total N Fertilizer Amounts (kg/ha) |
|---|---|---|---|---|
| I125N100 | 125% ET | 243.1 | 100% LOD | 151 |
| I100N100 | 100% ET | 205.8 | 100% LOD | 151 |
| I75N100 | 75% ET | 166.6 | 100% LOD | 151 |
| I50N100 | 50% ET | 128.0 | 100% LOD | 151 |
| I100N125 | 100% ET | 205.8 | 125% LOD | 189 |
| I100N75 | 100% ET | 205.8 | 75% LOD | 113 |
| Depth (cm) | Soil Water Retention | Vertical Ksat (cm/h) | Soil Root Growth Factors | |||||
|---|---|---|---|---|---|---|---|---|
| θ (cm) | λ | θs | θr | θ1/3 | θ15 | |||
| 0–5 | −8.96 | 0.17 | 0.35 | 0.10 | 0.24 | 0.17 | 3.15 | 1.00 |
| 5–15 | −17.00 | 0.33 | 0.37 | 0.13 | 0.22 | 0.16 | 3.22 | 0.90 |
| 15–30 | −7.38 | 0.35 | 0.47 | 0.15 | 0.23 | 0.17 | 3.46 | 0.80 |
| 30–45 | −23.89 | 0.16 | 0.28 | 0.11 | 0.22 | 0.17 | 1.81 | 0.70 |
| 45–60 | −10.47 | 0.18 | 0.30 | 0.13 | 0.22 | 0.18 | 2.83 | 0.50 |
| 60–90 | −5.53 | 0.15 | 0.31 | 0.10 | 0.21 | 0.16 | 2.83 | 0.30 |
| 90–120 | −6.79 | 0.22 | 0.32 | 0.11 | 0.20 | 0.14 | 2.33 | 0.15 |
| 120–150 | −16.68 | 0.30 | 0.40 | 0.07 | 0.20 | 0.12 | 3.02 | 0.05 |
| 150–179 | −14.65 | 0.32 | 0.40 | 0.04 | 0.17 | 0.08 | 2.59 | 0.01 |
| Parameter | Description | Value |
|---|---|---|
| P1 | Thermal time from seedling emergence to the end of the juvenile phase (°C·days). | 120 |
| P2 | Delay in development for each hour that day length is above 12.5 h (days/hr). | 0.875 |
| P5 | Thermal time from silking to physiological maturity (°C·days). | 800 |
| G2 | Maximum possible number of kernels per plant. | 800 |
| G3 | Kernel filling rate during linear grain filling stage under optimum conditions (mg/day). | 10 |
| PHINT | Phylochron interval between successive leaf tip appearance (°C·days). | 60 |
| Max | Maximum plant height at maturity (cm). | 320 |
| PB | Plant biomass at half of maximum height (g/plant [<=100] OR kg/ha [>100]). | 60 |
| Scenarios | VWC | LAI | Plant Height | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ObVWC | SimVWC | RRMSE | PBIAS | IoA | R2 | RRMSE | PBIAS | IoA | R2 | RRMSE | PBIAS | IoA | R2 | |
| I125N100 | 0.214 | 0.221 | 8.6% | −3.1% | 0.87 | 0.74 | 7.1% | 4.7% | 0.97 | 0.96 | 5.7% | −1.6% | 1.00 | 1.00 |
| I100N100 | 0.208 | 0.211 | 5.3% | −1.4% | 0.94 | 0.81 | 3.6% | 3.4% | 0.99 | 0.97 | 1.9% | 1.9% | 1.00 | 1.00 |
| I75N100 | 0.185 | 0.186 | 6.1% | −0.8% | 0.97 | 0.91 | 5.5% | 3.2% | 0.98 | 0.95 | 2.3% | 1.5% | 1.00 | 1.00 |
| I50N100 | 0.167 | 0.171 | 9.4% | −2.3% | 0.94 | 0.83 | 8.8% | 4.1% | 0.95 | 0.87 | 3.2% | −0.8% | 1.00 | 1.00 |
| I100N125 | 0.200 | 0.211 | 9.8% | −6.0% | 0.85 | 0.72 | 5.1% | 4.4% | 0.99 | 0.99 | 3.4% | 1.9% | 1.00 | 1.00 |
| I100N75 | 0.204 | 0.211 | 8.7% | −3.5% | 0.88 | 0.71 | 6.2% | 5.4% | 0.98 | 0.98 | 2.5% | 1.8% | 1.00 | 1.00 |
| Scenario | Yield (kg/ha) | WUE (kg/(ha·mm)) | TCN (kg/ha) | NUE (kg/kg) |
|---|---|---|---|---|
| I120N130 | 10516 * | 41.5 | 216 | 25.3 |
| I50N70 | 9559 | 47.3 * | 183 | 23.1 |
| I125N75 | 9754 | 37.4 | 161 | 30.2 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Yu, Q.; Abdalhi, M.A.M.; Li, F.; Qi, Z.; Zhu, T.; Cai, W.; Chen, X.; Feng, S. RZWQM2 Simulated Drip Fertigation Management to Improve Water and Nitrogen Use Efficiency of Maize in a Solar Greenhouse. Agriculture 2022, 12, 672. https://doi.org/10.3390/agriculture12050672
Cheng H, Yu Q, Abdalhi MAM, Li F, Qi Z, Zhu T, Cai W, Chen X, Feng S. RZWQM2 Simulated Drip Fertigation Management to Improve Water and Nitrogen Use Efficiency of Maize in a Solar Greenhouse. Agriculture. 2022; 12(5):672. https://doi.org/10.3390/agriculture12050672
Chicago/Turabian StyleCheng, Haomiao, Qilin Yu, Mohmed A. M. Abdalhi, Fan Li, Zhiming Qi, Tengyi Zhu, Wei Cai, Xiaoping Chen, and Shaoyuan Feng. 2022. "RZWQM2 Simulated Drip Fertigation Management to Improve Water and Nitrogen Use Efficiency of Maize in a Solar Greenhouse" Agriculture 12, no. 5: 672. https://doi.org/10.3390/agriculture12050672
APA StyleCheng, H., Yu, Q., Abdalhi, M. A. M., Li, F., Qi, Z., Zhu, T., Cai, W., Chen, X., & Feng, S. (2022). RZWQM2 Simulated Drip Fertigation Management to Improve Water and Nitrogen Use Efficiency of Maize in a Solar Greenhouse. Agriculture, 12(5), 672. https://doi.org/10.3390/agriculture12050672







