Abstract
Genotype and weather conditions play crucial roles in determining the volume and stability of a soybean yield. The aim of this study was to identify the key meteorological factors affecting the harvest date (model M_HARV) and yield of the soybean variety Augusta (model M_YIELD) using a neural network sensitivity analysis. The dates of the start of flowering and maturity, the yield data, the average daily temperatures and precipitation were collected, and the Selyaninov hydrothermal coefficients were calculated during a fifteen-year study (2005–2020 growing seasons). During the experiment, highly variable weather conditions occurred, strongly modifying the course of phenological phases in soybean and the achieved seed yield of Augusta cultivar. The harvesting of mature soybean seeds took place between 131 and 156 days after sowing, while the harvested yield ranged from 0.6 t·ha−1 to 2.6 t·ha−1. The sensitivity analysis of the MLP neural network made it possible to identify the factors which had the greatest impact on the tested dependent variables among all the analyzed factors. It was revealed that the variables assigned ranks 1 and 2 in the sensitivity analysis of the neural network forming the M_HARV model were total rainfall in the first decade of June and the first decade of August. The variables with the highest impact on the Augusta soybean seed yield (model M_YIELD) were the mean daily air temperature in the second decade of May and the Seljaninov coefficient values calculated for the sowing–flowering date period.
1. Introduction
Soybean (Glycine max [L.] Merrill) is the most important legume crop worldwide with a forecast of production at 353.8 million tonnes [1]. It is also the main source of valuable plant protein and the second source of oil, and the global demand for soybean has been constantly growing. Poland is highly dependent on soybean meal imports, a current volume of around 2.5 million tons. Independence from protein imports can be ensured by an increase of the acreage of soybean cultivation. Over the last ten years, the cultivation area has increased from <1000 to 25,552 hectares (in 2021) [2,3], but soybean is still considered to be a new crop for Polish farmers. One of the reasons for such a small acreage is the location of Poland, which is over 49 degrees latitude, north of the world’s main soybean cultivation regions. There are several major factors which limit soybean’s fitness for its purposes, and they are as follows: long daytime duration, low temperature at the time of germination and flowering, and requirements for rainfall [4]. The lack of suitable cultivars adapted to climatic conditions is the main problem for soybean cultivation in Poland. Primarily, early maturing cultivars (“000”) [5] have been promoted in Poland. However, the key issue for the higher latitude adaptation is the proper combination of allelic variants at the E1, E2, E3, and E4 loci [6]. The varieties having all four recessive alleles are insensitive in terms of photoperiod; for example Nawiko and Augusta, which was bred at the Department of Genetics and Plant Breeding, Poznań University of Life Sciences. Further, the very high variability and diversity of weather conditions observed in individual years, which is a characteristic of Poland’s transitional climate, can be considered an additional obstacle for soybean adaptation, causing significant fluctuations in the dates of the flowering initiation and maturity [7]. Unfavorable growing conditions—including cold stress—cause a reduction in soybean yield and its nutritional value [8,9].
There are many different factors that affect soybean adaptiveness around the world. In Central and South Germany, a positive correlation between seed yield with solar radiation (r = 0.32) and precipitation (r = 0.33) was found to be significant, but the same factor was negatively correlated with Crop Heat Units (CHU) (r = −0.42). Varieties from maturity group MG 00 were less correlated with the tested environmental factors than varieties from maturity group MG 000 [10]. In the far east, the yield-limiting, environmental factor is temperature, but for the Krasnodar region, the yield was positively related to the hydrothermal coefficient; a lack of moisture becomes a significant disadvantage for soybean in this region [11]. Also, in Argentina, the moisture availability during the period from flowering to pod formation is critical for productivity [12]. Precipitation is considered a major factor in the formation of soybean yield components in most regression models [13,14], and water deficiency is reported to be one of the most important environmental factors, reducing crop (including soybean) productivity more than any other factor [15,16]. Both too-high and too-low temperatures can reduce the yield of soybean. Cold stress at the flowering stage negatively affects the elements of the plant habits and seed yield of soybean, which results in a high level of yield decrease shown in late cultivars, while a smaller and similar yield decrease was observed in early and medium–early cultivars [17]. Both elevated temperature and water stresses post-flowering significantly affected plant growth and yield parameters negatively. The combined effects of the two factors were more severe than the individual stresses [18].
Moreover, global warming has been a new factor that has increased the incidence of extreme weather events in recent years. The effect of temperature rise may vary. Annual global mean temperatures varied from 15.0 to 15.3 °C and are likely to exert a positive impact on the average yield [19]. Tacarindua et al. [20,21] reported that temperature rise during the growing season from 26 to 30 °C affected the reduction of dry mass production, harvest index, seed number, pod number, and single-seed size, and thereby seed yield. Predicting models demonstrated a nonsignificant decrease in the global average soybean yield of 3.1% per °C increase with large uncertainties [22].
Thus, genotype and weather conditions have a significant impact on the amount and stability of soybean yield, which depends on many other cultivation factors [23,24]. Therefore, breeding new soybean cultivars for such conditions—as well as selecting European cultivars for cultivation—is much more difficult and requires long-term experiments. Analyses of the influence of weather factors on the phenological data and yield should be carried out on the same genotype. It is reported that Augusta is the only variety that has been cultivated in Poland for a long period of time (since 2002). For this reason, the results from 16 years of cultivation of this variety were used to determine the impact of meteorological conditions on the harvest date and soybean yield.
In this pilot study, the neural modeling method was used. Artificial neural networks (ANN) are a tool designed to implement various types of problems, including the performance of prognostic and deterministic analyses [25,26,27,28,29,30,31]. The reason for the great interest in neural networks is the fact that they are called “universal function estimators”, and they are capable of solving problems of a linear and non-linear nature. Often, the simultaneous use of multiple linear regression (MLR) and artificial neural networks can be found in the literature. Unfortunately, linear methods are characterized by much lower analysis results than ANNs [32,33,34]. It should be noted that artificial neural networks operate on a “black box” principle; that is, they do not provide complete information regarding the method of obtaining specific answers or detailed relations between the input and output variables [35]. To be able to extract as many clues and messages as possible from a trained network, several techniques were used, including neural network sensitivity analysis. This analysis is used to determine how “sensitive” the model is to changes in model parameter values and to changes in the model structure. The so-called “sensitivity of the network” is determined, among others, by the error ratio. A high network sensitivity to a given parameter suggests that the system’s performance may change drastically with a small change in that parameter. Conversely, a low sensitivity suggests a small change in performance [35,36]. In this way, it is easy to identify variables of high importance in influencing the variability of the output factors—i.e., the main problems set by the model developers, which are then solved by the network.
The aim of this study was to identify the key meteorological factors affecting the harvest date and yield of soybean using a neural network sensitivity analysis based on two deterministic models.
2. Materials and Methods
2.1. Plant Material
Polish soybean cultivar Augusta, one of the earliest soybean cultivars in Europe, was used as the plant material in this study. It was developed at the Department of Genetics and Plant Breeding of the Poznań University of Life Sciences (PULS) and registered in Poland in 2002. Augusta was selected from two crosses: (1) in the first step, the cross between Fiskeby V and line PI 194,643 was made and the line 104 was obtained; (2) in the second step, the line 104 was crossed with line 11, belonging to G. soja (Siebold & Zucc.) syn. G. ussuriensis (Regel & Maack) wild species. Line 11 of G. soja is growing in a natural environment in the far east latitude region of Russia, similar to Poland, and is a day-long tolerant genotype. Thus, Augusta has two sources of photoperiod insensitivity and chilling tolerance.
2.2. Field Test
The field experiment was conducted at the Agricultural Research Station Dłoń, Poznań University of Life Sciences, Poland (51°41′37″ N, 17°04′06″ E) during the 2005–2020 growing seasons. The plot soils are classified as Haplic Luvisols (LVh, WRB Soil Classification—FAO) [37] and the previous crop for the experiment was wheat. The Augusta seeds were sown from 20 to 28 of April at the density of 60 seeds per 1 m2. Just after sowing, a pre-emergence herbicide that contained linuron (0.1 g∙m−2) and S—metolachlor (0.14 g∙m−2) was applied. The fertilizer was used according to the conventional farming practices in this area (N 30 kg∙ha−1, P 80 kg∙ha−1, K 120 kg∙ha−1). The dates of the beginning of flowering and maturity were recorded due to the BBCH scale. The yield results were collected from the fields measuring from 0.5 to 5.0 hectares, on which the seeds of Augusta were multiplied.
The average daily temperatures and precipitation, measured according to the WMO guidelines for 2005–2020, were obtained from a Vantage Vue 6357 UE 9 meteorological station (Davis Instruments, United States) located approximately 400 m from the experimental field. Atmospheric conditions and information on vegetation length and yield from 2005 to 2020 are shown in Figure A1 and Figure A2.
2.3. Division of Experimental Data into Sets Used in the Analyses
All experimental data collected in the database were divided into two sets. This division resulted from the assumptions made about the use of deterministic models in indicating the independent variables with the greatest influence on the evaluated feature, i.e., harvest date (model M_HARV) and yield (model M_YIELD). The procedure for the experimental data intended for the development and specific verification of each of the deterministic models is presented below (Figure 1).
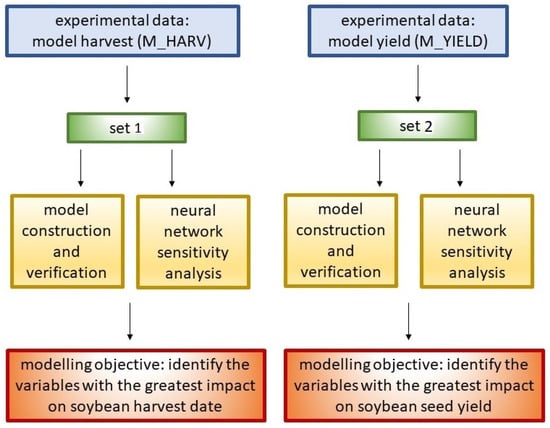
Figure 1.
The division of experimental data into sets according to the assumptions made about the construction and application of deterministic models.
2.4. Methodology for Predictive Model Development
Primary meteorological data were used to develop deterministic neural models (M_HARV, M_YIELD). These included: mean air temperature and precipitation totals for each decade, starting from the first decade of April to the third decade of September (M_HARV, M_YIELD) in the current agronomic season. Some of the proposed independent variables required additional calculations. For example, these included the values of Selyaninov hydrothermal coefficients (HTC) (Equation (1)), calculated for different time intervals depending on the deterministic assumptions of the selected models, growing degree days (GDD) > 6 °C and the total precipitation for selected vegetation periods.
where:
HTC = (P · 10)/Σt
- P—total monthly rainfall (mm),
- Σt—sum of monthly average daily air temperatures > 6 °C.
The duration of the soybean growing season (M_HARV, M_YIELD) was also determined. The independent variables in the developed models were the date of harvest (M_HARV) and yield (M_YIELD). The date of harvest was presented as a number of days since the beginning of the year, while the yield was t∙ha−1. A detailed list of independent and dependent variables taken into account in the development of each model, along with the range of their values, is presented in Table 1.

Table 1.
The neural models’ data structure.
The next step in performing the appropriate analyses was the selection of appropriate neural network architectures that make up the M_HARV and M_YIELD models. By using Statistica v.7.1. [38], it was possible to test the Automatic Network Designer, a tool that automatically evaluates a large number of different network architectures of varying complexity, selecting a set of those that best suit a given problem. In the first stage of work with the Automatic Network Designer, several types of neural networks were selected in order to test them in terms of the quality of implementation of deterministic problems. The tool allows for verifying 5 types of networks, i.e., multilayer perceptron (MLP) (three-layer and four-layer), radial basis function network (RBF), probabilistic neural network (PNN), and generalized regression neural network (GRNN). According to the literature data, the most popular type of network selected for the implementation of prognostic and deterministic issues is MLP with two hidden layers [39,40]. After verification of the preliminary results obtained during the pilot analyses, 3 types of networks were selected for further, more detailed testing: RBF and MLP (three-layer or four-layer). The linear transfer function and two activation functions—linear and logistic—were chosen for the MLP network. In the next step, the complexity of each type of network was determined. For the RBF network, the minimum number of neurons was assumed to be 5, while the maximum number was 80. For the MLP (three-layer) network, a minimum of 3 neurons and a maximum of 25 were assumed in the second layer. For the MLP (four-layer) network, the third layer contained a minimum of 3 neurons and a maximum of 25 neurons. After establishing the above assumptions, an analysis was carried out for 10,000 networks. This number of tested networks is most common in other studies. The interpretation of the values that characterize the learning quality and the error values for the networks developed allowed for the selection of the final network type, for which the analyses continued. The final analysis was of an MLP network with two hidden layers. The selection of the best final networks forming deterministic models was based on the most favourable values of parameters relating to their quality, i.e., standard deviation, mean value from error modules, the quotient of standard deviations, and correlation coefficient. With results which are ambiguous or difficult to evaluate, networks with high correlation coefficients and a low value of mean absolute error were sought. Finally, two MLP networks were selected with the following ratios: MLP 45:45-21-21-1:1 (M_HARV) and MLP 46:46-21-21-1:1 (M_YIELD). The structure of the two selected MLP networks, including the independent and dependent variables, is shown in Figure 2.
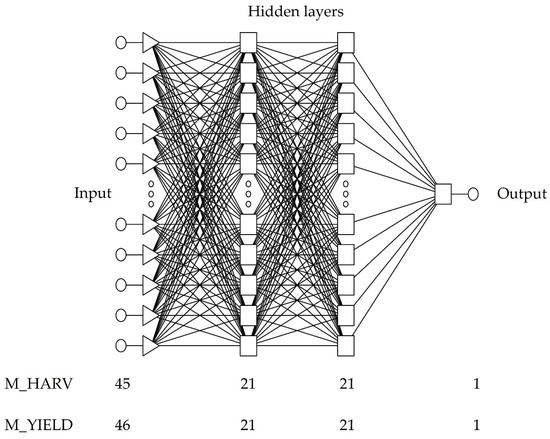
Figure 2.
The network structure for models Harvest (M_HARV) and Yield (M_YIELD).
The model Harvest (M_HARV) contained 45 neurons (nods) in the input, 21 in the first hidden layer, 21 in the second hidden layer, and 1 in the output.
The Yield model (M_YIELD) contained 46 neurons in the input, 21 in the first hidden layer, 21 in the second hidden layer, and 1 in the output.
To train and validate the selected MLP networks that formed the M_HARV and M_YIELD models, sets 1 and 2 were randomly divided into two sets: a training set (70% of cases) and a validation set (30% of cases). The data collected in the training set enabled the calculation of the gradient, weight, and value of any loads on the network. The role of the validation set was to control the training error of the network during the training procedure. If the validation set’s error increased for several consecutive epochs, the training process was halted. The most important task of this set was to prevent the overfitting of the neural network. Two error backpropagation methods were chosen to train the network forming M_HARV and M_YIELD models. As can be seen in Table 2, individual networks forming M_HARV and M_YIELD models were taught with different conditions ending the network training process. The best results were achieved at different epochs.

Table 2.
A number of epochs and training methods for neural networks.
2.5. Neural Network Sensitivity Analysis
The analysis of the sensitivity of the neural network makes it possible to identify the factors with the greatest impact on the tested dependent variables among all the analyzed factors. After removing a specific explanatory variable (independent feature) from the model, its influence on the value of the total error of the neural network is observed. This allows for the significance (validity) of the tested factors to be determined. To accomplish the above task, the error quotient and rank are used. The error quotient expresses the ratio of the error to the total error of all independent variables. As its value increases, the importance of a given variable increases. If for any of the independent variables the quotient drops below 1, such a variable should be removed from the model to improve its quality. A rank that acts as a place in the ranking list indicates the characteristics according to decreasing error. The rank value of 1 proved to be the most important influence on the explanation of the variability of the dependent variable.
3. Results
During the experiment, highly variable weather conditions were observed, which strongly altered the course of phenological phases in soybean and the achieved seed yield of Augusta cultivar. The soybean flowering phase was observed between 11 and 25 June in the interval from 52 to 62 days from the sowing of seeds. Harvesting of mature soybean seeds took place from 30–31 August (in 2012, 2016, and 2017) to 30 September in 2020, i.e., from 131 to 156 days after sowing in 2012 and 2020, respectively. Soybean yields obtained during the study years ranged from 0.6 t·ha−1 and 2.6 t·ha−1 in 2015 and 2020, respectively. Soybean yields were generally low mainly due to very variable weather conditions (Figure A1). During the sixteen study years, harvested yield ranged from 0.6 t·ha−1 during extreme drought in 2015 to 2.6 t·ha−1 in 2020. During the eight years, harvested yield was below 2 tons, from 1.2 to 1.8 t·ha−1. In only six years of the study, yields ranged from 2.0–2.2 t·ha−1 (Figure A2).
The growing degree days (GDD) from soybean sowing to flowering ranged from 873–893 in 2017 and 2009 to over 1100 in 2007 and 2012. It was during this period in the six years of the study (2008, 2015, 2011, 2006, and 2017) that very low rainfall was recorded to be less than 100 mm; and in 2020, the sum of rainfall in the period from sowing to flowering was 236 mm. Thus, dry or very dry years (only 37.5 mm of precipitation in 2008) were observed, associated with the occurrence of droughts in the first growing season, and extremely rainy years causing the flooding of the experimental fields in 2020.
GDD over the entire soybean growing season ranged from 2309 in 2017 to 2818 in 2018. During the entire soybean growing season in 2008, 2015, and 2019, a total of less than 200 mm of precipitation was recorded, while 584 mm of precipitation fell in the rainy year of 2020. A calculated HTC indicates catastrophic drought; 0.3–0.5-drought; 0.5–1.0 humidity below balance; 1–2 sufficient amount of water; 2–4 excess of water. The lowest value of HTC in the period from sowing to flowering was recorded in 2008 (0.369), while the highest value was 2.59 in 2020. Humidity below balance occurred until flowering in 2006, 2011, 2015, and 2019. Analyzing the results of HTC in the whole growing period of soybean, no drought was observed, while a level of humidity below balance was recorded in 2008, 2015, 2018, and 2019, as well as an excess of water in 2020.
Sensitivity analysis for the M_HARV model identified the factor “total precipitation in the first decade of June” as the factor that most influenced the timing of soybean harvest (rank 1). The second important factor of the M_HARV model (rank 2) was the total rainfall in the first decade of August. The third important variable was the value of the Seljaninov coefficient, calculated for the period from sowing to harvest (Table 3).

Table 3.
A sensitivity analysis of the neural networks.
The factor with the greatest influence on soybean seed yield (M_YIELD model) was the mean air temperature in the second decade of May. This variable was given a rank of 1 in the sensitivity analysis of the neural network. The factor that received rank 2 was the HTC values calculated for the period from sowing to flowering. The variable with rank 3 was also the HTC value but was determined for a different time interval, i.e., from sowing to harvesting (Table 3).
Comparison of Models M_HARV and M_YIELD Quality Characteristics
The best neural networks that allowed for the identification of factors with the greatest influence on harvest date (M_HARV) and soybean seed yield (M_YIELD model) were selected based on a detailed analysis of the quality parameters of the generated networks. Detailed results of the analyses are presented in Table 4.

Table 4.
The quality and structure of the neural models produced.
The results of the presented neural models were characterized in each of the considered cases by the best values of quality measures of the generated neural networks. When it was difficult to indicate the best network, the values of two quality parameters were considered: the correlation coefficient (r) and the mean absolute error. The principle followed was that the value of the correlation coefficient should be the highest with a simultaneous low value of the mean absolute error. In both analyzed cases, the values of the correlation coefficient were very high, i.e., for the model M_HARV: 0.898 and for the model M_YIELD: 0.75. The value of the mean absolute error was the highest for the model M_YIELD and it was 0.203 t∙ha−1. Another important parameter in assessing the quality of the generated neural networks was the error quotient, defined as the quotient of the standard deviation of the prediction errors and the standard deviation of the output variable. For the model to be useful for forecasting purposes, the value of this parameter should not exceed 0.7. In the three analyzed cases, this assumption was fulfilled.
The response plots are a visual representation of the results of the sensitivity analysis of the neural networks. It shows the relationship between variables of rank 1 and 2 from the sensitivity analysis and the dependent variable. On the x and y axes of the three-dimensional plot are placed the values of the selected independent variables, and on the z-axis are the values taken by the dependent variable. The response plots for MLP 45:45-21-21-1:1 and MLP 46:46-21-21-1:1 networks are shown in Figure 3 and Figure 4, respectively.
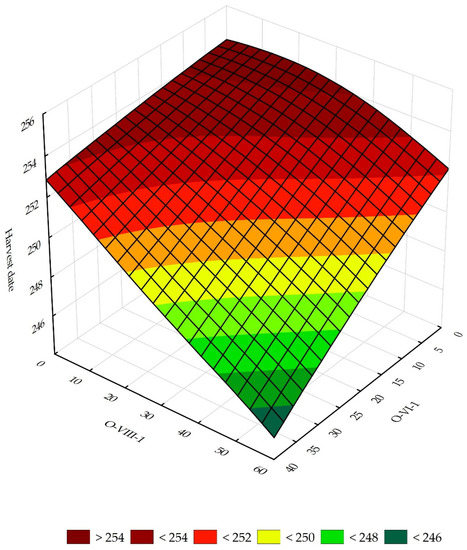
Figure 3.
The response surface for the harvest date and two variables, O-VII-1 and O-VI-1.
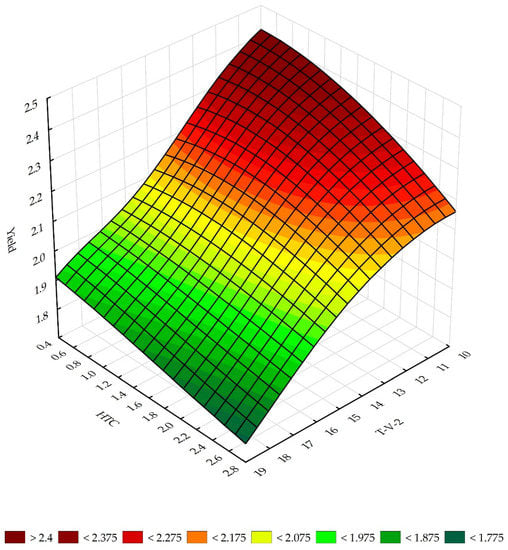
Figure 4.
The response surface for a yield and two variables, T-V-2 and HTC.
Figure 3 shows the response surface for the MLP network 45:45-21-21-1:1, where the explanatory variable is harvest date and the explanatory variables are precipitation in the first decade of June and precipitation in the first decade of August. The graph shows that the persistence of low average precipitation in the second decade of April and the first decade of April delays the date of the soybean harvest.
Figure 4 shows the response surface for the MLP 46:46-21-21-1:1 network forming the M_YIELD model, which shows the relationship between soybean seed yield levels and the average air temperature in the second decade of May, as well as the HTC values calculated for the sowing–flowering period. The highest soybean seed yield can be expected when the average air temperature in the second decade of May is about 10–12 °C, and the value of the HTC for the sowing–flowering period is relatively low, ranging from 0.4 to 0.8. It can be concluded that the first factor in question determines soybean yield to a greater extent than the second independent variable.
The results presented in the previous stages were supplemented with additional analyses and visualisations of the relations between the observed and predicted values of the harvest date and soybean yield. The results of the analyses are presented in Figure 5 and Figure 6.
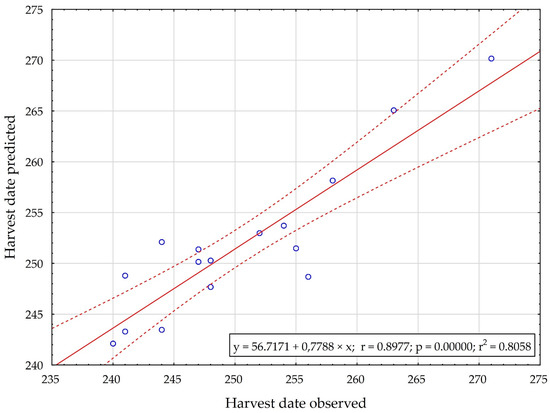
Figure 5.
The scatter plot between the observed and predicted values of the soybean harvest date in model M_HARV.
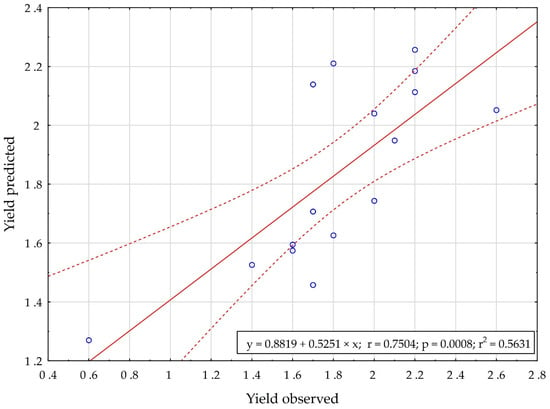
Figure 6.
The scatter plot between the observed and predicted values of the soybean seed yield in model M_YIELD.
4. Discussion
An important aspect of the use of neural networks in implementing deterministic problems is the choosing of an appropriate network topology and training method. A complex phase of testing different neural network topologies allowed us to indicate the most suitable type of network for the problems presented in this paper. Finally, the MLP network with two hidden layers was chosen. Training a neural network allows for the combining of certain behaviors of the model based on many experiences. The user enforces specific responses to given input signals from the network. The network remembers questions and answers based on selected patterns of behavior so that when a new “question” is asked, it gives an answer that is most similar to the original one. In the presented results, all neural networks were taught using the method of backward error propagation. This method allows for the creation of neural networks with very favorable quality parameters [25,35].
The selected neural networks forming the M_HARV and M_YIELD models were characterized by standard values of their quality metrics. The quality parameters of the M_YIELD model were less accurate than M_HARV. However, it turns out that the values of correlation coefficient (0.75), mean absolute error (0.2), and deviation quotient (0.663) obtained for the M_YIELD model fall within the generally accepted criteria related to the application of this type of tool in agricultural practice [41].
One of the most difficult steps in developing deterministic neural models is choosing the right independent variables to form the model. These variables should have a real influence on the development of the explained variable. The correct identification of explanatory variables requires excellent knowledge of the research object. Admittedly, the significance of selected variables can be verified by additional analyses and calculations [42], but it is practical experience that is the most valuable way to correctly match independent variables to explain the complexity and variability of a specific phenomenon. In our study, meteorological and phenological data were used with 45 and 46 selected variables for the M_HARV and M_YIELD models, respectively. We conclude that such a detailed approach to explaining the influence of weather conditions on the phenology and yield of soybean in Wielkopolska allowed for the precise identification of variables that have the greatest influence on harvest timing and seed yield.
Sensitivity analysis of neural networks was used to fully implement the issues presented in this paper. It is a method that allows for distinguishing important variables in the model from those that contribute little to the outcome of the network [43]. This method is widely used in typing the most important variables in issues related to the phenology and yield of crop species [44,45]. The result of the analysis is the value of the error quotient, based on which a rank (ranking place) is assigned to a particular trait. It is assumed that traits with an error quotient below one are not considered when interpreting the importance of variables.
The sensitivity analysis performed for the two described neural networks indicated different independent variables that determined to the greatest extent the variability of the next explained variables: harvest date and soybean seed yield. For the M_HARV model, these were precipitation amounts in the first decade of June and August. It should be noted, however, that the factors with an error quotient higher than 1.3 included the Seljaninov coefficient in the sowing–harvesting range, precipitation in the first and second decade of May, and temperature in the second decade of May and the second decade of July. These values testify to the high importance of the mentioned variables in the work to determine their influence on the optimal harvest date of soybean cv. Augusta. In the case of the M_YIELD model, all of the highly important factors responsible for yield were characterized by an error quotient above 1.1.
Both rainfall deficiency and significant excess strongly modify plant development and yield, and the developmental stage most sensitive to drought stress varies according to the cultivar used [46]. Drought occurring from late flowering to the beginning of pod filling results in a reduction in the number of seeds per pod, and drought occurring late in pod filling results in a reduction in seed size [47]. The results of our study are consistent with these findings.
The most important trait assessed by growers and later by farmers is yield potential, which depends on many factors, including climatic conditions during the growing season [48]. In the second M_YIELD model, the average air temperature in the second decade of May, the Seljaninov coefficient values calculated for the period from sowing to flowering, and then the values of this coefficient calculated for the whole growing season were found to be the most important variables. Multi-criteria analysis of the results generated by deterministic models should be carried out for each model separately. The values of the error quotients assigned to explanatory variables of rank 1 or 2 cannot be compared between the models M_HARV and M_YIELD. Still, these values must be analyzed for each model independently. In the M_HARV model, the significance of 43 out of 45 tested independent variables considered in the construction of the model was confirmed. For two variables, i.e., T-IV-2 and T-VIII-1, error quotient values below one were calculated. These results testify to a very good fit of the variables to explain the variability of the modeled phenomenon. Besides, in further analyses, it would be advisable to exclude the participation of variables T-IV-2 and T-VIII-1 in developing new deterministic or predictive models. In turn, for the M_YIELD model, the neural network sensitivity analysis confirmed the significance of 34 out of 46 tested independent variables. In the next stage of work with improving these models, the contribution of these variables can be eliminated. A detailed interpretation of the results of the sensitivity analysis of neural networks allows us to conclude that the harvest date is a factor more dependent on meteorological conditions than the yield of soybean of the Augusta cultivar.
For many years, the suitability of soybean genotypes for cultivation in Poland depended, among other things, on the tolerance of lower temperatures during the flowering and the harvest dates. The Augusta variety was bred in Poland, and during its breeding special attention was paid to these factors. The Fiskeby V cultivar from Sweden was used in crossbreeding, which is characterized by photoneutrality and resistance to cold stress. Despite this, as our research showed, it was the temperature in the initial period of plant growth that had the most significant effect on the yields obtained.
5. Conclusions
Presented deterministic models—M_HARV and M_YIELD—allowed us to use artificial neural networks for the preliminary identification of major factors affecting the harvest date and yield of soybean cultivar Augusta.
The sensitivity analysis of the neural network makes it possible to initially select the factors with the greatest influence on the explained variable while maintaining the adopted level of significance.
Total precipitation in the first decade of June and the first decade of August were the variables assigned ranks 1 and 2 in the sensitivity analysis of the neural network forming the M_HARV model. On the other hand, the variables with the highest impact on the Augusta soybean seed yield (model M_YIELD) were mean daily air temperature in the second decade of May and Seljaninov coefficient values calculated for the sowing–flowering date period.
Further research on the improvement of deterministic models in soybean cultivation should be carried out on multiple levels. It is worth exploring other analytical methods that optimize important production factors (controllable) which have a significant impact on soybean seed yield in terms of quantity and quality.
Author Contributions
Conceptualization, G.N. and D.K.-P.; methodology, G.N., D.K.-P. and M.P.; software, G.N., M.P. and T.W.; validation, G.N., D.K.-P., M.P., T.W., M.K. and J.N.; formal analysis, G.N.; investigation, D.K.-P., M.K. and J.N.; resources, G.N., D.K.-P., M.P., T.W., M.K. and J.N.; data curation, G.N. and D.K.-P.; writing—original draft preparation, G.N., D.K.-P., M.P., T.W. and J.N.; writing—review and editing, G.N., D.K.-P., M.P., T.W., M.K. and J.N.; visualization, G.N.; supervision, G.N., D.K.-P. and J.N.; project administration, G.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
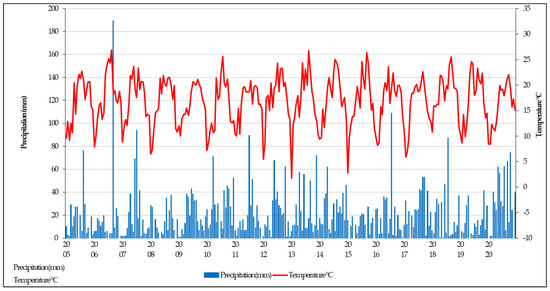
Figure A1.
Rainfall and average air temperatures between January 2005 and December 2020, ARS Dłoń, Poland.
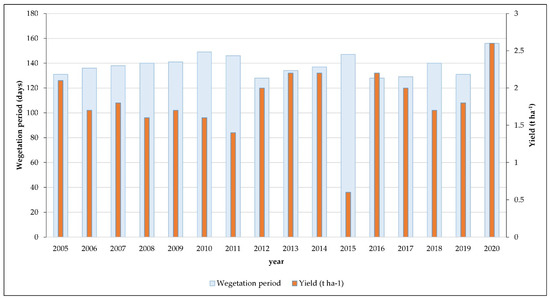
Figure A2.
The length of vegetation and the yield of soybean variety Augusta in the period 2005–2020, ARS Dłoń, Poland.
References
- World Agricultural Production. Available online: https://apps.fas.usda.gov/psdonline/circulars/production.pdf (accessed on 5 April 2022).
- Powierzchnie Upraw W Gminach. Available online: https://rejestrupraw.arimr.gov.pl/ (accessed on 5 April 2022).
- Niwińska, B.; Witaszek, K.; Niedbała, G.; Pilarski, K. Seeds of n-GM Soybean Varieties Cultivated in Poland and Their Processing Products as High-Protein Feeds in Cattle Nutrition. Agriculture 2020, 10, 174. [Google Scholar] [CrossRef]
- Gawęda, D.; Nowak, A.; Haliniarz, M.; Woźniak, A. Yield and Economic Effectiveness of Soybean Grown Under Different Cropping Systems. Int. J. Plant Prod. 2020, 14, 475–485. [Google Scholar] [CrossRef]
- Boerma, H.R.; Specht, J.E. Soybeans: Improvement, Production, and Uses, 3rd ed.; American Society of Agronomy, Crop Science Society of America, Soil Science Society of America: Madison, WI, USA, 2004. [Google Scholar]
- Miladinović, J.; Ćeran, M.; Đorđević, V.; Balešević-Tubić, S.; Petrović, K.; Đukić, V.; Miladinović, D. Allelic Variation and Distribution of the Major Maturity Genes in Different Soybean Collections. Front. Plant Sci. 2018, 9, 1286. [Google Scholar] [CrossRef]
- Krużel, J.; Ziernicka-Wojtaszek, A.; Borek, Ł.; Ostrowski, K. The changes in the duration of the meteorological vegetation period in Poland in the years 1971–2000 and 1981–2010. Inż. Ekol. 2015, 44, 47–52. [Google Scholar] [CrossRef]
- Michałek, S.; Borowski, E. Yielding, oil, fatty acids and protein content in the seeds of polish soybean cultivars under drought conditions. Acta Agrophysica 2006, 8, 459–471. [Google Scholar]
- Kołodziej, J.; Pisulewska, E. Effect of climatic factors on seed yield, fat yield and fat content in seeds of two soybean cultivars. Oilseed Crop. 2000, XXI, 759–776. [Google Scholar]
- Sobko, O.; Stahl, A.; Hahn, V.; Zikeli, S.; Claupein, W.; Gruber, S. Environmental Effects on Soybean (Glycine Max (L.) Merr) Production in Central and South Germany. Agronomy 2020, 10, 1847. [Google Scholar] [CrossRef]
- Novikova, L.Y.; Bulakh, P.P.; Nekrasov, A.Y.; Seferova, I.V. Soybean Response to Weather and Climate Conditions in the Krasnodar and Primorye Territories of Russia over the Past Decades. Agronomy 2020, 10, 1278. [Google Scholar] [CrossRef]
- Penalba, O.C.; Bettolli, M.L.; Vargas, W.M. The impact of climate variability on soybean yields in Argentina. Multivariate regression. Meteorol. Appl. 2007, 14, 3–14. [Google Scholar] [CrossRef]
- Choi, D.-H.; Ban, H.-Y.; Seo, B.-S.; Lee, K.-J.; Lee, B.-W. Phenology and Seed Yield Performance of Determinate Soybean Cultivars Grown at Elevated Temperatures in a Temperate Region. PLoS ONE 2016, 11, e0165977. [Google Scholar] [CrossRef]
- Gao, X.-B.; Guo, C.; Li, F.-M.; Li, M.; He, J. High Soybean Yield and Drought Adaptation Being Associated with Canopy Architecture, Water Uptake, and Root Traits. Agronomy 2020, 10, 608. [Google Scholar] [CrossRef]
- Lambers, H.; Chapin, F.S.; Pons, T.L. The Plant’s Energy Balance. In Plant Physiological Ecology; Springer: New York, NY, USA, 2008; pp. 225–236. [Google Scholar]
- Miladinov, Z.; Maksimovic, I.; Tubic, S.B.; Miladinovic, J.; Djordevic, V.; Vasiljevic, M.; Radic, V. The Impact of Water Deficit on The Soybean (Glycine max L.) Reproductive Stage of Development. Legum. Res.-AN Int. J. 2020, 43, 693–697. [Google Scholar] [CrossRef]
- Staniak, M.; Czopek, K.; Stępień-Warda, A.; Kocira, A.; Przybyś, M. Cold Stress during Flowering Alters Plant Structure, Yield and Seed Quality of Different Soybean Genotypes. Agronomy 2021, 11, 2059. [Google Scholar] [CrossRef]
- Ogunkanmi, L.; MacCarthy, D.S.; Adiku, S.G.K. Impact of Extreme Temperature and Soil Water Stress on the Growth and Yield of Soybean (Glycine max (L.) Merrill). Agriculture 2021, 12, 43. [Google Scholar] [CrossRef]
- Cheng-Zhi, C.; Cong-Jian, L.; Dan, X.; Xiao-Shan, Z.; Jin, Z. Global warming and world soybean yields. J. Agrometeorol. 2021, 23, 367–374. [Google Scholar] [CrossRef]
- Tacarindua, C.R.P.; Shiraiwa, T.; Homma, K.; Kumagai, E.; Sameshima, R. The response of soybean seed growth characteristics to increased temperature under near-field conditions in a temperature gradient chamber. F. Crop. Res. 2012, 131, 26–31. [Google Scholar] [CrossRef]
- Tacarindua, C.R.P.; Shiraiwa, T.; Homma, K.; Kumagai, E.; Sameshima, R. The effects of increased temperature on crop growth and yield of soybean grown in a temperature gradient chamber. F. Crop. Res. 2013, 154, 74–81. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Piao, S.; Wang, X.; Lobell, D.B.; Huang, Y.; Huang, M.; Yao, Y.; Bassu, S.; Ciais, P.; et al. Temperature increase reduces global yields of major crops in four independent estimates. Proc. Natl. Acad. Sci. USA 2017, 114, 9326–9331. [Google Scholar] [CrossRef] [PubMed]
- Nawracała, J. Analiza Genetyczno-Hodowlana Mieszańców i Linii Soi Otrzymanych z Krzyżowania Międzygatun-Kowego Glycine Max x Glycine Soja; Rozprawa naukowa w serii Rozprawy Naukowe Uniwersytetu Przyrodniczego w Poznaniu nr 394; Wydawnictwo Uniwersytetu Przyrodniczego w Poznaniu: Poznań, Poland, 2008. [Google Scholar]
- Mandić, V.; Đorđević, S.; Đorđević, N.; Bijelić, Z.; Krnjaja, V.; Petričević, M.; Brankov, M. Genotype and Sowing Time Effects on Soybean Yield and Quality. Agriculture 2020, 10, 502. [Google Scholar] [CrossRef]
- Piekutowska, M.; Niedbała, G.; Piskier, T.; Lenartowicz, T.; Pilarski, K.; Wojciechowski, T.; Pilarska, A.A.; Czechowska-Kosacka, A. The Application of Multiple Linear Regression and Artificial Neural Network Models for Yield Prediction of Very Early Potato Cultivars before Harvest. Agronomy 2021, 11, 885. [Google Scholar] [CrossRef]
- Hara, P.; Piekutowska, M.; Niedbała, G. Selection of Independent Variables for Crop Yield Prediction Using Artificial Neural Network Models with Remote Sensing Data. Land 2021, 10, 609. [Google Scholar] [CrossRef]
- Pentoś, K. The methods of extracting the contribution of variables in artificial neural network models—Comparison of inherent instability. Comput. Electron. Agric. 2016, 127, 141–146. [Google Scholar] [CrossRef]
- Niazian, M.; Niedbała, G. Machine Learning for Plant Breeding and Biotechnology. Agriculture 2020, 10, 436. [Google Scholar] [CrossRef]
- Kujawa, S.; Dach, J.; Kozłowski, R.J.; Przybył, K.; Niedbała, G.; Mueller, W.; Tomczak, R.J.; Zaborowicz, M.; Koszela, K. Maturity classification for sewage sludge composted with rapeseed straw using neural image analysis. In Proceedings of the SPIE—The International Society for Optical Engineering, Chengu, China, 20–22 May 2016; Volume 10033, p. 100332H. [Google Scholar]
- Wojciechowski, T.; Niedbala, G.; Czechlowski, M.; Nawrocka, J.R.; Piechnik, L.; Niemann, J. Rapeseed seeds quality classification with usage of VIS-NIR fiber optic probe and artificial neural networks. In Proceedings of the 2016 International Conference on Optoelectronics and Image Processing, ICOIP 2016, Warsaw, Poland, 10–12 June 2016. [Google Scholar]
- Niedbała, G.; Piekutowska, M.; Rudowicz-Nawrocka, J.; Adamski, M.; Wojciechowski, T.; Herkowiak, M.; Szparaga, A.; Czechowska-Kosacka, A. Application of artificial neural networks to analyze the emergence of soybean seeds after applying herbal treatments. J. Res. Appl. Agric. Eng. 2018, 63, 145–149. [Google Scholar]
- Majkovič, D.; O’Kiely, P.; Kramberger, B.; Vračko, M.; Turk, J.; Pažek, K.; Rozman, Č. Comparison of using regression modeling and an artificial neural network for herbage dry matter yield forecasting. J. Chemom. 2016, 30, 203–209. [Google Scholar] [CrossRef]
- Gorzelany, J.; Belcar, J.; Kuźniar, P.; Niedbała, G.; Pentoś, K. Modelling of Mechanical Properties of Fresh and Stored Fruit of Large Cranberry Using Multiple Linear Regression and Machine Learning. Agriculture 2022, 12, 200. [Google Scholar] [CrossRef]
- Sabzi-Nojadeh, M.; Niedbała, G.; Younessi-Hamzekhanlu, M.; Aharizad, S.; Esmaeilpour, M.; Abdipour, M.; Kujawa, S.; Niazian, M. Modeling the Essential Oil and Trans-Anethole Yield of Fennel (Foeniculum vulgare Mill. var. vulgare) by Application Artificial Neural Network and Multiple Linear Regression Methods. Agriculture 2021, 11, 1191. [Google Scholar] [CrossRef]
- Lu, M.; AbouRizk, S.M.; Hermann, U.H. Sensitivity Analysis of Neural Networks in Spool Fabrication Productivity Studies. J. Comput. Civ. Eng. 2001, 15, 299–308. [Google Scholar] [CrossRef]
- Nourani, V.; Sayyah Fard, M. Sensitivity analysis of the artificial neural network outputs in simulation of the evaporation process at different climatologic regimes. Adv. Eng. Softw. 2012, 47, 127–146. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015; ISBN 978-92-5-108369-7. [Google Scholar]
- TIBCO Statistica® Automated Neural Networks. Available online: https://community.tibco.com/wiki/tibco-statistica-automated-neural-networks (accessed on 10 January 2022).
- Bhojani, S.H.; Bhatt, N. Wheat crop yield prediction using new activation functions in neural network. Neural Comput. Appl. 2020, 32, 13941–13951. [Google Scholar] [CrossRef]
- Niedbała, G.; Piekutowska, M.; Weres, J.; Korzeniewicz, R.; Witaszek, K.; Adamski, M.; Pilarski, K.; Czechowska-Kosacka, A.; Krysztofiak-Kaniewska, A. Application of Artificial Neural Networks for Yield Modeling of Winter Rapeseed Based on Combined Quantitative and Qualitative Data. Agronomy 2019, 9, 781. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Mas, D.M.L.; Ahlfeld, D.P. Comparing artificial neural networks and regression models for predicting faecal coliform concentrations. Hydrol. Sci. J. 2007, 52, 713–731. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Nyarko, E.K.; Morić, D. A neural network based modelling and sensitivity analysis of damage ratio coefficient. Expert Syst. Appl. 2011, 38, 13405–13413. [Google Scholar] [CrossRef]
- Farjam, A.; Omid, M.; Akram, A.; Fazel Niari, Z. A neural network based modeling and sensitivity analysis of energy inputs forpredicting seed and grain corn yields. J. Agric. Sci. Technol. 2014, 16, 767–778. [Google Scholar]
- Niedbała, G.; Kozłowski, R.J. Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Wheat. J. Agric. Sci. Technol. 2019, 21, 51–61. [Google Scholar]
- Ku, Y.-S.; Au-Yeung, W.-K.; Yung, Y.-L.; Li, M.-W.; Wen, C.-Q.; Liu, X.; Lam, H.-M. Drought Stress and Tolerance in Soybean. In A Comprehensive Survey of International Soybean Research—Genetics, Physiology, Agronomy and Nitrogen Relationships; InTech: Palm Beach, FL, USA, 2013; Available online: https://books.google.co.jp/books?hl=zh-CN&lr=&id=87WiDwAAQBAJ&oi=fnd&pg=PA209&dq=Drought+Stress+and+Tolerance+in+Soybean&ots=fzzy8-mhTX&sig=Eqnob_LJ7Xh4MsPOQCWxpjwH6ng#v=onepage&q=Drought%20Stress%20and%20Tolerance%20in%20Soybean&f=false (accessed on 10 January 2022).
- Oya, T.; Lima Nepomuceno, A.; Neumaier, N.; Bouças Farias, J.R.; Tobita, S.; Ito, O. Drought Tolerance Characteristics of Brazilian Soybean Cultivars—Evaluation and characterization of drought tolerance of various Brazilian soybean cultivars in the field. Plant Prod. Sci. 2004, 7, 129–137. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Serbin, S.P. Impacts of recent climate change on Wisconsin corn and soybean yield trends. Environ. Res. Lett. 2008, 3, 34003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).