Estimation of Greenhouse Tomato Foliage Temperature Using DNN and ML Models
Abstract
:1. Introduction
1.1. Leaf Temperature—Its Importance and Methods of Measurement
1.2. Machine Learning and Neural Networks in Horticulture
2. Material and Methods
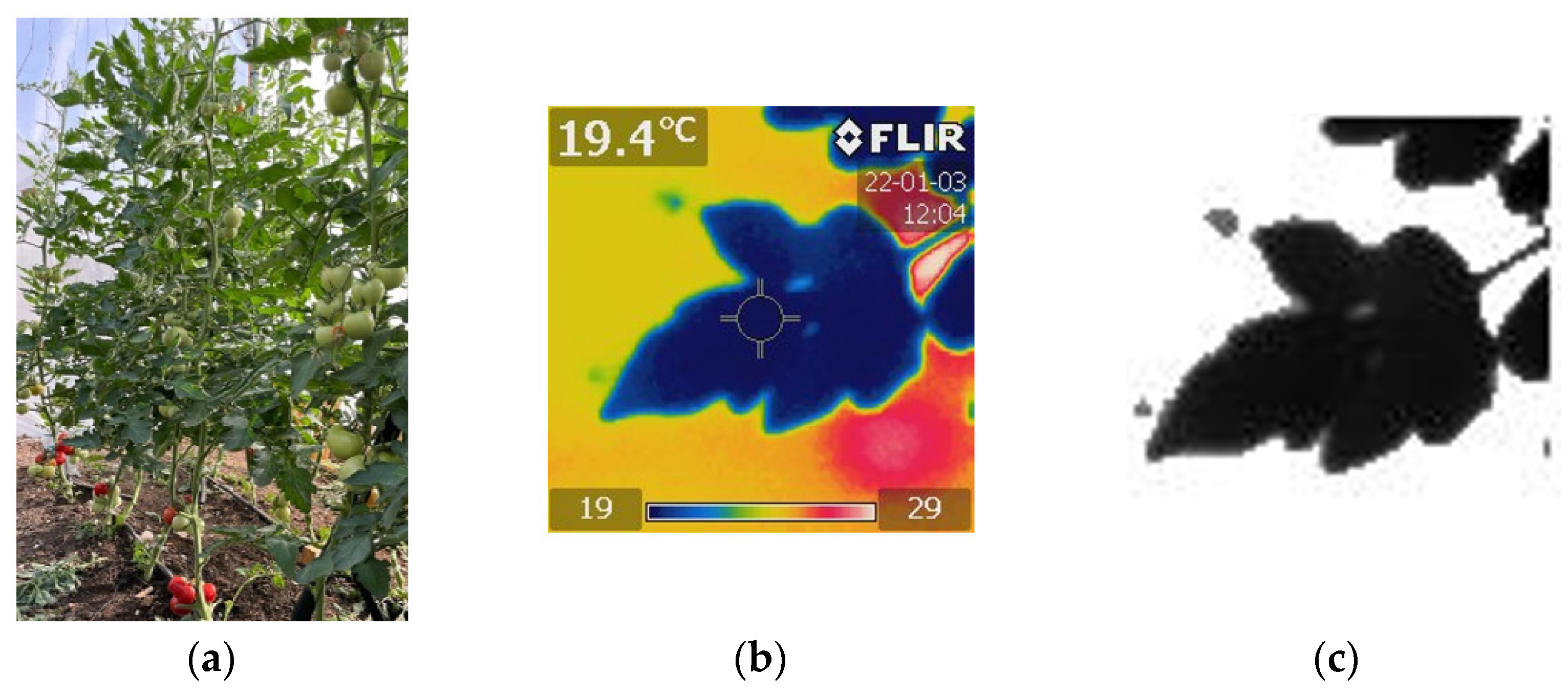
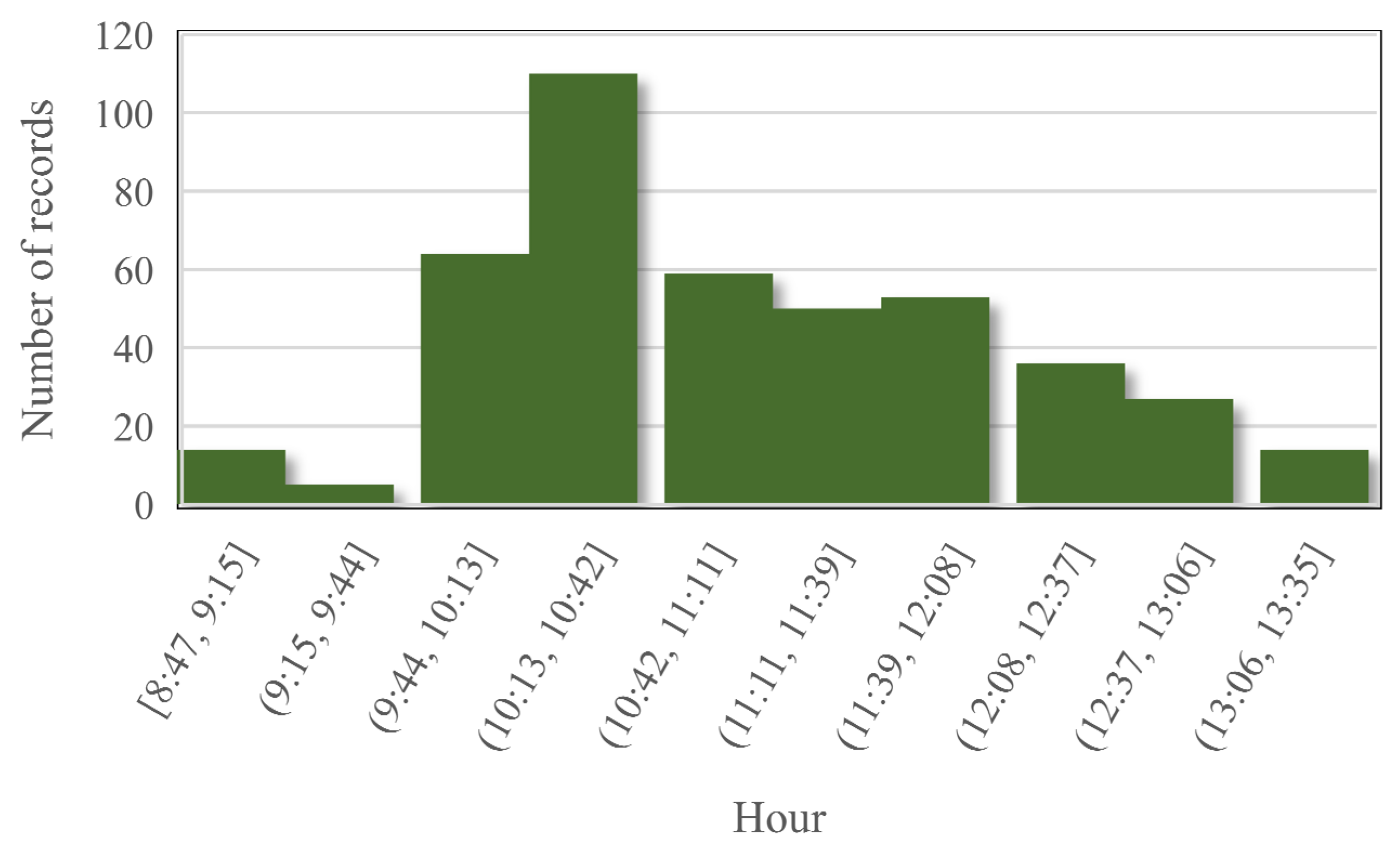
2.1. Experimental Work
2.2. Methods Used in the Models
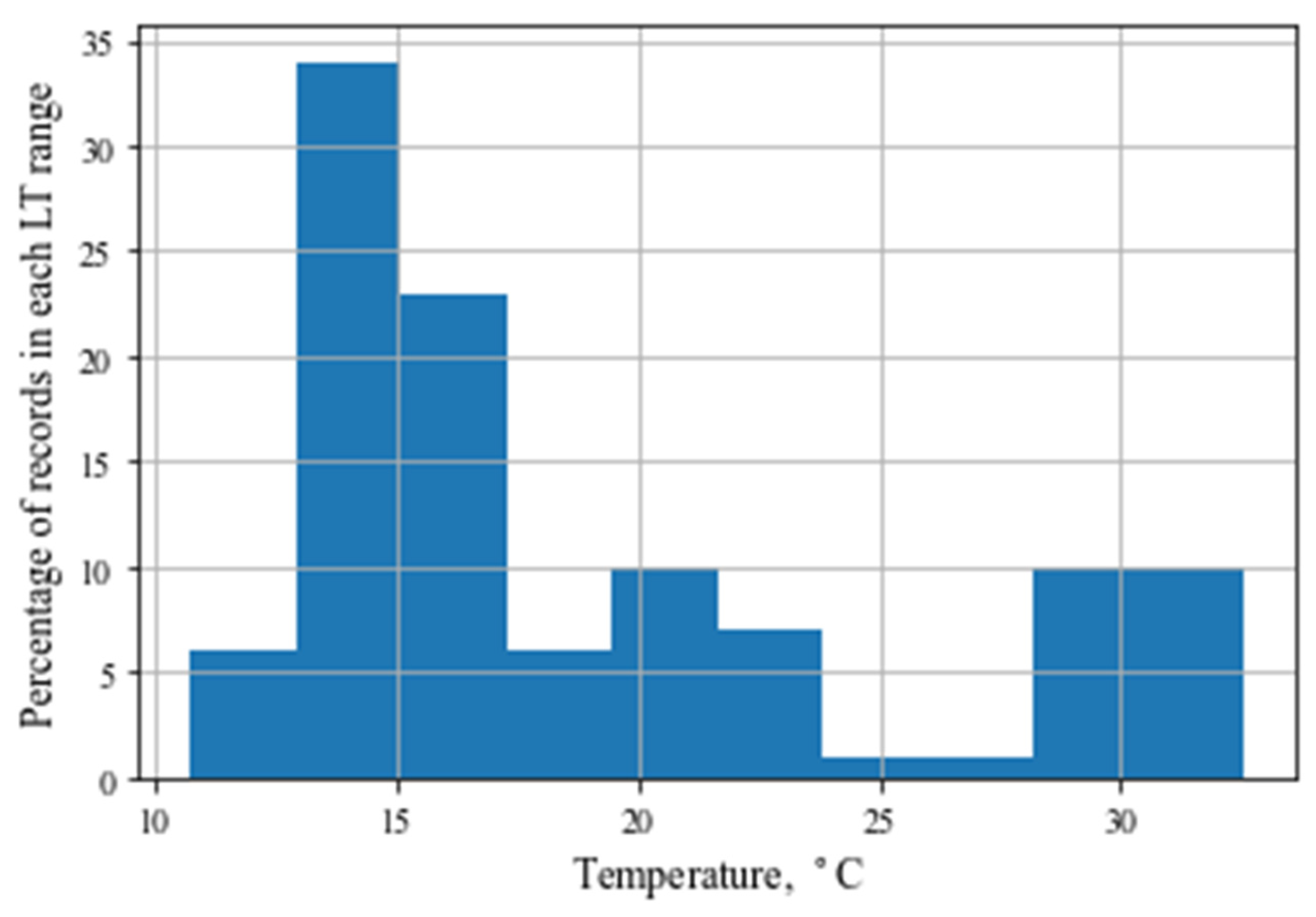
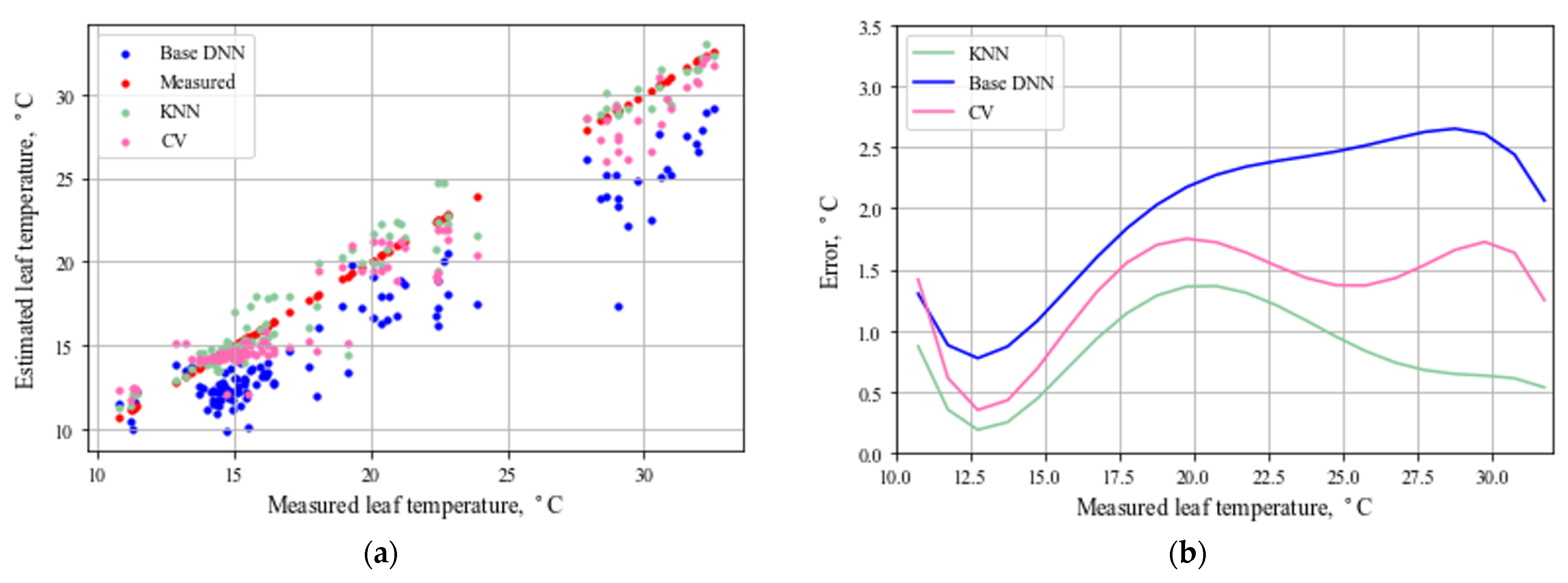
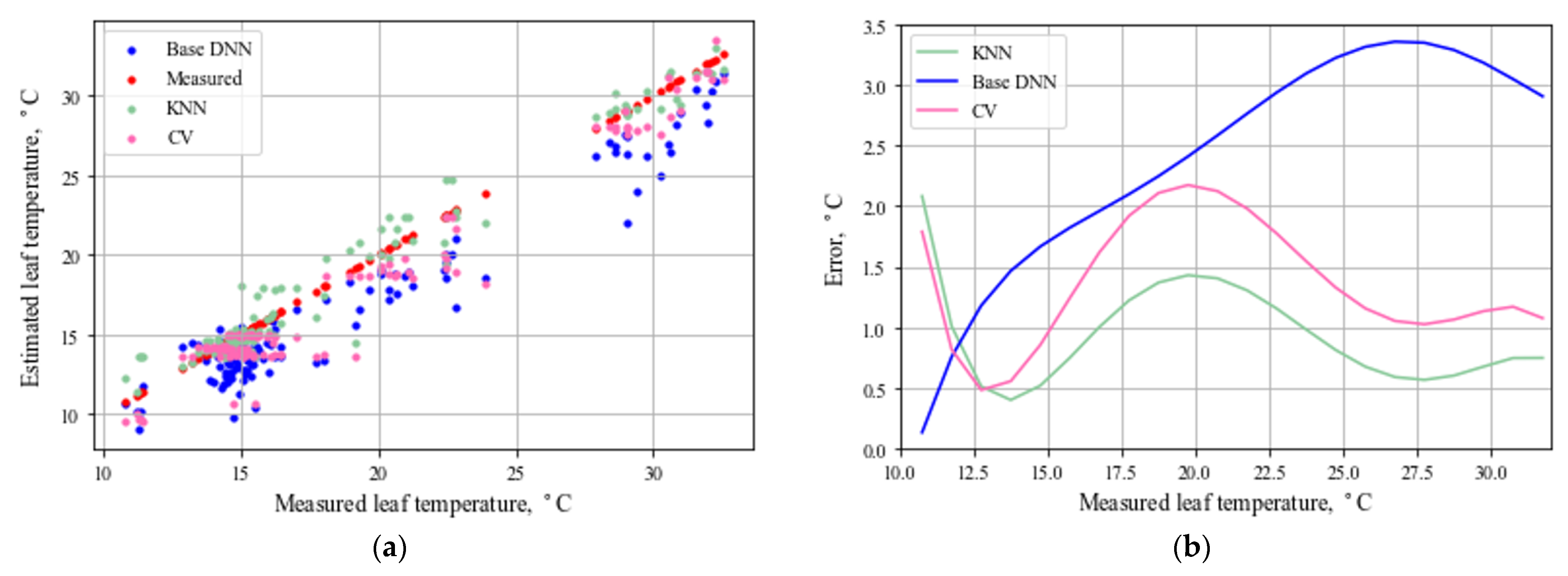
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. DNN Model Diagrams
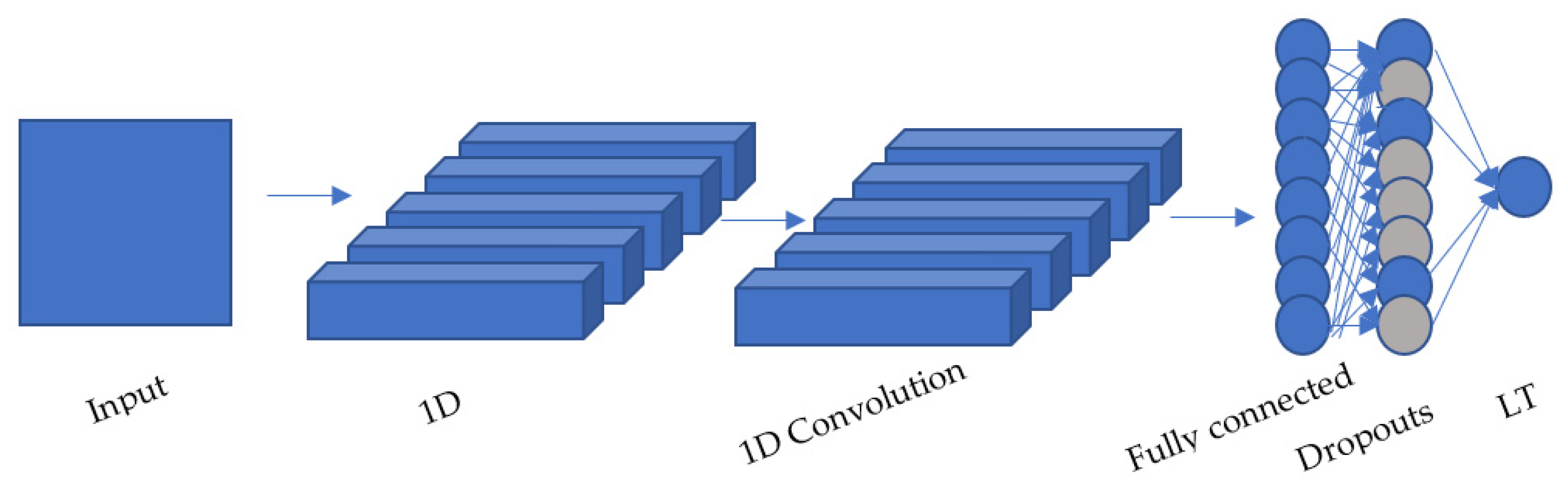

References
- Gutschick, V. Leaf energy balance: Basics, and modeling from leaves to canopies. Canopy Photosynth. Basics Appl. 2016, 42, 23–58. [Google Scholar]
- Urban, J.; Ingwers, W.M.; McGuire, M.A.; Teskey, R.O. Increase in leaf temperature opens stomata and decouples net photosynthesis from stomatal conductance in Pinus taeda and Populus deltoides x nigra. J. Exp. Bot. 2017, 68, 1757–1767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vijayakumar, A.; Shaji, S.; Beena, R.; Sarada, S.; Sajitha Rani, T.; Stephen, R.; Manju, R.V.; Viji, M.M. High temperature induced changes in quality and yield parameters of tomato (Solanum lycopersicum L.) and similarity coefficients among genotypes using SSR markers. Heliyon 2021, 7, e05988. [Google Scholar] [CrossRef] [PubMed]
- Niu, G.; Kozai, T.; Sabeh, N. Physical environmental factors and their properties. Plant Fact. 2020, 11, 185–195. [Google Scholar]
- Seginer, I. Alternative design formulae for the ventilation rate of greenhouses. J. Agric. Engng Res. 1997, 68, 355–365. [Google Scholar] [CrossRef]
- Stanghellini, C. Transpiration of Greenhouse Crops: An Aid to Climate Management. Ph.D. Thesis, Agriculture University Wageningen, Wageningen, The Netherlands, 1987; 150p. [Google Scholar]
- Papadakis, G.; Frangondakis, A.; Kyritsis, S. Experimental investigation and modelling of heat and mass transfer between a tomato crop and the greenhouse environment. J. Agric. Engng. Res. 1994, 57, 217–227. [Google Scholar] [CrossRef]
- Wang, S.; Deltour, J. An experimental model for leaf temperature of greenhouse-growm tomato. Int. Soc. Hortic. Sci. 2021, 491, 101–106. [Google Scholar]
- Yu, L.; Wang, W.; Zhang, X.; Zheng, W. A Review on leaf temperature sensor: Measurement Methods and Application. Comput. Comput. Technol. Agric. IX 2016, 478, 216–230. [Google Scholar]
- Tarnopolsky, M.; Seginer, I. Leaf temperature error from heat conduction along thermocouple wires. Agric. For. Meteorol. 1999, 93, 185–194. [Google Scholar] [CrossRef]
- Canopy Temperature and Its Measurement by the Hand-Held Infrared Thermometer in the Field. Available online: https://plantstress.com/leaf-canopy-temperature (accessed on 10 May 2022).
- Leigh, A.; Close, D.J.; Ball, C.M.; Siebke, K.; Nicotra, N.B. Leaf cooling curves: Measuring leaf temperature in sunlight. Funct. Plant Biol. 2006, 33, 515–519. [Google Scholar] [CrossRef] [PubMed]
- Dariouchy, A.; Aassif, E.; Lekouch, K.; Bouirden, L.; Maze, G. Prediction of the intern parameters tomato greenhouse in a semi-arid area using a time-series model of artificial neural networks. Measurement 2009, 42, 456–463. [Google Scholar] [CrossRef]
- Linker, R.; Seginer, I.; Gutman, P.O. Optimal CO2 control in a greenhouse modeled with neural networks. Comput. Electron. Agric. 1998, 19, 289–310. [Google Scholar] [CrossRef]
- Hu, H.-G.; Xu, L.-H.; Wei, R.-H.; Zhu, B.-K. RBF network based nonlinear model reference adaptive PD controller design for greenhouse climate. Int. J. Adv. Comput. Technol. 2011, 3, 357–366. [Google Scholar]
- King, B.A.; Shellie, K.C. Evaluation of neural network modeling to predict non-water-stressed leaf temperature in wine grape for calculation of crop water stress index. Agric. Water Manag. 2016, 167, 38–52. [Google Scholar] [CrossRef]
- Patil, R.R.; Kumar, S.; Rani, R. Comparison of artificial intelligence algorithms in plant disease prediction, Revue d’Intelligence Artificielle. Int. Inf. Eng. Technol. Assoc. 2022, 36, 185–193. [Google Scholar]
- Kaur, P.; Harnal, S.; Tiwari, R.; Upadhyay, S.; Bhatia, S.; Mashat, A.; Alabdali, A.M. Recognition of leaf disease using hybrid convolutional neural network by applying feature reduction. Sensors 2022, 22, 575. [Google Scholar] [CrossRef] [PubMed]
- Ramana, K.; Aluvala, R.; Kumar, M.R.; Nagaraja, G.; Krishna, A.V.; Nagendra, P. Leaf disease classification in smart agriculture using deep neural network architecture and IoT. J. Circuits Syst. Comput. 2022, 31, 2240004. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Ma, D.; Yang, C.; Meng, F. Prediction model of transpiration of greenhouse tomato based on LSTM. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2021, 52, 369–376. [Google Scholar]
- Qu, Y.; Clausen, A.; Jørgensen, B.N. Net photosynthesis prediction by deep learning for commercial greenhouse production. In Proceedings of the INES 2021—IEEE 25th International Conference on Intelligent Engineering Systems, Budapest, Hungary, 7–9 July 2021; Volume 9512919, pp. 139–144. [Google Scholar]
- Wang, L.; Wang, P.; Liang, S.; Qi, X.; Li, L.; Xu, L. Monitoring maize growth conditions by training a BP neural network with remotely sensed vegetation temperature condition index and leaf area index. Comput. Electron. Agric. 2019, 160, 82–90. [Google Scholar] [CrossRef]
- How Do I Know Which Test Train to Split? Available online: https://it-qa.com/how-do-i-know-which-test-train-to-split/ (accessed on 10 May 2022).
- Manikumri, N.; Vinodhini, G.; Murugappan, A. Modeling of reference evapotranspiration using climatic parameters for irrigation scheduling using machine learning with limited data. ISH J. Hydraul. Eng. 2021, 28, 272–281. [Google Scholar]


| Sensor | 2D Sonic Anemometer (Windsonic, Gill, UK) | Dry and Wet Bulb (Type T Thermocouples) | Pyranometer (LI-COR LI-200SZ, LI-200R) | Global Sun Radiation (CMP3) | Diffuse Sun Radiation (CMP3) |
|---|---|---|---|---|---|
| Number of sensors | 1 | 3, in each GH 1 in M | 1, in each GH 1 in M | 1 | 1 |
| Sensor location | M (at a height of 6 m) | GH: 0.5, 1.4, and 2 m above the ground M: about 4 m above ground | GH: at the top of the canopy in the southeastern side of the greenhouse | M: at a height of about 6 m | M: at a height of about 5 m |
| Sensor accuracy | ±2% at 12 ms−1 | ±0.5 °C | 3% | <20 Wm−2 | <20 Wm−2 |
| Season | Diffused Radiation Wm−2 | Global Radiation Wm−2 | Wind Speed ms−1 | Air Temperature °C | RH % |
|---|---|---|---|---|---|
| Summer | 140.57 ± 38.51 | 866.77 ± 41.87 | 2.13 ± 0.56 | 31.95 ± 1.63 | 53.61 ± 11.99 |
| Winter | 109.56 ± 48.45 | 264.17 ± 218.74 | 1.79 ± 0.58 | 14.48 ± 2.63 | 54.17 ± 14.91 |
| Greenhouse | Season | RH Gradient, %m−1 | Temperature Gradient °Cm−1 | Radiation Wm−2 | RH % | Air Temperature °C |
|---|---|---|---|---|---|---|
| Red OPV | Summer | −7.22 ± 2.61 | 1.29 ± 0.46 | 352.53 ± 78.05 | 55.92 ± 6.37 | 31.55 ± 1.24 |
| Winter | −4.19 ± 1.22 | 0.7 ± 0.34 | 176.96 ± 99.59 | 59.3 ± 15.31 | 15.83 ± 3.22 | |
| Blue OPV | Summer | −7 ± 2.87 | 1.23 ± 0.83 | 400.08 ± 64.29 | 48.59 ± 5.56 | 31.26 ± 1.34 |
| Winter | −4.99 ± 1.52 | 1.32 ± 0.88 | 182.14 ± 114.36 | 59.66 ± 15.53 | 16.17 ± 3.44 | |
| Control | Summer | −5.05 ± 5.14 | 0.84 ± 0.93 | 542.6 ± 30.06 | 57.41 ± 7.27 | 33.81 ± 1.1 |
| Winter | −1.85 ± 0.72 | 0.57 ± 0.31 | 197.83 ± 109.73 | 61.19 ± 16.18 | 15.57 ± 2.9 |
| BASE | CV |
|---|---|
| 1D convolution | Fully-connected (15) |
| 1D convolution | Fully-connected (10) |
| Fully-connected (10) | Dropouts (25%) |
| Dropouts (50%) | Fully-connected (1) |
| Fully-connected (1) |
| Parameter | BASE | CV | KNN |
|---|---|---|---|
| Err, °C | 1.76 | 0.93 | 0.69 |
| RMSE, °C | 2.27 | 1.29 | 1.01 |
| R2 | 0.96 | 0.98 | 0.99 |
| Parameter | BASE | CV | KNN | |||
|---|---|---|---|---|---|---|
| Err, °C | 2.09 | 1.76 | 1.18 | 0.93 | 0.8 | 0.69 |
| RMSE, °C | 2.51 | 2.27 | 1.63 | 1.29 | 1.13 | 1.01 |
| R2 | 0.96 | 0.96 | 0.98 | 0.98 | 0.98 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimberg, R.; Teitel, M.; Ozer, S.; Levi, A.; Levy, A. Estimation of Greenhouse Tomato Foliage Temperature Using DNN and ML Models. Agriculture 2022, 12, 1034. https://doi.org/10.3390/agriculture12071034
Grimberg R, Teitel M, Ozer S, Levi A, Levy A. Estimation of Greenhouse Tomato Foliage Temperature Using DNN and ML Models. Agriculture. 2022; 12(7):1034. https://doi.org/10.3390/agriculture12071034
Chicago/Turabian StyleGrimberg, Roei, Meir Teitel, Shay Ozer, Asher Levi, and Avi Levy. 2022. "Estimation of Greenhouse Tomato Foliage Temperature Using DNN and ML Models" Agriculture 12, no. 7: 1034. https://doi.org/10.3390/agriculture12071034
APA StyleGrimberg, R., Teitel, M., Ozer, S., Levi, A., & Levy, A. (2022). Estimation of Greenhouse Tomato Foliage Temperature Using DNN and ML Models. Agriculture, 12(7), 1034. https://doi.org/10.3390/agriculture12071034






