Novel Hybrid Statistical Learning Framework Coupled with Random Forest and Grasshopper Optimization Algorithm to Forecast Pesticide Use on Golf Courses
Abstract
:1. Introduction
2. Materials and Methods
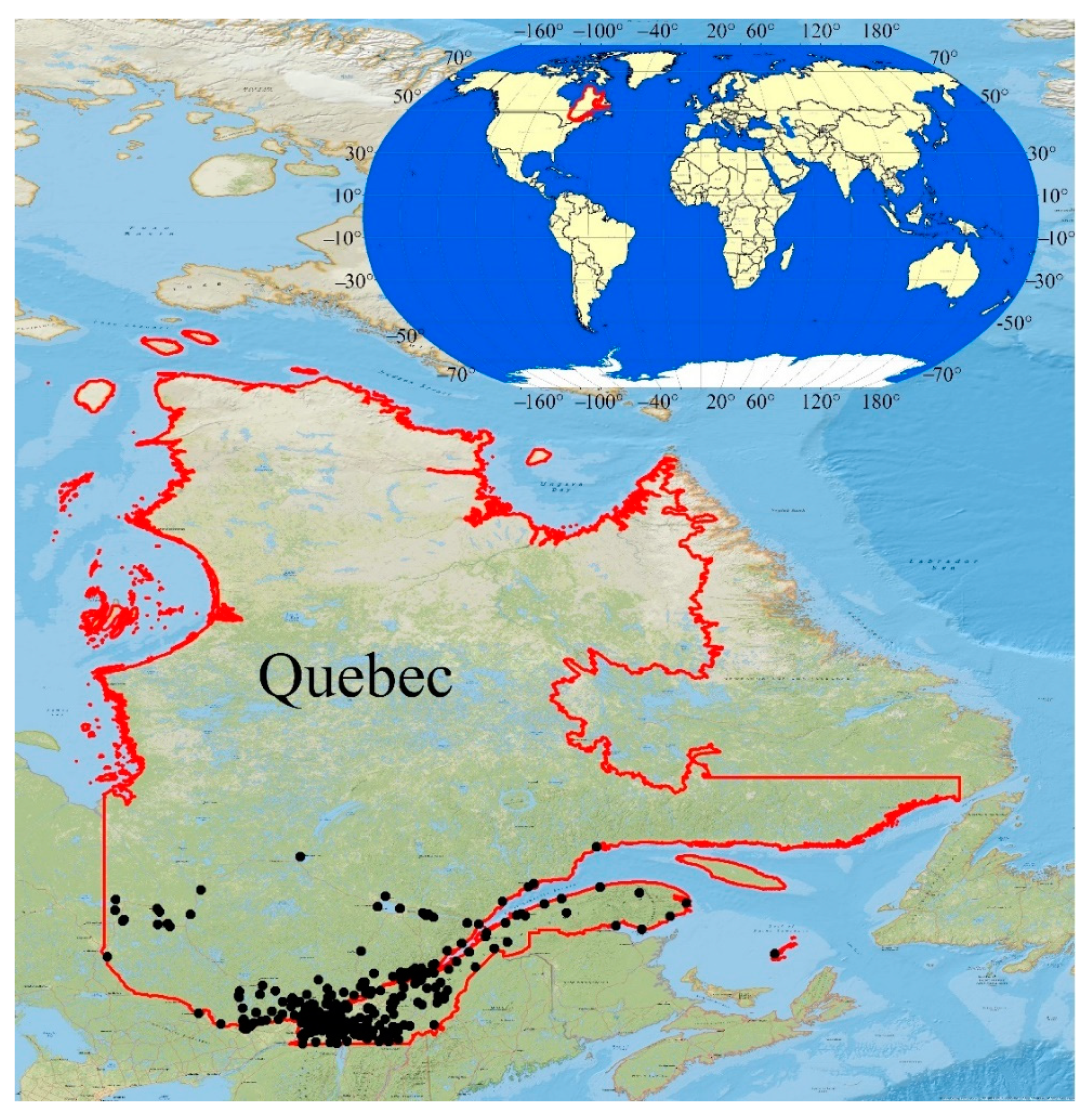
2.1. Golf Course Database
2.2. Theoretical Overview
2.2.1. Random Forest
2.2.2. Support Vector Machine (SVM)
2.2.3. Grasshopper Optimization Algorithm (GOA)
2.2.4. Developed Hybrid RF-SVM-GOA
2.3. Performance Evaluation Criteria
3. Results and Discussion
3.1. Tree-Based Methods in AIT Estimating
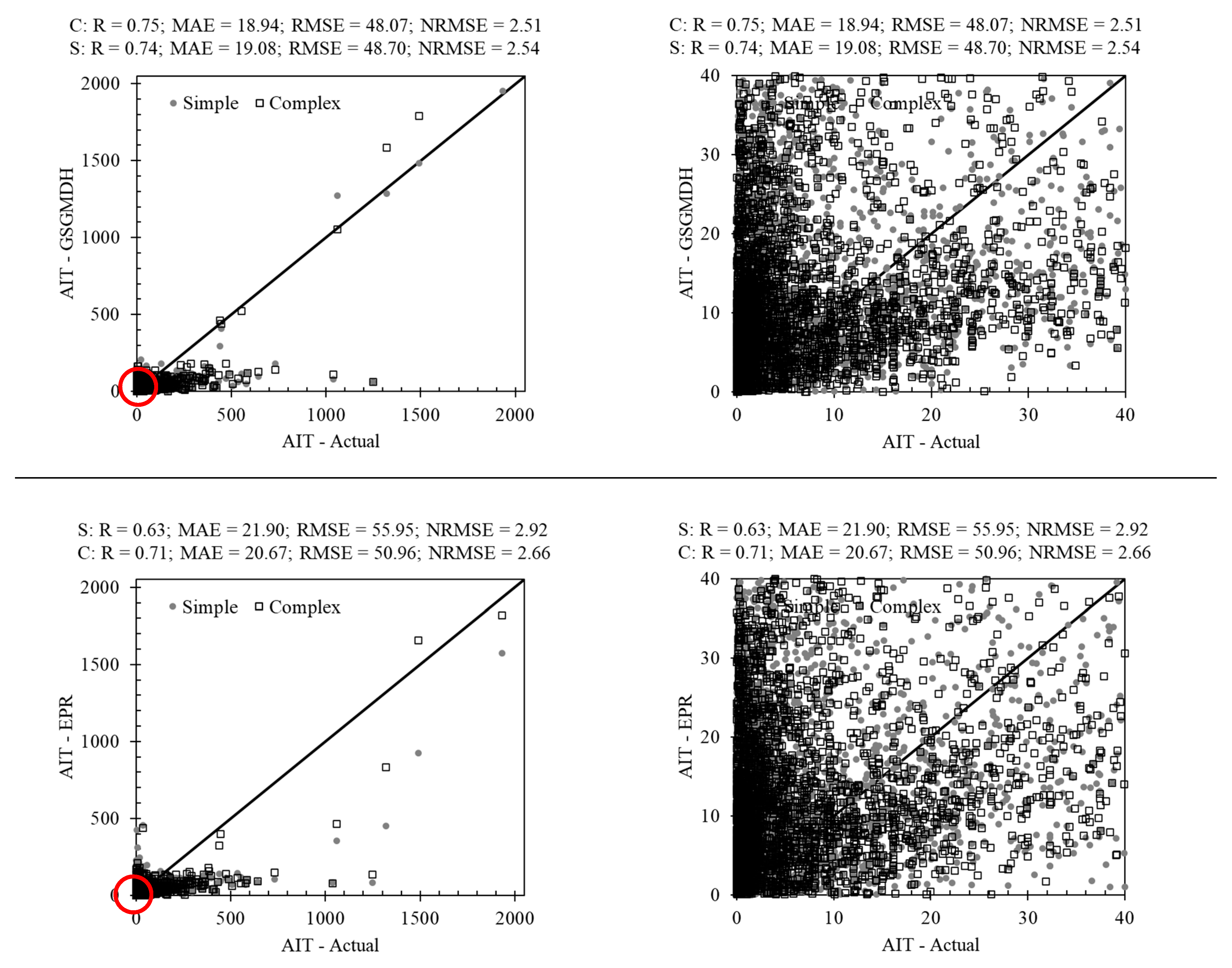
3.2. Non-Tree-Based Methods in AIT Estimating
3.3. AIT Estimating Using Hybrid Methods
3.4. Comparison of the Individual and Hybrid Methods in AIT Estimating
3.5. Evaluation of the Importance of Each of the Input Parameters in AIT Estimating
3.6. Sensitivity of the Developed Models on the Input Variables
4. Advantages, Limitations, and Future Improvements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stier, J.C.; Steinke, K.; Ervin, E.H.; Higginson, F.R.; McMaugh, P.E. Turfgrass Benefits and Issues. In Turfgrass: Biology, Use, and Management, 1st ed.; Stier, J.C., Horgan, B.P., Bonos, S.A., Eds.; Wiley: Hoboken, NJ, USA, 2013; Volume 56, pp. 105–145. [Google Scholar]
- Bekken, M.A.; Schimenti, C.S.; Soldat, D.J.; Rossi, F.S. A novel framework for estimating and analyzing pesticide risk on golf courses. Sci. Total Environ. 2021, 783, 146840. [Google Scholar] [CrossRef]
- Millington, B.; Wilson, B. An unexceptional exception: Golf, pesticides, and environmental regulation in Canada. Int. Rev. Sociol. Sport 2016, 51, 446–467. [Google Scholar] [CrossRef]
- Metcalfe, T.L.; Dillon, P.J.; Metcalfe, C.D. Detecting the transport of toxic pesticides from golf courses into watersheds in the Precambrian Shield region of Ontario, Canada. Environ. Toxicol. Chem. 2008, 27, 811–818. [Google Scholar] [CrossRef]
- Knopper, L.D.; Lean, D.R. Carcinogenic and genotoxic potential of turf pesticides commonly used on golf courses. J. Toxicol. Environ. Health Part B 2004, 7, 267–279. [Google Scholar] [CrossRef]
- Gouvernement du Québec. Ministère de l’Environnement et de la Lutte aux Changements ClimatiquesI; Loi sur les Pesticides, L.R.Q., Chapitre P-9.3; Gouvernement du Québec: Quebec City, QC, Canada, 2022.
- Baris, R.D.; Cohen, S.Z.; Barnes, N.L.; Lam, J.; Ma, Q. Quantitative analysis of over 20 years of golf course monitoring studies. Environ. Toxicol. Chem. 2010, 29, 1224–1236. [Google Scholar]
- Abadi, B. The determinants of cucumber farmers’ pesticide use behavior in central Iran: Implications for the pesticide use management. J. Clean. Prod. 2018, 205, 1069–1081. [Google Scholar] [CrossRef]
- Gan, H.; Wickings, K. Soil ecological responses to pest management in golf turf vary with management intensity, pesticide identity, and application program. Agric. Ecosyst. Environ. 2017, 246, 66–77. [Google Scholar] [CrossRef]
- Mackey, M.J.; Connette, G.M.; Peterman, W.E.; Semlitsch, R.D. Do golf courses reduce the ecological value of headwater streams for salamanders in the southern Appalachian Mountains? Landsc. Urban Plan. 2014, 125, 17–27. [Google Scholar] [CrossRef]
- Smith, M.D.; Conway, C.J.; Ellis, L.A. Burrowing owl nesting productivity: A comparison between artificial and natural burrows on and off golf courses. Wildl. Soc. Bull. 2005, 33, 454–462. [Google Scholar] [CrossRef]
- Wong, H.; Haith, D.A. Volatilization of Pesticides from Golf Courses in the United States: Mass Fluxes and Inhalation Health Risks. J. Environ. Qual. 2003, 42, 1615–1622. [Google Scholar] [CrossRef]
- Kearns, C.A.; Prior, L. Toxic greens: A preliminary study on pesticide usage on golf courses in Northern Ireland and potential risks to golfers and the environment. Saf. Secur. Eng. V 2013, 134, 173. [Google Scholar]
- Yang, M.; Cho, S.I. High-Resolution 3D Crop Reconstruction and Automatic Analysis of Phenotyping Index Using Machine Learning. Agriculture 2021, 11, 1010. [Google Scholar] [CrossRef]
- Diao, W.; Liu, G.; Zhang, H.; Hu, K.; Jin, X. Influences of Soil Bulk Density and Texture on Estimation of Surface Soil Moisture Using Spectral Feature Parameters and an Artificial Neural Network Algorithm. Agriculture 2021, 11, 710. [Google Scholar] [CrossRef]
- Huang, L.; Wu, K.; Huang, W.; Dong, Y.; Ma, H.; Liu, Y.; Liu, L. Detection of Fusarium Head Blight in Wheat Ears Using Continuous Wavelet Analysis and PSO-SVM. Agriculture 2021, 11, 998. [Google Scholar] [CrossRef]
- Carisse, O.; Fall, M.L. Decision Trees to Forecast Risks of Strawberry Powdery Mildew Caused by Podosphaera aphanis. Agriculture 2021, 11, 29. [Google Scholar] [CrossRef]
- Oman, K.; Barwicki, J.; Rzodkiewicz, W.; Dawidowski, M. Evaluation of mechanical and energetic properties of the forest residues shredded chips during briquetting process. Energies 2021, 14, 3270. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Bonakdari, H.; Jamshidi, A.; Pelletier, J.P.; Abram, F.; Tardif, G.; Martel-Pelletier, J.A. Warning machine learning algorithm for early knee osteoarthritis structural progressor patient screening. Ther. Adv. Musculoskelet. Dis. 2021, 13, 1759720X21993254. [Google Scholar] [CrossRef] [PubMed]
- Sharafi, H.; Ebtehaj, I.; Bonakdari, H.; Zaji, A.H. Design of a support vector machine with different kernel functions to predict scour depth around bridge piers. Nat. Hazards 2016, 84, 2145–2162. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 1st ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Azimi, H.; Bonakdari, H.; Ebtehaj, I. Design of radial basis function-based support vector regression in predicting the discharge coefficient of a side weir in a trapezoidal channel. Appl. Water Sci. 2019, 9, 78. [Google Scholar] [CrossRef] [Green Version]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Ebtehaj, I.; Bonakdari, H. A support vector regression-firefly algorithm-based model for limiting velocity prediction in sewer pipes. Water Sci. Technol. 2016, 73, 2244–2250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Rogers, S.M.; Matheson, T.; Despland, E.; Dodgson, T.; Burrows, M.; Simpson, S.J. Mechanosensory-induced behavioural gregarization in the desert locust Schistocerca gregaria. J. Exp. Biol. 2003, 206, 3991–4002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topaz, C.M.; Bernoff, A.J.; Logan, S.; Toolson, W. A model for rolling swarms of locusts. Eur. Phys. J. Spec. Top. 2008, 157, 93–109. [Google Scholar] [CrossRef] [Green Version]
- Akhbari, A.; Zaji, A.H.; Azimi, H.; Vafaeifard, M. Predicting the discharge coefficient of triangular plan form weirs using radian basis function and M5’methods. J. Appl. Res. Water Wastewater 2017, 4, 281–289. [Google Scholar]
- Kevric, J.; Jukic, S.; Subasi, A. An effective combining classifier approach using tree algorithms for network intrusion detection. Neural Comput. Appl. 2017, 28, 1051–1058. [Google Scholar] [CrossRef]
- Ojha, V.K.; Schiano, S.; Wu, C.Y.; Snášel, V.; Abraham, A. Predictive modeling of die filling of the pharmaceutical granules using the flexible neural tree. Neural Comput. Appl. 2018, 29, 467–481. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.J.; Jiang, T.H.; Ma, B.; You, Z.H.; Shi, W.L.; Cheng, L. HEMD: A highly efficient random forest-based malware detection framework for Android. Neural Comput. Appl. 2018, 30, 3353–3361. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Ebtehaj, I.; Bonakdari, H.; Es-haghi, M.S. Sediment transport modeling in rigid boundary open channels using generalize structure of group method of data handling. J. Hydrol. 2019, 577, 123951. [Google Scholar] [CrossRef]
- Bonakdari, H.; Ebtehaj, I.; Akhbari, A. Multi-objective evolutionary polynomial regression-based prediction of energy consumption probing. Water Sci. Technol. 2017, 75, 2791–2799. [Google Scholar] [CrossRef] [PubMed]
- Ebtehaj, I.; Bonakdari, H.; Shamshirband, S.; Mohammadi, K. A combined support vector machine-wavelet transform model for prediction of sediment transport in sewer. Flow Meas. Instrum. 2016, 47, 19–27. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Qian, S.S.; Anderson, C.W. Exploring factors controlling the variability of pesticide concentrations in the Willamette River Basin using tree-based models. Environ. Sci. Technol. 1999, 33, 3332–3340. [Google Scholar] [CrossRef]
- Yan, Y.; Feng, C.C.; Wan, M.P.H.; Chang, K.T.T. Multiple Regression and Artificial Neural Network for the Prediction of Crop Pest Risks. In Proceedings of the International Conference on Information Systems for Crisis Response and Management in Mediterranean Countries, Tunis, Tunisia, 28–30 October 2015; pp. 73–84. [Google Scholar]
- Shen, Y.; Zhao, E.; Zhang, W.; Baccarelli, A.A.; Gao, F. Predicting pesticide dissipation half-life intervals in plants with machine learning models. J. Hazard. Mater. 2022, 436, 129177. [Google Scholar] [CrossRef]
- Ibrahim, H.T.; Mazher, W.J.; Ucan, O.N.; Bayat, O. A grasshopper optimizer approach for feature selection and optimizing SVM parameters utilizing real biomedical data sets. Neural Comput. Appl. 2019, 31, 5965–5974. [Google Scholar] [CrossRef]








| Method | Parameter | Setting |
|---|---|---|
| RF | Bag size percentage | 100 |
| Batch size | 100 | |
| Maximum depth of tree | 10, 5 | |
| Number of decimal places | 2 | |
| Number of execution slots | 1 | |
| Number of features | 1 | |
| Number of iterations | 100 | |
| Seeds | 300, 10 | |
| RT | Number of randomly chosen attributes | 0 |
| Minimum total weights of instances in a leaf | 1 | |
| Minimum proportion of the variance of all data that need to be present at a node for splitting to be performed in regression trees | 0.001 | |
| Seed | 100 | |
| Maximum depth of tree | 5 | |
| REP Tree | Minimum total weights of instances in a leaf | 2 |
| Minimum proportion of the variance of all data that need to be present at a node for splitting to be performed in regression trees | 0.001 | |
| Seed | 100 | |
| Maximum tree depth | 5 | |
| M5P | Minimum number of instances to allow at a leaf node | 20 |
| Number of decimal places to be used for output of numbers in model | 20 | |
| GSGMDH | Maximum number of inputs for individual neurons | 3 |
| Maximal number of neurons in a layer | 10 | |
| Degree of polynomials in neurons | 3 | |
| EPR | Number of terms | 50, 200 |
| Maximum number of iterations | 50 | |
| Population size | 50 | |
| Crossover percentage | 0.35 | |
| Mutation percentage | 0.04 | |
| GOA | Maximum number of iterations | 1000 |
| Number of search agents | 70 | |
| cmin | 0.00001 | |
| cmax | 1 |
| AR | NH | GCI | Y | TA | Model No. | R2 | RMSE | NRMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| • | • | • | • | • | 1 | 0.999 | 0.839 | 0.843 | 0.044 |
| • | • | • | • | 2 | 0.003 | 303.782 | 480.594 | 25.072 | |
| • | • | • | • | 3 | 0.011 | 73.952 | 261.179 | 13.625 | |
| • | • | • | • | 4 | 0.020 | 54.141 | 204.369 | 10.661 | |
| • | • | • | • | 5 | 0.522 | 2.563 | 49.765 | 2.596 | |
| • | • | • | • | 6 | 0.522 | 2.563 | 49.766 | 2.596 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grégoire, G.; Fortin, J.; Ebtehaj, I.; Bonakdari, H. Novel Hybrid Statistical Learning Framework Coupled with Random Forest and Grasshopper Optimization Algorithm to Forecast Pesticide Use on Golf Courses. Agriculture 2022, 12, 933. https://doi.org/10.3390/agriculture12070933
Grégoire G, Fortin J, Ebtehaj I, Bonakdari H. Novel Hybrid Statistical Learning Framework Coupled with Random Forest and Grasshopper Optimization Algorithm to Forecast Pesticide Use on Golf Courses. Agriculture. 2022; 12(7):933. https://doi.org/10.3390/agriculture12070933
Chicago/Turabian StyleGrégoire, Guillaume, Josée Fortin, Isa Ebtehaj, and Hossein Bonakdari. 2022. "Novel Hybrid Statistical Learning Framework Coupled with Random Forest and Grasshopper Optimization Algorithm to Forecast Pesticide Use on Golf Courses" Agriculture 12, no. 7: 933. https://doi.org/10.3390/agriculture12070933








