Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method
Abstract
:1. Introduction
2. Determination of Intrinsic Soil Parameters
2.1. Soil Prototype and Particle Size Distribution
2.2. Soil Poisson’s Ratio Test
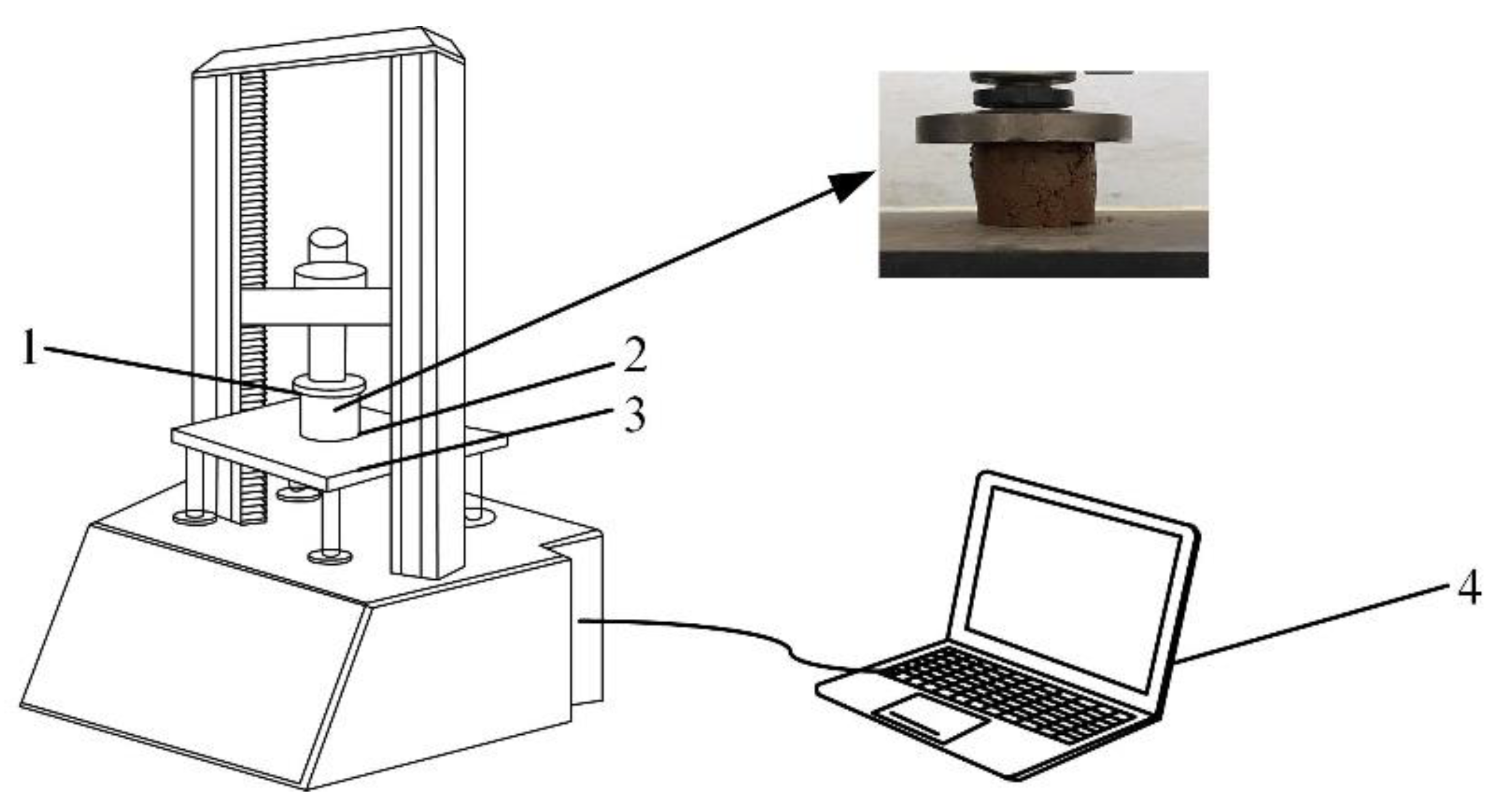
2.3. Soil Elastic Modulus and Shear Modulus Determination Test
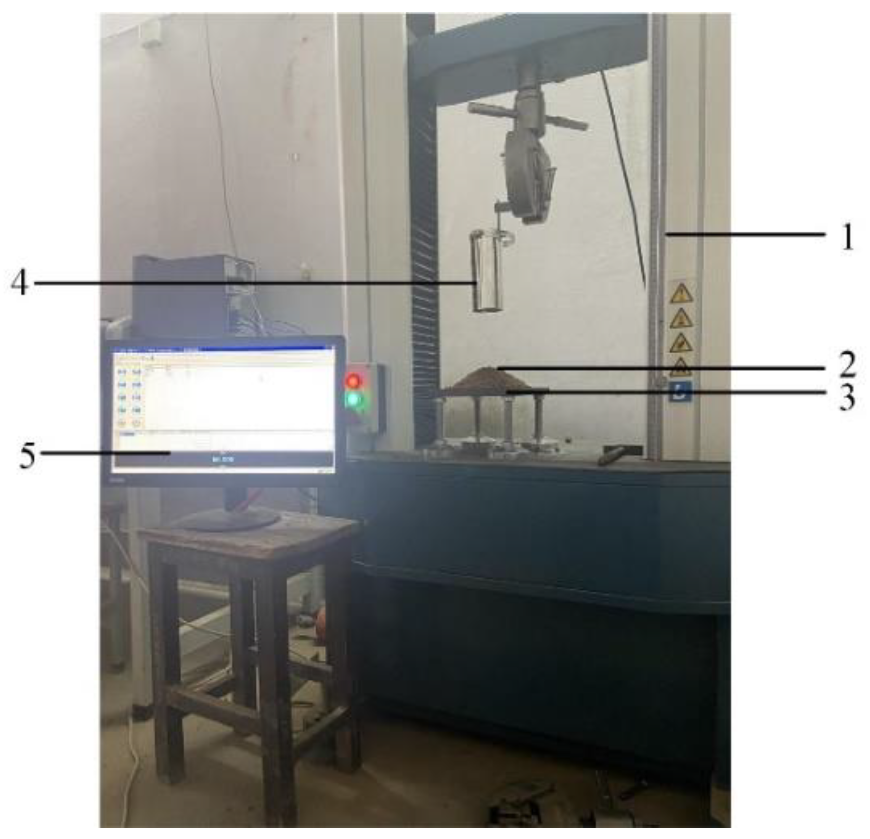
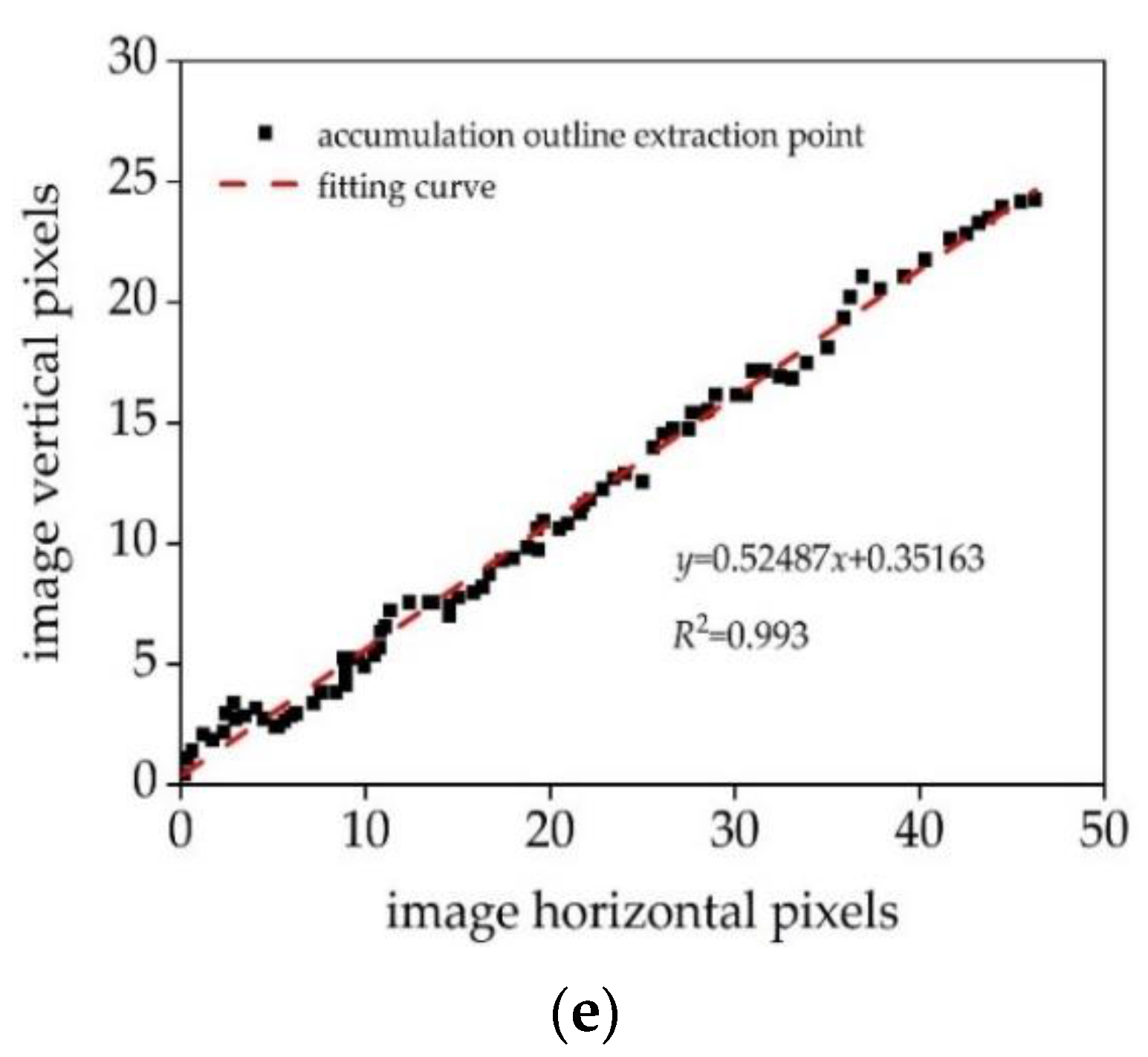
2.4. Soil Stacking Test
3. Simulation Calibration of Soil Simulation Parameters
3.1. Soil Simulation Model
3.2. Simulation Parameter Calibration Method
3.3. Results and Discussions
3.3.1. Plackett–Burman Test
3.3.2. Steepest Climb Test
3.3.3. Box–Behnken Test and Regression Model
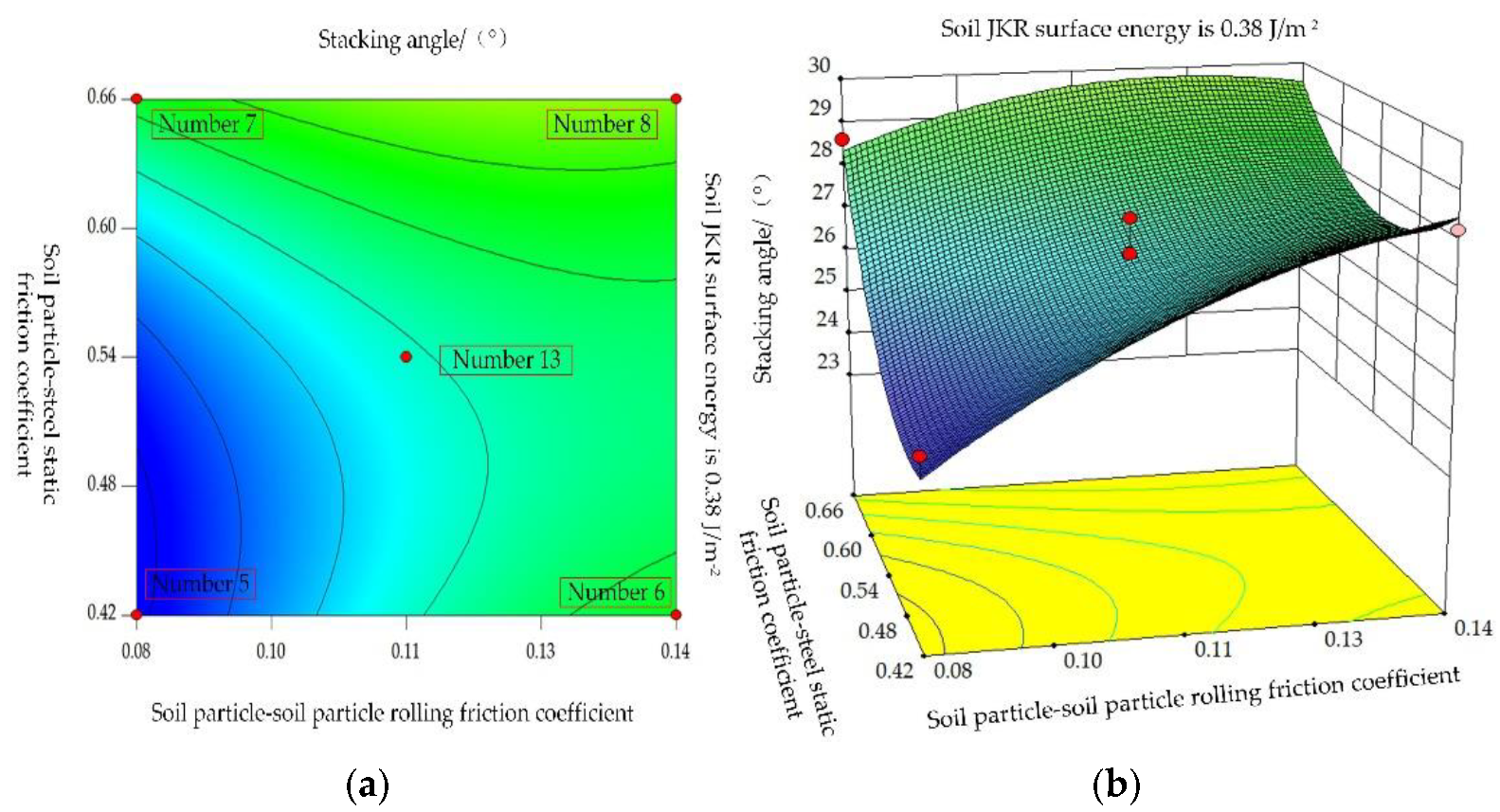
3.3.4. Regression Model Interaction Effect Analysis
3.4. Optimal Parameter Combination and Simulation Verification
4. Soil Cutting Resistance Test Verification
4.1. Experiment Purposes
4.2. Experiment Method and Index
4.2.1. Cutting Resistance Soil Bin Test
4.2.2. Cutting Resistance Simulation Test
4.3. Results and Discussions
5. Conclusions
- (1)
- Aiming at the cinnamon soil with yellow sandy soil characteristics commonly found in wheat fields in Luoyang, China, the Hertz–Mindlin with JKR as the contact model between soil particles, and the soil samples with a moisture content of 11.62% were simulated by using the method of combining physical test and simulation test. Through tests, we found that the average Poisson’s ratio of soil was 0.311. The average elastic modulus of soil was 10 MPa. The average shear modulus was 3.814 MPa. The mean value of the soil stacking angle was 27.69°.
- (2)
- On the basis of the physical test results, the Plackett–Burman test was carried out. The results of variance analysis showed that the cinnamon soil–cinnamon soil rolling friction coefficient (A), soil JKR surface energy (B), and cinnamon soil–steel static friction coefficient (C) had significant effects on the soil stacking angle.
- (3)
- The Box–Behnken test was carried out on the significant parameters, and the second-order regression model of the accumulation angle and the significant parameters was established. Taking the accumulation angle test value of 27.69° as the objective, the optimal solution was obtained: cinnamon soil–cinnamon soil rolling friction coefficient (A) was 0.08, soil JKR surface energy (B) was 0.37 J/m−2, and cinnamon soil–steel static friction coefficient (C) was 0.64. The relative error between the optimal parameter combination stacking angle and the actual physical stacking angle was 0.253%.
- (4)
- The working resistance test data were consistent with the analysis results, which showed that the directrixes forms of soil-engaging components has an important influence on its working resistance. Horizontal working resistance of the circular, parabolic, and bionic surface bulldozing plates decreased by 50.60%, 17.30%, and −5.35%, respectively, compared with the ruled surface. Exploring the influence mechanism between the directrix form of soil-engaging surface and working resistance in order to obtain lower working resistance will be one of the main research directions of energy-saving design of soil contact surface in the future.
- (5)
- To verify the accuracy of the calibrated and optimized parameters of the discrete element model, the indoor soil bin cutting resistance test and the simulation cutting resistance test were compared and analyzed. It was found that the test error of the simulation test compared with the measured test was within the acceptable range of 10.32%, indicating that the physical and mechanical properties of the simulation soil model were essentially consistent with the actual soil, which verified the accuracy and reliability of the cinnamon soil discrete element simulation parameter calibration results and research methods. The research results can provide basic data for the simulation of cutting resistance research of cinnamon-soil-engaging components.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, S.L.; Zhang, S.L.; Dang, Y.H.; Guo, L.P.; Li, L.J.; Gao, P.C.; Wang, R. Effect of field management practices on nitrogen and phosphate leaching in the cinnamon soil area of China. Chin. J. Eco-Agric. 2021, 29, 163–175. [Google Scholar]
- Han, W.; Xu, X.X.; Li, D.; Zhang, L.; Li, N.; Tan, B.Y.; Zhu, T.X.; Li, S.; Yi, Y.L. Effect of tillage methods on soil penetration resistance and its mechanism in the cinnamon soil area of western Liaoning Province. J. Soil Water Conserv. 2020, 34, 143–149. [Google Scholar]
- Mouazen, A.M.; Neményi, M. Tillage tool design by the finite element method: Part 1. Finite element modeling of soil plastic behaviour. J. Agric. Engng Res. 1999, 72, 37–51. [Google Scholar] [CrossRef]
- Abo-Elnor, M.; Hamilton, R.; Boyle, J.T. Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis. Soil Till. Res. 2004, 75, 61–73. [Google Scholar] [CrossRef]
- Zhang, R.; Li, J.Q.; Zhou, C.H.; Xu, S.C. Simulation of dynamic behavior of soil ahead of the bulldozing plates with different surface configurations by discrete element method. Trans. Chin. Soc. Agric. Eng. 2007, 23, 13–19. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Mak, J.; Chen, Y.; Sadek, M.A. Determining parameters of a discrete element model for soil-tool interaction. Soil Till. Res. 2012, 118, 117–122. [Google Scholar] [CrossRef]
- Chen, Y.; Munkholm, L.J.; Nyord, T. A discrete element model for soil-sweep interaction in three different soils. Soil Till. Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Zdancevičius, E.; Kačianauskas, R.; Zabulionis, D. Improvement of viscoelastic damping for the hertz contact of particles due to impact velocity. Procedia Eng. 2017, 172, 1286–1290. [Google Scholar] [CrossRef]
- Tong, J.; Mohammad, M.A.; Zhang, J.B.; Ma, Y.H.; Rong, B.J.; Chen, D.H.; Menon, C. DEM numerical simulation of abrasive wear characteristics of a bioinspired ridged surface. J. Bionic Eng. 2010, 7, 175–181. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.H.; Wang, X.C. Critical review of applications of discrete element method in agricultural engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modeling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Shi, L.R.; Zhao, W.Y.; Sun, W. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2017, 33, 181–187. [Google Scholar]
- Zhang, R.; Han, D.L.; Ji, Q.L.; He, Y.; Li, J.Q. Calibration methods of sandy soil parameters in simulation of discrete element method. Trans. Chin. Soc. Agric. Mach. 2017, 48, 49–56. [Google Scholar]
- Xing, J.J.; Zhang, R.; Wu, P.; Zhang, X.R.; Dong, X.H.; Chen, Y.; Ru, S.F. Parameter calibration of discrete element model for latosol particles in hot areas of Hainan Province. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–166. [Google Scholar]
- Li, J.W.; Tong, J.; Hu, B.; Wang, H.B.; Mao, C.Y.; Ma, Y.H. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China. Trans. Chin. Soc. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
- Zhong, W.Q.; Yu, A.B.; Liu, X.J.; Tong, Z.B.; Zhang, H. DEM/CFD-DEM modelling of non-spherical particulate systems: Theoretical developments and applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Wang, X.L.; Hu, H.; Wang, Q.J.; Li, H.W.; He, J.; Chen, W.Z. Calibration method of soil contact characteristic parameters based on DEM theory. Trans. Chin. Soc. Agric. Mach. 2017, 48, 78–85. [Google Scholar]
- Tian, X.L.; Cong, X.; Qi, J.T.; Guo, H.; Li, M.; Fan, X.H. Parameter calibration of discrete element model for corn straw and soil mixture in black soil areas. Trans. Chin. Soc. Agric. Mach. 2021, 52, 100–108+242. [Google Scholar]
- Muller, D.; Fimbinger, E.; Brand, C. Algorithm for the determination of the angle of repose in bulk material analysis. Powder Technol. 2021, 383, 598–605. [Google Scholar] [CrossRef]
- Wu, T.; Huang, W.F.; Chen, X.S.; Ma, X.; Han, Z.Q.; Pan, T. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles. J. South China Agric. Univ. 2017, 38, 93–98. [Google Scholar]
- Dai, F.; Song, X.F.; Zhao, W.Y.; Zhang, F.W.; Ma, H.J.; Ma, M.Y. Simulative calibration on contact parameters of discrete elements for covering soil on whole plastic film mulching on double ridges. Trans. Chin. Soc. Agric. Mach. 2019, 50, 49–56+77. [Google Scholar]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modeling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Xiang, W.; Wu, M.L.; Lü, J.N.; Quan, W.; Ma, L.; Liu, J.J. Calibration of simulation physical parameters of clay loam based on soil accumulation test. Trans. Chin. Soc. Agric. Eng. 2019, 35, 116–123. [Google Scholar]
- Hou, Z.F.; Dai, N.Z.; Chen, Z.; Chou, Y.; Zhang, X.W. Measurement and calibration of physical property parameters for Agropyron seeds in a discrete element simulation. Trans. Chin. Soc. Agric. Eng. 2020, 36, 46–54. [Google Scholar]
- Zhang, Y. Research on The Stress Fluctuation Behavior of Soil in the Working Process of Bulldozing Plates. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2015. [Google Scholar]
- Guo, Z.J.; Du, G.; Li, Z.L.; Li, X.P. Orthogonal experiment on resistance reduction by soil-engaging surfaces of bulldozer blade. Trans. Chin. Soc. Agric. Mach. 2015, 46, 372–378. [Google Scholar]
- Godwin, R.J. A review of the effect of implement geometry on soil failure and implement forces. Soil Till. Res. 2007, 97, 311–400. [Google Scholar] [CrossRef]
- Li, C.; Shen, J. Similarity analysis and scaling: An application to soil infiltration properties. Hydrol. Process. 1994, 8, 543–550. [Google Scholar] [CrossRef]




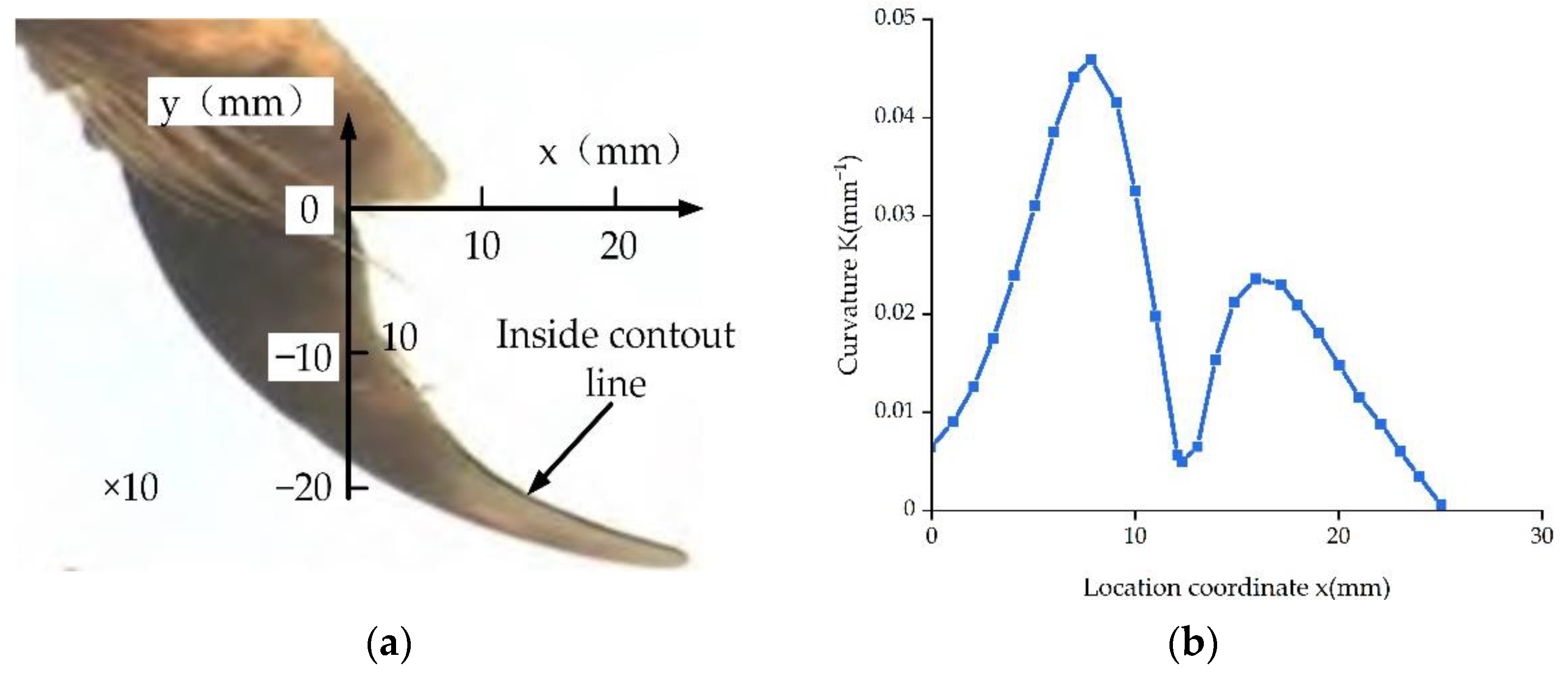

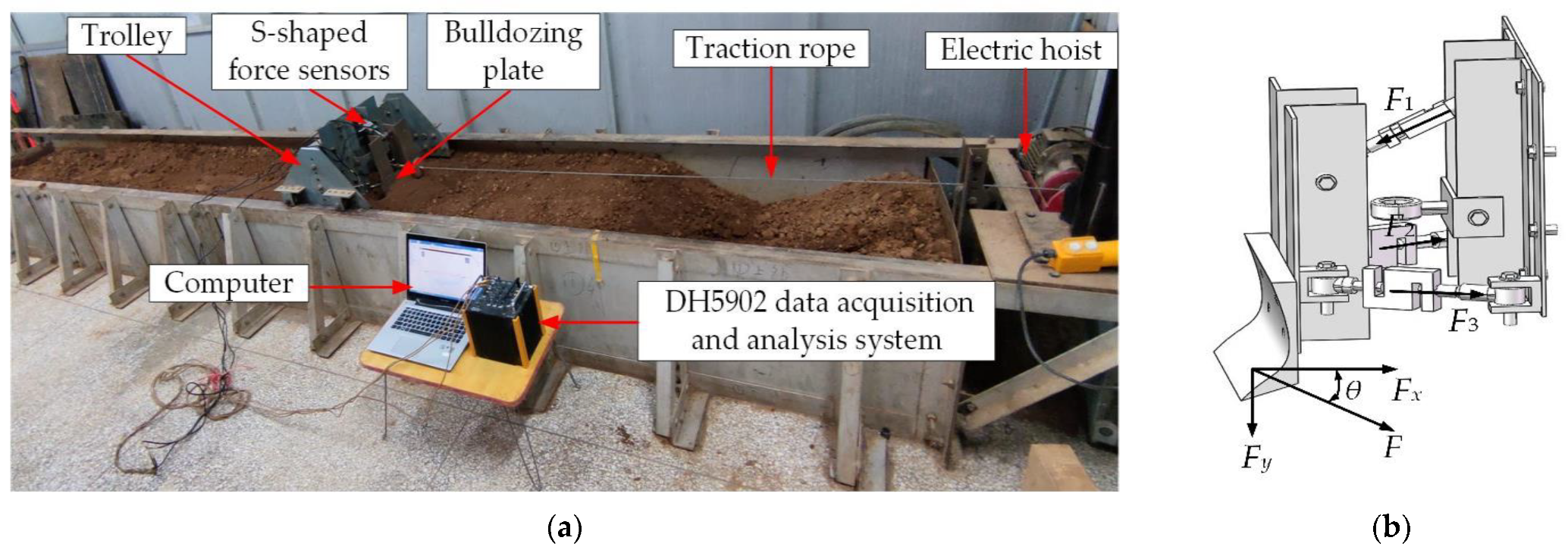

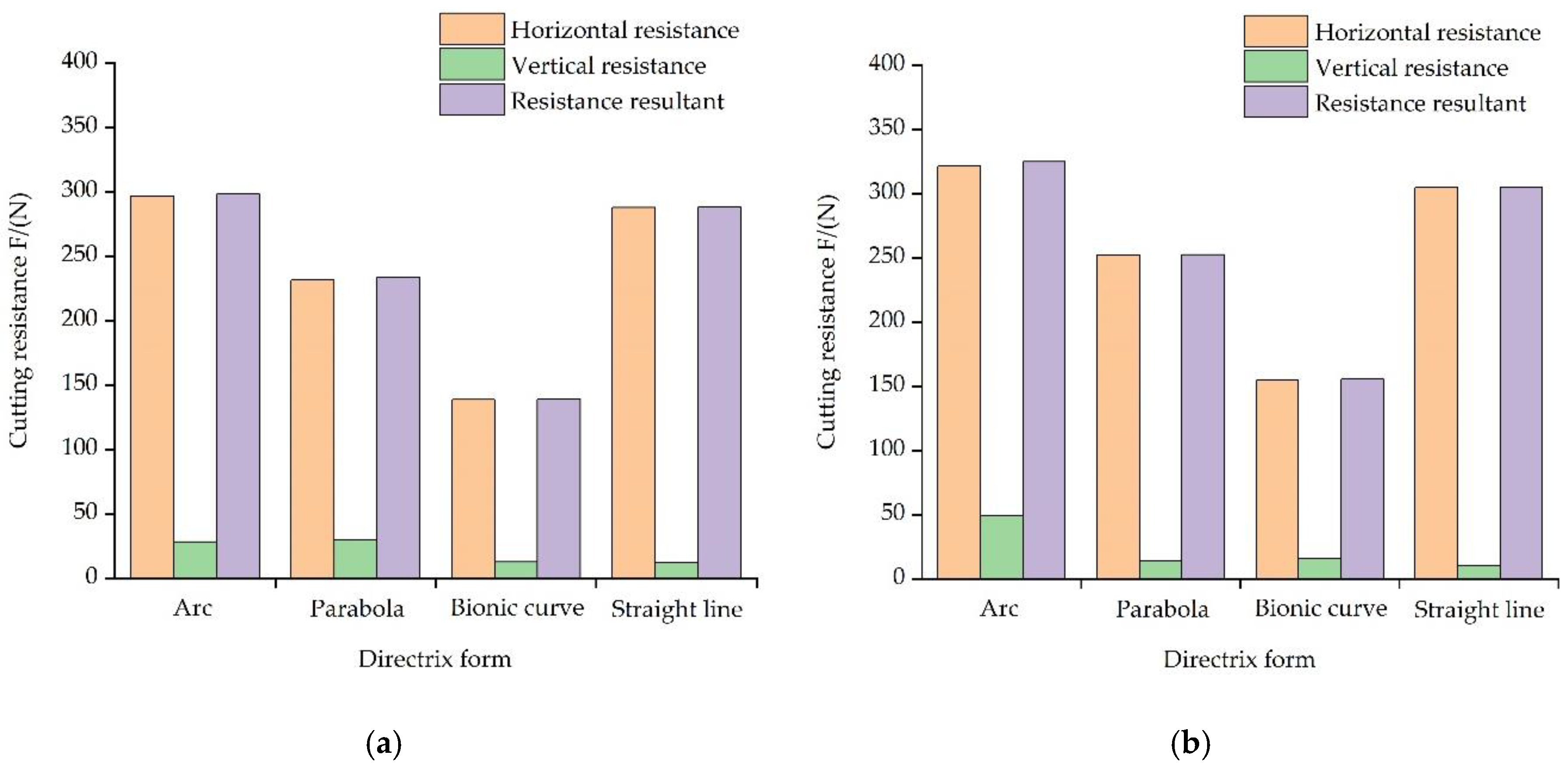
| Number | Particle Size Range/mm | Mass Fraction/% |
|---|---|---|
| 1 | >2 | 8.85 |
| 2 | 1–2 | 8.20 |
| 3 | 0.5–1 | 17.50 |
| 4 | 0.25–0.5 | 17.66 |
| 5 | 0–0.25 | 47.79 |
| Symbol | Parameter | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| X1 | Cinnamon soil–cinnamon soil recovery coefficient | 0.15 | 0.75 |
| X2 | Cinnamon soil–cinnamon soil static friction coefficient | 0.2 | 0.92 |
| X3 | Cinnamon soil–cinnamon soil rolling friction coefficient | 0.05 | 0.2 |
| X4 | Cinnamon soil–steel recovery coefficient | 0.2 | 0.7 |
| X5 | Cinnamon soil–steel static friction coefficient | 0.3 | 0.9 |
| X6 | Cinnamon soil–steel rolling friction coefficient | 0.05 | 0.2 |
| X7 | Surface energy of soil for JKR model/(J⋅m−2) | 0.1 | 0.8 |
| X8–X11 | Virtual parameters | - | - |
| Number | Simulation Test Factors | Test Result | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | Stacking Angle/(°) | |
| 1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | −1 | 1 | 1 | −1 | 30.2 |
| 2 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | 1 | −1 | 28.6 |
| 3 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 19.2 |
| 4 | −1 | 1 | −1 | 1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 19.0 |
| 5 | 1 | −1 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 49.3 |
| 6 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | 1 | −1 | 1 | 25.3 |
| 7 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 15.1 |
| 8 | −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | 1 | −1 | 35.2 |
| 9 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | −1 | 1 | 28.9 |
| 10 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | 1 | 37.0 |
| 11 | 1 | 1 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 14.9 |
| 12 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | 42.0 |
| Parameter | Sum of Squares | Contribution Degree | p-Value | Order of Significance |
|---|---|---|---|---|
| X1 | 13.02 | 1.0 | 0.4523 | 6 |
| X2 | 22.14 | 1.7 | 0.3391 | 5 |
| X3 | 1017.52 | 77.98 | 0.0018 | 1 |
| X4 | 39.24 | 3.01 | 0.2222 | 4 |
| X5 | 105.02 | 8.05 | 0.0775 | 3 |
| X6 | 0.52 | 0.04 | 0.8759 | 7 |
| X7 | 107.4 | 8.23 | 0.0753 | 2 |
| Number | Simulation Test Factors | Test Result | |||
|---|---|---|---|---|---|
| A | B | C | Stacking Angle/(°) | Relative Error of Stacking Angle/% | |
| 1 | 0.05 | 0.1 | 0.3 | 30.2 | 51.97 |
| 2 | 0.08 | 0.24 | 0.42 | 28.6 | 16.58 |
| 3 | 0.11 | 0.38 | 0.54 | 19.2 | 4.3 |
| 4 | 0.14 | 0.52 | 0.66 | 19.0 | 10.51 |
| 5 | 0.17 | 0.66 | 0.78 | 49.3 | 27.12 |
| 6 | 0.2 | 0.8 | 0.9 | 25.3 | 49.15 |
| Number | Simulation Test Factors | Test Result | ||
|---|---|---|---|---|
| A | B | C | Stacking Angle/(°) | |
| 1 | −1 | −1 | 0 | 25.7 |
| 2 | 1 | −1 | 0 | 29.8 |
| 3 | −1 | 1 | 0 | 27.5 |
| 4 | 1 | 1 | 0 | 30.8 |
| 5 | −1 | 0 | −1 | 24.2 |
| 6 | 1 | 0 | −1 | 28.2 |
| 7 | −1 | 0 | 1 | 28.6 |
| 8 | 1 | 0 | 1 | 29.1 |
| 9 | 0 | −1 | −1 | 28.1 |
| 10 | 0 | 1 | −1 | 30.1 |
| 11 | 0 | −1 | 1 | 31.2 |
| 12 | 0 | 1 | 1 | 33.1 |
| 13 | 0 | 0 | 0 | 27.6 |
| 14 | 0 | 0 | 0 | 26.8 |
| 15 | 0 | 0 | 0 | 26.6 |
| 16 | 0 | 0 | 0 | 26.1 |
| 17 | 0 | 0 | 0 | 26.7 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 78.71 | 9 | 8.75 | 24.94 | 0.0002 | ** |
| A | 17.70 | 1 | 17.70 | 50.48 | 0.0002 | ** |
| B | 5.61 | 1 | 5.61 | 16.00 | 0.0052 | ** |
| C | 16.25 | 1 | 16.25 | 46.33 | 0.0003 | ** |
| AB | 0.16 | 1 | 0.16 | 0.46 | 0.5210 | |
| AC | 3.06 | 1 | 3.06 | 8.73 | 0.0212 | * |
| BC | 0.0025 | 1 | 0.0025 | 0.00713 | 0.9351 | |
| A2 | 2.09 | 1 | 2.09 | 5.97 | 0.0446 | * |
| B2 | 24.15 | 1 | 24.15 | 68.88 | <0.0001 | ** |
| C2 | 9.10 | 1 | 9.10 | 25.95 | 0.0014 | ** |
| Residual | 2.45 | 7 | 0.35 | |||
| Lack of fit | 1.28 | 3 | 0.43 | 1.46 | 0.3515 | |
| Pure error | 1.17 | 4 | 0.29 | |||
| Cor Total | 81.16 | 16 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 78.55 | 7 | 11.22 | 38.59 | <0.0001 | ** |
| A | 17.70 | 1 | 17.70 | 60.88 | <0.0001 | ** |
| B | 5.61 | 1 | 5.61 | 19.30 | 0.0017 | ** |
| C | 16.25 | 1 | 16.25 | 55.87 | <0.0001 | ** |
| AC | 3.06 | 1 | 3.06 | 10.53 | 0.0101 | * |
| A2 | 2.09 | 1 | 2.09 | 7.20 | 0.0251 | * |
| B2 | 24.15 | 1 | 24.15 | 83.06 | <0.0001 | ** |
| C2 | 9.10 | 1 | 9.10 | 31.29 | 0.0003 | ** |
| Residual | 2.62 | 9 | 0.29 | |||
| Lack of fit | 1.44 | 5 | 0.29 | 0.99 | 0.5198 | |
| Pure error | 1.17 | 4 | 0.29 | |||
| Cor total | 81.16 | 16 |
| Number | Directrix | Cutting Angle δ | Front Roll Angle βk | Skew Angle ε | Clearance Angle α | Shovel Point Closed Angle β |
|---|---|---|---|---|---|---|
| 1 | Arc | 55° | 72.4° | 78° | 20° | 30° |
| 2 | Parabola | 55° | 80.2° | 78° | 20° | 30° |
| 3 | Bionic curve | 55° | 69.4° | 78° | 20° | 30° |
| 4 | Straight line | 78° | 102° | 78° | 30° | 48° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Guo, Z.; Jin, X.; Zhang, P.; Si, S.; Guo, F. Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method. Agriculture 2022, 12, 1082. https://doi.org/10.3390/agriculture12081082
Qiu Y, Guo Z, Jin X, Zhang P, Si S, Guo F. Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method. Agriculture. 2022; 12(8):1082. https://doi.org/10.3390/agriculture12081082
Chicago/Turabian StyleQiu, Yiqing, Zhijun Guo, Xin Jin, Pangang Zhang, Shengjie Si, and Fugui Guo. 2022. "Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method" Agriculture 12, no. 8: 1082. https://doi.org/10.3390/agriculture12081082
APA StyleQiu, Y., Guo, Z., Jin, X., Zhang, P., Si, S., & Guo, F. (2022). Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method. Agriculture, 12(8), 1082. https://doi.org/10.3390/agriculture12081082





