Determination of Vibration Picking Parameters of Camellia oleifera Fruit Based on Acceleration and Strain Response of Branches
Abstract
:1. Introduction
- Proposing the method of combining a simulation with an experimental test to determine the best vibration parameters of Camellia oleifera mechanized picking;
- Considering the plastic deformation of the Camellia oleifera branches during vibration picking;
- Establishing the correspondence between the simulation and experimental results that can predict the actual vibration response of the tea oil trees.
2. Materials and Methods
2.1. Material
2.2. Establishment of Three-Dimensional Model of Camellia Oleifera
2.3. Measurement of Physical Parameters of Camellia Oleifera
2.4. Research Methods
2.4.1. Finite Element Analysis
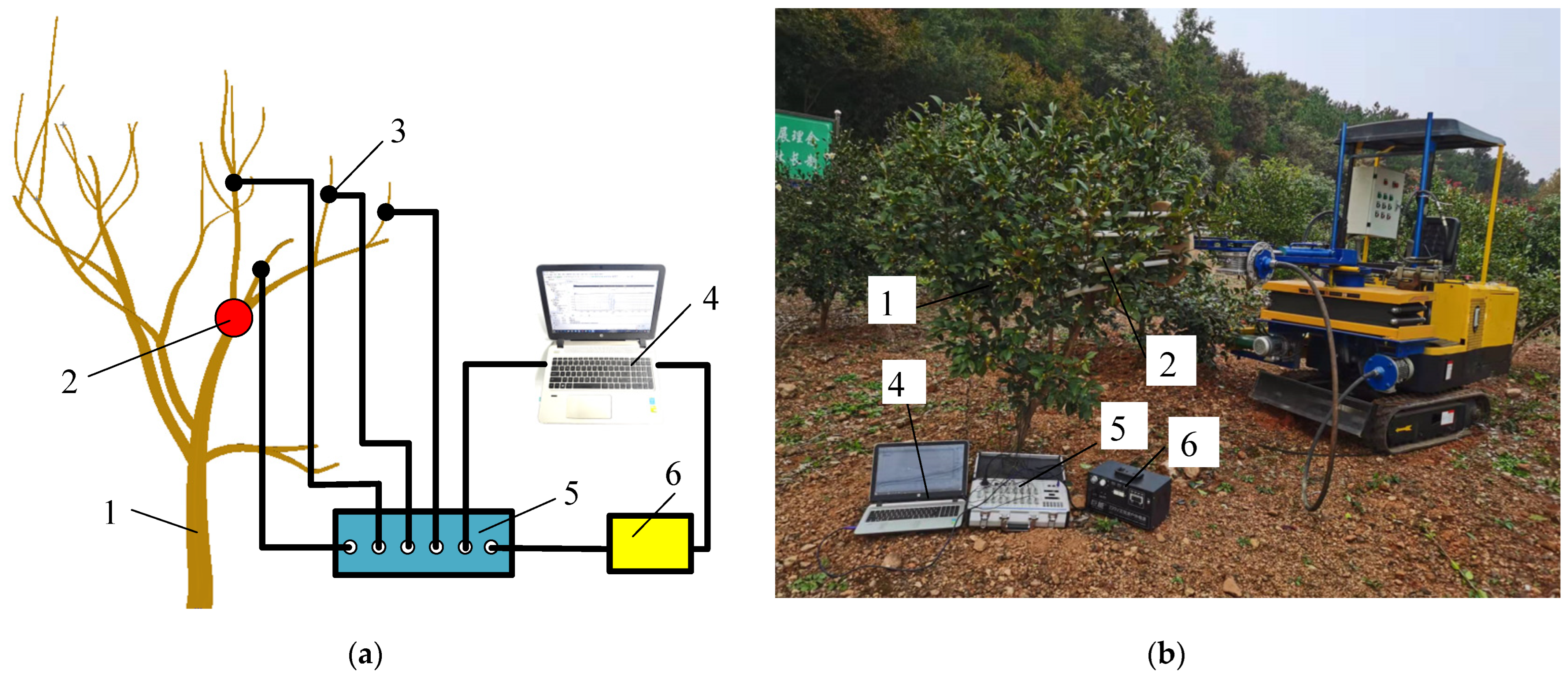
2.4.2. Vibration Test
3. Results and Discussions
3.1. Physical Characteristics of Camellia Oleifera
3.2. Free Mode Analysis of Camellia Oleifera
3.3. Harmonic Response Analysis of Camellia Oleifera
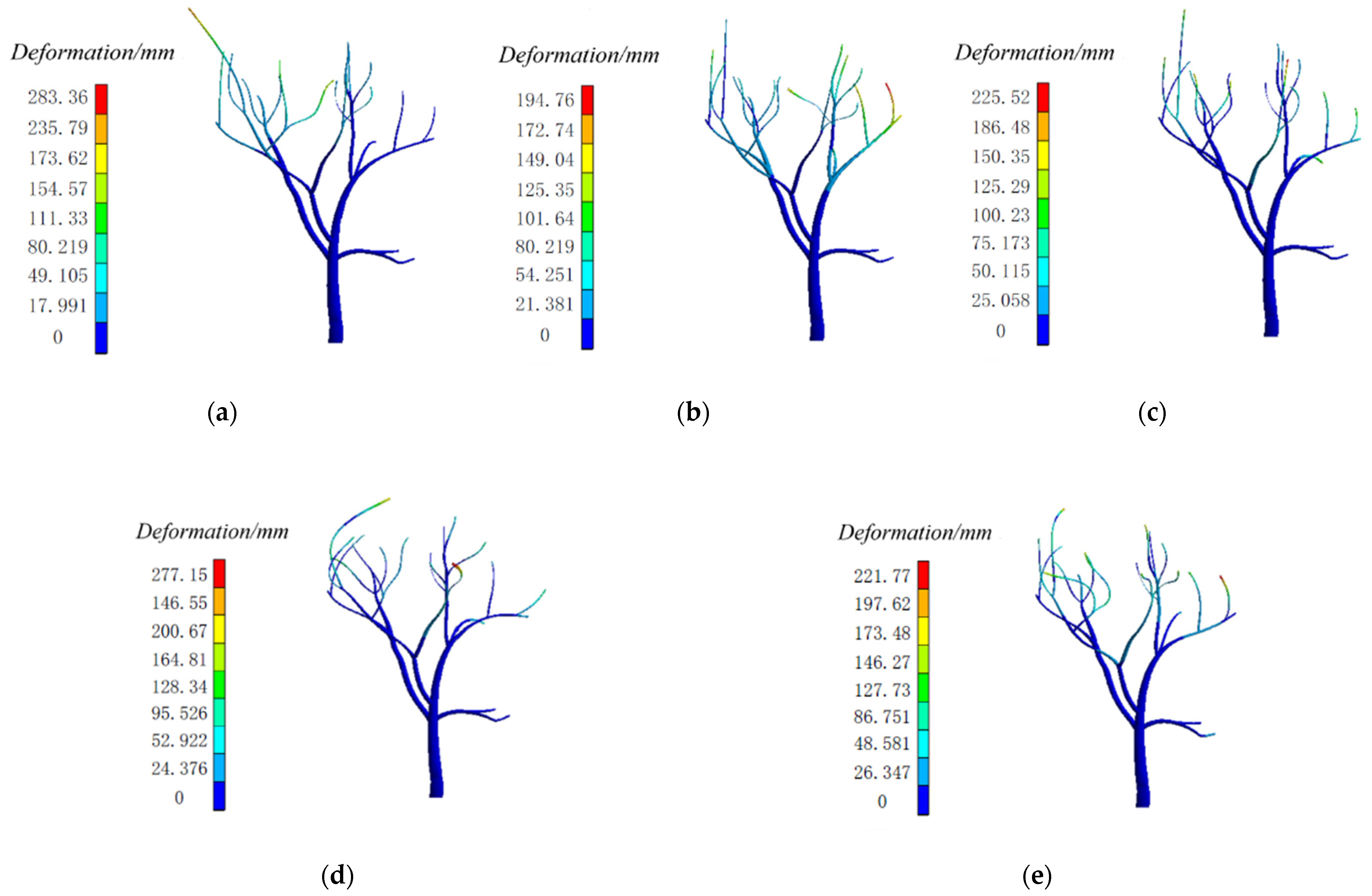
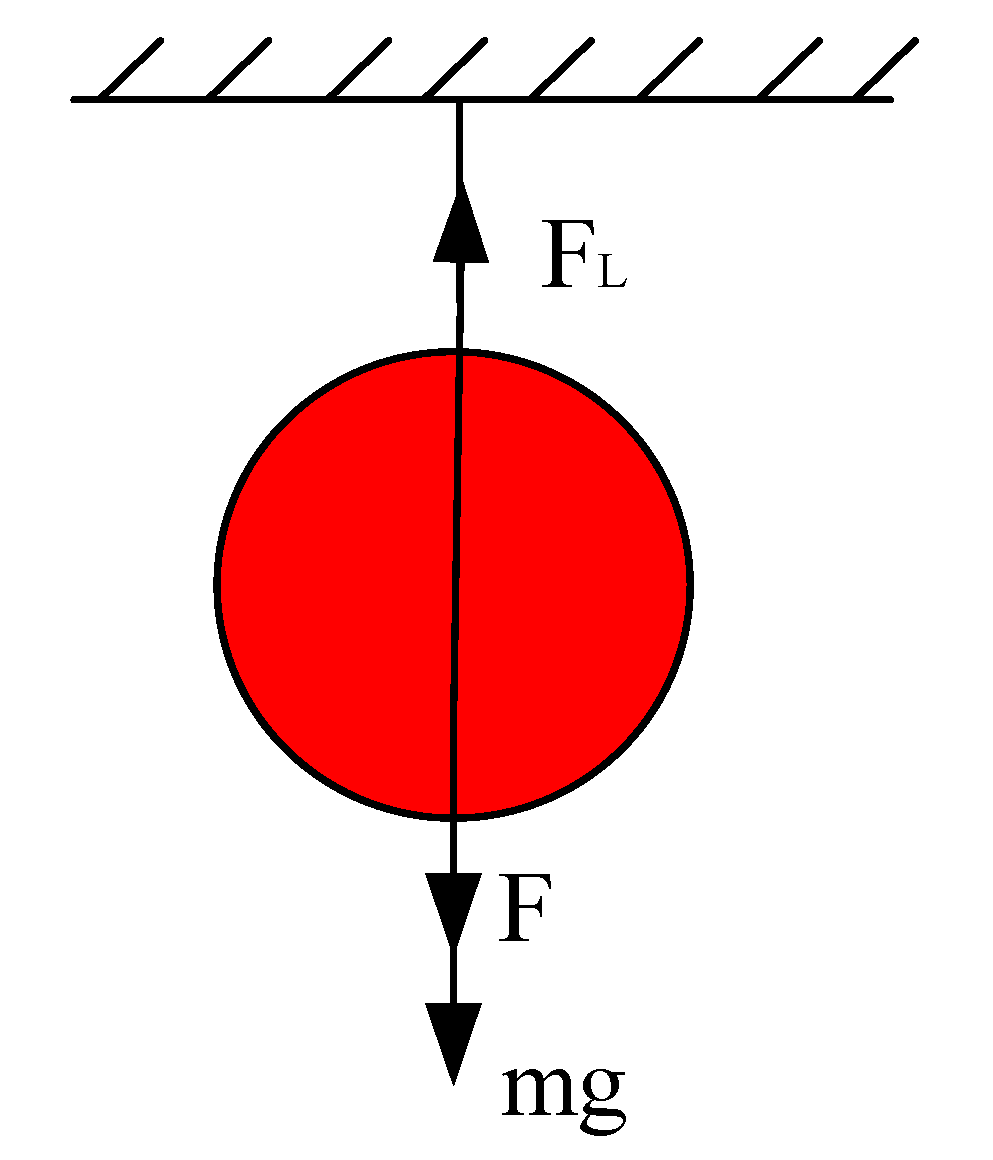
3.3.1. Analysis of Shedding Conditions of Camellia oleifera Fruit
3.3.2. Harmonic Response Analysis of Canopy under Stress
3.4. Comparison between Transient Analysis and Test Measurement Results
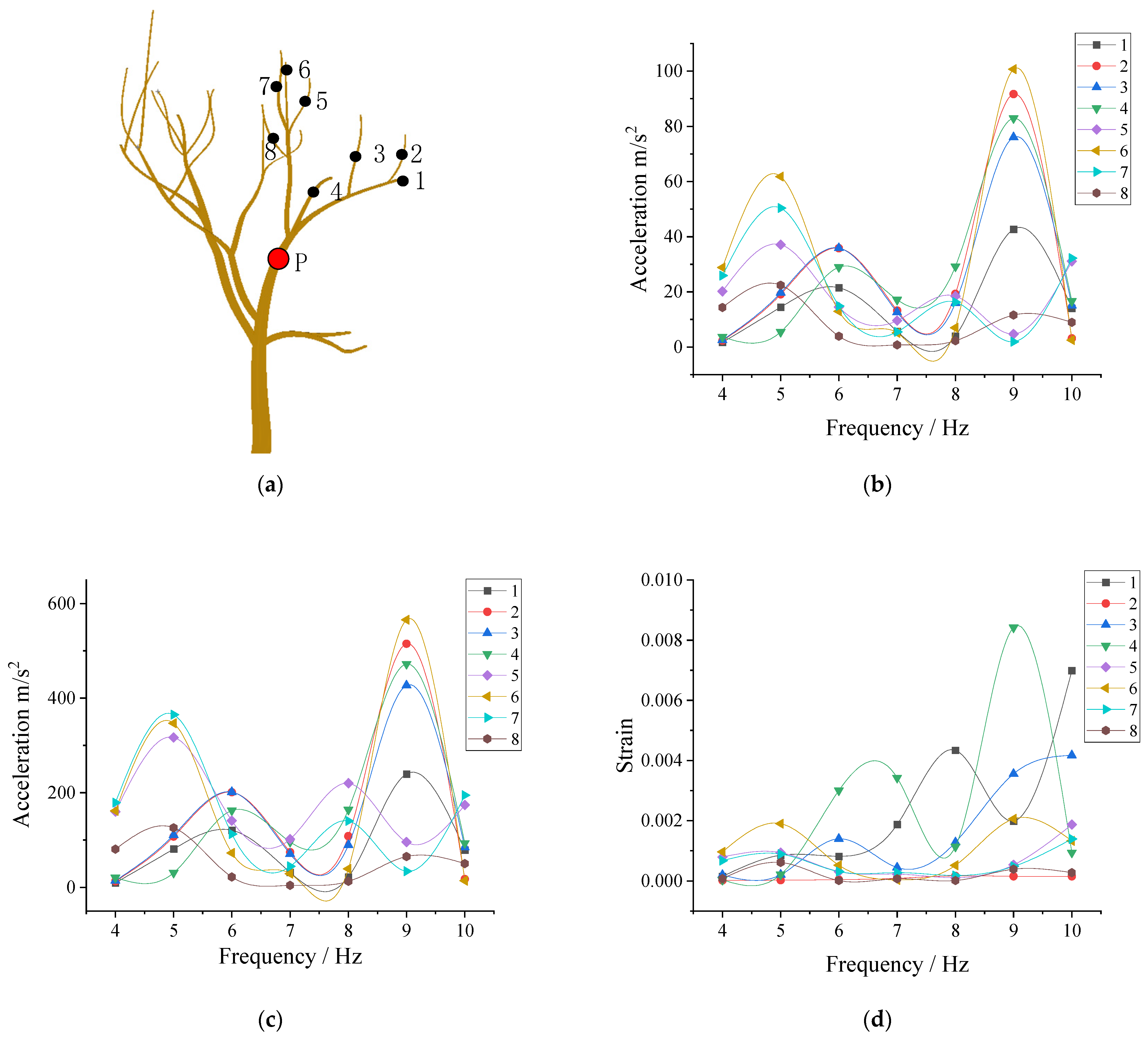
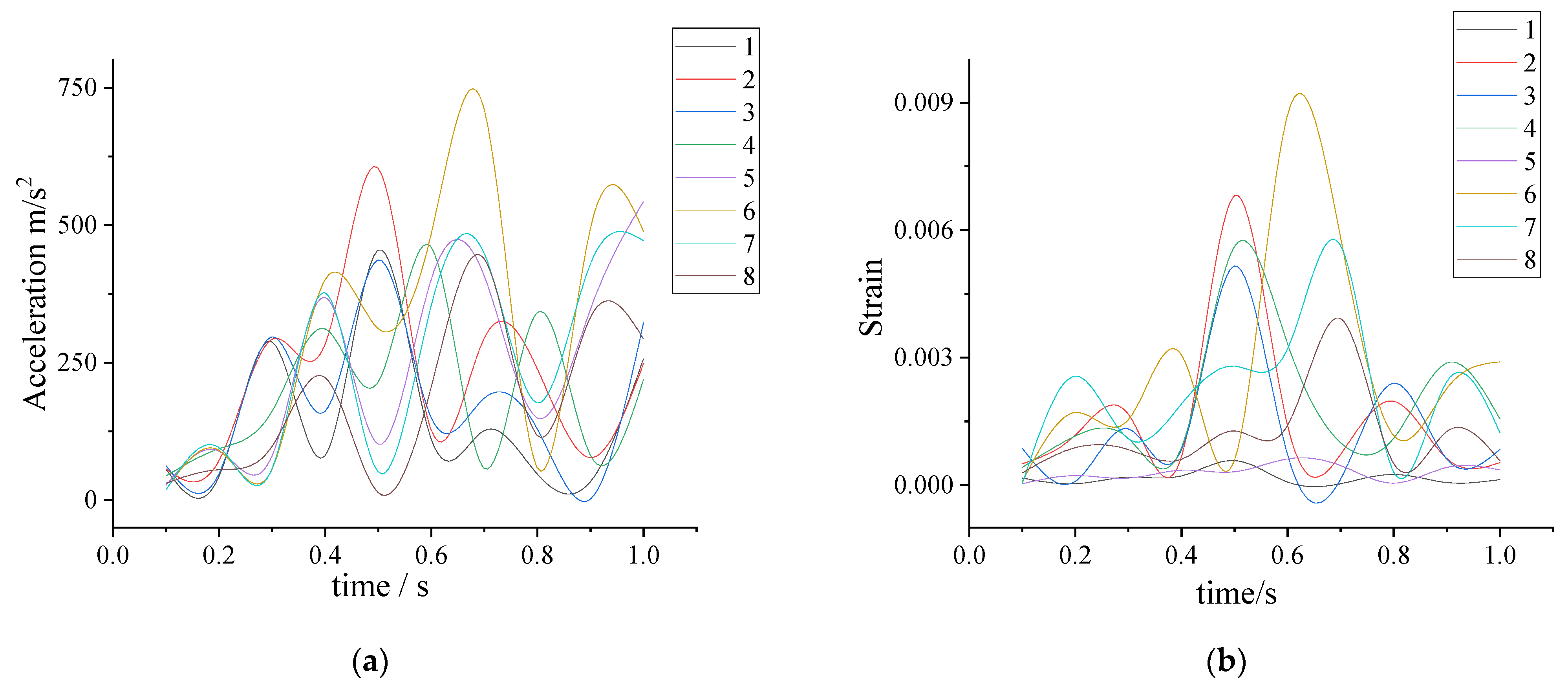
3.4.1. Acceleration Response of Each Detection Point
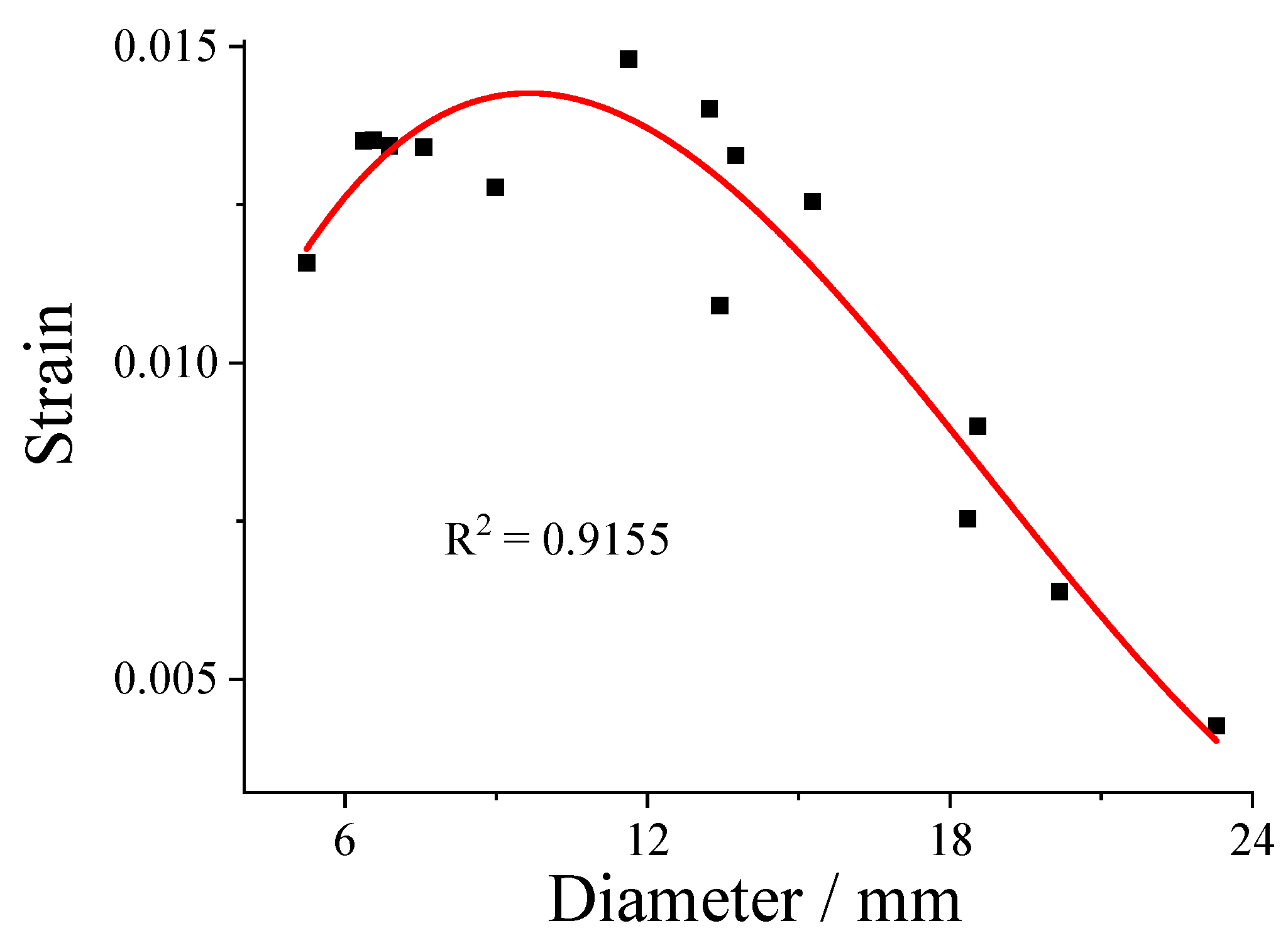
3.4.2. Strain at Each Test Point
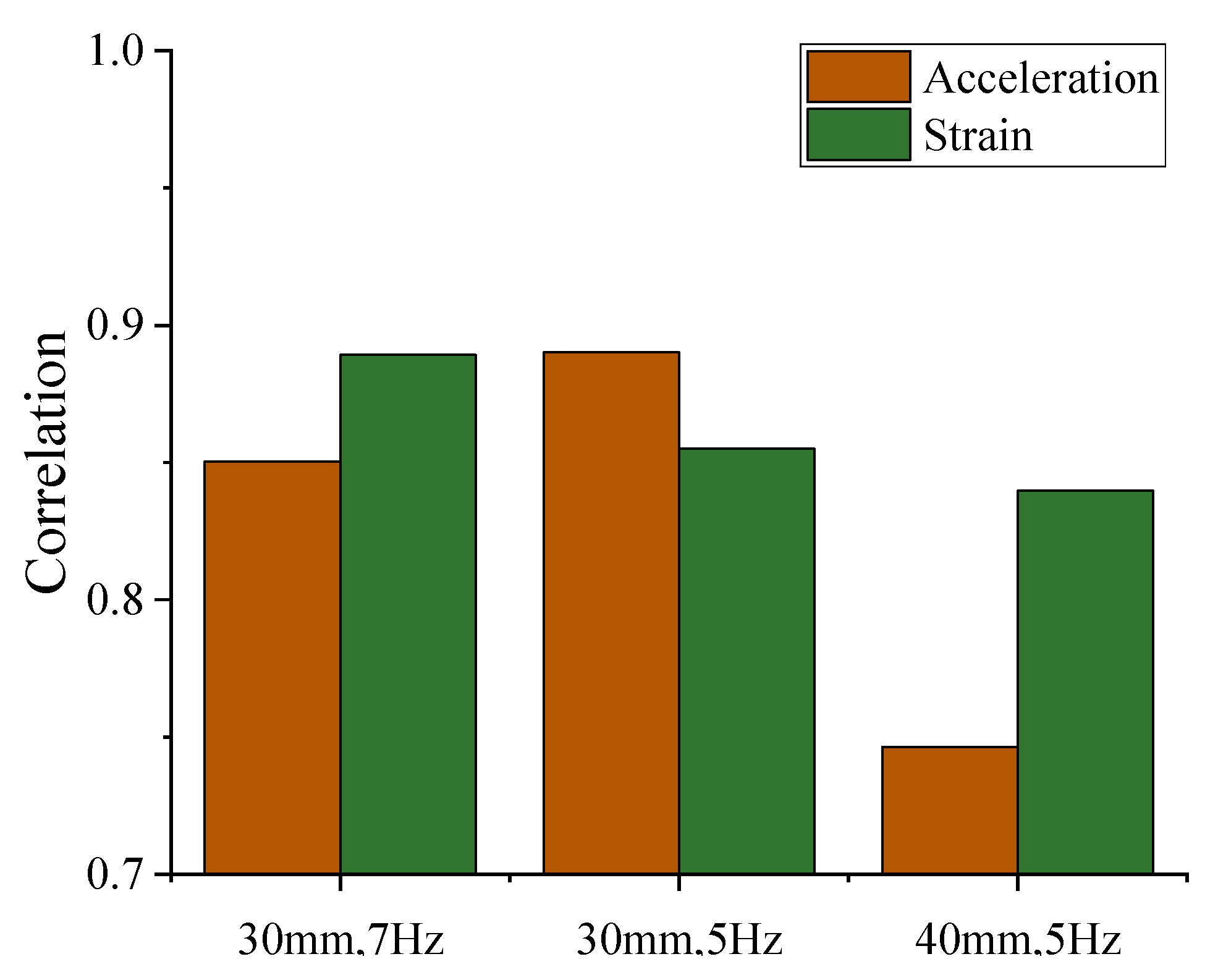
3.4.3. Correlation Coefficient Analysis
3.4.4. Curve Fitting Analysis
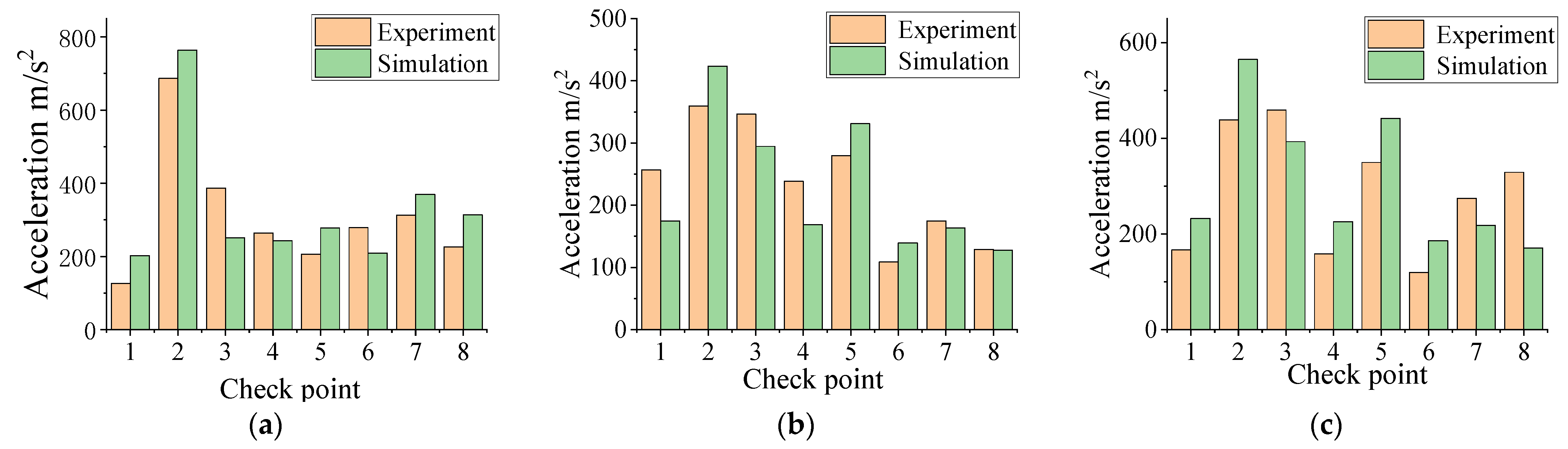
3.5. Test Verification
3.5.1. Verifying Harmonic Response Analysis Results
3.5.2. Vibration Picking of Camellia oleifera Tree Canopy
4. Discussion
5. Conclusions
- (1)
- The 3D model of the Camellia oleifera tree was established, and the free modal analysis of Camellia oleifera tree was carried out by ANSYS. It was determined that the optimal vibration frequency range for the Camellia oleifera tree was 4~10 Hz. The modal analysis determined that the optimal excitation frequency and amplitude of the Camellia oleifera tree were 9 Hz and 56 mm, respectively. The results show that the acceleration responses and strains in the test are close to the simulation value, but there are some errors. The correlation coefficient between the test value and the simulation value is 0.89;
- (2)
- When the frequency is 9 Hz and the amplitude is 56 mm, the acceleration of the detection points on the Camellia oleifera branches is greater than the acceleration required for the fruits to fall off, and the strain values of each detection point are less than the plastic deformation condition, that is, the Camellia oleifera tree will not undergo plastic deformation under this vibration parameter;
- (3)
- The best vibration parameters were further verified through field experiments. The test results showed that the vibration frequency of 9 Hz, the amplitude of 60 mm and the vibration time of 10 s were more suitable for the mechanized picking of Camellia oleifera. At this time, the fruit abscission rate of the Camellia oleifera was 90%, and the flower bud damage-rate was 13%. In general, this study can provide guidance for the production of harvesting machinery and improve the harvesting efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.W.; Wang, L.W. Development status and prospect of China oil tea industry. China Oils Fats 2021, 46, 6–9. [Google Scholar]
- Zhu, G.F.; Liu, H.; Li, W.; Liu, Y.H.; Xie, Y.; Zhang, Y.; Xie, Y.K. Change rule of storage quality and optimization of storage condition for Camellia oleifera seeds. Chin. Soc. Agric. Mach. 2020, 36, 301–311. [Google Scholar]
- Guo, S.; Li, Z.L.; Xue, J.H. Establishment and optimization of comprehensive evaluation model for seed and seed oil traits of Handeliodendron bodinieri. Chin. Soc. Agric. Mach. 2019, 35, 314–322. [Google Scholar]
- Yan, E.P.; Ji, Y.; Yin, X.M.; Mo, D.K. Rapid estimation of camellia oleifera yield based on automatic detection of canopy fruits using UAV images. Chin. Soc. Agric. Mach. 2021, 37, 39–46. [Google Scholar]
- He, L.; Zhou, J.; Du, X. Energy efficacy analysis of a mechanical shaker in sweet cherry harvesting. Biosyst. Eng. 2013, 116, 309–315. [Google Scholar] [CrossRef]
- Takeda, F.; Yang, W.Q.; Li, C.; Freivalds, A.; Sung, K.; Xu, R.; Hu, B.; Williamson, J.; Sargent, S. Applying New Technologies to Transform Blueberry Harvesting. Agronomy 2017, 7, 33. [Google Scholar] [CrossRef]
- Rao, H.H.; Huang, D.S.; Wang, Y.L.; Chen, B.; Liu, M.H. Design and Experiment of Hydraulic-driven Camellia Fruit Picking Machine. Trans. Chin. Soc. Agric. Mach. 2019, 50, 133–139, 147. [Google Scholar]
- Torregrosa, A.; Molina, J.M.; Pérez, M.; Ortí, E.; Xamani, P.; Ortiz, C. Mechanical Harvesting of Ornamental Citrus Trees in Valencia, Spain. Agronomy 2019, 9, 827. [Google Scholar] [CrossRef]
- Ortiz, C.; Torregrosa, A.; Castro-García, S. Citrus Fruit Movement Assessment Related to Fruit Damage during Harvesting with an Experimental Low-Frequency–High-Amplitude Device. Agronomy 2022, 12, 1337. [Google Scholar] [CrossRef]
- Ortiz, C.; Torregrosa, A.; Castro-García, S. Comparison of a Lightweight Experimental Shaker and an Orchard Tractor Mounted Trunk Shaker for Fresh Market Citrus Harvesting. Agriculture 2021, 11, 1092. [Google Scholar] [CrossRef]
- Blanco-Roldán, G.L.; Gil-Ribes, J.A.; Kouraba, K. Effects of Trunk Shaker Duration and Repetitions on Removal Efficiency for the Harvesting of Oil Olives. Appl. Eng. Agric. 2009, 25, 329–334. [Google Scholar] [CrossRef]
- Hoshyarmanesh, H.; Dastgerdi, H.R.; Ghodsi, M.; Khandan, R.; Zareinia, K. Numerical and experimental vibration analysis of olive tree for optimal mechanized harvesting efficiency and productivity. Comput. Electr. Agric. 2017, 132, 34–48. [Google Scholar] [CrossRef]
- Láng, Z. A one degree of freedom damped fruit tree model. Agric. Eng. Int. CIGR 2008, 51, 823–829. [Google Scholar] [CrossRef]
- Savary, S.; Ehsani, R.; Schueller, J.K.; Rajaraman, B.P. Simulation study of citrus tree canopy motion during harvesting using a canopy shaker. ASABE 2010, 53, 1557–1568. [Google Scholar]
- Liu, T.H.; Luo, G.; Ehsani, R.; Toudeshki, A.; Zou, X.J.; Wang, H.J. Simulation study on the effects of tine-shaking frequency and penetrating depth on fruit detachment for citrus canopy-shaker harvesting. Comput. Electr. Agric. 2018, 148, 54–62. [Google Scholar] [CrossRef]
- Xuan, Y.; Xu, L.; Liu, G.; Zhou, J. The Potential Influence of Tree Crown Structure on the Ginkgo Harvest. Forests 2021, 12, 366. [Google Scholar] [CrossRef]
- Zhao, J.; Tsuchikawa, S.; Ma, T.; Hu, G.; Chen, Y.; Wang, Z.; Chen, Q.; Gao, Z.; Chen, J. Modal Analysis and Experiment of a Lycium barbarum L. Shrub for Efficient Vibration Harvesting of Fruit. Agriculture 2021, 11, 519. [Google Scholar] [CrossRef]
- Chen, K.; Du, X.; Zhang, G.; Zhou, R.; Chen, K.; Du, X.; Zhang, G.; Zhou, R. Analysis on dynamics characteristics of vibratory harvesting for oil-tea Camellia fruit. In Proceedings of the ASABE 2019, Boston, MA, USA, 7–10 July 2019. [Google Scholar] [CrossRef]
- Du, X.; Chen, K.; Ma, Z.; Wu, C.; Zhang, G. Design construction and evaluation of a three-dimensional vibratory harvester for tree fruit. Appl. Eng. Agric. 2020, 36, 221–231. [Google Scholar] [CrossRef]
- Han, Y.; Xu, L.; Zhou, J.; Yu, B. Analysis of chestnut fruit shedding characteristics by vibration using high-speed videos. J. For. Eng. 2021, 6, 133–141. [Google Scholar]
- He, L.Y.; Liu, X.C.; Du, X.Q.; Wu, C.Y. In-situ identification of shaking frequency for adaptive vibratory fruit harvesting. Comput. Electr. Agric. 2020, 170, 105245. [Google Scholar] [CrossRef]
- Zhou, J.; He, L.; Zhang, Q.; Du, X.; Chen, D. Evaluation of the influence of shaking frequency and duration in mechanical harvesting of sweet cherry. Appl. Eng. Agric. 2013, 29, 607–612. [Google Scholar]
- Pu, Y.; Toudeshki, A.; Ehsani, R.; Yang, F. Design and evaluation of a two-section canopy shaker with variable frequency for mechanical harvesting of citrus. Int. J. Agric. Biol. Eng. 2018, 11, 77–87. [Google Scholar] [CrossRef]
- Udumala Savary, S.K.J.; Ehsani, R.; Salyani, M.; Hebel, M.A.; Bora, G.C. Study of force distribution in the citrus tree canopy during harvest using a continuous canopy shaker. Comput. Electr. Agric. 2011, 76, 51–58. [Google Scholar] [CrossRef]
- Wu, C.Y.; He, L.Y.; Du, X.Q.; Chen, S.D.; Ni, K.N. 3D reconstruction of Chinese hickory tree for dynamics analysis. Biosyst. Eng. 2014, 119, 69–79. [Google Scholar] [CrossRef]
- Sola-Guirado, R.R.; Bernardi, B.; Castro-Garcia, S.; Blanco-Roldán, G.L.; Benalia, S.; Fazari, A. Assessment of aerial and underground vibration transmission in mechanically trunk shaken olive trees. J. Agric. Eng. 2017, 49, 191–197. [Google Scholar] [CrossRef]
- Du, X.Q.; Jiang, F.; Li, S.T.; Xu, N.N.; Li, D.W.; Wu, C.Y. Design and experiment of vibratory harvesting mechanism for Chinese hickory nuts based on orthogonal eccentric masses. Comput. Electr. Agric. 2019, 156, 178–186. [Google Scholar] [CrossRef]
- Jing, X.; Lang, Z. Frequency domain analysis of a dimensionless cubic nonlinear damping system subject to harmonic input. Nonlinear Dyn. 2009, 58, 469–485. [Google Scholar] [CrossRef]
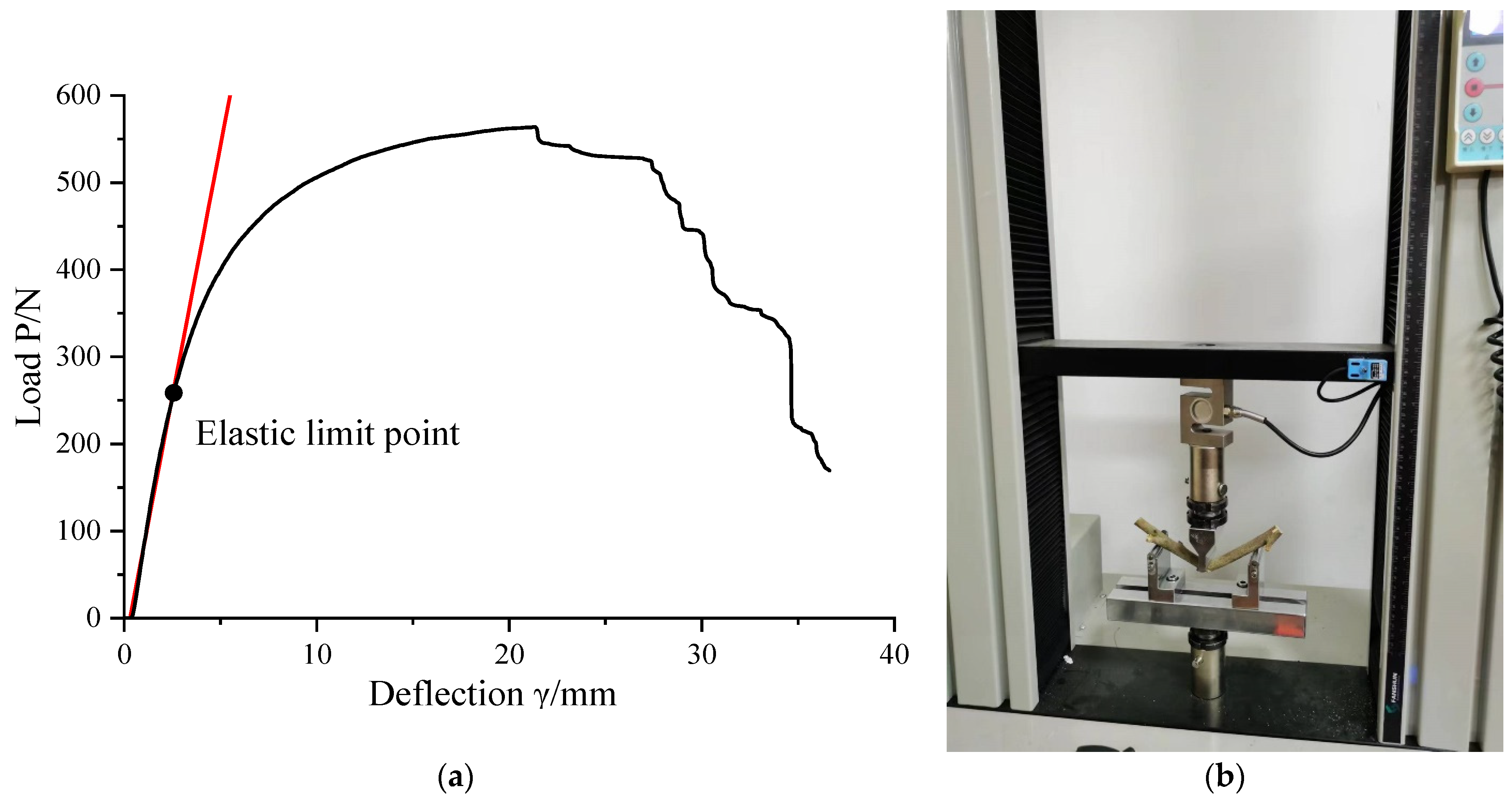
- ASABE S368; Compression Test of Food Materials of Convex Shape. ASABE: St. Joseph, MI, USA, 2008; pp. 671–678.
- Ashtiani, H.; Sadrnia, H.; Mohammadinezhad, M.H.; Aghkhani, M.; Khojastehpour, M.H. Abbaspour-Fard FEM-based simulation of the mechanical behavior of grapefruit under compressive loading. Sci. Hortic. 2019, 245, 39–46. [Google Scholar] [CrossRef]
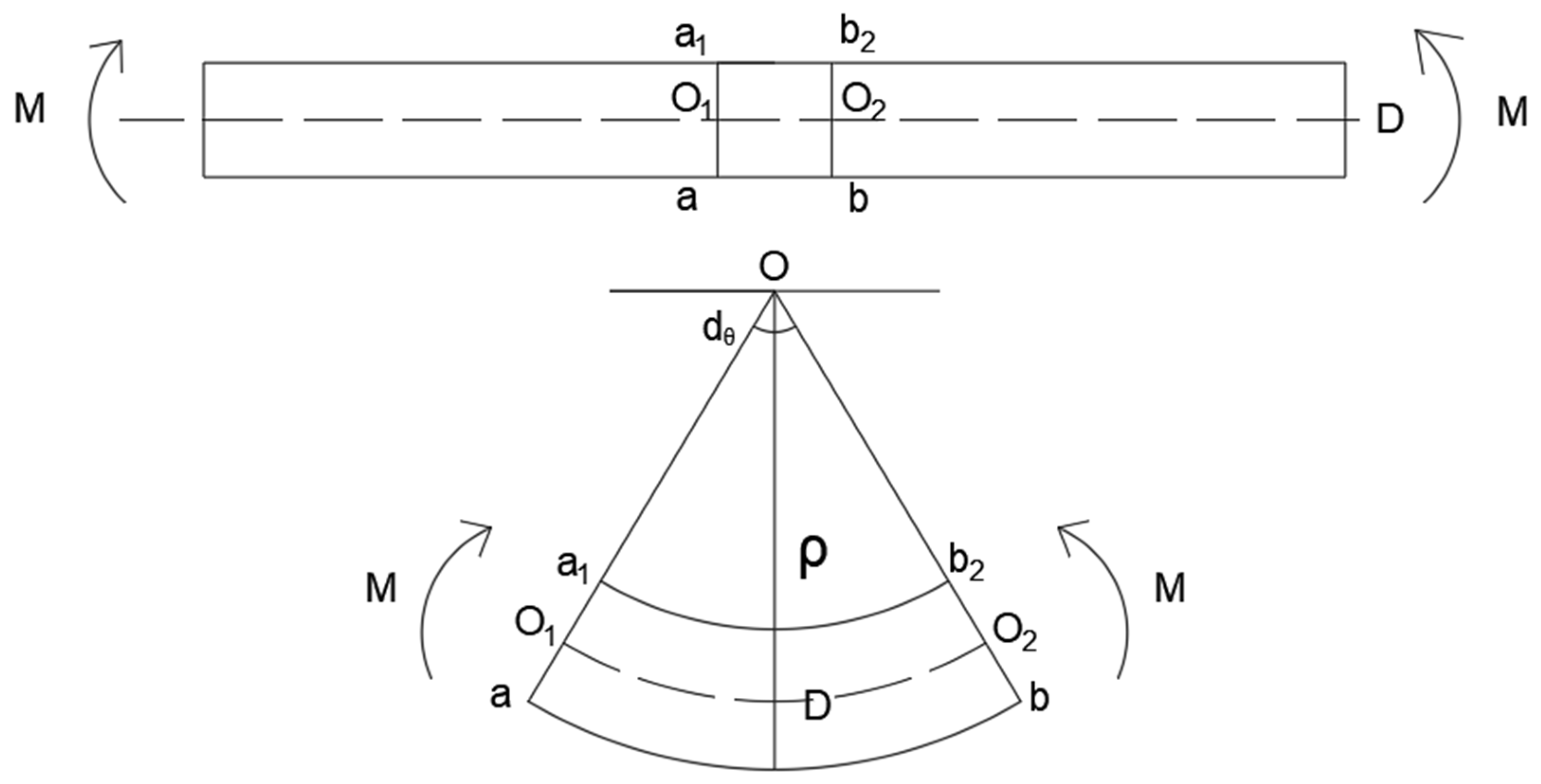
- Yu, H.R. Monitoring of Bending Deformation of Bridge Deck Based on Strain Measurement; Hefei University of Technology: Hefei, China, 2019. [Google Scholar]
- Fu, L.; Peng, J.; Nan, Q.; He, D.; Yang, Y.; Cui, Y. Simulation of vibration harvesting mechanism for sea buckthorn. Eng. Agric. Envi. Food 2016, 9, 101–108. [Google Scholar] [CrossRef]
- Peng, J.; Sun, S.; Fu, L. Research on dynamic characteristics of vibratory harvesting for sea buckthorn. J. Agric. Mech. 2017, 39, 32–37. [Google Scholar]
- Chen, K.Z. Design and Research on Vibration Picking Quipment of Camellia Fruit Tree Crown; Zhejiang Sci-Tech University: Hangzhou, China, 2020. [Google Scholar]
- Wu, D.L.; Li, C.; Cao, C.M.; Fan, E.B.; Wang, Q. Analysis and experiment of the operation process of branch-shaking type camellia oleifera fruit picking device. Trans. Chin. Soc. Agric. Eng. 2020, 36, 56–62. [Google Scholar] [CrossRef]
- Tang, X.Y.; Ren, J.R.; Liu, C.; Xiao, D. Simulation of Vibration Harvesting Mechanism for Wolfberry. ASABE 2011, 5, 4096–4110. [Google Scholar] [CrossRef]
- Wu, D.L.; Zhao, E.L.; Jiang, S.; Ding, D.; Liu, Y.Y.; Liu, L. Optimization Analysis and Test of Canopy Vibration Parameters of Camellia Fruit Based on Double Pendulum Model. Trans. Chin. Soc. Agric. Mach. 2021, 52, 96–104. [Google Scholar]



| NO. | Amplitude (mm) | Frequency (Hz) |
|---|---|---|
| 1 | 30 | 7 |
| 2 | 30 | 5 |
| 3 | 40 | 5 |
| Materials | Elasticity Modulus (Mpa) | Density (g/cm3) | Damping Ratio | Poisson’s Ratio |
|---|---|---|---|---|
| Camellia oleifera tree | 326.66 | 0.95 | 0.06 | 0.3 [34] |
| No. | Frequency (Hz) | Maximum Response Point | No. | Frequency (Hz) | Maximum Response Point | No. | Frequency (Hz) | Maximum Response Point |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.67 | c1 | 18 | 5.41 | b2 | 35 | 11.68 | a2 |
| 2 | 1.94 | a6 | 19 | 5.85 | a1 | 36 | 12.01 | a1 |
| 3 | 2.78 | a1 | 20 | 6.29 | a5 | 37 | 12.37 | b4 |
| 4 | 2.95 | b5 | 21 | 6.73 | a4 | 38 | 12.63 | b2 |
| 5 | 3.09 | c3 | 22 | 7.21 | a1 | 39 | 12.77 | a1 |
| 6 | 3.33 | b2 | 23 | 7.48 | a3 | 40 | 12.78 | a2 |
| 7 | 3.48 | c4 | 24 | 7.63 | b2 | 41 | 12.84 | a2 |
| 8 | 3.55 | b1 | 25 | 7.94 | c4 | 42 | 13.15 | b3 |
| 9 | 3.68 | c4 | 26 | 8.56 | c3 | 43 | 13.63 | c3 |
| 10 | 4.08 | c3 | 27 | 8.91 | a1 | 44 | 13.86 | c4 |
| 11 | 4.48 | a1 | 28 | 9.08 | a6 | 45 | 14.02 | a6 |
| 12 | 4.62 | a2 | 29 | 9.14 | b3 | 46 | 15.35 | b2 |
| 13 | 4.64 | b3 | 30 | 9.65 | c2 | 47 | 15.74 | a1 |
| 14 | 4.79 | c3 | 31 | 10.27 | a1 | 48 | 16.13 | a6 |
| 15 | 4.96 | a2 | 32 | 10.43 | c4 | 49 | 16.68 | c3 |
| 16 | 5.11 | a1 | 33 | 11.02 | c4 | 50 | 17.18 | a6 |
| 17 | 5.34 | c2 | 34 | 11.10 | c3 |
| Acceleration (m/s2) | Strain | |||
|---|---|---|---|---|
| Linear Fitting | Quadratic Fitting | Linear Fitting | Quadratic Fitting | |
| P1 | 72.28 | 81.12 | 0.00033 | 0.000024 |
| P2 | 0.71 | 0.66 | 0.74 | 0.98 |
| P3 | / | 0.000068 | / | −28.44 |
| R2 | 0.69 | 0.67 | 0.77 | 0.77 |
| Index | 5 s | 10 s | 15 s | |||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| Fruit shedding rate (%) | 68 | 11 | 90 | 5 | 91 | 5 |
| Bud abscission rate (%) | 11 | 3 | 13 | 4 | 18 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Zhao, E.; Fang, D.; Jiang, S.; Wu, C.; Wang, W.; Wang, R. Determination of Vibration Picking Parameters of Camellia oleifera Fruit Based on Acceleration and Strain Response of Branches. Agriculture 2022, 12, 1222. https://doi.org/10.3390/agriculture12081222
Wu D, Zhao E, Fang D, Jiang S, Wu C, Wang W, Wang R. Determination of Vibration Picking Parameters of Camellia oleifera Fruit Based on Acceleration and Strain Response of Branches. Agriculture. 2022; 12(8):1222. https://doi.org/10.3390/agriculture12081222
Chicago/Turabian StyleWu, Delin, Enlong Zhao, Dong Fang, Shan Jiang, Cheng Wu, Weiwei Wang, and Rongyan Wang. 2022. "Determination of Vibration Picking Parameters of Camellia oleifera Fruit Based on Acceleration and Strain Response of Branches" Agriculture 12, no. 8: 1222. https://doi.org/10.3390/agriculture12081222
APA StyleWu, D., Zhao, E., Fang, D., Jiang, S., Wu, C., Wang, W., & Wang, R. (2022). Determination of Vibration Picking Parameters of Camellia oleifera Fruit Based on Acceleration and Strain Response of Branches. Agriculture, 12(8), 1222. https://doi.org/10.3390/agriculture12081222






