Optimization Model and Application for Agricultural Machinery Systems Based on Timeliness Losses of Multiple Operations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Four-Dimensional Subscript Variable Setting
2.2. Objective Function Establishment
2.2.1. Model of Annual Fixed Cost of Machinery
2.2.2. Model for Annual Variable Cost of Operation Machinery Units
2.2.3. Model for Timeliness Loss Cost of Key Operations
2.3. Constraints of MINP Optimization Model
2.3.1. Operation Area Constraint
2.3.2. Tractor Allocation Constraint
2.3.3. Implement Allocation Constraint
2.3.4. Operation Sequence Constraint
2.3.5. Boundary Constraint for Start and End Dates of Key Operations
2.3.6. Non-Negative Variable and Integer Constraints
3. Results
3.1. Experiment on Timeliness Loss for Key Operations of Corn and Soybean
3.1.1. Experimental Materials
3.1.2. Experimental Design
3.1.3. Test Method
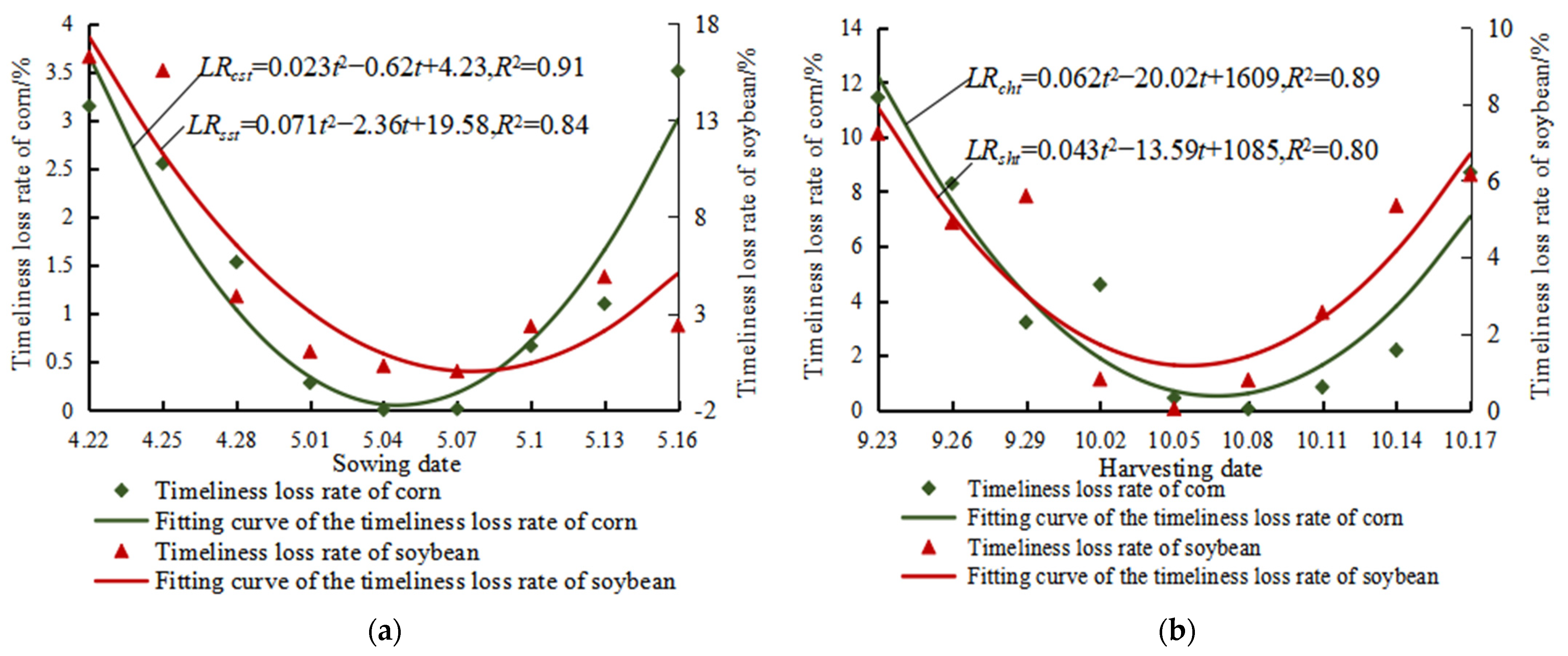
3.1.4. Determination of Timeliness Loss Functions of Key Operations
3.2. Corn–Soybean Rotation and Rotational Tillage Production Process
3.3. Determination of Agricultural Machinery Models and Parameters
3.4. Model Optimization Results
4. Discussion
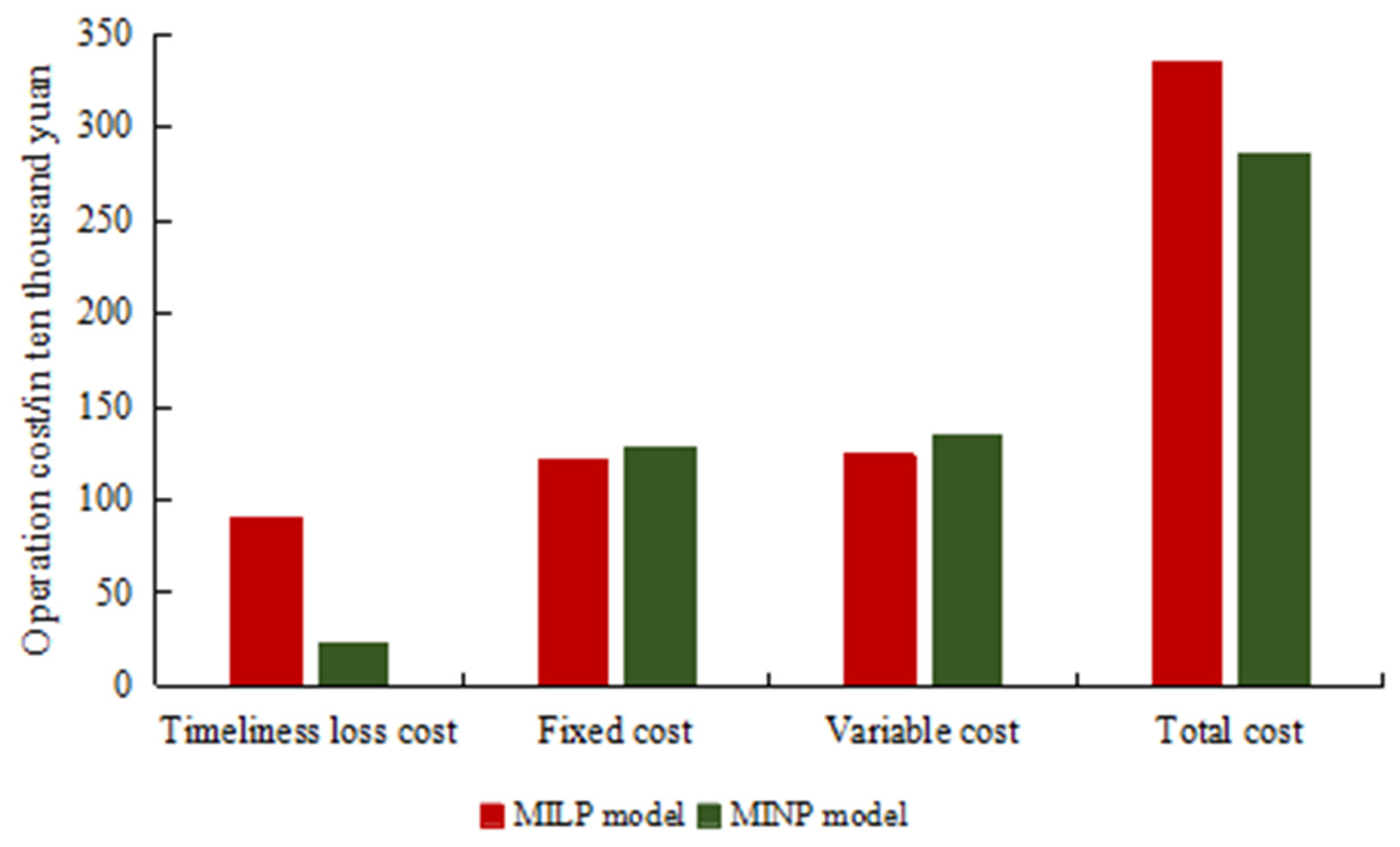
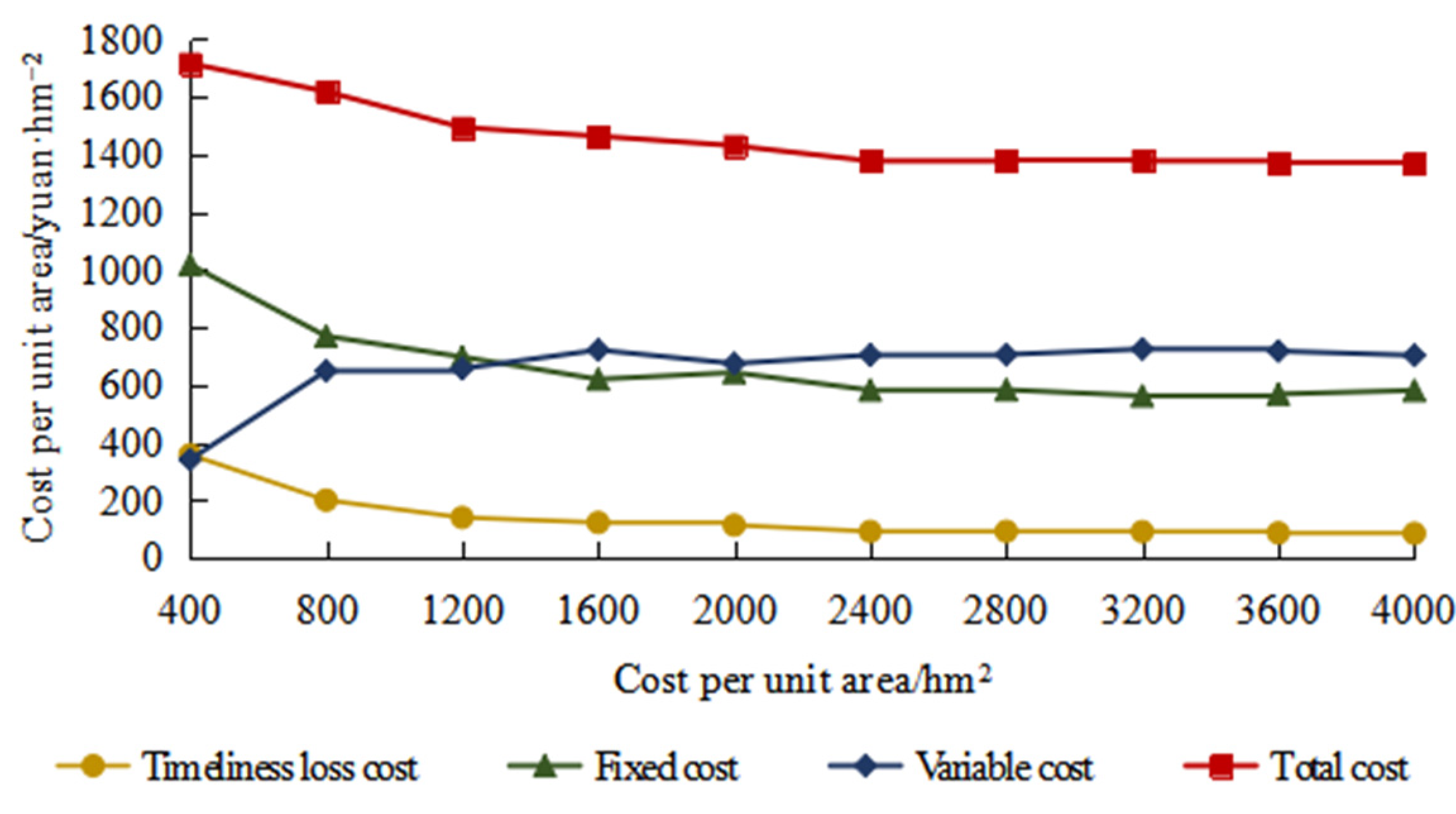
4.1. Analysis of the Impact of Timeliness Loss Rate Function on Total Operation Cost
4.2. Analysis of the Impact of Operation Sequence Constraints on Optimization Results
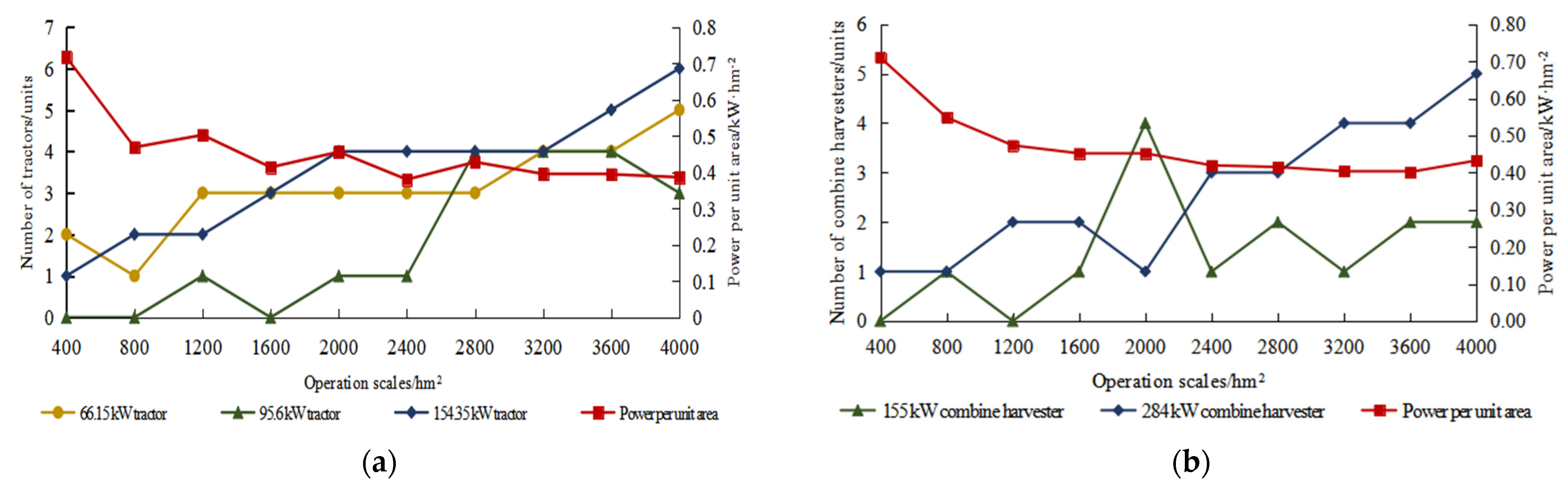
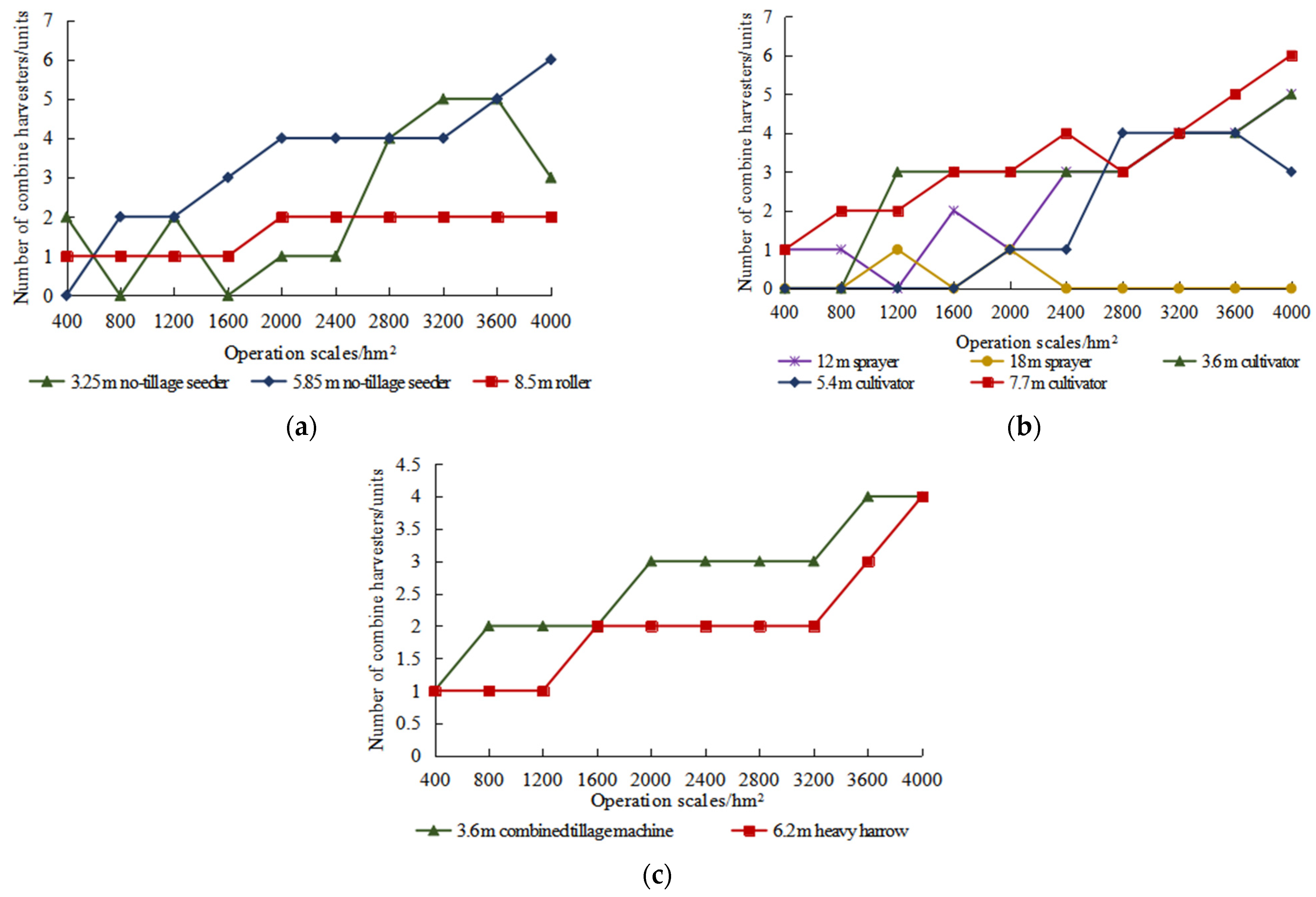
4.3. Analysis of Machinery Allocation Variation Rules for Different Operation Scales
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, B.; Tian, Z. Mechanism of factor substitution during rapid development of China’s agricultural mechanization. Trans. Chin. Soc. Agric. Eng. 2018, 34, 1–10. [Google Scholar]
- Hunt, D.R. A systems approach to farm machinery selection. Inst. Agric. Eng. J. Proc. 1969, 24, 25–27. [Google Scholar]
- Hughes, H.A.; Holtman, J.B. Machinery Complement Selection Based on Time Constraints. Trans. Asae 1976, 19, 812–814. [Google Scholar] [CrossRef]
- Wan, H.; Meng, F.; Zhang, X.; Gui, B. Methods to Determine Optimum Service Area for Certain Farm Machinery Group and to Select Reasonable Group for Given Service Area. Trans. Chin. Soc. Agric. Mach. 1984, 2, 77–88. [Google Scholar]
- Lu, H.; Zhao, Y.; Zhou, X.; Wei, Z. Selection of Agricultural Machinery Based on Improved CRITIC-Entropy Weight and GRA-TOPSIS Method. Processes 2022, 10, 266. [Google Scholar] [CrossRef]
- Hoose, A.; Yepes, V.; Kripka, M. Selection of Production Mix in the Agricultural Machinery Industry Considering Sustainability in Decision Making. Sustainability 2021, 13, 9110. [Google Scholar] [CrossRef]
- Najafi, B.; Dastgerduei, S.T. Optimization of Machinery Use on Farms with Emphasis on Timeliness Costs. J. Agr. Sci. Tech. 2015, 17, 533–541. [Google Scholar]
- Whitson, R.E.; Kay, R.D.; Lepori, W.A.; Rister, E.M. Machinery and Crop Selection with Weather Risk. Trans. ASAE 1981, 24, 288–291. [Google Scholar] [CrossRef]
- Audsley, E. An arable farm model to evaluate the commercial viability of new machines or techniques. J. Agric. Eng. Res. 1981, 26, 135–149. [Google Scholar] [CrossRef]
- Camarena, E.A.; Gracia, C.; Sixto, J.M.C. A Mixed Integer Linear Programming Machinery Selection Model for Multifarm Systems. Biosyst. Eng. 2004, 87, 145–154. [Google Scholar] [CrossRef]
- Cupia, M.; Kowalczyk, Z. Optimization of Selection of the Machinery Park in Sustainable Agriculture. Sustainability 2020, 12, 1380. [Google Scholar] [CrossRef]
- Filippi, C.; Mansini, R.; Stevanato, E. Mixed integer linear programming models for optimal crop selection. Comput. Oper. Res. 2017, 81, 26–39. [Google Scholar] [CrossRef]
- Meng, F.-Q.; Wan, H.-Q. The Effect of Timeliness Cost on the Quantity of Farm Machines Required. Trans. Chin. Soc. Agric. Mach. 1983, 1, 97–104. [Google Scholar]
- Zhou, T.; Cao, H. New Algorithms for the Optimum Disposition of Farm Machines—Integrated disposition algorithm. Trans. Chin. Soc. Agric. Mach. 1988, 1, 43–50. [Google Scholar]
- Srensen, C.G. Workability and Machinery Sizing for Combine Harvesting. CIGR E-J. 2003, 5, PM 03 003. [Google Scholar]
- Toro, A.D.; Hansson, P.A. Machinery Co-operatives—A Case Study in Sweden. Biosyst. Eng. 2004, 87, 13–25. [Google Scholar] [CrossRef]
- Toro, A.D.; Gunnarsson, C.; Lundin, G.; Jonsson, N. Cereal harvesting—Strategies and costs under variable weather conditions. Biosyst. Eng. 2012, 111, 429–439. [Google Scholar] [CrossRef]
- Depenbusch, L.; Farnworth, C.R.; Schreinemachers, P.; Myint, T.; Islam, M.M.; Kundu, N.D.; Myint, T.; San, A.M.; Jahan, R.; Nair, R.M. When Machines Take the Beans: Ex-Ante Socioeconomic Impact Evaluation of Mechanized Harvesting of Mungbean in Bangladesh and Myanmar. Agronomy 2021, 11, 925. [Google Scholar] [CrossRef]
- Wang, G.; Yi, Z.; Chen, C.; Cao, G. Effect of harvesting date on loss component characteristics of rice mechanical harvested in rice and wheat rotation area. Trans. Chin. Soc. Agric. Eng. 2016, 32, 36–42. [Google Scholar]
- Wang, J.; Sun, X.; Xu, Y.; Wang, Q.; Tang, H.; Zhou, W. The effect of harvest date on yield loss of long and short-grain rice cultivars (Oryza sativa L.) in Northeast China. Eur. J. Agron. 2021, 131, 126382. [Google Scholar] [CrossRef]
- Wang, J.; Sun, X.; Xu, Y.; Zhou, W.; Wang, Q. Timeliness Harvesting Loss of Rice in Cold Region under Different Mechanical Harvesting Methods. Sustainability 2021, 13, 6345. [Google Scholar] [CrossRef]
- Gao, H. Farm machinery system optimization under flow operation method. Trans. Chin. Soc. Agric. Mach. 1992, 04, 55–60. [Google Scholar]
- Khani, M.; Keyhani, A.; Alimardani, R.; Sharifnasab, H.; Peykani, G. A numerical and an analytical method for optimum planting date determination. Inf. Process. Agric. 2015, 2, 15–24. [Google Scholar] [CrossRef]
- Vatsa, D.K.; Saraswat, D.C. Selection of Power Tiller and Matching Equipment using Computer Program for Mechanizing Hill Agriculture. CIGR E-J. 2008, 10, 1–11. [Google Scholar]
- Tieppo, R.C.; Romanelli, T.L.; Milan, M.; Srensen, C.A.G.; Bochtis, D. Modeling cost and energy demand in agricultural machinery fleets for soybean and maize cultivated using a no-tillage system. Comput. Electron. Agric. 2019, 156, 282–292. [Google Scholar] [CrossRef]
- Qiao, J.; Li, C.; Han, Z.; Wu, J.; Yi, J.; Chen, H. Study on the Regularity of Timeliness Loss Changing with Soybean Sowing Date. Soybean Sci. 2016, 35, 70–73. [Google Scholar]
- Qiao, J.; Sun, J.; Qu, F.; Ma, L.; Wu, J.; Han, Z.; Chen, H. Study on regularities of timeliness loss changing with soybean harvesting date. J. Northeast Agric. Univ. 2017, 48, 76–81. [Google Scholar]
- Qiao, J.; Sun, J.; Tian, Y.; Wang, W.; Zhang, Y.; Xu, Y.; Chen, H. Experiments on the Regularities of Timeliness Loss Changing with Soybean Harvesting Date in Beian. Soybean Sci. 2017, 36, 803–807. [Google Scholar]
- Qiao, J.; Zhang, X.; Yi, J.; Sun, J.; Wang, F.; Chen, H. Optimization model and application of agricultural machinery system based on nonlinear programming. J. Northeast Agric. Univ. 2017, 48, 80–88. [Google Scholar]
- Wang, F.; Dai, Y. Improvement and analysis of the modeling method of linear programming for the equipment of agricultural machinery systems. J. Agric. Mech. Res. 1988, 3, 5–9. [Google Scholar]
- Wang, Y.; Qiao, J.; Ren, G.; Zhang, Q. The research on depreciation methods of agricultural machinery. J. Agric. Mech. Res. 2016, 38, 129–132+151. [Google Scholar]
- Qiao, J.; Yi, J.; Li, C.; Chen, H.; Han, Z. Study on the optimum distribution problem of agricultural operation period. J. Northeast Agric. Univ. 2016, 47, 72–76. [Google Scholar]
- GB/T 10362-2008; Inspection of Grain and Oils—Determination of Moisture Content of Maize. Standardization Administration of China: Beijing, China, 4 November 2008. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=4340D08D86E5257B6ADFB000A6A2EBDB (accessed on 6 October 2023).
- GB 1352-2023; Soybean. China. Standardization Administration of China: Beijing, China, 23 May 2023. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=738C8F5A5E434CF4A0E68BA738366882 (accessed on 6 October 2023).
- Wang, H.; Chen, H.; Ji, W. Design and experiment of cleaning and covering mechanism for no-till seeder in wheat stubble fields. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2012, 28, 7–12. [Google Scholar]
- Capowiez, Y.; Cadoux, S.; Bouchant, P.; Ruy, S.; Roger-Estrade, J.; Richard, G.; Boizard, H. The effect of tillage type and cropping system on earthworm communities, macroporosity and water infiltration. Soil Till Res. 2009, 105, 209–216. [Google Scholar] [CrossRef]
- Meidute-Kavaliauskiene, I.; Davidaviciene, V.; Ghorbani, S.; Sahebi, I.G. Optimal Allocation of Gas Resources to Different Consumption Sectors Using Multi-Objective Goal Programming. Sustainability 2021, 13, 5663. [Google Scholar] [CrossRef]

| Tractors | Implements | Operation Machinery Units | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | Power (kW) | (CNY 10,000) | (years) | (CNY 10,000) | Variables | Kind | The Width of the Implements (m) | (CNY 10,000) | (years) | (CNY 10,000) | Operating Item | (CNY/hm2) | (hm2/d) |
| 66.15 | 12.37 | 13 | 1.39 | No-till straw mulching precision seeders | 3.25 | 14 | 8 | 2.22 | No-tillage and sowing with straw mulching | 17.16 | 124 | ||
| Precision sowing | 20.59 | 111.60 | |||||||||||
| Rollers | 8.5 | 3.74 | 8 | 0.59 | Rolling | 69.12 | 19.47 | ||||||
| Sprayers | 12 | 3.85 | 8 | 0.61 | Weeding | 61.09 | 17.33 | ||||||
| Culti-vators | 3.6 | 3.8 | 8 | 0.60 | Deep loosening, intertill, and ridging | 28.96 | 66.67 | ||||||
| 95.6 | 18.13 | 13 | 2.03 | No-till straw mulching precision seeders | 3.25 | 14 | 8 | 2.22 | No-tillage and sowing with straw mulching | 19.50 | 121.37 | ||
| Precision sowing | 23.40 | 109.24 | |||||||||||
| Rollers | 12.8 | 5.6 | 8 | 0.89 | Rolling | 99.36 | 22.13 | ||||||
| Sprayers | 18 | 6.3 | 8 | 1 | Weeding | 84.00 | 20 | ||||||
| Culti-vators | 5.4 | 4.8 | 8 | 0.76 | Deep loosening, intertill, and ridging | 43.52 | 73 | ||||||
| 154.35 | 68 | 16 | 6.72 | No-till straw mulching precision seeders | 5.85 | 19.6 | 8 | 3.10 | No-tillage and sowing with straw mulching | 35.10 | 111.23 | ||
| Precision sowing | 42.12 | 100.11 | |||||||||||
| Culti-vators | 7.7 | 7.2 | 8 | 1.44 | Deep loosening, intertill, and ridging | 68.96 | 84 | ||||||
| Combined tillage machines | 3.6 | 18.5 | 8 | 2.93 | Combined tilling | 30.40 | 216 | ||||||
| Heavy harrows | 6.2 | 6.8 | 8 | 1.08 | Harrowing | 55.52 | 84 | ||||||
| 271 | 131 | 16 | 12.95 | Combined tillage machines | 6.8 | 31 | 8 | 4.91 | Combined tilling | 43.20 | 300 | ||
| Heavy harrows | 7.8 | 7.1 | 8 | 1.12 | Harrowing | 81.92 | 100 | ||||||
| — | Combine harvesters | 155 | 98 | 16 | 9.69 | Harvesting | 23.66 | 261.20 | |||||
| — | 239 | 275 | 16 | 27.18 | 31.55 | ||||||||
| — | 284 | 206 | 16 | 20.36 | 50.08 | ||||||||
| Machinery Type | Variables | Number of Machines | Fixed Cost (In CNY 10,000) | ||
|---|---|---|---|---|---|
| Current | MINP | Current | MINP | ||
| Tractors | 3 | 3 | 4.17 | 4.17 | |
| 3 | 1 ↓ | 6.09 | 2.03 ↓ | ||
| 5 | 4 ↓ | 33.60 | 26.88 ↓ | ||
| 1 | 0 ↓ | 12.95 | 0.00 ↓ | ||
| Subtotal | 12 | 8 ↓ | 56.81 | 33.08 | |
| Seeders | 3 | 1 ↓ | 6.66 | 2.22 ↓ | |
| 4 | 4 | 12.40 | 12.40 | ||
| Subtotal | 7 | 5 ↓ | 19.06 | 14.62 ↓ | |
| Rollers | 2 | 2 | 1.18 | 1.18 | |
| 1 | 0 ↓ | 0.89 | 0.00 ↓ | ||
| Subtotal | 3 | 2 ↓ | 2.07 | 1.18 ↓ | |
| Sprayers | 1 | 1 | 0.61 | 0.61 | |
| 2 | 1 ↓ | 2 | 1 ↓ | ||
| Subtotal | 3 | 2 ↓ | 2.61 | 1.61 ↓ | |
| Cultivators | 5 | 3 ↓ | 3.00 | 1.80 ↓ | |
| 3 | 1 ↓ | 2.28 | 0.76 ↓ | ||
| 3 | 3 | 3.42 | 3.42 | ||
| Subtotal | 11 | 7 ↓ | 8.70 | 5.98 ↓ | |
| Combine harvesters | 2 | 0 ↓ | 19.38 | 0.00 ↓ | |
| 2 | 0 ↓ | 54.36 | 0.00 ↓ | ||
| 2 | 3 ↑ | 40.72 | 61.08 ↑ | ||
| Subtotal | 6 | 3 | 114.46 | 61.08 ↓ | |
| Combined tillage machines | 3 | 3 | 8.79 | 8.79 | |
| 1 | 0 ↓ | 4.91 | 0.00 ↓ | ||
| Subtotal | 4 | 3 ↓ | 13.70 | 8.79 ↓ | |
| Heavy harrows | 3 | 2 ↓ | 3.24 | 2.16 ↓ | |
| 1 | 0 ↓ | 1.12 | 0.00 ↓ | ||
| Subtotal | 4 | 2 ↓ | 4.36 | 2.16 ↓ | |
| Total | 50 | 32 ↓ | 221.77 | 128.50 ↓ | |
| Agricultural Stage | I1 | I2 | I3 | I4 | I5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Working date (month·day) | 5.2 | 5.3 | 5.4 | 5.5 | 5.6 | 5.7 | 5.89 | 5.9 | 5.10 | |
| Daily sowing area (hm2) | 77 | 84 | 84 | 84 | 84 | 84 | 85 | 85 | ||
| Cumulative sowing area (hm2) | 77 | 161 | 245 | 329 | 413 | 497 | 582 | 667 | ||
| Daily post-sow tolling area without restraint conditions (hm2) | 138 | 29 | 28 | 28 | 28 | 138 | 138 | 140 | ||
| Cumulative post-sow tolling area without restraint conditions (hm2) | 138 | 167 | 195 | 223 | 251 | 389 | 527 | 667 | ||
| Daily post-sow tolling area under restraint conditions (hm2) | 77 | 56 | 56 | 56 | 56 | 122 | 122 | 122 | ||
| Cumulative post-sow tolling area under restraint conditions (hm2) | 77 | 133 | 189 | 245 | 301 | 423 | 545 | 667 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Zhang, Y.; Chen, H.; Qiao, J. Optimization Model and Application for Agricultural Machinery Systems Based on Timeliness Losses of Multiple Operations. Agriculture 2023, 13, 1969. https://doi.org/10.3390/agriculture13101969
Sun J, Zhang Y, Chen H, Qiao J. Optimization Model and Application for Agricultural Machinery Systems Based on Timeliness Losses of Multiple Operations. Agriculture. 2023; 13(10):1969. https://doi.org/10.3390/agriculture13101969
Chicago/Turabian StyleSun, Jian, Yiming Zhang, Haitao Chen, and Jinyou Qiao. 2023. "Optimization Model and Application for Agricultural Machinery Systems Based on Timeliness Losses of Multiple Operations" Agriculture 13, no. 10: 1969. https://doi.org/10.3390/agriculture13101969
APA StyleSun, J., Zhang, Y., Chen, H., & Qiao, J. (2023). Optimization Model and Application for Agricultural Machinery Systems Based on Timeliness Losses of Multiple Operations. Agriculture, 13(10), 1969. https://doi.org/10.3390/agriculture13101969






