Land Cover Classification from Hyperspectral Images via Weighted Spatial–Spectral Joint Kernel Collaborative Representation Classifier
Abstract
1. Introduction
2. Methodology
2.1. WSSKCRT
2.2. JCRC
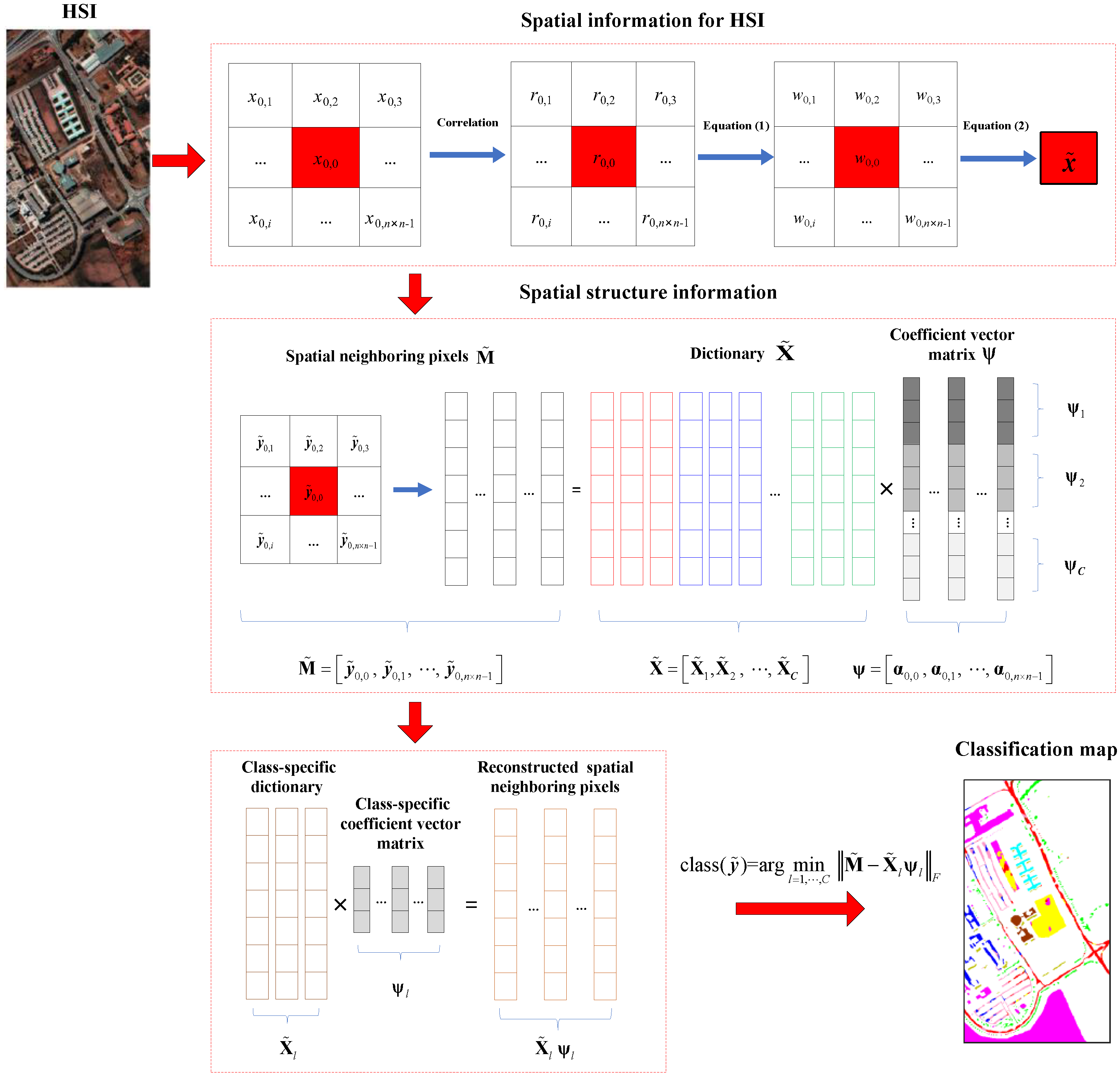
2.3. Proposed WSSJCRC
2.4. Proposed WSSJKCRC
3. Experimental Results and Analysis
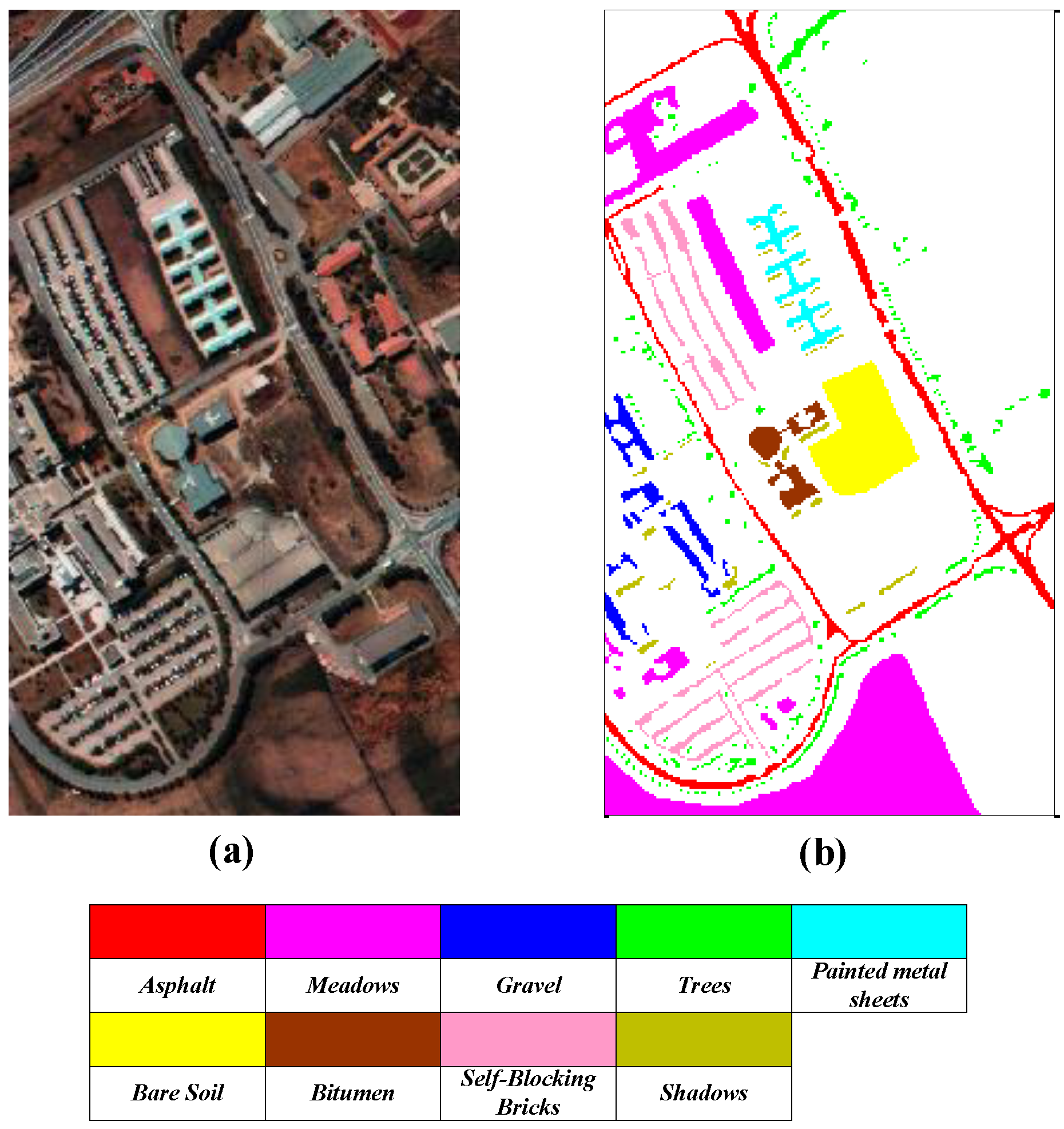
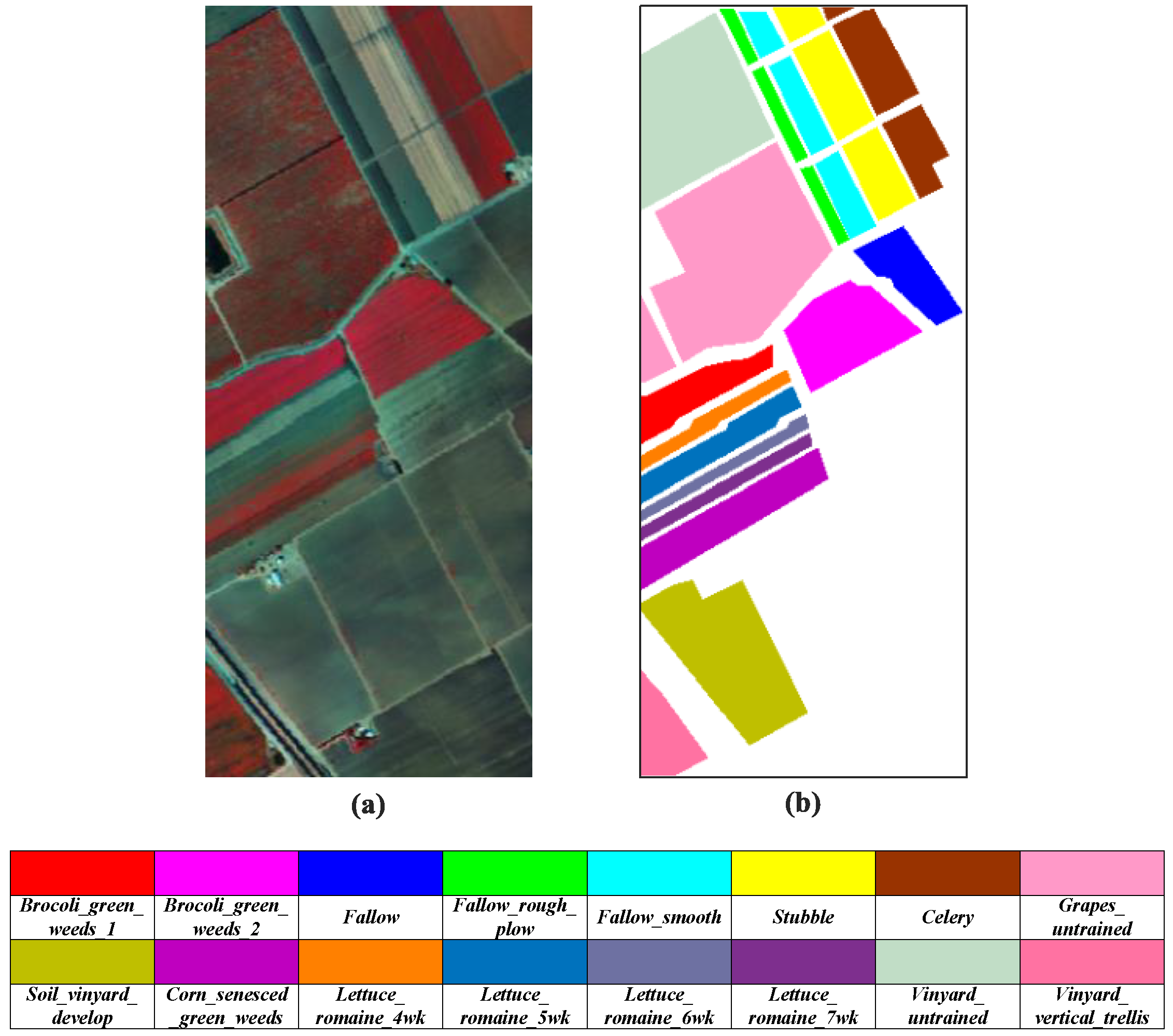
3.1. Experimental Data
3.2. Data Preprocessing
3.3. Parameter Optimization
3.3.1. Parameter Optimization of the Compared Methods
3.3.2. Parameter Optimization of the Proposed Methods
3.4. Classification Results and Discussion
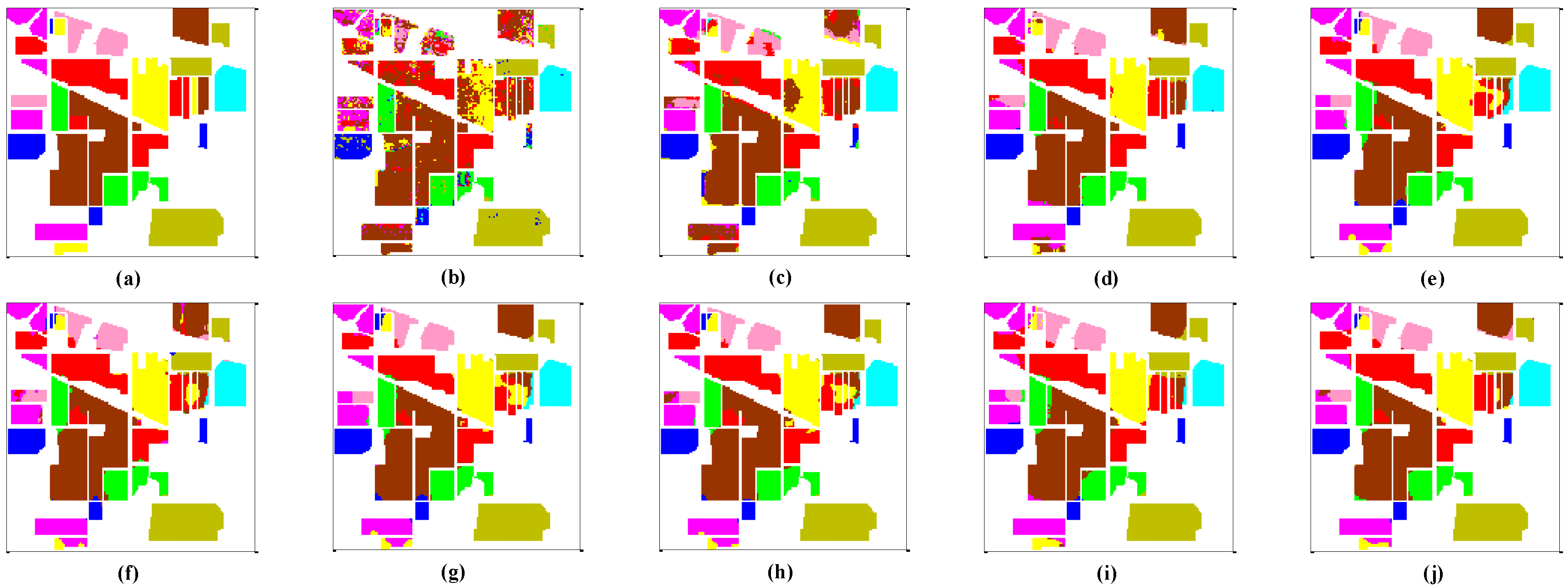
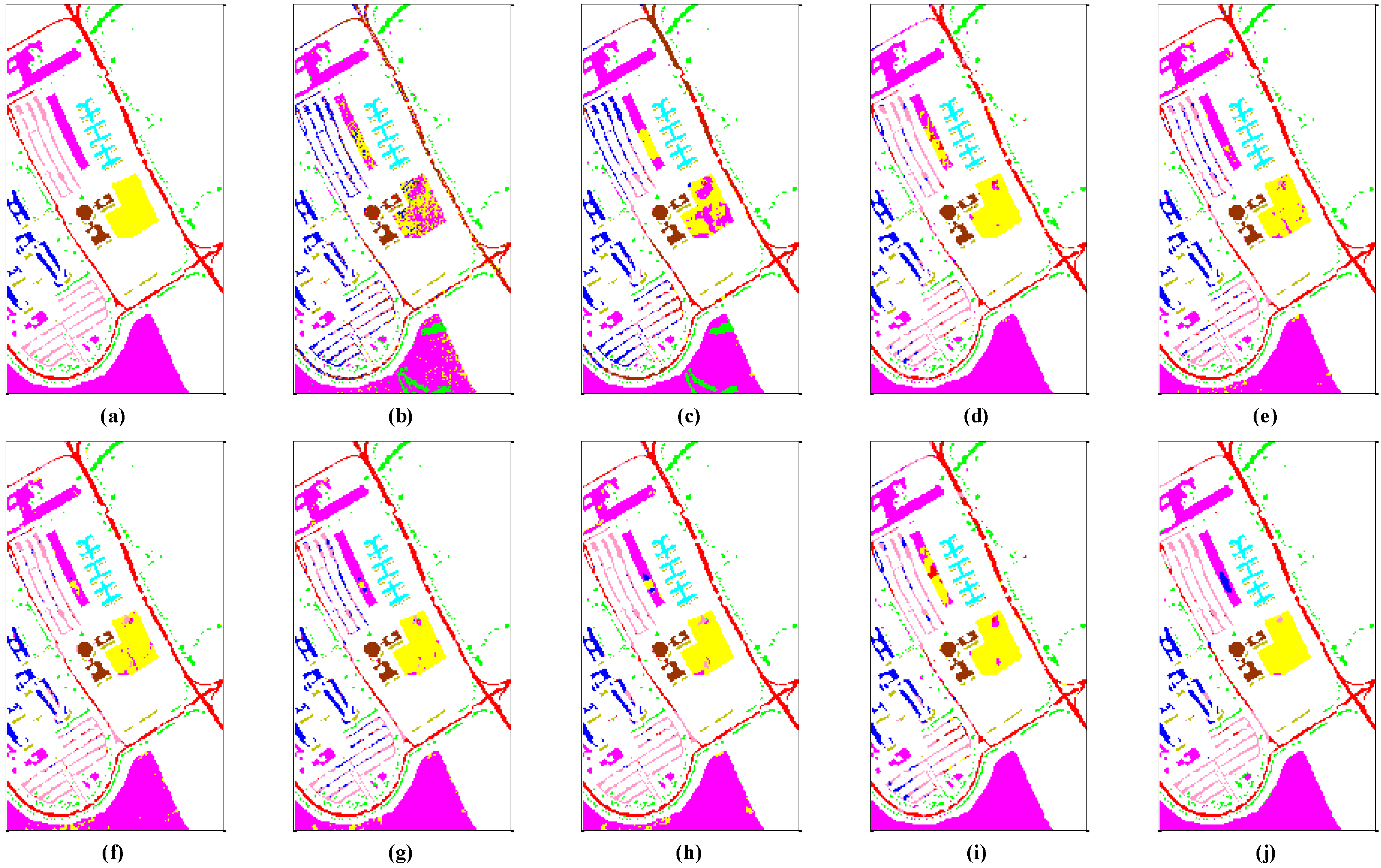
3.4.1. Analysis of Classification Performance
3.4.2. Stability Analysis for Classification Performance
3.4.3. Significance Analysis for Classification Performance
3.5. Comparison of Running Time
4. Conclusions
- (1)
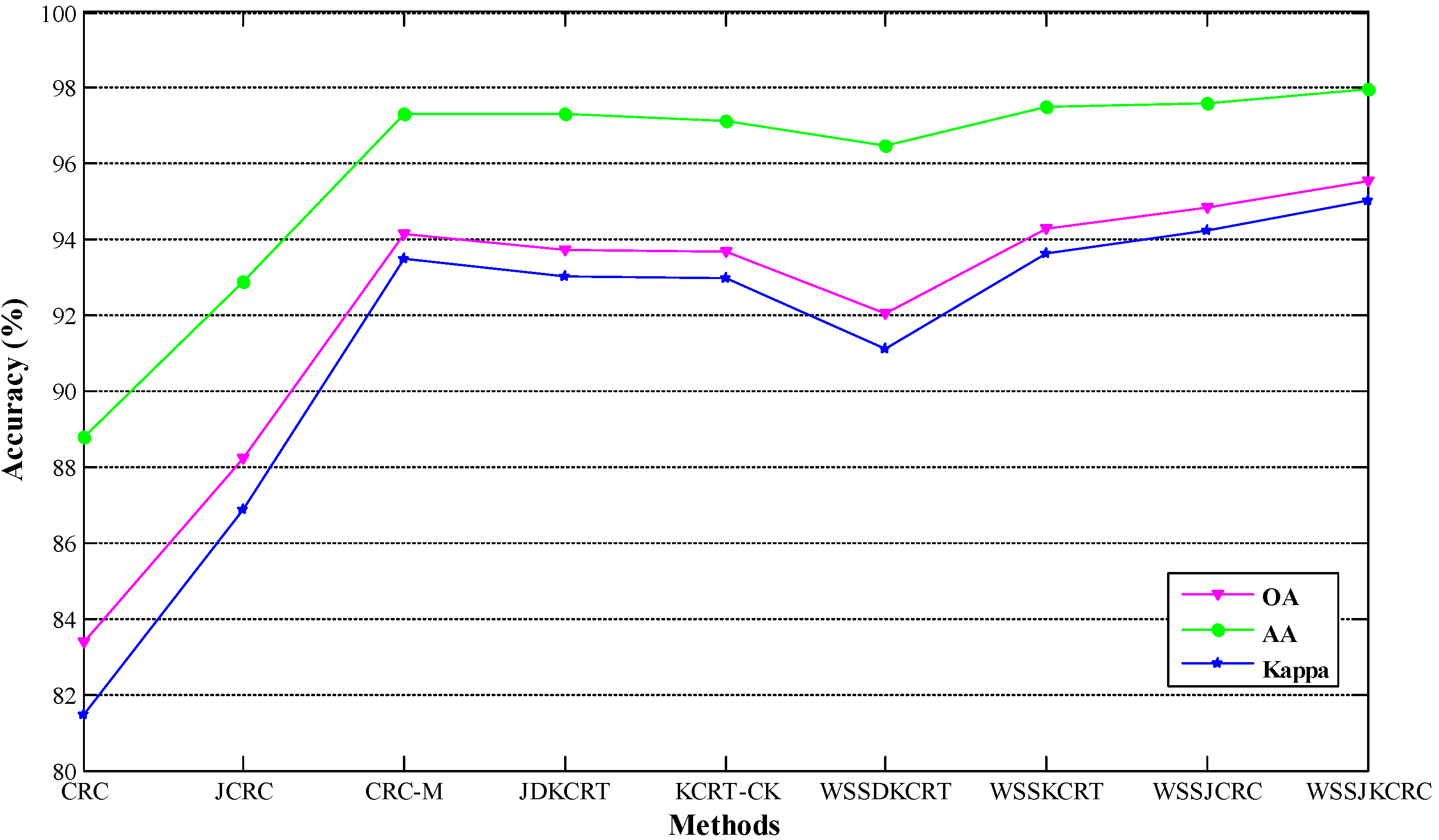
- The proposed WSSJCRC method significantly outperforms the traditional CRC and JCRC methods for land cover classification on the three hyperspectral scenes;
- (2)
- The proposed WSSJKCRC method achieves the best land cover classification performance on the three hyperspectral scenes among all the compared methods. The OA, AA, and Kappa of WSSJKCRC reach 96.21%, 96.20%, and 0.9555 for the Indian Pines scene, 97.02%, 96.64%, and 0.9605 for the Pavia University scene, 95.55%, 97.97%, and 0.9504 for the Salinas scene, respectively;
- (3)
- WSSJKCRC can achieve the promising performance for land cover classification with OA over 95% on the three hyperspectral scenes under the situation of small-scale labeled samples, thus effectively reducing the labeling cost for HSI.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, S.; Liu, L.Y.; Zhang, X.; Yang, J.N. Mapping the annual dynamics of land cover in Beijing from 2001 to 2020 using Landsat dense time series stack. ISPRS J. Photogramm. Remote Sens. 2022, 185, 201–218. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land cover classification using google earth engine and random forest classifier-the role of image composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Agapiou, A. Land cover mapping from colorized CORONA archived greyscale satellite data and feature extraction classification. Land 2021, 10, 771. [Google Scholar] [CrossRef]
- Akar, O.; Gormus, E.T. Land use/land cover mapping from airborne hyperspectral images with machine learning algorithms and contextual information. Geocarto Int. 2022, 37, 3963–3990. [Google Scholar] [CrossRef]
- Wasniewski, A.; Hoscilo, A.; Chmielewska, M. Can a hierarchical classification of sentinel-2 data improve land cover mapping? Remote Sens. 2022, 14, 989. [Google Scholar] [CrossRef]
- Yu, Y.T.; Guan, H.Y.; Li, D.L.; Gu, T.N.; Wang, L.F.; Ma, L.F.; Li, J. A hybrid capsule network for land cover classification using multispectral LiDAR data. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1263–1267. [Google Scholar] [CrossRef]
- Hong, D.F.; Hu, J.L.; Yao, J.; Chanussot, J.; Zhu, X.X. Multimodal remote sensing benchmark datasets for land cover classification with a shared and specific feature learning model. ISPRS J. Photogramm. Remote Sens. 2021, 178, 68–80. [Google Scholar] [CrossRef]
- Zafari, A.; Zurita-Milla, R.; Izquierdo-Verdiguier, E. Evaluating the performance of a random forest kernel for land cover classification. Remote Sens. 2019, 11, 575. [Google Scholar] [CrossRef]
- Li, X.Y.; Sun, C.; Meng, H.M.; Ma, X.; Huang, G.H.; Xu, X. A novel efficient method for land cover classification in fragmented agricultural landscapes using sentinel satellite imagery. Remote Sens. 2022, 14, 2045. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.T.; Fang, L.Y.; Jia, X.P.; Benediktsson, J.A. From subpixel to superpixel: A novel fusion framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4398–4411. [Google Scholar] [CrossRef]
- Gao, Q.S.; Lim, S.; Jia, X.P. Improved joint sparse models for hyperspectral image classification based on a novel neighbour selection strategy. Remote Sens. 2018, 10, 905. [Google Scholar] [CrossRef]
- Yu, H.Y.; Shang, X.D.; Song, M.P.; Hu, J.C.; Jiao, T.; Guo, Q.D.; Zhang, B. Union of class-dependent collaborative representation based on maximum margin projection for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 553–566. [Google Scholar] [CrossRef]
- Bigdeli, B.; Samadzadegan, F.; Reinartz, P. A multiple SVM system for classification of hyperspectral remote sensing data. J. Indian Soc. Remote Sens. 2013, 41, 763–776. [Google Scholar] [CrossRef]
- Waske, B.; van der Linden, S.; Benediktsson, J.A.; Rabe, A.; Hostert, P. Sensitivity of support vector machines to random feature selection in classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2880–2889. [Google Scholar] [CrossRef]
- Lopez-Fandino, J.; Quesada-Barriuso, P.; Heras, D.B.; Arguello, F. Efficient ELM-based techniques for the classification of hyperspectral remote sensing images on commodity GPUs. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2884–2893. [Google Scholar] [CrossRef]
- Huang, F.; Lu, J.; Tao, J.; Li, L.; Tan, X.C.; Liu, P. Research on optimization methods of ELM classification algorithm for hyperspectral remote sensing images. IEEE Access 2019, 7, 108070–108089. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Cao, G.; Li, X.S.; Wang, B.S. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, F.; Hu, W. Collaborative-representation-based nearest neighbor classifier for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2015, 12, 389–393. [Google Scholar] [CrossRef]
- Su, H.J.; Zhao, B.; Du, Q.; Du, P.J. Kernel collaborative representation with local correlation features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1230–1241. [Google Scholar] [CrossRef]
- Ye, M.C.; Qian, Y.T.; Zhou, J.; Tang, Y.Y. Dictionary learning-based feature-level domain adaptation for cross-scene hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1544–1562. [Google Scholar] [CrossRef]
- Chen, H.; Ye, M.C.; Lei, L.; Lu, H.J.; Qian, Y.T. Semisupervised dual-dictionary learning for heterogeneous transfer learning on cross-scene hyperspectral images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 3164–3178. [Google Scholar] [CrossRef]
- Shen, J.Y.; Cao, X.B.; Li, Y.; Xu, D. Feature adaptation and augmentation for cross-scene hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 622–626. [Google Scholar] [CrossRef]
- Yang, R.C.; Zhou, Q.B.; Fan, B.L.; Wang, Y.T. Land cover classification from hyperspectral images via local nearest neighbor collaborative representation with Tikhonov regularization. Land 2022, 11, 702. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.S. Transferring CNN ensemble for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 876–880. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.T.; Lu, X.Q. A supervised segmentation network for hyperspectral image classification. IEEE Trans. Image Process. 2021, 30, 2810–2825. [Google Scholar] [CrossRef] [PubMed]
- Du, P.J.; Gan, L.; Xia, J.S.; Wang, D.M. Multikernel adaptive collaborative representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4664–4677. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, F.; Hu, W. Hyperspectral image classification by fusing collaborative and sparse representations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4178–4187. [Google Scholar] [CrossRef]
- Chen, X.; Li, S.Y.; Peng, J.T. Hyperspectral imagery classification with multiple regularized collaborative representations. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1121–1125. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Xiong, M.M. Kernel collaborative representation with Tikhonov regularization for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 48–52. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, M.; Feng, X.C. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 471–478. [Google Scholar]
- Li, W.; Tramel, E.W.; Prasad, S.; Fowler, J.E. Nearest regularized subspace for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 477–489. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.X.; Liu, N.; Du, Q.; Tao, R. Structure-aware collaborative representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7246–7261. [Google Scholar] [CrossRef]
- Yang, R.C.; Kan, J.M. Euclidean distance-based adaptive collaborative representation with Tikhonov regularization for hyperspectral image classification. Multimed. Tools Appl. 2022. [Google Scholar] [CrossRef]
- Liu, H.; Li, W.; Xia, X.G.; Zhang, M.M.; Gao, C.Z.; Tao, R. Spectral shift mitigation for cross-scene hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 6624–6638. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Li, H.; Mei, X.G.; Ma, J.Y. Hyperspectral image classification with discriminative kernel collaborative representation and Tikhonov regularization. IEEE Geosci. Remote Sens. Lett. 2018, 15, 587–591. [Google Scholar] [CrossRef]
- Su, H.J.; Hu, Y.Z.; Lu, H.L.; Sun, W.W.; Du, Q. Diversity-driven multikernel collaborative representation ensemble for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 2861–2876. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Joint within-class collaborative representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2200–2208. [Google Scholar] [CrossRef]
- Shaw, G.A.; Burke, H.K. Spectral imaging for remote sensing. Lincoln Lab. J. 2003, 14, 3–28. [Google Scholar]
- Yang, R.C.; Fan, B.L.; Wei, R.; Wang, Y.T.; Zhou, Q.B. Land cover classification from hyperspectral images via weighted spatial-spectral kernel collaborative representation with Tikhonov regularization. Land 2022, 11, 263. [Google Scholar] [CrossRef]
- Yang, J.H.; Qian, J.X. Hyperspectral image classification via multiscale joint collaborative representation with locally adaptive dictionary. IEEE Geosci. Remote Sens. Lett. 2018, 15, 112–116. [Google Scholar] [CrossRef]








| Indian Pines | Pavia University | Salinas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Class | Training Samples | Test Samples | No. | Class | Training Samples | Test Samples | No. | Class | Training Samples | Test Samples |
| 1 | Corn-notill | 72 | 1356 | 1 | Asphalt | 60 | 6571 | 1 | Brocoli_green_weeds_1 | 20 | 1949 |
| 2 | Corn-mintill | 42 | 788 | 2 | Meadows | 60 | 18,589 | 2 | Brocoli_green_weeds_2 | 20 | 3666 |
| 3 | Grass-pasture | 25 | 458 | 3 | Gravel | 60 | 2039 | 3 | Fallow | 20 | 1916 |
| 4 | Grass-trees | 37 | 693 | 4 | Trees | 60 | 3004 | 4 | Fallow_rough_plow | 20 | 1334 |
| 5 | Hay-windrowed | 24 | 454 | 5 | Painted metal sheets | 60 | 1285 | 5 | Fallow_smooth | 20 | 2618 |
| 6 | Soybean-notill | 49 | 923 | 6 | Bare Soil | 60 | 4969 | 6 | Stubble | 20 | 3899 |
| 7 | Soybean-mintill | 123 | 2332 | 7 | Bitumen | 60 | 1270 | 7 | Celery | 20 | 3519 |
| 8 | Soybean-clean | 30 | 563 | 8 | Self-Blocking Bricks | 60 | 3622 | 8 | Grapes_untrained | 20 | 11,211 |
| 9 | Woods | 64 | 1201 | 9 | Shadows | 60 | 887 | 9 | Soil_vinyard_develop | 20 | 6143 |
| 10 | Corn_senesced_green_weeds | 20 | 3218 | ||||||||
| 11 | Lettuce_romaine_4wk | 20 | 1008 | ||||||||
| 12 | Lettuce_romaine_5wk | 20 | 1867 | ||||||||
| 13 | Lettuce_romaine_6wk | 20 | 856 | ||||||||
| 14 | Lettuce_romaine_7wk | 20 | 1010 | ||||||||
| 15 | Vinyard_untrained | 20 | 7208 | ||||||||
| 16 | Vinyard_vertical_trellis | 20 | 1747 | ||||||||
| All class | 466 | 8768 | All class | 540 | 42,236 | All class | 320 | 53,169 | |||
| Method | Indian Pines | Pavia University | Salinas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | β | Wf | Ws | λ | β | Wf | Ws | λ | β | Wf | Ws | |
| CRC | 10−6 | NA | NA | NA | 10−5 | NA | NA | NA | 10−7 | NA | NA | NA |
| JCRC | 10−7 | NA | NA | 7 × 7 | 10−7 | NA | NA | 5 × 5 | 10−8 | NA | NA | 3 × 3 |
| CRC-M | 10−8 | NA | 13 × 13 | NA | 10−8 | NA | 13 × 13 | NA | 10−11 | NA | 11 × 11 | NA |
| JDKCRT | 10−3 | 10−2 | 19 × 19 | NA | 10−3 | 10−4 | 5 × 5 | NA | 10−4 | 10−4 | 9 × 9 | NA |
| KCRT-CK | 10−5 | NA | 15 × 15 | NA | 10−2 | NA | 5 × 5 | NA | 10−3 | NA | 9 × 9 | NA |
| WSSDKCRT | 10−4 | 10−3 | 19 × 19 | NA | 10−3 | 10−4 | 7 × 7 | NA | 10−3 | 10−4 | 5 × 5 | NA |
| WSSKCRT | 10−4 | NA | 19 × 19 | NA | 10−2 | NA | 9 × 9 | NA | 10−8 | NA | 9 × 9 | NA |
| Method | Indian Pines | Pavia University | Salinas | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λ | Wf | Ws | λ | Wf | Ws | λ | Wf | Ws | |
| WSSJCRC | 10−8 | 21 × 21 | 13 × 13 | 10−7 | 13 × 13 | 3 × 3 | 10−9 | 11 × 11 | 7 × 7 |
| WSSJKCRC | 10−3 | 15 × 15 | 7 × 7 | 10−4 | 13 × 13 | 7 × 7 | 10−4 | 11 × 11 | 7 × 7 |
| Class | CRC | JCRC | CRC-M | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | WSSJCRC | WSSJKCRC |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 64.76 ± 4.26 | 83.33 ± 4.65 | 89.73 ± 2.24 | 89.59 ± 2.16 | 92.88 ± 1.41 | 91.57 ± 2.17 | 93.25 ± 3.16 | 85.96 ± 3.90 | 92.43 ± 1.98 |
| 2 | 32.60 ± 6.43 | 60.36 ± 3.33 | 94.24 ± 2.59 | 94.71 ± 1.77 | 94.09 ± 2.98 | 94.49 ± 4.42 | 95.66 ± 2.86 | 92.54 ± 2.63 | 94.51 ± 1.57 |
| 3 | 76.92 ± 5.27 | 88.47 ± 2.81 | 92.29 ± 4.66 | 95.87 ± 3.05 | 94.17 ± 4.50 | 96.83 ± 2.06 | 97.88 ± 2.43 | 93.08 ± 5.74 | 95.44 ± 3.76 |
| 4 | 91.24 ± 2.36 | 98.56 ± 0.86 | 98.82 ± 1.02 | 97.73 ± 0.83 | 97.59 ± 1.45 | 97.60 ± 1.69 | 96.22 ± 2.31 | 97.53 ± 1.12 | 98.25 ± 1.04 |
| 5 | 98.37 ± 1.03 | 100.00 ± 0.00 | 99.91 ± 0.26 | 99.71 ± 0.36 | 98.96 ± 1.40 | 99.49 ± 0.69 | 99.01 ± 1.27 | 99.96 ± 0.13 | 99.98 ± 0.07 |
| 6 | 42.05 ± 5.23 | 62.95 ± 6.19 | 90.10 ± 2.61 | 92.09 ± 2.41 | 93.43 ± 2.57 | 93.10 ± 2.54 | 93.38 ± 2.41 | 87.28 ± 2.26 | 92.29 ± 2.56 |
| 7 | 81.93 ± 1.82 | 86.42 ± 1.84 | 97.36 ± 0.76 | 95.19 ± 1.49 | 96.24 ± 1.35 | 95.81 ± 1.28 | 96.83 ± 1.63 | 93.66 ± 2.19 | 97.94 ± 1.20 |
| 8 | 18.76 ± 3.63 | 65.56 ± 6.54 | 93.21 ± 3.62 | 94.33 ± 3.16 | 92.38 ± 4.05 | 94.03 ± 3.24 | 92.65 ± 6.42 | 88.56 ± 4.07 | 95.74 ± 1.95 |
| 9 | 97.31 ± 0.67 | 99.92 ± 0.07 | 99.74 ± 0.47 | 99.15 ± 0.76 | 98.23 ± 0.94 | 99.41 ± 0.42 | 99.13 ± 0.94 | 99.06 ± 0.76 | 99.20 ± 0.46 |
| OA (%) | 70.02 ± 0.66 | 83.41 ± 0.77 | 95.18 ± 0.58 | 94.91 ± 0.56 | 95.40 ± 0.52 | 95.51 ± 0.64 | 95.98 ± 0.92 | 92.71 ± 0.90 | 96.21 ± 0.44 |
| AA (%) | 67.10 ± 0.80 | 82.84 ± 0.88 | 95.04 ± 0.83 | 95.38 ± 0.44 | 95.33 ± 0.67 | 95.82 ± 0.66 | 96.00 ± 1.14 | 93.07 ± 1.05 | 96.20 ± 0.52 |
| Kappa | 0.6395 ± 0.0086 | 0.8031 ± 0.0092 | 0.9433 ± 0.0069 | 0.9404 ± 0.0065 | 0.9459 ± 0.0060 | 0.9474 ± 0.0074 | 0.9527 ± 0.0108 | 0.9145 ± 0.0106 | 0.9555 ± 0.0052 |
| Class | CRC | JCRC | CRC-M | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | WSSJCRC | WSSJKCRC |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 26.08 ± 6.00 | 41.70 ± 8.62 | 72.75 ± 4.04 | 92.15 ± 1.57 | 91.62 ± 2.39 | 93.68 ± 1.81 | 91.41 ± 2.63 | 72.42 ± 2.80 | 94.03 ± 2.23 |
| 2 | 78.54 ± 3.75 | 82.10 ± 3.43 | 93.85 ± 3.21 | 95.76 ± 1.29 | 93.77 ± 2.84 | 97.34 ± 1.48 | 96.57 ± 1.44 | 91.42 ± 2.93 | 98.20 ± 1.15 |
| 3 | 91.44 ± 1.39 | 95.52 ± 2.18 | 93.29 ± 2.94 | 95.27 ± 1.35 | 87.68 ± 1.55 | 96.58 ± 1.29 | 90.30 ± 2.41 | 96.38 ± 1.22 | 95.23 ± 3.00 |
| 4 | 95.27 ± 1.74 | 96.69 ± 1.06 | 91.23 ± 1.58 | 96.77 ± 1.44 | 96.32 ± 1.23 | 96.82 ± 0.87 | 97.15 ± 0.88 | 92.71 ± 1.27 | 95.32 ± 1.24 |
| 5 | 99.89 ± 0.07 | 100.00 ± 0.00 | 99.84 ± 0.06 | 100.00 ± 0.00 | 99.98 ± 0.03 | 99.77 ± 0.13 | 99.67 ± 0.07 | 100.00 ± 0.00 | 99.98 ± 0.04 |
| 6 | 52.76 ± 6.60 | 69.48 ± 3.53 | 98.25 ± 1.52 | 94.90 ± 1.90 | 93.25 ± 1.34 | 96.88 ± 0.94 | 95.95 ± 1.38 | 98.73 ± 0.87 | 99.29 ± 0.96 |
| 7 | 88.38 ± 3.22 | 98.17 ± 0.47 | 99.75 ± 0.26 | 98.77 ± 0.49 | 96.83 ± 1.22 | 99.15 ± 0.53 | 97.70 ± 0.77 | 99.96 ± 0.12 | 99.98 ± 0.05 |
| 8 | 18.39 ± 3.95 | 22.73 ± 5.69 | 77.63 ± 3.06 | 67.10 ± 5.28 | 88.80 ± 2.21 | 71.48 ± 4.94 | 91.22 ± 1.56 | 73.96 ± 3.77 | 94.50 ± 3.74 |
| 9 | 90.20 ± 2.07 | 98.56 ± 0.77 | 90.86 ± 1.66 | 99.59 ± 0.22 | 99.59 ± 0.16 | 98.55 ± 0.66 | 97.77 ± 0.67 | 93.45 ± 1.92 | 93.25 ± 1.57 |
| OA (%) | 65.19 ± 1.47 | 72.30 ± 1.43 | 89.78 ± 1.58 | 92.99 ± 0.60 | 93.24 ± 1.18 | 94.58 ± 0.56 | 95.13 ± 0.63 | 88.72 ± 1.53 | 97.02 ± 0.77 |
| AA (%) | 71.22 ± 0.57 | 78.33 ± 0.94 | 90.83 ± 0.67 | 93.37 ± 0.52 | 94.20 ± 0.37 | 94.47 ± 0.37 | 95.30 ± 0.20 | 91.00 ± 0.78 | 96.64 ± 0.70 |
| Kappa | 0.5547 ± 0.0148 | 0.6442 ± 0.0172 | 0.8656 ± 0.0199 | 0.9073 ± 0.0077 | 0.9109 ± 0.0150 | 0.9282 ± 0.0073 | 0.9355 ± 0.0082 | 0.8525 ± 0.0194 | 0.9605 ± 0.0102 |
| Class | CRC | JCRC | CRC-M | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | WSSJCRC | WSSJKCRC |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.65 ± 0.43 | 99.17 ± 0.26 | 100.00 ± 0.00 | 99.16 ± 0.96 | 98.79 ± 1.01 | 99.68 ± 0.39 | 98.76 ± 1.51 | 100.00 ± 0.00 | 99.73 ± 0.44 |
| 2 | 99.20 ± 0.63 | 99.99 ± 0.01 | 99.99 ± 0.02 | 99.45 ± 0.61 | 99.25 ± 1.02 | 99.80 ± 0.19 | 99.88 ± 0.11 | 100.00 ± 0.00 | 99.93 ± 0.07 |
| 3 | 92.62 ± 2.57 | 98.48 ± 1.59 | 99.87 ± 0.23 | 99.54 ± 0.36 | 99.92 ± 0.10 | 99.88 ± 0.11 | 99.78 ± 0.27 | 100.00 ± 0.00 | 99.78 ± 0.16 |
| 4 | 96.26 ± 1.24 | 98.45 ± 0.91 | 99.03 ± 0.75 | 99.11 ± 0.67 | 99.03 ± 0.54 | 99.60 ± 0.32 | 99.00 ± 0.63 | 99.74 ± 0.22 | 97.93 ± 0.39 |
| 5 | 96.53 ± 1.32 | 98.14 ± 0.79 | 95.91 ± 1.54 | 96.21 ± 2.18 | 96.48 ± 4.62 | 97.23 ± 1.88 | 97.46 ± 1.09 | 96.98 ± 1.55 | 98.42 ± 1.00 |
| 6 | 99.91 ± 0.06 | 99.99 ± 0.02 | 99.95 ± 0.09 | 99.69 ± 0.69 | 99.35 ± 1.40 | 99.26 ± 1.02 | 98.94 ± 1.60 | 99.86 ± 0.27 | 98.76 ± 2.80 |
| 7 | 99.82 ± 0.06 | 99.92 ± 0.04 | 99.99 ± 0.03 | 98.68 ± 0.91 | 98.10 ± 0.98 | 99.15 ± 0.45 | 99.24 ± 0.45 | 100.00 ± 0.00 | 99.35 ± 0.44 |
| 8 | 65.41 ± 7.32 | 79.27 ± 6.64 | 82.62 ± 3.61 | 77.77 ± 8.09 | 80.38 ± 2.88 | 77.79 ± 4.44 | 81.82 ± 3.91 | 87.24 ± 3.18 | 86.78 ± 3.51 |
| 9 | 99.71 ± 0.24 | 99.97 ± 0.10 | 99.98 ± 0.03 | 99.62 ± 0.38 | 99.45 ± 0.57 | 99.53 ± 0.51 | 99.81 ± 0.10 | 99.99 ± 0.02 | 99.90 ± 0.19 |
| 10 | 86.79 ± 1.40 | 91.33 ± 1.18 | 95.93 ± 2.60 | 97.96 ± 0.93 | 97.44 ± 1.47 | 95.99 ± 1.40 | 97.51 ± 1.67 | 96.14 ± 2.60 | 97.39 ± 1.54 |
| 11 | 95.46 ± 1.15 | 97.65 ± 1.24 | 99.76 ± 0.27 | 99.54 ± 0.94 | 100.00 ± 0.00 | 99.20 ± 0.73 | 99.75 ± 0.30 | 99.66 ± 0.49 | 100.00 ± 0.00 |
| 12 | 71.75 ± 5.26 | 89.04 ± 5.23 | 99.26 ± 0.43 | 99.87 ± 0.32 | 99.97 ± 0.04 | 100.00 ± 0.00 | 99.77 ± 0.40 | 99.14 ± 1.10 | 99.96 ± 0.04 |
| 13 | 74.99 ± 4.38 | 83.45 ± 4.75 | 98.47 ± 1.02 | 100.00 ± 0.00 | 99.72 ± 0.35 | 99.43 ± 0.83 | 99.92 ± 0.12 | 99.33 ± 0.57 | 99.82 ± 0.24 |
| 14 | 90.67 ± 1.92 | 95.89 ± 2.05 | 99.39 ± 0.52 | 98.66 ± 1.04 | 98.82 ± 0.93 | 96.90 ± 3.07 | 99.16 ± 0.68 | 97.97 ± 2.05 | 99.19 ± 1.19 |
| 15 | 54.81 ± 5.17 | 57.01 ± 12.57 | 88.17 ± 5.19 | 93.00 ± 3.22 | 89.84 ± 4.82 | 80.95 ± 5.27 | 90.36 ± 4.90 | 85.48 ± 3.35 | 91.44 ± 3.57 |
| 16 | 97.70 ± 0.60 | 98.44 ± 0.45 | 99.14 ± 0.76 | 99.11 ± 0.54 | 97.82 ± 2.43 | 99.14 ± 0.67 | 98.75 ± 0.98 | 99.93 ± 0.08 | 99.07 ± 1.52 |
| OA (%) | 83.36 ± 1.24 | 88.23 ± 1.06 | 94.15 ± 0.71 | 93.72 ± 1.42 | 93.70 ± 0.65 | 92.04 ± 0.97 | 94.28 ± 0.89 | 94.85 ± 0.65 | 95.55 ± 0.70 |
| AA (%) | 88.77 ± 0.60 | 92.89 ± 0.72 | 97.34 ± 0.27 | 97.34 ± 0.37 | 97.15 ± 0.48 | 96.47 ± 0.51 | 97.49 ± 0.38 | 97.59 ± 0.29 | 97.97 ± 0.30 |
| Kappa | 0.8147 ± 0.0134 | 0.8686 ± 0.0120 | 0.9349 ± 0.0079 | 0.9303 ± 0.0157 | 0.9299 ± 0.0073 | 0.9114 ± 0.0108 | 0.9363 ± 0.0099 | 0.9426 ± 0.0073 | 0.9504 ± 0.0078 |
| Indicators | Datasets | CRC | JCRC | CRC-M | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | WSSJCRC |
|---|---|---|---|---|---|---|---|---|---|
| p-value for OA | Indian Pines | 4.110 × 10−26 | 1.082 × 10−19 | 4.661 × 10−4 | 3.155 × 10−5 | 1.961 × 10−3 | 1.423 × 10−2 | 4.923 × 10−1 | 4.526 × 10−9 |
| Pavia University | 7.786 × 10−22 | 4.743 × 10−20 | 3.202 × 10−10 | 3.189 × 10−10 | 2.293 × 10−7 | 4.501 × 10−7 | 2.141 × 10−5 | 2.235 × 10−11 | |
| Salinas | 1.214 × 10−15 | 1.183 × 10−12 | 5.536 × 10−4 | 2.899 × 10−3 | 1.747 × 10−5 | 6.662 × 10−8 | 3.532 × 10−3 | 4.346 × 10−2 | |
| p-value for AA | Indian Pines | 1.860 × 10−25 | 6.762 × 10−19 | 2.346 × 10−3 | 1.928 × 10−3 | 6.447 × 10−3 | 1.911 × 10−1 | 6.467 × 10−1 | 2.305 × 10−7 |
| Pavia University | 6.868 × 10−25 | 2.903 × 10−20 | 5.771 × 10−13 | 1.280 × 10−9 | 2.867 × 10−8 | 1.531 × 10−7 | 3.041 × 10−5 | 3.740 × 10−12 | |
| Salinas | 2.773 × 10−19 | 1.637 × 10−13 | 2.110 × 10−4 | 8.763 × 10−4 | 3.891 × 10−4 | 5.278 × 10−7 | 9.463 × 10−3 | 1.542 × 10−2 | |
| p-value for Kappa | Indian Pines | 9.274 × 10−26 | 1.168 × 10−19 | 4.704 × 10−4 | 3.291 × 10−5 | 1.987 × 10−3 | 1.534 × 10−2 | 4.970 × 10−1 | 4.409 × 10−9 |
| Pavia University | 4.011 × 10−23 | 2.287 × 10−20 | 1.875 × 10−10 | 2.673 × 10−10 | 1.705 × 10−7 | 3.780 × 10−7 | 1.969 × 10−5 | 1.577 × 10−11 | |
| Salinas | 8.783 × 10−16 | 1.351 × 10−12 | 5.487 × 10−4 | 2.894 × 10−3 | 1.839 × 10−5 | 6.549 × 10−8 | 3.596 × 10−3 | 4.189 × 10−2 |
| Datasets | CRC | JCRC | CRC-M | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | WSSJCRC | WSSJKCRC |
|---|---|---|---|---|---|---|---|---|---|
| Indian Pines | 0.47 | 10.75 | 13.49 | 24.33 | 15.36 | 27.34 | 27.90 | 4669.58 | 463.77 |
| Pavia University | 1.10 | 49.60 | 66.40 | 50.65 | 48.48 | 52.19 | 52.74 | 211.30 | 1094.92 |
| Salinas | 1.38 | 18.01 | 37.63 | 29.25 | 29.22 | 48.74 | 30.73 | 1136.04 | 1267.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Zhou, Q.; Fan, B.; Wang, Y.; Li, Z. Land Cover Classification from Hyperspectral Images via Weighted Spatial–Spectral Joint Kernel Collaborative Representation Classifier. Agriculture 2023, 13, 304. https://doi.org/10.3390/agriculture13020304
Yang R, Zhou Q, Fan B, Wang Y, Li Z. Land Cover Classification from Hyperspectral Images via Weighted Spatial–Spectral Joint Kernel Collaborative Representation Classifier. Agriculture. 2023; 13(2):304. https://doi.org/10.3390/agriculture13020304
Chicago/Turabian StyleYang, Rongchao, Qingbo Zhou, Beilei Fan, Yuting Wang, and Zhemin Li. 2023. "Land Cover Classification from Hyperspectral Images via Weighted Spatial–Spectral Joint Kernel Collaborative Representation Classifier" Agriculture 13, no. 2: 304. https://doi.org/10.3390/agriculture13020304
APA StyleYang, R., Zhou, Q., Fan, B., Wang, Y., & Li, Z. (2023). Land Cover Classification from Hyperspectral Images via Weighted Spatial–Spectral Joint Kernel Collaborative Representation Classifier. Agriculture, 13(2), 304. https://doi.org/10.3390/agriculture13020304





