Application of Computational Intelligence Methods in Agricultural Soil–Machine Interaction: A Review
Abstract
:1. Introduction
2. Traditional Modeling Methods
2.1. Analytical Method
2.2. Empirical Method
2.3. Semi-Empirical Method
2.4. Numerical Method
3. Computational Intelligence: An Overview
3.1. Data Preprocessing
- (i)
- Data Normalization: This is the most rudimentary form of preprocessing. Each field of the data are normalized separately so that the entries lie in some desired range, usually or .
- (ii)
- Data Cleaning: Experimental data may contain some missing entries. One option to deal with the issue is to remove every sample, which contains a missing (scalar) field. This practice may be wasteful, particularly when the data are limited. If so, missing fields may be filled with means, medians, or interpolated values. Corrupted entries can also be treated in this manner [37]. Noise reduction is another form of data cleaning. When the noise follows a non-skewed distribution around a zero mean, noise removal may not be necessary in regression tasks. Convolution with Gaussian or other filters is a common filtering tool for time series data [38].
- (iii)
- (iv)
- Spectral Transformation: This technique can be used with periodic data. The classical Fourier transform is regularly used to extract frequency components of such data; it does not preserve the time information of the input. Wavelet transforms can be used when the data must incorporate frequency and temporal components.
3.2. Loss Functions
- (i)
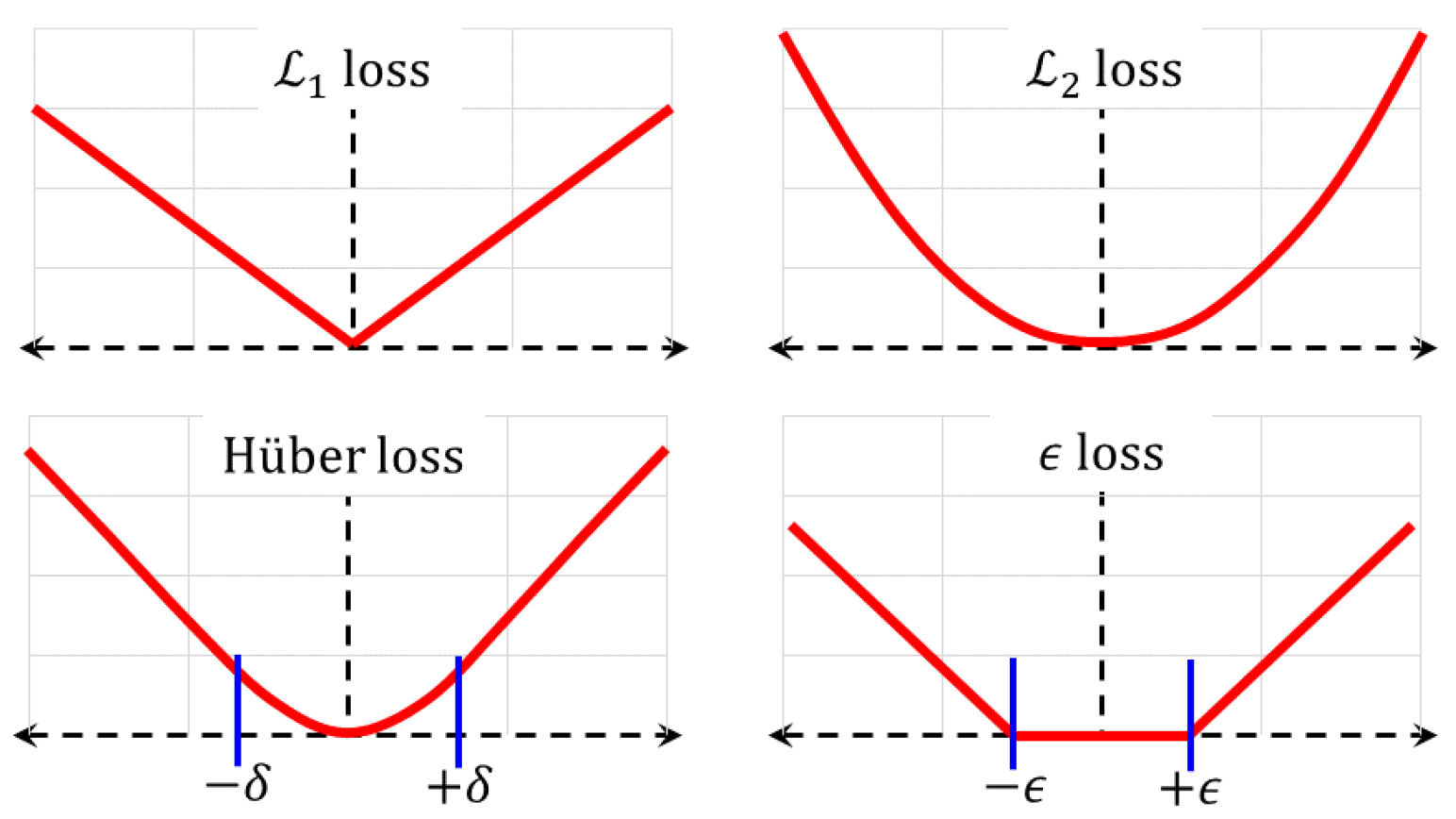
- Mean squared () loss: For scalars, this loss is the average of the squared differences between the network’s outputs , for inputs and the corresponding targets, so that, . For vector outputs, the Euclidean norm is used, where is the model’s vector output. The loss is the most commonly used function. Using quadratic penalty terms makes the function quite sensitive to statistical outliers.
- (ii)
- Averaged absolute () loss: This is the average of the absolute difference, . The loss is used to avoid assigning excessive penalties to noisier samples. On the other hand, its effectiveness is compromised for data with copious noise.
- (iii)
- Hüber loss: The Hüber loss represents a trade-off between the and losses [43]. Samples where the absolute difference is less than a threshold incur a quadratic penalty, while the remaining ones have a linear penalty. It is obtained as the average , where is the penalty of the nth sample,As the Hüber loss function is not twice differentiable at , the similarly shaped log-cosh function below can be used in its place,
- (iv)
- -Loss: This loss does not apply a penalty when the difference lies within a tolerable range , for some constant . A linear penalty is incurred whenever the numerical difference lies outside this range. In other words, , where,
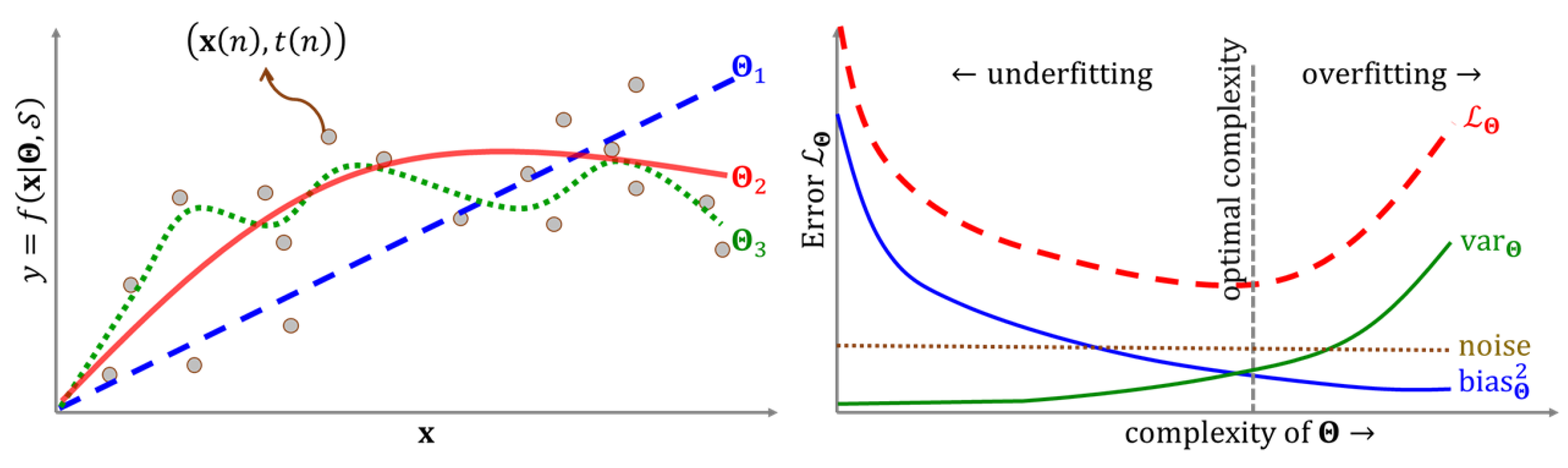
3.3. Model Selection
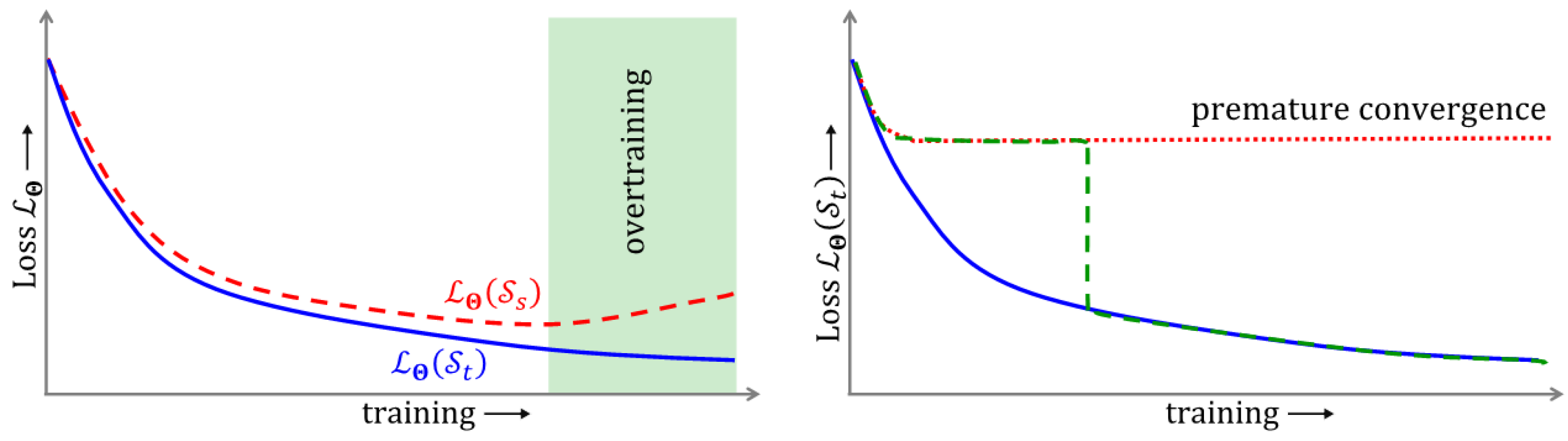
3.4. Training Algorithms
3.5. Optimization Metaheuristics
4. Current Computational Intelligence Models
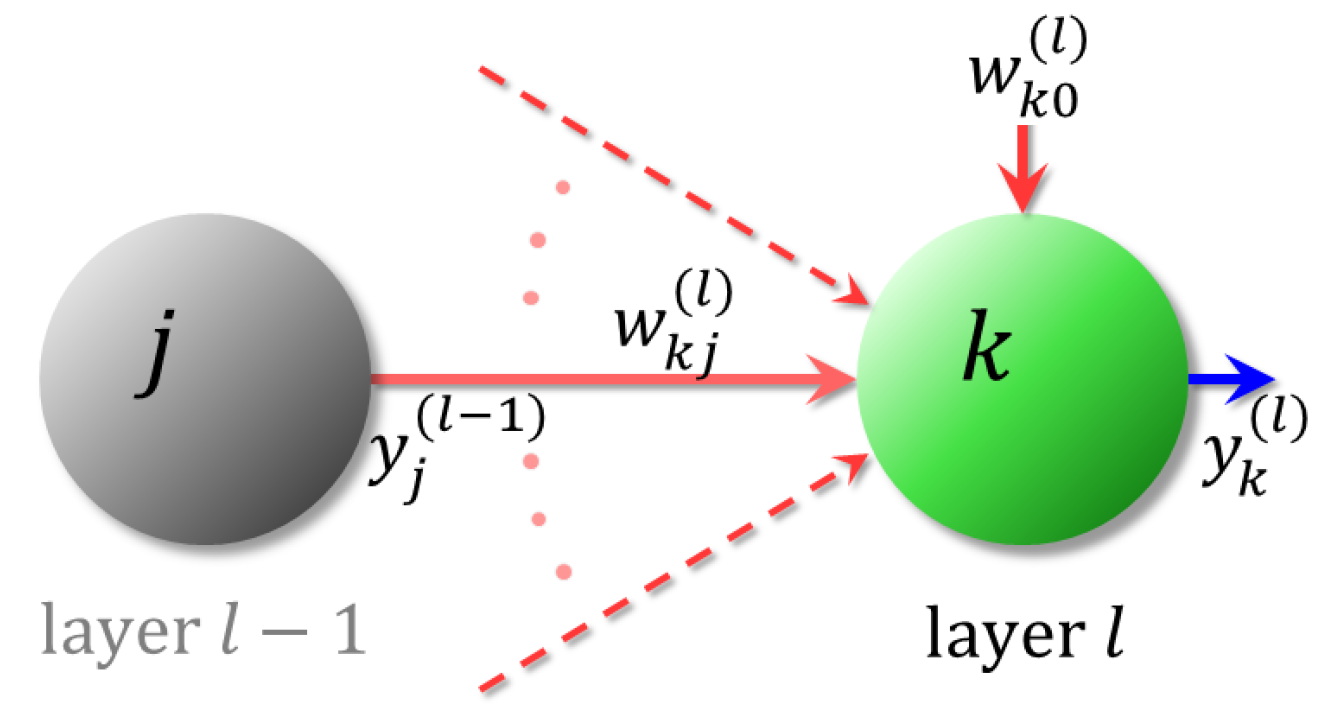
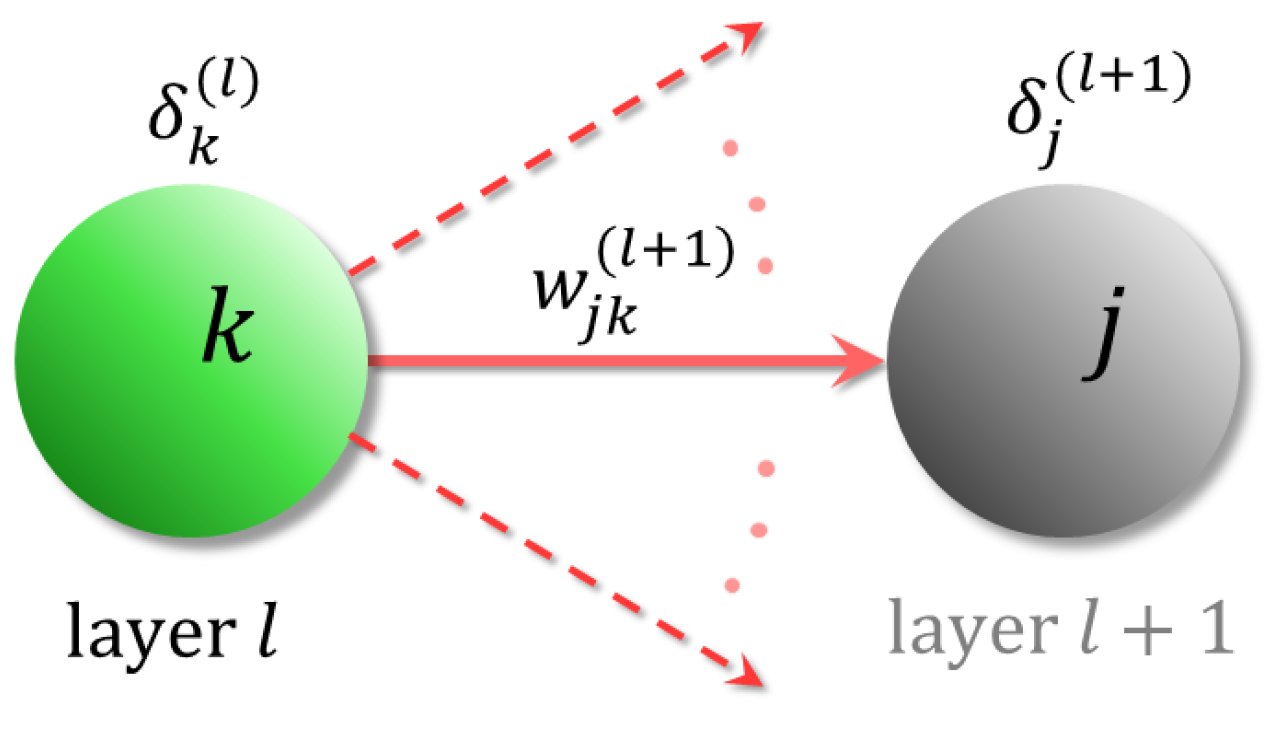
4.1. Neural Networks
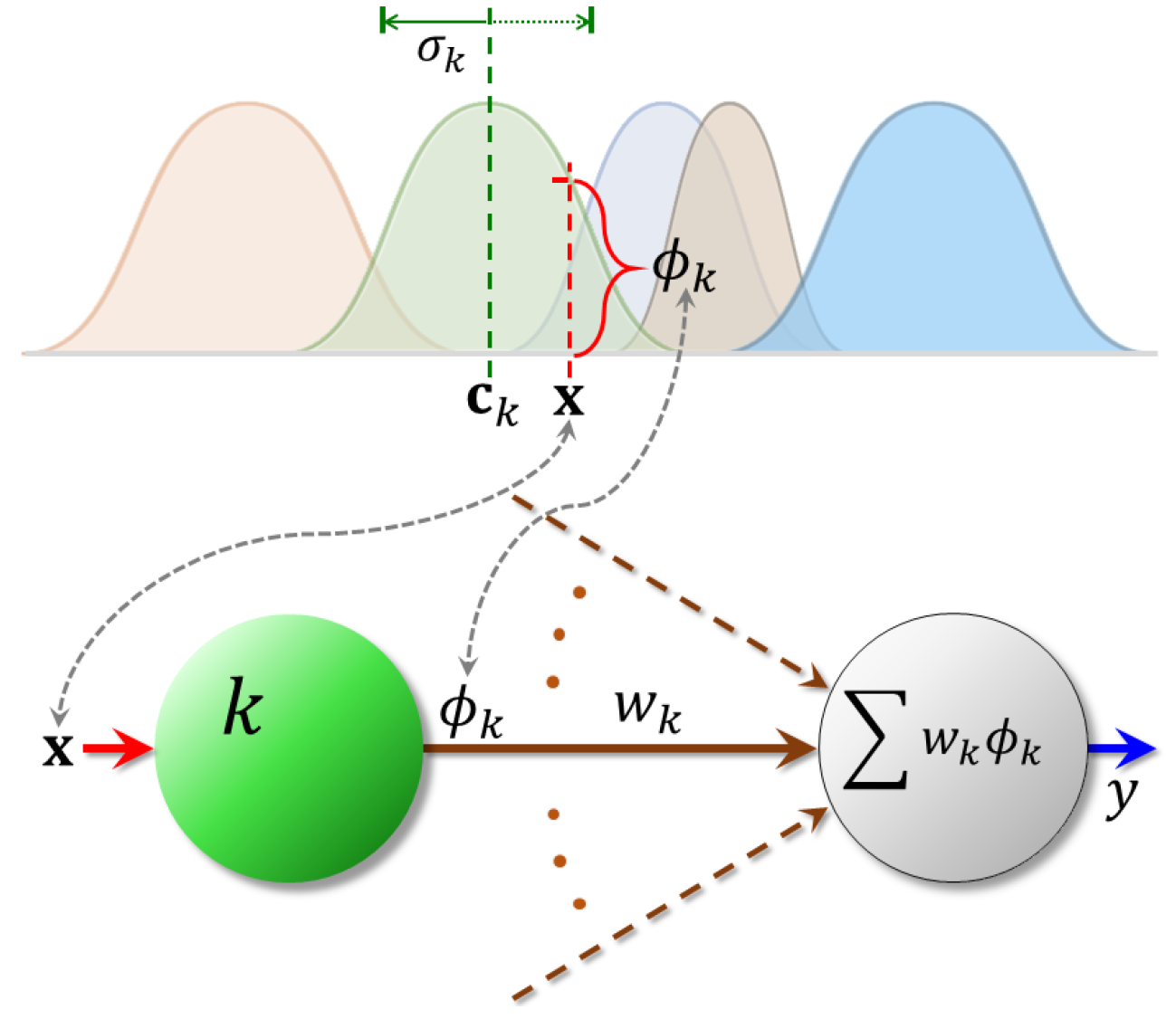
4.2. Radial Basis Function Networks
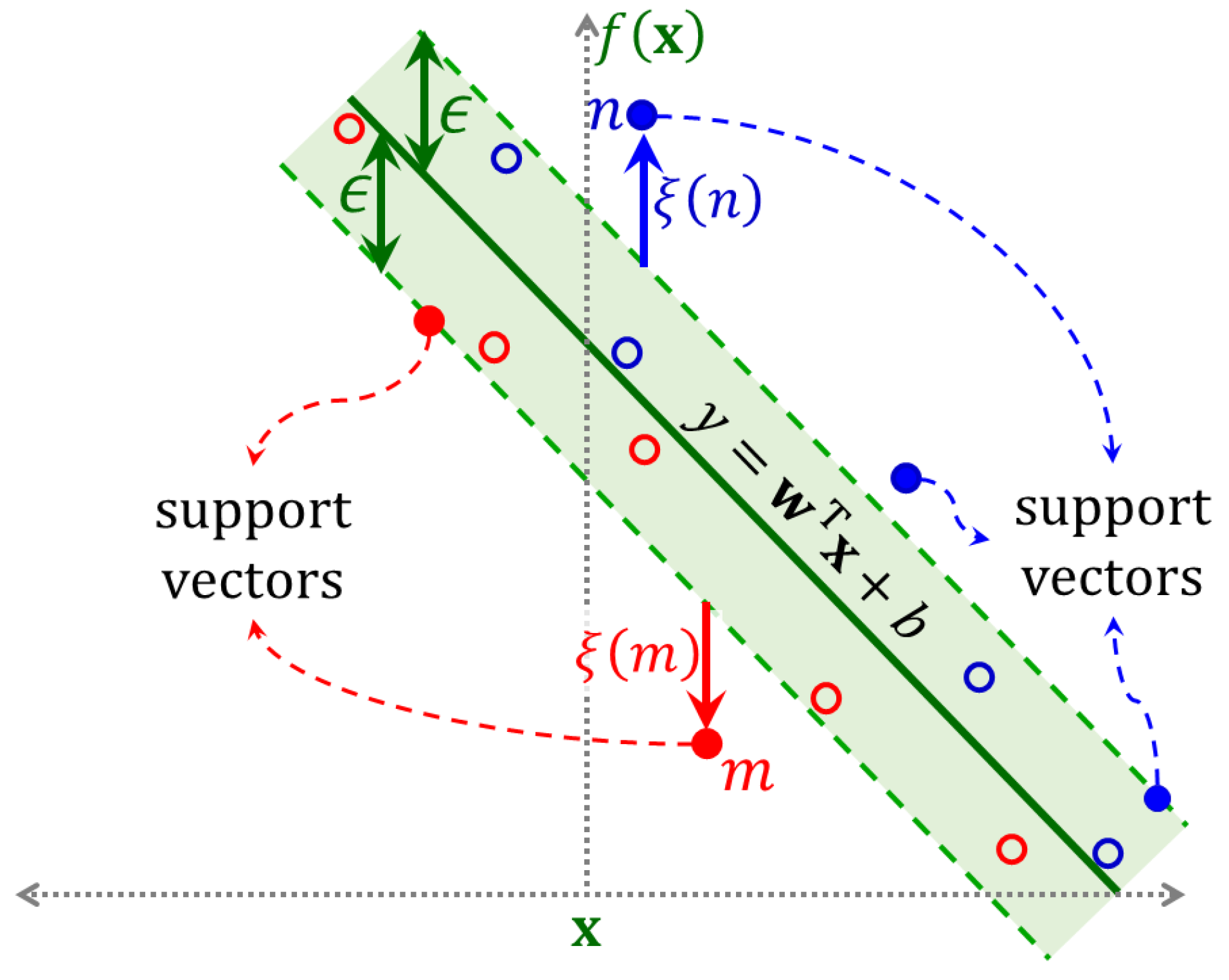
4.3. Support Vector Regression
4.4. Fuzzy Inference Systems
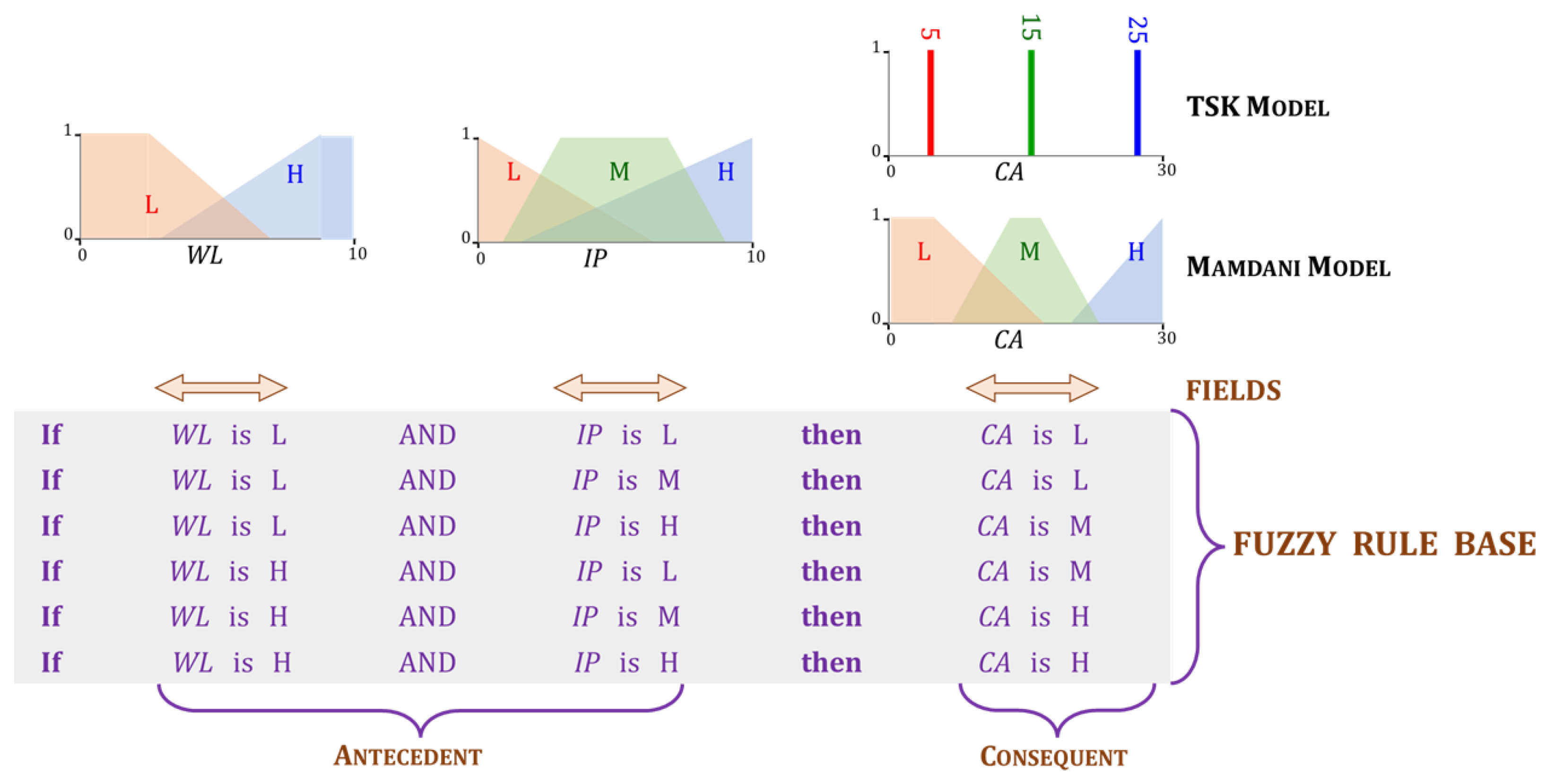
- (i)
- Fuzzification: This step is carried out separately in each antecedent field “” and for each rule k. It involves computing the values of the memberships using the numerical values of the input element .
- (ii)
- Aggregation: In this step, AND and OR operations are applied as appropriate to each rule in the FIS. The rules in the FIS shown in Figure 10 and Figure 11 only involve conjunctions (AND) that are implemented through the t-norm. The aggregated membership is referred to as its rule strength. The strength of rule k is,
- (iii)
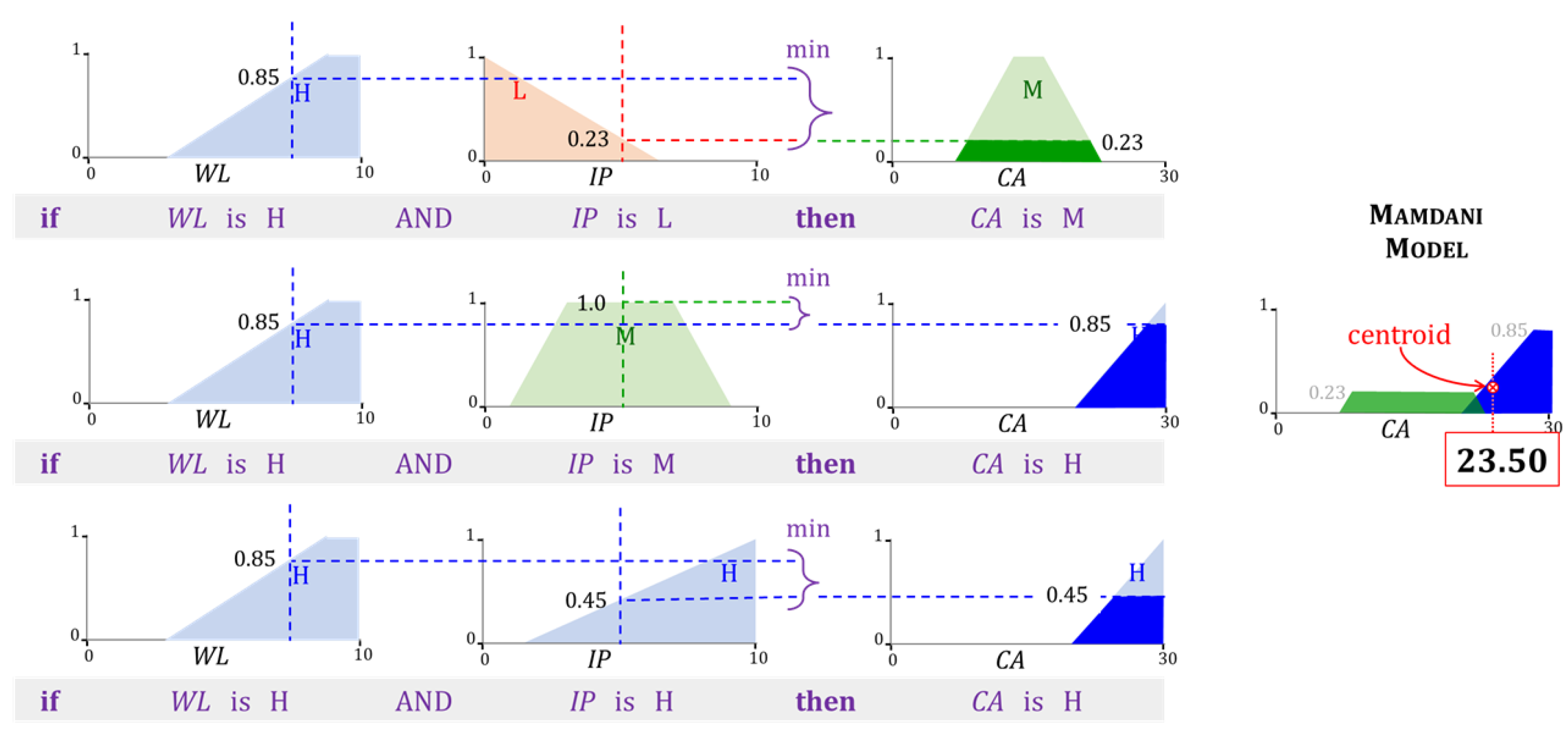
- Inference: The strength of each rule is applied to its consequent. Each rule k in our example contains only one consequent field. Its membership function is limited to a maximum of . For every rule, k in k, a two-dimensional region is identified in the Mamdani model. Since the TSK model involves only singletons at this step, only a two-dimensional point is necessary. Accordingly,In the example shown in Figure 10, the upper limit .
- (iv)
- Defuzzification: The value of the FIS’s output is determined in the last step. The Mamdani FIS in Figure 10 uses the centroid defuzzification method. The regions are unified into a single region . The final output is the x-coordinate of the centroid of . The TSK model in Figure 11 uses a weighted sum to obtain the output y of the FIS. Mathematically,In the above expression, . It is evident from the above description, that the inference and defuzzification step in a Mamdani FIS is more computationally intensive in comparison to that in the TSK model. There are several other methods to obtain the output of a FIS. For details, the interested reader is referred to [78,79]. The Mamdani model [80,81,82] as well as the TSK model [83,84,85,86,87] have been used frequently in agricultural research.
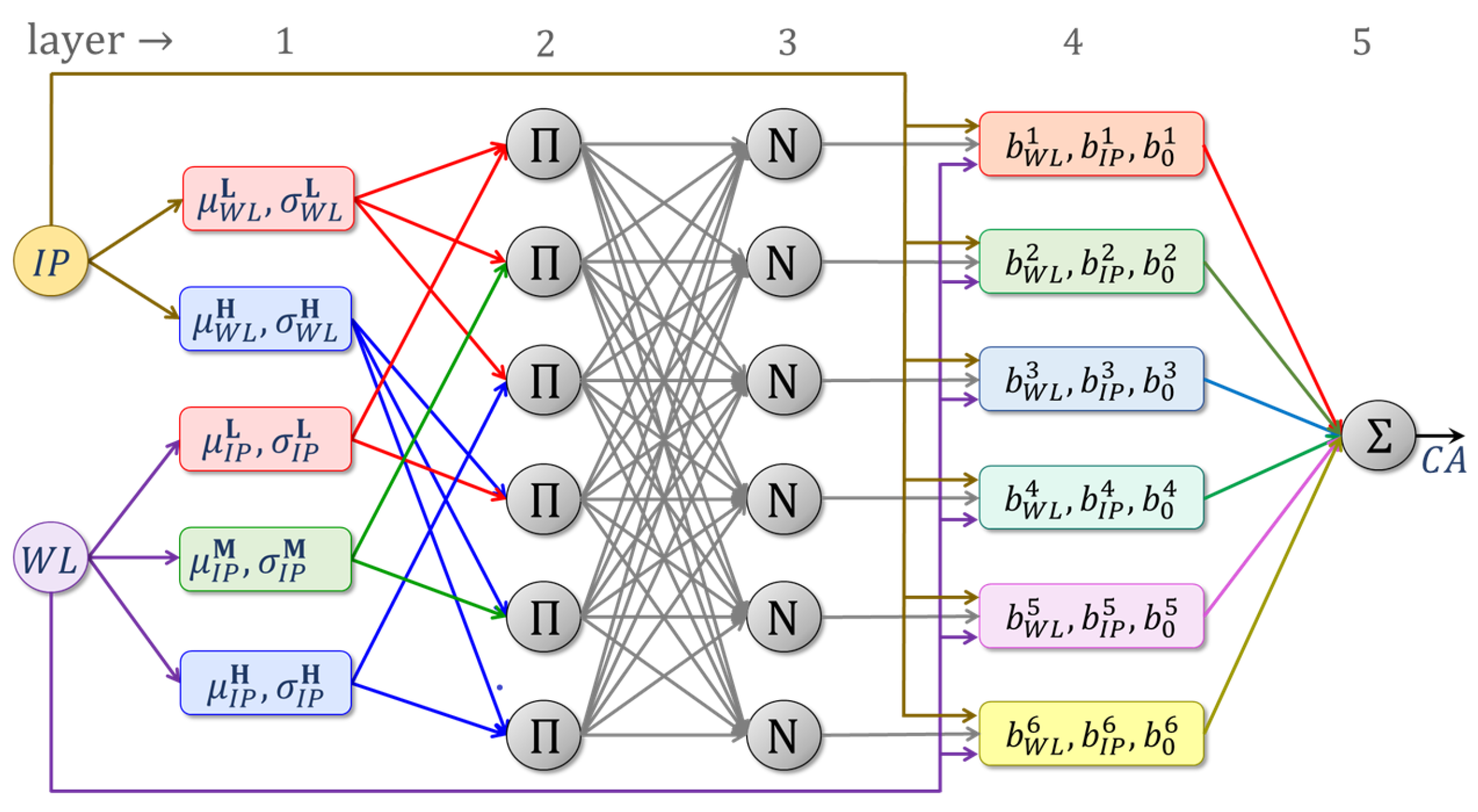
4.5. Adaptive Neuro-Fuzzy Inference Systems
- (i)
- Fuzzifying layer: The role of the first layer is to fuzzify scalar elements of the input . It involves computing the memberships in (31).
- (ii)
- Aggregating layer: This layer performs aggregation. When all ⋄ operators in (30) are conjunctions, the output of the kth unit in the second layer is obtained using the expression,
- (iii)
- Normalizing layer: This is the third layer of the ANFIS, whose role is to normalize the incoming aggregated memberships, from the previous layer. The output of its kth unit is,
- (iv)
- Consequent layer: The output of the kth unit of the fourth layer is,
- (v)
- Output layer: The final layer of the ANFIS performs a summation of the consequent outputs ,The quantity y is the output of the ANFIS.
5. Soil–Machine Interaction Studies: A Brief Survey
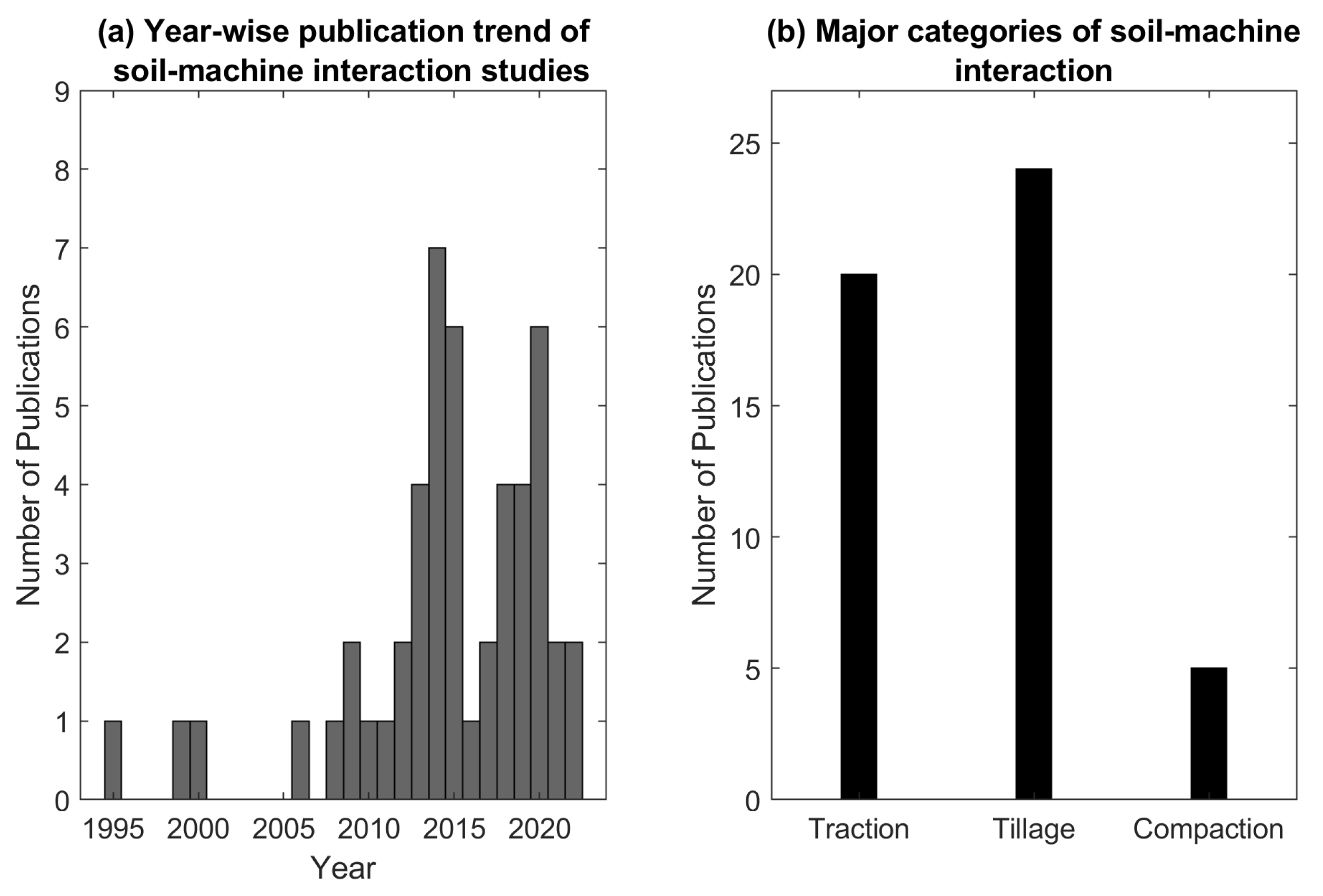
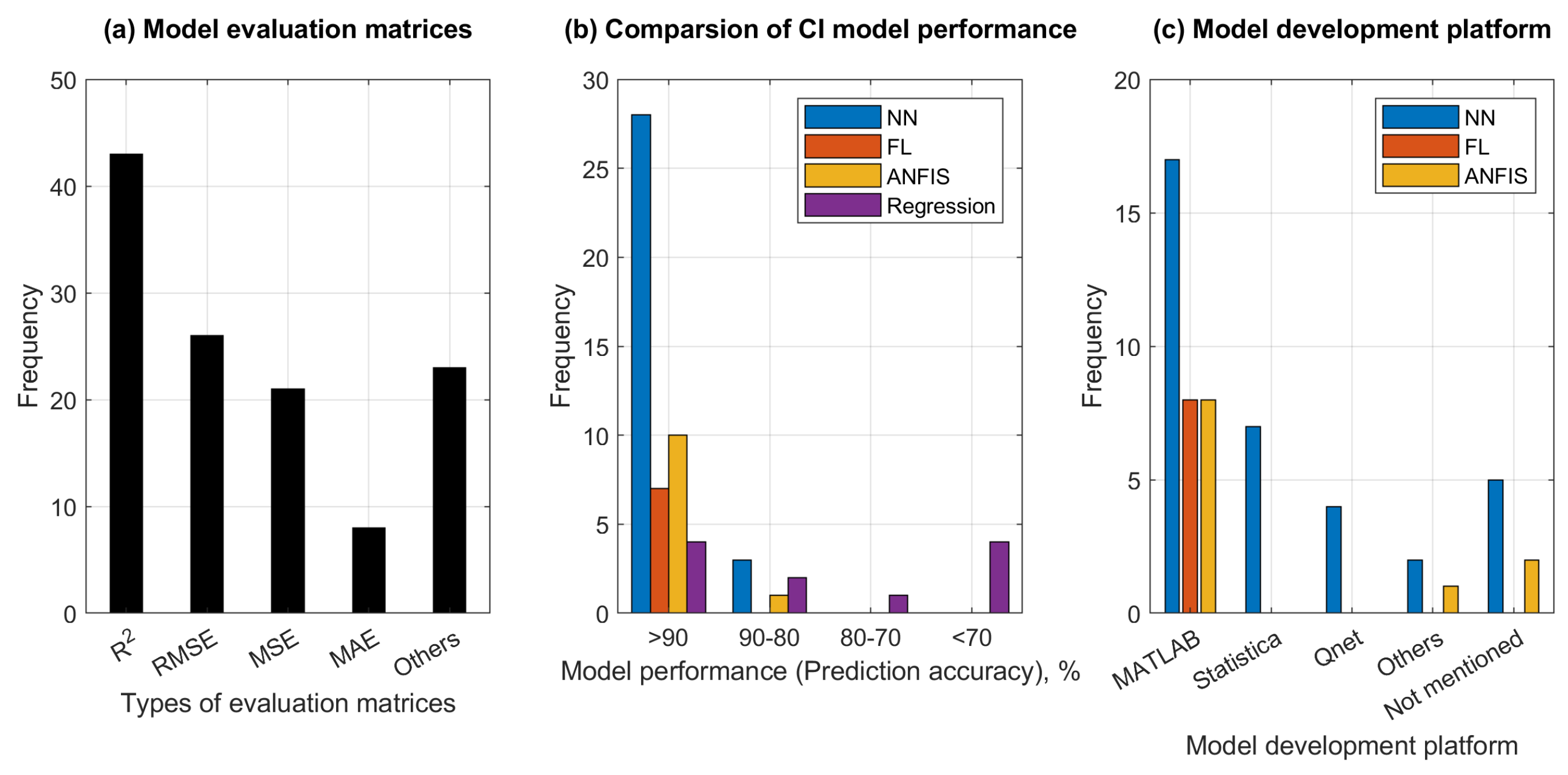
5.1. Literature Survey Methodology
5.2. Traction
| Author & Year | Traction Device | Method | Input | Output |
|---|---|---|---|---|
| Hassan and Tohmaz (1995) [101] | Rubber-tire skidder | NN | Tire size, tire pressure, normal load, line of pull angle | Drawbar pull |
| Çarman and Taner (2012) [106] | Driven wheel | NN | Travel reduction | Traction efficiency |
| Taghavifar et al. (2013) [113] | Driven wheel | NN | Velocity, tire pressure, normal load | Rolling resistance |
| Taghavifar and Mardani (2013) [114] | Driven wheel | FIS | Velocity, tire pressure, normal load | Motion resistance coeff. |
| Taghavifar and Mardani (2014) [107] | Driven wheel | ANFIS | Velocity, wheel load, slip | Energy efficiency indices (Traction coeff. and traction efficiency) |
| Taghavifar and Mardani (2014) [108] | Driven wheel | NN | Velocity, wheel load, slip | Energy efficiency indices (Traction coeff. and traction efficiency) |
| Taghavifar and Mardani (2014) [109] | Driven wheel | NN | Soil texture, tire type, wheel load, speed, slip, inflation pressure | Traction force |
| Taghavifar and Mardani (2014) [115] | Driven wheel | NN & SVR | Wheel load, inflation pressure, velocity | Energy wasted |
| Taghavifar and Mardani (2015) [50] | Driven wheel | ANFIS | Wheel load, inflation pressure, velocity | Drawbar pull energy |
| Taghavifar et al. (2015) [102] | Driven wheel | NN-GA | Wheel load, inflation pressure, velocity | Available power |
| Ekinci et al. (2015) [110] | Single wheel tester | NN & SVR | Lug height, axle load, inflation pressure, drawbar pull | Traction efficiency |
| Almaliki et al. (2016) [116] | Tractor | NN | Moisture content, cone index, tillage depth, inflation pressure, engine speed, forward speed | Traction efficiency, drawbar pull, rolling resistance, fuel consumption |
| Pentos et al. (2017) [111] | Micro tractor | NN | Vertical load, horizontal deformation, soil Coeff., compaction, moisture content | Traction force and traction efficiency |
| Shafaei et al. (2018) [94] | Tractor | ANFIS, NN | Forward speed, plowing depth, tractor mode | Traction efficiency |
| Shafaei et al. (2019) [117] | Tractor | ANFIS, NN | Forward speed, plowing depth, tractor mode | Wheel slip |
| Shafaei et al. (2020) [103] | Tractor | FIS | Tractor weight, wheel slip, tractor driving mode | Drawbar pull |
| Pentos et al. (2020) [112] | Micro tractor | NN, ANFIS | Vertical load, horizontal deformation, soil Coeff., compaction, moisture content | Traction force and traction efficiency |
| Hanifi et al. (2021) [118] | Tractor (60 HP) | NN | Inflation pressure, axle load, drawbar force | Specific fuel consumption |
| Badgujar et al. (2022) [119] | AGV | NN | Slope, speed, drawbar | Traction efficiency, slip and power number |
| Cutini et al. (2022) [104] | Tractor | NN | Tire geometric parameters (area, length, width, depth), slip | Drawbar pull |
5.3. Tillage
| Author and Year | Tillage Tool | CI Method | Input | Output |
|---|---|---|---|---|
| Zhang and Kushwaha (1999) [137] | Narrow blades (five) | RBF neural network | Forward speed, tool types, soil type | Draft |
| Choi et al. (2000) [120] | MB plow, Janggi plow, model tool | Time lagged RNN | One step ahead prediction | Dynamic draft |
| Aboukarima (2006) [127] | Chisel plow | NN | Soil parameters (textural index, moisture, bulk density), tractor power, plow parameters (depth, width, speed) | Draft |
| Alimardani et al. (2009) [130] | Subsoiler | NN | Travel speed, tillage depth, soil parameters (physical) | Draft and tillage energy |
| Roul et al. (2009) [21] | MB plow, cultivator, disk harrow | NN | Plow parameters (depth, width, speed), bulk density, moisture | Draft |
| Marakoğlu and Çarman(2010) [135] | Duckfoot cultivator share | FIS | Travel speed, working depth | Draft efficiency and soil loosening |
| Rahman et al. (2011) [143] | Rectangular tillage tool | NN | Plow depth, travel speed, moisture | Energy requirement |
| Mohammadi et al. (2012) [138] | Winged share tool | FIS | Share depth, width, speed | Draft requirement |
| Al-Hamed et al. (2013) [125] | Disk plow | NN | Soil parameters (texture, moisture, soil density), tool parameters (disk dia., tilt and disk angle), plow depth, plow speed | Draft, Unit draft and energy requirement |
| Saleh and Aly (2013) [144] | Multi-flat plowing tines | NN | Plow parameters (geometry, speed, lift angle, orientation, depth), soil conditions (moisture, density, strength) | Draft force, vertical force, side force, soil finess |
| Akbarnia et al. (2014) [139] | Winged share tool | NN | Working depth, speed, share width | Draft force |
| Abbaspour-Gilandeh and Sedghi (2015) [134] | Combine tillage | FIS | Moisture, speed, soil sampling depth | Median weight diameter |
| Shafaei et al (2017) [86] | Chisel plow | ANFIS | Plowing depth, speed | Draft force |
| Shafaei et al. (2018) [145] | MB plow | ANFIS | Plowing depth, speed | Draft (specific force and draft force) |
| Shafaei et al. (2018) [123] | Disk plow | NN, MLR | Plowing depth, speed | Draft |
| Shafaei et al. (2018) [126] | Disk plow | ANFIS, NN | Plowing depth, speed | Fuel efficiency |
| Shafaei et al. (2019) [117] | Conservation tillage | NN, ANFIS | Plowing depth, speed, tractor mode | Energy indices |
| Askari and Abbaspour-Gilandeh (2019) [132] | Subsoiler tines | MLR, ANFIS, RSM | Tine type, speed, working depth, width | Draft |
| Çarman et al. (2019) [124] | MB plow | NN | Tillage depth, speed | Draft, fuel consumption |
| Marey et al. (2020) [128] | Chisel plow | NN | Tractor power, soil texture, density, moisture, plow speed, depth | Draft, rate of soil volume plowed, fuel consumption |
| Al-Janobi et al. (2020) [122] | MB plow | NN | Soil texture, field working index | Draft, energy |
| Abbaspour-Gilandeh et al. (2020) [136] | MB plow, para-plow | ANFIS | Velocity, depth, type of implement | Draft, vertical and lateral force |
| Abbaspour-Gilandeh et al. (2020) [133] | Chisel cultivator | NN, MLR | Depth, moisture, cone index, speed | Draft |
| Shafaei et al. (2021) [146] | MB plow | FIS | Tillage depth, speed, tractor mode | Power consumption efficiency |
5.4. Compaction
| Author and Year | Traction Device | CI Method | Input | Output |
|---|---|---|---|---|
| Çarman (2008) [147] | Radial tire (2) | FIS | Tire contact pressure, velocity | Bulk density, penetration resistance, soil pressure at 20 cm depth |
| Taghavifar et al. (2013) [148] | Tire | NN | Wheel load, inflation pressure, wheel pass, velocity, slip | Penetration resistance, soil sinkage |
| Taghavifar and Mardani (2014) [149] | Tire | FIS | Wheel load, inflation pressure | Contact area, contact pressure |
| Taghavifar and Mardani (2014) [150] | Tire (size 220/65R21) | WNN, NN | Wheel load, velocity, slip | Contact pressure |
| Taghavifar (2015) [151] | Tire (size 220/65R21 and 9.5L-14) | NN | Soil texture, tire type, slip, wheel pass, load, velocity | Contact pressure, bulk density |
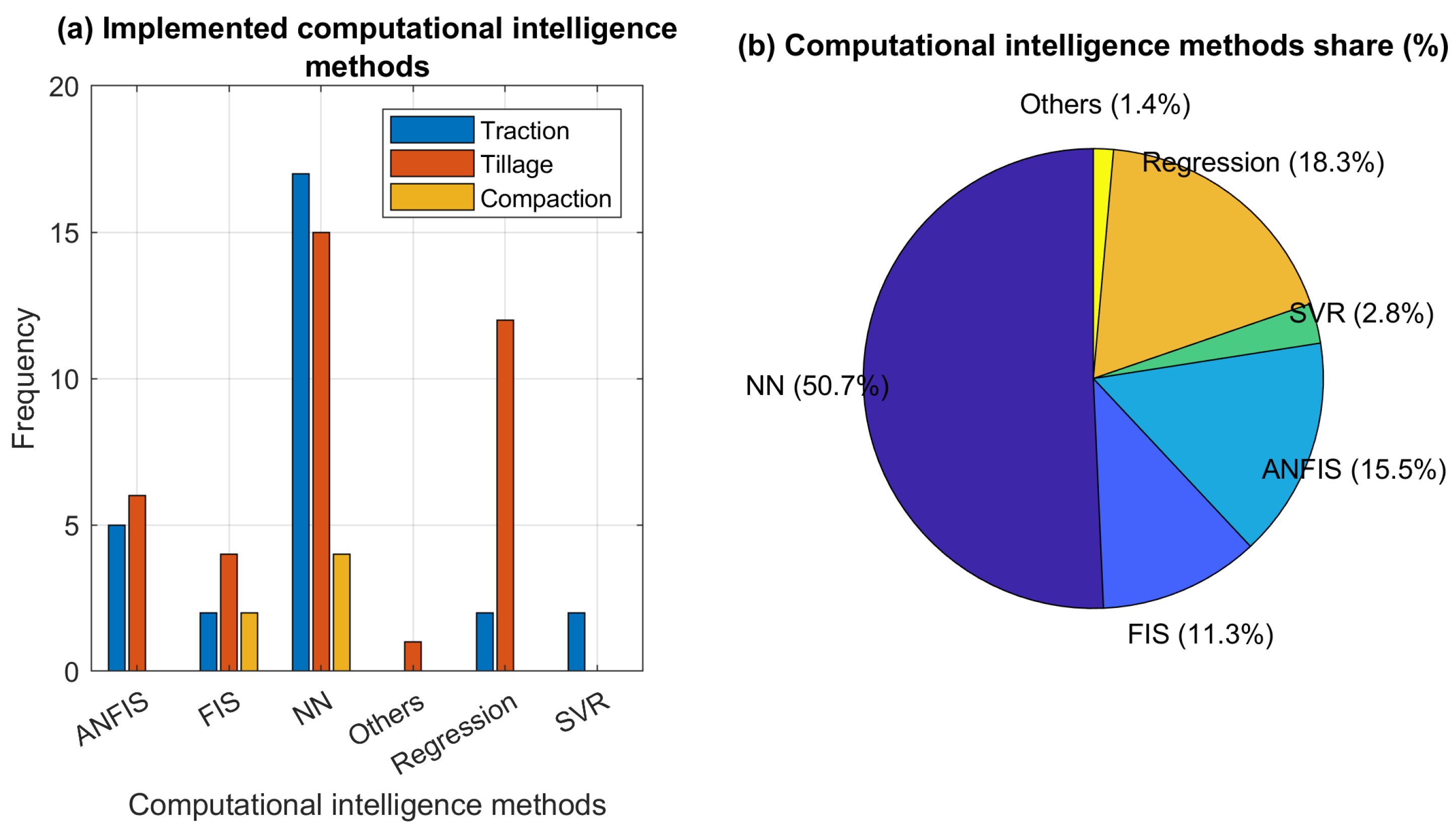
5.5. Implemented CI Methods
6. Strengths and Limitations of CI Methods
- (i)
- Data-driven models can handle copious amounts of data with relative ease [152]. With increasing data size, the corresponding growth in computational overheads is generally between linear and quadratic orders of magnitude. For instance, the number of iterations (called epochs) needed to train a neural network is fixed regardless of data size [53]. On the other hand, traditional methods regularly witness quadratic or higher growths.
- (ii)
- To further enhance their performances after initial offline training, data-driven CI models (e.g., NNs and DNNs) can learn online during actual deployment [153]. In other words, they are capable of learning from experience.
- (iii)
- FIS models can directly benefit from human domain experts; their expert knowledge can be incorporated into the model [154].
- (iv)
- Conversely, FIS model outputs are amenable to direct human interpretation. NNs endowed with such capability have been recently proposed [155].
- (v)
- (vi)
- (vii)
- (i)
- Interpretability: Several CI models such as NN & SVR are black box approaches. Unlike physics-based approaches, the nonlinear input-output relationships expressed by these models are not self-explanatory, i.e., do not render themselves to common sense interpretations. Although various schemes towards making these relationships more explainable are currently being explored, [162,163,164,165], this research is only at a preliminary stage.
- (ii)
- Computational requirements: The development of CI models often requires specialized software (e.g., MATLAB). Moreover, training DNNs with reasonably sized data may prove to be too time-consuming unless using GPUs (graphics processing units), where processors can be run as a pipeline or in parallel [166].
- (iii)
- Data requirements: In comparison to classical methods, CI models require relatively copious amounts of data for training. As such models are not equipped for extrapolation, data samples must adequately cover the entire input range of real-world inputs. In order to effectively train certain CI models such as RBFNs, the data should not be skewed in any direction. Unfortunately, experimentally generating such data can often be a resource-intensive and time-consuming process.
- (iv)
7. Emergent Computational Intelligence Models
7.1. Deep Neural Networks
7.2. Regression Trees and Random Forests
7.3. Extreme Learning Machines
7.4. Bayesian Methods
7.5. Ensemble Models
8. Future Direction and Scope
8.1. Online Traction Control
8.2. Online Tillage Control
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ani, O.A.; Uzoejinwa, B.; Ezeama, A.; Onwualu, A.; Ugwu, S.; Ohagwu, C. Overview of soil-machine interaction studies in soil bins. Soil Tillage Res. 2018, 175, 13–27. [Google Scholar] [CrossRef]
- ASABE. Terminology and Definitions for Soil Tillage and Soil-Tool Relationships; Technical Report ASAE EP291.3 Feb2005 (R2018); American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2018. [Google Scholar]
- Sunusi, I.I.; Zhou, J.; Zhen Wang, Z.; Sun, C.; Eltayeb Ibrahim, I.; Opiyo, S.; korohou, T.; Ahmed Soomro, S.; Alhaji Sale, N.; Olanrewaju, T.O. Intelligent tractors: Review of online traction control process. Comput. Electron. Agric. 2020, 170, 105176. [Google Scholar] [CrossRef]
- Zoz, F.; Grisso, R. Traction and Tractor Performance; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2012. [Google Scholar]
- Upadhyaya, S.K.; Way, T.R.; Upadhyaya, S.K.; Chancellor, W.J. Chapter 2. Traction Mechanics. Part V. Traction Prediction Equations. In Advances in Soil Dynamics Volume 3, 1st ed.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2009; pp. 161–186. [Google Scholar] [CrossRef]
- Karmakar, S.; Kushwaha, R.L. Dynamic modeling of soil–tool interaction: An overview from a fluid flow perspective. J. Terramech. 2006, 43, 411–425. [Google Scholar] [CrossRef]
- Johnson, C.E.; Bailey, A.C. Soil Compaction. In Advances in Soil Dynamics Volume 2, 1st ed.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2002; pp. 155–178. [Google Scholar] [CrossRef] [Green Version]
- Acquah, K.; Chen, Y. Soil Compaction from Wheel Traffic under Three Tillage Systems. Agriculture 2022, 12, 219. [Google Scholar] [CrossRef]
- Soane, B.; van Ouwerkerk, C. Soil Compaction Problems in World Agriculture. In Developments in Agricultural Engineering; Elsevier: Amsterdam, The Netherlands, 1994; Volume 11, pp. 1–21. [Google Scholar] [CrossRef]
- Brus, D.J.; van den Akker, J.J.H. How serious a problem is subsoil compaction in the Netherlands? A survey based on probability sampling. Soil 2018, 4, 37–45. [Google Scholar] [CrossRef] [Green Version]
- Zabrodskyi, A.; Šarauskis, E.; Kukharets, S.; Juostas, A.; Vasiliauskas, G.; Andriušis, A. Analysis of the Impact of Soil Compaction on the Environment and Agricultural Economic Losses in Lithuania and Ukraine. Sustainability 2021, 13, 7762. [Google Scholar] [CrossRef]
- Keller, T. Soil Compaction and Soil Tillage—Studies in Agricultural Soil Mechanics. Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2004. [Google Scholar]
- DeJong-Hughes, J.; Moncrief, J.; Voorhees, W.; Swan, J. Soil Compaction: Causes, Effects and Control; The University of Minnesota Extension Service: St. Paul, MN, USA, 2001; Available online: https://hdl.handle.net/11299/55483 (accessed on 24 October 2022).
- Badalíková, B. Influence of Soil Tillage on Soil Compaction. In Soil Engineering; Dedousis, A.P., Bartzanas, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 20, pp. 19–30. [Google Scholar] [CrossRef]
- Tiwari, V.; Pandey, K.; Pranav, P. A review on traction prediction equations. J. Terramechan. 2010, 47, 191–199. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley: New York, NY, USA, 2001. [Google Scholar]
- Godwin, R.; Spoor, G. Soil failure with narrow tines. J. Agric. Eng. Res. 1977, 22, 213–228. [Google Scholar] [CrossRef]
- Makanga, J.; Salokhe, V.; Gee-Clough, D. Effect of tine rake angle and aspect ratio on soil failure patterns in dry loam soil. J. Terramech. 1996, 33, 233–252. [Google Scholar] [CrossRef]
- Karmakar, S. Numerical Modeling of Soil Flow and Pressure Distribution on a Simple Tillage Tool Using Computational Fluid Dynamics. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Tagar, A.; Ji, C.; Ding, Q.; Adamowski, J.; Chandio, F.; Mari, I. Soil failure patterns and draft as influenced by consistency limits: An evaluation of the remolded soil cutting test. Soil Tillage Res. 2014, 137, 58–66. [Google Scholar] [CrossRef]
- Roul, A.; Raheman, H.; Pansare, M.; Machavaram, R. Predicting the draught requirement of tillage implements in sandy clay loam soil using an artificial neural network. Biosyst. Eng. 2009, 104, 476–485. [Google Scholar] [CrossRef]
- Fielke, J.; Riley, T. The universal earthmoving equation applied to chisel plough wings. J. Terramech. 1991, 28, 11–19. [Google Scholar] [CrossRef]
- Godwin, R.; Seig, D.; Allott, M. Soil failure and force prediction for soil engaging discs. Soil Use Manag. 1987, 3, 106–114. [Google Scholar] [CrossRef]
- Kushwaha, R.L.; Shen, J. Finite Element Analysis of the Dynamic Interaction Between Soil and Tillage Tool. Trans. ASAE 1995, 38, 1315–1319. [Google Scholar] [CrossRef]
- Upadhyaya, S.K.; Rosa, U.A.; Wulfsohn, D. Application of the Finite Element Method in Agricultural Soil Mechanics. In Advances in Soil Dynamics Volume 2, 1st ed.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2002; pp. 117–153. [Google Scholar] [CrossRef]
- Shmulevich, I.; Rubinstein, D.; Asaf, Z. Chapter 5. Discrete Element Modeling of Soil-Machine Interactions. In Advances in Soil Dynamics Volume 3, 1st ed.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2009; pp. 399–433. [Google Scholar] [CrossRef]
- Liu, J.; Kushwaha, R.L. Two-decade Achievements in Modeling of Soil—Tool Interactions. In Proceedings of the ASABE Annual International Meeting 2008, Providence, RI, USA, 29 June–2 July 2008; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2008. [Google Scholar] [CrossRef]
- Taheri, S.; Sandu, C.; Taheri, S.; Pinto, E.; Gorsich, D. A technical survey on Terramechanics models for tire–terrain interaction used in modeling and simulation of wheeled vehicles. J. Terramech. 2015, 57, 1–22. [Google Scholar] [CrossRef]
- Ghosh, S.; Konar, A. An Overview of Computational Intelligence Algorithms. In Call Admission Control in Mobile Cellular Networks; Springer: Berlin/Heidelberg, Germany, 2013; pp. 63–94. [Google Scholar] [CrossRef]
- Vasant, P. Handbook of Research on Novel Soft Computing Intelligent Algorithms: Theory and Practical Applications; IGI Global: Hershey, PA, USA, 2013. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.J. Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Springer: Manhattan, NY, USA, 2014; Volume 62. [Google Scholar]
- Ibrahim, D. An overview of soft computing. Procedia Comput. Sci. 2016, 102, 34–38. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary artificial neural networks: A review. Artif. Intell. Rev. 2013, 39, 251–260. [Google Scholar] [CrossRef]
- Stanley, K.O.; Clune, J.; Lehman, J.; Miikkulainen, R. Designing neural networks through neuroevolution. Nat. Mach. Intell. 2019, 1, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Elbes, M.; Alzubi, S.; Kanan, T.; Al-Fuqaha, A.; Hawashin, B. A survey on particle swarm optimization with emphasis on engineering and network applications. Evol. Intell. 2019, 12, 113–129. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive network based fuzzy inference system (ANFIS) training approaches: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2263–2293. [Google Scholar] [CrossRef]
- Ridzuan, F.; Zainon, W.M.N.W. A review on data cleansing methods for big data. Procedia Comput. Sci. 2019, 161, 731–738. [Google Scholar] [CrossRef]
- Badgujar, C.; Das, S.; Flippo, D.; Welch, S.M.; Martinez-Figueroa, D. A Deep Neural Network-Based Approach to Predict the Traction, Mobility, and Energy Consumption of Autonomous Ground Vehicle on Sloping Terrain Field. Comput. Electron. Agric. 2022, 196, 106867. [Google Scholar] [CrossRef]
- Scholz, M. Validation of nonlinear PCA. Neural Process. Lett. 2012, 36, 21–30. [Google Scholar] [CrossRef]
- Stone, J.V. Independent component analysis: An introduction. Trends Cogn. Sci. 2002, 6, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Cherkassky, V.; Ma, Y. Comparison of loss functions for linear regression. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 1, pp. 395–400. [Google Scholar] [CrossRef]
- Čížek, P.; Sadıkoğlu, S. Robust nonparametric regression: A review. Wiley Interdiscip. Rev. Comput. Stat. 2020, 12, e1492. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Wu, Q. Robust pairwise learning with Huber loss. J. Complex. 2021, 66, 101570. [Google Scholar] [CrossRef]
- Vapnik, V.; Levin, E.; Le Cun, Y. Measuring the VC-dimension of a learning machine. Neural Comput. 1994, 6, 851–876. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Wilamowski, B.M.; Yu, H. Improved computation for Levenberg–Marquardt training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Koduru, P.; Gui, M.; Cochran, M.; Wareing, A.; Welch, S.M.; Babin, B.R. Adding local search to particle swarm optimization. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 428–433. [Google Scholar]
- Taghavifar, H.; Mardani, A. Energy loss optimization of run-off-road wheels applying imperialist competitive algorithm. Inf. Process. Agric. 2014, 1, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Taghavifar, H.; Mardani, A. Evaluating the effect of tire parameters on required drawbar pull energy model using adaptive neuro-fuzzy inference system. Energy 2015, 85, 586–593. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Sapna, S.; Tamilarasi, A.; Kumar, M.P. Backpropagation learning algorithm based on Levenberg Marquardt Algorithm. Comput. Sci. Inf. Technol. (CS IT) 2012, 2, 393–398. [Google Scholar]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning from Data; AMLBook: New York, NY, USA, 2012. [Google Scholar]
- Ghosh, J.; Nag, A. An overview of radial basis function networks. In Radial Basis Function Networks 2; Springer: New York, NY, USA, 2001; pp. 1–36. [Google Scholar]
- Ruß, G. Data mining of agricultural yield data: A comparison of regression models. In Proceedings of the Industrial Conference on Data Mining, Leipzig, Germany, 20–22 July 2009; Springer: New York, NY, USA, 2009; pp. 24–37. [Google Scholar]
- da Silva, E.M., Jr.; Maia, R.D.; Cabacinha, C.D. Bee-inspired RBF network for volume estimation of individual trees. Comput. Electron. Agric. 2018, 152, 401–408. [Google Scholar] [CrossRef]
- Zhang, D.; Zang, G.; Li, J.; Ma, K.; Liu, H. Prediction of soybean price in China using QR-RBF neural network model. Comput. Electron. Agric. 2018, 154, 10–17. [Google Scholar] [CrossRef]
- Ashraf, T.; Khan, Y.N. Weed density classification in rice crop using computer vision. Comput. Electron. Agric. 2020, 175, 105590. [Google Scholar] [CrossRef]
- Eide, Å.J.; Lindblad, T.; Paillet, G. Radial-basis-function networks. In Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bock, H.H. Clustering methods: A history of k-means algorithms. Selected Contributions in Data Analysis and Classification; Springer: New York, NY, USA, 2007; pp. 161–172. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Pisner, D.A.; Schnyer, D.M. Support vector machine. In Machine learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–121. [Google Scholar]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Mucherino, A.; Papajorgji, P.; Pardalos, P.M. A survey of data mining techniques applied to agriculture. Oper. Res. 2009, 9, 121–140. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Using MARS, SVM, GEP and empirical equations for estimation of monthly mean reference evapotranspiration. Comput. Electron. Agric. 2017, 139, 103–114. [Google Scholar] [CrossRef]
- Patrício, D.I.; Rieder, R. Computer vision and artificial intelligence in precision agriculture for grain crops: A systematic review. Comput. Electron. Agric. 2018, 153, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Kok, Z.H.; Shariff, A.R.M.; Alfatni, M.S.M.; Khairunniza-Bejo, S. Support vector machine in precision agriculture: A review. Comput. Electron. Agric. 2021, 191, 106546. [Google Scholar] [CrossRef]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Hindi, H. A tutorial on convex optimization. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 4, pp. 3252–3265. [Google Scholar]
- Hindi, H. A tutorial on convex optimization II: Duality and interior point methods. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 11. [Google Scholar]
- Chapelle, O. Training a support vector machine in the primal. Neural Comput. 2007, 19, 1155–1178. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Li, Y. Incremental support vector machine learning in the primal and applications. Neurocomputing 2009, 72, 2249–2258. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.G. Iterative Learning in Support Vector Regression with Heterogeneous Variances. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 1–10. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Iancu, I. A Mamdani type fuzzy logic controller. Fuzzy Log. -Control. Concepts Theor. Appl. 2012, 15, 325–350. [Google Scholar]
- Guerra, T.M.; Kruszewski, A.; Lauber, J. Discrete Tagaki–Sugeno models for control: Where are we? Annu. Rev. Control 2009, 33, 37–47. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Nakanishi, H.; Turksen, I.; Sugeno, M. A review and comparison of six reasoning methods. Fuzzy Sets Syst. 1993, 57, 257–294. [Google Scholar] [CrossRef]
- Ying, H.; Ding, Y.; Li, S.; Shao, S. Comparison of necessary conditions for typical Takagi-Sugeno and Mamdani fuzzy systems as universal approximators. IEEE Trans. Syst. Man Cybern. -Part A Syst. Humans 1999, 29, 508–514. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Lan, Y.; Thomson, S.J.; Fang, A.; Hoffmann, W.C.; Lacey, R.E. Development of soft computing and applications in agricultural and biological engineering. Comput. Electron. Agric. 2010, 71, 107–127. [Google Scholar] [CrossRef] [Green Version]
- Touati, F.; Al-Hitmi, M.; Benhmed, K.; Tabish, R. A fuzzy logic based irrigation system enhanced with wireless data logging applied to the state of Qatar. Comput. Electron. Agric. 2013, 98, 233–241. [Google Scholar] [CrossRef]
- Zareiforoush, H.; Minaei, S.; Alizadeh, M.R.; Banakar, A.; Samani, B.H. Design, development and performance evaluation of an automatic control system for rice whitening machine based on computer vision and fuzzy logic. Comput. Electron. Agric. 2016, 124, 14–22. [Google Scholar] [CrossRef]
- Kisi, O.; Sanikhani, H.; Zounemat-Kermani, M.; Niazi, F. Long-term monthly evapotranspiration modeling by several data-driven methods without climatic data. Comput. Electron. Agric. 2015, 115, 66–77. [Google Scholar] [CrossRef]
- Valdés-Vela, M.; Abrisqueta, I.; Conejero, W.; Vera, J.; Ruiz-Sánchez, M.C. Soft computing applied to stem water potential estimation: A fuzzy rule based approach. Comput. Electron. Agric. 2015, 115, 150–160. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Piri, J. Daily suspended sediment concentration simulation using hydrological data of Pranhita River Basin, India. Comput. Electron. Agric. 2017, 138, 20–28. [Google Scholar] [CrossRef]
- Shafaei, S.; Loghavi, M.; Kamgar, S. Appraisal of Takagi-Sugeno-Kang type of adaptive neuro-fuzzy inference system for draft force prediction of chisel plow implement. Comput. Electron. Agric. 2017, 142, 406–415. [Google Scholar] [CrossRef]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Iturraran-Viveros, U.; Bagherzadeh, A.; Mousavi, R.; Karimi, S. Modeling soil cation exchange capacity using soil parameters: Assessing the heuristic models. Comput. Electron. Agric. 2017, 135, 242–251. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Babuška, R.; Verbruggen, H. Neuro-fuzzy methods for nonlinear system identification. Annu. Rev. Control 2003, 27, 73–85. [Google Scholar] [CrossRef]
- Shihabudheen, K.; Pillai, G.N. Recent advances in neuro-fuzzy system: A survey. Knowl.-Based Syst. 2018, 152, 136–162. [Google Scholar] [CrossRef]
- de Campos Souza, P.V. Fuzzy neural networks and neuro-fuzzy networks: A review the main techniques and applications used in the literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Wu, W.; Li, L.; Yang, J.; Liu, Y. A modified gradient-based neuro-fuzzy learning algorithm and its convergence. Inf. Sci. 2010, 180, 1630–1642. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H. An adaptive fuzzy hierarchical control for maintaining solar greenhouse temperature. Comput. Electron. Agric. 2018, 155, 251–256. [Google Scholar] [CrossRef]
- Shafaei, S.; Loghavi, M.; Kamgar, S. An extensive validation of computer simulation frameworks for neural prognostication of tractor tractive efficiency. Comput. Electron. Agric. 2018, 155, 283–297. [Google Scholar] [CrossRef]
- Petković, B.; Petković, D.; Kuzman, B.; Milovančević, M.; Wakil, K.; Ho, L.S.; Jermsittiparsert, K. Neuro-fuzzy estimation of reference crop evapotranspiration by neuro fuzzy logic based on weather conditions. Comput. Electron. Agric. 2020, 173, 105358. [Google Scholar] [CrossRef]
- Wiktorowicz, K. RFIS: Regression-based fuzzy inference system. Neural Comput. Appl. 2022, 34, 12175–12196. [Google Scholar] [CrossRef]
- Cheng, C.B.; Cheng, C.J.; Lee, E. Neuro-fuzzy and genetic algorithm in multiple response optimization. Comput. Math. Appl. 2002, 44, 1503–1514. [Google Scholar] [CrossRef] [Green Version]
- Shihabudheen, K.; Mahesh, M.; Pillai, G.N. Particle swarm optimization based extreme learning neuro-fuzzy system for regression and classification. Expert Syst. Appl. 2018, 92, 474–484. [Google Scholar] [CrossRef]
- Castellano, G.; Castiello, C.; Fanelli, A.M.; Jain, L. Evolutionary neuro-fuzzy systems and applications. In Advances in Evolutionary Computing for System Design; Springer: New York, NY, USA, 2007; pp. 11–45. [Google Scholar]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Kisi, O. Comparison of three different bio-inspired algorithms to improve ability of neuro fuzzy approach in prediction of agricultural drought, based on three different indexes. Comput. Electron. Agric. 2020, 170, 105279. [Google Scholar] [CrossRef]
- Hassan, A.; Tohmaz, A. Performance of Skidder Tires in Swamps—Comparison between Statistical and Neural Network Models. Trans. ASAE 1995, 38, 1545–1551. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A.; Hosseinloo, A.H. Appraisal of artificial neural network-genetic algorithm based model for prediction of the power provided by the agricultural tractors. Energy 2015, 93, 1704–1710. [Google Scholar] [CrossRef]
- Shafaei, S.; Loghavi, M.; Kamgar, S. Benchmark of an intelligent fuzzy calculator for admissible estimation of drawbar pull supplied by mechanical front wheel drive tractor. Artif. Intell. Agric. 2020, 4, 209–218. [Google Scholar] [CrossRef]
- Cutini, M.; Costa, C.; Brambilla, M.; Bisaglia, C. Relationship between the 3D Footprint of an Agricultural Tire and Drawbar Pull Using an Artificial Neural Network. Appl. Eng. Agric. 2022, 38, 293–301. [Google Scholar] [CrossRef]
- American National Standard ANSI/ASAE S296.5 DEC2003 (R2018); General Terminology for Traction of Agricultural Traction and Transport Devices and Vehicles. ASABE: St. Joseph, MI, USA, 2018.
- Carman, K.; Taner, A. Prediction of Tire Tractive Performance by Using Artificial Neural Networks. Math. Comput. Appl. 2012, 17, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Taghavifar, H.; Mardani, A. On the modeling of energy efficiency indices of agricultural tractor driving wheels applying adaptive neuro-fuzzy inference system. J. Terramech. 2014, 56, 37–47. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. Applying a supervised ANN (artificial neural network) approach to the prognostication of driven wheel energy efficiency indices. Energy 2014, 68, 651–657. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. Use of artificial neural networks for estimation of agricultural wheel traction force in soil bin. Neural Comput. Appl. 2014, 24, 1249–1258. [Google Scholar] [CrossRef]
- Ekinci, S.; Carman, K.; Kahramanlı, H. Investigation and modeling of the tractive performance of radial tires using off-road vehicles. Energy 2015, 93, 1953–1963. [Google Scholar] [CrossRef]
- Pentoś, K.; Pieczarka, K. Applying an artificial neural network approach to the analysis of tractive properties in changing soil conditions. Soil Tillage Res. 2017, 165, 113–120. [Google Scholar] [CrossRef]
- Pentoś, K.; Pieczarka, K.; Lejman, K. Application of Soft Computing Techniques for the Analysis of Tractive Properties of a Low-Power Agricultural Tractor under Various Soil Conditions. Complexity 2020. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A.; Karim-Maslak, H.; Kalbkhani, H. Artificial Neural Network estimation of wheel rolling resistance in clay loam soil. Appl. Soft Comput. 2013, 13, 3544–3551. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. A knowledge-based Mamdani fuzzy logic prediction of the motion resistance coefficient in a soil bin facility for clay loam soil. Neural Comput. Appl. 2013, 23, 293–302. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. A comparative trend in forecasting ability of artificial neural networks and regressive support vector machine methodologies for energy dissipation modeling of off-road vehicles. Energy 2014, 66, 569–576. [Google Scholar] [CrossRef]
- Almaliki, S.; Alimardani, R.; Omid, M. Artificial Neural Network Based Modeling of Tractor Performance at Different Field Conditions. Agric. Eng. Int. CIGR J. 2016, 18, 262–274. [Google Scholar]
- Shafaei, S.; Loghavi, M.; Kamgar, S. Feasibility of implementation of intelligent simulation configurations based on data mining methodologies for prediction of tractor wheel slip. Inf. Process. Agric. 2019, 6, 183–199. [Google Scholar] [CrossRef]
- Küçüksariyildiz, H.; Çarman, K.; Sabanci, K. Prediction of Specific Fuel Consumption of 60 HP 2WD Tractor Using Artificial Neural Networks. Int. J. Automot. Sci. Technol. 2021, 5, 436–444. [Google Scholar] [CrossRef]
- Badgujar, C.; Flippo, D.; Welch, S. Artificial neural network to predict traction performance of autonomous ground vehicle on a sloped soil bin and uncertainty analysis. Comput. Electron. Agric. 2022, 196, 106867. [Google Scholar] [CrossRef]
- Choi, Y.S.; Lee, K.S.; Park, W.Y. Application of a Neural Network to Dynamic Draft Model. Agric. Biosyst. Eng. 2000, 1, 67–72. [Google Scholar]
- ASABE. Agricultural Machinery Management Data; Technical Report ASAE D497.4 MAR99; American Society of Agricultural and Biological Engineers (ASABE): St. Joseph, MI, USA, 2000. [Google Scholar]
- Al-Janobi, A.; Al-Hamed, S.; Aboukarima, A.; Almajhadi, Y. Modeling of Draft and Energy Requirements of a Moldboard Plow Using Artificial Neural Networks Based on Two Novel Variables. Eng. Agrícola 2020, 40, 363–373. [Google Scholar] [CrossRef]
- Shafaei, S.; Loghavi, M.; Kamgar, S.; Raoufat, M. Potential assessment of neuro-fuzzy strategy in prognostication of draft parameters of primary tillage implement. Ann. Agrar. Sci. 2018, 16, 257–266. [Google Scholar] [CrossRef]
- Çarman, K.; Çıtıl, E.; Taner, A. Artificial Neural Network Model for Predicting Specific Draft Force and Fuel Consumption Requirement of a Mouldboard Plough. Selcuk J. Agric. Food Sci. 2019, 33, 241–247. [Google Scholar] [CrossRef]
- Al-Hamed, S.A.; Wahby, M.F.; Al-Saqer, S.M.; Aboukarima, A.M.; Ahmed, A.S. Artificial neural network model for predicting draft and energy requirements of a disk plow. J. Anim. Plant Sci. 2013, 23, 1714–1724. [Google Scholar]
- Shafaei, S.M.; Loghavi, M.; Kamgar, S. A comparative study between mathematical models and the ANN data mining technique in draft force prediction of disk plow implement in clay loam soil. Agric. Eng. Int. CIGR J. 2018, 20, 71–79. [Google Scholar]
- Aboukarima, A.; Saad, A.F. Assessment of Different Indices Depicting Soil Texture for Predicting Chisel Plow Draft Using Neural Networks. Alex. Sci. Exch. J. 2006, 27, 170–180. [Google Scholar]
- Marey, S.; Aboukarima, A.; Almajhadi, Y. Predicting the Performance Parameters of Chisel Plow Using Neural Network Model. Eng. Agrícola 2020, 40, 719–731. [Google Scholar] [CrossRef]
- DeJong-Hughes, J. Tillage Implements, 2021; The University of Minnesota Extension Service: St. Paul, MN, USA, 2021. [Google Scholar]
- Alimardani, R.; Abbaspour-Gilandeh, Y.; Khalilian, A.; Keyhani, A.; Sadati, S.H. Prediction of draft force and energy of subsoiling operation using ANN model. J. Food, Agric. Environ. 2009, 7, 537–542. [Google Scholar]
- Bergtold, J.; Sailus, M.; Jackson, T. Conservation Tillage Systems in the Southeast: Production, Profitability and Stewardship; USDA: Washington, DC, USA; Sustainable Agriculture Research & Education: College Park, MD, USA, 2020. [Google Scholar]
- Askari, M.; Abbaspour-Gilandeh, Y. Assessment of adaptive neuro-fuzzy inference system and response surface methodology approaches in draft force prediction of subsoiling tines. Soil Tillage Res. 2019, 194, 104338. [Google Scholar] [CrossRef]
- Abbaspour-Gilandeh, M.; Shahgoli, G.; Abbaspour-Gilandeh, Y.; Herrera-Miranda, M.A.; Hernández-Hernández, J.L.; Herrera-Miranda, I. Measuring and Comparing Forces Acting on Moldboard Plow and Para-Plow with Wing to Replace Moldboard Plow with Para-Plow for Tillage and Modeling It Using Adaptive Neuro-Fuzzy Interface System (ANFIS). Agriculture 2020, 10, 633. [Google Scholar] [CrossRef]
- Abbaspour-Gilandeh, Y.; Sedghi, R. Predicting soil fragmentation during tillage operation using fuzzy logic approach. J. Terramech. 2015, 57, 61–69. [Google Scholar] [CrossRef]
- Marakoğlu, T.; Çarman, K. Fuzzy knowledge-based model for prediction of soil loosening and draft efficiency in tillage. J. Terramech. 2010, 47, 173–178. [Google Scholar] [CrossRef]
- Abbaspour-Gilandeh, Y.; Fazeli, M.; Roshanianfard, A.; Hernández-Hernández, M.; Gallardo-Bernal, I.; Hernández-Hernández, J.L. Prediction of Draft Force of a Chisel Cultivator Using Artificial Neural Networks and Its Comparison with Regression Model. Agronomy 2020, 10, 451. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.X.; Kushwaha, R. Applications of neural networks to simulate soil-tool interaction and soil behavior. Can. Agric. Eng. 1999, 41, 119–125. [Google Scholar]
- Mohammadi, A. Modeling of Draft Force Variation in a Winged Share Tillage Tool Using Fuzzy Table Look-Up Scheme. Agric. Eng. Int. CIGR J. 2012, 14, 262–268. [Google Scholar]
- Akbarnia, A.; Mohammadi, A.; Alimardani, R.; Farhani, F. Simulation of draft force of winged share tillage tool using artificial neural network model. Agric. Eng. Int. CIGR J. 2014, 16, 57–65. [Google Scholar]
- Usaborisut, P.; Prasertkan, K. Specific energy requirements and soil pulverization of a combined tillage implement. Heliyon 2019, 5, e02757. [Google Scholar] [CrossRef]
- Upadhyay, G.; Raheman, H. Comparative assessment of energy requirement and tillage effectiveness of combined (active-passive) and conventional offset disc harrows. Biosyst. Eng. 2020, 198, 266–279. [Google Scholar] [CrossRef]
- Shafaei, S.; Loghavi, M.; Kamgar, S. Prognostication of energy indices of tractor-implement utilizing soft computing techniques. Inf. Process. Agric. 2019, 6, 132–149. [Google Scholar] [CrossRef]
- Rahman, A.; Kushwaha, R.L.; Ashrafizadeh, S.R.; Panigrahi, S. Prediction of Energy Requirement of a Tillage Tool in a Soil Bin using Artificial Neural Network. In Proceedings of the 2011 ASABE Annual International Meeting, Louisville, KY, USA, 7–10 August 2011; ASABE: St. Joseph, MI, USA, 2011. [Google Scholar] [CrossRef]
- Saleh, B.; Aly, A. Artificial Neural Network Model for Evaluation of the Ploughing Process Performance. Int. J. Control Autom. Syst. 2013, 2, 1–11. [Google Scholar]
- Shafaei, S.; Loghavi, M.; Kamgar, S. On the neurocomputing based intelligent simulation of tractor fuel efficiency parameters. Inf. Process. Agric. 2018, 5, 205–223. [Google Scholar] [CrossRef]
- Shafaei, S.M.; Loghavi, M.; Kamgar, S. On the Reliability of Intelligent Fuzzy System for Multivariate Pattern Scrutinization of Power Consumption Efficiency of Mechanical Front Wheel Drive Tractor. J. Biosyst. Eng. 2021, 46, 1–15. [Google Scholar] [CrossRef]
- Carman, K. Prediction of soil compaction under pneumatic tires a using fuzzy logic approach. J. Terramech. 2008, 45, 103–108. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A.; Taghavifar, L. A hybridized artificial neural network and imperialist competitive algorithm optimization approach for prediction of soil compaction in soil bin facility. Measurement 2013, 46, 2288–2299. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. Fuzzy logic system based prediction effort: A case study on the effects of tire parameters on contact area and contact pressure. Appl. Soft Comput. 2014, 14, 390–396. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. Wavelet neural network applied for prognostication of contact pressure between soil and driving wheel. Inf. Process. Agric. 2014, 1, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Taghavifar, H. A supervised artificial neural network representational model based prediction of contact pressure and bulk density. J. Adv. Veh. Eng. 2015, 1, 14–21. [Google Scholar]
- Chen, X.W.; Lin, X. Big data deep learning: Challenges and perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Hoi, S.C.; Sahoo, D.; Lu, J.; Zhao, P. Online learning: A comprehensive survey. Neurocomputing 2021, 459, 249–289. [Google Scholar] [CrossRef]
- Wagner, C.; Smith, M.; Wallace, K.; Pourabdollah, A. Generating uncertain fuzzy logic rules from surveys: Capturing subjective relationships between variables from human experts. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2033–2038. [Google Scholar]
- Evans, R.; Grefenstette, E. Learning explanatory rules from noisy data. J. Artif. Intell. Res. 2018, 61, 1–64. [Google Scholar] [CrossRef]
- Mashwani, W.K. Comprehensive survey of the hybrid evolutionary algorithms. Int. J. Appl. Evol. Comput. 2013, 4, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1–40. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Abdella, M.; Marwala, T. The use of genetic algorithms and neural networks to approximate missing data in database. In Proceedings of the IEEE 3rd International Conference on Computational Cybernetics, Hotel Le Victoria, Mauritius, 13–16 April 2005; pp. 207–212. [Google Scholar]
- Amiri, M.; Jensen, R. Missing data imputation using fuzzy-rough methods. Neurocomputing 2016, 205, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Capuano, N.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E.; Loia, V. Fuzzy group decision making with incomplete information guided by social influence. IEEE Trans. Fuzzy Syst. 2017, 26, 1704–1718. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Sheu, Y.h. Illuminating the Black Box: Interpreting Deep Neural Network Models for Psychiatric Research. Front. Psychiatry 2020, 11, 551299. [Google Scholar] [CrossRef]
- Jeyakumar, J.V.; Noor, J.; Cheng, Y.H.; Garcia, L.; Srivastava, M. How can i explain this to you? an empirical study of deep neural network explanation methods. Adv. Neural Inf. Process. Syst. 2020, 33, 4211–4222. [Google Scholar]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A survey on neural network interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Awan, A.A.; Subramoni, H.; Panda, D.K. An in-depth performance characterization of CPU- and GPU-based DNN training on modern architectures. In Proceedings of the Machine Learning on HPC Environments, New. York, NY, USA, 12–17 November 2017; pp. 1–8. [Google Scholar]
- Lázaro, M.; Santamaría, I.; Pérez-Cruz, F.; Artés-Rodríguez, A. Support vector regression for the simultaneous learning of a multivariate function and its derivatives. Neurocomputing 2005, 69, 42–61. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z.; Zhang, K. Multivariate output global sensitivity analysis using multi-output support vector regression. Struct. Multidiscip. Optim. 2019, 59, 2177–2187. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Rusk, N. Deep learning. Nat. Methods 2016, 13, 35. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.; Tufail, M.; Khan, M.T.; Khan, Z.A.; Iqbal, J.; Wasim, A. Real-time recognition of spraying area for UAV sprayers using a deep learning approach. PLoS ONE 2021, 16, e0249436. [Google Scholar] [CrossRef]
- Saleem, M.H.; Potgieter, J.; Arif, K.M. Automation in agriculture by machine and deep learning techniques: A review of recent developments. Precis. Agric. 2021, 22, 2053–2091. [Google Scholar] [CrossRef]
- Hu, K.; Coleman, G.; Zeng, S.; Wang, Z.; Walsh, M. Graph weeds net: A graph-based deep learning method for weed recognition. Comput. Electron. Agric. 2020, 174, 105520. [Google Scholar] [CrossRef]
- Godara, S.; Toshniwal, D. Deep Learning-based query-count forecasting using farmers’ helpline data. Comput. Electron. Agric. 2022, 196, 106875. [Google Scholar] [CrossRef]
- Altalak, M.; Alajmi, A.; Rizg, A. Smart Agriculture Applications Using Deep Learning Technologies: A Survey. Appl. Sci. 2022, 12, 5919. [Google Scholar] [CrossRef]
- Hryniowski, A.; Wong, A. DeepLABNet: End-to-end learning of deep radial basis networks with fully learnable basis functions. arXiv 2019, arXiv:1911.09257. [Google Scholar]
- Li, Y.; Zhang, T. Deep neural mapping support vector machines. Neural Netw. 2017, 93, 185–194. [Google Scholar] [CrossRef]
- Zhang, Y.; Ishibuchi, H.; Wang, S. Deep Takagi–Sugeno–Kang fuzzy classifier with shared linguistic fuzzy rules. IEEE Trans. Fuzzy Syst. 2017, 26, 1535–1549. [Google Scholar] [CrossRef]
- Das, R.; Sen, S.; Maulik, U. A survey on fuzzy deep neural networks. ACM Comput. Surv. (CSUR) 2020, 53, 1–25. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Peng, Z. Rice diseases detection and classification using attention based neural network and bayesian optimization. Expert Syst. Appl. 2021, 178, 114770. [Google Scholar] [CrossRef]
- Hanin, B. Which neural net architectures give rise to exploding and vanishing gradients? Adv. Neural Inf. Process. Syst. 2018, 3, 1–18. [Google Scholar] [CrossRef]
- Talathi, S.S.; Vartak, A. Improving performance of recurrent neural network with relu nonlinearity. arXiv 2015, arXiv:1511.03771. [Google Scholar]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Santoro, A.; Marris, L.; Akerman, C.J.; Hinton, G. Backpropagation and the brain. Nat. Rev. Neurosci. 2020, 21, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep learning techniques: An overview. In Proceedings of the International Conference on Advanced Machine Learning Technologies and Applications, Jaipur, India, 13–15 February 2020; Springer: New York, NY, USA, 2020; pp. 599–608. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhang, Z.; Liu, H.; Meng, Z.; Chen, J. Deep learning-based automatic recognition network of agricultural machinery images. Comput. Electron. Agric. 2019, 166, 104978. [Google Scholar] [CrossRef]
- Jin, X.B.; Yang, N.X.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Kong, J.L. Hybrid deep learning predictor for smart agriculture sensing based on empirical mode decomposition and gated recurrent unit group model. Sensors 2020, 20, 1334. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.; Kim, J.; Lee, H.; Shin, J. Guiding deep molecular optimization with genetic exploration. Adv. Neural Inf. Process. Syst. 2020, 33, 12008–12021. [Google Scholar]
- Navada, A.; Ansari, A.N.; Patil, S.; Sonkamble, B.A. Overview of use of decision tree algorithms in machine learning. In Proceedings of the 2011 IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 27–28 June 2011; pp. 37–42. [Google Scholar]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B.; Gao, Y. Symmetric Binary Tree Based Co-occurrence Texture Pattern Mining for Fine-grained Plant Leaf Image Retrieval. Pattern Recognit. 2022, 129, 108769. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Zhang, L.; Traore, S.; Ge, J.; Li, Y.; Wang, S.; Zhu, G.; Cui, Y.; Fipps, G. Using boosted tree regression and artificial neural networks to forecast upland rice yield under climate change in Sahel. Comput. Electron. Agric. 2019, 166, 105031. [Google Scholar] [CrossRef]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Da Silva Júnior, J.C.; Medeiros, V.; Garrozi, C.; Montenegro, A.; Gonçalves, G.E. Random forest techniques for spatial interpolation of evapotranspiration data from Brazilian’s Northeast. Comput. Electron. Agric. 2019, 166, 105017. [Google Scholar] [CrossRef]
- Zhang, Y.; Sui, B.; Shen, H.; Ouyang, L. Mapping stocks of soil total nitrogen using remote sensing data: A comparison of random forest models with different predictors. Comput. Electron. Agric. 2019, 160, 23–30. [Google Scholar] [CrossRef]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Ismail, M.F.; Tan, N.P.; Karam, D.S. Hyperspectral remote sensing for assessment of chlorophyll sufficiency levels in mature oil palm (Elaeis guineensis) based on frond numbers: Analysis of decision tree and random forest. Comput. Electron. Agric. 2020, 169, 105221. [Google Scholar] [CrossRef]
- Karimi, S.; Shiri, J.; Marti, P. Supplanting missing climatic inputs in classical and random forest models for estimating reference evapotranspiration in humid coastal areas of Iran. Comput. Electron. Agric. 2020, 176, 105633. [Google Scholar] [CrossRef]
- Obsie, E.Y.; Qu, H.; Drummond, F. Wild blueberry yield prediction using a combination of computer simulation and machine learning algorithms. Comput. Electron. Agric. 2020, 178, 105778. [Google Scholar] [CrossRef]
- Ramos, A.P.M.; Osco, L.P.; Furuya, D.E.G.; Gonçalves, W.N.; Santana, D.C.; Teodoro, L.P.R.; da Silva Junior, C.A.; Capristo-Silva, G.F.; Li, J.; Baio, F.H.R.; et al. A random forest ranking approach to predict yield in maize with uav-based vegetation spectral indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
- Rastgou, M.; Bayat, H.; Mansoorizadeh, M.; Gregory, A.S. Estimating the soil water retention curve: Comparison of multiple nonlinear regression approach and random forest data mining technique. Comput. Electron. Agric. 2020, 174, 105502. [Google Scholar] [CrossRef]
- dos Santos Luciano, A.C.; Picoli, M.C.A.; Duft, D.G.; Rocha, J.V.; Leal, M.R.L.V.; Le Maire, G. Empirical model for forecasting sugarcane yield on a local scale in Brazil using Landsat imagery and random forest algorithm. Comput. Electron. Agric. 2021, 184, 106063. [Google Scholar] [CrossRef]
- Mariano, C.; Monica, B. A random forest-based algorithm for data-intensive spatial interpolation in crop yield mapping. Comput. Electron. Agric. 2021, 184, 106094. [Google Scholar] [CrossRef]
- Dhaliwal, J.K.; Panday, D.; Saha, D.; Lee, J.; Jagadamma, S.; Schaeffer, S.; Mengistu, A. Predicting and interpreting cotton yield and its determinants under long-term conservation management practices using machine learning. Comput. Electron. Agric. 2022, 199, 107107. [Google Scholar] [CrossRef]
- Yoo, B.H.; Kim, K.S.; Park, J.Y.; Moon, K.H.; Ahn, J.J.; Fleisher, D.H. Spatial portability of random forest models to estimate site-specific air temperature for prediction of emergence dates of the Asian Corn Borer in North Korea. Comput. Electron. Agric. 2022, 199, 107113. [Google Scholar] [CrossRef]
- Elavarasan, D.; Vincent, D.R.; Sharma, V.; Zomaya, A.Y.; Srinivasan, K. Forecasting yield by integrating agrarian factors and machine learning models: A survey. Comput. Electron. Agric. 2018, 155, 257–282. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, K.; Shamshirband, S.; Motamedi, S.; Petković, D.; Hashim, R.; Gocic, M. Extreme learning machine based prediction of daily dew point temperature. Comput. Electron. Agric. 2015, 117, 214–225. [Google Scholar] [CrossRef]
- Gocic, M.; Petković, D.; Shamshirband, S.; Kamsin, A. Comparative analysis of reference evapotranspiration equations modelling by extreme learning machine. Comput. Electron. Agric. 2016, 127, 56–63. [Google Scholar] [CrossRef]
- Patil, A.P.; Deka, P.C. An extreme learning machine approach for modeling evapotranspiration using extrinsic inputs. Comput. Electron. Agric. 2016, 121, 385–392. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Sadgrove, E.J.; Falzon, G.; Miron, D.; Lamb, D. Fast object detection in pastoral landscapes using a colour feature extreme learning machine. Comput. Electron. Agric. 2017, 139, 204–212. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Downs, N.J.; Maraseni, T. Multi-stage committee based extreme learning machine model incorporating the influence of climate parameters and seasonality on drought forecasting. Comput. Electron. Agric. 2018, 152, 149–165. [Google Scholar] [CrossRef]
- Shi, P.; Li, G.; Yuan, Y.; Huang, G.; Kuang, L. Prediction of dissolved oxygen content in aquaculture using Clustering-based Softplus Extreme Learning Machine. Comput. Electron. Agric. 2019, 157, 329–338. [Google Scholar] [CrossRef]
- Gong, D.; Hao, W.; Gao, L.; Feng, Y.; Cui, N. Extreme learning machine for reference crop evapotranspiration estimation: Model optimization and spatiotemporal assessment across different climates in China. Comput. Electron. Agric. 2021, 187, 106294. [Google Scholar] [CrossRef]
- Nahvi, B.; Habibi, J.; Mohammadi, K.; Shamshirband, S.; Al Razgan, O.S. Using self-adaptive evolutionary algorithm to improve the performance of an extreme learning machine for estimating soil temperature. Comput. Electron. Agric. 2016, 124, 150–160. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Ma, X.; Zhou, H.; Zeng, W. Hybrid extreme learning machine with meta-heuristic algorithms for monthly pan evaporation prediction. Comput. Electron. Agric. 2020, 168, 105115. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Yu, W.; Zhuang, F.; He, Q.; Shi, Z. Learning deep representations via extreme learning machines. Neurocomputing 2015, 149, 308–315. [Google Scholar] [CrossRef]
- Tissera, M.D.; McDonnell, M.D. Deep extreme learning machines: Supervised autoencoding architecture for classification. Neurocomputing 2016, 174, 42–49. [Google Scholar] [CrossRef]
- Abdelghafour, F.; Rosu, R.; Keresztes, B.; Germain, C.; Da Costa, J.P. A Bayesian framework for joint structure and colour based pixel-wise classification of grapevine proximal images. Comput. Electron. Agric. 2019, 158, 345–357. [Google Scholar] [CrossRef]
- Khanal, A.R.; Mishra, A.K.; Lambert, D.M.; Paudel, K.P. Modeling post adoption decision in precision agriculture: A Bayesian approach. Comput. Electron. Agric. 2019, 162, 466–474. [Google Scholar] [CrossRef]
- Tetteh, G.O.; Gocht, A.; Conrad, C. Optimal parameters for delineating agricultural parcels from satellite images based on supervised Bayesian optimization. Comput. Electron. Agric. 2020, 178, 105696. [Google Scholar] [CrossRef]
- Fang, Y.; Xu, L.; Chen, Y.; Zhou, W.; Wong, A.; Clausi, D.A. A Bayesian Deep Image Prior Downscaling Approach for High-Resolution Soil Moisture Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4571–4582. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Hrycej, T. Gibbs sampling in Bayesian networks. Artif. Intell. 1990, 46, 351–363. [Google Scholar] [CrossRef]
- Chapman, R.; Cook, S.; Donough, C.; Lim, Y.L.; Ho, P.V.V.; Lo, K.W.; Oberthür, T. Using Bayesian networks to predict future yield functions with data from commercial oil palm plantations: A proof of concept analysis. Comput. Electron. Agric. 2018, 151, 338–348. [Google Scholar] [CrossRef]
- Kocian, A.; Massa, D.; Cannazzaro, S.; Incrocci, L.; Di Lonardo, S.; Milazzo, P.; Chessa, S. Dynamic Bayesian network for crop growth prediction in greenhouses. Comput. Electron. Agric. 2020, 169, 105167. [Google Scholar] [CrossRef]
- Bilmes, J.A. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. Int. Comput. Sci. Inst. 1998, 4, 126. [Google Scholar]
- Lu, J. A survey on Bayesian inference for Gaussian mixture model. arXiv 2021, arXiv:2108.11753. [Google Scholar]
- Mouret, F.; Albughdadi, M.; Duthoit, S.; Kouamé, D.; Rieu, G.; Tourneret, J.Y. Reconstruction of Sentinel-2 derived time series using robust Gaussian mixture models—Application to the detection of anomalous crop development. Comput. Electron. Agric. 2022, 198, 106983. [Google Scholar] [CrossRef]
- Zhu, C.; Ding, J.; Zhang, Z.; Wang, J.; Wang, Z.; Chen, X.; Wang, J. SPAD monitoring of saline vegetation based on Gaussian mixture model and UAV hyperspectral image feature classification. Comput. Electron. Agric. 2022, 200, 107236. [Google Scholar] [CrossRef]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Wilson, A.G.; Knowles, D.A.; Ghahramani, Z. Gaussian process regression networks. arXiv 2011, arXiv:1110.4411. [Google Scholar]
- Smola, A.; Bartlett, P. Sparse greedy Gaussian process regression. Adv. Neural Inf. Process. Syst. 2000, 13, 1–7. [Google Scholar]
- Azadbakht, M.; Ashourloo, D.; Aghighi, H.; Radiom, S.; Alimohammadi, A. Wheat leaf rust detection at canopy scale under different LAI levels using machine learning techniques. Comput. Electron. Agric. 2019, 156, 119–128. [Google Scholar] [CrossRef]
- Shabani, S.; Samadianfard, S.; Sattari, M.T.; Shamshirband, S.; Mosavi, A.; Kmet, T.; Várkonyi-Kóczy, A.R. Modeling daily pan evaporation in humid climates using gaussian process regression. arXiv 2019, arXiv:1908.04267. [Google Scholar]
- Nieto, P.G.; García-Gonzalo, E.; Puig-Bargués, J.; Solé-Torres, C.; Duran-Ros, M.; Arbat, G. A new predictive model for the outlet turbidity in micro-irrigation sand filters fed with effluents using Gaussian process regression. Comput. Electron. Agric. 2020, 170, 105292. [Google Scholar] [CrossRef]
- Rastgou, M.; Bayat, H.; Mansoorizadeh, M.; Gregory, A.S. Prediction of soil hydraulic properties by Gaussian process regression algorithm in arid and semiarid zones in Iran. Soil Tillage Res. 2021, 210, 104980. [Google Scholar] [CrossRef]
- Nguyen, L.; Nguyen, D.K.; Nghiem, T.X.; Nguyen, T. Least square and Gaussian process for image based microalgal density estimation. Comput. Electron. Agric. 2022, 193, 106678. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar]
- Zhou, Z.H. Ensemble learning. In Machine Learning; Springer: New York, NY, USA, 2021; pp. 181–210. [Google Scholar]
- Chaudhary, A.; Kolhe, S.; Kamal, R. A hybrid ensemble for classification in multiclass datasets: An application to oilseed disease dataset. Comput. Electron. Agric. 2016, 124, 65–72. [Google Scholar]
- Haagsma, M.; Page, G.F.; Johnson, J.S.; Still, C.; Waring, K.M.; Sniezko, R.A.; Selker, J.S. Model selection and timing of acquisition date impacts classification accuracy: A case study using hyperspectral imaging to detect white pine blister rust over time. Comput. Electron. Agric. 2021, 191, 106555. [Google Scholar] [CrossRef]
- Kar, S.; Purbey, V.K.; Suradhaniwar, S.; Korbu, L.B.; Kholová, J.; Durbha, S.S.; Adinarayana, J.; Vadez, V. An ensemble machine learning approach for determination of the optimum sampling time for evapotranspiration assessment from high-throughput phenotyping data. Comput. Electron. Agric. 2021, 182, 105992. [Google Scholar] [CrossRef]
- Chaudhary, A.; Thakur, R.; Kolhe, S.; Kamal, R. A particle swarm optimization based ensemble for vegetable crop disease recognition. Comput. Electron. Agric. 2020, 178, 105747. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Improving reference evapotranspiration estimation using novel inter-model ensemble approaches. Comput. Electron. Agric. 2021, 187, 106227. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W.; Jiao, X.; Guo, W.; Hamoud, Y.A. Evaluation of stacking and blending ensemble learning methods for estimating daily reference evapotranspiration. Comput. Electron. Agric. 2021, 184, 106039. [Google Scholar] [CrossRef]
- Koyama, K.; Lyu, S. Soft-labeling approach along with an ensemble of models for predicting subjective freshness of spinach leaves. Comput. Electron. Agric. 2022, 193, 106633. [Google Scholar] [CrossRef]
- Xu, C.; Ding, J.; Qiao, Y.; Zhang, L. Tomato disease and pest diagnosis method based on the Stacking of prescription data. Comput. Electron. Agric. 2022, 197, 106997. [Google Scholar] [CrossRef]
- Aiken, V.C.F.; Dórea, J.R.R.; Acedo, J.S.; de Sousa, F.G.; Dias, F.G.; de Magalhães Rosa, G.J. Record linkage for farm-level data analytics: Comparison of deterministic, stochastic and machine learning methods. Comput. Electron. Agric. 2019, 163, 104857. [Google Scholar] [CrossRef]
- Weber, V.A.M.; de Lima Weber, F.; da Silva Oliveira, A.; Astolfi, G.; Menezes, G.V.; de Andrade Porto, J.V.; Rezende, F.P.C.; de Moraes, P.H.; Matsubara, E.T.; Mateus, R.G.; et al. Cattle weight estimation using active contour models and regression trees Bagging. Comput. Electron. Agric. 2020, 179, 105804. [Google Scholar] [CrossRef]
- Genedy, R.A.; Ogejo, J.A. Using machine learning techniques to predict liquid dairy manure temperature during storage. Comput. Electron. Agric. 2021, 187, 106234. [Google Scholar] [CrossRef]
- Mohammed, S.; Elbeltagi, A.; Bashir, B.; Alsafadi, K.; Alsilibe, F.; Alsalman, A.; Zeraatpisheh, M.; Széles, A.; Harsányi, E. A comparative analysis of data mining techniques for agricultural and hydrological drought prediction in the eastern Mediterranean. Comput. Electron. Agric. 2022, 197, 106925. [Google Scholar] [CrossRef]
- Ayan, E.; Erbay, H.; Varçın, F. Crop pest classification with a genetic algorithm-based weighted ensemble of deep convolutional neural networks. Comput. Electron. Agric. 2020, 179, 105809. [Google Scholar] [CrossRef]
- Barbosa, A.; Hovakimyan, N.; Martin, N.F. Risk-averse optimization of crop inputs using a deep ensemble of convolutional neural networks. Comput. Electron. Agric. 2020, 178, 105785. [Google Scholar] [CrossRef]
- e Lucas, P.d.O.; Alves, M.A.; e Silva, P.C.d.L.; Guimarães, F.G. Reference evapotranspiration time series forecasting with ensemble of convolutional neural networks. Comput. Electron. Agric. 2020, 177, 105700. [Google Scholar] [CrossRef]
- Gonzalo-Martín, C.; García-Pedrero, A.; Lillo-Saavedra, M. Improving deep learning sorghum head detection through test time augmentation. Comput. Electron. Agric. 2021, 186, 106179. [Google Scholar] [CrossRef]
- Gu, Z.; Zhu, T.; Jiao, X.; Xu, J.; Qi, Z. Neural network soil moisture model for irrigation scheduling. Comput. Electron. Agric. 2021, 180, 105801. [Google Scholar] [CrossRef]
- Khanramaki, M.; Asli-Ardeh, E.A.; Kozegar, E. Citrus pests classification using an ensemble of deep learning models. Comput. Electron. Agric. 2021, 186, 106192. [Google Scholar] [CrossRef]
- Li, Q.; Jia, W.; Sun, M.; Hou, S.; Zheng, Y. A novel green apple segmentation algorithm based on ensemble U-Net under complex orchard environment. Comput. Electron. Agric. 2021, 180, 105900. [Google Scholar] [CrossRef]
- Gonzalez, R.; Iagnemma, K. Slippage estimation and compensation for planetary exploration rovers. State of the art and future challenges. J. Field Robot. 2018, 35, 564–577. [Google Scholar] [CrossRef]
- Gonzalez, R.; Chandler, S.; Apostolopoulos, D. Characterization of machine learning algorithms for slippage estimation in planetary exploration rovers. J. Terramech. 2019, 82, 23–34. [Google Scholar] [CrossRef]
- Jørgensen, M. Adaptive tillage systems. Agron. Res. 2014, 12, 95–100. [Google Scholar]
- Jia, H.; Guo, M.; Yu, H.; Li, Y.; Feng, X.; Zhao, J.; Qi, J. An adaptable tillage depth monitoring system for tillage machine. Biosyst. Eng. 2016, 151, 187–199. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badgujar, C.; Das, S.; Figueroa, D.M.; Flippo, D. Application of Computational Intelligence Methods in Agricultural Soil–Machine Interaction: A Review. Agriculture 2023, 13, 357. https://doi.org/10.3390/agriculture13020357
Badgujar C, Das S, Figueroa DM, Flippo D. Application of Computational Intelligence Methods in Agricultural Soil–Machine Interaction: A Review. Agriculture. 2023; 13(2):357. https://doi.org/10.3390/agriculture13020357
Chicago/Turabian StyleBadgujar, Chetan, Sanjoy Das, Dania Martinez Figueroa, and Daniel Flippo. 2023. "Application of Computational Intelligence Methods in Agricultural Soil–Machine Interaction: A Review" Agriculture 13, no. 2: 357. https://doi.org/10.3390/agriculture13020357
APA StyleBadgujar, C., Das, S., Figueroa, D. M., & Flippo, D. (2023). Application of Computational Intelligence Methods in Agricultural Soil–Machine Interaction: A Review. Agriculture, 13(2), 357. https://doi.org/10.3390/agriculture13020357








