Quantitative Description and Classification of Growing Media Particle Morphology through Dynamic Image Analysis
Abstract
:1. Introduction
- To define shape descriptors (aspect ratio, elongation, circularity, convexity, and roundness) and the parameters used for their calculations, then to discuss their relevance for describing growing media particles with the QicPic device;
- To propose a classification adapted from Blott and Pye to describe the particle shapes of growing media constituents [21];
- To catalog particle shapes of materials tested according to the classification proposed;
- To analyze relationships between particle shape and size descriptors;
- To propose a first classification of growing media constituents based on their particle size and shape, and to discuss its robustness.
2. Materials and Methods
2.1. Dynamic Image Analysis
2.2. Shape Descriptors
- Aspect ratio: indicator of width/length ratio (Figure 2, Equation (1)) where width and length are respectively calculated from the minimum (FeretMIN) and maximum (FeretMAX) Feret diameters. Feret diameters are defined as the distance between two parallels tangents of the particle contour. Thus, Feret MIN is the smallest and Feret MAX the biggest distance among all Feret diameters of a particle.
- Elongation: another indicator of width/length ratio (Figure 2, Equation (2)). The length of fiber (LeFi) is calculated using the skeletonization technique, and corresponds to the longest direct path from one end to another within the particle contour. The diameter of fiber (DiFi) is calculated by dividing the projection area by the sum of all lengths of the branches of the fibre skeleton.
- Circularity: indicator of the deformation of the perimeter of a particle from a circle having the same area [33]. This shape descriptor is sometime wrongly called sphericity, but its measurement is done in two dimensions [21]. The circularity is calculated from the particle perimeter and area. An equal projection area circle (EQPC) is calculated from the measured area of the particle, and the perimeter of the EQPC is compared to the real perimeter of the particle (Figure 2, Equation (3)). Particle circularity decreases as the perimeter increases for a given area. As discussed by Blott and Pye [21], circularity is distinct from roundness. As an example, a square has high a circularity equal to 0.89, but a roundness equal to zero.
- Convexity: indicator of the compactness of a particle. Convexity corresponds to the ratio of the projection area itself (A) and the area of the convex hull (A + B) (Figure 2, Equation (4)), where (B) is the open concave region of the particle. The convex hull is a surface delimited by the line of shortest distance, which connects the maximum projections on a particle outline.
- Roundness: indicator of the relative sharpness of the corner of a particle [34]. Various formulas are available to assess the roundness of the particle [21]. Here, roundness measured by the QicPic is defined as the ratio of the average radius of curvature of all convex regions to the circumscribed circle of the particle (Figure 2, Equation (5)), in contrast with Wadell [34], who suggested to consider the largest inscribed circle of the particle as denominator in the roundness calculation equation.
2.3. Shape Classification
2.4. Particle Size Measurement
2.5. Data Treatment and Statistical Analysis
3. Results
3.1. Global Analysis of Particle Shapes for the 22 Growing Media Constituents
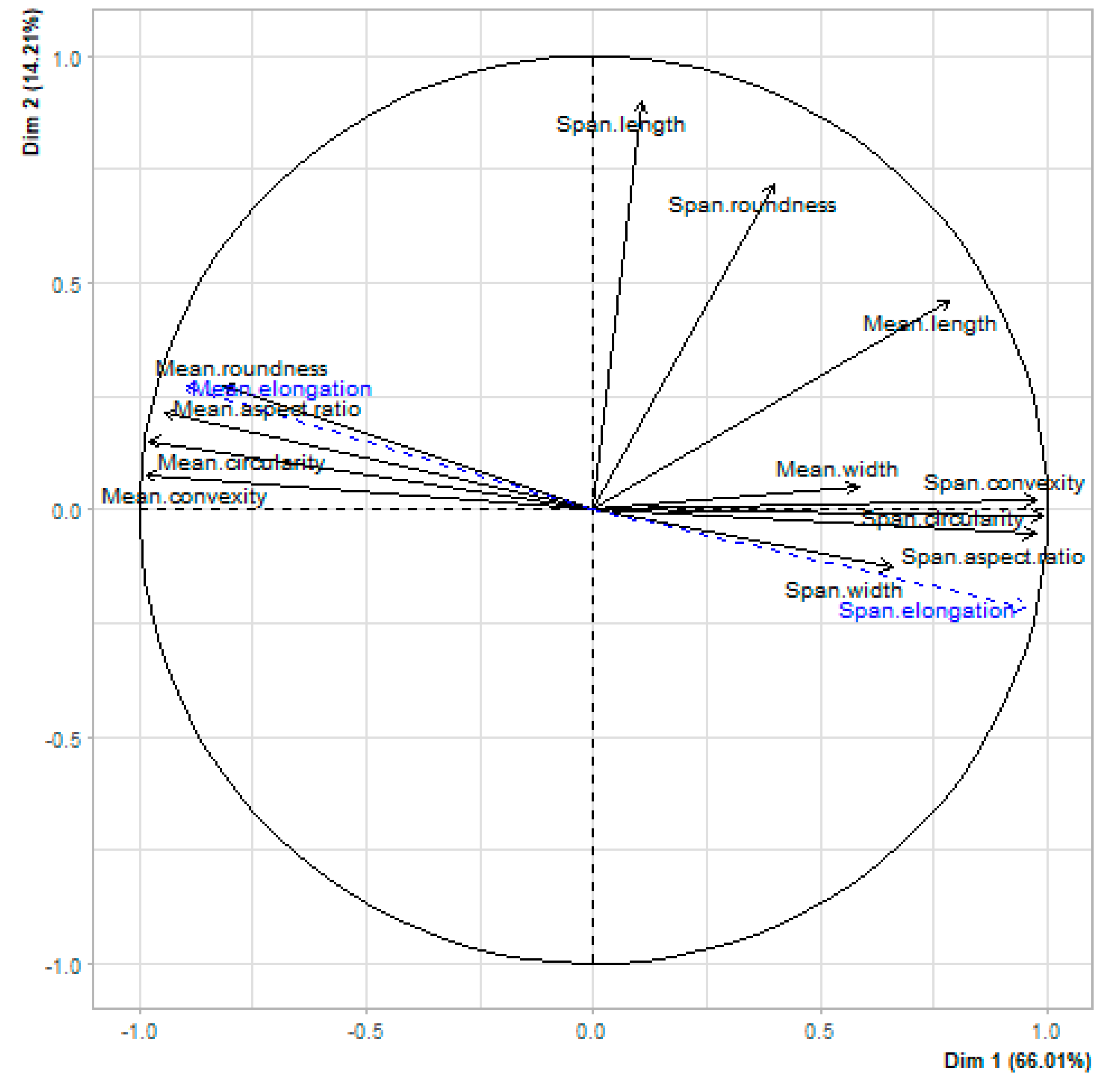
3.2. Correlations between Morphological Descriptors & Identification of Relevant Parameters
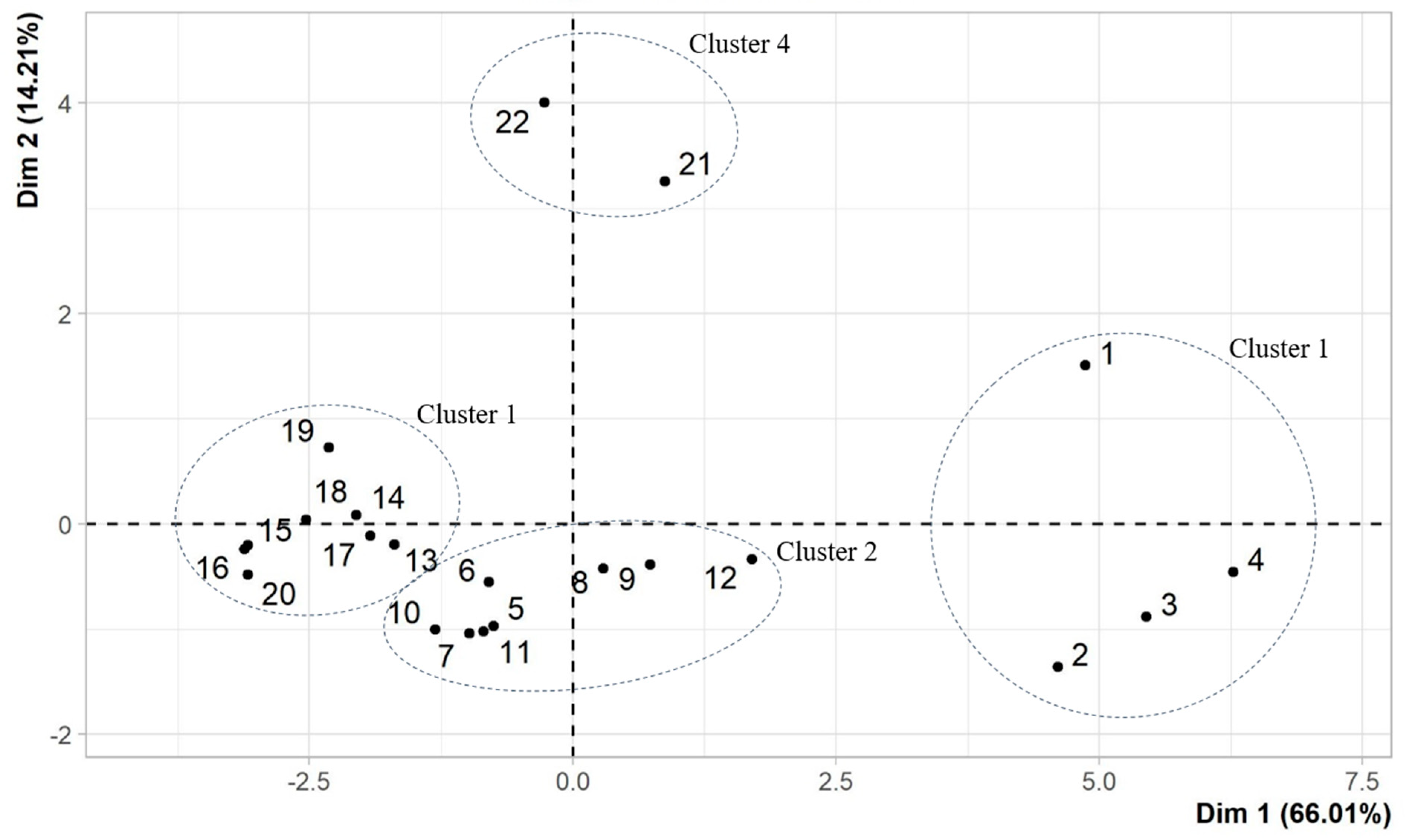
3.3. Hierarchical Clustering Analysis (HCA) of Growing Media Constituents
3.4. Shape Diversity as a Function of Particle Length
4. Discussion
4.1. Relevance of Shape Descriptors for Characterizing Growing Media Constituents
- Both aspect ratio (Equation (1)) and elongation (Equation (2)) describe the width/length ratio. However, elongation calculated from Equation (2) assumes that the particle width is equal to its surface divided by its length, which is only true for elongated-rectangular shaped particles (e.g., fibers). For non-elongated particles, the particle length (LeFi) is overestimated, and consequently, the width/length ratio underestimated. In contrast, the aspect ratio is most appropriate for non-curved particles. Indeed, for curved particles, FeretMIN overestimates the particle width, and FeretMAX minimizes its length, resulting in an overestimation of the width/length ratio.
- Convexity is a relevant shape descriptor for non-curved particles, where concave areas are clearly defined (cf. area B on Figure 2). Indeed, for curved particles such as fibers, concave regions correspond to the inner area between the extremities of curved particles, thus resulting in underestimating the convexity.
- Although circularity is not based on particle length and width, but on particle area and perimeter, it is highly related to the width/length ratio of particles. The perimeter of a particle increases while its width/length ratio decreases for a given area. Moreover, circularity is also related to the convexity of a particle. Indeed, the more a particle has concavities, the more its perimeter increases compared to its area, which is reflected by the circularity. In contrast with previously mentioned shape descriptors, circularity is then adapted for all particle shapes, and could be considered as a strong indicator to differentiate materials.
- Roundness calculation also considers particle length, but is not influenced by the width/length ratio of particles, in terms of either its perimeter or area, nor its curvature. As observed, this shape descriptor was the less correlated with the others.
4.2. Relevance of Growing Media Classification According to Particle Size and Shape
4.3. Two-Dimensional Analysis
5. Conclusions
- (1)
- Fine and coarse wood and coir fibers;
- (2)
- Sphagnum white peats, regardless of their particle sizes (fine and medium) and extraction processes (milled and sod);
- (3)
- Black peats, sedge peat, coir fine, fresh and composted pine bark, green waste compost, and fine perlite.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blok, C.; Eveleens, B.; Van Winkel, A. Growing media for food and quality of life in the period 2020–2050. Acta Hortic. 2021, 1305, 341–356. [Google Scholar] [CrossRef]
- Caron, J.; Michel, J.-C. Understanding and optimizing the physical properties of growing media for soilless cultivation. In Advances in Horticultural Soilless Culture, 1st ed.; Gruda, N., Ed.; Burleigh Dodds Science Publishing: Cambridge, UK, 2021; pp. 107–138. [Google Scholar]
- Paquet, J.M.; Caron, J.; Banton, O. In situ determination of the water desorption characteristics of peat substrates. Can. J. Soil Sci. 1993, 73, 329–339. [Google Scholar] [CrossRef]
- Heiskanen, J.; Tervo, L.; Heinonen, J. Effects of mechanical container-filling methods on texture and water retention of peat growth media. Scand. J. For. Res. 1996, 11, 351–355. [Google Scholar] [CrossRef]
- Gruda, N.; Schnitzler, W.H. Suitability of wood fiber substrates for production of vegetable transplants II: The effect of wood fiber substrates and their volume weights on the growth of tomato transplants. Sci. Hortic. 2004, 100, 333–340. [Google Scholar] [CrossRef]
- Bilderback, T.E.; Fonteno, W.C. Effects of container geometry and media physical properties on air and water volumes in containers. J. Environ. Hortic. 2004, 5, 180–182. [Google Scholar] [CrossRef]
- Raviv, M.; Wallach, R.; Silber, A.; Bar-Tal, A. Substrates and their analysis. In Hydroponic Production of Vegetables and Ornamentals, 1st ed.; Savvas, D., Passam, H., Eds.; Embryo Publication: Athens, Greece, 2002; pp. 25–102. [Google Scholar]
- Owen, J.S.; Altland, J.E. Container Height and Douglas Fir Bark Texture Affect Substrate Physical Properties. HortScience 2008, 43, 505–508. [Google Scholar] [CrossRef]
- Michel, J.-C.; Kerloch, E. Evolution of hydraulic properties and wettability of organic growing media during cultivation according to irrigation strategies. Sci. Hortic. 2017, 217, 28–35. [Google Scholar] [CrossRef]
- Michel, J.-C. Relevant hydraulic properties of peat-based mixes for explaining root development according to irrigation strategies. Acta Hortic. 2019, 1266, 353–360. [Google Scholar] [CrossRef]
- Bunt, A.C. Physical properties of mixtures of peats and minerals of different particle size and bulk density for potting substrate. Acta Hortic. 1983, 150, 143–145. [Google Scholar] [CrossRef]
- Handreck, K.A. Particle size and the physical properties of growing media for containers. Commun. Soil Sci. Plant Anal. 1983, 14, 209–222. [Google Scholar] [CrossRef]
- Caron, J.; Rivière, L.-M.; Guillemain, G. Gas diffusion and air-filled porosity: Effect of some oversize fragments in growing media. Can. J. Soil Sci. 2005, 85, 57–65. [Google Scholar] [CrossRef]
- Fields, J.S.; Owen, J.S.; Scoggins, H.L. Exploring the Influence of Particle Size on Plant Water Availability in Pine Bark Substrates. In Proceedings of the 60th SNA Research Conference, McMinnville, TN, USA, October 2015; pp. 19–27. [Google Scholar]
- Nguyen, V.T.H.; Kraska, T.; Winkler, W.; Aydinlik, S.; Jackson, B.E.; Pude, R. Primary Mechanical Modification to Improve Performance of Miscanthus as Stand-Alone Growing Substrates. Agronomy 2022, 12, 420. [Google Scholar] [CrossRef]
- Bartley, P.C.; Fonteno, W.C.; Jackson, B.E. A Review and Analysis of Horticultural Substrate Characterization by Sieve Analysis. HortScience 2022, 57, 715–725. [Google Scholar] [CrossRef]
- Bartley, P.C. Multidimensional Characterization of Horticultural Substrates. Doctoral Dissertation, North Carolina State University, Raleigh, NC, USA, 2019. [Google Scholar]
- Durand, S.; Jackson, B.E.; Bartley, P.C.; Fonteno, W.C.; Michel, J.-C. New tools for particle shape analysis of substrate components: Initial results and future prospects. Acta Hortic. 2021, 1317, 335–342. [Google Scholar] [CrossRef]
- Trubetskaya, A.; Beckmann, G.; Wadenbäck, J.; Holm, J.K.; Velaga, S.P.; Weber, R. One way of representing the size and shape of biomass particles in combustion modeling. Fuel 2017, 206, 675–683. [Google Scholar] [CrossRef]
- Durand, S.; Jackson, B.E.; Fonteno, W.C.; Michel, J.-C. Particle size distribution of growing media constituents using dynamic image analysis: Parametrization and comparison to sieving. Soil Sci. Soc. Am. J. 2023. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. Particle shape: A review and new methods of characterization and classification. Sedimentology 2008, 55, 31–63. [Google Scholar] [CrossRef]
- Lim, M.S.; Wijeyesekera, D.; Zainorabidin, A.; Bakar, I. The Effects of Particle Morphology (Shape and Sizes) Characteristics on its Engineering Behaviour and Sustainable Engineering Performance of Sand. Int. J. Integr. Eng. 2012, 4, 27–37. [Google Scholar]
- Wu, Y.; Cui, J.; Huang, J.; Zhang, W.; Yoshimoto, N.; Wen, L. Correlation of Critical State Strength Properties with Particle Shape and Surface Fractal Dimension of Clinker Ash. Int. J. Geomech. 2021, 21, 04021071. [Google Scholar] [CrossRef]
- Ulusoy, U. A Review of Particle Shape Effects on Material Properties for Various Engineering Applications: From Macro to Nanoscale. Minerals 2023, 13, 91. [Google Scholar] [CrossRef]
- Puri, V.M.; Mancino, C.F. Importance of Particle Shape and Size on Rootzone Sands’ Bulk Mechanical Behavior. USGA Turfgrass Environ. Res. 2002, 1, 1–9. [Google Scholar]
- Miller, N.; Henderson, J. Correlating Particle Shape Parameters to Bulk Properties and Load Stress at Two Water Contents. Agron. J. 2011, 103, 1514–1523. [Google Scholar] [CrossRef]
- Yi, H.; Mittal, B.; Puri, V.M.; Li, F.; Mancino, C.F. Measurement of Bulk Mechanical Properties and Modeling the Load-Response of Rootzone Sands. Part 1: Round and Angular Monosize and Binary Mixtures. Part. Sci. Technol. 2001, 19, 145–173. [Google Scholar] [CrossRef]
- Liu, Z.; Dugan, B.; Masiello, C.A.; Gonnermann, H.M. Biochar particle size, shape, and porosity act together to influence soil water properties. PLoS ONE 2017, 12, e0179079. [Google Scholar] [CrossRef]
- Gil, M.; Teruel, E.; Arauzo, I. Analysis of standard sieving method for milled biomass through image processing. Effects of particle shape and size for poplar and corn stover. Fuel 2014, 116, 328–340. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, X.; Liu, H. Experimental research on shape and size distribution of biomass particle. Fuel 2012, 94, 551–555. [Google Scholar] [CrossRef]
- Schmilewski, G. Growing media constituents used in the EU in 2013. Acta Hortic. 2017, 1168, 85–92. [Google Scholar] [CrossRef]
- Afnor, NF EN 13041; Soil Improvers and Growing Media—Determination of Physical Properties—Dry Bulk Density, Air Volume, Water Volume, Shrinkage Value and Total Pore Space. European Standard: Plzeň, Czech Republic, 2000.
- Wadell, H. Sphericity and roundness of rock particles. J. Geol. 1933, 41, 310–331. [Google Scholar] [CrossRef]
- Wadell, H. Volume, Shape, and Roundness of Rock Particles. J. Geol. 1932, 40, 443–451. [Google Scholar] [CrossRef]
- Igathinathane, C.; Pordesimo, L.O.; Columbus, E.P.; Batchelor, W.D.; Sokhansanj, S. Sieveless particle size distribution analysis of particulate materials through computer vision. Comput. Electron. Agric. 2009, 66, 147–158. [Google Scholar] [CrossRef]
- Bitra, V.S.P.; Womac, A.R.; Yang, Y.T.; Igathinathane, C.; Miu, P.I.; Chevanan, N.; Sokhansanj, S. Knife mill operating factors effect on switchgrass particle size distributions. Bioresour. Technol. 2009, 100, 5176–5188. [Google Scholar] [CrossRef]
- Vaissie, P.; Monge, A.; Husson, F. Factoshiny: Perform Factorial Analysis from ‘FactoMineR’ with a Shiny. Package to perform statistical analysis on R software. 2021. Available online: https://cran.r-project.org/web/packages/Factoshiny/ (accessed on 23 December 2022).
- Blott, S.J.; Pye, K. GRADISTAT: A grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 2001, 26, 1237–1248. [Google Scholar] [CrossRef]
- Li, L.; Iskander, M. Evaluation of Dynamic Image Analysis for Characterizing Granular Soils. Geotech. Test. J. 2020, 43, 1149–1173. [Google Scholar] [CrossRef]


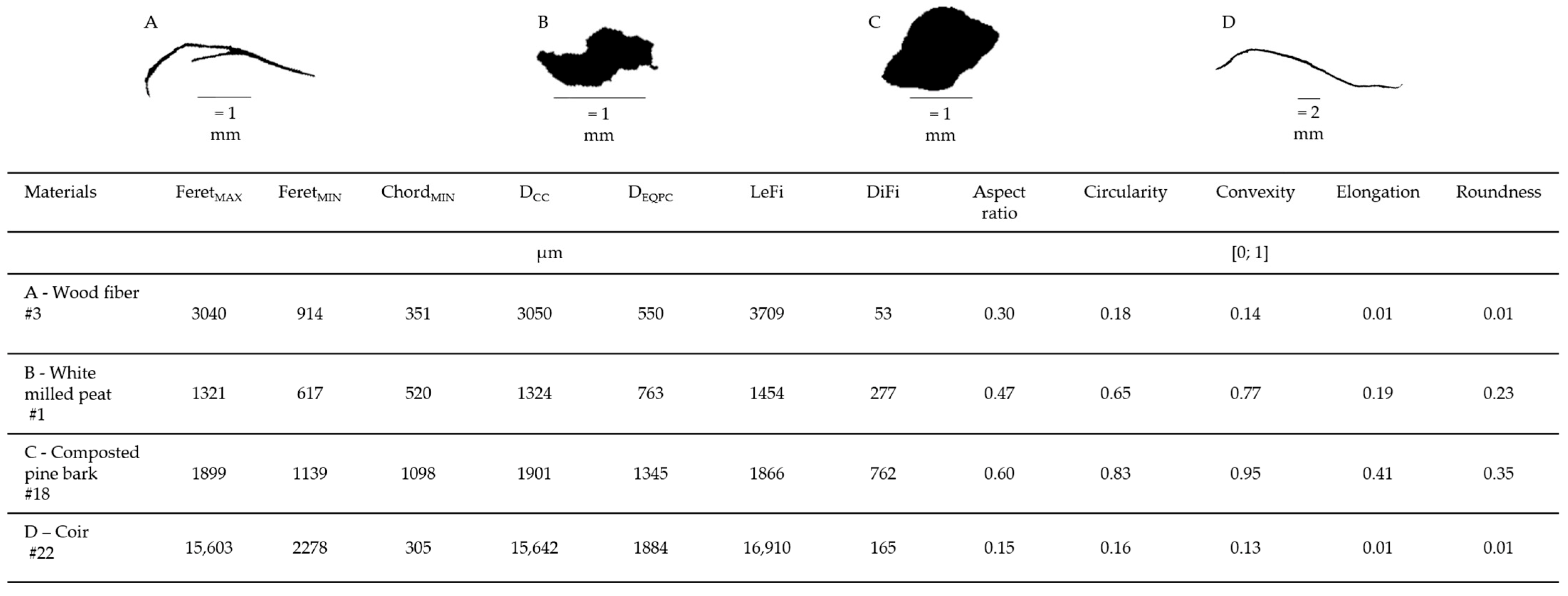

| #ID Number | Materials | Supplier 1 | Origin | Extraction/Process | Bulk Density 2 | Indicated Particle Size Range 3 |
|---|---|---|---|---|---|---|
| g cm−3 | mm | |||||
| #1 | Coir fiber | PTH | Ivory Coast | Grounded, sieved | 0.07 | 5–25 |
| #2 | Wood fiber (fine) | KD | Germany | Defibrated | 0.08 | 0–2 |
| #3 | Wood fiber (medium) | KD | Germany | Defibrated | 0.09 | 2–4 |
| #4 | Wood fiber (medium) | FLO | Germany | Defibrated | 0.09 | N/A |
| #5 | White peat (fine), H5 4 | PTH | Ireland | Milled, screened | 0.10 | 0–5 |
| #6 | White peat (fine), H1–H3 | PTH | Canada | Milled, screened | 0.11 | N/A |
| #7 | White peat (fine), H2–H6 | KD | Lithuania | Milled | 0.10 | 0–7 |
| #8 | White peat (fine), H2–H5 | FLO | Latvia | Milled | 0.10 | 0–5 |
| #9 | White peat (fine), H2–H5 | FLO | Germany | Sod | 0.08 | 0–7 |
| #10 | White peat (fine), H2–H5 | KD | Lithuania | Sod | 0.11 | 0–7 |
| #11 | White peat (medium), H2–H6 | KD | Lithuania | Milled | 0.11 | 0–25 |
| #12 | White peat (medium), H2–H5 | FLO | Latvia | Milled | 0.10 | 5–20 |
| #13 | Black peat, H6–H8 | KD | Lithuania | Frozen, milled, sieved | 0.17 | 0–5 |
| #14 | Black peat, H5–H8 | FLO | Germany | Frozen | 0.18 | 0–7 |
| #15 | Sedge peat | ETF | France | Excavated | 0.24 | 0–10 |
| #16 | Coir pith | PTH | Sri Lanka | Grounded, sieved | 0.08 | 0–5 |
| #17 | Fresh pine bark (fine) | PTH | France | Screened | 0.22 | 0–5 |
| #18 | Composted pine bark (fine) | PTH | France | Screened | 0.25 | 0–5 |
| #19 | Green waste compost | KD | Germany | 0.50 | 0–5 | |
| #20 | Perlite (fine) | KD | Germany | 0.06 | 0.6–2.5 | |
| #21 | Coir (medium) | PTH | Ivory Coast | Grounded | 0.08 | 0–25 |
| #22 | Coir (medium) | ETB | Sri Lanka | N/A | 0.05 | 5–25 |
| Shape Descriptor | Classes |
|---|---|
| Aspect ratio | 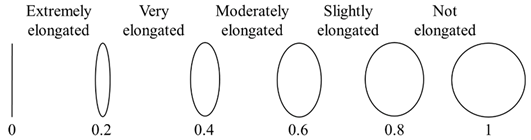 |
| Elongation |  |
| Circularity | 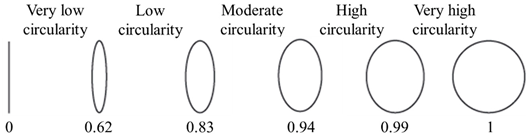 |
| Roundness | 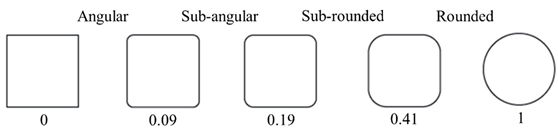 |
| Convexity | 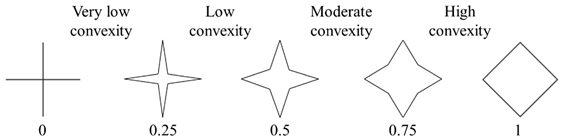 |
| Aspect Ratio | Circularity | Roundness | Convexity | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Extre-mely | Very | Mode-rately | Slightly | Not | Very Low | Low | ModE-Rate | High | Very High | Angular | Sub-Angular | Sub-Rounded | Rounded | Very Low | Low | ModE-Rate | High | |
| #ID | Elongated | |||||||||||||||||
| #1 | 24 2 | 17 | 23 | 29 | 8 | 44 | 32 | 22 | 2 | 0 | 48 | 21 | 22 | 9 | 9 | 14 | 15 | 62 |
| #2 | 12 | 34 | 30 | 21 | 3 | 59 | 26 | 13 | 2 | 0 | 61 | 28 | 9 | 2 | 3 | 18 | 36 | 44 |
| #3 | 15 | 32 | 28 | 22 | 4 | 58 | 20 | 19 | 4 | 0 | 66 | 26 | 7 | 2 | 5 | 19 | 32 | 44 |
| #4 | 14 | 37 | 28 | 19 | 4 | 60 | 22 | 15 | 3 | 0 | 66 | 25 | 7 | 2 | 4 | 17 | 33 | 46 |
| #5 | 2 | 22 | 37 | 33 | 7 | 19 | 52 | 26 | 3 | 0 | 26 | 32 | 32 | 9 | 0 | 2 | 16 | 82 |
| #6 | 2 | 20 | 35 | 36 | 7 | 18 | 46 | 33 | 4 | 0 | 36 | 34 | 22 | 8 | 0 | 2 | 16 | 82 |
| #7 | 2 | 18 | 33 | 39 | 8 | 17 | 44 | 36 | 4 | 0 | 36 | 40 | 19 | 6 | 0 | 2 | 16 | 82 |
| #8 | 2 | 19 | 35 | 35 | 8 | 26 | 47 | 24 | 3 | 0 | 31 | 34 | 26 | 9 | 0 | 3 | 21 | 76 |
| #9 | 6 | 26 | 33 | 29 | 6 | 28 | 43 | 27 | 3 | 0 | 44 | 32 | 18 | 6 | 1 | 5 | 19 | 74 |
| #10 | 1 | 15 | 31 | 43 | 10 | 15 | 39 | 41 | 5 | 0 | 35 | 42 | 17 | 6 | 0 | 2 | 15 | 83 |
| #11 | 2 | 18 | 34 | 39 | 8 | 17 | 43 | 35 | 4 | 0 | 35 | 40 | 19 | 6 | 0 | 2 | 16 | 82 |
| #12 | 5 | 19 | 33 | 35 | 9 | 35 | 35 | 25 | 6 | 0 | 35 | 38 | 21 | 5 | 2 | 5 | 24 | 70 |
| #13 | 1 | 12 | 30 | 46 | 11 | 11 | 37 | 46 | 7 | 0 | 29 | 36 | 24 | 11 | 0 | 2 | 11 | 87 |
| #14 | 1 | 10 | 28 | 47 | 14 | 10 | 37 | 48 | 5 | 0 | 22 | 28 | 29 | 21 | 0 | 2 | 9 | 89 |
| #15 | 0 | 3 | 29 | 55 | 12 | 2 | 17 | 67 | 13 | 0 | 17 | 45 | 25 | 13 | 0 | 0 | 4 | 96 |
| #16 | 1 | 4 | 26 | 52 | 16 | 4 | 42 | 51 | 3 | 0 | 16 | 23 | 37 | 25 | 1 | 1 | 3 | 96 |
| #17 | 1 | 12 | 30 | 45 | 12 | 8 | 45 | 43 | 4 | 0 | 18 | 32 | 34 | 16 | 0 | 0 | 5 | 95 |
| #18 | 1 | 9 | 28 | 49 | 14 | 4 | 36 | 53 | 7 | 0 | 17 | 36 | 31 | 16 | 0 | 0 | 3 | 97 |
| #19 | 1 | 6 | 24 | 53 | 16 | 7 | 22 | 61 | 10 | 0 | 23 | 38 | 24 | 16 | 0 | 2 | 5 | 93 |
| #20 | 0 | 2 | 27 | 55 | 16 | 1 | 41 | 52 | 6 | 0 | 6 | 26 | 48 | 20 | 0 | 0 | 3 | 97 |
| #21 | 12 | 8 | 22 | 45 | 13 | 20 | 27 | 50 | 4 | 0 | 40 | 27 | 19 | 14 | 4 | 6 | 8 | 82 |
| #22 | 4 | 8 | 26 | 49 | 13 | 12 | 29 | 53 | 6 | 0 | 30 | 29 | 25 | 16 | 4 | 3 | 5 | 87 |
| Mean | 5.0 | 16.0 | 29.5 | 39.8 | 10.0 | 21.6 | 35.5 | 38.2 | 4.9 | 0.0 | 33.5 | 32.4 | 23.4 | 10.8 | 1.5 | 4.9 | 14.3 | 79.4 |
| SD 1 | 6.4 | 9.9 | 4.1 | 11.0 | 4.0 | 18.5 | 9.9 | 15.4 | 2.6 | 0.0 | 16.1 | 6.5 | 9.7 | 6.5 | 2.4 | 6.1 | 10.1 | 16.8 |
| Elongation | Aspect Ratio | Roundness | Circularity | Convexity | Width | Length | |
|---|---|---|---|---|---|---|---|
| Elongation | 1 | ||||||
| Aspect ratio | 0.95 *** | 1 | |||||
| Roundness | 0.77 *** | 0.88 *** | 1 | ||||
| Circularity | 0.97 *** | 0.97 *** | 0.82 *** | 1 | |||
| Convexity | 0.92 *** | 0.96 *** | 0.86 *** | 0.98 *** | 1 | ||
| Width | −0.56 ** | −0.42 | −0,14 | −0.57 ** | −0.48 * | 1 | |
| Length | −0.60 ** | −0.60 ** | −0.36 | −0.70 *** | −0.70 *** | 0.75 *** | 1 |
| Cluster | #ID 1 Material | Aspect Ratio | Circularity | Convexity | Roundness | Width (mm) | Length (mm) |
|---|---|---|---|---|---|---|---|
| Mean [Relative Span] | |||||||
| 1 | #1 Coir fiber | 0.46 2 [1.3] | 0.60 [0.9] | 0.71 [0.8] | 0.16 [3.8] | 0.62 3 [3.8] | 3.85 [5.2] |
| #2 Wood fiber (fine) | 0.43 [1.3] | 0.57 [1.1] | 0.68 [0.7] | 0.10 [2.4] | 0.48 [5.8] | 1.71 [4.3] | |
| #3 Wood fiber (medium) | 0.44 [1.3] | 0.58 [1.1] | 0.67 [0.9] | 0.09 [2.8] | 0.47 [9.2] | 1.86 [5.6] | |
| #4 Wood fiber (medium) | 0.42 [1.3] | 0.57 [1.1] | 0.68 [0.7] | 0.09 [2.7] | 0.82 [10.3] | 2.96 [7.3] | |
| Cluster 1 value range | 0.42–0.46 [1.3] | 0.57–0.60 [0.9–1.1] | 0.67–0.71 [0.7–0.9] | 0.09–0.16 [2.4–3.8] | 0.47–0.82 [3.8–10.3] | 1.71–3.85 [4.3–7.3] | |
| 2 | #5 White peat, H5 | 0.54 [0.8] | 0.74 [0.5] | 0.83 [0.3] | 0.20 [2.2] | 0.35 [2.7] | 0.81 [2.5] |
| #6 White peat, H1–H3 | 0.55 [0.8] | 0.76 [0.5] | 0.83 [0.3] | 0.17 [2.7] | 0.23 [2.6] | 0.60 [3.0] | |
| #7 White peat (fine), H2–H6 | 0.57 [0.8] | 0.76 [0.5] | 0.82 [0.3] | 0.15 [2.3] | 0.20 [2.4] | 0.52 [3.1] | |
| #8 White peat (fine), H2–H5 | 0.55 [0.9] | 0.71 [0.5] | 0.81 [0.3] | 0.18 [2.5] | 0.48 [4.2] | 1.21 [4.9] | |
| #9 White peat (fine), H2–H5 | 0.50 [1.0] | 0.71 [0.6] | 0.79 [0.4] | 0.15 [3.0] | 0.25 [2.9] | 0.82 [4.2] | |
| #10 White peat (fine), H2–H5 | 0.59 [0.8] | 0.78 [0.4] | 0.83 [0.3] | 0.15 [2.2] | 0.20 [2.7] | 0.49 [3.6] | |
| #11 White peat (medium), H2–H6 | 0.56 [0.8] | 0.76 [0.5] | 0.82 [0.3] | 0.15 [2.3] | 0.23 [2.7] | 0.56 [3.4] | |
| #12 White peat (medium), H2–H5 | 0.55 [0.9] | 0.69 [0.7] | 0.78 [0.4] | 0.16 [2.2] | 0.68 [6.4] | 1.89 [7.1] | |
| Cluster 2 value range | 0.50–0.59 [0.8–1.0] | 0.69–0.78 [0.4–0.7] | 0.78–0.83 [0.3–0.4] | 0.15–0.20 [2.2–3.0] | 0.20–0.68 [2.6–6.4] | 0.49–1.89 [2.5–7.1] | |
| 3 | #13 Black peat, H6–H8 | 0.61 [0.7] | 0.80 [0.4] | 0.85 [0.2] | 0.19 [2.8] | 0.23 [3.6] | 0.49 [4.0] |
| #14 Black peat, H5–H8 | 0.62 [0.7] | 0.80 [0.4] | 0.86 [0.2] | 0.25 [2.7] | 0.33 [3.6] | 0.64 [3.9] | |
| #15 Sedge peat | 0.64 [0.5] | 0.87 [0.2] | 0.90 [0.2] | 0.21 [2.5] | 0.12 [4.8] | 0.23 [5.3] | |
| #16 Coir pith | 0.65 [0.6] | 0.82 [0.2] | 0.88 [0.1] | 0.29 [2.0] | 0.41 [3.2] | 0.86 [3.9] | |
| #17 Fresh pine bark (fine) | 0.61 [0.7] | 0.80 [0.3] | 0.88 [0.2] | 0.24 [2.3] | 0.47 [4.3] | 1.00 [5.5] | |
| #18 Composted pine bark (fine) | 0.63 [0.6] | 0.83 [0.3] | 0.88 [0.2] | 0.24 [2.4] | 0.33 [4.2] | 0.70 [5.6] | |
| #19 Green waste compost | 0.65 [0.6] | 0.84 [0.3] | 0.87 [0.2] | 0.22 [3.1] | 0.28 [4.3] | 0.79 [5.9] | |
| #20 Perlite (fine) | 0.67 [0.5] | 0.84 [0.2] | 0.91 [0.2] | 0.29 [1.6] | 0.63 [4.5] | 1.00 [4.6] | |
| Cluster 3 value range | 0.61–0.67 [0.5–0.7] | 0.80–0.87 [0.2–0.4] | 0.85–0.91 [0.1–0.2] | 0.19–0.29 [1.6–3.1] | 0.12–0.63 [3.2–4.8] | 0.23–1.00 [3.9–5.9] | |
| 4 | #21 Coir (medium) | 0.58 [1.0] | 0.75 [0.7] | 0.80 [0.5] | 0.19 [3.9] | 0.28 [2.6] | 1.81 [19.6] |
| #22 Coir (medium) | 0.61 [0.7] | 0.79 [0.5] | 0.83 [0.3] | 0.22 [3.3] | 0.43 [4.5] | 2.47 [27.1] | |
| Cluster 4 value range | 0.58–0.61 [0.7–1.0] | 0.75–0.79 [0.5–0.7] | 0.80–0.83 [0.3–0.5] | 0.19–0.22 [3.3–3.9] | 0.28–0.43 [2.6–4.5] | 1.81–2.47 [19.6–27.1] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durand, S.; Jackson, B.E.; Fonteno, W.C.; Michel, J.-C. Quantitative Description and Classification of Growing Media Particle Morphology through Dynamic Image Analysis. Agriculture 2023, 13, 396. https://doi.org/10.3390/agriculture13020396
Durand S, Jackson BE, Fonteno WC, Michel J-C. Quantitative Description and Classification of Growing Media Particle Morphology through Dynamic Image Analysis. Agriculture. 2023; 13(2):396. https://doi.org/10.3390/agriculture13020396
Chicago/Turabian StyleDurand, Stan, Brian E. Jackson, William C. Fonteno, and Jean-Charles Michel. 2023. "Quantitative Description and Classification of Growing Media Particle Morphology through Dynamic Image Analysis" Agriculture 13, no. 2: 396. https://doi.org/10.3390/agriculture13020396
APA StyleDurand, S., Jackson, B. E., Fonteno, W. C., & Michel, J.-C. (2023). Quantitative Description and Classification of Growing Media Particle Morphology through Dynamic Image Analysis. Agriculture, 13(2), 396. https://doi.org/10.3390/agriculture13020396








