Imaging Sensor-Based High-Throughput Measurement of Biomass Using Machine Learning Models in Rice
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Set Up and Growth Condition
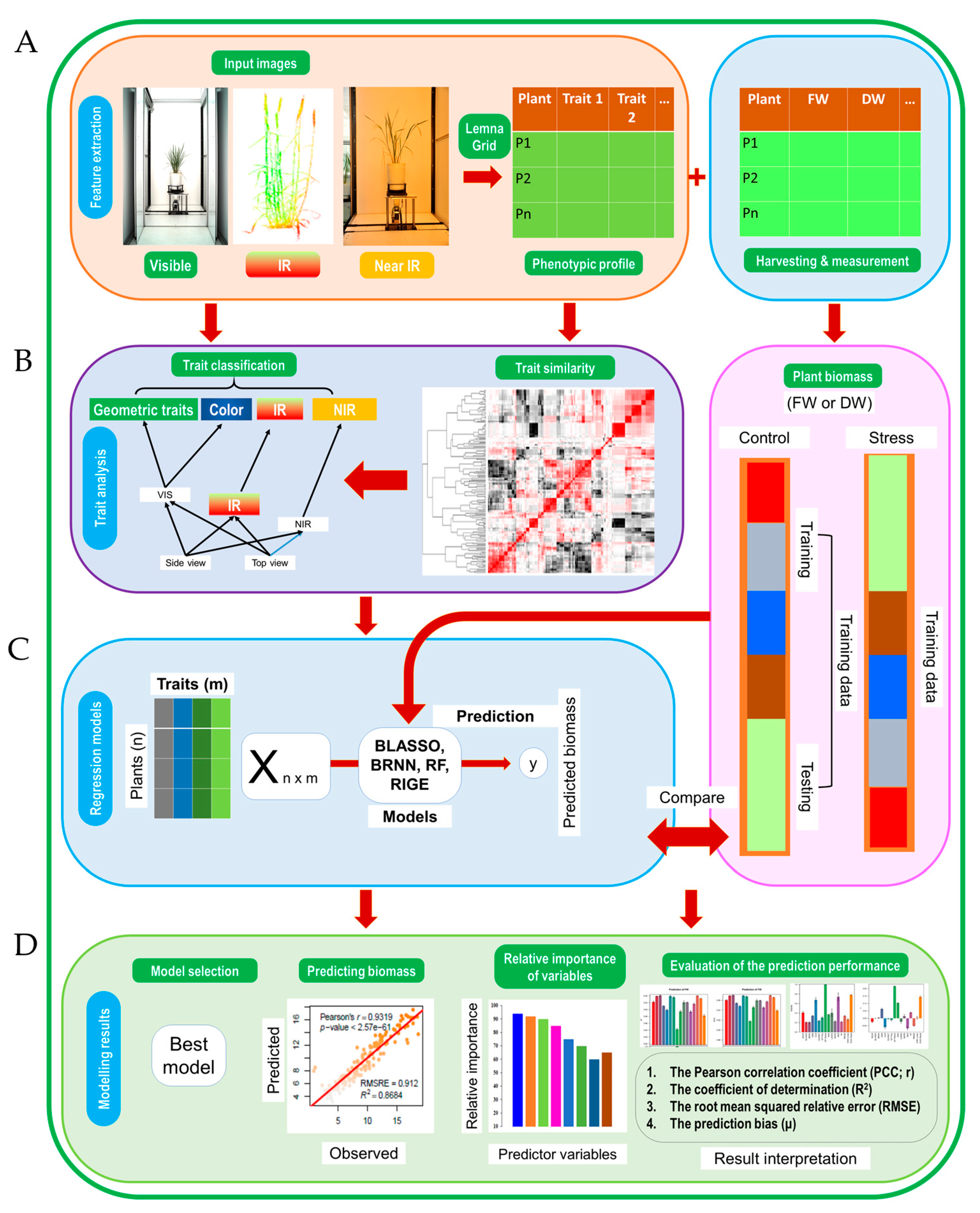
2.2. Image Data Acquisition, Processing and Analysis
2.3. Image Trait Feature Extraction
2.4. Machine Learning Modelling for Predicting Biomass
2.5. Machine Learning Algorithms
2.6. Evaluation of the Prediction Model
2.7. Data Analysis
3. Results
3.1. Image-Based Feature Extraction and Trait Selection
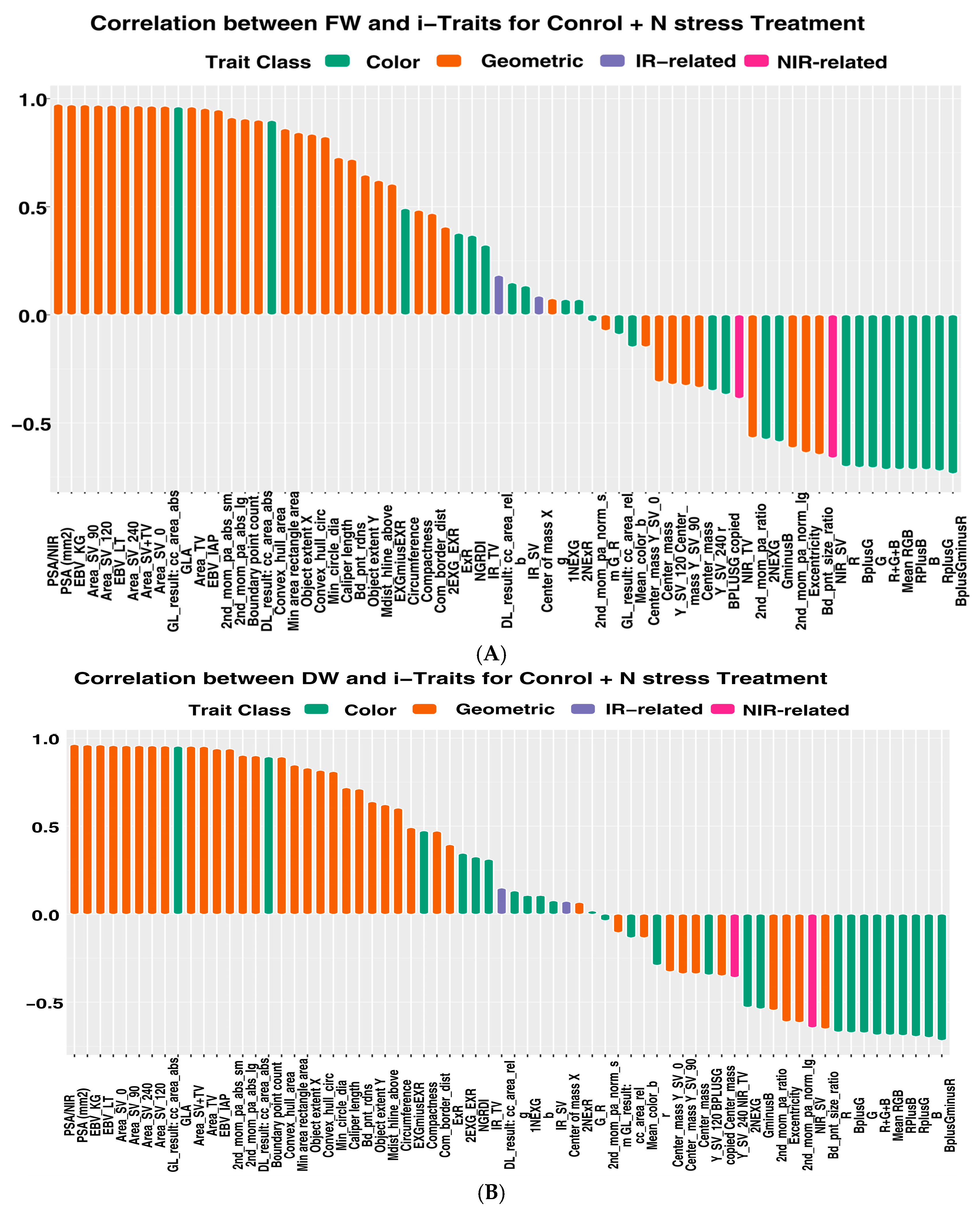
3.2. Trait Relationship among Each Other and Superior Trait for Biomass Prediction
3.3. Machine Learning Models for Prediction of Above-Ground Biomass
3.4. Evaluation of Multivariate Models Using Performance Indicators
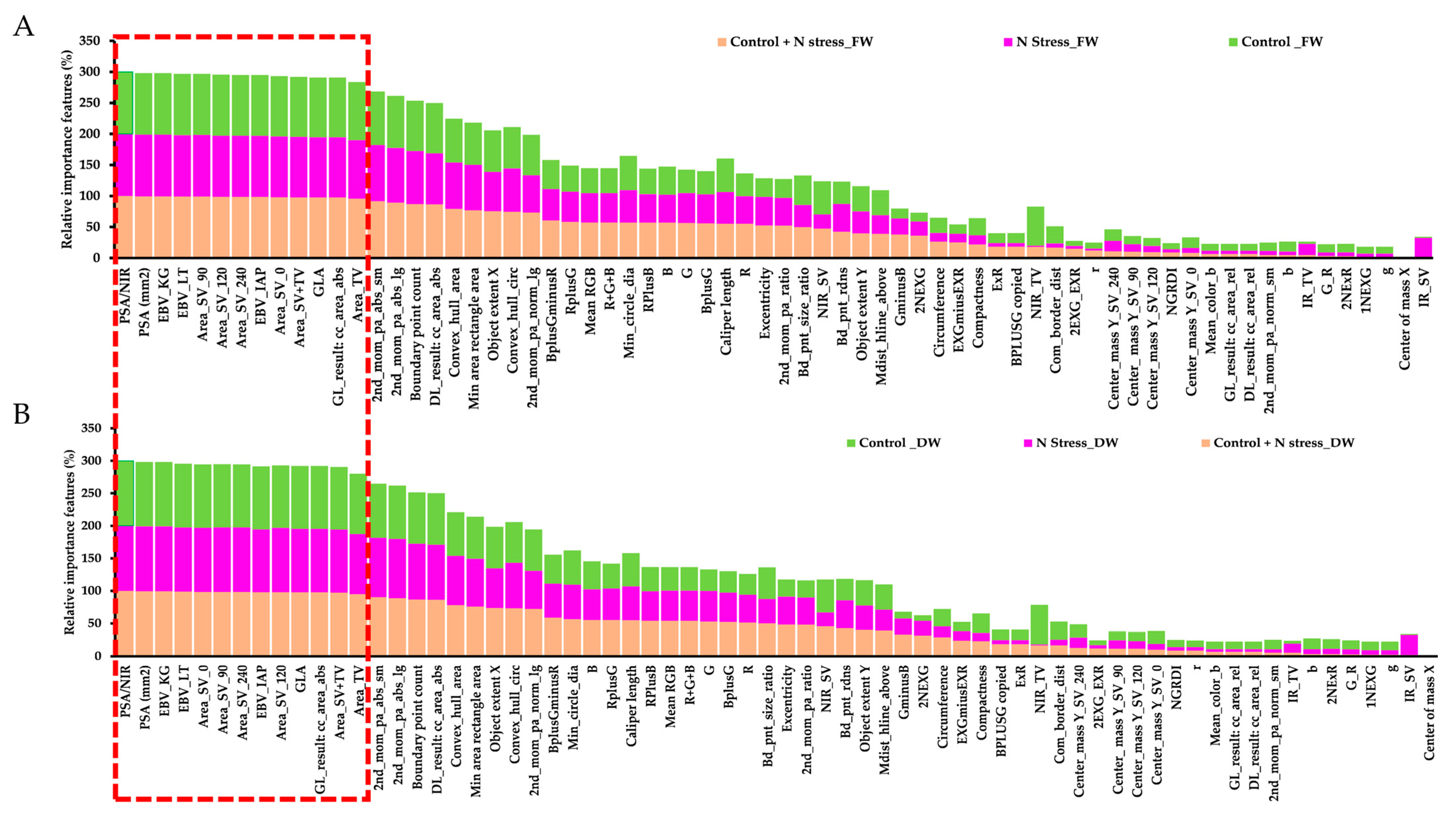
3.5. Relative Significance of Various Image-Based Features in Predicting Plant Biomass
4. Discussion
High-Throughput Phenotypic Traits Precisely Estimate Biomass
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Y.; Shen, J.; Qi, Y. Estimation of Rice Biomass at Different Growth Stages by Using Fractal Dimension in Image Processing. Appl. Sci. 2021, 11, 7151. [Google Scholar] [CrossRef]
- Toda, Y.; Wakatsuki, H.; Aoike, T.; Kajiya-Kanegae, H.; Yamasaki, M.; Yoshioka, T.; Ebana, K.; Hayashi, T.; Nakagawa, H.; Hasegawa, T. Predicting Biomass of Rice with Intermediate Traits: Modeling Method Combining Crop Growth Models and Genomic Prediction Models. PLoS ONE 2020, 15, e0233951. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Peng, S.; Huang, J.; Cui, K.; Nie, L.; Wang, F. Genetic Improvements in Rice Yield and Concomitant Increases in Radiation-and Nitrogen-Use Efficiency in Middle Reaches of Yangtze River. Sci. Rep. 2016, 6, 21049. [Google Scholar] [CrossRef] [Green Version]
- Matsubara, K.; Yamamoto, E.; Kobayashi, N.; Ishii, T.; Tanaka, J.; Tsunematsu, H.; Yoshinaga, S.; Matsumura, O.; Yonemaru, J.; Mizobuchi, R. Improvement of Rice Biomass Yield through QTL-Based Selection. PLoS ONE 2016, 11, e0151830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corales, M.; Nguyen, N.T.A.; Abiko, T.; Mochizuki, T. Mapping Quantitative Trait Loci for Water Uptake of Rice under Aerobic Conditions. Plant Prod. Sci. 2020, 23, 436–451. [Google Scholar] [CrossRef]
- Rakotoson, T.; Dusserre, J.; Letourmy, P.; Frouin, J.; Ratsimiala, I.R.; Rakotoarisoa, N.V.; Vom Brocke, K.; Ramanantsoanirina, A.; Ahmadi, N.; Raboin, L.-M. Genome-Wide Association Study of Nitrogen Use Efficiency and Agronomic Traits in Upland Rice. Rice Sci. 2021, 28, 379–390. [Google Scholar] [CrossRef]
- Li, J.; Xin, W.; Wang, W.; Zhao, S.; Xu, L.; Jiang, X.; Duan, Y.; Zheng, H.; Yang, L.; Liu, H. Mapping of Candidate Genes in Response to Low Nitrogen in Rice Seedlings. Rice 2022, 15, 51. [Google Scholar] [CrossRef]
- Bhandari, A.; Sandhu, N.; Bartholome, J.; Cao-Hamadoun, T.-V.; Ahmadi, N.; Kumari, N.; Kumar, A. Genome-Wide Association Study for Yield and Yield Related Traits under Reproductive Stage Drought in a Diverse Indica-Aus Rice Panel. Rice 2020, 13, 53. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Wang, X.; Zhao, Y.; Khan, N.U.; Zhao, Z.; Zhang, Y.; Wen, X.; Tang, F.; Wang, F.; Li, Z. Genetic Basis and Identification of Candidate Genes for Salt Tolerance in Rice by GWAS. Sci. Rep. 2020, 10, 9958. [Google Scholar] [CrossRef]
- Klukas, C.; Chen, D.; Pape, J.-M. Integrated Analysis Platform: An Open-Source Information System for High-Throughput Plant Phenotyping. Plant Physiol. 2014, 165, 506–518. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Neumann, K.; Friedel, S.; Kilian, B.; Chen, M.; Altmann, T.; Klukas, C. Dissecting the Phenotypic Components of Crop Plant Growth and Drought Responses Based on High-Throughput Image Analysis. Plant Cell 2014, 26, 4636–4655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahaman, M.M.; Chen, D.; Gillani, Z.; Klukas, C.; Chen, M. Advanced Phenotyping and Phenotype Data Analysis for the Study of Plant Growth and Development. Front. Plant Sci. 2015, 6, 619. [Google Scholar] [CrossRef] [Green Version]
- Fahlgren, N.; Feldman, M.; Gehan, M.A.; Wilson, M.S.; Shyu, C.; Bryant, D.W.; Hill, S.T.; McEntee, C.J.; Warnasooriya, S.N.; Kumar, I.; et al. A Versatile Phenotyping System and Analytics Platform Reveals Diverse Temporal Responses to Water Availability in Setaria. Mol. Plant 2015, 8, 1520–1535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Golzarian, M.R.; Frick, R.A.; Rajendran, K.; Berger, B.; Roy, S.; Tester, M.; Lun, D.S. Accurate Inference of Shoot Biomass from High-Throughput Images of Cereal Plants. Plant Methods 2011, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Arvidsson, S.; Pérez-Rodríguez, P.; Mueller-Roeber, B. A Growth Phenotyping Pipeline for Arabidopsis Thaliana Integrating Image Analysis and Rosette Area Modeling for Robust Quantification of Genotype Effects. New Phytol. 2011, 191, 895–907. [Google Scholar] [CrossRef] [PubMed]
- Hairmansis, A.; Berger, B.; Tester, M.; Roy, S.J. Image-Based Phenotyping for Non-Destructive Screening of Different Salinity Tolerance Traits in Rice. Rice 2014, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Campbell, M.T.; Knecht, A.C.; Berger, B.; Brien, C.J.; Wang, D.; Walia, H. Integrating Image-Based Phenomics and Association Analysis to Dissect the Genetic Architecture of Temporal Salinity Responses in Rice. Plant Physiol. 2015, 168, 1476–1489. [Google Scholar] [CrossRef] [Green Version]
- Parent, B.; Shahinnia, F.; Maphosa, L.; Berger, B.; Rabie, H.; Chalmers, K.; Kovalchuk, A.; Langridge, P.; Fleury, D. Combining Field Performance with Controlled Environment Plant Imaging to Identify the Genetic Control of Growth and Transpiration Underlying Yield Response to Water-Deficit Stress in Wheat. J. Exp. Bot. 2015, 66, 5481–5492. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Shi, R.; Pape, J.-M.; Neumann, K.; Arend, D.; Graner, A.; Chen, M.; Klukas, C. Predicting Plant Biomass Accumulation from Image-Derived Parameters. GigaScience 2018, 7, giy001. [Google Scholar] [CrossRef] [Green Version]
- Neilson, E.H.; Edwards, A.M.; Blomstedt, C.K.; Berger, B.; Møller, B.L.; Gleadow, R.M. Utilization of a High-Throughput Shoot Imaging System to Examine the Dynamic Phenotypic Responses of a C4 Cereal Crop Plant to Nitrogen and Water Deficiency over Time. J. Exp. Bot. 2015, 66, 1817–1832. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, N.; Huang, C.; Fang, W.; Yang, W.; Chen, G.; Xiong, L.; Liu, Q. A Hyperspectral Imaging System for an Accurate Prediction of the Above-Ground Biomass of Individual Rice Plants. Rev. Sci. Instrum. 2013, 84, 95107. [Google Scholar] [CrossRef]
- Muraya, M.M.; Chu, J.; Zhao, Y.; Junker, A.; Klukas, C.; Reif, J.C.; Altmann, T. Genetic Variation of Growth Dynamics in Maize (Zea mays L.) Revealed through Automated Non-Invasive Phenotyping. Plant J. 2017, 89, 366–380. [Google Scholar] [CrossRef] [Green Version]
- Neumann, K.; Zhao, Y.; Chu, J.; Keilwagen, J.; Reif, J.C.; Kilian, B.; Graner, A. Genetic Architecture and Temporal Patterns of Biomass Accumulation in Spring Barley Revealed by Image Analysis. BMC Plant Biol. 2017, 17, 137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, W.; Guo, Z.; Huang, C.; Duan, L.; Chen, G.; Jiang, N.; Fang, W.; Feng, H.; Xie, W.; Lian, X.; et al. Combining high-throughput phenotyping and genome-wide association studies to reveal natural genetic variation in rice. Nat. Commun. 2014, 5, 5087. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Huang, C.; Wu, D.; Qiao, F.; Li, W.; Duan, L.; Wang, K.; Xiao, Y.; Chen, G.; Liu, Q.; et al. High-Throughput Phenotyping and QTL Mapping Reveals the Genetic Architecture of Maize Plant Growth. Plant Physiol. 2017, 173, 1554–1564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Busemeyer, L.; Ruckelshausen, A.; Möller, K.; Melchinger, A.E.; Alheit, K.V.; Maurer, H.P.; Hahn, V.; Weissmann, E.A.; Reif, J.C.; Würschum, T. Precision phenotyping of biomass accumulation in triticale reveals temporal genetic patterns of regulation. Sci. Rep. 2013, 3, 2442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, Q.; Miao, Y.; Wang, H.; Huang, S.; Cheng, S.; Khosla, R.; Jiang, R. Non-Destructive Estimation of Rice Plant Nitrogen Status with Crop Circle Multispectral Active Canopy Sensor. Field Crops Res. 2013, 154, 133–144. [Google Scholar] [CrossRef]
- Erdle, K.; Mistele, B.; Schmidhalter, U. Comparison of Active and Passive Spectral Sensors in Discriminating Biomass Parameters and Nitrogen Status in Wheat Cultivars. Field Crops Res. 2011, 124, 74–84. [Google Scholar] [CrossRef]
- Fernandez, M.G.S.; Bao, Y.; Tang, L.; Schnable, P.S. High-Throughput Phenotyping for Biomass Crops. Plant Physiol. 2017, 10, 17-00707. [Google Scholar]
- Misra, T.; Arora, A.; Marwaha, S.; Ray, M.; Raju, D.; Kumar, S.; Goel, S.; Sahoo, R.N.; Chinnusamy, V. Artificial neural network for estimating leaf fresh weight of rice plant through visual-nir imaging. Indian J. Agric. Sci. 2019, 89, 146–150. [Google Scholar] [CrossRef]
- Vishal, M.K.; Saluja, R.; Aggrawal, D.; Banerjee, B.; Raju, D.; Kumar, S.; Chinnusamy, V.; Sahoo, R.N.; Adinarayana, J. Leaf Count Aided Novel Framework for Rice (Oryza sativa L.) Genotypes Discrimination in Phenomics: Leveraging Computer Vision and Deep Learning Applications. Plants 2022, 11, 2663. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Fu, L.-Y.; Hu, D.; Klukas, C.; Chen, M.; Kaufmann, K. The HTPmod Shiny Application Enables Modeling and Visualization of Large-Scale Biological Data. Commun. Biol. 2018, 1, 89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, W.; Ratkowsky, D.A.; Hui, C.; Wang, P.; Su, J.; Shi, P. Leaf Fresh Weight versus Dry Weight: Which Is Better for Describing the Scaling Relationship between Leaf Biomass and Leaf Area for Broad-Leaved Plants? Forests 2019, 10, 256. [Google Scholar] [CrossRef] [Green Version]
- Koehrsen, W. Introduction to Bayesian Linear Regression—Towards Data Science. Medium. 2018. Available online: https://towardsdatascience.com/introduction-to-bayesian-linear-regression-e66e60791ea7 (accessed on 3 February 2023).
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.-S. A Weakly Informative Default Prior Distribution for Logistic and Other Regression Models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]
- Vasquez, M.M.; Hu, C.; Roe, D.J.; Chen, Z.; Halonen, M.; Guerra, S. Least Absolute Shrinkage and Selection Operator Type Methods for the Identification of Serum Biomarkers of Overweight and Obesity: Simulation and Application. BMC Med. Res. Methodol. 2016, 16, 154. [Google Scholar] [CrossRef] [Green Version]
- Park, T.; Casella, G. The Bayesian Lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Burden, F.; Winkler, D. Bayesian Regularization of Neural Networks. In Artificial Neural Networks. Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2008; Volume 458. [Google Scholar] [CrossRef]
- Bai, Z.; Fahey, G.; Golub, G. Some Large-Scale Matrix Computation Problems. J. Comput. Appl. Math. 1996, 74, 71–89. [Google Scholar] [CrossRef] [Green Version]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Gianola, D.; Okut, H.; Weigel, K.A.; Rosa, G.J.M. Predicting Complex Quantitative Traits with Bayesian Neural Networks: A Case Study with Jersey Cows and Wheat. BMC Genet. 2011, 12, 87. [Google Scholar] [CrossRef] [Green Version]
- Elsinghorst, D.S. Machine Learning Basics—Gradient Boosting & XGBoost. Shirin’s PlaygRound. 2018. Available online: https://shirinsplayground.netlify.app/2018/11/ml_basics_gbm/ (accessed on 3 February 2023).
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Generalized Linear Model. Available online: https://arxiv.org/pdf/2102.05497.pdf (accessed on 3 February 2023).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Tamimi, N.; Brien, C.; Oakey, H.; Berger, B.; Saade, S.; Ho, Y.S.; Schmöckel, S.M.; Tester, M.; Negrão, S. Salinity Tolerance Loci Revealed in Rice Using High-Throughput Non-Invasive Phenotyping. Nat. Commun. 2016, 7, 13342. [Google Scholar] [CrossRef] [Green Version]
- Trevor, H.; Qian, J.; Tay, K. An Introduction to ‘glmnet’. Available online: https://glmnet.stanford.edu/articles/glmnet.html (accessed on 3 February 2023).
- Tibshirani, R.; Bien, J.; Friedman, J.; Hastie, T.; Simon, N.; Taylor, J.; Tibshirani, R.J. Strong Rules for Discarding Predictors in Lasso-type Problems. J. R. Stat. Soc. Ser. B 2012, 74, 245–266. [Google Scholar] [CrossRef] [Green Version]
- Bach, F.R.; Jordan, M.I. Predictive Low-Rank Decomposition for Kernel Methods. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 33–40. [Google Scholar]
- Wu, T.-F.; Lin, C.-J.; Weng, R. Probability Estimates for Multi-Class Classification by Pairwise Coupling. J. Mach. Learn. Res. 2003, 5, 975–1005. [Google Scholar]
- Zhiting, H. Gaussian Process and Deep Kernel Learning. In Probabilistic Graphical Models; Carnegie Mellon University: Pittsburgh, PA, USA, 2017; pp. 1–8. [Google Scholar]
- Lee, S.; Wang, C. Probabilistic Graphical Models. 2017. Available online: https://www.ism.ac.jp/events/2017/meeting0222_24.html (accessed on 3 February 2023).
- IBM. What Is the K-Nearest Neighbors Algorithm? IBM: Armonk, NY, USA, 2023. [Google Scholar]
- Hechenbichler, K.; Schliep, K. Weighted K-Nearest-Neighbor Techniques and Ordinal Classification. 2004. Available online: https://epub.ub.uni-muenchen.de/1769/1/paper_399.pdf (accessed on 3 February 2023).
- Columbia University Least Absolute Shrinkage and Selection Operator (LASSO). Available online: https://www.publichealth.columbia.edu/research/population-health-methods/least-absolute-shrinkage-and-selection-operator-lasso (accessed on 3 February 2023).
- Januaviani, T.M.A.; Bon, A.T. The LASSO (Least Absolute Shrinkage and Selection Operator) Method to Predict Indonesian Foreign Exchange Deposit Data. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bangkok, Thailand, 5–7 March 2019. [Google Scholar]
- Dodig, D.; Božinović, S.; Nikolić, A.; Zorić, M.; Vančetović, J.; Ignjatović-Micić, D.; Delić, N.; Weigelt-Fischer, K.; Junker, A.; Altmann, T. Image-Derived Traits Related to Mid-Season Growth Performance of Maize under Nitrogen and Water Stress. Front. Plant Sci. 2019, 10, 814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brownlee, J. Multivariate Adaptive Regression Splines (MARS) in Python—MachineLearningMastery.Com. 2021. Available online: https://machinelearningmastery.com/multivariate-adaptive-regression-splines-mars-in-python/ (accessed on 3 February 2023).
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Liang, Z.; Pandey, P.; Stoerger, V.; Xu, Y.; Qiu, Y.; Ge, Y.; Schnable, J.C. Conventional and Hyperspectral Time-Series Imaging of Maize Lines Widely Used in Field Trials. Gigascience 2018, 7, gix117. [Google Scholar] [CrossRef] [Green Version]
- Voxco. Multivariate Regression: Definition, Example and Steps; Voxco: Surry Hills, Australia, 2023. [Google Scholar]
- RColorBrewer, S.; Liaw, M.A. Package ‘Randomforest’; University of California: Berkeley, CA, USA, 2018. [Google Scholar]
- Liu, Y.; Wang, Y.; Zhang, J. New Machine Learning Algorithm: Random Forest BT. In BT—Information Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 246–252. [Google Scholar]
- Saunders, C.; Gammerman, A.; Vovk, V. Ridge Regression Learning Algorithm in Dual Variables. In Proceedings of the Proceedings of the Fifteenth International Conference on Machine Learning (ICML 1998), Madison, WI, USA, 24–27 July 1998. [Google Scholar]
- Anish Singh, W. Radial Kernel Support Vector Classifier. Available online: https://datascienceplus.com/radial-kernel-support-vector-classifier/ (accessed on 3 February 2023).
- Shi, Y.; Li, P.; Yuan, H.; Miao, J.; Niu, L. Fast Kernel Extreme Learning Machine for Ordinal Regression. Knowledge-Based Syst. 2019, 177, 44–54. [Google Scholar] [CrossRef]
- Yusof, K.W.; Babangida, N.M.; Mustafa, M.R.; Isa, M.H. Linear Kernel Support Vector Machines for Modeling Pore-Water Pressure Responses. J. Eng. Sci. Technol. 2017, 12, 2202–2212. [Google Scholar]
- Peizhuang, W. Pattern Recognition with Fuzzy Objective Function Algorithms (James C. Bezdek). Siam Rev. 1983, 25, 442. [Google Scholar] [CrossRef]


| Fresh Weight (Control+ N Stress) | Dry Weight (Control+ N Stress) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simple Linear Regression Model | Models * | ρ2 | R2 | PCC | RMSE | µ | ρ2 | R2 | PCC | RMSE | µ |
| SLRM_Area_TV | 0.90 | 0.91 | 0.95 | 6.27 | 0.06 | 0.89 | 0.90 | 0.95 | 1.39 | 0.08 | |
| SLRM_Area_SV | 0.86 | 0.93 | 0.97 | 5.50 | −0.48 | 0.83 | 0.94 | 0.97 | 1.10 | −0.01 | |
| SLRM_PSAhc | 0.90 | 0.95 | 0.97 | 4.95 | −0.20 | 0.87 | 0.95 | 0.97 | 1.04 | 0.03 | |
| SLRM_EBVIAP | 0.90 | 0.90 | 0.95 | 6.42 | −0.38 | 0.88 | 0.90 | 0.95 | 1.33 | −0.00 | |
| SLRM_EBVLT | 0.91 | 0.93 | 0.98 | 5.26 | −0.17 | 0.89 | 0.93 | 0.97 | 1.11 | 0.04 | |
| SLRM_EBVKG | 0.91 | 0.94 | 0.97 | 4.95 | −0.20 | 0.90 | 0.94 | 0.97 | 1.04 | 0.03 | |
| SLRM_GLA | 0.89 | 0.92 | 0.96 | 5.82 | −0.44 | 0.89 | 0.93 | 0.97 | 1.15 | −0.02 | |
| SLRM_PSA:NIR | 0.92 | 0.95 | 0.98 | 4.73 | −0.04 | 0.90 | 0.95 | 0.97 | 1.01 | 0.06 | |
| Multivariate Machine Learning Model | BRNN | 0.95 | 0.96 | 0.98 | 0.20 | 0.02 | 0.92 | 0.95 | 0.97 | 0.21 | 0.02 |
| BLASSO | 0.94 | 0.96 | 0.98 | 0.22 | 0.01 | 0.92 | 0.95 | 0.97 | 0.23 | 0.01 | |
| GP−Poly | 0.95 | 0.96 | 0.98 | 0.23 | 0.02 | 0.92 | 0.95 | 0.97 | 0.24 | 0.02 | |
| GLMNET | 0.94 | 0.96 | 0.98 | 0.23 | 0.01 | 0.92 | 0.94 | 0.97 | 0.25 | 0.01 | |
| RIDGE | 0.94 | 0.96 | 0.98 | 0.29 | 0.01 | 0.92 | 0.94 | 0.97 | 0.25 | 0.02 | |
| SVM−Linear | 0.94 | 0.96 | 0.98 | 0.25 | 0.03 | 0.92 | 0.94 | 0.97 | 0.30 | 0.01 | |
| MARS | 0.94 | 0.96 | 0.98 | 0.21 | 0.03 | 0.90 | 0.94 | 0.97 | 0.33 | 0.00 | |
| BGLM | 0.94 | 0.96 | 0.98 | 0.33 | 0.00 | 0.92 | 0.94 | 0.97 | 0.31 | 0.02 | |
| LASSO | 0.94 | 0.95 | 0.98 | 0.36 | 0.01 | 0.68 | 0.94 | 0.97 | 0.32 | 0.01 | |
| MLR | 0.93 | 0.95 | 0.98 | 0.38 | 0.00 | 0.91 | 0.94 | 0.97 | 0.34 | 0.01 | |
| GLM | 0.93 | 0.95 | 0.98 | 0.38 | 0.01 | 0.91 | 0.93 | 0.96 | 0.23 | 0.04 | |
| RF | 0.94 | 0.94 | 0.97 | 0.22 | 0.03 | 0.91 | 0.92 | 0.96 | 0.34 | 0.07 | |
| GBM | 0.92 | 0.94 | 0.97 | 0.36 | 0.08 | 0.89 | 0.91 | 0.96 | 0.33 | 0.07 | |
| KNN | 0.88 | 0.93 | 0.96 | 0.38 | 0.10 | 0.86 | 0.90 | 0.95 | 0.60 | 0.10 | |
| SVM−Radial | 0.89 | 0.92 | 0.96 | 0.60 | 0.11 | 0.87 | 0.89 | 0.94 | 0.64 | 0.11 | |
| GP−Radial | 0.86 | 0.91 | 0.95 | 0.68 | 0.14 | 0.84 | 0.63 | 0.69 | 0.36 | # | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elangovan, A.; Duc, N.T.; Raju, D.; Kumar, S.; Singh, B.; Vishwakarma, C.; Gopala Krishnan, S.; Ellur, R.K.; Dalal, M.; Swain, P.; et al. Imaging Sensor-Based High-Throughput Measurement of Biomass Using Machine Learning Models in Rice. Agriculture 2023, 13, 852. https://doi.org/10.3390/agriculture13040852
Elangovan A, Duc NT, Raju D, Kumar S, Singh B, Vishwakarma C, Gopala Krishnan S, Ellur RK, Dalal M, Swain P, et al. Imaging Sensor-Based High-Throughput Measurement of Biomass Using Machine Learning Models in Rice. Agriculture. 2023; 13(4):852. https://doi.org/10.3390/agriculture13040852
Chicago/Turabian StyleElangovan, Allimuthu, Nguyen Trung Duc, Dhandapani Raju, Sudhir Kumar, Biswabiplab Singh, Chandrapal Vishwakarma, Subbaiyan Gopala Krishnan, Ranjith Kumar Ellur, Monika Dalal, Padmini Swain, and et al. 2023. "Imaging Sensor-Based High-Throughput Measurement of Biomass Using Machine Learning Models in Rice" Agriculture 13, no. 4: 852. https://doi.org/10.3390/agriculture13040852









