Self-Excited-Resonance of Soil-Engaging Surface Spectrum: A New Method of Soil Cutting Resistance Reduction
Abstract
:1. Introduction
2. Materials and Methods
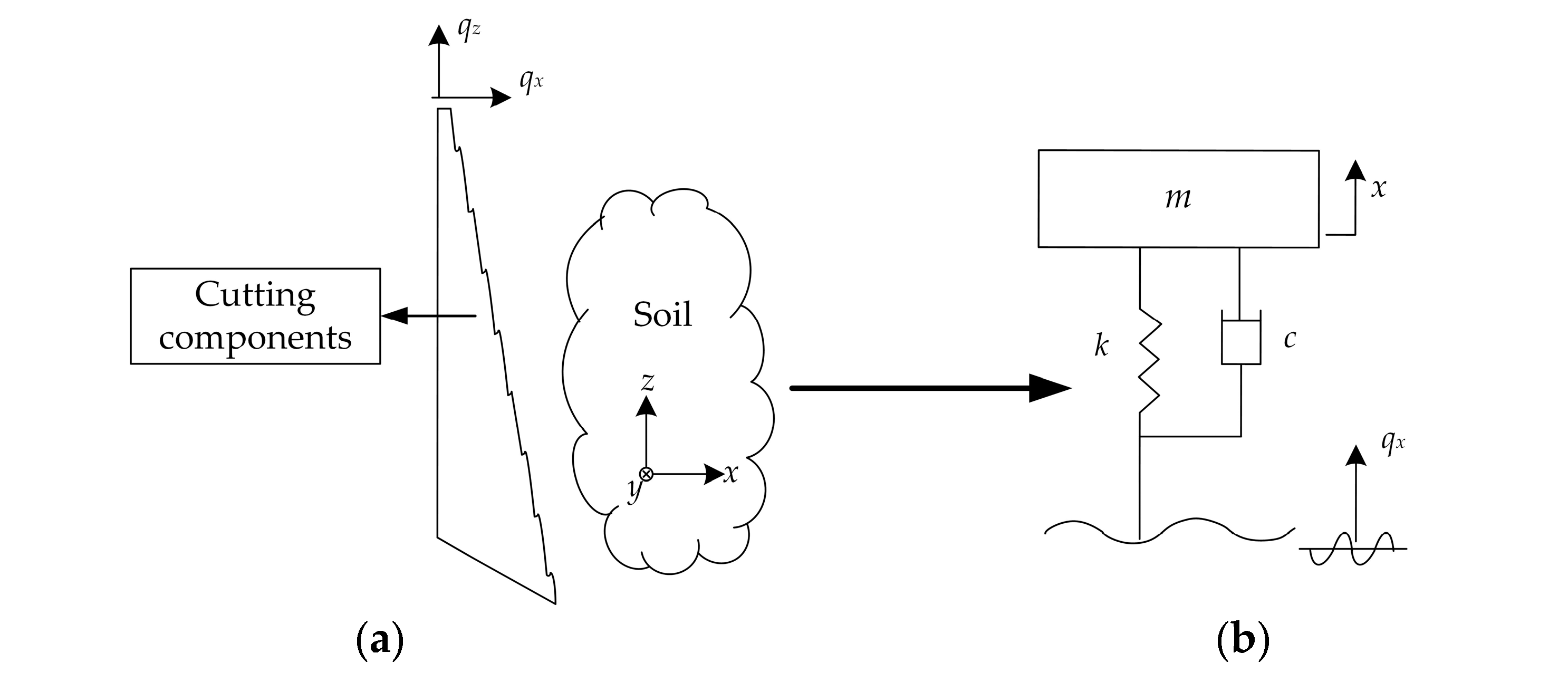
2.1. Soil-Engaging Components-Soil Vibration Cutting Model
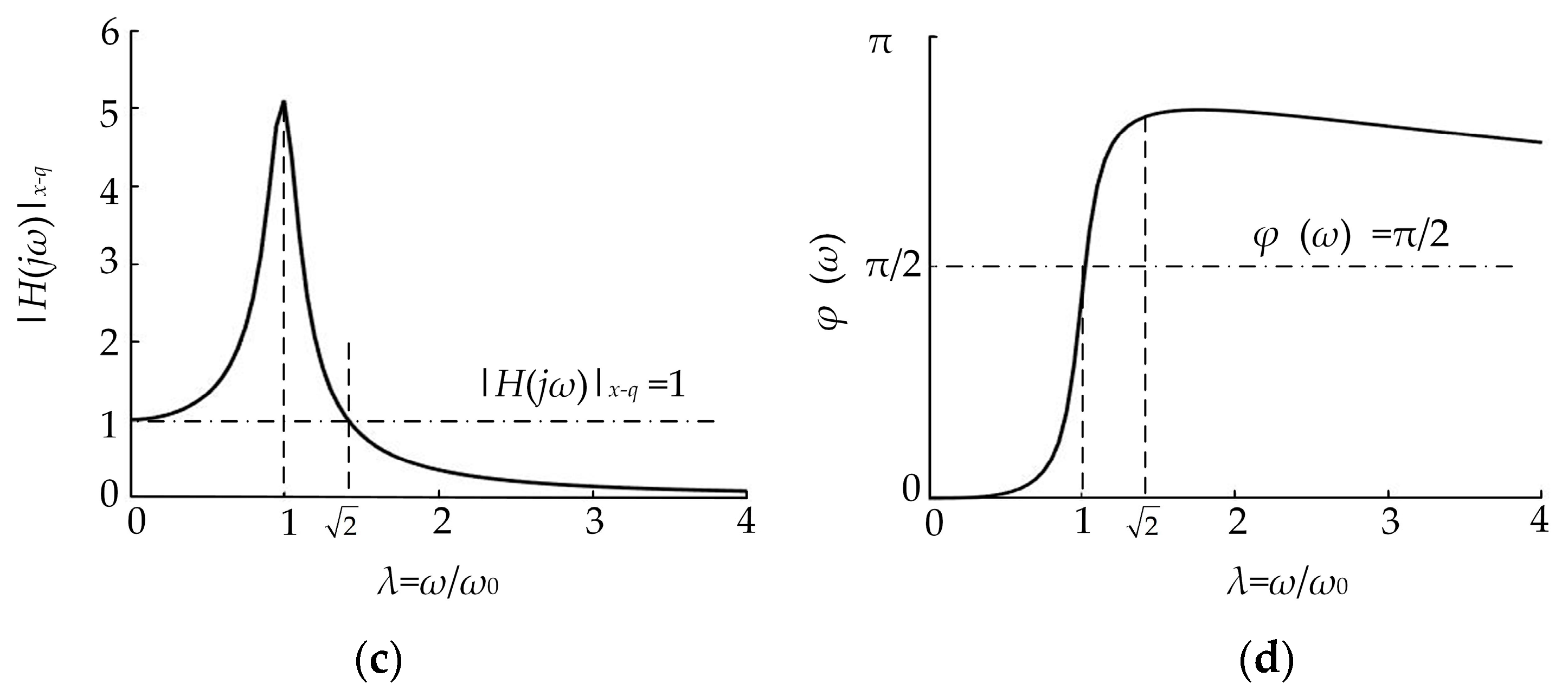
2.2. Soil Natural Vibration Frequency
2.3. Model Bulldozing Plate for Test
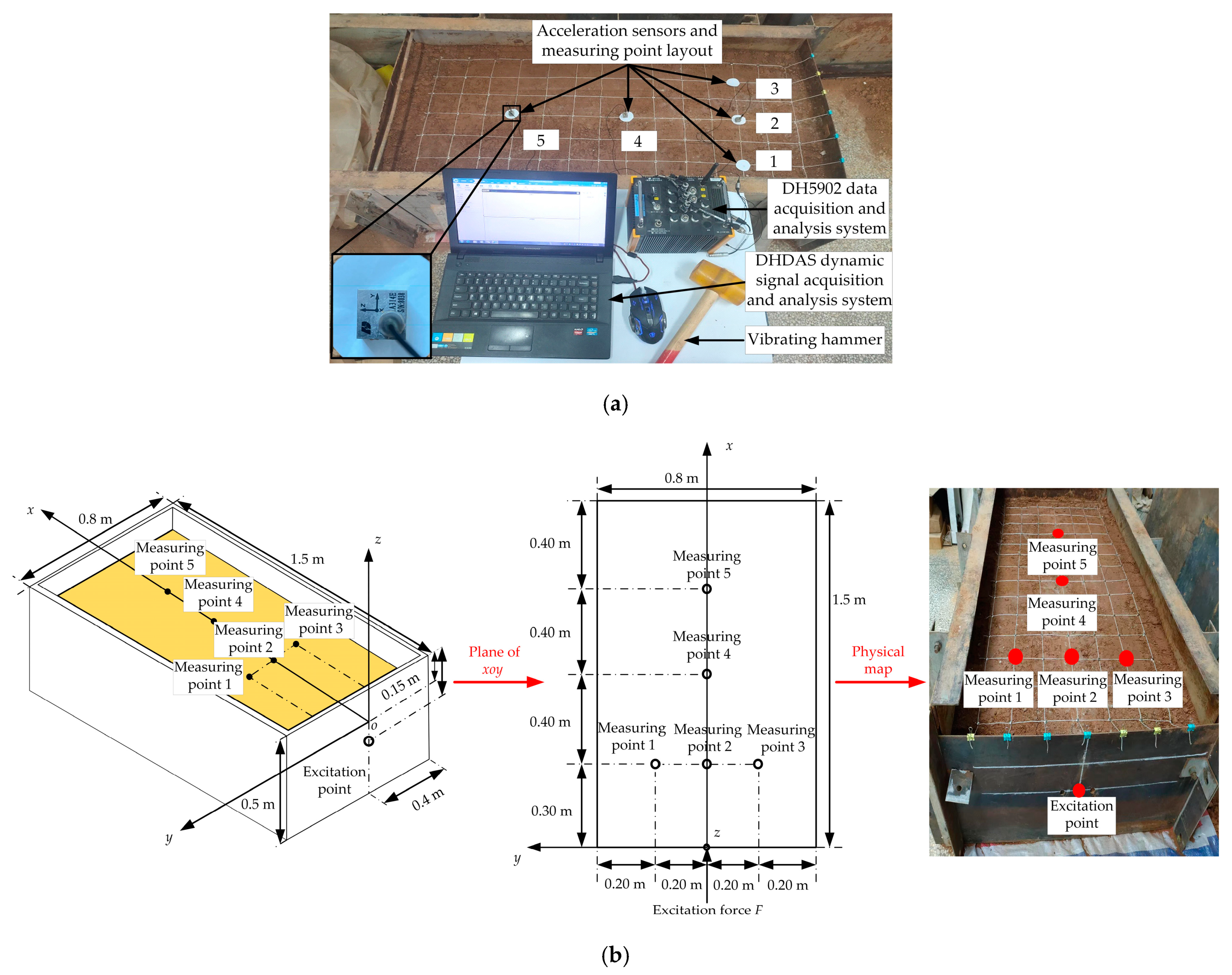
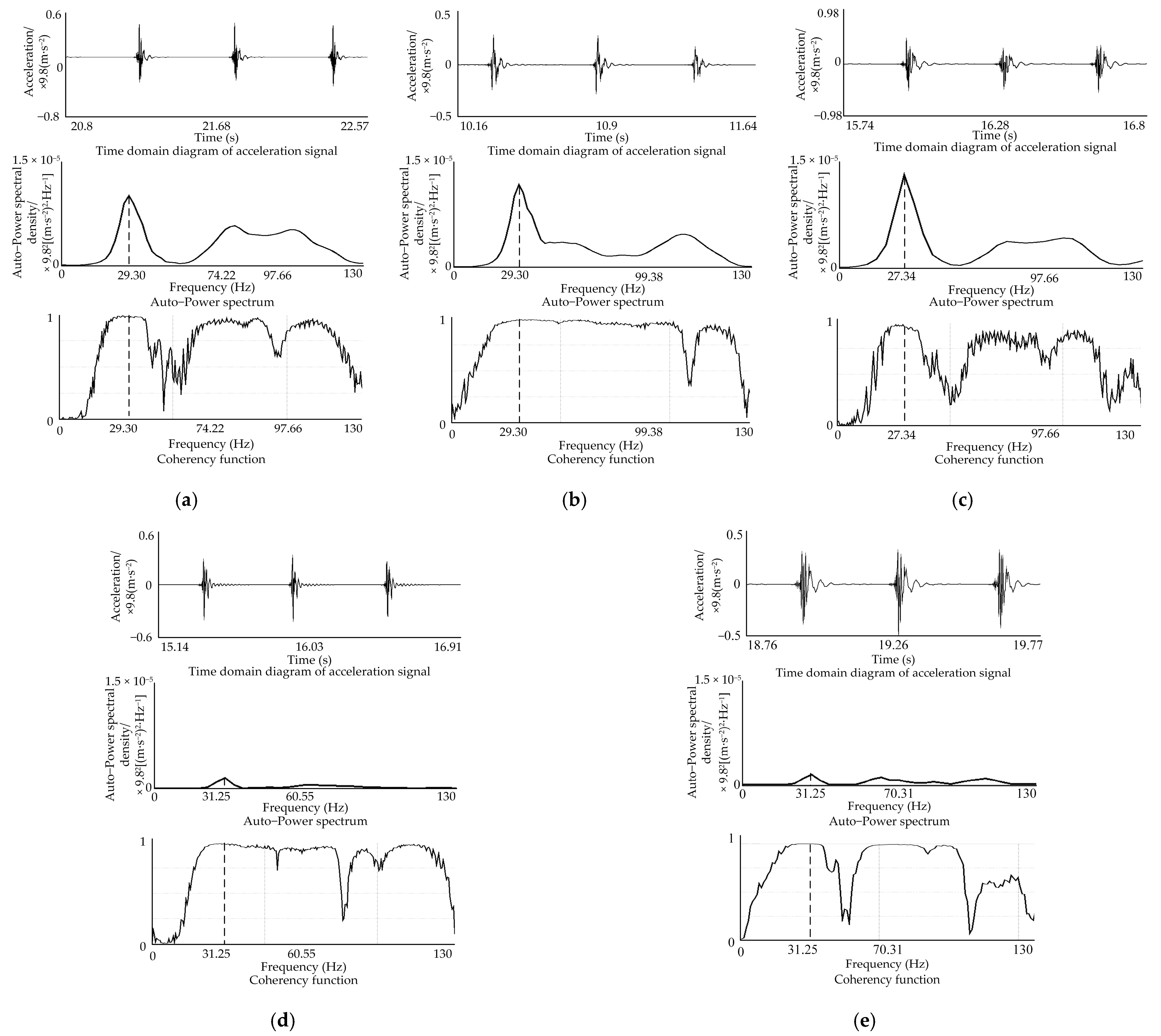
2.4. Soil Bin Test
3. Results and Discussion
3.1. Law of Resistance Reduction
3.2. Law of Soil Adhesion
3.3. Adaptive Law of Resonance Resistance Reduction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Awuah, E.; Zhou, J.; Liang, Z.; Aikins, K.A.; Gbenontin, B.V.; Mecha, P.; Makange, N.R. Parametric analysis and numerical optimization of Jerusalem artichoke vibrating digging shovel using discrete element method. Soil Till. Res. 2022, 219, 105344. [Google Scholar] [CrossRef]
- Manuwa, S.I. Performance evaluation of tillage tines operating under different depths in a sandy clay loam soil. Soil Till. Res. 2009, 103, 399–405. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Azali, S.T.; Zhao, J. Introduction of an empirical TBM cutter wear prediction model for pyroclastic and mafic igneous rocks; a case history of Karaj water conveyance tunnel, Iran. Tunn. Undergr. Space Technol. 2014, 43, 222–231. [Google Scholar] [CrossRef]
- Arvidsson, J.; Keller, T.; Gustafsson, K. Specific draught for mouldboard plough, chisel plough and disc harrow at different water contents. Soil Till. Res. 2004, 79, 221–232. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Ji, J. Effect of Mounting Angle on Bending Subsoiling Tool–Soil Interactions Using DEM Simulations. Agriculture 2022, 12, 1830. [Google Scholar] [CrossRef]
- Godwin, R.J. A review of the effect of implement geometry on soil failure and implement forces. Soil Till. Res. 2007, 92, 331–400. [Google Scholar] [CrossRef]
- Li, Q.D.; Guo, J.Y.; Hu, J.; Zhang, W.; Wang, H.L.; Dai, H.Q. Research status of wear resistance and drag reduction treatment of soil cultivation components. Surf. Technol. 2017, 46, 119–126. [Google Scholar]
- Han, Z.W.; Mu, Z.Z.; Yin, W.; Niu, S.; Zhang, J.Q.; Ren, L.Q. Biomimetic multifunctional surfaces inspired from animals. Adv. Colloid Interface Sci. 2016, 234, 27–50. [Google Scholar] [CrossRef]
- Xi, X.B.; Zhang, R.H.; Shan, X.; Ye, W.W.; Shi, Y.J.; Ma, G.L.; Tao, D.Q. Optimization of gas explosion subsoiling parameters based on soil fissure trace equation and soil disturbance model. Trans. Chin. Soc. Agric. Eng. 2018, 34, 15–24. [Google Scholar]
- Zhou, W.; Ni, X.; Song, K.; Wen, N.; Wang, J.; Fu, Q.; Na, M.; Tang, H.; Wang, Q. Bionic Optimization Design and Discrete Element Experimental Design of Carrot Combine Harvester Ripping Shovel. Processes 2023, 11, 1526. [Google Scholar] [CrossRef]
- Yu, J.; Ma, Y.; Wang, S.; Xu, Z.; Liu, X.; Wang, H.; Qi, H.; Han, L.; Zhuang, J. 3D finite element simulation and experimental validation of a mole rat’s digit inspired biomimetic potato digging shovel. Appl. Sci. 2022, 12, 1761. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Chen, Y.; Lin, P.; Zhang, Q.; Cheng, Y.; Yang, Z.; Huang, G. Research on Ditching Mechanism of Self-Excited Vibration Ditching Machine. Agronomy 2023, 13, 905. [Google Scholar] [CrossRef]
- Wang, W.M.; Wang, T.Y.; Guo, B.; Chen, X.; Zhou, F.J. Design and experiment of key components of rotary cultivator based on vibration reducing resistance principle. Trans. Chin. Soc. Agric. Mach. 2019, 50, 35–45. [Google Scholar]
- Gholamhossein, S.; Chris, S.; Jacky, D.; John, F. The effect of oscillation angle on the performance of oscillatory tillage. Soil Till. Res. 2009, 104, 97–105. [Google Scholar]
- Gholamhossein, S.; John, F.; Jacky, D.; Chris, S. Optimising oscillation frequency in oscillatory tillage. Soil Till. Res. 2010, 106, 202–210. [Google Scholar]
- Zhang, X.Y.; Chen, Y. Soil disturbance and cutting forces of four different sweeps for mechanical weeding. Soil Till. Res. 2017, 169, 167–175. [Google Scholar] [CrossRef]
- Lisowski, A.; Klonowski, J.; Green, O.; Swietochowski, A.; Sypula, M.; Struzyk, A.; Nowakowski, T.; Chlebowski, J.; Kamiński, J.; Kostyra, K.; et al. Duckfoot tools connected with flexible and stiff tines: Three components of resistances and soil disturbance. Soil Till. Res. 2016, 158, 76–90. [Google Scholar] [CrossRef]
- Niyamapa, T.; Salokhe, V.M. Soil distribution and force mechanics of vibrating tillage tool. J. Terramech. 2000, 37, 151–166. [Google Scholar] [CrossRef]
- Wang, Y.X.; Zhang, D.; Li, Y.; Cui, T.; Jing, H.; Zhong, X.J. Modeling the interaction of soil and a vibrating subsoiler using the discrete element method. Comput. Electron. Agric. 2000, 174, 105518. [Google Scholar] [CrossRef]
- Cui, T.; Zhong, X.J. Optimized design and field experiment of a staggered vibrating subsoiler for conservation tillage. Int. J. Agric. Biol. Eng. 2019, 174, 59–65. [Google Scholar]
- Niyamapa, T.; Salokhe, V.M. Force and pressure distribution under vibratory tillage tool. J. Terramech. 2000, 37, 139–150. [Google Scholar] [CrossRef]
- Sahay, C.S.; Thomas, E.V.; Satapathy, K.K.; Anthonis, J. Performance evaluation of a novel power-tiller-operated oscillatory tillage implement for dry land tillage. Biosyst. Eng. 2009, 102, 385–391. [Google Scholar] [CrossRef]
- Elyas, R.; Yuness, S. Vibratory soil cutting a new approach for the mathematical analysis. Soil Till. Res. 2016, 159, 33–40. [Google Scholar]
- Sakai, K.; Hata, S.I.; Takai, M.; Nambu, S. Design parameters of four-shank vibrating subsoiler. Trans. Amer. Soc. Agric. Eng. 1993, 36, 23–26. [Google Scholar] [CrossRef]
- Wang, D.W.; Wang, J.S.; Shang, S.Q. Experimental research on soil digging resistance and energy consumption based on vibration. Trans. Chin. Soc. Agric. Mach. 2020, 51, 267–272. [Google Scholar]
- Berntsen, R.; Bere, B.; Torp, T.; Aasen, H. Tine forces established by a two-level model and the draught requirement of rigid and flexible tines. Soil Till. Res. 2006, 90, 230–241. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Duerinckx, K.; Ramon, H.; Anthonis, J. Soil influences on the mechanical actions of a flexible spring tine during selective weed harrowing. Biosyst. Eng. 2007, 96, 7–18. [Google Scholar] [CrossRef]
- Berntsen, R.; Bere, B. Soil fragmentation and the efficiency of tillage implements. Soil Till. Res. 2002, 64, 137–147. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, W.L.; Yang, Q.J.; Li, D.D.; Xia, J.F. Design and experiment of sliding cutting self-excited vibration drag reduction subsoiling device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 71–78. [Google Scholar]
- Cui, T.; Shi, Z.D.; Yang, L.; Wang, Y.X.; Han, D.D.; Zhang, D.X. Design and experiment of vibration subsoiler with adjustable spring pre-tightening force. Trans. Chin. Soc. Agric. Mach. 2016, 47, 96–102. [Google Scholar]
- Zhang, P. Design and Experiment of Drag Reduction on Self-Exciting Vibrating Soil-engaging Surface of Bulldozing Plates with Parabolic Basement. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2022. [Google Scholar]
- Zhang, Y.M. Forced vibration of single degree of freedom systems. In Mechanical Vibration; Tsinghua University Press: Beijing, China, 2007; pp. 38–39. [Google Scholar]
- Zong, Q.; Wang, H.B.; Zhou, S.B. Research on monitoring and controlling techniques considering effects of seismic shock. Chin. J. Rock Mech. Eng. 2008, 27, 938–945. [Google Scholar]
- Qiu, Y.Q.; Guo, Z.J.; Jin, X.; Zhang, P.G.; Si, S.J.; Guo, F.G. Calibration and verification test of cinnamon soil simulation parameters based on discrete element method. Agriculture 2022, 12, 1082. [Google Scholar] [CrossRef]
- Quan, L.Z.; Tong, J.; Zeng, B.G.; Chen, D.H. Finite element mode analysis and experiment of cornstubble harvester. Trans. Chin. Soc. Agric. Eng. 2011, 27, 15–20. [Google Scholar]
- Guo, Z.J.; Xing, Y.S.; Du, G.; Zhang, S. Influence of intrinsic geometrical quantity of soil-engaging surface on working resistance of bulldozing plate. Trans. Chin. Soc. Agric. Mach. 2014, 45, 328–333. [Google Scholar]
- Guo, Z.J.; Zhou, D.Y.; Zhou, Z.L. Simulation research on mechanical performances of several kinds of cultivating components with different soil-engaging surfaces. J. Mech. Eng. 2010, 46, 71–75. [Google Scholar] [CrossRef]
- Yang, J.J. Similar concepts and definitions. In Similitude Theory and Structural Model Test; Wuhan University of Technology Press: Wuhan, China, 2005; pp. 10–12. [Google Scholar]
- Guo, Z.J.; Du, G.; Li, Z.L.; Li, X.P. Orthogonal experiment on resistance reduction by soil-engaging surfaces of bulldozer blade. Trans. Chin. Soc. Agric. Mach. 2015, 46, 372–378. [Google Scholar]
- Ren, L.Q.; Han, Z.W.; Li, J.Q.; Tong, J. Experimental investigation of bionic rough curved soil cutting blade surface to reduce soil adhesion and friction. Soil Till. Res. 2006, 85, 1–12. [Google Scholar] [CrossRef]
- Yu, Z.S. The comfort of a car. In Automobile Theory, 6th ed.; China Machine Press: Beijing, China, 2019; pp. 246–247. [Google Scholar]
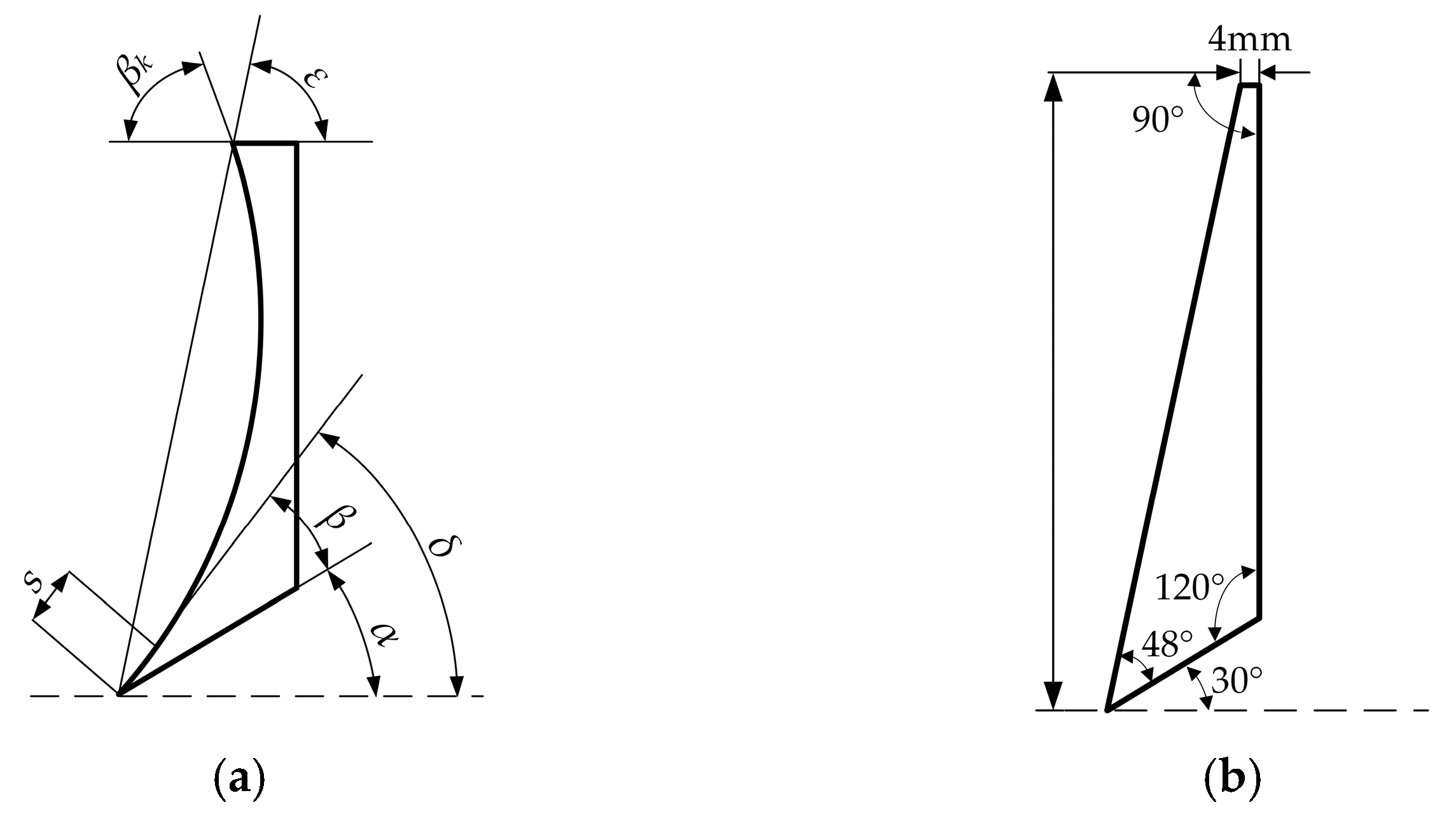






| Parameter | Test Results of Cinnamon Soil | Standard Deviation |
|---|---|---|
| Mean soil hardness (MPa) | 1.006 | 0.223 |
| Soil shear modulus (MPa) | 3.846 | 0.211 |
| Soil internal fraction angle (°) | 28.5 | 1.388 |
| Soil cohesion (kPa) | 45.9 | 0.303 |
| Soil moisture content (%) | 12.82 | 0.019 |
| Soil bulk density (kg·m−3) | 1164 | 6.986 |
| Soil Poisson’s ratio (μ) | 0.3 | 0.0086 |
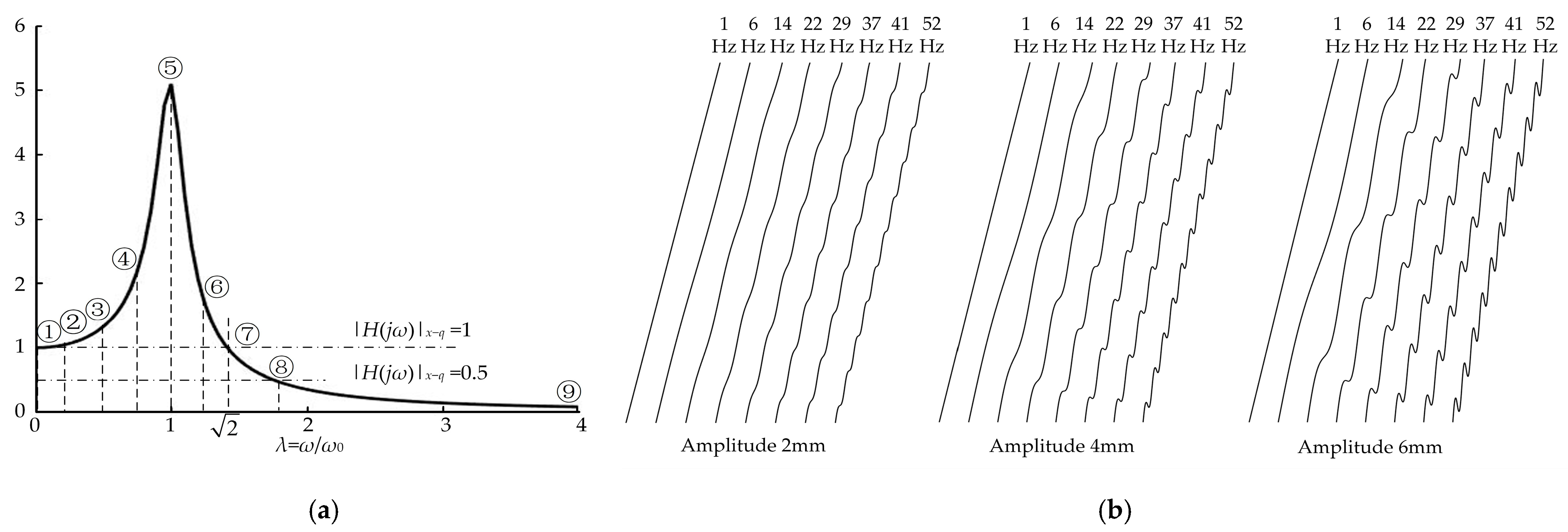
| Number | Frequency Ratio | Impact Frequency (Hz) | Working Speed (m·s−1) | Spatial Geometric Frequency (mm−1) | Wavelengths (mm) | Directrix Equation |
|---|---|---|---|---|---|---|
| 1 | 0.034 | 1 | 0.16 | 0.00625 | 160 | z = 4.7x + Aisin(0.039x) |
| 2 | 0.205 | 6 | 0.16 | 0.0375 | 26.7 | z = 4.7x + Aisin(0.236x) |
| 3 | 0.47 | 14 | 0.16 | 0.0875 | 11.4 | z = 4.7x + Aisin(0.550x) |
| 4 | 0.75 | 22 | 0.16 | 0.1375 | 7.3 | z = 4.7x + Aisin(0.864x) |
| 5 | 1 | 29 | 0.16 | 0.18125 | 5.5 | z = 4.7x + Aisin(1.138x) |
| 6 | 1.25 | 37 | 0.16 | 0.23125 | 4.3 | z = 4.7x + Aisin(1.452x) |
| 7 | 1.414 | 41 | 0.16 | 0.25625 | 3.9 | z = 4.7x + Aisin(1.609x) |
| 8 | 1.758 | 52 | 0.16 | 0.325 | 3.1 | z = 4.7x + Aisin(2.041x) |
| 9 | Tend to ∞ | Plane | 0.16 | ∞ | 0 | z = 4.7x + 0 |
| Level | Factors | |
|---|---|---|
| A Impact Frequency (Hz) | B Amplitude (mm) | |
| 1 | 1 | 2 |
| 2 | 6 | 4 |
| 3 | 14 | 6 |
| 4 | 22 | |
| 5 | 29 | |
| 6 | 37 | |
| 7 | 41 | |
| 8 | 52 | |
| Number | Factor | Horizontal Resistance (Fx/N) | Vertical Resistance (Fz/N) | Resultant Force (F/N) | Fx/F | Resistance Reduction Ratio of Fx Relative to Plane Bulldozing Plate | Resistance Reduction Ratio of Fz Relative to Plane Bulldozing plate | |
|---|---|---|---|---|---|---|---|---|
| A Frequency (Hz) | B Amplitude (mm) | |||||||
| 1 | 1(1) | 1(2) | 403.63 | 12.33 | 403.82 | 0.9995 | 8.97% | −21.78% |
| 2 | 2(6) | 1(2) | 401.03 | 16.16 | 401.36 | 0.9992 | 9.56% | −59.70% |
| 3 | 3(14) | 1(2) | 401.18 | 12.76 | 401.39 | 0.9995 | 9.53% | −26.08% |
| 4 | 4(22) | 1(2) | 443.09 | 15.11 | 443.35 | 0.9994 | 0.08% | −49.28% |
| 5 | 5(29) | 1(2) | 387.08 | 13.65 | 387.32 | 0.9994 | 12.71% | −34.86% |
| 6 | 6(37) | 1(2) | 421.61 | 14.81 | 421.87 | 0.9994 | 4.92% | −46.31% |
| 7 | 7(41) | 1(2) | 403.06 | 13.62 | 403.29 | 0.9994 | 9.10% | −34.59% |
| 8 | 8(52) | 1(2) | 355.56 | 11.99 | 355.76 | 0.9994 | 19.82% | −18.48% |
| 9 | 1(1) | 2(4) | 364.59 | 11.73 | 364.78 | 0.9995 | 17.78% | −15.87% |
| 10 | 2(6) | 2(4) | 372.39 | 11.02 | 372.56 | 0.9995 | 16.02% | −8.88% |
| 11 | 3(14) | 2(4) | 401.08 | 11.32 | 401.24 | 0.9996 | 9.55% | −11.82% |
| 12 | 4(22) | 2(4) | 375.77 | 10.72 | 375.92 | 0.9996 | 15.26% | −5.88% |
| 13 | 5(29) | 2(4) | 342.89 | 6.83 | 342.96 | 0.9998 | 22.67% | 32.55% |
| 14 | 6(37) | 2(4) | 370.60 | 11.13 | 370.77 | 0.9995 | 16.42% | −9.92% |
| 15 | 7(41) | 2(4) | 362.81 | 8.09 | 362.90 | 0.9998 | 18.18% | 20.06% |
| 16 | 8(52) | 2(4) | 399.78 | 8.06 | 399.86 | 0.9998 | 9.84% | 20.39% |
| 17 | 1(1) | 3(6) | 439.15 | 13.73 | 439.37 | 0.9995 | 0.96% | −35.67% |
| 18 | 2(6) | 3(6) | 400.89 | 11.46 | 401.06 | 0.9996 | 9.59% | −13.18% |
| 19 | 3(14) | 3(6) | 349.58 | 6.63 | 349.64 | 0.9998 | 21.16% | 34.52% |
| 20 | 4(22) | 3(6) | 381.34 | 8.45 | 381.44 | 0.9997 | 14.00% | 16.54% |
| 21 | 5(29) | 3(6) | 381.37 | 7.83 | 381.45 | 0.9998 | 13.99% | 22.62% |
| 22 | 6(37) | 3(6) | 354.51 | 8.35 | 354.61 | 0.9997 | 20.05% | 17.51% |
| 23 | 7(41) | 3(6) | 444.82 | 13.80 | 445.03 | 0.9995 | −0.31% | −36.33% |
| 24 | 8(52) | 3(6) | 453.97 | 9.97 | 454.08 | 0.9998 | −2.38% | 1.47% |
| 25 | Plane bulldozing plate | 443.43 | 10.12 | 443.54 | 0.9998 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Qiu, Y.; Yan, X.; Wang, J.; Zhang, Y.; Zhang, P.; Zhang, F. Self-Excited-Resonance of Soil-Engaging Surface Spectrum: A New Method of Soil Cutting Resistance Reduction. Agriculture 2023, 13, 1154. https://doi.org/10.3390/agriculture13061154
Guo Z, Qiu Y, Yan X, Wang J, Zhang Y, Zhang P, Zhang F. Self-Excited-Resonance of Soil-Engaging Surface Spectrum: A New Method of Soil Cutting Resistance Reduction. Agriculture. 2023; 13(6):1154. https://doi.org/10.3390/agriculture13061154
Chicago/Turabian StyleGuo, Zhijun, Yiqing Qiu, Xianghai Yan, Jiajia Wang, Yin Zhang, Pangang Zhang, and Fu Zhang. 2023. "Self-Excited-Resonance of Soil-Engaging Surface Spectrum: A New Method of Soil Cutting Resistance Reduction" Agriculture 13, no. 6: 1154. https://doi.org/10.3390/agriculture13061154
APA StyleGuo, Z., Qiu, Y., Yan, X., Wang, J., Zhang, Y., Zhang, P., & Zhang, F. (2023). Self-Excited-Resonance of Soil-Engaging Surface Spectrum: A New Method of Soil Cutting Resistance Reduction. Agriculture, 13(6), 1154. https://doi.org/10.3390/agriculture13061154







