Assessing Spatial Variation and Driving Factors of Available Phosphorus in a Hilly Area (Gaozhou, South China) Using Modeling Approaches and Digital Soil Mapping
Abstract
:1. Introduction
- The performance of four popular models (RF, IDW, RBF, and OK) for DSM of AP are shown and compared in a typical hilly area in a subtropical monsoon climate, i.e., Gaozhou.
- The spatial distribution and variation characteristics of AP in the study area are analyzed.
- The importance of driving factors that influence the spatial distribution and variation of AP are ranked and analyzed based on RF.
- The correlation between AP and the influence of environmental variables at different spatial locations and directions are investigated, which reveals the spatial heterogeneity of the influence strength of the environmental factors.
2. Materials and Methods
2.1. Materials
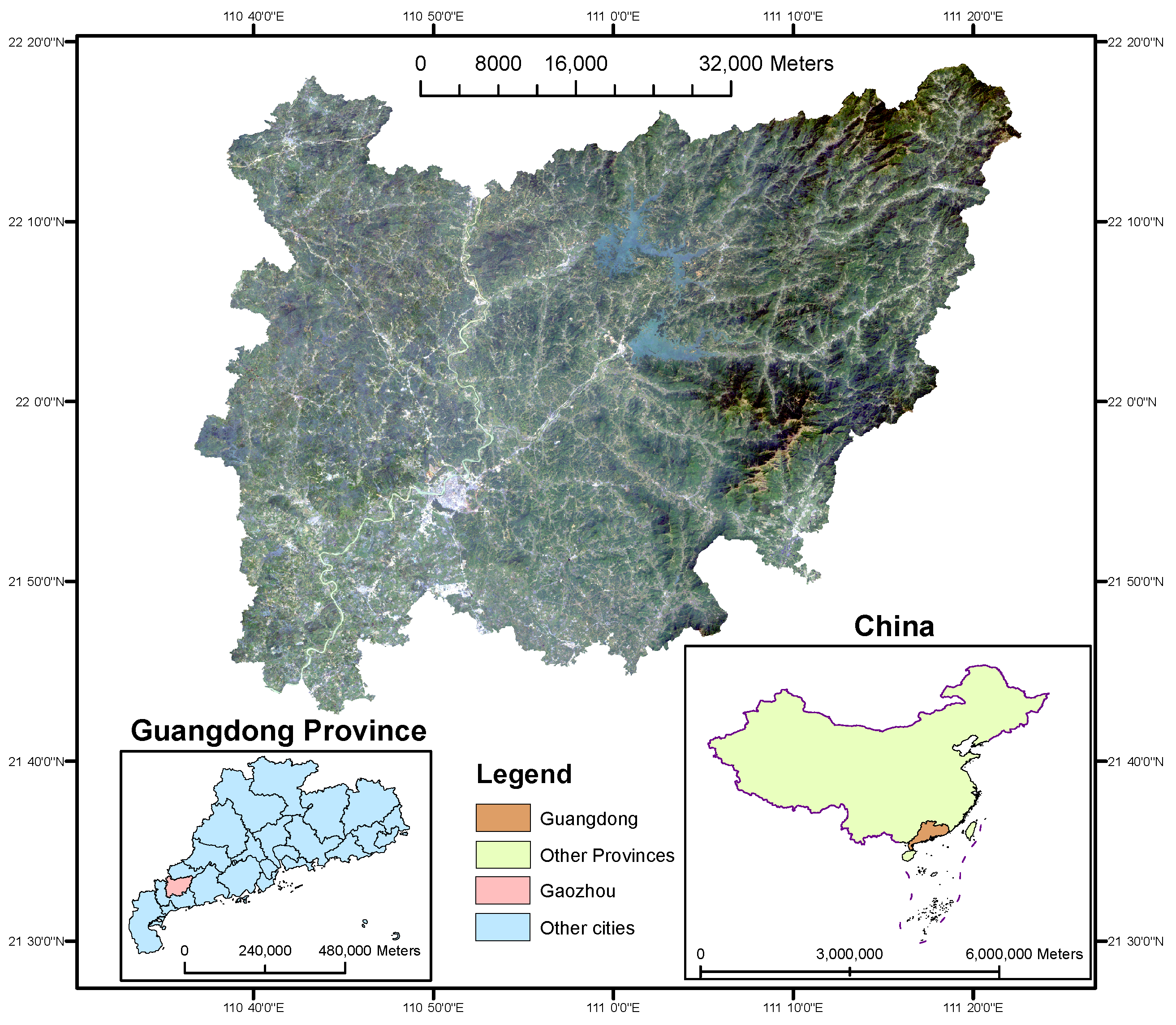
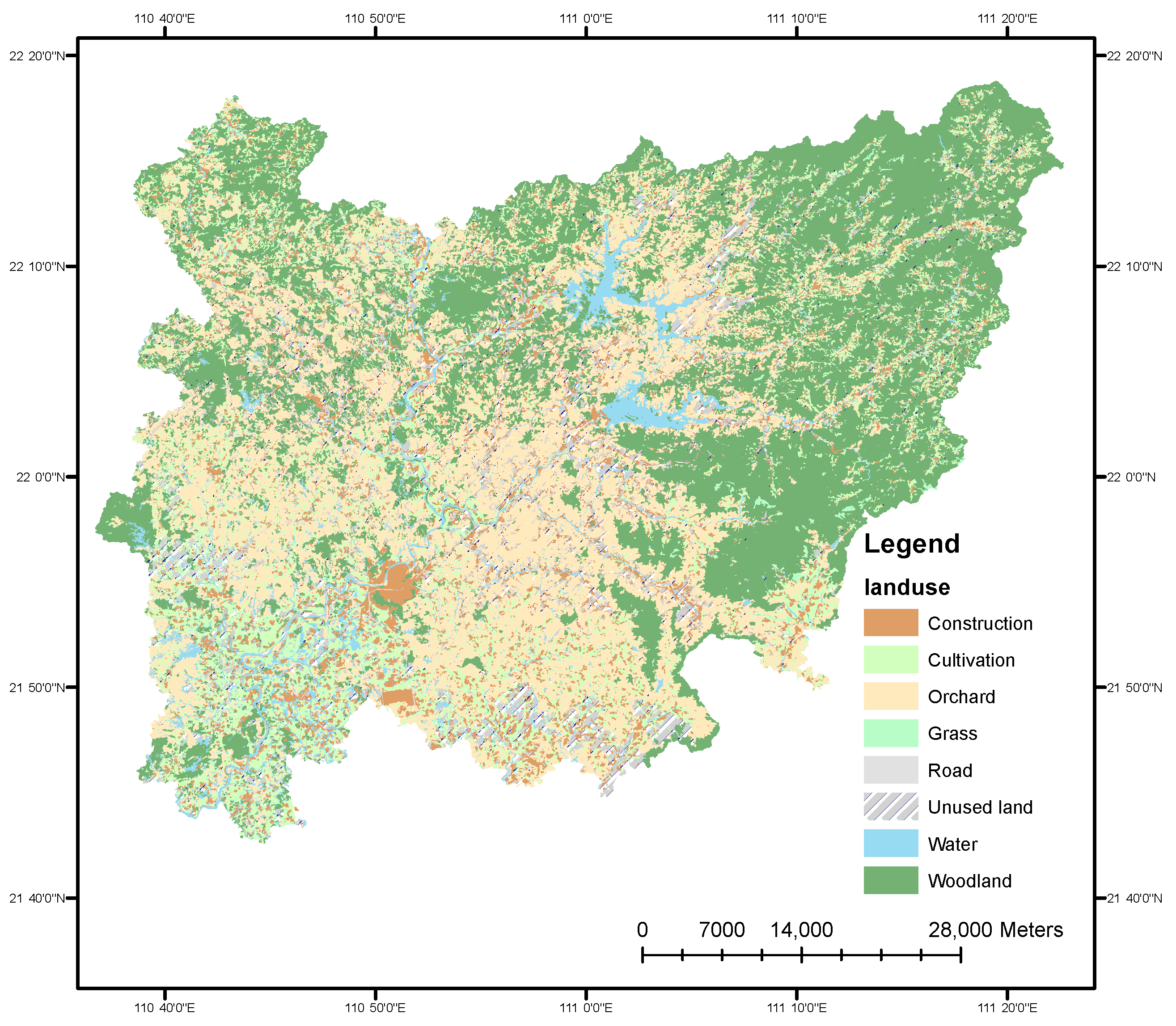
2.1.1. Study Area
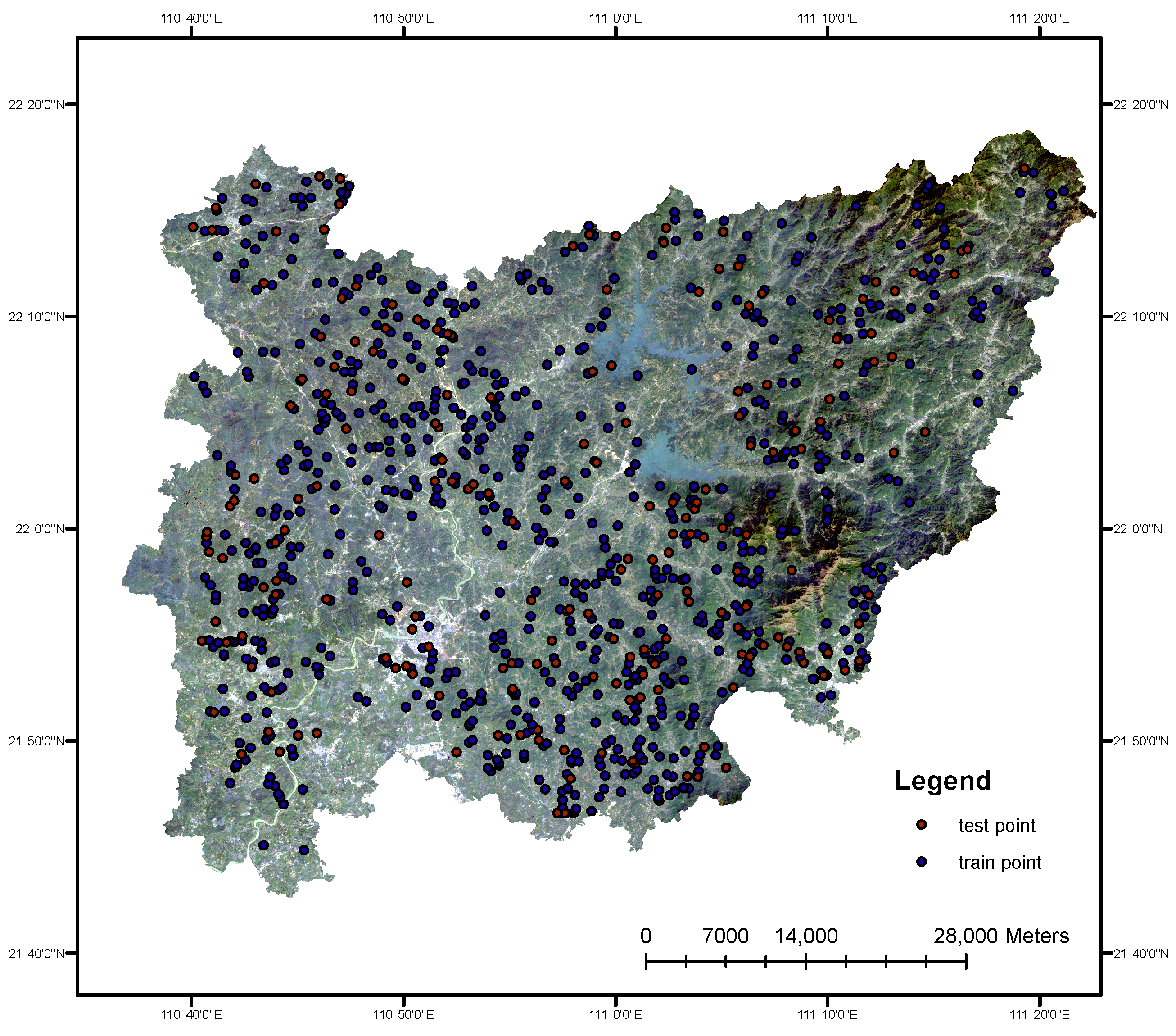
2.1.2. Data
2.2. Methods
2.2.1. Random Forest for Spatial Interpolation
2.2.2. Validation Methods
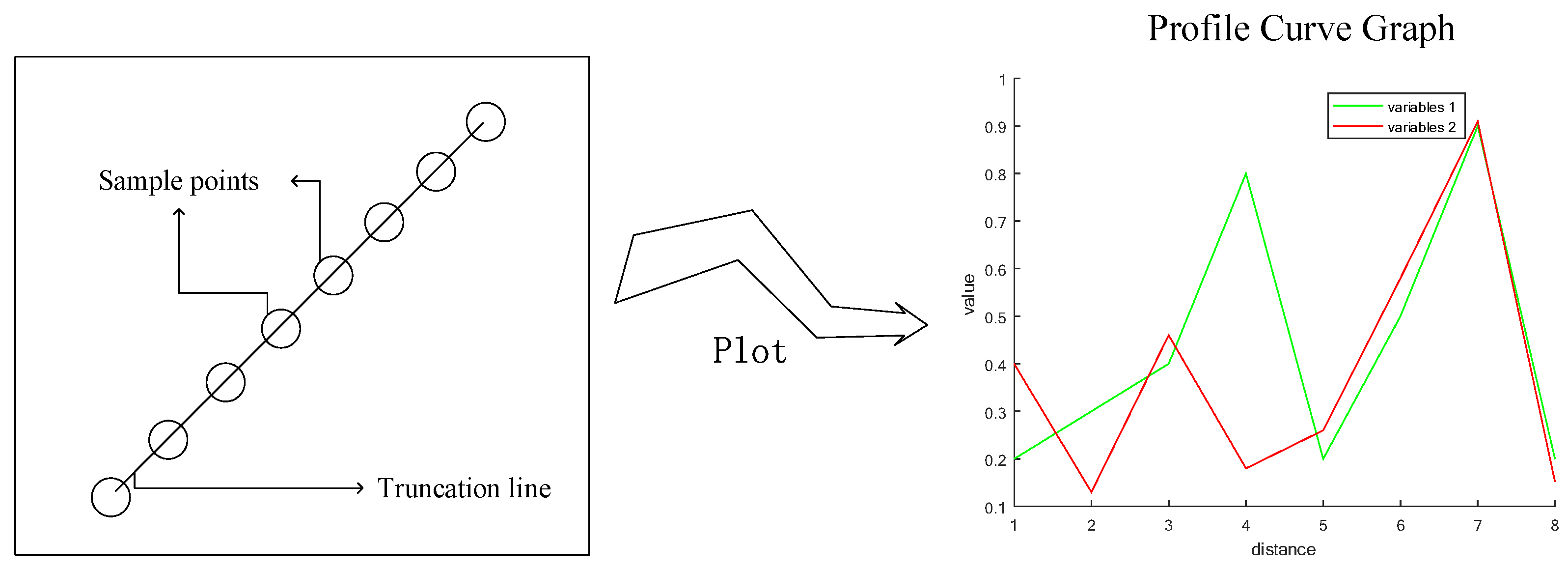
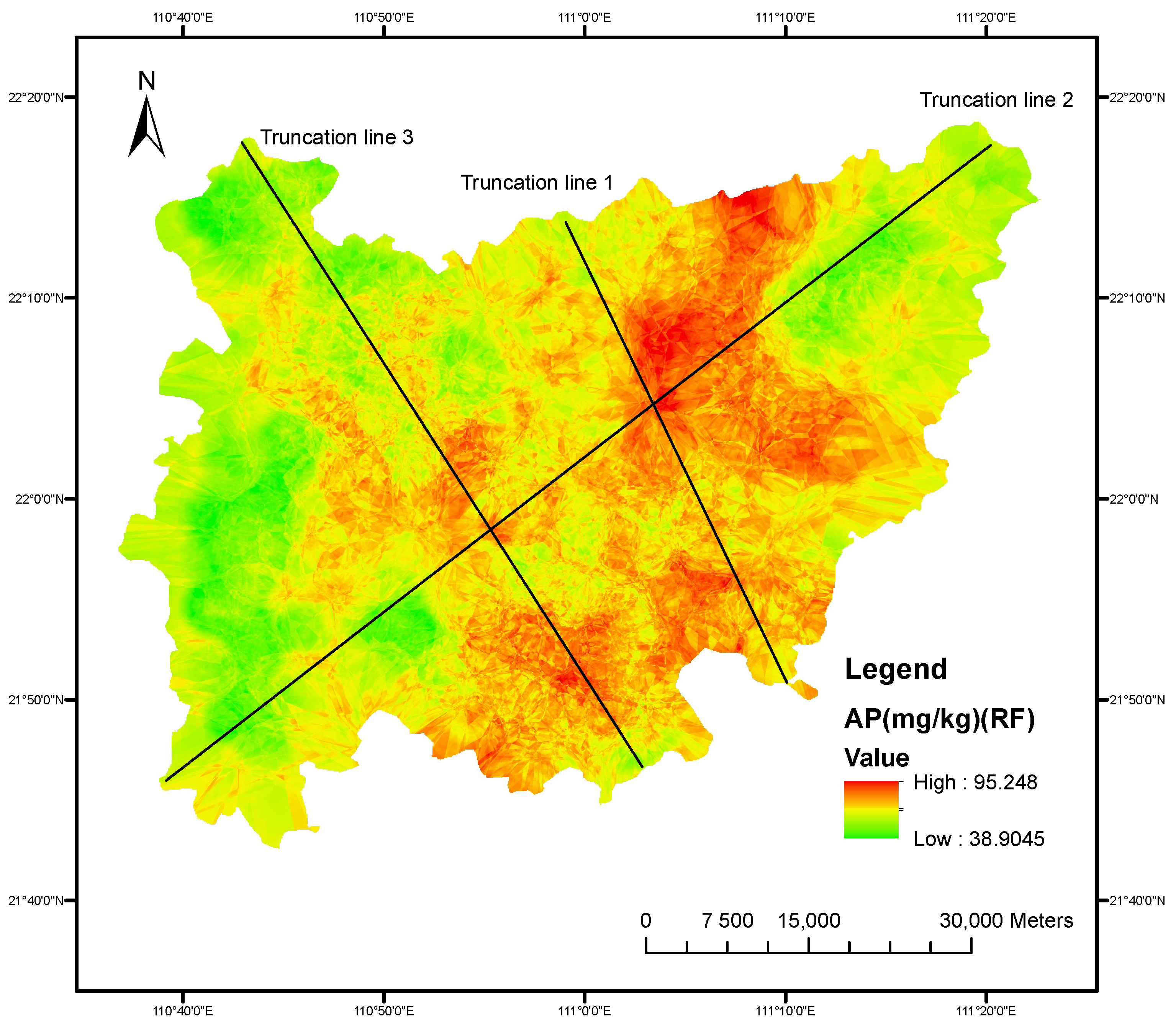
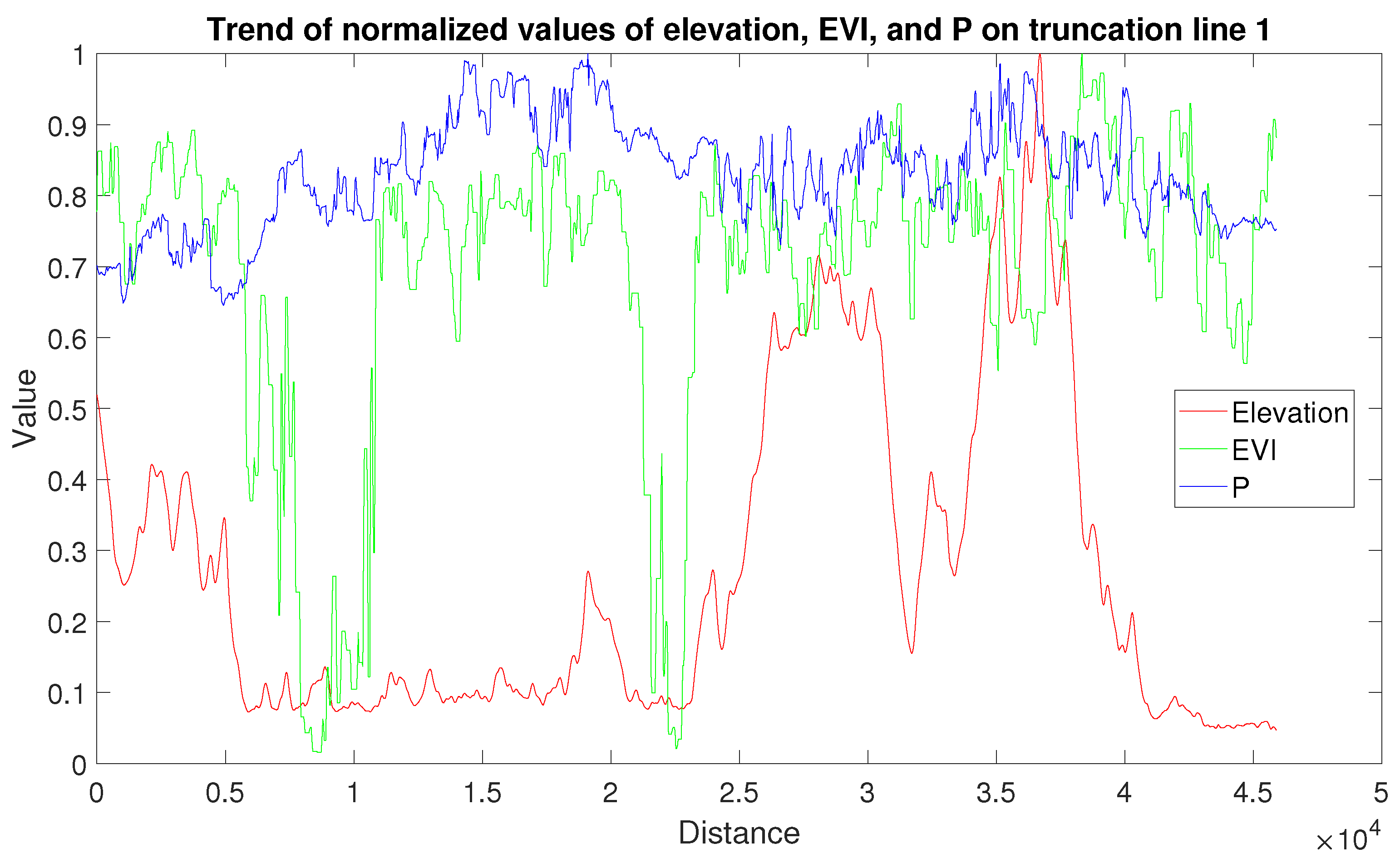
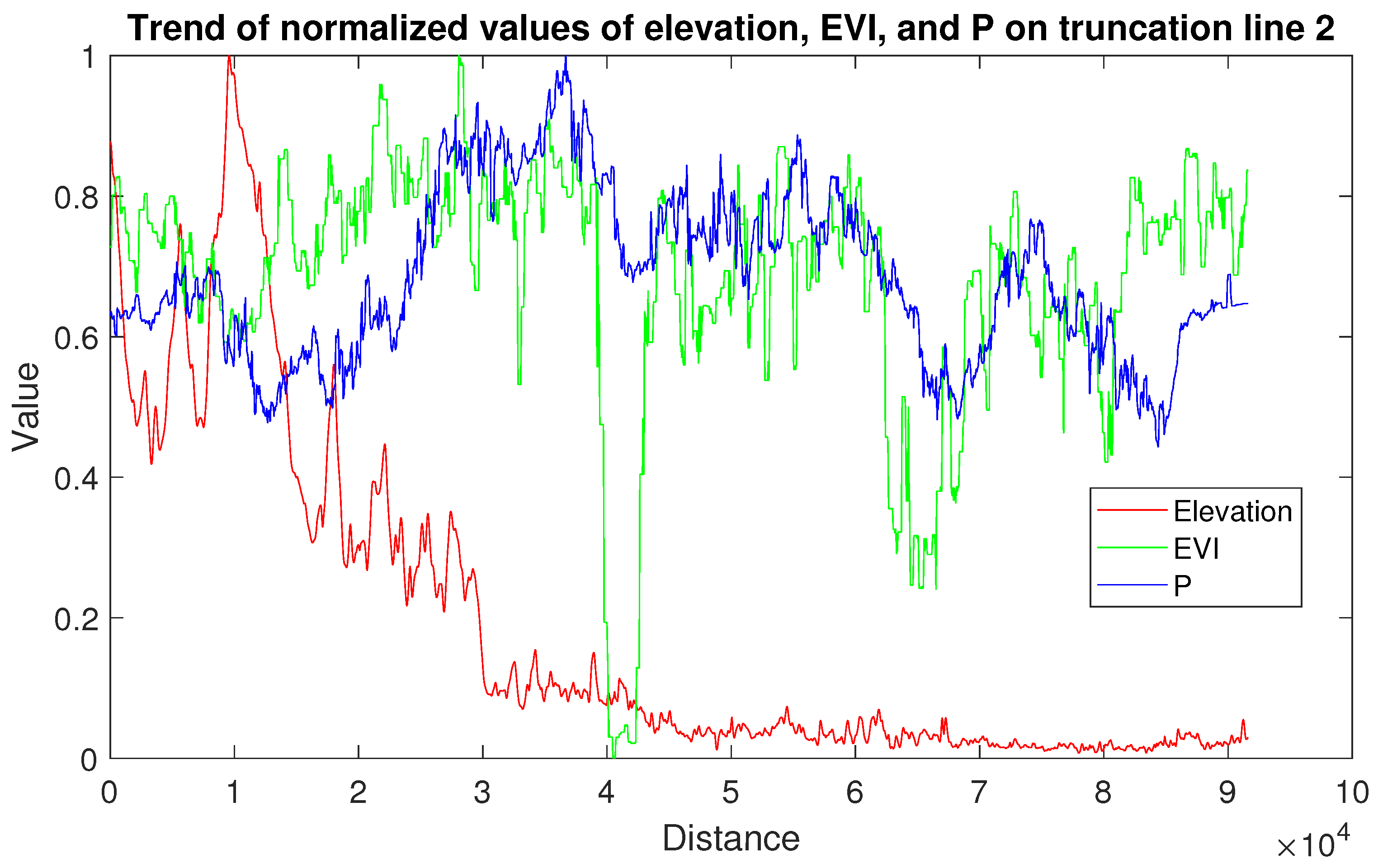
2.2.3. The Truncation Line Analysis Method
2.2.4. Statistical Analysis
3. Results
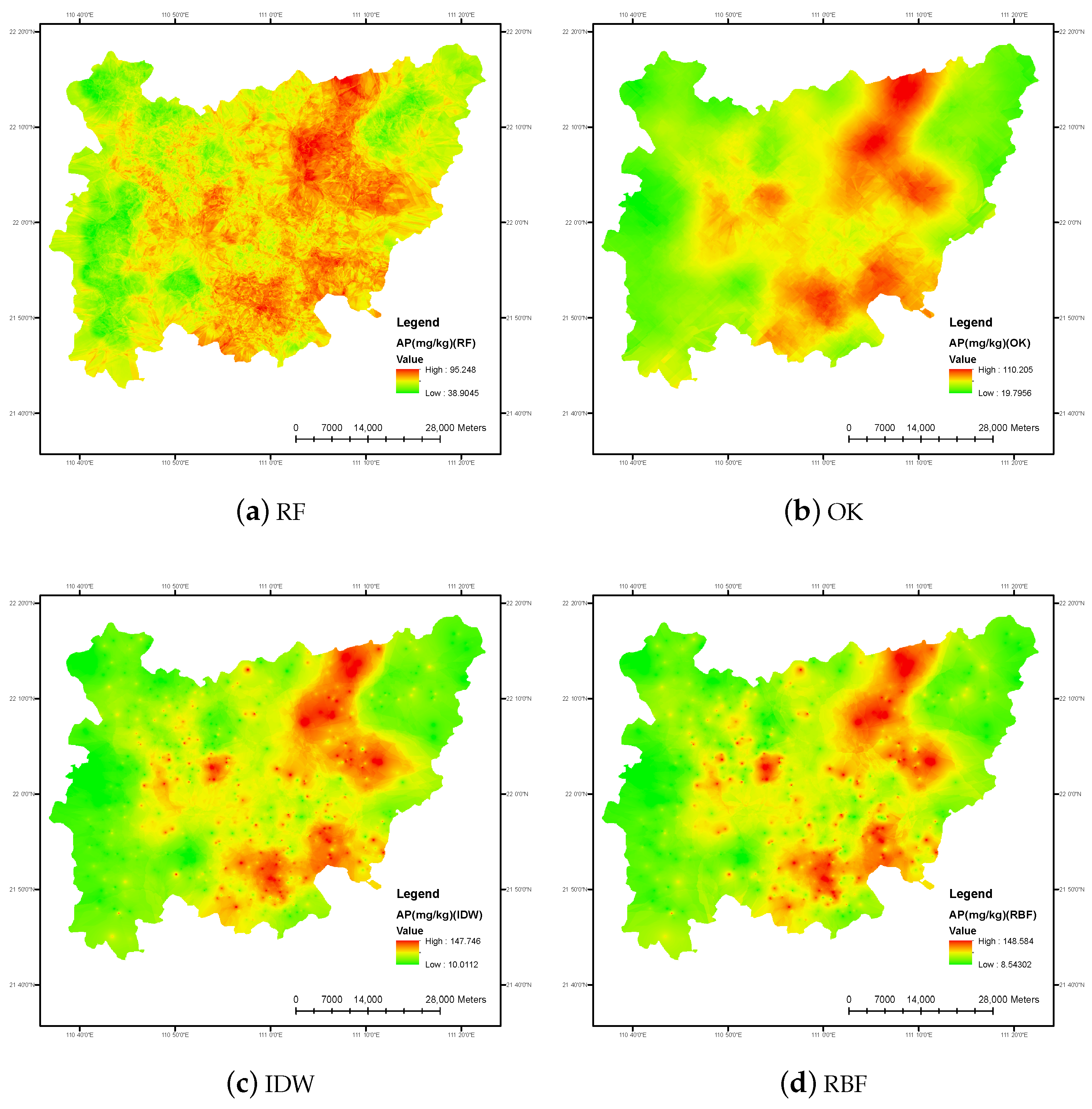
3.1. Results of the Digital Soil Mapping Based on Four Different Spatial Interpolation Models
3.1.1. Parameters Setting
- For OK, the nugget, partial sill, lag size, and the number of lags were set to 958.4114, 277.2129, 1150.591, and 12, respectively. The Gaussian Model was chosen as the semivariogram model.
- For IDW, the power was set to 1.
- For RBF, the kernel function and parameter were set to Completely Regularized Spline and 0.0846, respectively.
- The mapping unit for all models, i.e., pixel size, was set to 30 m.
3.1.2. Mapping Results Analysis of Different Models
3.2. Spatial Variation Analysis of Available Phosphorus over the Study Area
4. Discussion
4.1. Diagnosis for Collinearity of Key Driving Factors
4.2. The Performance Comparison between the Four Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, M.; Wang, L.; Ge, F.; Xie, B. Understanding the Dynamic Mechanism of Urban Land Use and Population Distribution Evolution from a Microscopic Perspective. ISPRS Int. J. Geo-Inf. 2022, 11, 536. [Google Scholar] [CrossRef]
- Xu, T.; Yi, S.; Zhou, Y.; Li, Q.; Liu, Y. Temporal and Spatial Changes and Driving Forces of Soil Properties in Subtropical Mountainous Areas from 2017 to 2020: A Case Study of Baokang County, Hubei Province, China. Land 2022, 11, 1735. [Google Scholar] [CrossRef]
- Grunwald, S.; Thompson, J.; Boettinger, J. Digital soil mapping and modeling at continental scales: Finding solutions for global issues. Soil Sci. Soc. Am. J. 2011, 75, 1201–1213. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.L.; Feng, L.; Song, X.D. Recent progress and future prospect of digital soil mapping: A review. J. Integr. Agric. 2017, 16, 2871–2885. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, A.X.; Liu, J.; Ma, T.; Yang, L.; Zhou, C. An adaptive uncertainty-guided sampling method for geospatial prediction and its application in digital soil mapping. Int. J. Geogr. Inf. Sci. 2023, 37, 476–498. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wu, Z.; Wang, B.; Wang, S. Geographical detector-based stratified regression kriging strategy for mapping soil organic carbon with high spatial heterogeneity. Catena 2021, 196, 104953. [Google Scholar] [CrossRef]
- Minasny, B.; Berglund, Ö.; Connolly, J.; Hedley, C.; de Vries, F.; Gimona, A.; Kempen, B.; Kidd, D.; Lilja, H.; Malone, B.; et al. Digital mapping of peatlands—A critical review. Earth-Sci. Rev. 2019, 196, 102870. [Google Scholar] [CrossRef]
- Yasrebi, J.; Saffari, M.; Fathi, H.; Karimian, N.; Moazallahi, M.; Gazni, R. Evaluation and comparison of ordinary kriging and inverse distance weighting methods for prediction of spatial variability of some soil chemical parameters. Res. J. Biol. Sci. 2009, 4, 93–102. [Google Scholar]
- Bhunia, G.S.; Shit, P.K.; Maiti, R. Spatial variability of soil organic carbon under different land use using radial basis function (RBF). Model. Earth Syst. Environ. 2016, 2, 17. [Google Scholar] [CrossRef]
- Apaydin, H.; Sonmez, F.K.; Yildirim, Y.E. Spatial interpolation techniques for climate data in the GAP region in Turkey. Clim. Res. 2004, 28, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Hani, A.; Abari, S.A.H. Determination of Cd, Zn, K, pH, TNV, organic material and electrical conductivity (EC) distribution in agricultural soils using geostatistics and GIS (case study: South-Western of Natanz-Iran). Int. J. Agric. Biosyst. Eng. 2011, 5, 852–855. [Google Scholar]
- Gia Pham, T.; Kappas, M.; Van Huynh, C.; Hoang Khanh Nguyen, L. Application of ordinary kriging and regression kriging method for soil properties mapping in hilly region of Central Vietnam. ISPRS Int. J. Geo-Inf. 2019, 8, 147. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Webster, R.; Shi, Z. Mapping soil salinity in the Yangtze delta: REML and universal kriging (E-BLUP) revisited. Geoderma 2015, 237, 71–77. [Google Scholar] [CrossRef]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil organic carbon concentrations and stocks on Barro Colorado Island—Digital soil mapping using Random Forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Pereira, G.W.; Valente, D.S.M.; de Queiroz, D.M.; Santos, N.T.; Fernandes-Filho, E.I. Soil mapping for precision agriculture using support vector machines combined with inverse distance weighting. Precis. Agric. 2022, 23, 1189–1204. [Google Scholar] [CrossRef]
- Bodaghabadi, M.B.; Martínez-Casasnovas, J.; Salehi, M.H.; Mohammadi, J.; Borujeni, I.E.; Toomanian, N.; Gandomkar, A. Digital soil mapping using artificial neural networks and terrain-related attributes. Pedosphere 2015, 25, 580–591. [Google Scholar] [CrossRef] [Green Version]
- Holleran, M.; Levi, M.; Rasmussen, C. Quantifying soil and critical zone variability in a forested catchment through digital soil mapping. Soil 2015, 1, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Dai, F.; Zhou, Q.; Lv, Z.; Wang, X.; Liu, G. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Suleymanov, A.; Gabbasova, I.; Komissarov, M.; Suleymanov, R.; Garipov, T.; Tuktarova, I.; Belan, L. Random Forest Modeling of Soil Properties in Saline Semi-Arid Areas. Agriculture 2023, 13, 976. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, Random Forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Dong, W.; Wu, T.; Luo, J.; Sun, Y.; Xia, L. Land parcel-based digital soil mapping of soil nutrient properties in an alluvial-diluvia plain agricultural area in China. Geoderma 2019, 340, 234–248. [Google Scholar] [CrossRef]
- Pahlavan-Rad, M.R.; Khormali, F.; Toomanian, N.; Brungard, C.W.; Kiani, F.; Komaki, C.B.; Bogaert, P. Legacy soil maps as a covariate in digital soil mapping: A case study from Northern Iran. Geoderma 2016, 279, 141–148. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, S.; Geng, W.; Ding, Y.; Jiang, X. Use of geographically weighted regression (GWR) to reveal spatially varying relationships between Cd Accumulation and soil properties at field scale. Land 2022, 11, 635. [Google Scholar] [CrossRef]
- Osterholz, W.; King, K.; Williams, M.; Hanrahan, B.; Duncan, E. Stratified soil sampling improves predictions of P concentration in surface runoff and tile discharge. Soil Syst. 2020, 4, 67. [Google Scholar] [CrossRef]
- Sims, J.T. Soil test phosphorus: Olsen P. In Methods Phosphorus Analysis Soils, Sediments, Residuals, Waters; North Carolina State University: Raleigh, NC, USA, 2000; Volume 20. [Google Scholar]
- Records, R.M.; Wohl, E.; Arabi, M. Phosphorus in the river corridor. Earth-Sci. Rev. 2016, 158, 65–88. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Onodera, S.I.; Saito, M.; Okuda, N.; Okubo, T. Estimation of phosphorus transport influenced by climate change in a rice paddy catchment using SWAT. Int. J. Environ. Res. 2021, 15, 759–772. [Google Scholar] [CrossRef]
- Pistocchi, C.; Mészáros, É.; Tamburini, F.; Frossard, E.; Bünemann, E.K. Biological processes dominate phosphorus dynamics under low phosphorus availability in organic horizons of temperate forest soils. Soil Biol. Biochem. 2018, 126, 64–75. [Google Scholar] [CrossRef] [Green Version]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens. 2006, 27, 1135–1158. [Google Scholar] [CrossRef]
- Wang, R.; Zou, R.; Liu, J.; Liu, L.; Hu, Y. Spatial distribution of soil nutrients in farmland in a hilly region of the pearl river delta in China based on geostatistics and the inverse distance weighting method. Agriculture 2021, 11, 50. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Behrens, T.; Schmidt, K.; Viscarra Rossel, R.A.; Gries, P.; Scholten, T.; MacMillan, R.A. Spatial modelling with Euclidean distance fields and machine learning. Eur. J. Soil Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuchs, C.; Benjamini, Y. Multivariate profile charts for statistical process control. Technometrics 1994, 36, 182–195. [Google Scholar] [CrossRef]
- Yang, J.; Hendrix, T.D.; Chang, K.H.; Umphress, D. An empirical validation of complexity profile graph. In Proceedings of the 43rd Annual Southeast Regional Conference, Kennesaw, GA, USA, 18 March 2005; Volume 1, pp. 143–149. [Google Scholar]
- Craney, T.A.; Surles, J.G. Model-dependent variance inflation factor cutoff values. Qual. Eng. 2002, 14, 391–403. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77, 733–742. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Hegde, R.; Singh, S. Spatial prediction of major soil properties using Random Forest techniques—A case study in semi-arid tropics of South India. Geoderma Reg. 2017, 10, 154–162. [Google Scholar] [CrossRef]
- Chiao, L.Y.; Hsieh, C.H.; Chiu, T.S. Exploring spatiotemporal ecological variations by the multiscale interpolation. Ecol. Model. 2012, 246, 26–33. [Google Scholar] [CrossRef]
- Foster, M.P.; Evans, A.N. An evaluation of interpolation techniques for reconstructing ionospheric TEC maps. IEEE Trans. Geosci. Remote. Sens. 2008, 46, 2153–2164. [Google Scholar] [CrossRef]
- da Silva Júnior, J.C.; Medeiros, V.; Garrozi, C.; Montenegro, A.; Gonçalves, G.E. Random forest techniques for spatial interpolation of evapotranspiration data from Brazilian’s Northeast. Comput. Electron. Agric. 2019, 166, 105017. [Google Scholar] [CrossRef]
- Messenzehl, K.; Meyer, H.; Otto, J.C.; Hoffmann, T.; Dikau, R. Regional-scale controls on the spatial activity of rockfalls (Turtmann Valley, Swiss Alps)—A multivariate modeling approach. Geomorphology 2017, 287, 29–45. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Huang, Z.; Daniell, J.J. Can we improve the spatial predictions of seabed sediments? A case study of spatial interpolation of mud content across the southwest Australian margin. Cont. Shelf Res. 2011, 31, 1365–1376. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Bing, H.; Yang, Z.; Wang, J.; Sun, H.; Sun, S.; Luo, J. Variations in soil phosphorus biogeochemistry across six vegetation types along an altitudinal gradient in SW China. Catena 2016, 142, 102–111. [Google Scholar] [CrossRef]
- Liu, Z.P.; Shao, M.A.; Wang, Y.Q. Scale-dependent correlations between soil properties and environmental factors across the Loess Plateau of China. Soil Res. 2013, 51, 112–123. [Google Scholar] [CrossRef]
- Vidal-Vázquez, E.; Camargo, O.d.; Vieira, S.; Miranda, J.; Menk, J.; Siqueira, G.; Mirás-Avalos, J.; González, A.P. Multifractal analysis of soil properties along two perpendicular transects. Vadose Zone J. 2013, 12, vzj2012.0188. [Google Scholar] [CrossRef]




| Model | RMSE |
|---|---|
| RF | 32.01 |
| OK | 32.08 |
| RBF | 33.08 |
| IDW | 32.74 |
| Environment Variables | TPI | TWI | Aspect | Profile Curvature | Slope | Plane Curvature |
|---|---|---|---|---|---|---|
| importance | 31,970.42 (6) | 31,555.20 (7) | 28,539.34 (11) | 30,073.59 (10) | 32,466.85 (5) | 30706.98 (9) |
| Environment Variables | Altitude | Surface Fluctuation | Average Annual Temperature | Average Annual Precipitation | EVI | |
| importance | 35,362.74 (2) | 31,330.63 (8) | 33,080.58 (4) | 33,367.12 (3) | 37,989.11(1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Cheng, L.; Xu, R.; He, X.; Mo, W.; Xu, J. Assessing Spatial Variation and Driving Factors of Available Phosphorus in a Hilly Area (Gaozhou, South China) Using Modeling Approaches and Digital Soil Mapping. Agriculture 2023, 13, 1541. https://doi.org/10.3390/agriculture13081541
Zhang W, Cheng L, Xu R, He X, Mo W, Xu J. Assessing Spatial Variation and Driving Factors of Available Phosphorus in a Hilly Area (Gaozhou, South China) Using Modeling Approaches and Digital Soil Mapping. Agriculture. 2023; 13(8):1541. https://doi.org/10.3390/agriculture13081541
Chicago/Turabian StyleZhang, Wenhui, Liangwei Cheng, Ruitao Xu, Xiaohua He, Weihan Mo, and Jianbo Xu. 2023. "Assessing Spatial Variation and Driving Factors of Available Phosphorus in a Hilly Area (Gaozhou, South China) Using Modeling Approaches and Digital Soil Mapping" Agriculture 13, no. 8: 1541. https://doi.org/10.3390/agriculture13081541
APA StyleZhang, W., Cheng, L., Xu, R., He, X., Mo, W., & Xu, J. (2023). Assessing Spatial Variation and Driving Factors of Available Phosphorus in a Hilly Area (Gaozhou, South China) Using Modeling Approaches and Digital Soil Mapping. Agriculture, 13(8), 1541. https://doi.org/10.3390/agriculture13081541






