UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Research Area
2.2. Data Acquisition and Pre-Processing
2.2.1. UAV Multispectral Data
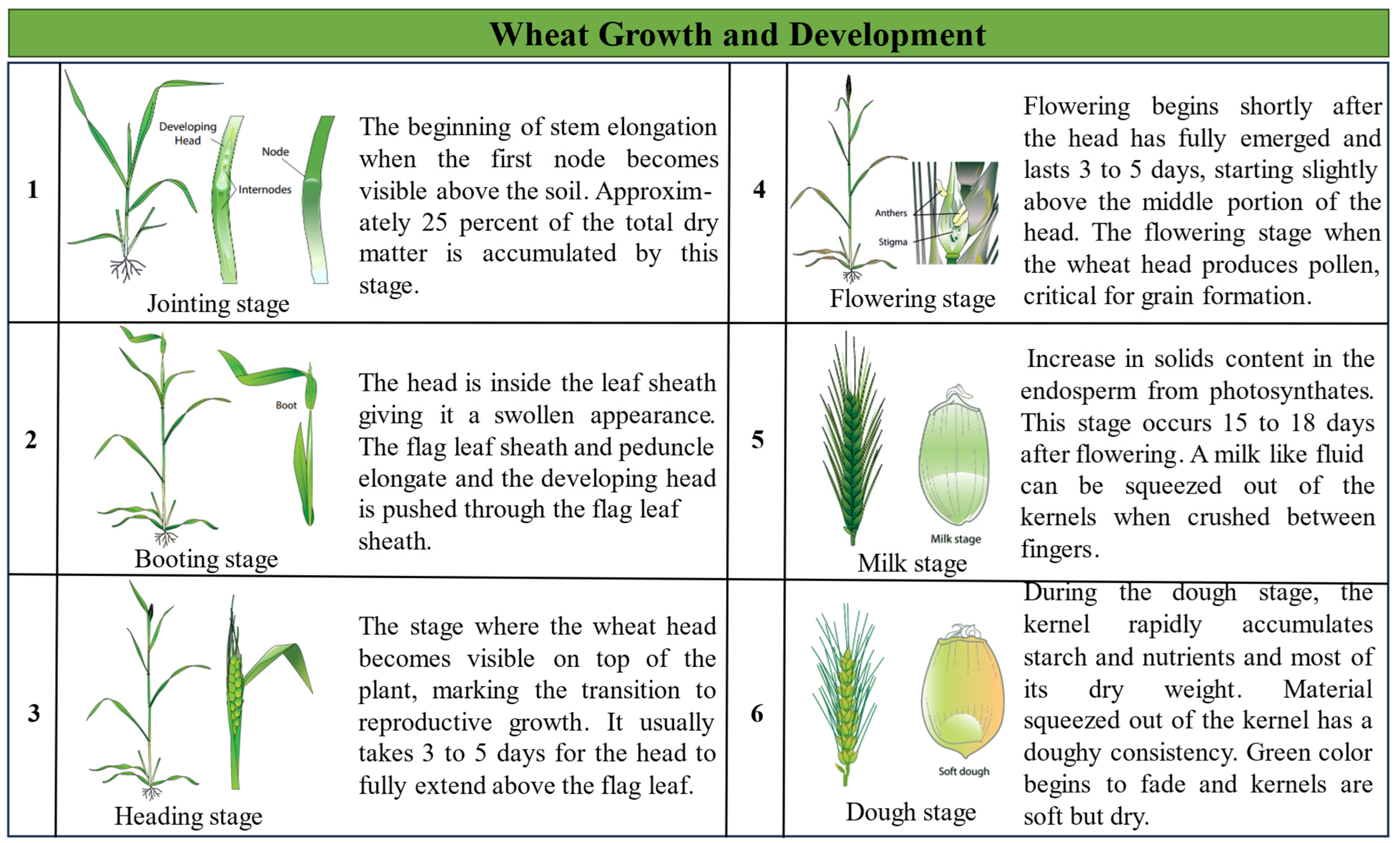
2.2.2. Field Data
- (1)
- Chlorophyll Content Measurement
- (2)
- Leaf Area Index Measurement
- (3)
- Plant Height Measurement
- (4)
- Biomass Measurement
- (5)
- Plant Water Content Measurement
- (6)
- Yield Measurement
2.3. Research Methods
2.3.1. Selection of Vegetation Index
2.3.2. Modeling Method
2.3.3. Comprehensive Growth Index (CGI)
- (1)
- CGI construction based on the equal-weight method
- (2)
- CGI construction based on the coefficient of variation method
- (3)
- CGI construction based on the contribution of single indicators to yield
- (1)
- Principle of Construction
- (2)
- Data Pre-processing and Feature Matrix Construction
- (3)
- Calculation of the weight matrix
- (4)
- Calculation of the CGIac
2.3.4. Evaluation Metrics
3. Results
3.1. Construction of CGIac
3.2. Performance Analysis of CGIac in Crop Yield
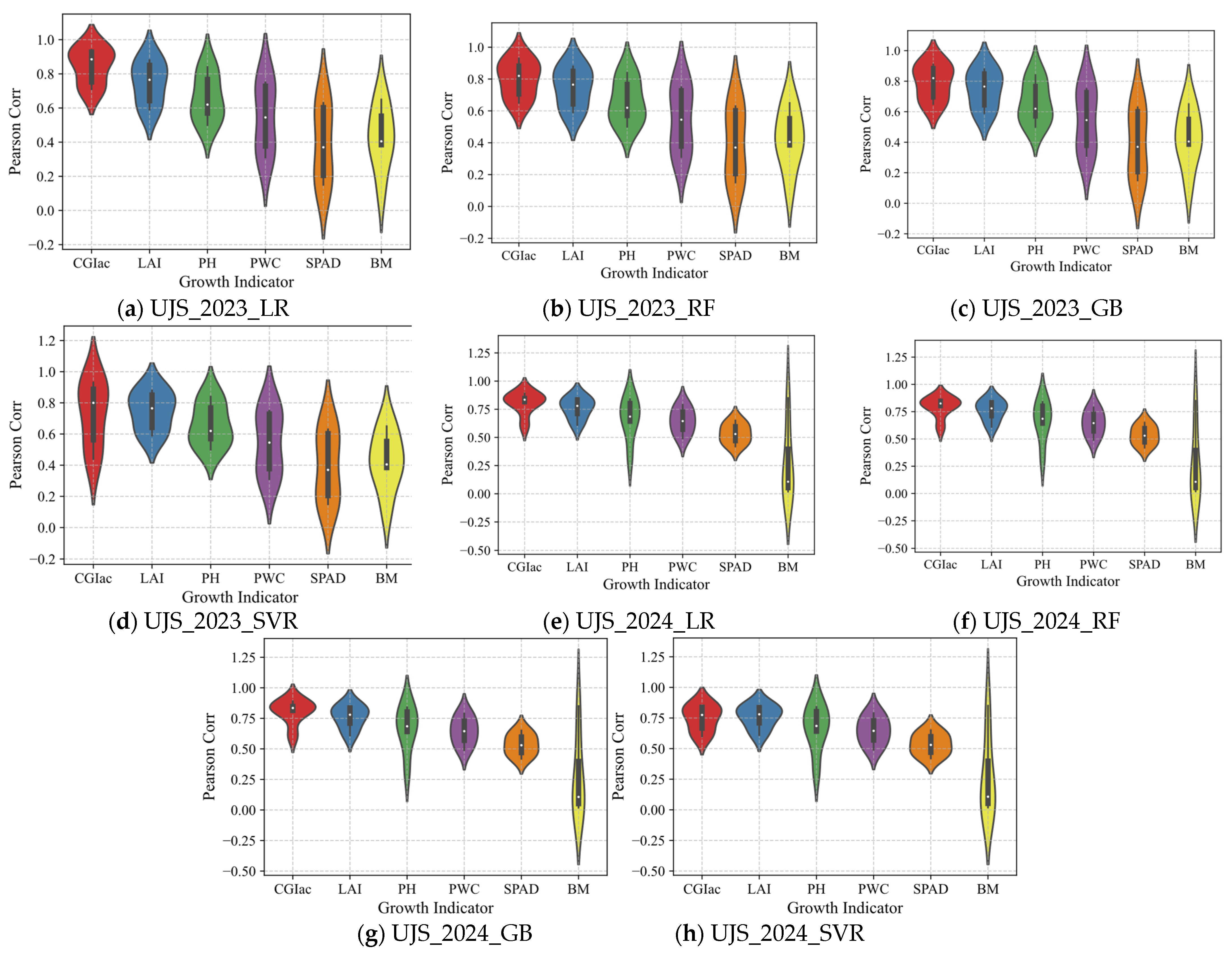
3.2.1. Correlation Analysis Between CGIac and Yield
3.2.2. Comparative Analysis of the Correlation Between Different CGI and Crop Yield
3.2.3. Evaluation of the Accuracy Variations in Yield Prediction with CGIac
3.3. Construction of CGI Inversion Model
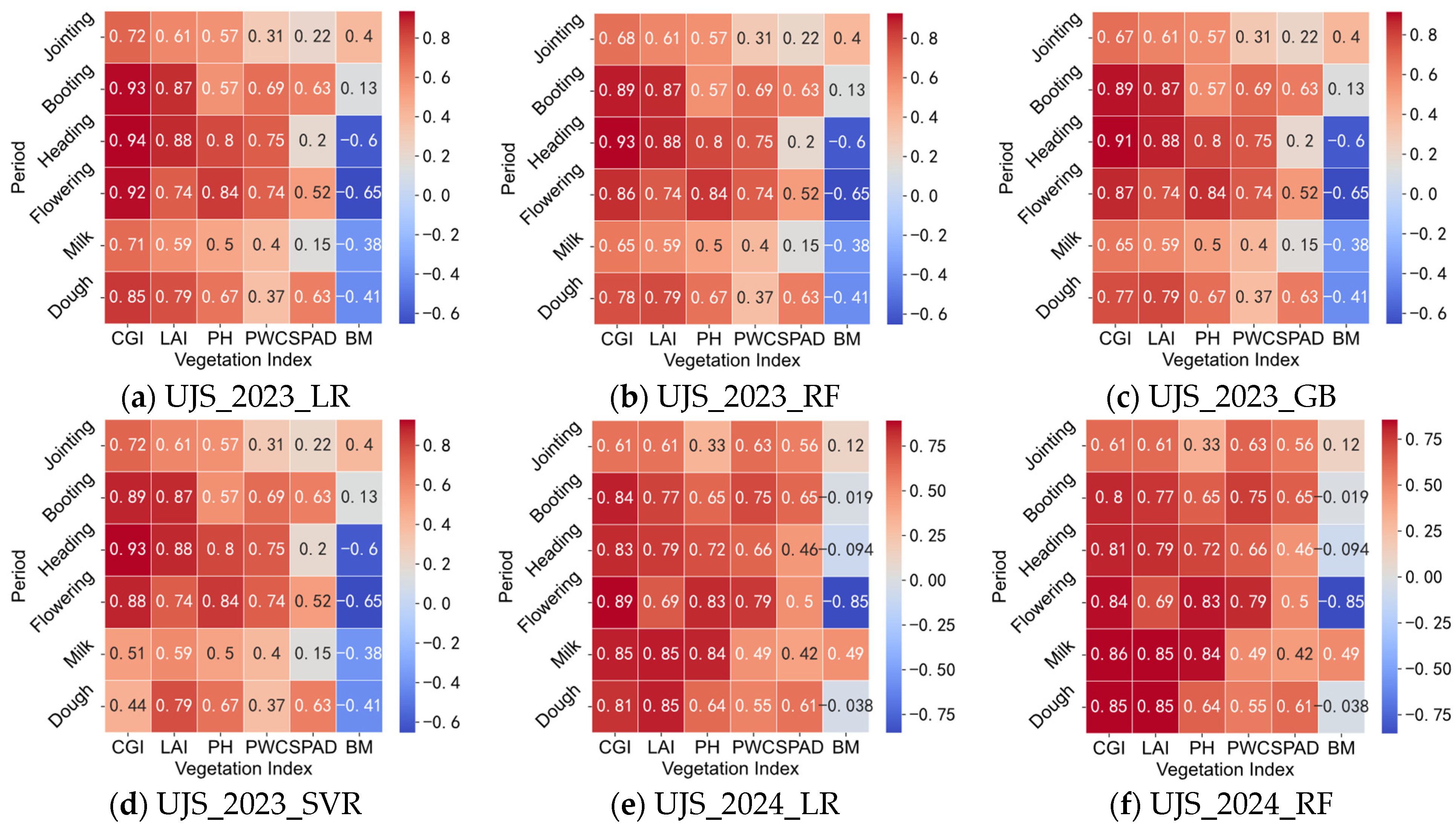
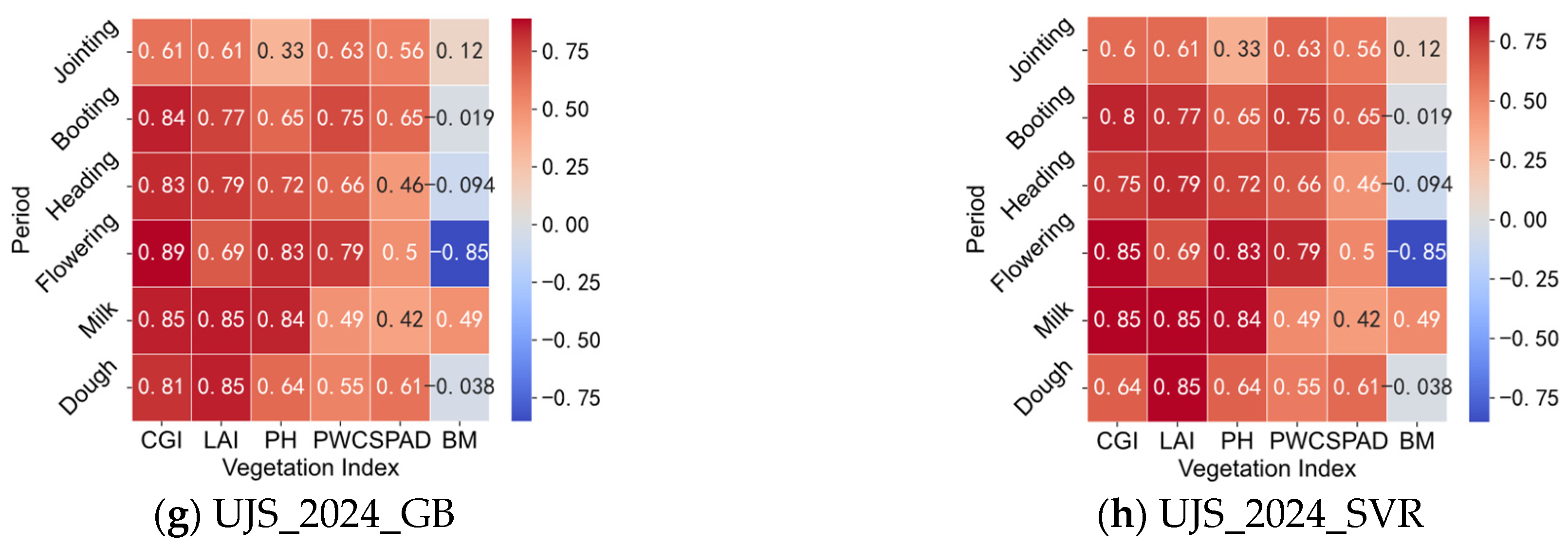
3.3.1. Correlation Analysis Between Vegetation Indices and CGIac
3.3.2. Selection of Input Features
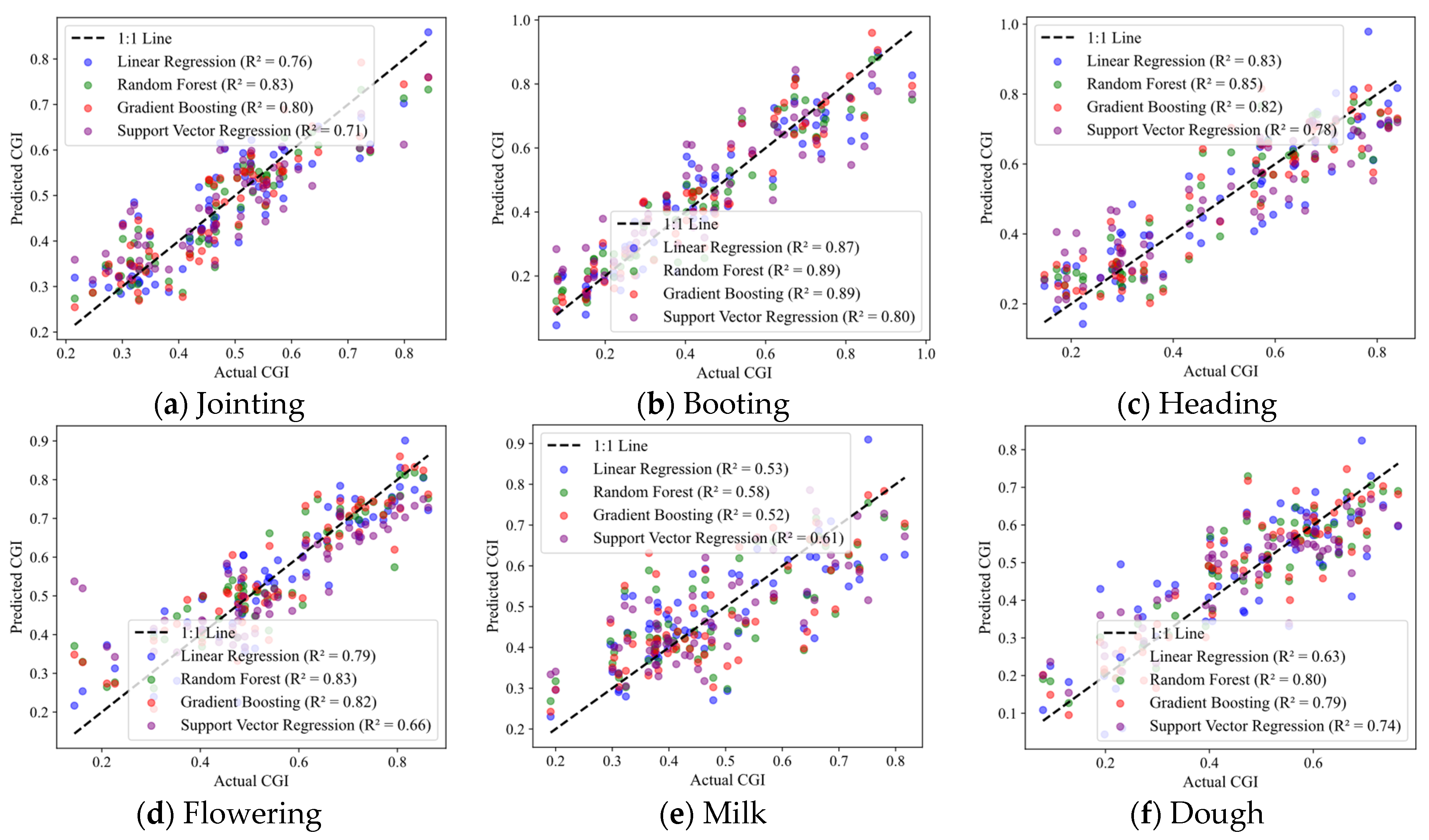
3.3.3. Results of the CGIac Inversion Model
3.4. Application of the Optimal Inversion Model in Regional Growth Monitoring
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Karmakar, P.; Teng, S.W.; Murshed, M.; Pang, S.; Li, Y.; Lin, H. Crop monitoring by multimodal remote sensing: A review. Remote Sens. Appl. Soc. Environ. 2024, 33, 101093. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, M.; Zeng, H.; Tian, F.; Potgieter, A.B.; Qin, X.; Yan, N.; Chang, S.; Zhao, Y.; Dong, Q.; et al. Challenges and Opportunities in Remote Sensing-Based Crop Monitoring: A Review. Natl. Sci. Rev. 2023, 10, nwac290. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Fang, W. UV-NDVI for real-time crop health monitoring in vertical farms. Smart Agric. Technol. 2024, 8, 100462. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, Z.; Dai, S.; Zhang, P.; Wei, X. Using UAV multispectral remote sensing with appropriate spatial resolution and machine learning to monitor wheat scab. Agriculture 2022, 12, 1785. [Google Scholar] [CrossRef]
- Ahmed, S.; Xin, H.; Faheem, M.; Qiu, B. Stability analysis of a sprayer uav with a liquid tank with different outer shapes and inner structures. Agriculture 2022, 12, 379. [Google Scholar] [CrossRef]
- Ahmed, S.; Qiu, B.; Ahmad, F.; Kong, C.W.; Xin, H. A state-of-the-art analysis of obstacle avoidance methods from the perspective of an agricultural sprayer UAV’s operation scenario. Agronomy 2021, 11, 1069. [Google Scholar] [CrossRef]
- Ahmed, S.; Qiu, B.; Kong, C.W.; Xin, H.; Ahmad, F.; Lin, J. A data-driven dynamic obstacle avoidance method for liquid-carrying plant protection UAVs. Agronomy 2022, 12, 873. [Google Scholar] [CrossRef]
- Zhang, S.; Qiu, B.; Xue, X.; Sun, T.; Gu, W.; Zhou, F.; Sun, X. Effects of crop protection unmanned aerial system flight speed, height on effective spraying width, droplet deposition and penetration rate, and control effect analysis on wheat aphids, powdery mildew, and head blight. Appl. Sci. 2021, 11, 712. [Google Scholar] [CrossRef]
- Memon, M.S.; Chen, S.; Niu, Y.; Zhou, W.; Elsherbiny, O.; Liang, R.; Du, Z.; Guo, X. Evaluating the Efficacy of Sentinel-2B and Landsat-8 for Estimating and Mapping Wheat Straw Cover in Rice–Wheat Fields. Agronomy 2023, 13, 2691. [Google Scholar] [CrossRef]
- Olson, D.; Anderson, J. Review on unmanned aerial vehicles, remote sensors, imagery processing, and their applications in agriculture. Agron. J. 2021, 113, 971–992. [Google Scholar] [CrossRef]
- Liu, X.; Wu, L.; Chen, L.; Ma, Y.; Li, T.; Wu, T. LAI inversion and growth evaluation of winter wheat using semi-empirical and semi-mechanistic modeling. Trans. Chin. Soc. Agric. Eng. 2024, 40, 162–170. [Google Scholar]
- Wang, R.; Tuerxun, N.; Zheng, J. Improved estimation of SPAD values in walnut leaves by combining spectral, texture, and structural information from UAV-based multispectral image. Sci. Hortic. 2024, 328, 112940. [Google Scholar] [CrossRef]
- Shu, M.; Li, Q.; Ghafoor, A.; Zhu, J.; Li, B.; Ma, Y. Using the plant height and canopy coverage to estimation maize aboveground biomass with UAV digital images. Eur. J. Agron. 2023, 151, 126957. [Google Scholar] [CrossRef]
- Pei, H.; Feng, H.; Li, C.; Jin, X.; Li, Z.; Yang, G. Remote sensing monitoring of winter wheat growth with UAV based on comprehensive index. Trans. Chin. Soc. Agric. Eng. 2017, 33, 74–82. [Google Scholar]
- Xu, Y.; Cheng, Q.; Wei, X.; Yang, B.; Xia, S.; Rui, T.; Zhang, S. Monitoring of winter wheat growth under UAV using variation coefficient method and optimized neural network. Trans. Chin. Soc. Agric. Eng. 2021, 37, 71–80. [Google Scholar]
- El-Hendawy, S.; Al-Suhaibani, N.; Al-Ashkar, I.; Alotaibi, M.; Tahir, M.U.; Solieman, T.; Hassan, W.M. Combining genetic analysis and multivariate modeling to evaluate spectral reflectance indices as indirect selection tools in wheat breeding under water deficit stress conditions. Remote Sens. 2020, 12, 1480. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, F.; Zhang, L.; Lin, Y.; Wang, S.; Xie, Y. UNVI-based time series for vegetation discrimination using separability analysis and random forest classification. Remote Sens. 2020, 12, 529. [Google Scholar] [CrossRef]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Bannari, A.; Asalhi, H.; Teillet, P.M. Transformed difference vegetation index (TDVI) for vegetation cover mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 3053–3055. [Google Scholar] [CrossRef]
- Burns, B.W.; Green, V.S.; Hashem, A.A.; Massey, J.H.; Shew, A.M.; Adviento-Borbe, M.A.A.; Milad, M. Determining nitrogen deficiencies for maize using various remote sensing indices. Precis. Agric. 2022, 23, 791–811. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Yan, K.; Gao, S.; Chi, H.; Qi, J.; Song, W.; Tong, Y.; Mu, X.; Yan, G. Evaluation of the vegetation-index-based dimidiate pixel model for fractional vegetation cover estimation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4400514. [Google Scholar] [CrossRef]
- Sewiko, R.; Sagala, H.A.M.U. The use of drone and visible atmospherically resistant index (VARI) algorithm implementation in mangrove ecosystem health’s monitoring. Asian J. Aquat. Sci. 2022, 5, 322–329. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, L.; Liu, B.; Wu, Y.; Ma, J.; Zhang, W.; Wang, B.; Chen, Z. Estimation of Winter Wheat Yield using multiple temporal vegetation indices derived from UAV-Based multispectral and hyperspectral imagery. Remote Sens. 2023, 15, 4800. [Google Scholar] [CrossRef]
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2015, 16, 62–76. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from Hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, G. Determination of green aboveground biomass in desert steppe using litter-soil-adjusted vegetation index. Eur. J. Remote Sens. 2014, 47, 611–625. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial color infrared photography for determining early in-season nitrogen requirements in corn. Agron. J. 2006, 98, 968–977. [Google Scholar] [CrossRef]
- Mehrotra, S.; Kumar, A.; Roy, A. Classifying Pinus roxburghii Using an Innovative Training Approach of Fuzzy Models While Handling Heterogeneity Within Class in Western Himalayan Forests. J. Indian. Soc. Remote Sens. 2024, 52, 1269–1283. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Kim, Y.S. Comparison of the decision tree, artificial neural network, and linear regression methods based on the number and types of independent variables and sample size. Expert Syst. Appl. 2008, 34, 1227–1234. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar] [CrossRef]
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Tao, H.; Xu, L.; Feng, H.; Yang, G.; Miao, M.; Lin, B. Monitoring of winter wheat growth based on UAV hyperspectral growth index. Trans. Chin. Soc. Agric. Mach. 2020, 51, 180–191. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, W.; Qiu, S.; Wang, J.; Wei, Z. Collaborative analysis on the marked ages of rice wines by electronic tongue and nose based on different feature data sets. Sensors 2020, 20, 1065. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Stone, M. Cross-validation: A review. Stat. J. Theor. Appl. Stat. 1978, 9, 127–139. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, T.; Ding, F.; Ding, D.; Wu, W.; Yao, Z.; Liu, T.; Huo, Z.; Sun, C. Wheat LAI Estimation in Main Growth Period Based on UAV Images. J. Agric. Sci. Technol. 2021, 23, 89–97. Available online: https://www.nkdb.net/EN/10.13304/j.nykjdb.2019.0515 (accessed on 12 September 2024).
- Brisco, B.; Brown, R.J.; Hirose, T.; McNairn, H.; Staenz, K. Precision Agriculture and the Role of Remote Sensing: A Review. Can. J. Remote Sens. 1998, 24, 315–327. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
- Quemada, C.; Pérez-Escudero, J.M.; Gonzalo, R.; Ederra, I.; Santesteban, L.G.; Torres, N.; Iriarte, J.C. Remote Sensing for Plant Water Content Monitoring: A Review. Remote Sens. 2021, 13, 2088. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, Y.; Cheng, M.; Sun, C. Comprehensive Growth Index (CGI): A Comprehensive Indicator from UAV-Observed Data for Winter Wheat Growth Status Monitoring. Agronomy 2023, 13, 2883. [Google Scholar] [CrossRef]
- Prasad, N.R.; Patel, N.R.; Danodia, A. Crop Yield Prediction in Cotton for Regional Level Using Random Forest Approach. Spat. Inf. Res. 2021, 29, 195–206. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]


| Vegetation Index | Formula | References |
|---|---|---|
| Normalized difference vegetation index (NDVI) | [19,20] | |
| Transformed difference vegetation index (TDVI) | [19] | |
| Green normalized difference vegetation index (GNDVI) | [20,21] | |
| Normalized difference red-edge (NDRE) | [20,22] | |
| Renormalized difference vegetation index (RDVI) | [23,24] | |
| Difference vegetation index (DVI) | [23,25] | |
| Visible atmospherically resistant index (VARI) | [26] | |
| Ratio vegetation index (RVI) | [23] | |
| Simple ratio (SR) | [24,27] | |
| Modified simple ratio (MSR) | [24,28] | |
| Enhanced vegetation index (EVI) | [23] | |
| Enhanced vegetation index 2 (EVI2) | [23] | |
| Soil adjusted vegetation index (SAVI) | [29] | |
| Optimized soil adjusted vegetation index (OSAVI) | [28] | |
| Green soil-adjusted vegetation index (GSAVI) | [30] | |
| Green optimized soil-adjusted vegetation index (GOSAVI) | [31] | |
| Modified soil-adjusted vegetation index 2 (MSAVI2) | [32] | |
| Green chlorophyll index (GCI) | [20] | |
| Red-edge chlorophyll index (RECI) | [33] | |
| Green-red vegetation index (GRVI) | [34] | |
| Green-blue vegetation index (GBVI) | [34] | |
| Simplified canopy chlorophyll content index (SCCCI) | [35] | |
| Modified chlorophyll absorption in reflectance index (MCARI) | [28,34] | |
| Transformed chlorophyll absorption in reflectance index (TCARI) | [28,34] | |
| MCARI/OSAVI | MCARI/OSAVI | [28] |
| TACRI/OSAVI | TACRI/OSAVI | [28] |
| Wide dynamic range vegetation index (WDRVI) | [36] | |
| Non-linear index (NLI) | [24] | |
| Modified non-linear index (MNLI) | [24] | |
| Triangular vegetation index (TVI) | [37] |
| Model | Growth Stage | CGIac |
|---|---|---|
| LR | Jointing | G1 = 0.271758 × BM + 0.304704 × LAI + 0.104303 × PH + 0.02197 × SPAD + 0.297265 × PWC |
| Booting | G2 = 0.034661 × BM + 0.433267 × LAI + 0.006892 × PH + 0.253023 × SPAD + 0.272156 × PWC | |
| Heading | G3 = 0.011324 × BM + 0.489689 × LAI + 0.236703 × PH + 0.099299 × SPAD + 0.162987 × PWC | |
| Flowering | G4 = −0.0766 × BM + 0.277624 × LAI + 0.440874 × PH + 0.066658 × SPAD + 0.138243 × PWC | |
| Milk | G5 = −0.30049 × BM + 0.324447 × LAI + 0.250528 × PH − 0.06709 × SPAD − 0.05745 × PWC | |
| Dough | G6 = −0.18787 × BM + 0.441084 × LAI + 0.135365 × PH + 0.00168 × SPAD − 0.234 × PWC | |
| RF | Jointing | G1 = 0.17298 × BM + 0.341312 × LAI + 0.259386 × PH + 0.123208 × SPAD + 0.103113 × PWC |
| Booting | G2 = 0.014361 × BM + 0.829011 × LAI + 0.018984 × PH + 0.046781 × SPAD + 0.090864 × PWC | |
| Heading | G3 = 0.041499 × BM + 0.602172 × LAI + 0.209805 × PH + 0.062957 × SPAD + 0.083567 × PWC | |
| Flowering | G4 = 0.058259 × BM + 0.088018 × LAI + 0.747809 × PH + 0.052486 × SPAD + 0.053429 × PWC | |
| Milk | G5 = 0.080248 × BM + 0.406717 × LAI + 0.188087 × PH + 0.098313 × SPAD + 0.226635 × PWC | |
| Dough | G6 = 0.065111 × BM + 0.721612 × LAI + 0.080778 × PH + 0.049925 × SPAD + 0.082573 × PWC | |
| GB | Jointing | G1 = 0.213924 × BM + 0.354581 × LAI + 0.171247 × PH + 0.164739 × SPAD + 0.095509 × PWC |
| Booting | G2 = 0.010774 × BM + 0.816524 × LAI + 0.020577 × PH + 0.045704 × SPAD + 0.106421 × PWC | |
| Heading | G3 = 0.032358 × BM + 0.722393 × LAI + 0.099169 × PH + 0.084201 × SPAD + 0.061879 × PWC | |
| Flowering | G4 = 0.057654 × BM + 0.097934 × LAI + 0.739065 × PH + 0.06869 × SPAD + 0.036656 × PWC | |
| Milk | G5 = 0.07444 × BM + 0.461609 × LAI + 0.139829 × PH + 0.102316 × SPAD + 0.221806 × PWC | |
| Dough | G6 = 0.079261 × BM + 0.702568 × LAI + 0.079209 × PH + 0.036209 × SPAD + 0.102752 × PWC | |
| SVR | Jointing | G1 = 0.29722 × BM + 0.21063 × LAI + 0.113377 × PH + 0.070007 × SPAD + 0.308767 × PWC |
| Booting | G2 = 0.126434 × BM + 0.285509 × LAI + 0.212022 × PH + 0.164219 × SPAD + 0.211816 × PWC | |
| Heading | G3 = 0.153201 × BM + 0.357273 × LAI + 0.206744 × PH + 0.092045 × SPAD + 0.190736 × PWC | |
| Flowering | G4 = 0.13485 × BM + 0.222092 × LAI + 0.406385 × PH + 0.107272 × SPAD + 0.129401 × PWC | |
| Milk | G5 = 0.292152 × BM + 0.230943 × LAI + 0.273961 × PH + 0.078397 × SPAD + 0.124547 × PWC | |
| Dough | G6 = 0.415469 × BM + 0.322669 × LAI + 0.120148 × PH + 0.072594 × SPAD + 0.069119 × PWC |
| Growth Stages | Model | Without CGI | CGIac | CGIav | CGIcv | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (t/ha) | R2 | RMSE (t/ha) | R2 | RMSE (t/ha) | R2 | RMSE (t/ha) | ||
| Jointing | LR | 0.370 | 0.0593 | 0.377 | 0.0587 | 0.370 | 0.0593 | 0.375 | 0.0589 |
| RF | 0.379 | 0.0586 | 0.433 | 0.0535 | 0.337 | 0.0625 | 0.448 | 0.052 | |
| GB | 0.460 | 0.0508 | 0.478 | 0.0492 | 0.360 | 0.0603 | 0.478 | 0.0492 | |
| SVR | 0.366 | 0.0597 | 0.360 | 0.0603 | 0.366 | 0.0597 | 0.368 | 0.0595 | |
| Booting | LR | 0.643 | 0.0336 | 0.643 | 0.0336 | 0.643 | 0.0336 | 0.644 | 0.0336 |
| RF | 0.613 | 0.0365 | 0.622 | 0.0356 | 0.603 | 0.0374 | 0.605 | 0.0372 | |
| GB | 0.604 | 0.0373 | 0.623 | 0.0355 | 0.626 | 0.0352 | 0.619 | 0.0359 | |
| SVR | 0.499 | 0.0472 | 0.527 | 0.0446 | 0.497 | 0.0474 | 0.503 | 0.0468 | |
| Heading | LR | 0.573 | 0.0402 | 0.573 | 0.0402 | 0.573 | 0.0402 | 0.575 | 0.0400 |
| RF | 0.523 | 0.0450 | 0.541 | 0.0433 | 0.477 | 0.0493 | 0.474 | 0.0495 | |
| GB | 0.522 | 0.0451 | 0.530 | 0.0443 | 0.499 | 0.0472 | 0.532 | 0.0441 | |
| SVR | 0.380 | 0.0584 | 0.396 | 0.0569 | 0.376 | 0.0588 | 0.376 | 0.0588 | |
| Flowering | LR | 0.757 | 0.0229 | 0.757 | 0.0229 | 0.757 | 0.0229 | 0.755 | 0.0231 |
| RF | 0.756 | 0.0230 | 0.780 | 0.0207 | 0.762 | 0.0224 | 0.757 | 0.0229 | |
| GB | 0.755 | 0.0231 | 0.772 | 0.0215 | 0.768 | 0.0219 | 0.736 | 0.0249 | |
| SVR | 0.571 | 0.0404 | 0.586 | 0.0390 | 0.573 | 0.0402 | 0.607 | 0.037 | |
| Milk | LR | 0.380 | 0.0584 | 0.468 | 0.0501 | 0.341 | 0.0621 | 0.268 | 0.069 |
| RF | 0.588 | 0.0389 | 0.637 | 0.0342 | 0.560 | 0.0415 | 0.426 | 0.0541 | |
| GB | 0.584 | 0.0392 | 0.551 | 0.0423 | 0.602 | 0.0375 | 0.239 | 0.0717 | |
| SVR | 0.363 | 0.0600 | 0.411 | 0.0555 | 0.384 | 0.0580 | 0.235 | 0.0721 | |
| Dough | LR | 0.544 | 0.0429 | 0.544 | 0.0429 | 0.544 | 0.0429 | 0.546 | 0.0428 |
| RF | 0.600 | 0.0377 | 0.589 | 0.0387 | 0.594 | 0.0382 | 0.575 | 0.0400 | |
| GB | 0.574 | 0.0402 | 0.545 | 0.0429 | 0.557 | 0.0417 | 0.507 | 0.0464 | |
| SVR | 0.362 | 0.0601 | 0.381 | 0.0584 | 0.375 | 0.0589 | 0.374 | 0.0590 | |
| VI | Jointing | Booting | Heading | Flowering | Milk | Dough |
|---|---|---|---|---|---|---|
| RECI | 0.775 ** | 0.748 ** | 0.760 ** | 0.906 ** | 0.815 ** | 0.923 ** |
| NDRE | 0.761 ** | 0.743 ** | 0.757 ** | 0.908 ** | 0.828 ** | 0.919 ** |
| SCCCI | 0.739 ** | 0.736 ** | 0.753 ** | 0.873 ** | 0.826 ** | 0.904 ** |
| GOSAVI | 0.753 ** | 0.896 ** | 0.892 ** | 0.894 ** | 0.780 ** | 0.890 ** |
| GCI | 0.743 ** | 0.701 ** | 0.710 ** | 0.916 ** | 0.789 ** | 0.919 ** |
| GSAVI | 0.771 ** | 0.911 ** | 0.910 ** | 0.864 ** | 0.752 ** | 0.860 ** |
| OSAVI | 0.762 ** | 0.883 ** | 0.887 ** | 0.861 ** | 0.718 ** | 0.852 ** |
| GNDVI | 0.716 ** | 0.676 ** | 0.686 ** | 0.910 ** | 0.806 ** | 0.905 ** |
| MSAVI2 | 0.774 ** | 0.904 ** | 0.906 ** | 0.845 ** | 0.707 ** | 0.822 ** |
| RDVI | 0.772 ** | 0.899 ** | 0.902 ** | 0.848 ** | 0.712 ** | 0.837 ** |
| EVI | 0.776 ** | 0.903 ** | 0.908 ** | 0.837 ** | 0.711 ** | 0.841 ** |
| MNLI | 0.781 ** | 0.90 ** | 0.905 ** | 0.844 ** | 0.710 ** | 0.841 ** |
| SAVI | 0.767 ** | 0.900 ** | 0.904 ** | 0.841 ** | 0.706 ** | 0.824 ** |
| SR | 0.734 ** | 0.690 ** | 0.689 ** | 0.889 ** | 0.718 ** | 0.897 ** |
| EVI2 | 0.771 ** | 0.903 ** | 0.905 ** | 0.840 ** | 0.705 ** | 0.821 ** |
| NLI | 0.716 ** | 0.786 ** | 0.806 ** | 0.873 ** | 0.719 ** | 0.865 ** |
| MSR | 0.725 ** | 0.675 ** | 0.674 ** | 0.887 ** | 0.722 ** | 0.896 ** |
| TDVI | 0.767 ** | 0.903 ** | 0.907 ** | 0.831 ** | 0.697 ** | 0.797 ** |
| DVI | 0.771 ** | 0.907 ** | 0.907 ** | 0.824 ** | 0.688 ** | 0.768 ** |
| WDRVI | 0.703 ** | 0.648 ** | 0.651 ** | 0.880 ** | 0.722 ** | 0.895 ** |
| TVI | 0.749 ** | 0.902 ** | 0.904 ** | 0.815 ** | 0.668 ** | 0.747 ** |
| NDVI | 0.684 ** | 0.628 ** | 0.630 ** | 0.872 ** | 0.714 ** | 0.867 ** |
| VARI | 0.612 ** | 0.602 ** | 0.585 ** | 0.765 ** | 0.396 * | 0.766 ** |
| MCARI | 0.512 ** | 0.725 ** | 0.738 ** | 0.664 ** | 0.453 ** | 0.662 ** |
| GRVI | 0.468 ** | 0.460 ** | 0.360 * | 0.679 ** | 0.302 | 0.719 ** |
| MCAR/IOSAVI | 0.381 * | 0.628 ** | 0.643 ** | 0.565 ** | 0.253 | 0.313 |
| TCARI/OSAVI | 0.568 ** | 0.621 ** | 0.613 ** | 0.759 ** | 0.685 ** | 0.893 ** |
| TCARI | 0.568 ** | 0.682 ** | 0.671 ** | 0.777 ** | 0.685 ** | 0.918 ** |
| GBVI | 0.550 ** | 0.682 ** | 0.775 ** | 0.734 ** | 0.740 ** | 0.805 ** |
| RVI | 0.679 ** | 0.624 ** | 0.626 ** | 0.871 ** | 0.711 ** | 0.852 ** |
| Growth Stages | λ (log10) | α |
|---|---|---|
| Jointing | −4 | 0.95 |
| Booting | −3.428 | 1.0 |
| Heading | −3.674 | 1.0 |
| Flowering | −3.837 | 0.9 |
| Milk | −2.937 | 1.0 |
| Dough | −1.798 | 0.1 |
| VI | Jointing | Booting | Heading | Flowering | Milk | Dough |
|---|---|---|---|---|---|---|
| DVI | 0.2513 | 0.0000 | 0.0000 | 0.1197 | 0.0191 | 0.0000 |
| EVI2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0137 | 0.0000 |
| EVI | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0160 | 0.0000 |
| GBVI | −0.1370 | 0.0000 | 0.1892 | 0.1895 | −0.0705 | −0.0866 |
| GCI | −0.3909 | 0.0000 | −0.1293 | 0.0212 | 0.0284 | 0.0751 |
| GNDVI | 0.1826 | 0.0000 | −0.8979 | 0.0582 | 0.0500 | 0.0609 |
| GOSAVI | 0.0057 | 0.0000 | 0.0000 | 0.0000 | 0.0333 | 0.0255 |
| GRVI | 0.1198 | 0.0000 | 0.0608 | −0.1715 | 0.0000 | 0.0000 |
| GSAVI | 0.0567 | 0.0000 | 0.0000 | 0.0000 | 0.0293 | 0.0000 |
| MCARI/OSAVI | −0.0058 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| MCARI | −0.0173 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| MNLI | 0.5396 | 1.0156 | 0.0000 | 0.2467 | 0.0233 | 0.0000 |
| MSAVI2 | 0.0000 | 0.0000 | 1.0549 | 0.0434 | 0.0148 | 0.0000 |
| MSR | 0.2019 | 0.0000 | 0.0000 | 0.0000 | 0.0006 | 0.0469 |
| NDRE | 0.0000 | 0.0000 | 0.0000 | 0.1745 | 0.0814 | 0.0585 |
| NDVI | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0223 |
| NLI | −0.3420 | 0.0000 | 0.0000 | −0.1883 | 0.0000 | 0.0137 |
| OSAVI | −0.3324 | 0.0000 | 0.0000 | 0.0000 | 0.0027 | 0.0000 |
| RDVI | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0096 | 0.0000 |
| RECI | 0.1256 | 0.0000 | 0.0000 | 0.1635 | 0.0597 | 0.0641 |
| RVI | 0.0000 | 0.0335 | 0.0000 | 0.0000 | 0.0000 | −0.0086 |
| SAVI | −0.1239 | 0.0000 | 0.0000 | 0.0000 | 0.0096 | 0.0000 |
| SCCCI | −0.0186 | 0.2110 | 0.9070 | 0.2833 | 0.1112 | 0.0556 |
| SR | 0.3274 | 0.0000 | 0.0000 | 0.0112 | 0.0000 | 0.0529 |
| TCARI/OSAVI | 0.0000 | 0.3374 | 0.0000 | −0.0456 | −0.0236 | −0.0561 |
| TCARI | 0.1684 | 0.0000 | 0.0000 | −0.2001 | −0.0345 | −0.1043 |
| TDVI | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0145 | 0.0000 |
| TVI | 0.1003 | 0.0000 | 0.0000 | 0.1035 | 0.0121 | 0.0000 |
| VARI | 0.0351 | 0.0000 | 0.0000 | −0.2165 | 0.0000 | 0.0000 |
| WDRVI | 0.0788 | 0.0000 | 0.0000 | 0.0000 | 0.0035 | 0.0483 |
| Growth Stages | LR | RF | GB | SVR | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Jointing | 0.759 | 0.0045 | 0.827 | 0.0032 | 0.803 | 0.0037 | 0.710 | 0.0054 |
| Booting | 0.869 | 0.0072 | 0.895 | 0.0058 | 0.891 | 0.0060 | 0.802 | 0.0109 |
| Heading | 0.830 | 0.0074 | 0.851 | 0.0066 | 0.823 | 0.0078 | 0.784 | 0.0094 |
| Flowering | 0.794 | 0.0063 | 0.831 | 0.0052 | 0.816 | 0.0056 | 0.663 | 0.0104 |
| Milk | 0.533 | 0.0103 | 0.581 | 0.0092 | 0.522 | 0.0105 | 0.613 | 0.0085 |
| Dough | 0.627 | 0.0111 | 0.801 | 0.0059 | 0.793 | 0.0062 | 0.738 | 0.0078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, X.; Zhang, H.; Zhang, B.; Zhang, J.; Hu, X.; Du, X.; Cai, J.; Jia, W.; Wu, C. UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation. Agriculture 2024, 14, 1900. https://doi.org/10.3390/agriculture14111900
Zhang L, Wang X, Zhang H, Zhang B, Zhang J, Hu X, Du X, Cai J, Jia W, Wu C. UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation. Agriculture. 2024; 14(11):1900. https://doi.org/10.3390/agriculture14111900
Chicago/Turabian StyleZhang, Lulu, Xiaowen Wang, Huanhuan Zhang, Bo Zhang, Jin Zhang, Xinkang Hu, Xintong Du, Jianrong Cai, Weidong Jia, and Chundu Wu. 2024. "UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation" Agriculture 14, no. 11: 1900. https://doi.org/10.3390/agriculture14111900
APA StyleZhang, L., Wang, X., Zhang, H., Zhang, B., Zhang, J., Hu, X., Du, X., Cai, J., Jia, W., & Wu, C. (2024). UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation. Agriculture, 14(11), 1900. https://doi.org/10.3390/agriculture14111900






