The More the Better? Reconsidering the Welfare Effect of Crop Insurance Premium Subsidy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Analysis
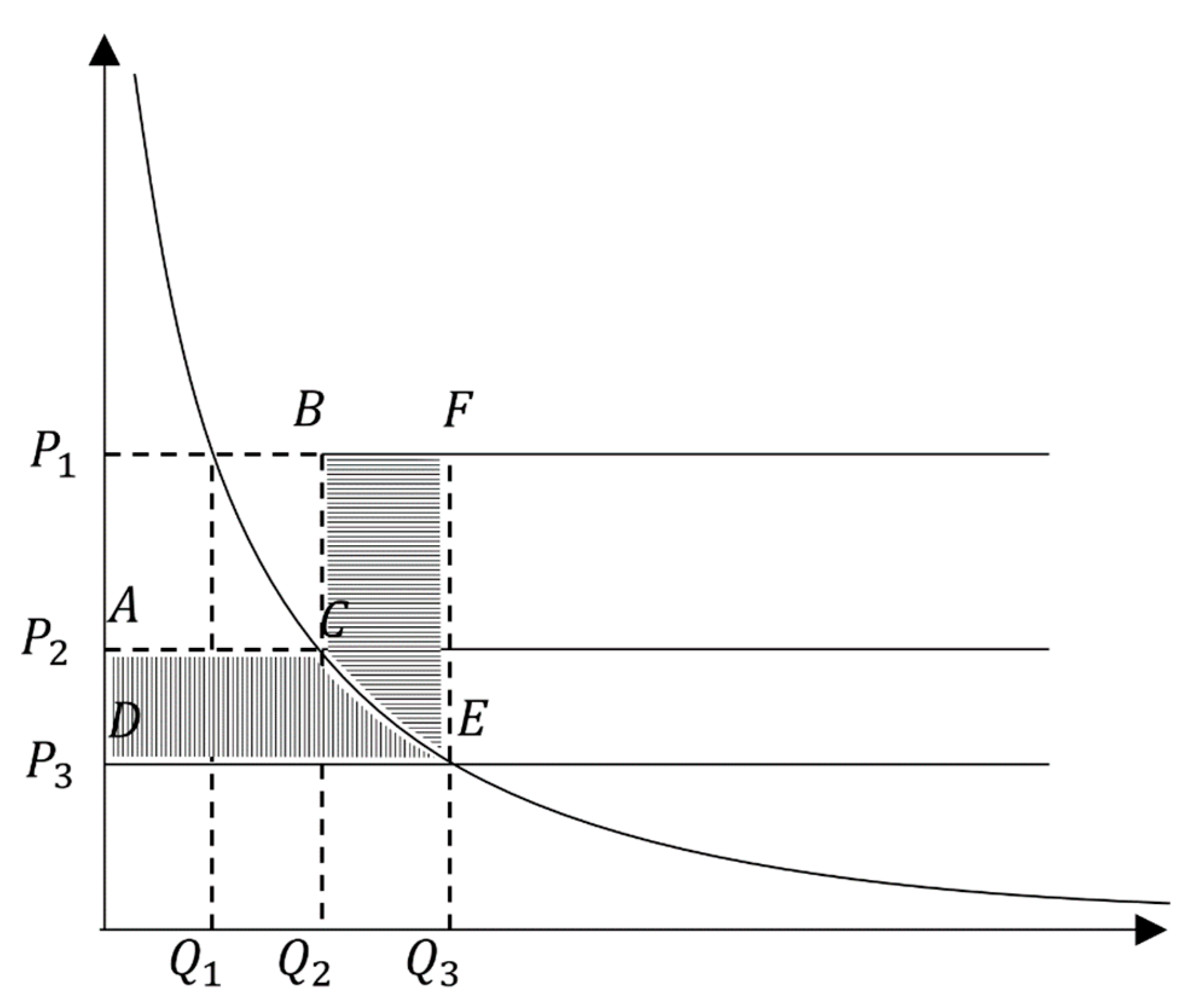
2.1.1. Welfare Analysis Under a Linear but Irrational Demand Model
2.1.2. Welfare Analysis Under Non-Linear Real Model
2.2. Data Source
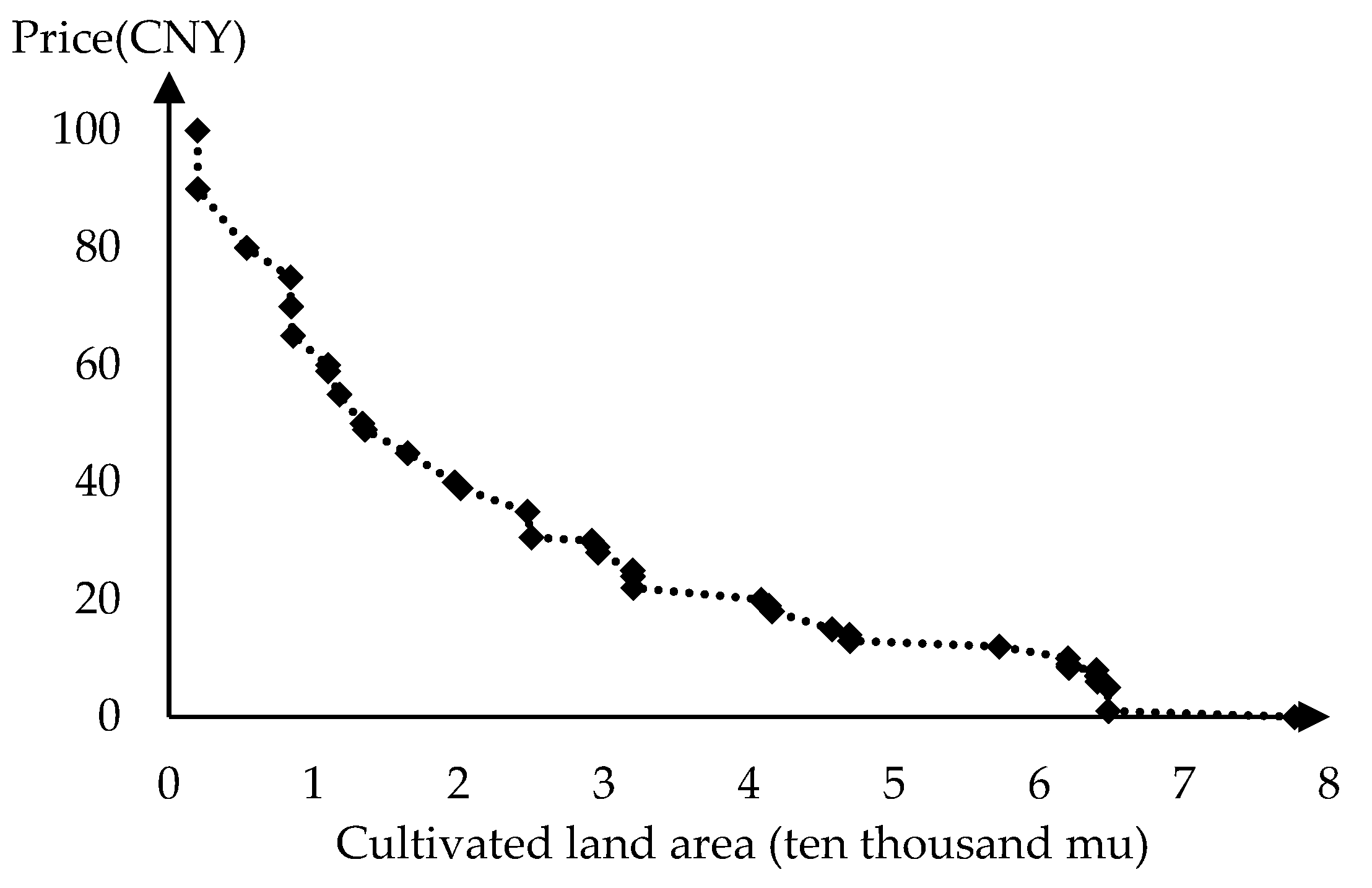
2.3. Descriptive Analysis
3. Results
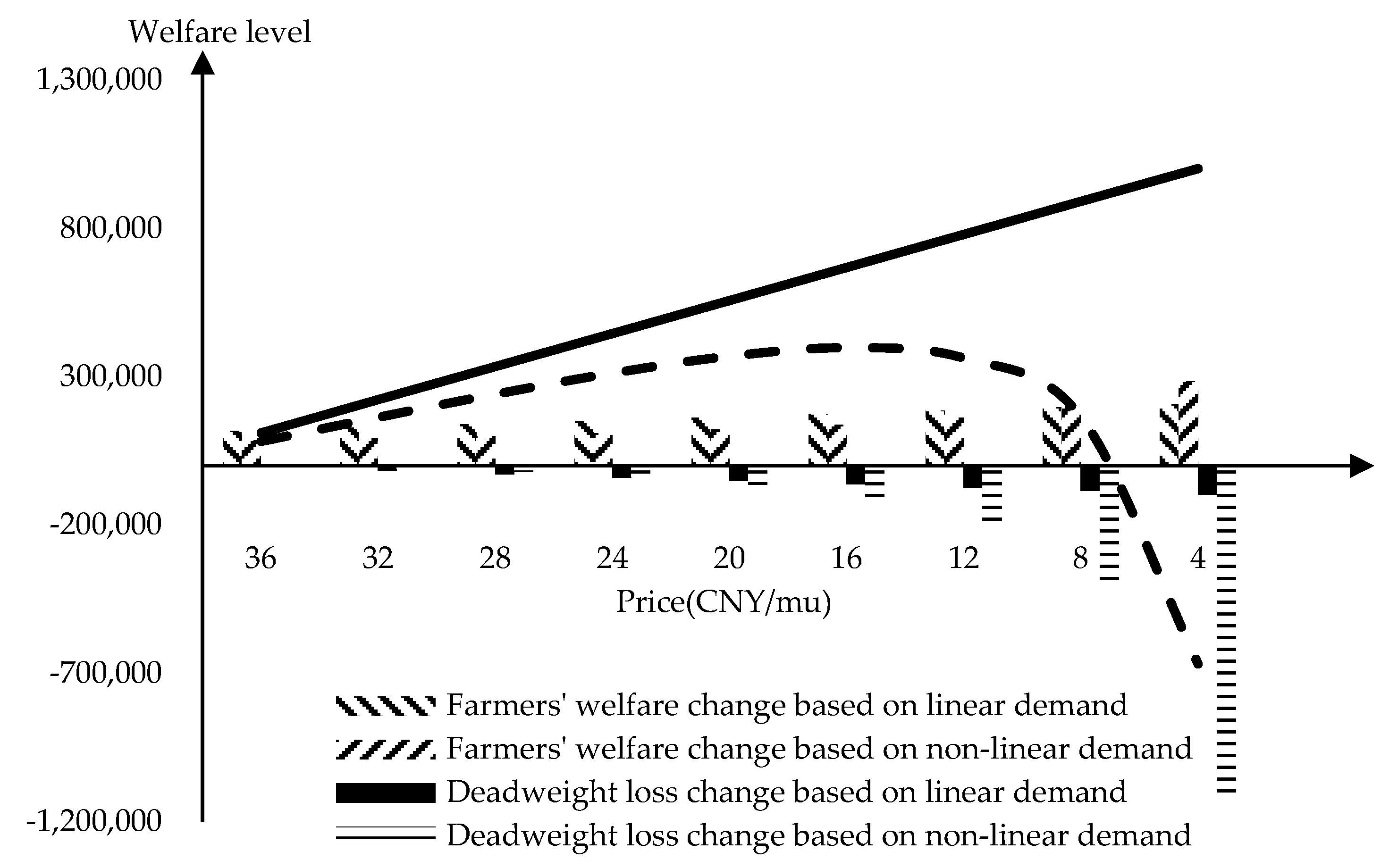
3.1. Regression Results and Welfare Measurement
3.2. Robustness Test
3.3. Heterogeneity Analysis
3.3.1. Regional Heterogeneity
3.3.2. Risk Appetite Heterogeneity
3.3.3. Planting Scale Heterogeneity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wagner, K.R.H. Designing Insurance for Climate Change. Nat. Clim. Chang. 2022, 12, 1070–1072. [Google Scholar] [CrossRef]
- Gao, Y.; Shu, Y.; Cao, H.; Zhou, S.; Shi, S. Fiscal Policy Dilemma in Resolving Agricultural Risks: Evidence from China’s Agricultural Insurance Subsidy Pilot. Int. J. Environ. Res. Public Health 2021, 18, 7577. [Google Scholar] [CrossRef]
- Guo, Y.M.; Shi, Y.R. Impact of the VAT Reduction Policy on Local Fiscal Pressure in China in Light of the COVID-19 Pandemic: A Measurement Based on a Computable General Equilibrium Model. Econ. Anal. Policy 2021, 69, 253–264. [Google Scholar] [CrossRef]
- Fang, L.; Hu, R.; Mao, H.; Chen, S. How Crop Insurance Influences Agricultural Green Total Factor Productivity: Evidence from Chinese Farmers. J. Clean. Prod. 2021, 321, 128977. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Bai, W.; Liu, B. Evaluation of the Crop Insurance Management for Soybean Risk of Natural Disasters in Jilin Province, China. Nat. Hazards 2015, 76, 587–599. [Google Scholar] [CrossRef]
- Yu, J.; Smith, A.; Sumner, D.A. Effects of Crop Insurance Premium Subsidies on Crop Acreage. Am. J. Agric. Econ. 2018, 100, 91–114. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Q.; Kimura, S.; Akter, S. Is the Crop Insurance Program Effective in China? Evidence from Farmers Analysis in Five Provinces. J. Integr. Agric. 2015, 14, 2109–2120. [Google Scholar] [CrossRef]
- Schaffitzel, F.; Jakob, M.; Soria, R.; Vogt-Schilb, A.; Ward, H. Can Government Transfers Make Energy Subsidy Reform Socially Acceptable? A Case Study on Ecuador. Energy Policy 2020, 137, 111120. [Google Scholar] [CrossRef]
- Fadhliani, Z.; Luckstead, J.; Wailes, E.J. The Impacts of Multiperil Crop Insurance on Indonesian Rice Farmers and Production. Agric. Econ. 2019, 50, 15–26. [Google Scholar] [CrossRef]
- Gassler, B.; Rehermann, R. Risk Preferences and the Adoption of Subsidised Crop Insurance: Evidence from Lithuania. Ger. J. Agric. Econ. 2022, 71, 36–52. [Google Scholar] [CrossRef]
- Sharma, S.; Walters, C.G. Influence of Farm Size and Insured Type on Crop Insurance Returns. Agribusiness 2020, 36, 440–452. [Google Scholar] [CrossRef]
- Hou, D.; Wang, X. Inhibition or Promotion?–The Effect of Agricultural Insurance on Agricultural Green Development. Front. Public Health 2022, 10, 910534. [Google Scholar] [CrossRef]
- Yan, F.; Yi, F.; Chen, H. Effect of Education on Crop Insurance Knowledge: Evidence from a RCT in China. China Agric. Econ. Rev. 2024. [Google Scholar] [CrossRef]
- Ricome, A.; Affholder, F.; Gérard, F.; Muller, B.; Poeydebat, C.; Quirion, P.; Sall, M. Are Subsidies to Weather-Index Insurance the Best Use of Public Funds? A Bio-Economic Farm Model Applied to the Senegalese Groundnut Basin. Agric. Syst. 2017, 156, 149–176. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, W.; Liu, J. Impact of Government Subsidy on Agricultural Production and Pollution: A Game-Theoretic Approach. J. Clean. Prod. 2021, 285, 124806. [Google Scholar] [CrossRef]
- Ye, T.; Wang, M.; Hu, W.; Liu, Y.; Shi, P. High Liabilities or Heavy Subsidies: Farmers’ Preferences for Crop Insurance Attributes in Hunan, China. China Agric. Econ. Rev. 2017, 9, 588–606. [Google Scholar] [CrossRef]
- Ramirez, O.A.; Carpio, C.E. Are the Federal Crop Insurance Subsidies Equitably Distributed? Evidence from a Monte Carlo Simulation Analysis. J. Agric. Resour. Econ. 2015, 40, 457–475. [Google Scholar] [CrossRef]
- Alizamir, S.; Iravani, F.; Mamani, H. An Analysis of Price vs. Revenue Protection: Government Subsidies in the Agriculture Industry. Manag. Sci. 2019, 65, 32–49. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Bai, Y.; Liu, X.; Ye, T. Residents’ Preferences for Rural Housing Disaster Insurance Attributes in Central and Western Tibet. Int. J. Disaster Risk Sci. 2023, 14, 697–711. [Google Scholar] [CrossRef]
- Zhong, L.; Nie, J.; Yue, X.; Jin, M. Optimal Design of Agricultural Insurance Subsidies under the Risk of Extreme Weather. Int. J. Prod. Econ. 2023, 263, 108920. [Google Scholar] [CrossRef]
- Okubo, M. Model Uncertainty, Economic Development, and Welfare Costs of Business Cycles. J. Macroecon. 2023, 76, 103514. [Google Scholar] [CrossRef]
- Mazzoleni, P.; Pagani, E.; Perali, F. On the Curvature Properties of “Long” Social Welfare Functions. Mathematics 2023, 11, 1674. [Google Scholar] [CrossRef]
- Ohdoi, R.; Futagami, K. Welfare Implications of Non-Unitary Time Discounting. Theory Decis. 2021, 90, 85–115. [Google Scholar] [CrossRef]
- Huang, J.-C.; Zhao, M.Q. Model Selection and Misspecification in Discrete Choice Welfare Analysis. Appl. Econ. 2015, 47, 4153–4167. [Google Scholar] [CrossRef]
- Vercammen, J.; Pannell, D.J. The Economics of Crop Hail Insurance. Can. J. Agri. Econ. 2000, 48, 87–98. [Google Scholar] [CrossRef]
- Hill, R.V.; Kumar, N.; Magnan, N.; Makhija, S.; De Nicola, F.; Spielman, D.J.; Ward, P.S. Ex Ante and Ex Post Effects of Hybrid Index Insurance in Bangladesh. J. Dev. Econ. 2019, 136, 1–17. [Google Scholar] [CrossRef]
- Yi, F.; Zhou, M.; Zhang, Y.Y. Value of Incorporating ENSO Forecast in Crop Insurance Programs. Am. J. Agric. Econ. 2020, 102, 439–457. [Google Scholar] [CrossRef]
- Heyne, P.; Boettke, P.; Prychitko, D.L. The Economic Way of Thinking; Science Research Associates: Chicago, IL, USA, 1987. [Google Scholar]
- Rubinstein, M. An Aggregation Theorem for Securities Markets. J. Financ. Econ. 1974, 1, 225–244. [Google Scholar] [CrossRef]
- Dai, J.; Meng, W. A Risk-Averse Newsvendor Model under Marketing-Dependency and Price-Dependency. Int. J. Prod. Econ. 2015, 160, 220–229. [Google Scholar] [CrossRef]
- Lynch, M.Á.; Nolan, S.; Devine, M.T.; O’Malley, M. The Impacts of Demand Response Participation in Capacity Markets. Appl. Energy 2019, 250, 444–451. [Google Scholar] [CrossRef]
- Stark, O.; Budzinski, W. A Social-psychological Reconstruction of Amartya Sen’s Measures of Inequality and Social Welfare. Kyklos 2021, 74, 552–566. [Google Scholar] [CrossRef]
- Zou, H. The Social Welfare Effect of Environmental Regulation: An Analysis Based on Atkinson Social Welfare Function. J. Clean. Prod. 2024, 434, 140022. [Google Scholar] [CrossRef]
- Ahmed, S.; McIntosh, C.; Sarris, A. The Impact of Commercial Rainfall Index Insurance: Experimental Evidence from Ethiopia. Am. J. Agric. Econ. 2020, 102, 1154–1176. [Google Scholar] [CrossRef]
- Cole, S.; Fernando, A.N.; Stein, D.; Tobacman, J. Field Comparisons of Incentive-Compatible Preference Elicitation Techniques. J. Econ. Behav. Organ. 2020, 172, 33–56. [Google Scholar] [CrossRef]
- Palm-Forster, L.H.; Swinton, S.M.; Shupp, R.S. Farmer Preferences for Conservation Incentives That Promote Voluntary Phosphorus Abatement in Agricultural Watersheds. J. Soil Water Conserv. 2017, 72, 493–505. [Google Scholar] [CrossRef]
- Khalid, S.A.; Salman, V. Welfare Impact of Electricity Subsidy Reforms in Pakistan: A Micro Model Study. Energy Policy 2020, 137, 111097. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, B. Performance of Alternative Electricity Prices on Residential Welfare in China. Energy Policy 2021, 153, 112233. [Google Scholar] [CrossRef]
- Goolsbee, A. The Value of Broadband and the Deadweight Loss of Taxing New Technology. Contrib. Econ. Anal. Policy 2006, 5, 0000101515153806451505. [Google Scholar] [CrossRef]
- Anderson, S.P.; Renault, R. Efficiency and Surplus Bounds in Cournot Competition. J. Econ. Theory 2003, 113, 253–264. [Google Scholar] [CrossRef]
- Berry-Stölzle, T.R. Evaluating Liquidation Strategies for Insurance Companies. J. Risk Insur. 2008, 75, 207–230. [Google Scholar] [CrossRef]
- Zhu, X.; Van Ommeren, J.; Rietveld, P. Indirect Benefits of Infrastructure Improvement in the Case of an Imperfect Labor Market. Transp. Res. Part B Methodol. 2009, 43, 57–72. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Mendes Lopes, A.; Machado, J.A.T. A Review of Power Laws in Real Life Phenomena. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3558–3578. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The Area and Population of Cities: New Insights from a Different Perspective on Cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Bulut, H. Managing Catastrophic Risk in Agriculture through Ex Ante Subsidized Insurance or Ex Post Disaster Aid. J. Agric. Resour. Econ. 2017, 42, 406–426. [Google Scholar]
- Amoah, A.; Ferrini, S.; Schaafsma, M. Electricity Outages in Ghana: Are Contingent Valuation Estimates Valid? Energy Policy 2019, 135, 110996. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Liu, Y. Can Product-Information Disclosure Increase Chinese Consumer’s Willingness to Pay for GM Foods? The Case of Fad-3 GM Lamb. China Agric. Econ. Rev. 2017, 9, 415–437. [Google Scholar] [CrossRef]
- Drichoutis, A.C.; Lusk, J.L.; Pappa, V. Elicitation Formats and the WTA/WTP Gap: A Study of Climate Neutral Foods. Food Policy 2016, 61, 141–155. [Google Scholar] [CrossRef]
- Orlowski, J.; Wicker, P. Monetary Valuation of Non-Market Goods and Services: A Review of Conceptual Approaches and Empirical Applications in Sports. Eur. Sport Manag. Q. 2019, 19, 456–480. [Google Scholar] [CrossRef]
- Heinzen, R.R.; Bridges, J.F.P. Comparison of Four Contingent Valuation Methods to Estimate the Economic Value of a Pneumococcal Vaccine in Bangladesh. Int. J. Technol. Assess. Health Care 2008, 24, 481–487. [Google Scholar] [CrossRef]
- Bageant, E.R.; Barrett, C.B. Are There Gender Differences in Demand for Index-Based Livestock Insurance? J. Dev. Stud. 2017, 53, 932–952. [Google Scholar] [CrossRef]
- Islam, M.D.I.; Rahman, A.; Sarker, M.N.I.; Sarker, M.S.; Jianchao, L. Factors Influencing Rice Farmers’ Risk Attitudesand Perceptions in Bangladesh amidEnvironmental and Climatic Issues. Pol. J. Environ. Stud. 2020, 30, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Cai, H.; Liu, R. Farmers’ Demand for Informal Risk Management Strategy and Weather Index Insurance: Evidence from China. Int. J. Disaster Risk Sci. 2021, 12, 281–297. [Google Scholar] [CrossRef]
- Goodwin, B.K. An Empirical Analysis of the Demand for Multiple Peril Crop Insurance. Am. J. Agric. Econ. 1993, 75, 425–434. [Google Scholar] [CrossRef]
- Kim, Y.; Yu, J.; Pendell, D.L. Effects of Crop Insurance on Farm Disinvestment and Exit Decisions. Eur. Rev. Agric. Econ. 2019, 47, 324–347. [Google Scholar] [CrossRef]
- Lusk, J.L. Distributional Effects of Crop Insurance Subsidies. Appl. Econ. Perspect. Policy 2017, 39, 1–15. [Google Scholar] [CrossRef]
- Hagquist, C.; Stenbeck, M. Goodness of Fit in Regression Analysis—R2 and G2 Reconsidered. Qual. Quant. 1998, 32, 229–245. [Google Scholar] [CrossRef]
- Brick, K.; Visser, M. Risk Preferences, Technology Adoption and Insurance Uptake: A Framed Experiment. J. Econ. Behav. Organ. 2015, 118, 383–396. [Google Scholar] [CrossRef]
- Ward, P.S.; Ortega, D.L.; Spielman, D.J.; Kumar, N.; Minocha, S. Demand for Complementary Financial and Technological Tools for Managing Drought Risk. Econ. Dev. Cult. Change 2020, 68, 607–653. [Google Scholar] [CrossRef]
- Philippi, T.; Schiller, J. Abandoning Disaster Relief and Stimulating Insurance Demand through Premium Subsidies. J. Risk Insur. 2024, 91, 339–382. [Google Scholar] [CrossRef]
- Wong, H.L.; Wei, X.; Kahsay, H.B.; Gebreegziabher, Z.; Gardebroek, C.; Osgood, D.E.; Diro, R. Effects of Input Vouchers and Rainfall Insurance on Agricultural Production and Household Welfare: Experimental Evidence from Northern Ethiopia. World Dev. 2020, 135, 105074. [Google Scholar] [CrossRef]
- Qin, T.; Gu, X.; Tian, Z.; Pan, H.; Deng, J.; Wan, L. An Empirical Analysis of the Factors Influencing Farmer Demand for Forest Insurance: Based on Surveys from Lin’an County in Zhejiang Province of China. J. For. Econ. 2016, 24, 37–51. [Google Scholar] [CrossRef]
- Glauber, J.W. Crop Insurance Reconsidered. Am. J. Agri. Econ. 2004, 86, 1179–1195. [Google Scholar] [CrossRef]
- Connor, L.; Katchova, A.L. Crop Insurance Participation Rates and Asymmetric Effects on U.S. Corn and Soybean Yield Risk. J. Agric. Resour. Econ. 2020, 45, 1–19. [Google Scholar] [CrossRef]
- Miao, R. Climate, Insurance and Innovation: The Case of Drought and Innovations in Drought-Tolerant Traits in US Agriculture. Eur. Rev. Agric. Econ. 2020, 47, 1826–1860. [Google Scholar] [CrossRef]
- Tsiboe, F.; Turner, D. The Crop Insurance Demand Response to Premium Subsidies: Evidence from U.S. Agriculture. Food Policy 2023, 119, 102505. [Google Scholar] [CrossRef]

| Next you will be introduced to a wheat insurance policy that will be available to you in 2022. This insurance provides you with a maximum benefit of $1000 per mu, triggered by a 10 per cent reduction in your wheat yield, with a final benefit amount based on your actual losses. Also, different percentages are payable for different growing seasons, as you can read about in the policy description provided to you. | |
| Would you like to purchase this wheat insurance? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 70–80) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 60–70) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 50–60) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 40–50) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 30–40) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 20–30) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 10–20) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Would you be willing to pay [CNY 0–10) per mu for it? | 0 = No (Skip this table); 1 = Yes |
| Variables | Description | Mean | Sd | Min. | Max. |
|---|---|---|---|---|---|
| Gender | 0 = Male; 1 = Female | 0.08 | 0.26 | 0 | 1 |
| Age | Year | 56.35 | 10.52 | 25 | 80 |
| Marriage | 0 = Unmarried; 1 = Married | 0.98 | 0.13 | 0 | 1 |
| Education | Year | 8.57 | 3.49 | 0 | 16 |
| Health | 0 = Unhealthy; 1 = Healthy | 0.93 | 0.26 | 0 | 1 |
| Planting scale | 0 = Small-scale Farmer; 1 = Large-scale Farmer | 0.55 | 0.50 | 0 | 1 |
| Crop insurance premium | CNY/mu | 10.37 | 7.89 | 0 | 43 |
| Income | Annual Revenue (CNY 10,000) | 36.33 | 91.28 | 0 | 1450 |
| Disasters | 0 = No Disaster in 2021; 1 = Disaster in 2021 | 0.68 | 0.47 | 0 | 1 |
| Liquidity constraints | 0 = No Constraint in 2021; 1 = Constraint in 2021 | 0.39 | 0.49 | 0 | 1 |
| Parameter | Linear Demand | Power-Law Demand |
|---|---|---|
| 56,300.840 *** | 220,326.600 *** | |
| (2308.652) | (25,035.180) | |
| −711.647 *** | −0.642 *** | |
| (51.318) | (0.045) | |
| 0.861 | 0.970 | |
| 0.857 | 0.968 |
| Subsidy Level | Linear Demand | Power-Law Demand | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Welfare Effect Change | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Welfare Effect Change | |||
| 10% | 117,033 | 5693 | 20.56 | 111,340 | 111,340 | 85,407 | 2972 | 28.74 | 82,434 | 82,434 |
| 20% | 128,419 | 17,080 | 7.52 | 222,680 | 111,340 | 91,737 | 10,521 | 8.72 | 163,650 | 81,216 |
| 30% | 139,806 | 28,466 | 4.91 | 334,019 | 111,340 | 99,427 | 21,477 | 4.63 | 241,600 | 77,950 |
| 40% | 151,192 | 39,852 | 3.79 | 445,359 | 111,340 | 109,019 | 38,023 | 2.87 | 312,596 | 70,996 |
| 50% | 162,578 | 51,239 | 3.17 | 556,699 | 111,340 | 121,406 | 64,393 | 1.89 | 369,609 | 57,014 |
| 60% | 173,965 | 62,625 | 2.78 | 668,039 | 111,340 | 138,193 | 109,740 | 1.26 | 398,062 | 28,453 |
| 70% | 185,351 | 74,011 | 2.50 | 779,379 | 111,340 | 162,612 | 197,193 | 0.82 | 363,481 | −34,581 |
| 80% | 196,737 | 85,398 | 2.30 | 890,719 | 111,340 | 202,518 | 401,657 | 0.50 | 164,342 | −199,139 |
| 90% | 208,124 | 96,784 | 2.15 | 1,002,058 | 111,340 | 284,844 | 1,117,149 | 0.25 | −667,962 | −832,304 |
| Subsidy Level | Linear Demand | Power-Law Demand | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Welfare Effect Change | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Welfare Effect Change | |||
| 10% | 531 | 29 | 8.31 | 502 | 502 | 366 | 14 | 26.14 | 352 | 352 |
| 20% | 588 | 86 | 6.84 | 1004 | 502 | 397 | 51 | 7.78 | 698 | 346 |
| 30% | 645 | 143 | 4.51 | 1507 | 502 | 434 | 106 | 4.09 | 1026 | 328 |
| 40% | 703 | 200 | 3.52 | 2009 | 502 | 482 | 190 | 2.54 | 1318 | 292 |
| 50% | 760 | 258 | 2.95 | 2511 | 502 | 544 | 326 | 1.67 | 1536 | 218 |
| 60% | 817 | 315 | 2.59 | 3013 | 502 | 630 | 564 | 1.12 | 1602 | 66 |
| 70% | 874 | 372 | 2.35 | 3515 | 502 | 757 | 1035 | 0.73 | 1324 | −278 |
| 80% | 932 | 429 | 2.17 | 4018 | 502 | 969 | 2170 | 0.45 | 123 | −1201 |
| 90% | 989 | 487 | 2.03 | 4520 | 502 | 1425 | 6324 | 0.23 | −4776 | −4899 |
| Subsidy Level | Suqian City | Yancheng City | Huai’an City | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | ||||
| 10% | 11,131 | 380 | 29.29 | 10,751 | 29,397 | 911 | 32.28 | 28,486 | 46,982 | 1688 | 27.83 | 45,294 |
| 20% | 11,940 | 1343 | 8.89 | 21,348 | 31,331 | 3201 | 9.79 | 56,617 | 50,580 | 5988 | 8.45 | 89,886 |
| 30% | 12,921 | 2738 | 4.72 | 31,532 | 33,662 | 6478 | 5.20 | 83,801 | 54,962 | 12,254 | 4.49 | 132,594 |
| 40% | 14,143 | 4839 | 2.92 | 40,836 | 36,541 | 11,355 | 3.22 | 108,987 | 60,442 | 21,758 | 2.78 | 171,277 |
| 50% | 15,718 | 8178 | 1.92 | 48,376 | 40,219 | 19,004 | 2.12 | 130,202 | 67,543 | 36,976 | 1.83 | 201,844 |
| 60% | 17,847 | 13,903 | 1.28 | 52,321 | 45,139 | 31,931 | 1.41 | 143,410 | 77,202 | 63,279 | 1.22 | 215,767 |
| 70% | 20,936 | 24,904 | 0.84 | 48,354 | 52,181 | 56,356 | 0.93 | 139,235 | 91,320 | 114,311 | 0.80 | 192,776 |
| 80% | 25,965 | 50,509 | 0.51 | 23,810 | 63,445 | 112,009 | 0.57 | 90,671 | 114,537 | 234,526 | 0.49 | 72,787 |
| 85% | 16,195 | 48,726 | 0.33 | −8720 | 38,785 | 105,961 | 0.37 | 23,495 | 72,262 | 228,771 | 0.32 | −83,721 |
| 90% | 36,281 | 139,515 | 0.26 | −79,424 | 47,158 | 193,482 | 0.24 | −122,829 | 90,635 | 431,193 | 0.21 | −424,280 |
| Subsidy Level | Risk-Averse | Risk-Neutral | Risk-Seeking | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | ||||
| 10% | 33,627 | 1426 | 23.58 | 32,202 | 15,748 | 539 | 29.23 | 15,209 | 30,129 | 853 | 35.33 | 29,276 |
| 20% | 36,681 | 5118 | 7.17 | 63,764 | 16,895 | 1905 | 8.87 | 30,199 | 31,936 | 2982 | 10.71 | 58,230 |
| 30% | 40,452 | 10,629 | 3.81 | 93,587 | 18,286 | 3884 | 4.71 | 44,602 | 34,101 | 5999 | 5.68 | 86,332 |
| 40% | 45,244 | 19,194 | 2.36 | 119,637 | 20,020 | 6865 | 2.92 | 57,757 | 36,758 | 10,441 | 3.52 | 112,650 |
| 50% | 51,569 | 33,272 | 1.55 | 137,935 | 22,254 | 11,605 | 1.92 | 68,406 | 40,127 | 17,332 | 2.32 | 135,445 |
| 60% | 60,364 | 58,322 | 1.04 | 139,978 | 25,276 | 19,734 | 1.28 | 73,948 | 44,592 | 28,832 | 1.55 | 151,205 |
| 70% | 73,576 | 108,599 | 0.68 | 104,955 | 29,661 | 35,361 | 0.84 | 68,248 | 50,910 | 50,249 | 1.01 | 151,866 |
| 75% | 44,276 | 132,958 | 0.33 | 16,272 | 17,232 | 45,133 | 0.38 | 40,347 | 28,830 | 67,500 | 0.43 | 113,196 |
| 80% | 51,827 | 188,172 | 0.28 | −120,073 | 19,572 | 61,184 | 0.32 | −1265 | 32,038 | 88,456 | 0.36 | 56,778 |
| 85% | 63,170 | 292,402 | 0.22 | −349,305 | 22,967 | 90,291 | 0.25 | −68,589 | 36,578 | 125,352 | 0.29 | −31,997 |
| 90% | 82,510 | 534,043 | 0.15 | −800,838 | 28,498 | 154,328 | 0.18 | −194,419 | 43,732 | 203,474 | 0.21 | −191,739 |
| Subsidy Level | Smallholder | Large-Scale Household | ||||||
|---|---|---|---|---|---|---|---|---|
| Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | Farmers’ Welfare Change | Deadweight Loss Change | Total Welfare Effect | |||
| 10% | 1841 | 74 | 24.96 | 1767 | 84,908 | 2868 | 29.61 | 82,040 |
| 20% | 1998 | 264 | 7.58 | 3502 | 91,011 | 10,131 | 8.98 | 162,920 |
| 30% | 2192 | 545 | 4.03 | 5149 | 98,408 | 20,633 | 4.77 | 240,695 |
| 40% | 2437 | 977 | 2.49 | 6609 | 107,611 | 36,431 | 2.95 | 311,875 |
| 50% | 2758 | 1682 | 1.64 | 7684 | 119,462 | 61,502 | 1.94 | 369,835 |
| 60% | 3201 | 2923 | 1.09 | 7961 | 135,464 | 104,413 | 1.30 | 400,886 |
| 70% | 3859 | 5385 | 0.72 | 6436 | 158,642 | 186,718 | 0.85 | 372,810 |
| 75% | 2299 | 6654 | 0.35 | 2082 | 91,990 | 239,042 | 0.38 | 225,759 |
| 80% | 2668 | 9306 | 0.29 | −4556 | 104,312 | 323,272 | 0.32 | 6799 |
| 85% | 3218 | 14,255 | 0.23 | −15,593 | 122,161 | 475,685 | 0.26 | −346,725 |
| 90% | 4142 | 25,560 | 0.16 | −37,012 | 151,160 | 810,049 | 0.19 | −1,005,614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Yi, F.; Zhou, H.; Yan, F. The More the Better? Reconsidering the Welfare Effect of Crop Insurance Premium Subsidy. Agriculture 2024, 14, 2050. https://doi.org/10.3390/agriculture14112050
Hu M, Yi F, Zhou H, Yan F. The More the Better? Reconsidering the Welfare Effect of Crop Insurance Premium Subsidy. Agriculture. 2024; 14(11):2050. https://doi.org/10.3390/agriculture14112050
Chicago/Turabian StyleHu, Mingyu, Fujin Yi, Hong Zhou, and Feier Yan. 2024. "The More the Better? Reconsidering the Welfare Effect of Crop Insurance Premium Subsidy" Agriculture 14, no. 11: 2050. https://doi.org/10.3390/agriculture14112050
APA StyleHu, M., Yi, F., Zhou, H., & Yan, F. (2024). The More the Better? Reconsidering the Welfare Effect of Crop Insurance Premium Subsidy. Agriculture, 14(11), 2050. https://doi.org/10.3390/agriculture14112050





