Simulation and Experiment of Optimal Conditions for Apple Harvesting with High Fruit Stalk Retention Rate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Apple Fruit Modeling
2.1.1. Geometric Feature Measurement of the Fruit
2.1.2. Apple Fruit Mode
2.2. Apple Branch and Stalk Modeling
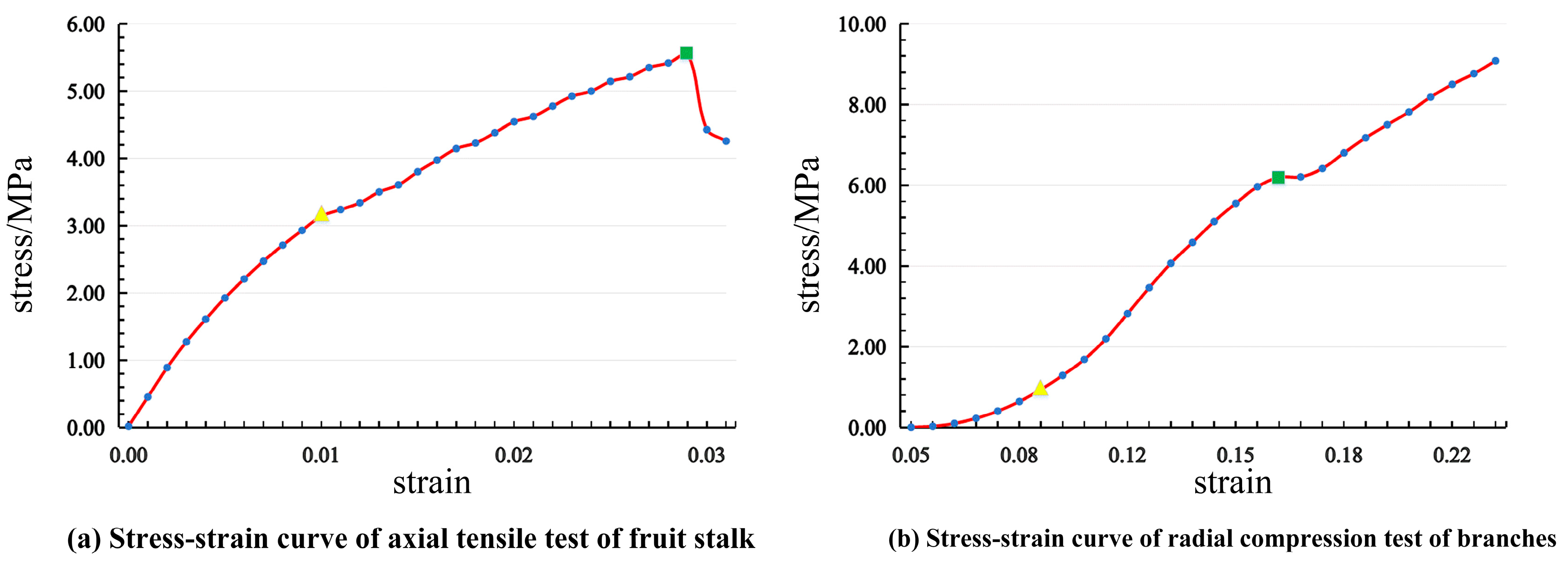
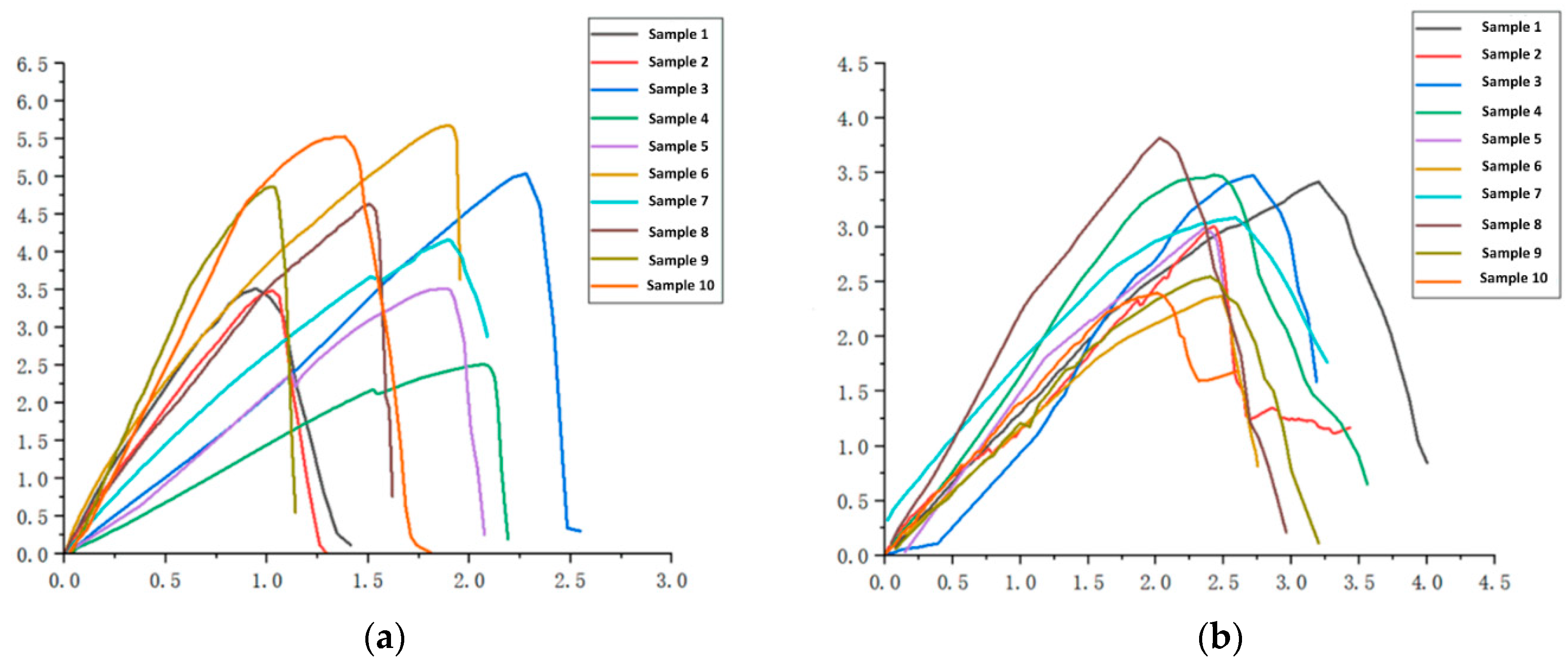
2.2.1. Mechanical Property Measurement of Branches and Stalks
2.2.2. Branch and Fruit Stalk Mode
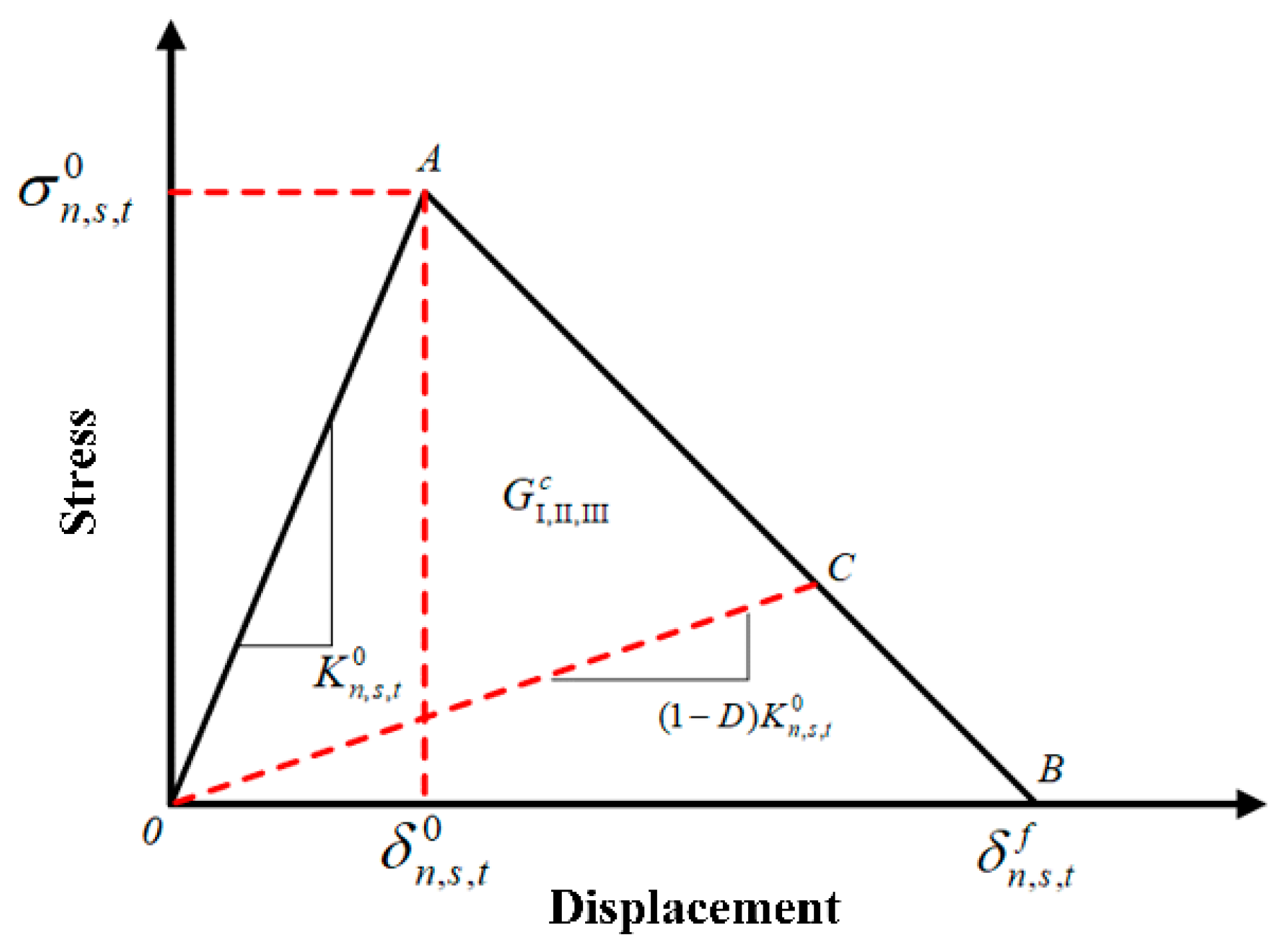
2.3. Modelling of the Abscission Layer
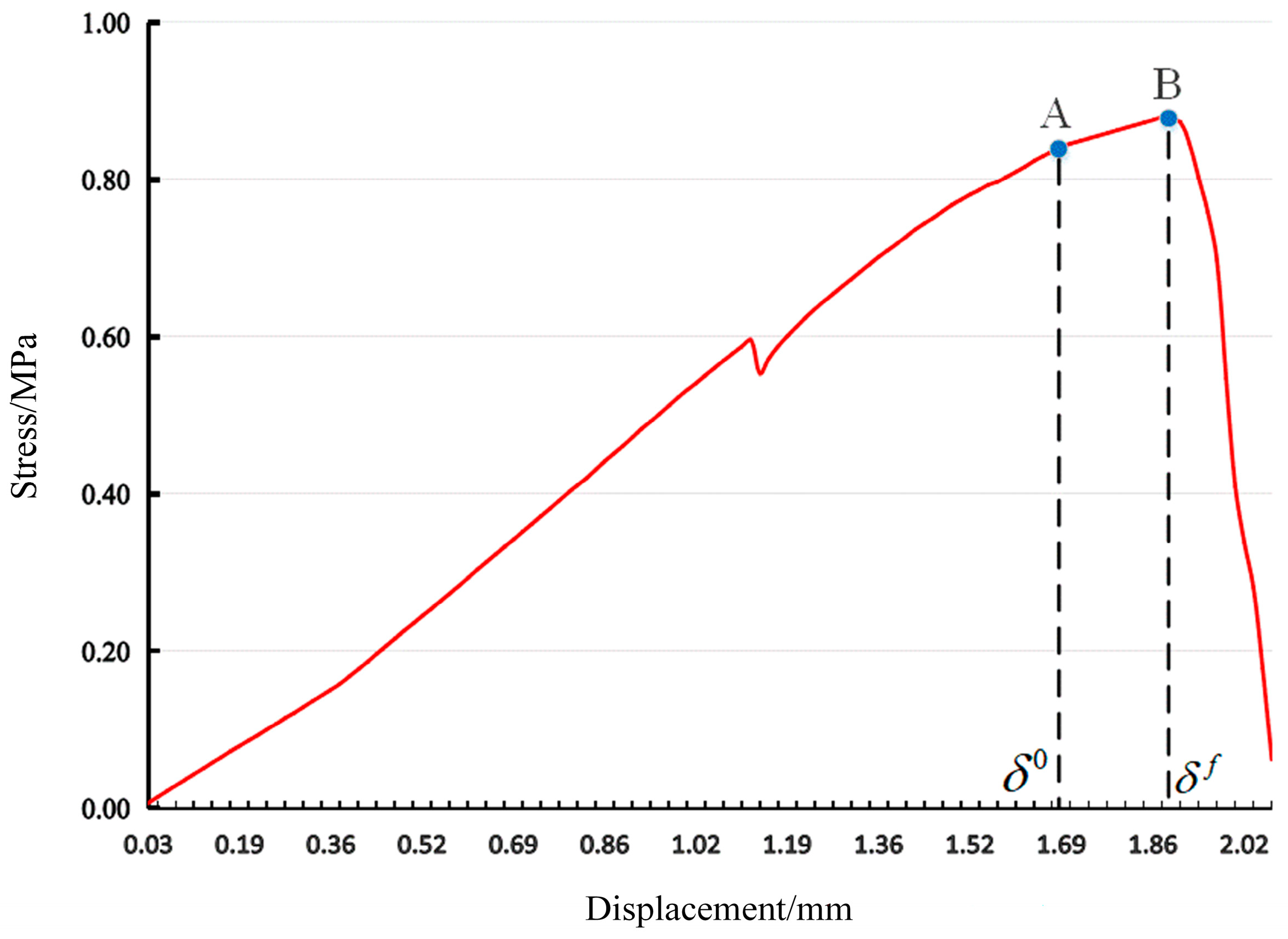
2.3.1. Measurement of Abscission Layer Mechanical Properties
2.3.2. Abscission Layer Model Parameters
2.4. Branch–Stalk–Fruit Finite Element Model
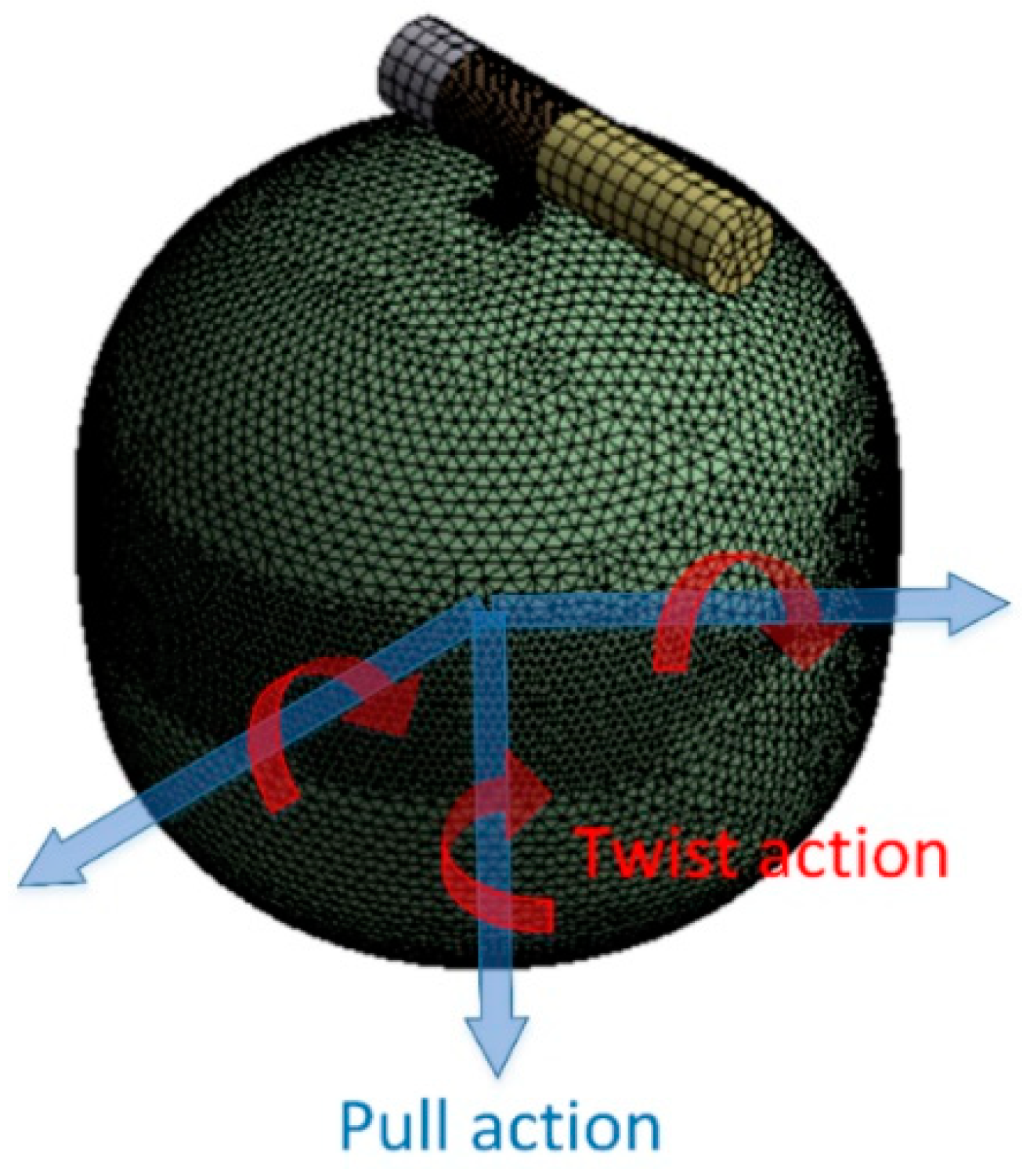
2.5. Fruit Abscission Process Simulation
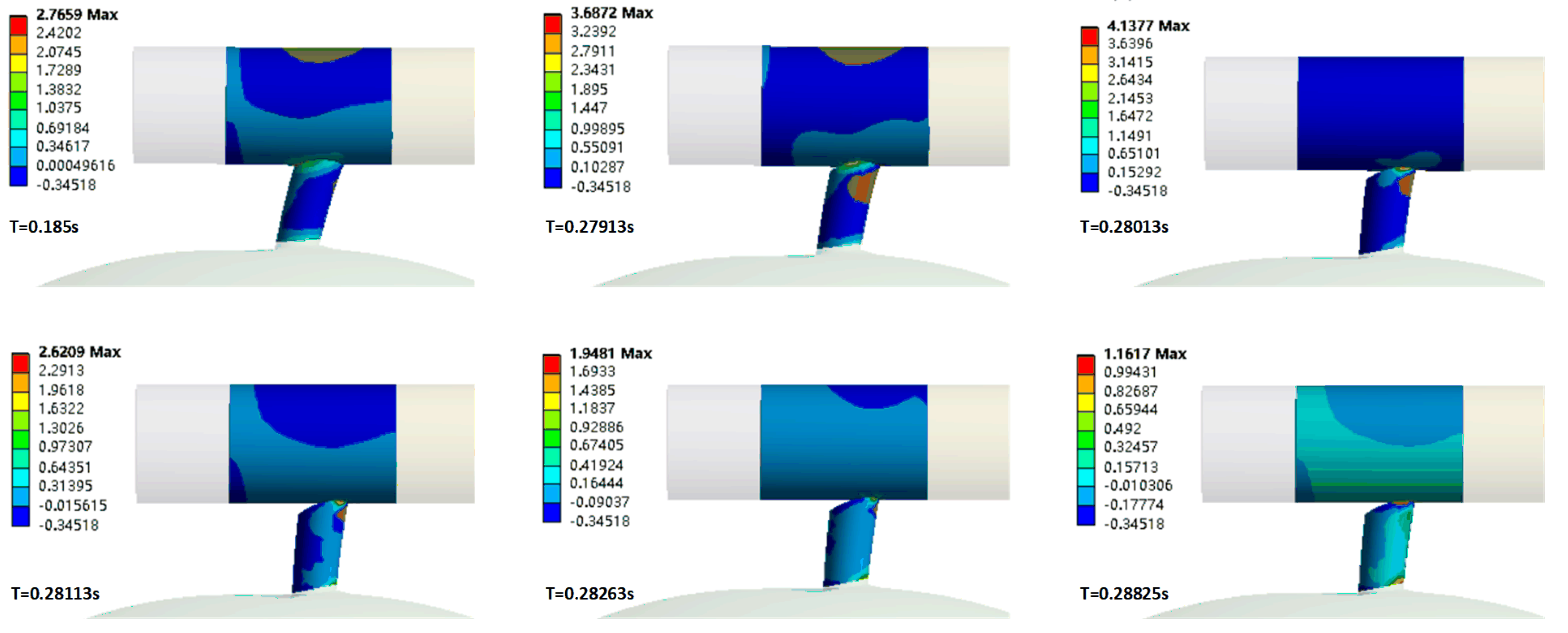
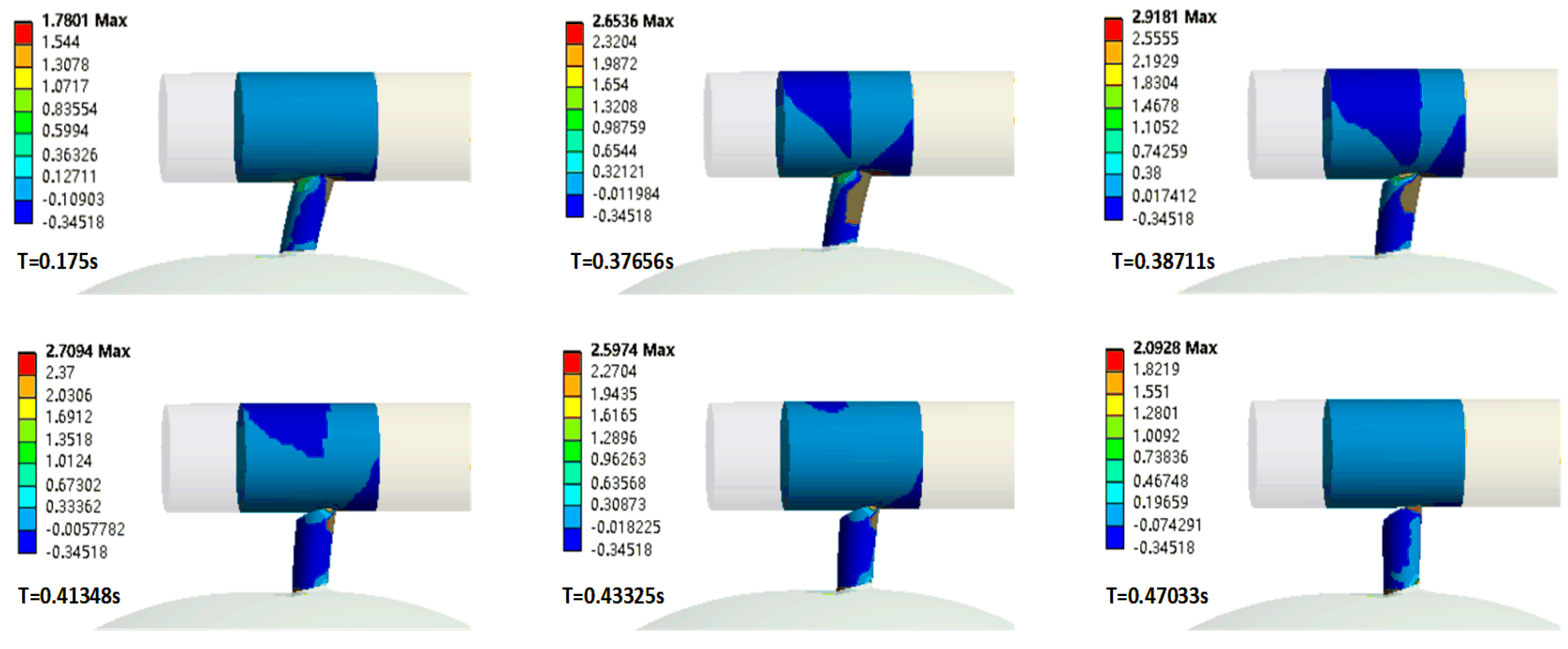
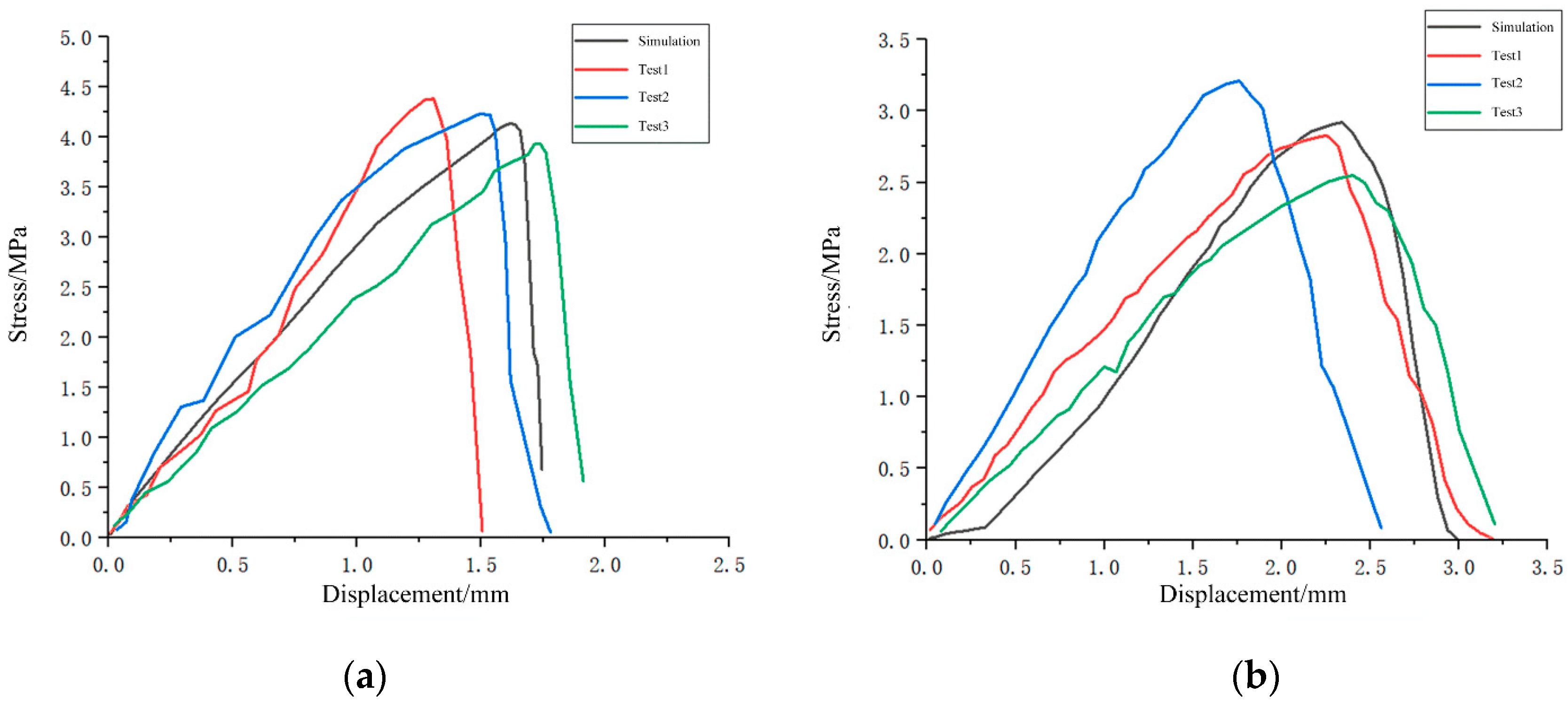
2.6. Model Abscission Process Accuracy Verification
2.7. Optimal Harvesting Mode Study
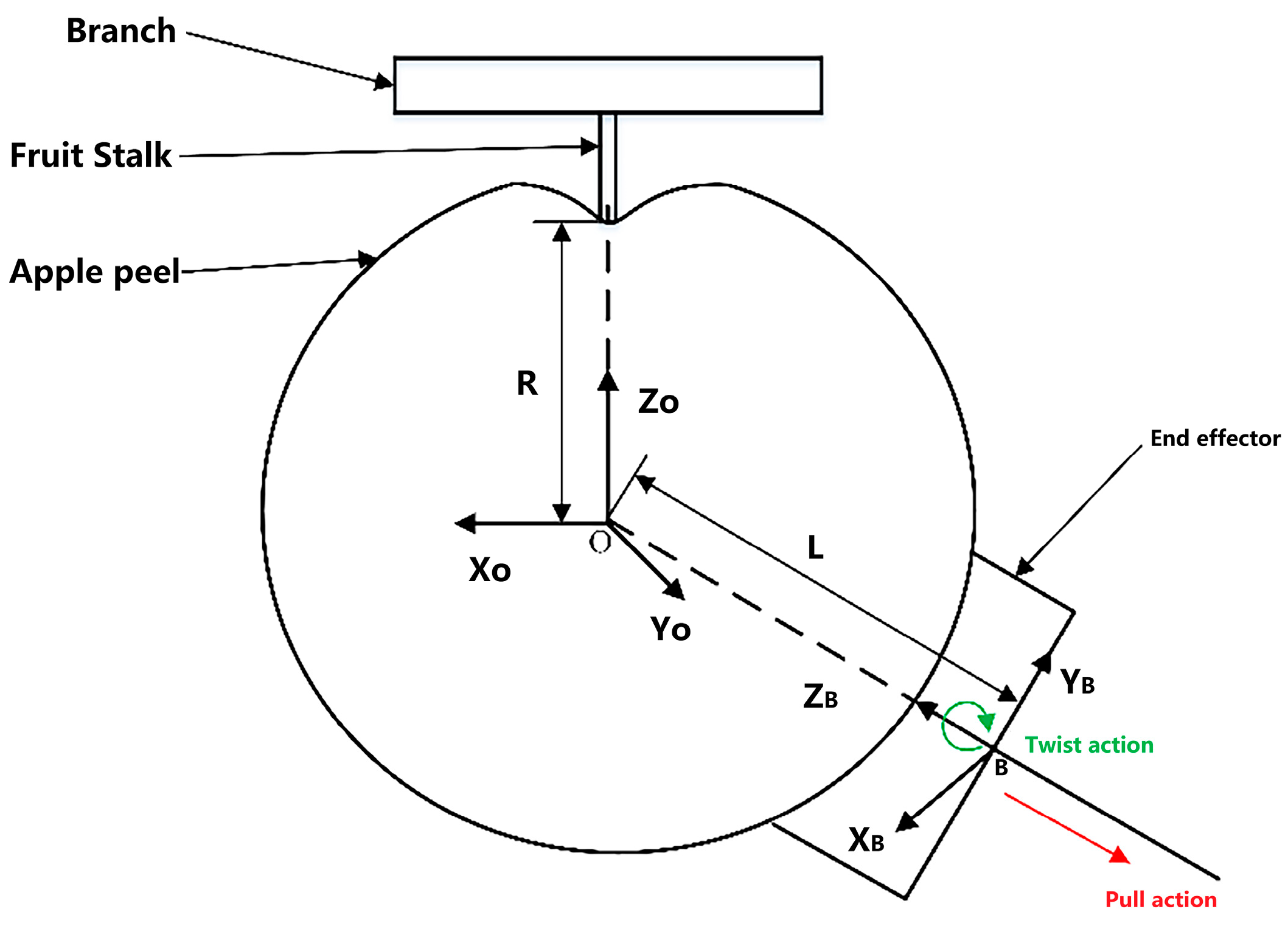
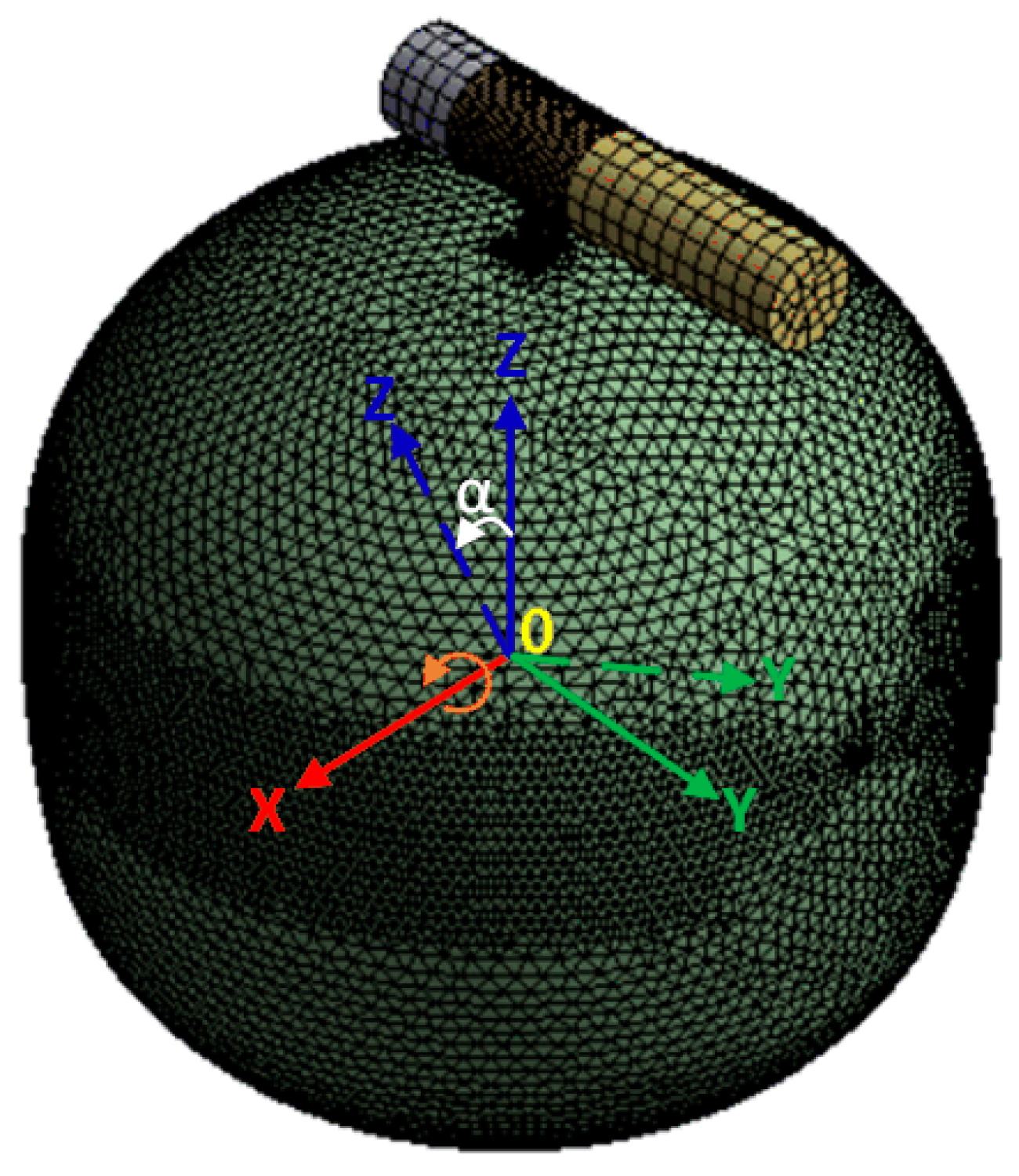
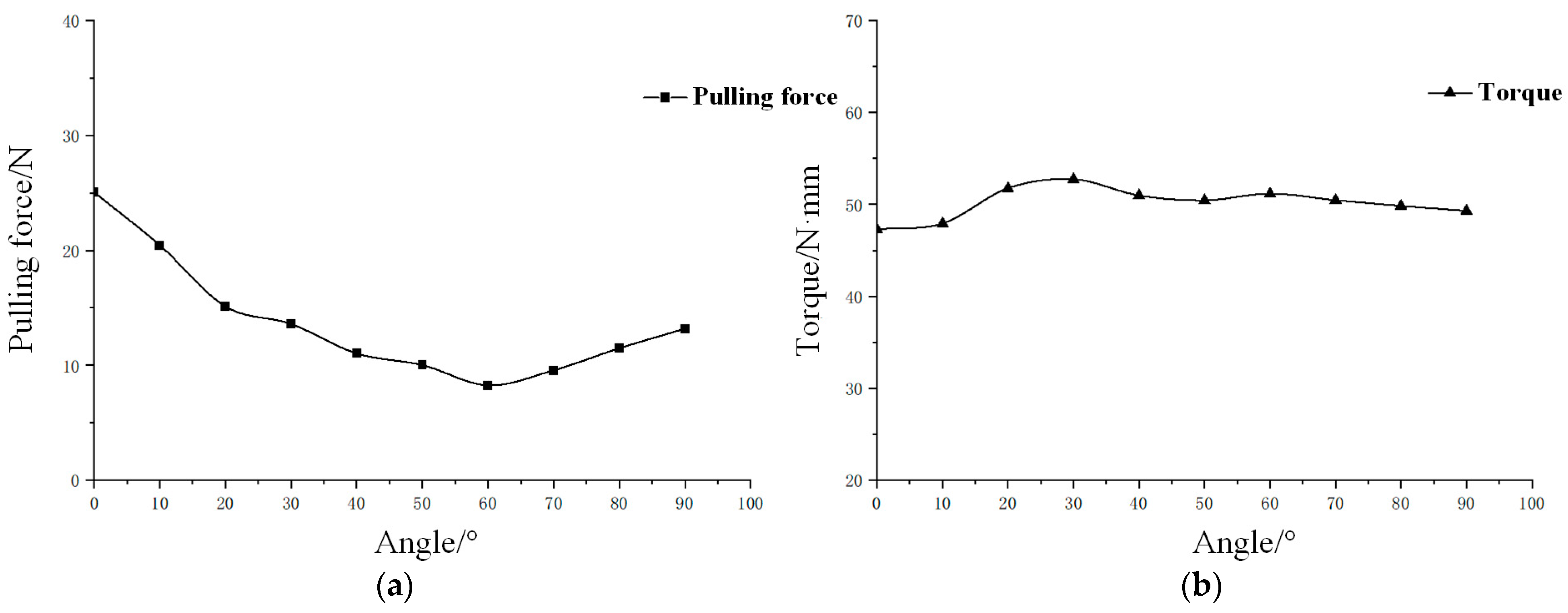
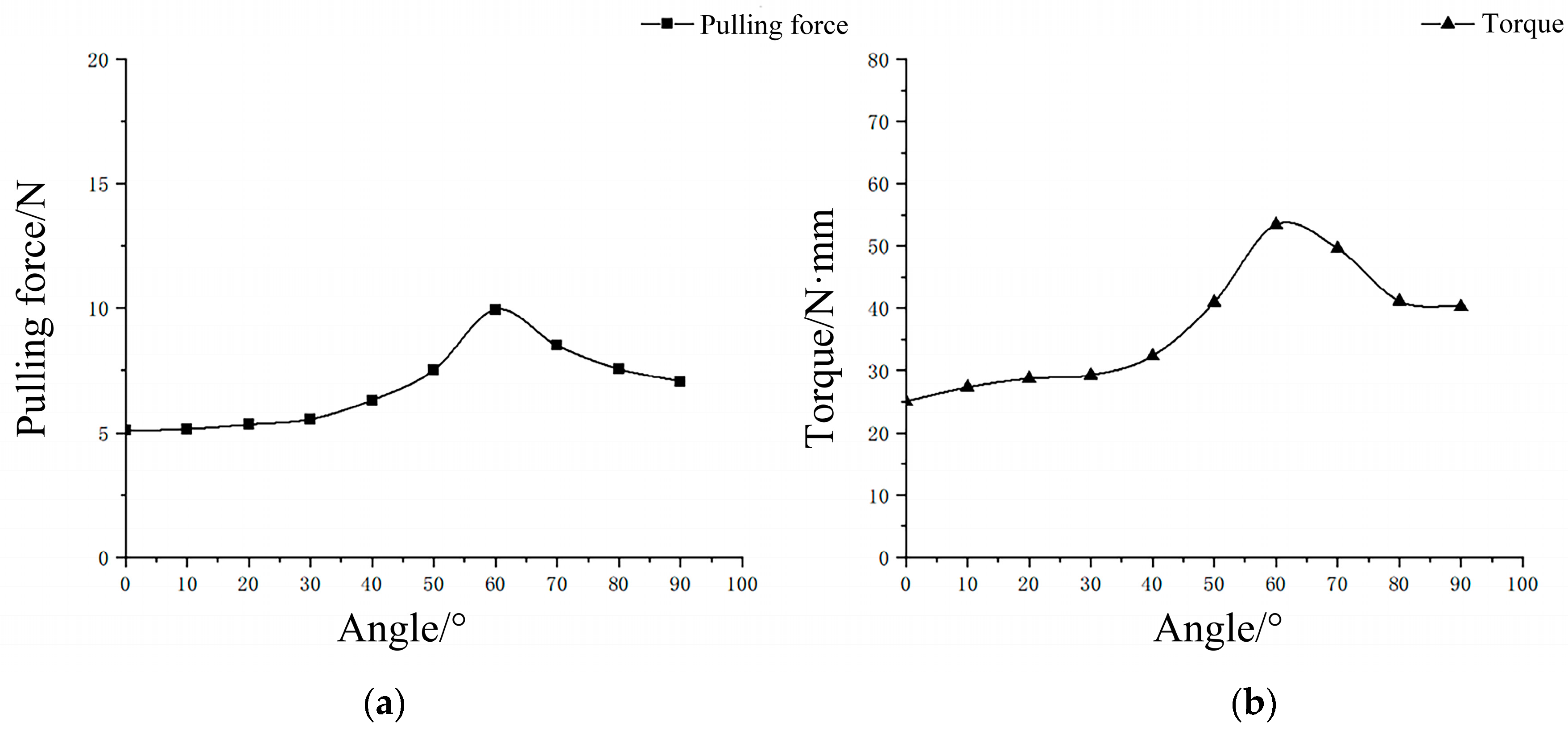
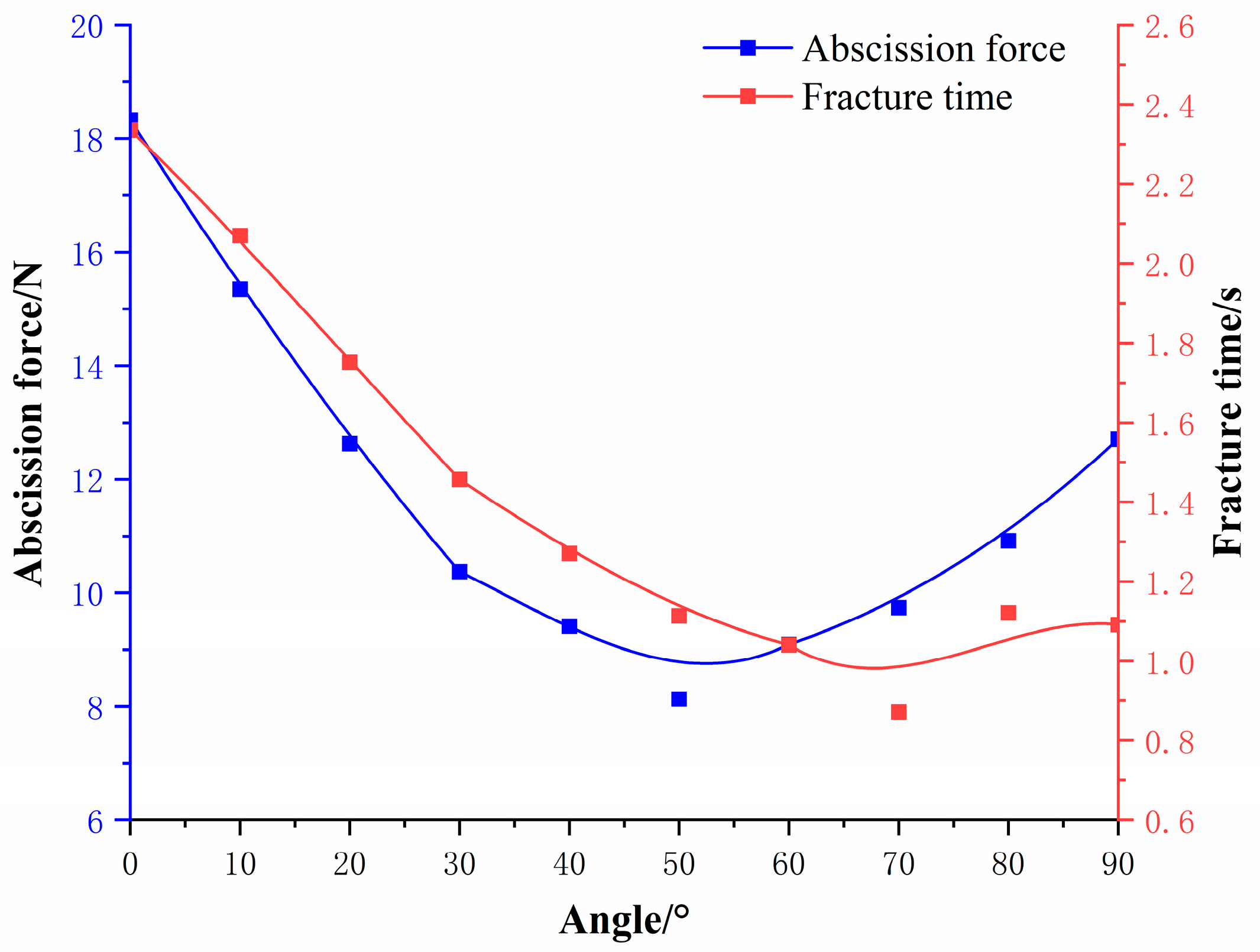
2.7.1. Estimation of the Best Harvesting Angle Based on Finite Element Simulation
2.7.2. Simulation of Pulling Action at Different Angles
2.7.3. Simulation of Twisting Action at Different Angles
3. Results and Discussion
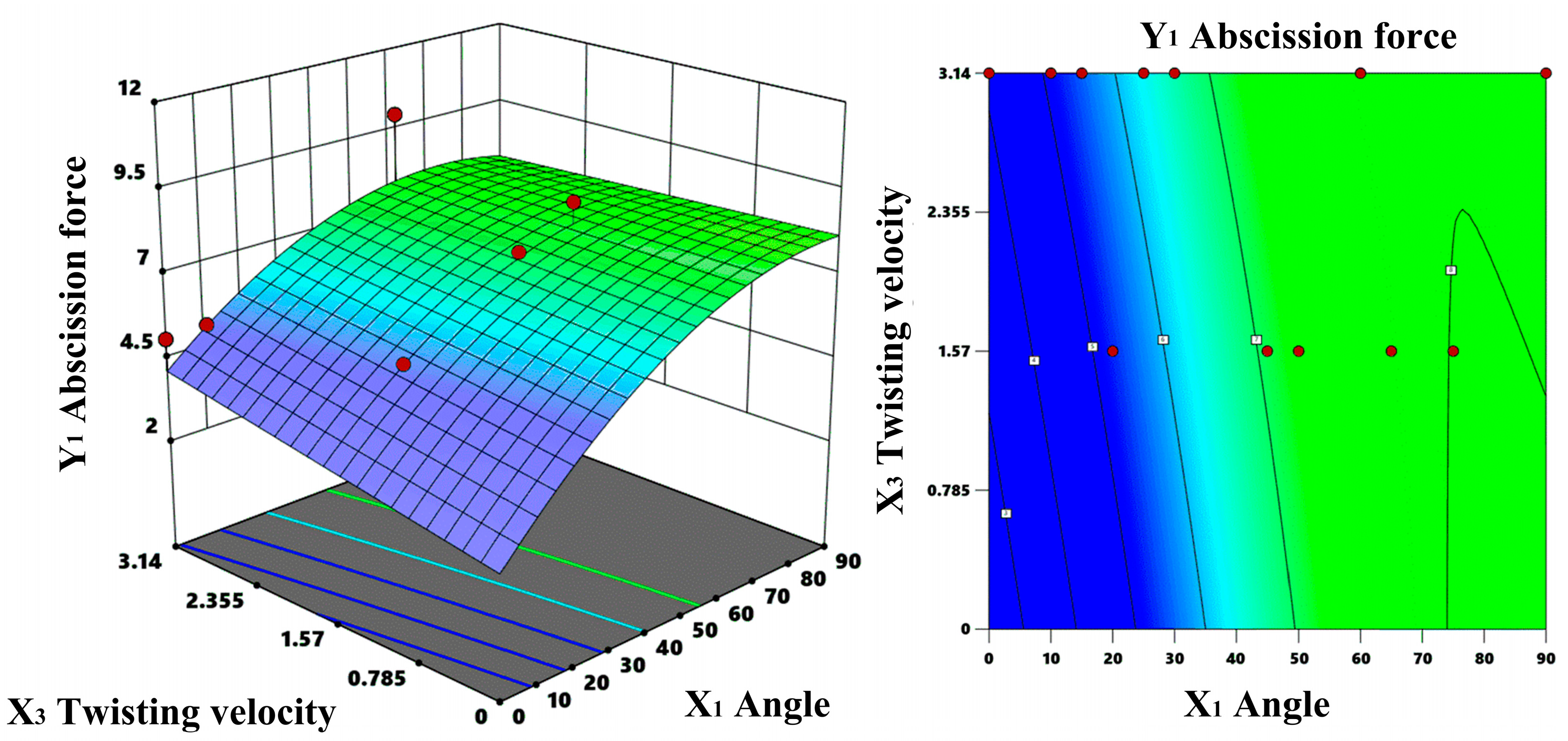
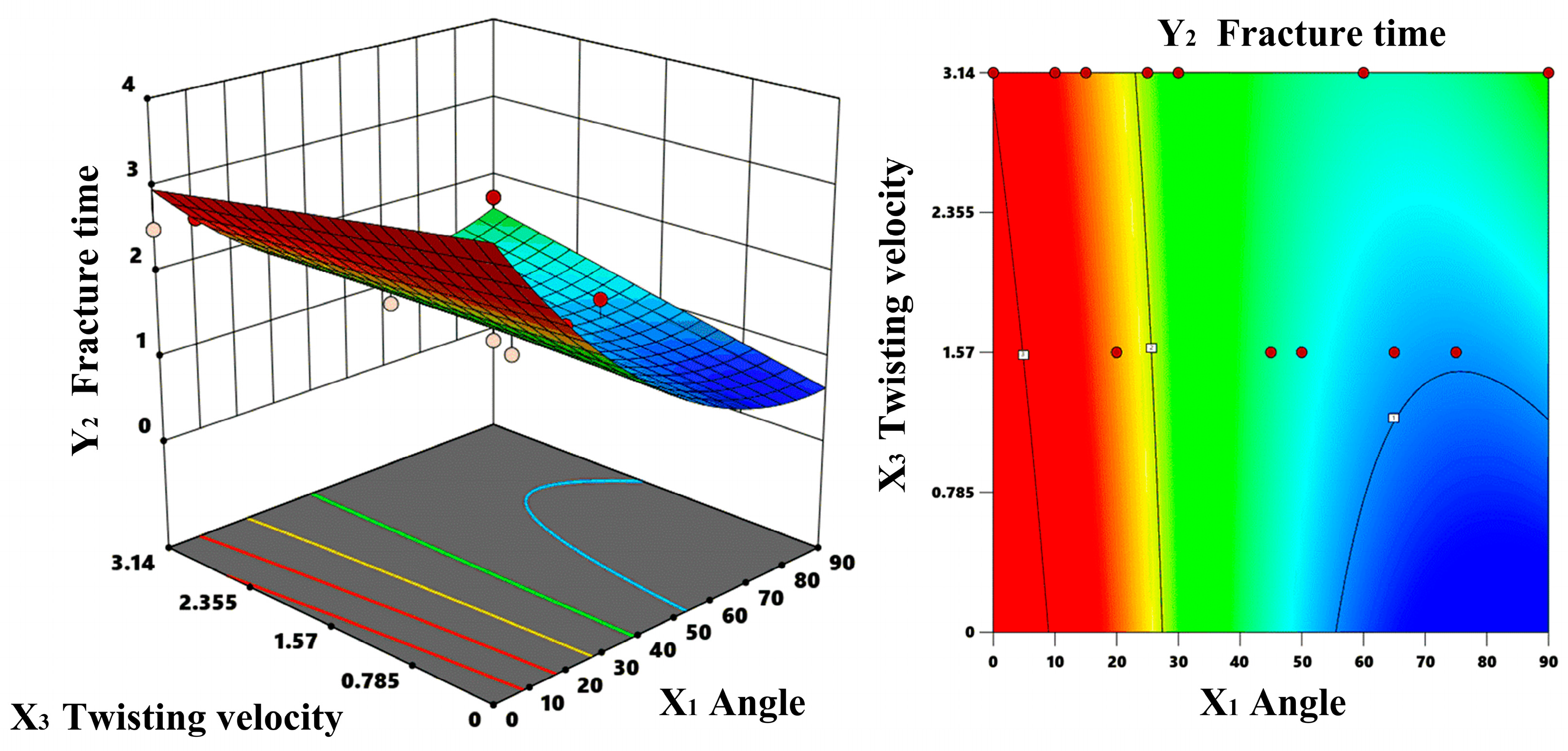
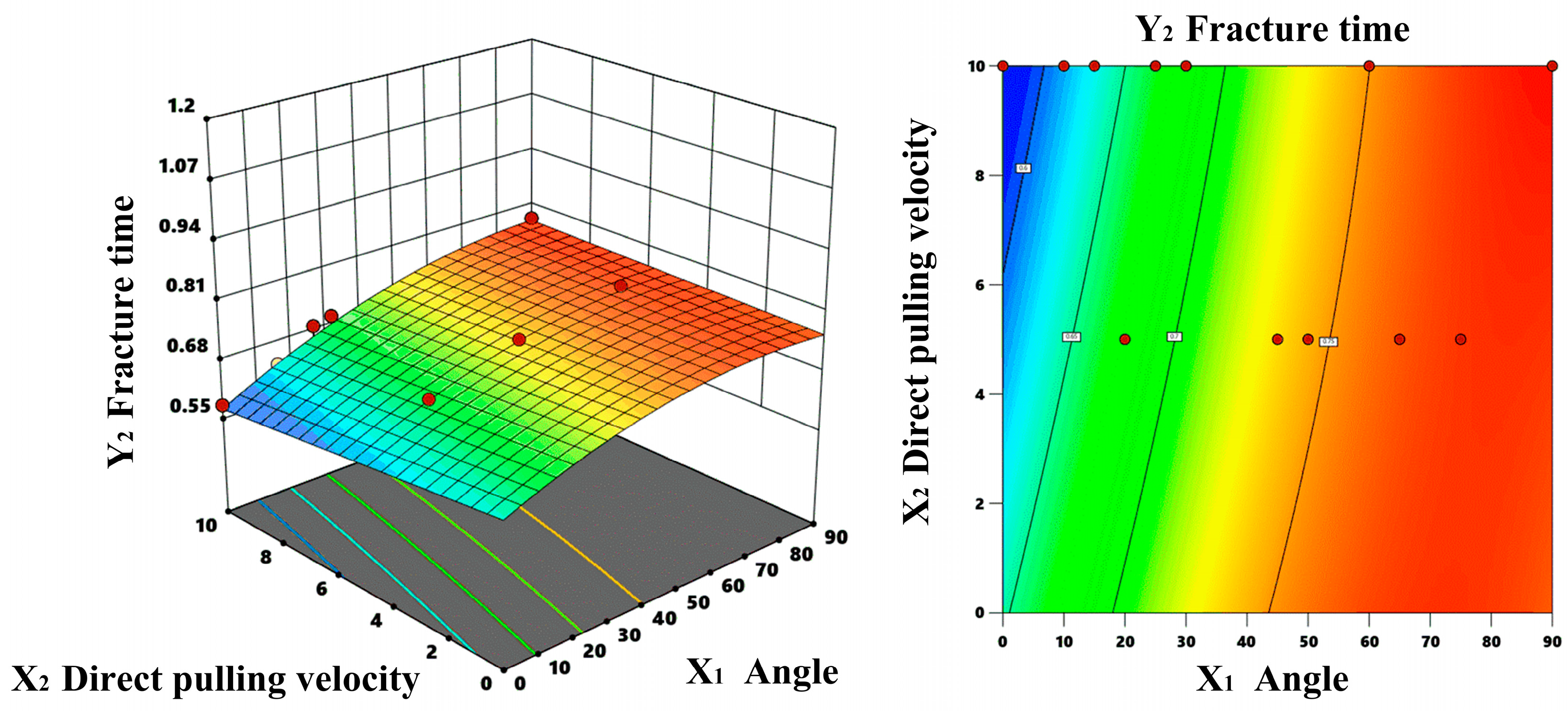
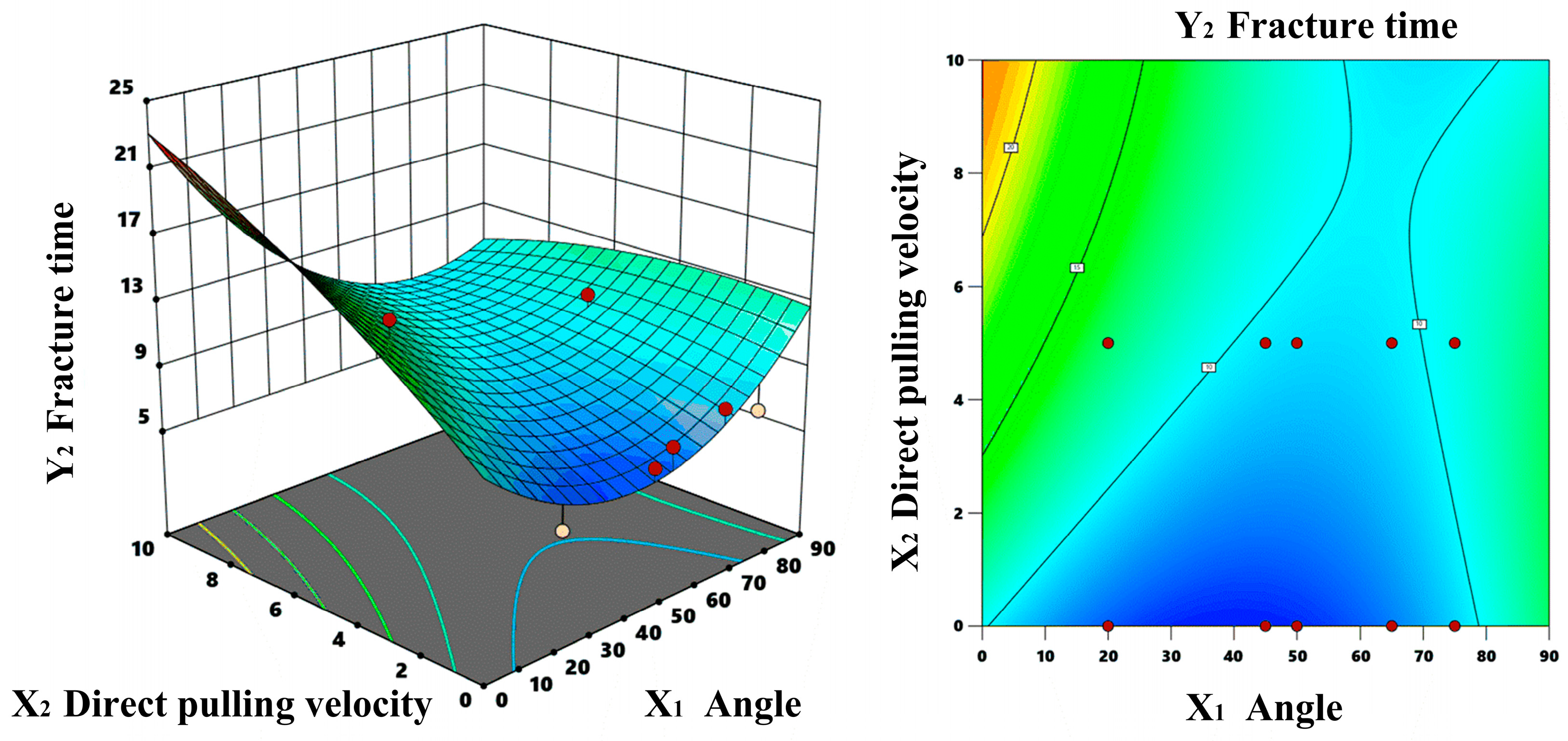
3.1. Response Surface Analysis of Optimal Picking Angle
3.1.1. Multivariate Regression Analysis
3.1.2. Response Surface Methodology
3.1.3. Parameter Optimization and Optimal Solution
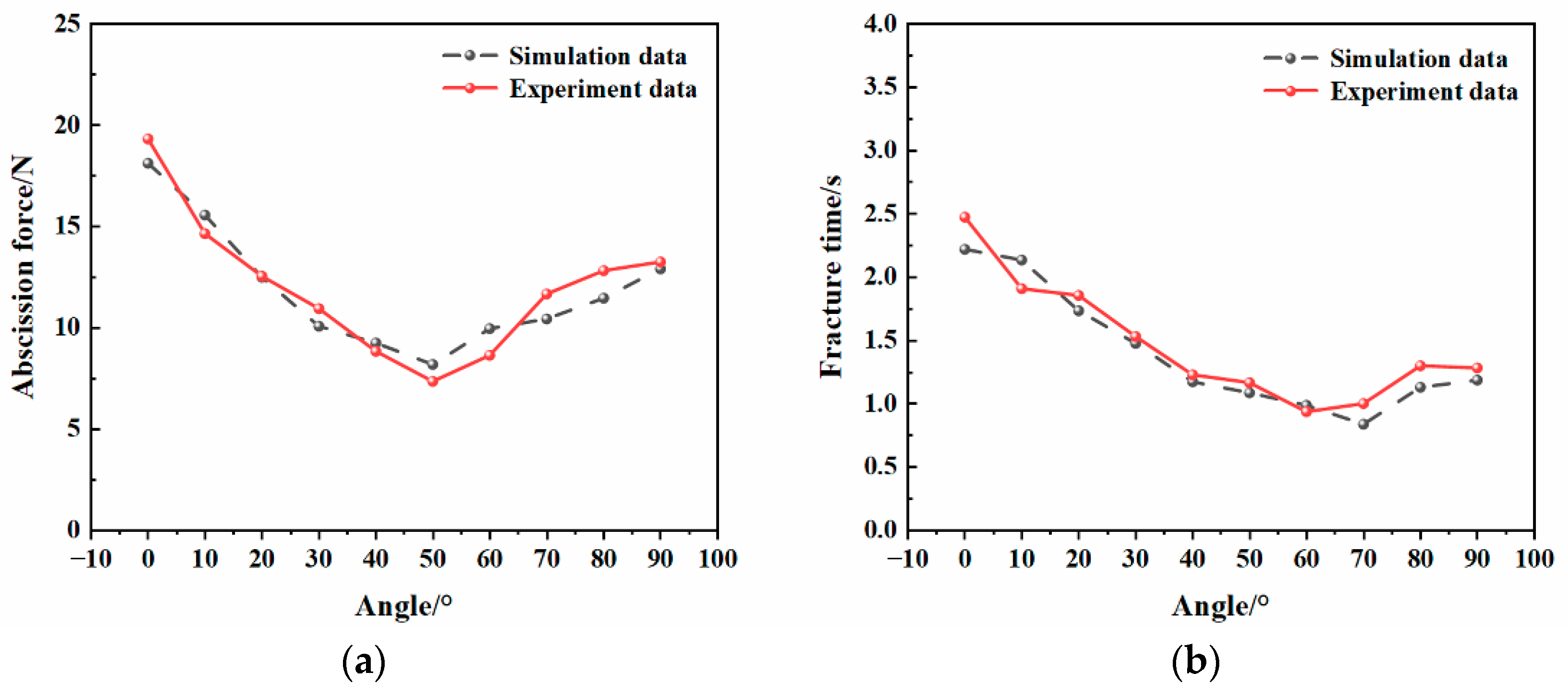
3.2. Fruit Abscission Process Validation Experiment
3.3. Apple-Picking Robot Orchard Picking Experiment and Result Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, J. Research progress analysis of robotics selective harvesting technologies. Trans. Chin. Soc. Agric. Mach. 2020, 51, 1–17. [Google Scholar] [CrossRef]
- Baeten, J.; Donné, K.; Boedrij, S.; Beckers, W.; Claesen, E. Autonomous fruit picking machine: A robotic apple harvester. In Field and Service Robotics: Results of the 6th International Conference; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gu, B.; Ji, C.; Wang, H.; Tian, G.; Zhang, G.; Wang, L. Design and experiment of intelligent mobile fruit picking robot. Trans. Chin. Soc. Agric. Mach. 2012, 43, 153–160. [Google Scholar] [CrossRef]
- Aljanobi, A.A.; Al-Hamed, S.A.; Al-Suhaibani, S.A. A setup of mobile robotic unit for fruit harvesting. In Proceedings of the 19th International Workshop on Robotics in Alpe-Adria-Danube Region (RAAD 2010), Budapest, Hungary, 24–26 June 2010. [Google Scholar]
- Bac, C.W.; van Henten, E.J.; Hemming, J.; Edan, Y. Harvesting robots for high-value crops: State-of-the-art review and challenges ahead. J. Field Robot. 2014, 31, 888–911. [Google Scholar] [CrossRef]
- Zhang, Z.; Igathinathane, C.; Li, J.; Cen, H.; Lu, Y.; Flores, P. Technology progress in mechanical harvest of fresh market apples. Comput. Electron. Agric. 2020, 175, 105606. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z. The Vision-Based Target Recognition, Localization, and Control for Harvesting Robots: A Review. Int. J. Precis. Eng. Manuf. 2024, 25, 409–428. [Google Scholar] [CrossRef]
- Yuri, J.A.; Moggia, C.; Sepulveda, A.; Poblete-Echeverría, C.; Valdés-Gómez, H.; Torres, C.A. Effect of cultivar, rootstock, and growing conditions on fruit maturity and postharvest quality as part of a six-year apple trial in Chile. Sci. Hortic. 2019, 253, 70–79. [Google Scholar] [CrossRef]
- Sun, C.Y.; Yan, J.; Fugui, Z.; Yuanmin, G.; Yong, X. Research progress of vegetable picking robot and its key technologies. J. Chin. Agric. Mech. 2023, 44, 63. [Google Scholar] [CrossRef]
- De Kleine, M.E.; Karkee, M. A semi-automated harvesting prototype for shaking fruit tree limbs. Trans. ASABE 2015, 58, 1461–1470. [Google Scholar] [CrossRef]
- Fruit, F.D. World Markets and Trade (Apples, Grapes, & Pears); Foreign Agricultural Service: Washington, DC, USA, 2018; pp. 1–30. [Google Scholar]
- Zhang, K.; Lammers, K.; Chu, P.; Li, Z.; Lu, R. An automated apple harvesting robot—From system design to field evaluation. J. Field Robot. 2024, 41, 2384–2400. [Google Scholar] [CrossRef]
- Janisiewicz, W.J.; Peterson, D.L. Susceptibility of the stem pull area of mechanically harvested apples to blue mold decay and its control with a biocontrol agent. Plant Dis. 2004, 88, 662–664. [Google Scholar] [CrossRef]
- Bulanon, D.M.; Kataoka, T. Fruit detection system and an end effector for robotic harvesting of Fuji apples. Agric. Eng. Int. CIGR J. 2010, 12, 203–210. [Google Scholar]
- Silwal, A.; Davidson, J.R.; Karkee, M.; Mo, C.; Zhang, Q.; Lewis, K. Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 2017, 34, 1140–1159. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.; Chen, L.; Chukwu, O.; Opara, U.L. Susceptibility of apples to bruising inside ventilated corrugated paperboard packages during simulated transport damage. Postharvest Biol. Technol. 2016, 118, 111–119. [Google Scholar] [CrossRef]
- He, L.; Fu, H.; Sun, D.; Karkee, M.; Zhang, Q. Shake-and-Catch Harvesting for Fresh Market Apples in Trellis-Trained Trees. Trans. ASABE 2017, 60, 353–360. [Google Scholar] [CrossRef]
- Hohimer, C.J.; Wang, H.; Bhusal, S.; Miller, J.; Mo, C.; Karkee, M. Design and Field Evaluation of a Robotic Apple Harvesting System with a 3D-Printed Soft-Robotic End-Effector. Trans. ASABE 2019, 62, 405–414. [Google Scholar] [CrossRef]
- Wang, Z.; Xun, Y.; Wang, Y.; Yang, Q. Review of smart robots for fruit and vegetable picking in agriculture. Int. J. Agric. Biol. Eng. 2022, 15, 33–54. [Google Scholar] [CrossRef]
- Bu, L.; Hu, G.; Chen, C.; Sugirbay, A.; Chen, J. Experimental and simulation analysis of optimum picking patterns for robotic apple harvesting. Sci. Hortic. 2020, 261, 108937. [Google Scholar] [CrossRef]
- Beyaz, A. Harvest glove and LabView based mechanical damage determination on apples. Sci. Hortic. 2018, 228, 49–55. [Google Scholar] [CrossRef]
- Bu, L.; Chen, C.; Hu, G.; Zhou, J.; Sugirbay, A.; Chen, J. Investigating the dynamic behavior of an apple branch-stem-fruit model using experimental and simulation analysis. Comput. Electron. Agric. 2021, 186, 106224. [Google Scholar] [CrossRef]
- Guoli, L.; Changying, J.; Baoxing, G.; Weiyue, X.; Mang, D. Kinematics analysis and experiment of apple harvesting robot manipulator with multiple end-effectors. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2016, 47, 14–21. [Google Scholar] [CrossRef]
- Torregrosa, A.; Albert, F.; Aleixos, N.; Ortiz, C.; Blasco, J. Analysis of the detachment of citrus fruits by vibration using artificial vision. Biosyst. Eng. 2014, 119, 1–12. [Google Scholar] [CrossRef]
- Gongal, A.; Amatya, S.; Karkee, M.; Zhang, Q.; Lewis, K. Sensors and systems for fruit detection and localization: A review. Comput. Electron. Agric. 2015, 116, 8–19. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Singh, K.; Pardeshi, I.; Kumar, M.; Srinivas, K.; Srivastva, A. Optimisation of machine parameters of a pedal-operated paddy thresher using RSM. Biosyst. Eng. 2008, 100, 591–600. [Google Scholar] [CrossRef]
- Stagnari, F.; Galieni, A.; Pisante, M. Shading and nitrogen management affect quality, safety and yield of greenhouse-grown leaf lettuce. Sci. Hortic. 2015, 192, 70–79. [Google Scholar] [CrossRef]
- Zhao, J.; Sugirbay, A.; Zhang, S.; Liu, F.; Bu, L.; Chen, Y.; Wang, Z.; Chen, J. FEM explicit dynamics simulation and NIR hyperspectral reflectance imaging for determination of impact bruises of Lycium barbarum L. Postharvest Biol. Technol. 2019, 155, 102–110. [Google Scholar] [CrossRef]
- Zulkifli, N.; Hashim, N.; Harith, H.H.; Shukery, M.F.M. Finite element modelling for fruit stress analysis—A review. Trends Food Sci. Technol. 2020, 97, 29–37. [Google Scholar] [CrossRef]
- Shen, C.; Li, X.; Tian, K.; Zhang, B.; Huang, J.; Chen, Q. Experimental analysis on mechanical model of ramie stalk. Trans. Chin. Soc. Agric. Eng. 2015, 31, 26–33. [Google Scholar] [CrossRef]
- Yamada, T.; Kobayashi, T.; Tabuchi, T. Anatomical and histochemical studies of separation process on the juncture tissues between peduncle and bourse on apple fruit. Acta Hortic. 2018, 1206, 129–136. [Google Scholar] [CrossRef]
- Horbens, M.; Branke, D.; Gärtner, R.; Voigt, A.; Stenger, F.; Neinhuis, C. Multi-scale simulation of plant stem reinforcement by brachysclereids: A case study in apple fruit peduncles. J. Struct. Biol. 2015, 192, 116–126. [Google Scholar] [CrossRef]
- Qiu, L.P.; Zhu, E.C.; van de Kuilen, J.W.G. Modeling crack propagation in wood by extended finite element method. Eur. J. Wood Wood Prod. 2013, 72, 273–283. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials. NASA/TM-2002-211737. 2002. Available online: https://ntrs.nasa.gov/citations/20020053651 (accessed on 9 December 2024).
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Liu, P.; Islam, M. A nonlinear cohesive model for mixed-mode delamination of composite laminates. Compos. Struct. 2013, 106, 47–56. [Google Scholar] [CrossRef]
- Mi, Y.; Crisfield, M.A.; Davies, G.A.O.; Hellweg, H.B. Progressive Delamination Using Interface Elements. J. Compos. Mater. 1998, 32, 1246–1272. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. An interface damage model for the simulation of delamination under variable-mode ratio in composite materials. Int. J. Adv. Robot. Syst. 2004. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Ezzine, M.C.; Amiri, A.; Tarfaoui, M. Experimental and numerical investigation of the fracture behavior of adhesive shear tests single lap joints. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 382. [Google Scholar] [CrossRef]
- Applications of the Newton-Raphson Method in Decision Sciences and Education. Adv. Decis. Sci. 2019, 23, 52–80. [CrossRef]
- Ji, W.; Li, J.; Yang, J.; Ding, S.; Zhao, D. Analysis and validation for mechanical damage of apple by gripper in harvesting robot based on finite element method. Trans. Chin. Soc. Agric. Mach. 2015, 31, 17–22. [Google Scholar] [CrossRef]
- Tien Thanh Nguyen, T.T.; Eessen, D.V.; Baerdemaeker, J.D.; Saeys, W. Optimum detaching movement for apples-harvesting robot. In Proceedings of the International Conference of Agricultural Engineering—CIGR-AgEng 2012: Agriculture and Engineering for a Healthier Life, Valencia, Spain, 8–12 July 2012. [Google Scholar]
- Daily, J.W. Design and analysis of experiments. Exp. Therm. Fluid Sci. 1988, 1, 105. [Google Scholar] [CrossRef]



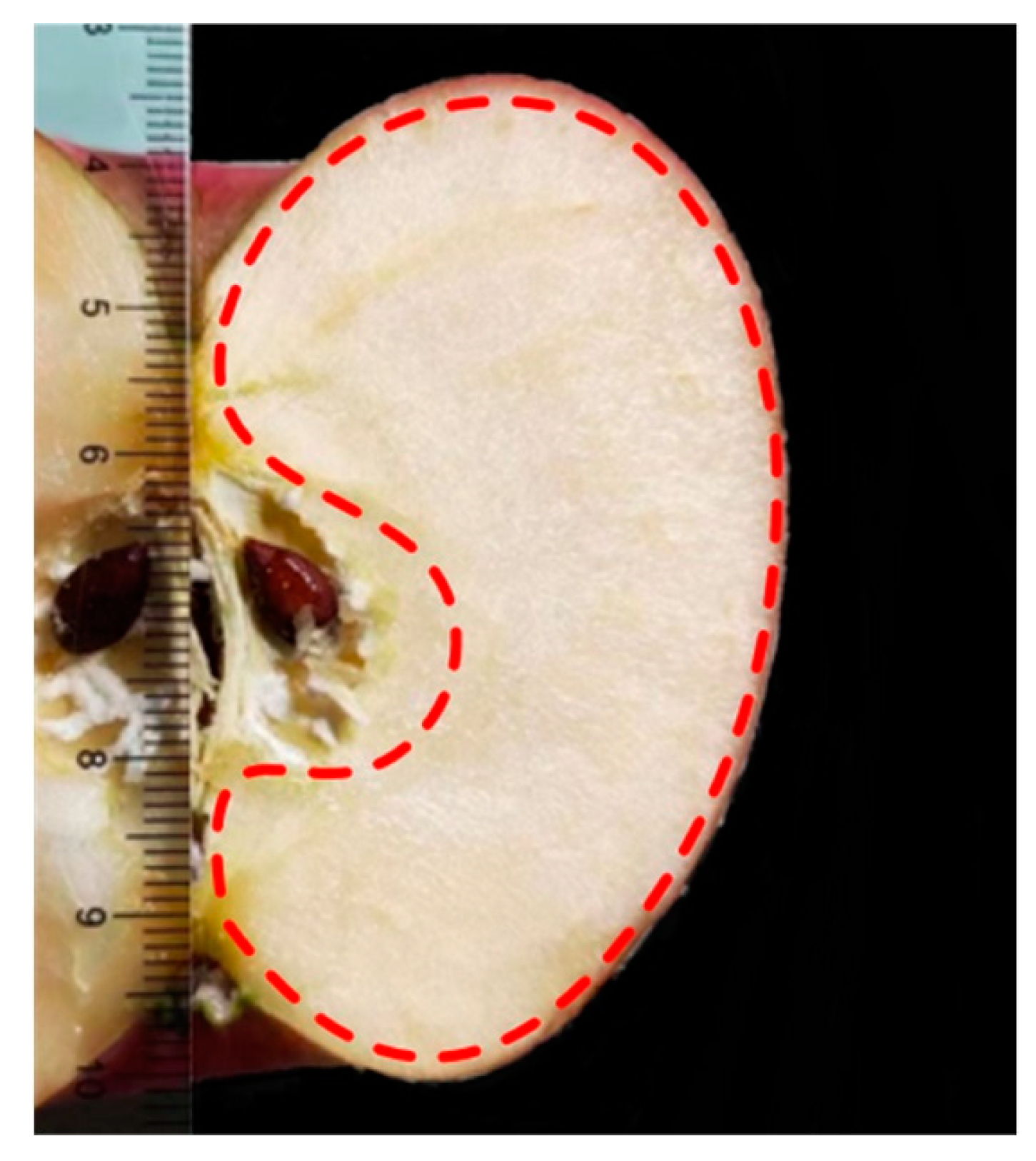
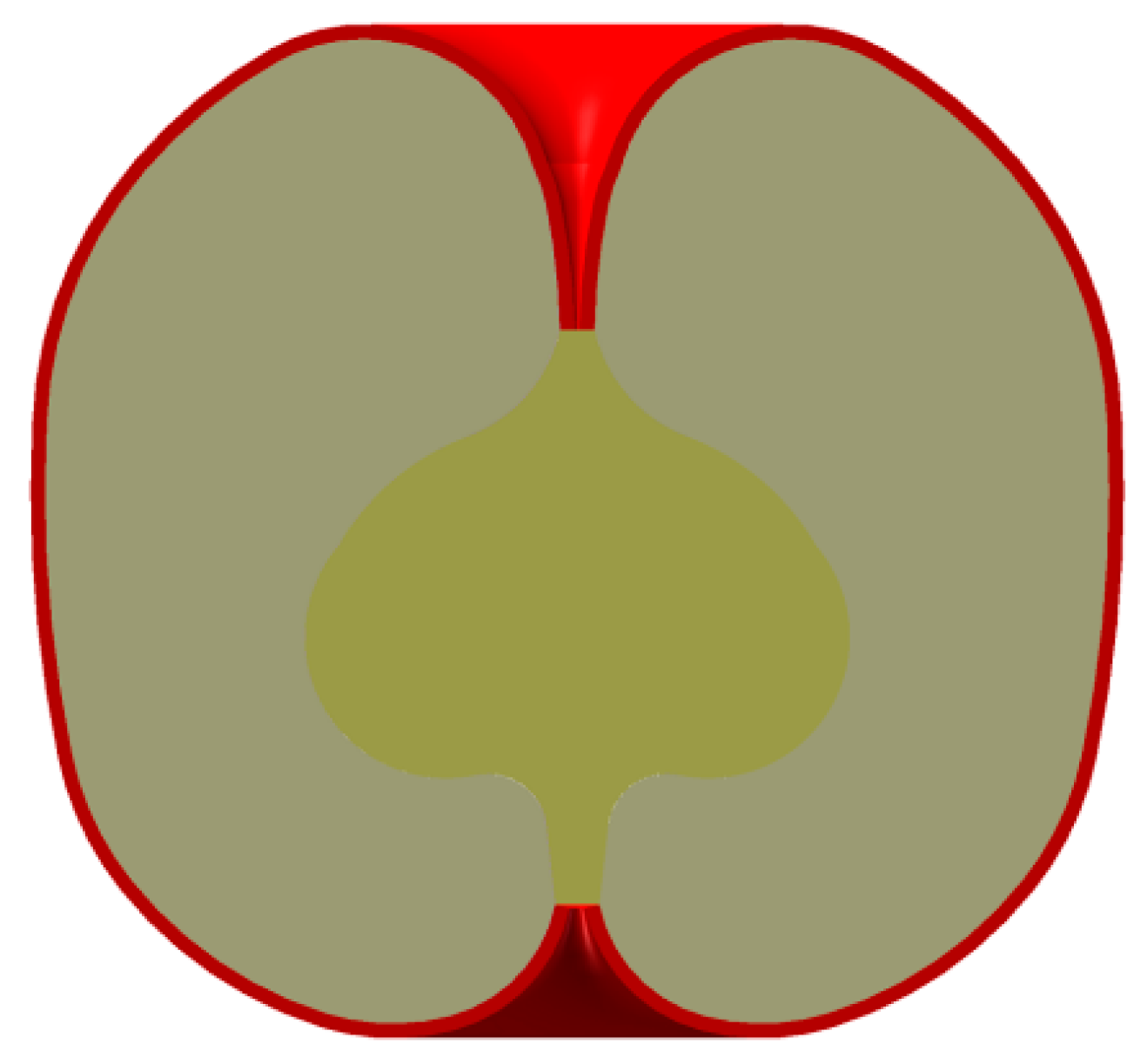
















| Geometric Feature | Minimum Value | Maximum Value | Average Value |
|---|---|---|---|
| Axial diameter (mm) | 59.6 | 92.8 | 72.3 |
| Radial diameter (mm) | 69.7 | 107.5 | 85.2 |
| Fruit stalk length (mm) | 10.1 | 30.4 | 19.3 |
| Fruit weight (g) | 175.2 | 389.1 | 287.6 |
| Material | Elastic Modulus E/MPa | Yield Stress /MPa | Failure Stress | Bulk Modulus | Shear Modulus | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Stalk | 141.37 | 3.14 | 5.56 | 235.62 | 50.49 | 0.4 |
| Branch | 58.94 | 0.65 | 6.21 | 98.23 | 21.05 | 0.4 |
| Maximum Normal Stress (Mpa) | Normal Fracture Energy Release Rate (KJ/m2) | Maximum Tangential Stress (Mpa) | Tangential Fracture Energy Release Rate (KJ/m2) |
|---|---|---|---|
| 4.283 | 0.516 | 2.976 | 1.083 |
| Material | Density Kg/m3 | Elastic Modulus Mpa | Poisson’s Ratio |
|---|---|---|---|
| Apple peel | 840 | 12 | 0.35 |
| Apple flesh | 840 | 5 | 0.35 |
| Apple core | 950 | 7 | 0.35 |
| Factors/Responses | Unit |
|---|---|
| The angle between the center axis of the robotic arm’s end and the fruit axis, ) | ° |
| Direct-pulling velocity ) | mm/s |
| ) | rad/s |
| The maximum pulling force experienced when the abscission layer fractures, ) | N |
| The time from when the abscission layer begins to experience the load until it fractures, ) | s |
| Order | (°) | (mm/s) | (rad/s) | (N) | (s) |
|---|---|---|---|---|---|
| 1 | 0 | 10 | 0 | 25.05 | 0.58 |
| 2 | 0 | 0 | 3.14 | 5.088 | 2.51 |
| 3 | 0 | 10 | 3.14 | 24.28 | 1.86 |
| 4 | 10 | 10 | 0 | 20.45 | 0.58 |
| 5 | 10 | 0 | 3.14 | 5.147 | 2.51 |
| 6 | 10 | 10 | 3.14 | 19.78 | 1.86 |
| 7 | 15 | 10 | 0 | 17.22 | 0.63 |
| 8 | 15 | 0 | 3.14 | 5.231 | 2.48 |
| 9 | 15 | 10 | 3.14 | 16.474 | 1.99 |
| 10 | 20 | 5 | 0 | 15.12 | 0.68 |
| 11 | 20 | 0 | 1.57 | 5.329 | 2.47 |
| 12 | 20 | 5 | 1.57 | 13.847 | 2.01 |
| 13 | 25 | 10 | 0 | 14.48 | 0.69 |
| 14 | 25 | 0 | 3.14 | 5.443 | 2.38 |
| 15 | 25 | 10 | 3.14 | 13.031 | 1.66 |
| 16 | 30 | 10 | 0 | 13.59 | 0.7 |
| 17 | 30 | 0 | 3.14 | 5.543 | 2.03 |
| 18 | 30 | 10 | 3.14 | 12.856 | 1.45 |
| 19 | 45 | 5 | 0 | 10.58 | 0.74 |
| 20 | 45 | 0 | 1.57 | 6.662 | 1.21 |
| 21 | 45 | 5 | 1.57 | 9.178 | 0.89 |
| 22 | 50 | 5 | 0 | 10.02 | 0.74 |
| 23 | 50 | 0 | 1.57 | 7.512 | 0.96 |
| 24 | 50 | 5 | 1.57 | 8.954 | 0.82 |
| 25 | 60 | 10 | 0 | 8.26 | 0.73 |
| 26 | 60 | 0 | 3.14 | 9.954 | 0.76 |
| 27 | 60 | 10 | 3.14 | 7.423 | 0.62 |
| 28 | 65 | 5 | 0 | 9.57 | 0.75 |
| 29 | 65 | 0 | 1.57 | 8.504 | 1.08 |
| 30 | 65 | 5 | 1.57 | 8.72 | 0.85 |
| 31 | 75 | 5 | 0 | 11.48 | 0.78 |
| 32 | 75 | 0 | 1.57 | 7.563 | 1.26 |
| 33 | 75 | 5 | 1.57 | 11.304 | 1.04 |
| 34 | 90 | 10 | 0 | 13.19 | 0.78 |
| 35 | 90 | 0 | 3.14 | 7.062 | 1.73 |
| 36 | 90 | 10 | 3.14 | 11.964 | 1.11 |
| Source | Sum of Squares | df | Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 864.67 | 9 | 96.07 | 26 | <0.0001 *** |
| 61.21 | 1 | 61.21 | 16.56 | <0.0004 *** | |
| 74.41 | 1 | 74.41 | 20.14 | <0.0001 *** | |
| 13.26 | 1 | 13.26 | 3.59 | 0.0693 | |
| 114.27 | 1 | 114.27 | 30.92 | <0.0001 *** | |
| 0.2592 | 1 | 0.2592 | 0.0701 | 0.7932 | |
| 4.19 | 1 | 4.19 | 1.32 | 0.2966 | |
| 99.40 | 1 | 99.40 | 26.90 | <0.0001 *** | |
| 4.89 | 1 | 4.89 | 1.32 | 0.2606 | |
| 0.1188 | 1 | 0.1188 | 0.0322 | 0.38591 | |
| Residual | 96.07 | 26 | 3.70 | ||
| Cor Total | 960.75 | 35 | |||
| Fit Statistics | |||||
| Std. Dev. | 1.92 | 0.9000 | |||
| Mean | 11.27 | 0.8654 | |||
| C.V.% | 14.68 | 0.6667 | |||
| PRESS | 144.08 | Adeq Precision | 19.3187 |
| Source | Sum of Squares | df | Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 12.76 | 9 | 1.42 | 14.31 | <0.0001 *** |
| 1.81 | 1 | 1.81 | 18.24 | <0.0002 *** | |
| 0.6223 | 1 | 0.6223 | 6.28 | 0.0188 ** | |
| 1.09 | 1 | 1.09 | 11.04 | 0.0026 ** | |
| 0.2015 | 1 | 0.2015 | 2.03 | 0.1659 | |
| 0.6217 | 1 | 0.6217 | 6.27 | 0.0189 * | |
| 0.0018 | 1 | 0.0018 | 0.0184 | 0.8931 | |
| 0.5911 | 1 | 0.5911 | 5.96 | 0.0217 ** | |
| 0.0094 | 1 | 0.0094 | 0.0943 | 0.7612 | |
| 0.0358 | 1 | 0.0358 | 0.3609 | 0.5532 | |
| Residual | 2.58 | 26 | 0.0991 | ||
| Cor Total | 0.0358 | 35 | |||
| Fit Statistics | |||||
| Std. Dev. | 0.3149 | 0.8320 | |||
| Mean | 1.28 | 0.7738 | |||
| C.V.% | 14.68 | 0.5664 | |||
| PRESS | 1137.99 | Adeq Precision | 14.4491 |
| Item | Goal | Lower Limit | Upper Limit |
|---|---|---|---|
| Angle (°) | Within range | 0 | 90 |
| Direct-pulling velocity (mm/s) | Within range | 0 | 10 |
| Twisting velocity (rad/s) | Within range | 0 | 1.57 |
| Abscission force (N) | Minimum value | 5 | 15 |
| Fracture time (s) | Minimum value | 0.7 | 1.3 |
| Angle (°) | Direct-Pulling Velocity (mm/s) | Twisting Velocity (rad/s) | Abscission Force (N) | Fracture Time (s) |
|---|---|---|---|---|
| 58.402 | 3.000 | 2.115 | 8.100 | 0.942 |
| Variety | Picking Methods | Number of Pickings | Number of Successful Pickings | Average Picking Period | Number of Stalks Retained | Stalk Retention Rate |
|---|---|---|---|---|---|---|
| Red Fuji | optimal picking methods | 100 | 83 | 11.2 s | 78 | 94.0% |
| point-to-point | 100 | 74 | 8.4 s | 56 | 75.7% | |
| Mingyue | optimal picking methods | 100 | 87 | 10.9 s | 80 | 92.0% |
| point-to-point | 100 | 72 | 7.6 s | 52 | 72.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, M.; Xu, Z.; Hui, B.; Zhou, Q. Simulation and Experiment of Optimal Conditions for Apple Harvesting with High Fruit Stalk Retention Rate. Agriculture 2024, 14, 2280. https://doi.org/10.3390/agriculture14122280
Bao M, Xu Z, Hui B, Zhou Q. Simulation and Experiment of Optimal Conditions for Apple Harvesting with High Fruit Stalk Retention Rate. Agriculture. 2024; 14(12):2280. https://doi.org/10.3390/agriculture14122280
Chicago/Turabian StyleBao, Muze, Zhipeng Xu, Boxu Hui, and Qiaojun Zhou. 2024. "Simulation and Experiment of Optimal Conditions for Apple Harvesting with High Fruit Stalk Retention Rate" Agriculture 14, no. 12: 2280. https://doi.org/10.3390/agriculture14122280
APA StyleBao, M., Xu, Z., Hui, B., & Zhou, Q. (2024). Simulation and Experiment of Optimal Conditions for Apple Harvesting with High Fruit Stalk Retention Rate. Agriculture, 14(12), 2280. https://doi.org/10.3390/agriculture14122280






