Simulation Analysis and Optimization Design of Paddy Field Mud Spreader Blades for Uniform Dispersion
Abstract
:1. Introduction
2. Materials and Methods
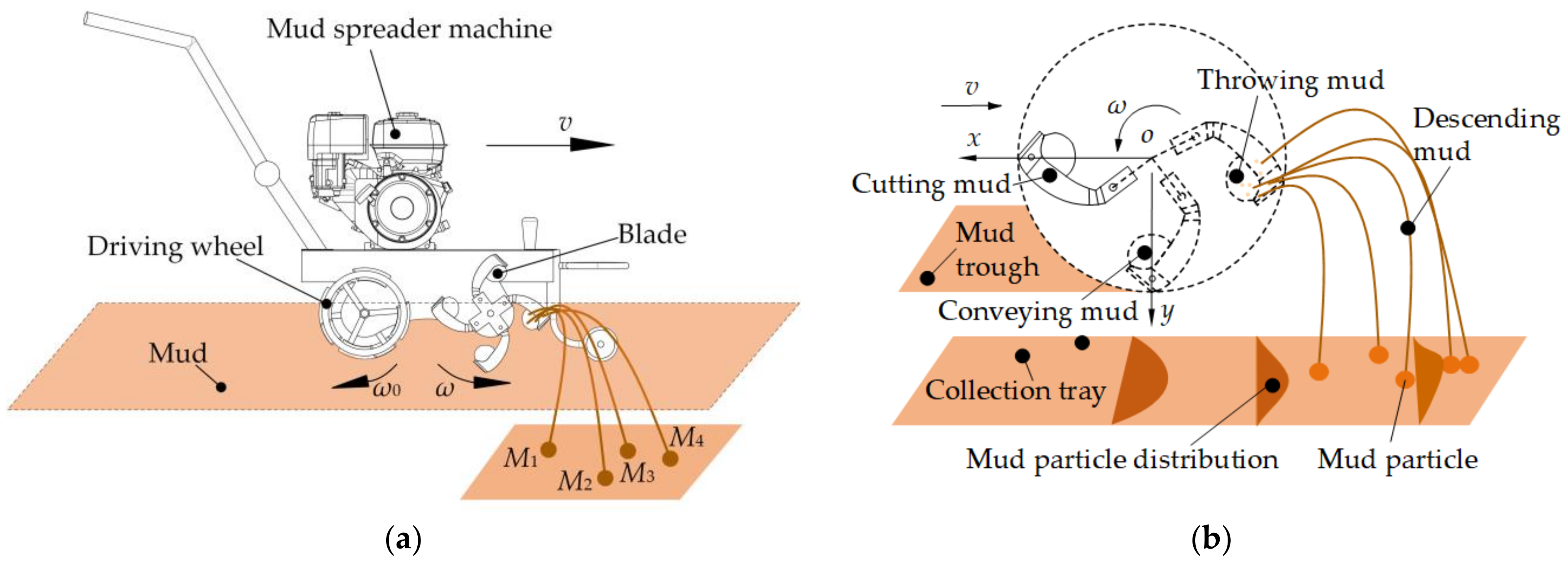
2.1. Operational Principle of Mud Spreader
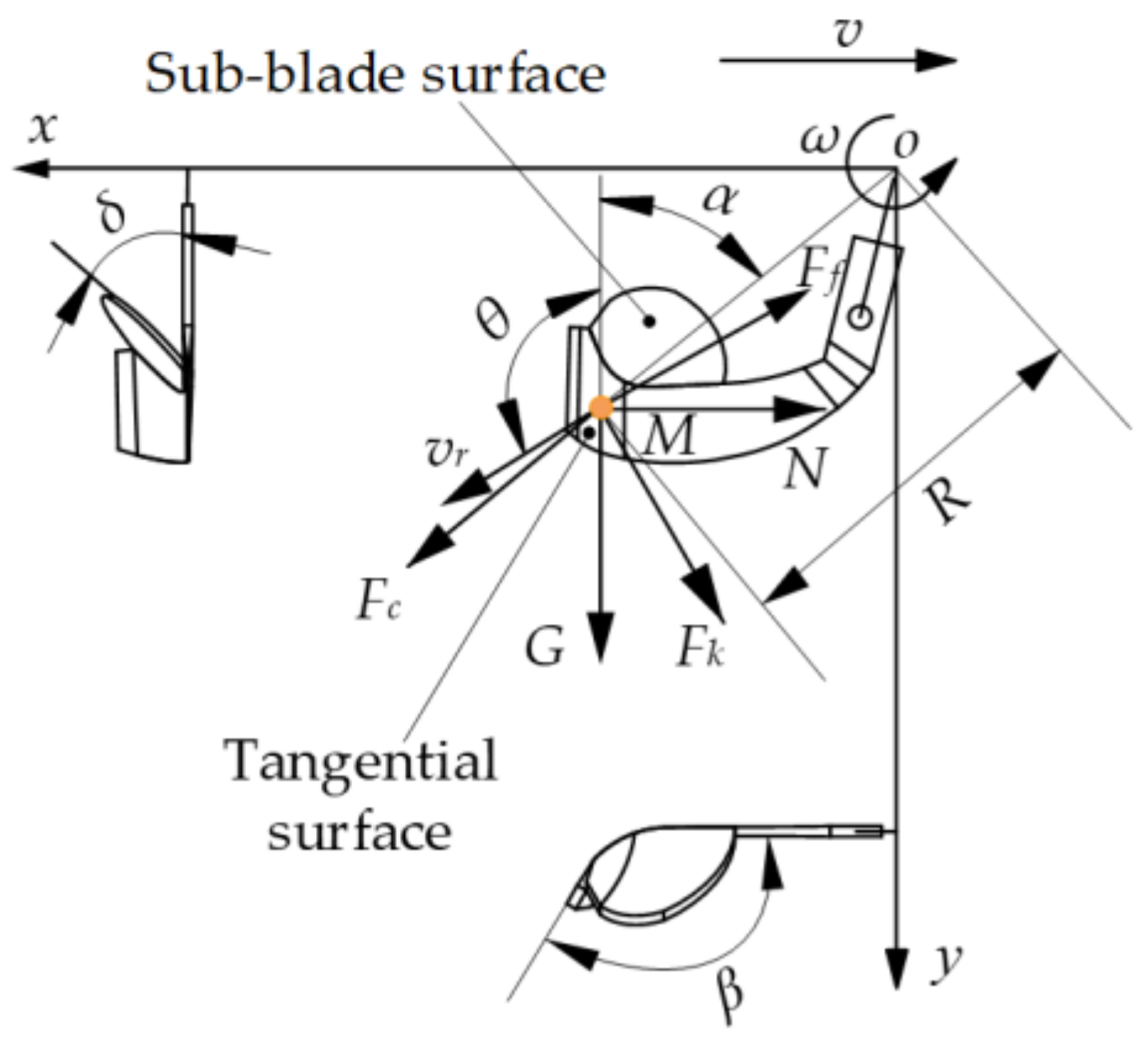
2.2. Mechanics Model of Mud Particle Motion
2.2.1. Force Analysis on Particles
2.2.2. Differential Equation of Particle Motion
2.2.3. Trajectory Equation of Particle Motion
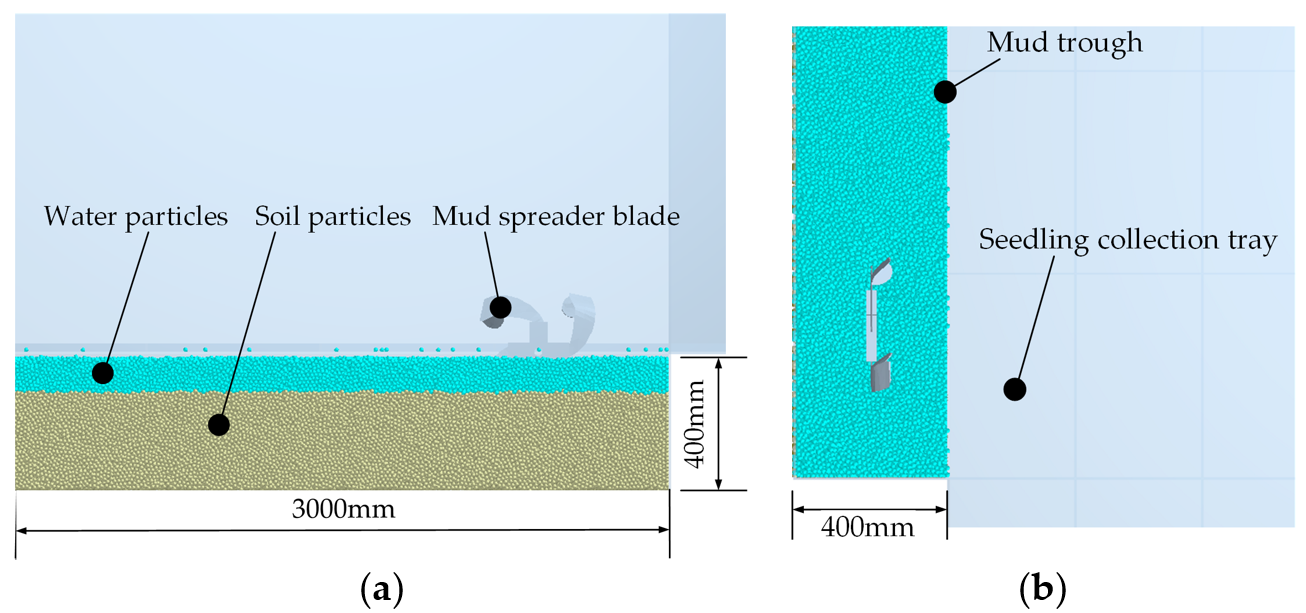
2.3. Simulation Model
2.3.1. Discrete Element Model
2.3.2. Single-Factor Experiment
2.3.3. Secondary Orthogonal Rotational Combination Design Experiment
2.3.4. Calculation Method of Experimental Index
3. Results and Discussion
3.1. Single-Factor Experiment Results and Discussion
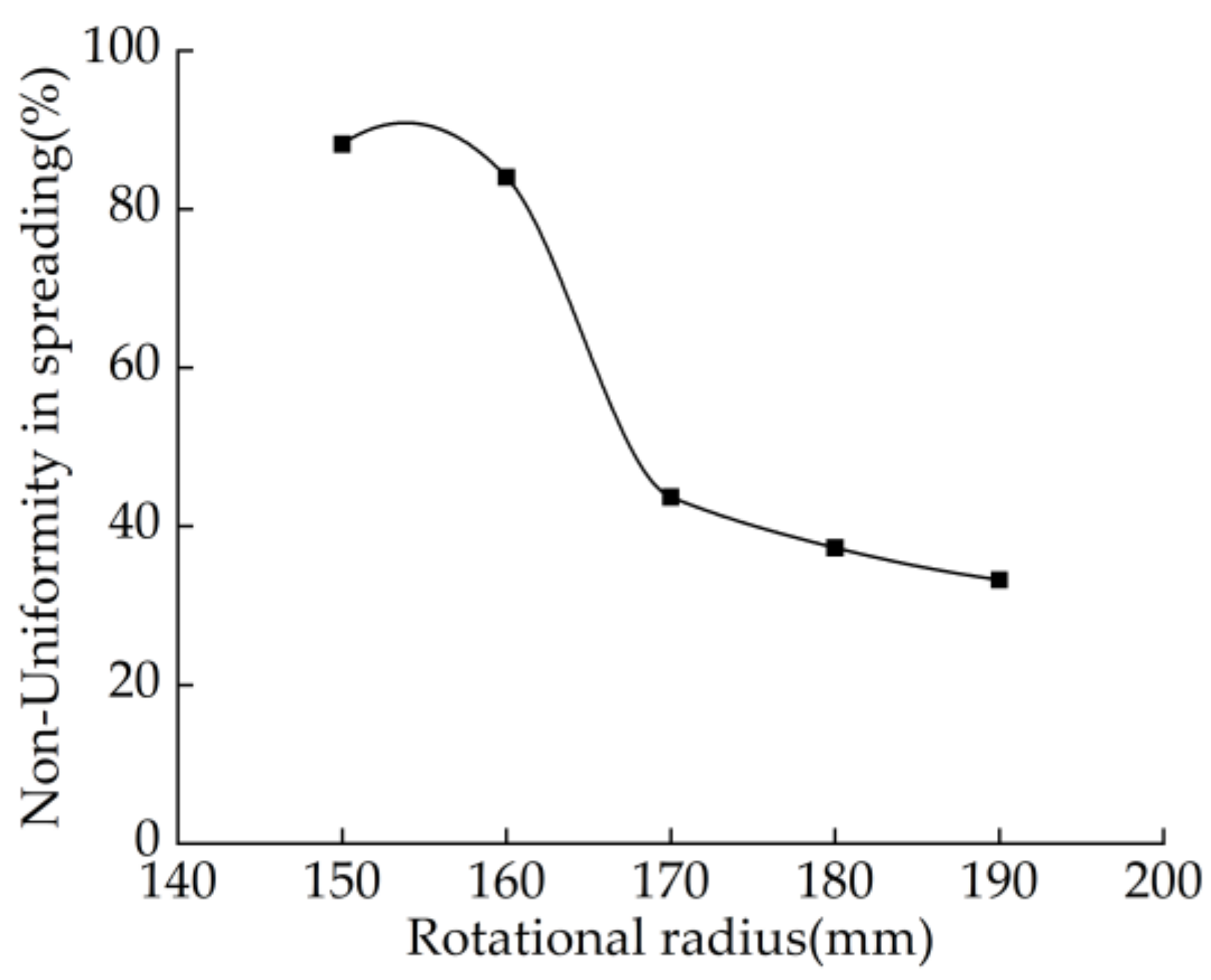
3.1.1. Influence of Rotating Radius on Non-Uniformity in Spreading
3.1.2. Influence of Bending Angle on Non-Uniformity in Spreading
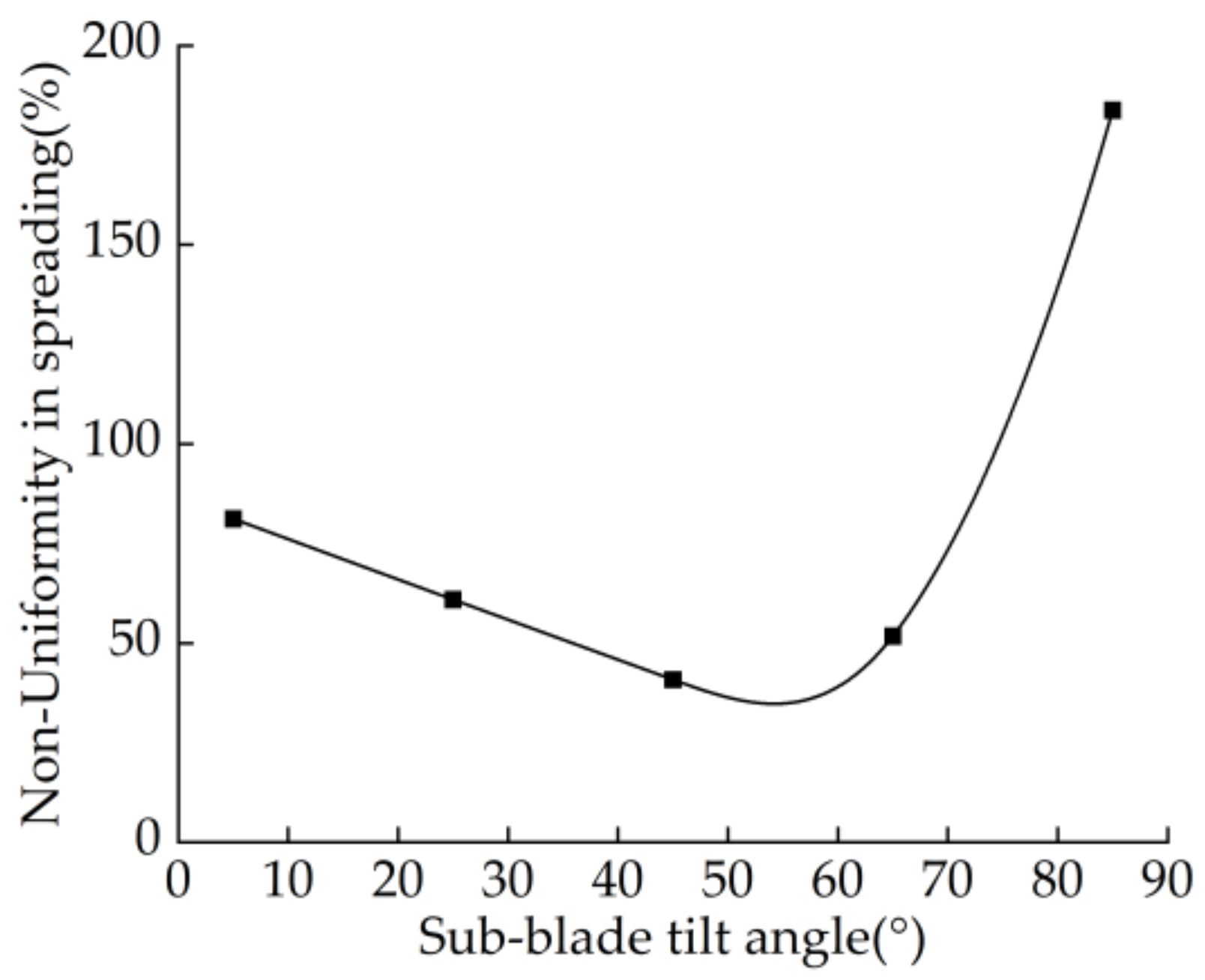
3.1.3. Influence of Sub-Blade Tilt Angle on Non-Uniformity in Spreading
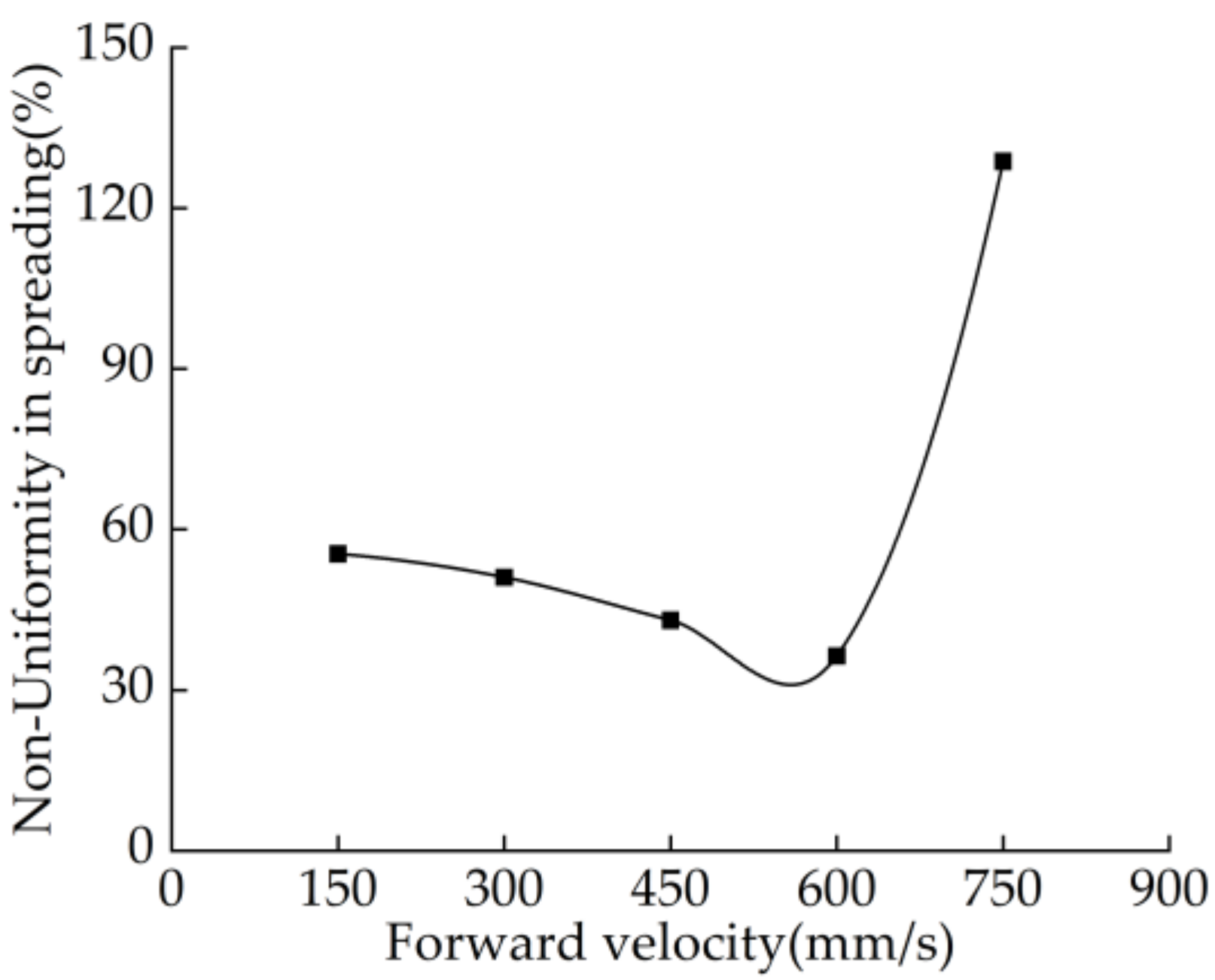
3.1.4. Impact of Forward Velocity on Non-Uniformity in Spreading
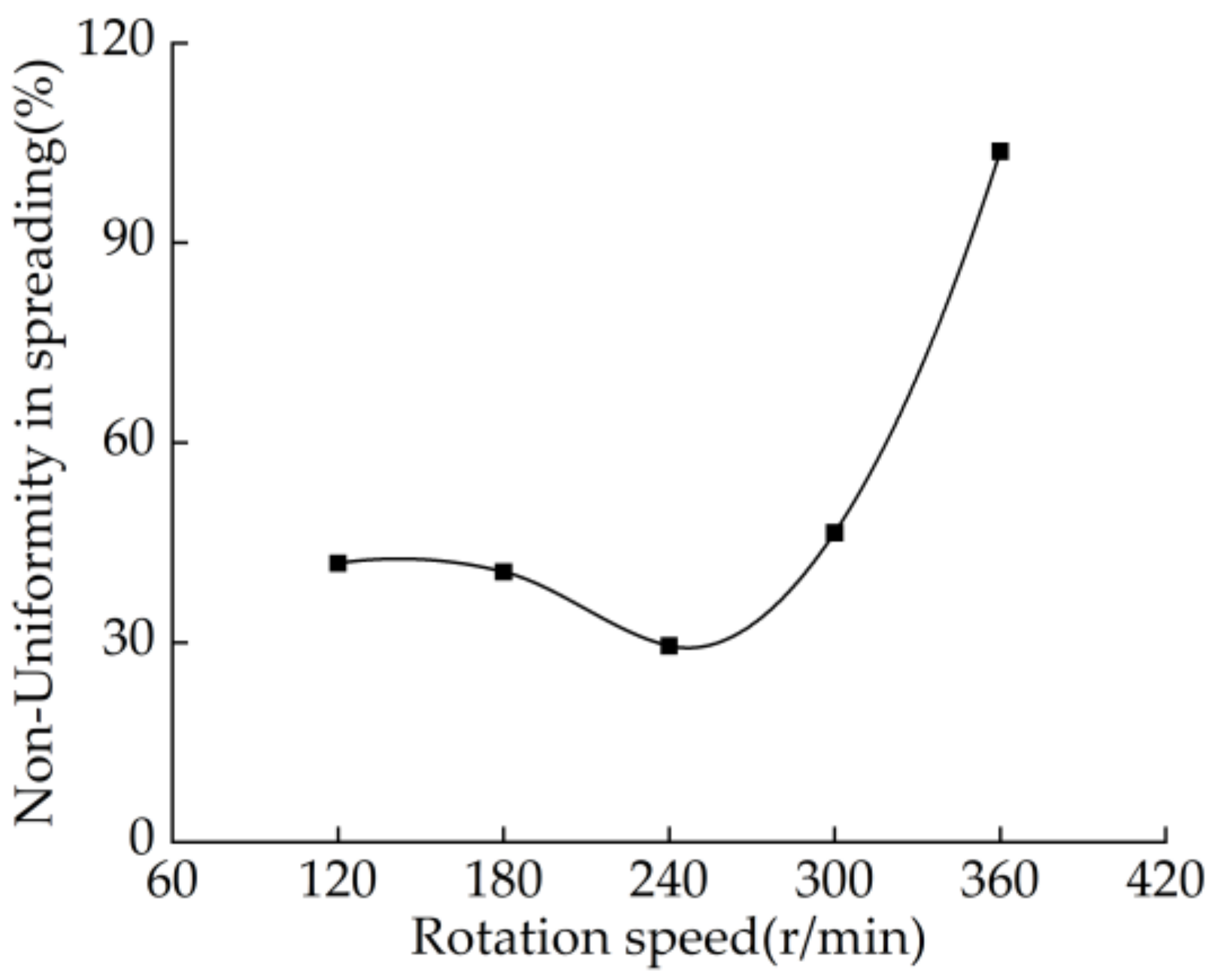
3.1.5. Influence of Rotation Speed on Non-Uniformity in Spreading
3.2. Results and Analysis of the Secondary Orthogonal Rotational Combination Design Experiment
3.2.1. Experimental Results
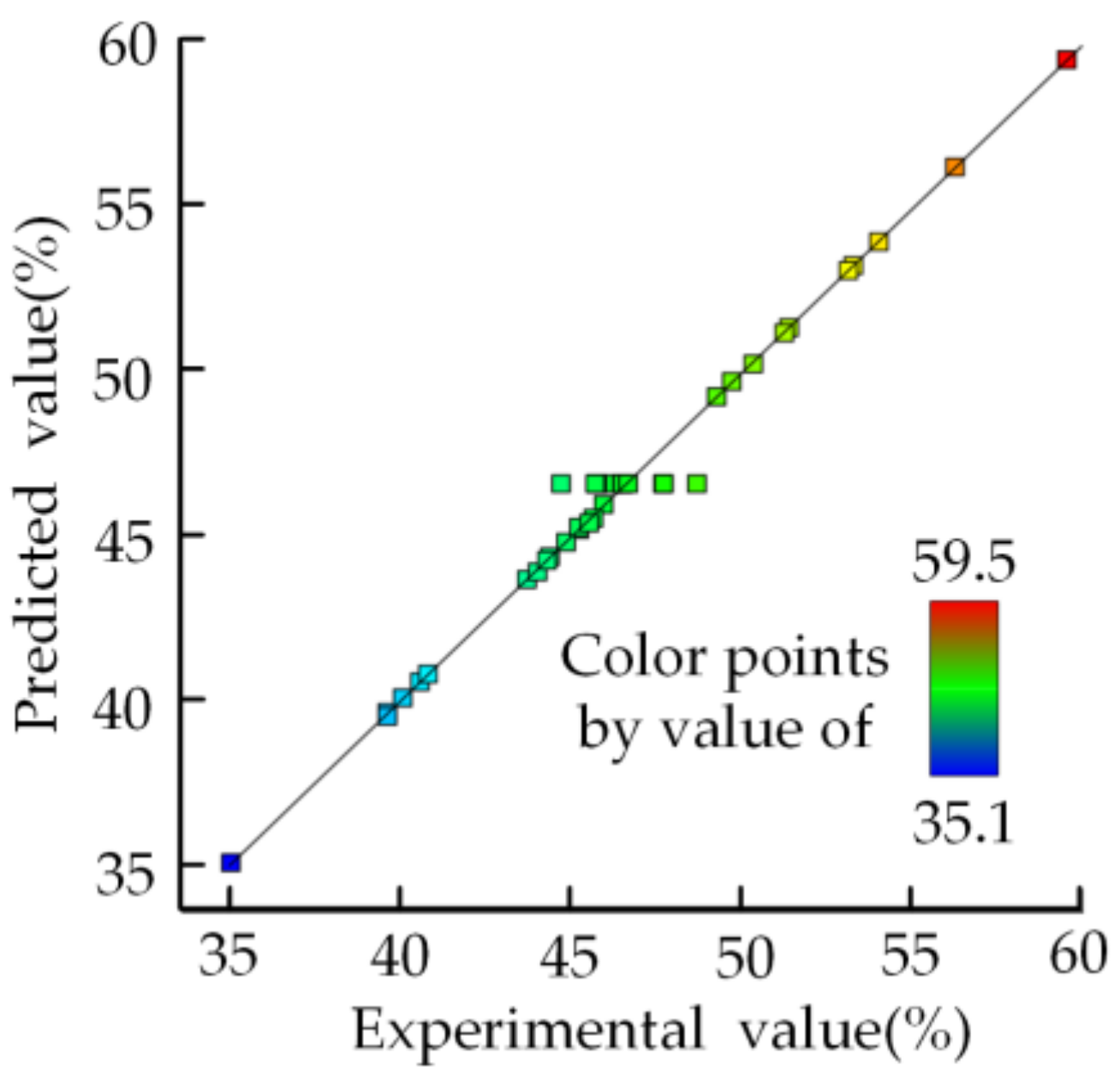
3.2.2. Regression Prediction Model
3.2.3. Analysis of the Impact Intensity of Factors
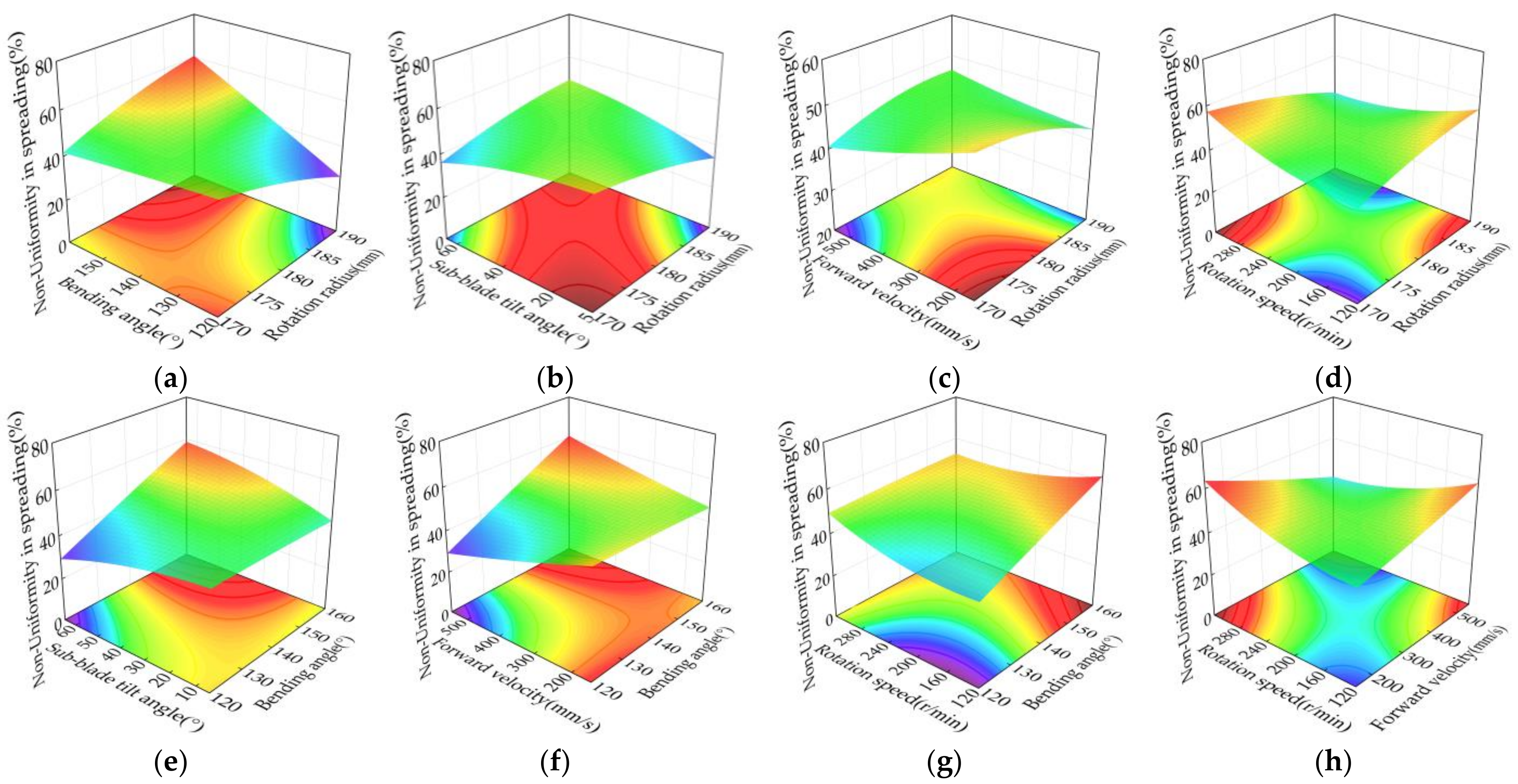
3.2.4. Analysis of the Impact Effects of Interaction Factors on Non-Uniformity in Spreading
3.3. Optimization Model
3.4. Bench Experiment
4. Conclusions
- The trajectory equations governing the movement of mud particles were established, and a discrete element simulation model was developed to simulate the interaction between the mud spreader blade and mud particles. A second-order orthogonal rotation combined design experiment was conducted to obtain a regression predictive model for quantifying the non-uniformity in spreading with respect to the blade parameters. The accuracy of both the proposed simulation model and regression predictive model was validated through bench tests.
- The response surface methodology was utilized to construct a regression model for the objective function, and analysis of variance was employed to determine the significance of first-order, square terms, and interaction terms on the objective function. The results of the variance analysis indicated that the first-order terms, including rotation radius, bending angle, and forward velocity, significantly influenced non-uniformity in spreading. Additionally, the square terms for rotation radius, sub-blade tilt angle, and rotational speed had a significant impact on non-uniformity in spreading. Among the interaction terms of the second order, the interaction effects of the sub-blade tilt angle with forward velocity and the sub-blade tilt angle with rotational speed were not significant, while the interactions of other factors demonstrated significant effects on the non-uniformity in spreading.
- A multivariate single-objective optimization approach was employed to establish an optimization model for the non-uniformity in spreading. The results indicated that the optimized value for non-uniformity in spreading was achieved at a rotation radius of 188 mm, a bending angle of 121°, a sub-blade tilt angle of 30°, a forward velocity of 400 mm/s, and a rotational speed of the blade at 191 r/min.
- The optimized blade parameters were validated through bench tests. The experimental results closely aligned with the simulated results, with a relative error of 7.67% for non-uniformity in spreading. Furthermore, the optimized uniformity of mud spreading increased by 31.19%, indicating that the optimized parameters can meet the planting requirements for rice seedling cultivation in paddy fields.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liao, P.; Meng, Y.; Chen, Y.; Weng, W.; Chen, L.; Xing, Z.; Guo, B.; Wei, H.; Gao, H.; Zhang, H. Potted-Seedling Machine Transplantation Simultaneously Promotes Rice Yield, Grain Quality, and Lodging Resistance in China: A Meta-Analysis. Agronomy 2022, 12, 3003. [Google Scholar] [CrossRef]
- Xing, Z.P.; Hu, Y.J.; Qian, H.J.; Cao, W.W.; Guo, B.W.; Wei, H.Y.; Xu, K.; Huo, Z.Y.; Zhou, G.S.; Dai, Q.G. Comparison of yield traits in rice among three mechanized planting methods in a rice-wheat rotation system. J. Integr. Agric. 2017, 16, 1451–1466. [Google Scholar] [CrossRef]
- Liu, W.; Tian, S.; Wang, Q.; Jiang, H. Key Technologies of Plug Tray Seedling Transplanters in Protected Agriculture: A Review. Agriculture 2023, 13, 1488. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, Y.; Zhang, X.; Liao, Q.; Fu, H.; Cheng, Q.; Chen, Z.; Sun, Y.; Ma, J.; Zhang, J.; et al. Unmanned Aerial Vehicle Direct Seeding or Integrated Mechanical Transplanting, Which Will Be the Next Step for Mechanized Rice Production in China?—A Comparison Based on Energy Use Efficiency and Economic Benefits. Energy 2023, 273, 127223. [Google Scholar] [CrossRef]
- Arredondo-Arredondo, J.J.; Ortiz-Laurel, H.; Rössel-Kipping, D.; Morales-García, D. Evaluation of the Performance of Three Types of Draught Animal Plows. Agrociencia 2003, 37, 187–194. [Google Scholar]
- Li, L.; Chen, J.; Ma, C.; Meng, H.; Qi, J.; Li, Y.; Zhang, P.; Lian, G.; Qi, Z. Study on Soil Throwing Performance and Ditch Depth Stability of Ditching Device in Sandy Orchards in Southern Xinjiang. Appl. Sci. 2021, 11, 12058. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, Y.; Xi, G. Numerical Simulation of the Flow in Straight Blade Agitator with the Mps Method. Int. J. Numer. Methods Fluids 2011, 67, 1960–1972. [Google Scholar] [CrossRef]
- Liu, M.; Hu, C.; Ku, H.; Cai, H. Investigation of Operating Performance of Single-Side Paddy Field Ridger Based on Discrete Element Method and Test Verification. J. Agric. Sci. Technol. 2022, 24, 603–616. [Google Scholar]
- Modak, S.P.; Dogra, B.; Dogra, R.; Kumar, D. Design of Rotary Weeder Blade. AMA Agric. Mech. Asia Afr. Lat. A. 2016, 47, 32–40. [Google Scholar]
- Jia, H.; Ma, C.; Tong, J. Study on universal blade rotor for rototilling and stubble-breaking machine. Soil Tillage Res. 2007, 94, 201–208. [Google Scholar]
- Wang, Y.; Li, D.; Nie, C.; Gong, P.; Yang, J.; Hu, Z.; Li, B.; Ma, M. Research Progress on the Wear Resistance of Key Components in Agricultural Machinery. Materials 2023, 16, 7646. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, D.; He, X.; Shang, S.; Zhao, Z.; Wang, H.; Tan, Y.; Shi, Y. Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting. Machines 2022, 10, 562. [Google Scholar] [CrossRef]
- Wang, B.; Chen, M.; Wei, J.; Liang, G.; Liang, K. Bionic Optimization Design of Rotary Tiller Based on Fuzzy Algorithm. Mob. Inf. Syst. 2022, 2022, 1203973. [Google Scholar] [CrossRef]
- Yang, Y.; Tong, J.; Huang, Y.; Li, J.; Jiang, X. Biomimetic Rotary Tillage Blade Design for Reduced Torque and Energy Requirement. Appl. Bionics Biomech. 2021, 2021, 8573897. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Xie, Y.; Liang, L.; Ding, Q.; Xie, H.; Wang, J. Straw-Soil-Rotary Blade Interaction: Interactive Effects of Multiple Operation Parameters on the Straw Movement. Agronomy 2022, 12, 847. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, M.; Chen, W.; Yuan, D.; Wu, C.; Zhu, J. Simulation Analysis and Experiments for Blade-Soil-Straw Interaction under Deep Ploughing Based on the Discrete Element Method. Agriculture 2023, 13, 136. [Google Scholar] [CrossRef]
- Cheng, J.; Zheng, K.; Xia, J.; Liu, G.; Jiang, L.; Li, D. Analysis of Adhesion between Wet Clay Soil and Rotary Tillage Part in Paddy Field Based on Discrete Element Method. Processes 2021, 9, 845. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, X.; Pan, R.; Guo, S.; Yang, J. Numerical Simulation of Spiral Cutter–Soil Interaction in Deep Vertical Rotary Tillage. Agriculture 2023, 13, 1850. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Hu, X.; Wang, H.; Shi, X.; Ma, X. Simulation of Soil Cutting and Power Consumption Optimization of a Typical Rotary Tillage Soil Blade. Appl. Sci. 2022, 12, 8177. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, J.; Zhang, X.; Zhao, S. Effect of Rotary Speed on Soil and Straw Throwing Process by Stubble-Crushing Blade for Strip Tillage Using DEM-CFD. Agriculture 2023, 13, 877. [Google Scholar] [CrossRef]
- Wang, J.; Xiang, Y.; Wang, C.; Xu, C.; Zhu, G.; Gu, Z.; Wang, J.; Tang, H. The Method and Experiment of Kinetic Determination for the Rotary Soil-Engaging Components of Agricultural Machinery Using a Compacting Device in a Paddy Field as an Example. Agronomy 2023, 13, 775. [Google Scholar] [CrossRef]
- Ahmad, F.; Qiu, B.; Ding, Q.; Ding, W.; Khan, Z.; Shoaib, M.; Chandio, F.A.; Rehim, A.; Khaliq, A. Discrete Element Method Simulation of Disc Type Furrow Openers in Paddy Soil. Int. J. Agric. Biol. Eng. 2020, 13, 103–110. [Google Scholar] [CrossRef]
- Du, J.; Heng, Y.; Zheng, K.; Luo, C.; Zhu, Y.; Zhang, J.; Xia, J. Investigation of the Burial and Mixing Performance of a Rotary Tiller Using Discrete Element Method. Soil Tillage Res. 2022, 220, 105349. [Google Scholar] [CrossRef]
- Gao, J.; Shen, Y.; Ma, B. Optimized Design of Touching Parts of Soil Disinfection Machine Based on Strain Sensing and Discrete Element Simulation. Sensors 2023, 23, 6369. [Google Scholar] [CrossRef]
- Cheng, J.; Xia, J.; Zheng, K.; Liu, G.; Wei, Y.; Liu, Z.; Li, P.; Liu, H. Construction and Analysis of a Discrete Element Model for Calculating Friction Resistance of the Typical Rotary Blades. Comput. Electron. Agric. 2023, 214, 108303. [Google Scholar] [CrossRef]
- Li, X.; Zhu, L.; Gong, S. Soil-Cutting Simulation and Dual-Objective Optimization on Tillage Process Parameters of Micro-Tiller by Smoothed Particle Galerkin Modeling and Genetic Algorithm. Comput. Electron. Agric. 2022, 198, 107021. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Z.; Xiao, M.; Bartos, P.; Bohata, A. Soil-Cutting Simulation and Parameter Optimization of Rotary Blade’s Three-Axis Resistances by Response Surface Method. Comput. Electron. Agric. 2019, 164, 104902. [Google Scholar] [CrossRef]
- Xin, F.; Xiao, X.; Dong, J.; Zhang, G.; Zhang, Y.; Wu, X.; Li, X.; Zou, Z.; Ma, J.; Du, G.; et al. Large Increases of Paddy Rice Area, Gross Primary Production, And Grain Production in Northeast China During 2000–2017. Sci. Total Environ. 2020, 711, 135183. [Google Scholar] [CrossRef]
- Hu, L.; Xu, Y.; He, J.; Du, P.; Zhao, R.; Luo, X. Design and Test of Tractor-Attached Laser-Controlled Rotary Scraper Land Leveler for Paddy Fields. J. Irrig. Drain. Eng. 2020, 146, 04020002. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Comparison of the Discrete Element and Finite Element Methods to Model the Interaction of Soil and Tool Cutting Edge. Biosyst. Eng. 2018, 169, 199–208. [Google Scholar] [CrossRef]
- Barr, J.B.; Desbiolles, J.M.A.; Fielke, J.M.; Mustafa, U. Development and Field Evaluation of a High-Speed No–till Seeding System. Soil Tillage Res. 2019, 194, 104337. [Google Scholar] [CrossRef]
- Xie, Y.; Ferng, Y.; Miao, J.; Ren, J.; Zhang, X. Numerical and Experimental Study on Optimization of Paddy Field Blade Used in Initial Mud-Cutting Process. Comput. Electron. Agric. 2020, 170, 105243. [Google Scholar] [CrossRef]
- Xie, Y.; Hong, Y.; Zhang, X.; Ren, J. Analysis of Mud Splashing Pattern of Paddy Field Blade Using Computational Fluid Dynamics. Comput. Electron. Agric. 2020, 176, 105639. [Google Scholar] [CrossRef]
- Ani, O.A.; Uzoejinwa, B.B.; Ezeama, A.O.; Onwualu, A.P.; Ugwu, S.N.; Ohagwu, C.J. Overview of Soil-Machine Interaction Studies in Soil Bins. Soil Tillage Res. 2018, 175, 13–27. [Google Scholar] [CrossRef]
- Lee, K.S.; Park, S.H.; Park, W.Y.; Lee, C.S. Strip Tillage Characteristics of Rotary Tiller Blades for Use in a Dryland Direct Rice Seeder. Soil Tillage Res. 2003, 71, 25–32. [Google Scholar] [CrossRef]
- Chen, C.; Di, Z.; Chen, W.; Zheng, S.; Ren, J. Structure Parameter Design and Bench Test Research of Paddy Field Blades. Sci. Rep. 2022, 12, 14733. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Zhang, B.; You, J. Mechanism of Drag Reduction in Floating Plate of Paddy Field Based on CFD. Complexity 2020, 2020, 8852941. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, L.; Cao, C.; Zhu, C.; Qin, K.; Ge, J. Optimization and Validation of Blade Parameters for Inter-Row Weeding Wheel in Paddy Fields. Front. Plant Sci. 2022, 13, 1003471. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Shi, M.; Yu, C.; Yu, Z.; Kuang, F.; Xiong, W.; Xue, K. Tool-Straw-Paddy Soil Coupling Model of Mechanical Rotary-Tillage Process Based on DEM-FEM. Comput. Electron. Agric. 2023, 215, 108410. [Google Scholar] [CrossRef]
- Ding, Q.; Lu, X.; Sun, K.; Li, Y.; He, R.; Wang, X. Performance and Design Parameter Definition on Puddling Knife Using Reverse Engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 68–74. (In Chinese) [Google Scholar]
- Matin, M.A.; Hossain, M.I.; Gathala, M.K.; Timsina, J.; Krupnik, T.J. Optimal Design and Setting of Rotary Strip-Tiller Blades to Intensify Dry Season Cropping in Asian Wet Clay Soil Conditions. Soil Tillage Res. 2021, 207, 104854. [Google Scholar] [CrossRef] [PubMed]
- Torotwa, I.; Ding, Q.; Awuah, E.; He, R. Biomimetic Tool Design Improves Tillage Efficiency, Seedbed Quality, And Straw Incorporation During Rototilling in Conservation Farming. J. Agric. Eng. 2023, 54, 1327. [Google Scholar] [CrossRef]
- Pang, C.; Zhuomao, E. Study on the Mud Bedding Device Used on the Rice Seeders. J. China Agric. Univ. 2000, 5, 40–42. [Google Scholar]
- Zhang, X.; Xia, J.; Zhang, J.; He, X.; Liang, S.; Zhang, S.; Wu, H.; Wan, S. Working performance experiment of combination blade roller for straw returning in paddy field and dry land. Trans. Chin. Soc. Agric. Eng. 2016, 32, 9–15. [Google Scholar]
- Xie, Y.; Ren, J.; Zhang, X. Process Analysis and Optimization Design of Blades in Rice Seedling Raising Tray for Mud Homogenizing. J. China Agric. Univ. 2020, 25, 85–94. [Google Scholar]
- Johnson, K.; Kendall, K.; Roberts, A. Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. [Google Scholar]
- Wang, H.; Yang, K.; Wang, H.; Wu, J.; Xiao, Q. Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure. Energies 2023, 16, 2045. [Google Scholar] [CrossRef]



| Horizontal Coded Value | Rotating Radius X1 (mm) | Bending Angle X2 (°) | Sub-Blade Tilt Angle X2 (°) | Forward Velocity X4 (mm/s) | Rotation Speed X5 (r/min) |
|---|---|---|---|---|---|
| Upper asterisk arm (r = 2) | 190 | 160 | 65 | 550 | 320 |
| Upper level (r = 1) | 185 | 150 | 50 | 450 | 270 |
| Zero level (r = 0) | 180 | 140 | 35 | 350 | 220 |
| Lower level (r = −1) | 175 | 130 | 20 | 250 | 170 |
| Lower asterisk arm (r = −2) | 170 | 120 | 5 | 150 | 120 |
| Variation interval (∆j) | 5 | 10 | 15 | 100 | 50 |
| Test No. | X1 | X2 | X3 | X4 | X5 | Y (%) |
|---|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | −1 | 1 | 59.55 |
| 2 | 1 | −1 | −1 | −1 | −1 | 40.60 |
| 3 | −1 | 1 | −1 | −1 | −1 | 44.41 |
| 4 | 1 | 1 | −1 | −1 | 1 | 45.27 |
| 5 | −1 | −1 | 1 | −1 | −1 | 40.83 |
| 6 | 1 | −1 | 1 | −1 | 1 | 44.88 |
| 7 | −1 | 1 | 1 | −1 | 1 | 51.42 |
| 8 | 1 | 1 | 1 | −1 | −1 | 54.05 |
| 9 | −1 | −1 | −1 | 1 | −1 | 45.26 |
| 10 | 1 | −1 | −1 | 1 | 1 | 35.06 |
| 11 | −1 | 1 | −1 | 1 | 1 | 45.98 |
| 12 | 1 | 1 | −1 | 1 | −1 | 56.27 |
| 13 | −1 | −1 | 1 | 1 | 1 | 39.65 |
| 14 | 1 | −1 | 1 | 1 | −1 | 40.10 |
| 15 | −1 | 1 | 1 | 1 | −1 | 49.74 |
| 16 | 1 | 1 | 1 | 1 | 1 | 53.30 |
| 17 | −2 | 0 | 0 | 0 | 0 | 45.69 |
| 18 | 2 | 0 | 0 | 0 | 0 | 43.74 |
| 19 | 0 | −2 | 0 | 0 | 0 | 39.65 |
| 20 | 0 | 2 | 0 | 0 | 0 | 53.15 |
| 21 | 0 | 0 | −2 | 0 | 0 | 44.05 |
| 22 | 0 | 0 | 2 | 0 | 0 | 44.32 |
| 23 | 0 | 0 | 0 | −2 | 0 | 49.29 |
| 24 | 0 | 0 | 0 | 2 | 0 | 45.56 |
| 25 | 0 | 0 | 0 | 0 | −2 | 50.37 |
| 26 | 0 | 0 | 0 | 0 | 2 | 51.28 |
| 27 | 0 | 0 | 0 | 0 | 0 | 46.26 |
| 28 | 0 | 0 | 0 | 0 | 0 | 47.72 |
| 29 | 0 | 0 | 0 | 0 | 0 | 46.53 |
| 30 | 0 | 0 | 0 | 0 | 0 | 45.79 |
| 31 | 0 | 0 | 0 | 0 | 0 | 46.53 |
| 32 | 0 | 0 | 0 | 0 | 0 | 46.70 |
| 33 | 0 | 0 | 0 | 0 | 0 | 44.73 |
| 34 | 0 | 0 | 0 | 0 | 0 | 47.74 |
| 35 | 0 | 0 | 0 | 0 | 0 | 48.71 |
| 36 | 0 | 0 | 0 | 0 | 0 | 45.73 |
| Source of Variance | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Significance Level p |
|---|---|---|---|---|---|
| Model | 855.36 | 20 | 42.77 | 53.10 | <0.0001 |
| X1 | 5.22 | 1 | 5.22 | 6.48 | 0.0224 |
| X2 | 276.87 | 1 | 276.87 | 343.78 | <0.0001 |
| X3 | 0.1849 | 1 | 0.1849 | 0.2296 | 0.6387 |
| X4 | 22.25 | 1 | 22.25 | 27.62 | <0.0001 |
| X5 | 1.34 | 1 | 1.34 | 1.66 | 0.2165 |
| X1X2 | 110.15 | 1 | 110.15 | 136.77 | <0.0001 |
| X1X3 | 51.40 | 1 | 51.40 | 63.83 | <0.0001 |
| X1X4 | 15.07 | 1 | 15.07 | 18.71 | 0.0006 |
| X1X5 | 52.02 | 1 | 52.02 | 64.59 | <0.0001 |
| X2X3 | 62.31 | 1 | 62.31 | 77.36 | <0.0001 |
| X2X4 | 80.74 | 1 | 80.74 | 100.25 | <0.0001 |
| X2X5 | 27.16 | 1 | 27.16 | 33.72 | <0.0001 |
| X3X4 | 0.0822 | 1 | 0.0822 | 0.1021 | 0.7538 |
| X3X5 | 1.70 | 1 | 1.70 | 2.11 | 0.1673 |
| X4X5 | 93.12 | 1 | 93.12 | 115.62 | <0.0001 |
| X12 | 7.89 | 1 | 7.89 | 9.79 | 0.0069 |
| X22 | 0.1761 | 1 | 0.1761 | 0.2186 | 0.6468 |
| X32 | 12.61 | 1 | 12.61 | 15.65 | 0.0013 |
| X42 | 1.06 | 1 | 1.06 | 1.31 | 0.2696 |
| X52 | 34.02 | 1 | 34.02 | 42.24 | <0.0001 |
| Residue | 12.08 | 15 | 0.8054 | ||
| Lack of fit | 0.0535 | 6 | 0.0089 | 0.0067 | 1.0000 |
| Error | 12.03 | 9 | 1.34 | ||
| Sum total | 867.44 | 35 | |||
| R2 = 0.9861; Adjusted R2 = 0.9675; Predicted R2 = 0.9815; Signal-to-noise ratio = 35.70 | |||||
| Test Number | Theoretical Value (%) | Test Results (%) | Relative Error (%) |
|---|---|---|---|
| 1 | 29.63 | 31.83 | 6.91 |
| 2 | 29.63 | 32.62 | 9.17 |
| 3 | 29.63 | 32.86 | 9.83 |
| 4 | 29.63 | 30.89 | 4.08 |
| 5 | 29.63 | 32.33 | 8.35 |
| Average value | 29.63 | 32.11 | 7.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Chen, C.; Bao, D.; Wu, X.; Zheng, S. Simulation Analysis and Optimization Design of Paddy Field Mud Spreader Blades for Uniform Dispersion. Agriculture 2024, 14, 344. https://doi.org/10.3390/agriculture14030344
Ren J, Chen C, Bao D, Wu X, Zheng S. Simulation Analysis and Optimization Design of Paddy Field Mud Spreader Blades for Uniform Dispersion. Agriculture. 2024; 14(3):344. https://doi.org/10.3390/agriculture14030344
Chicago/Turabian StyleRen, Jinbo, Chongcheng Chen, Difa Bao, Xinhui Wu, and Shuhe Zheng. 2024. "Simulation Analysis and Optimization Design of Paddy Field Mud Spreader Blades for Uniform Dispersion" Agriculture 14, no. 3: 344. https://doi.org/10.3390/agriculture14030344




