Simulation Analysis and Parameter Optimization of Residual Film Pickup Process Based on Finite Element Method
Abstract
:1. Introduction
2. Materials and Methods
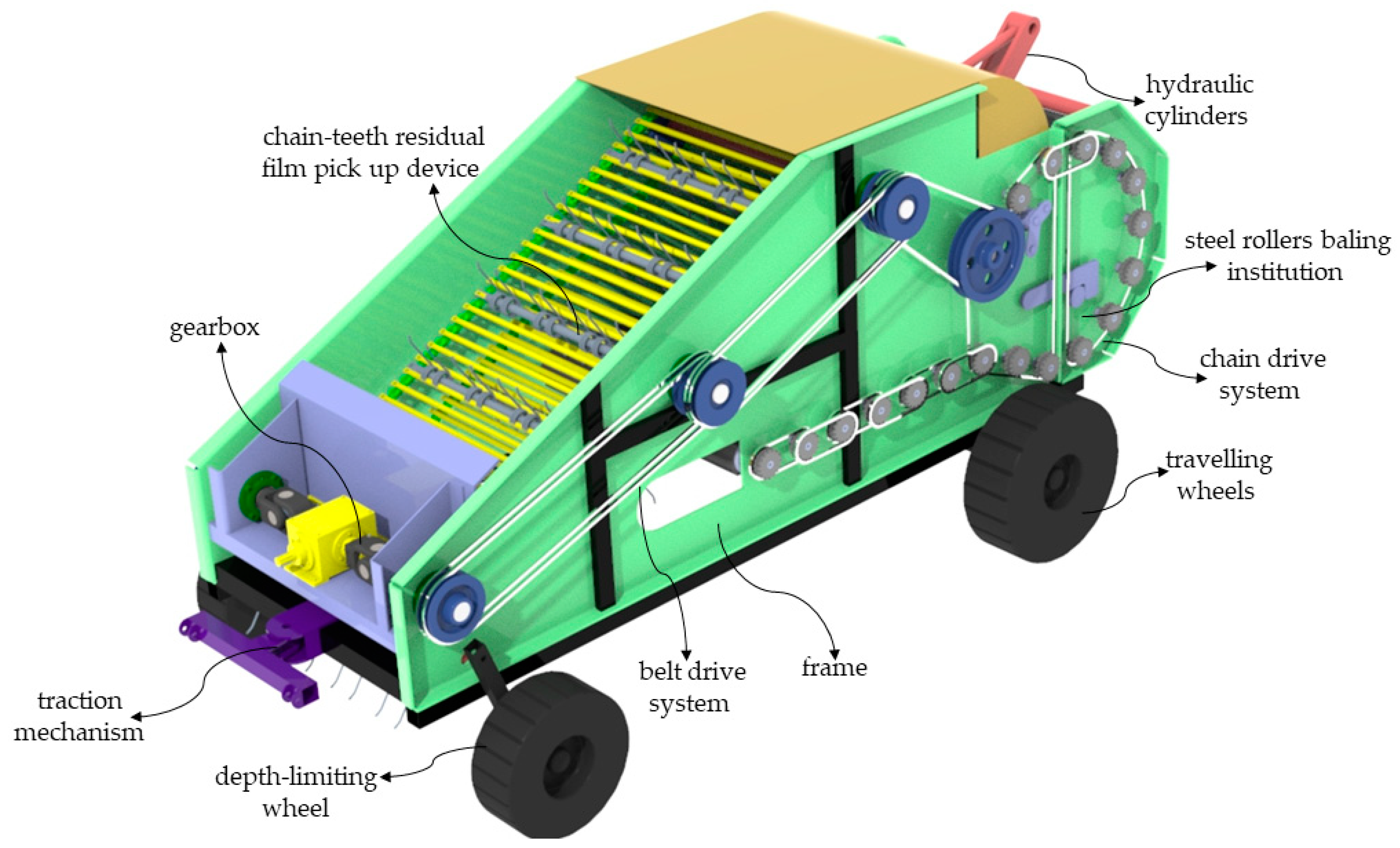
2.1. Residual Film Recycling Machines and Principles of Operation
2.1.1. Structure of Machine
2.1.2. Working Process
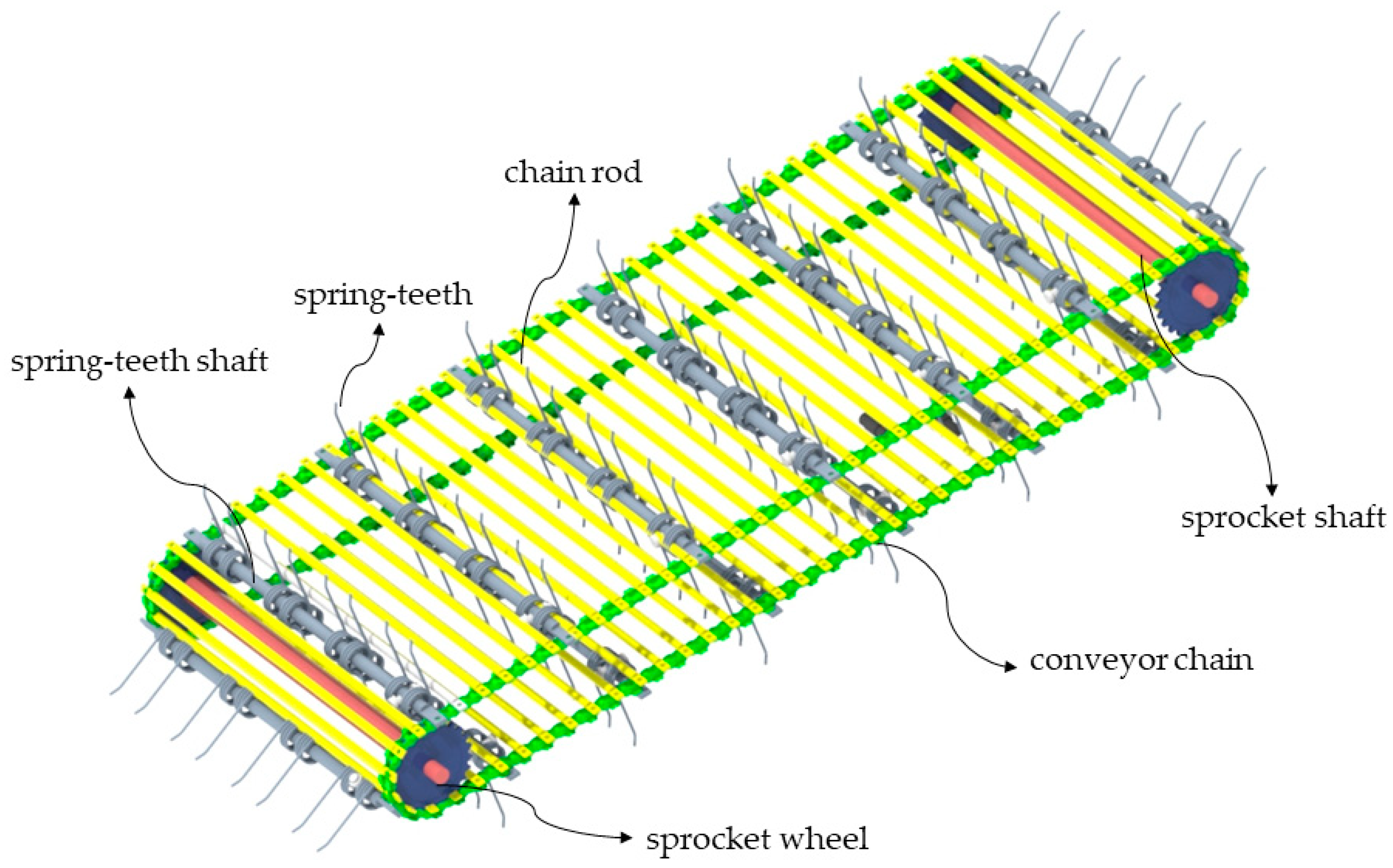
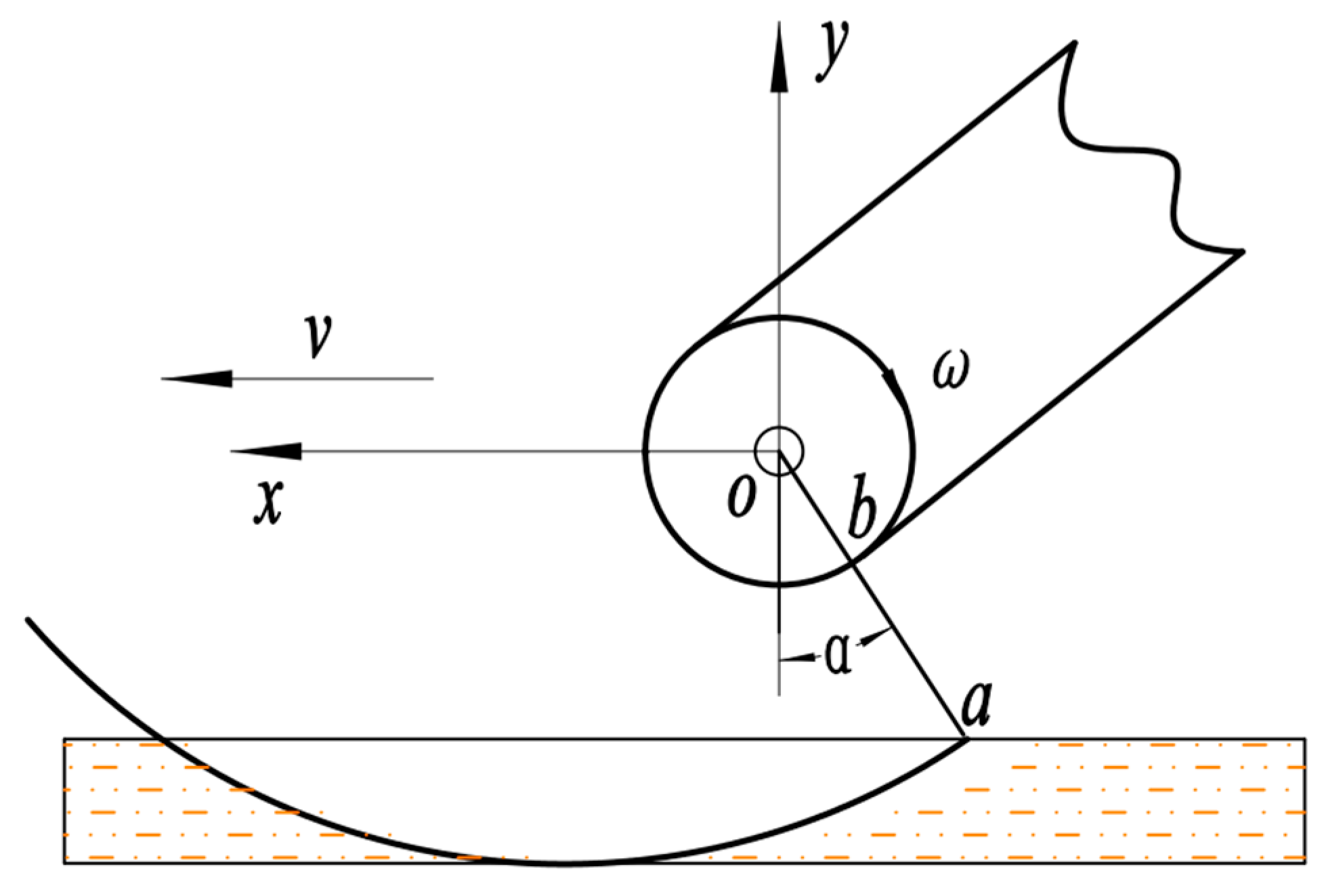
2.2. Analysis of Operation Process Mechanism of Residual Film Picking Mechanism
2.2.1. Mechanism Structure
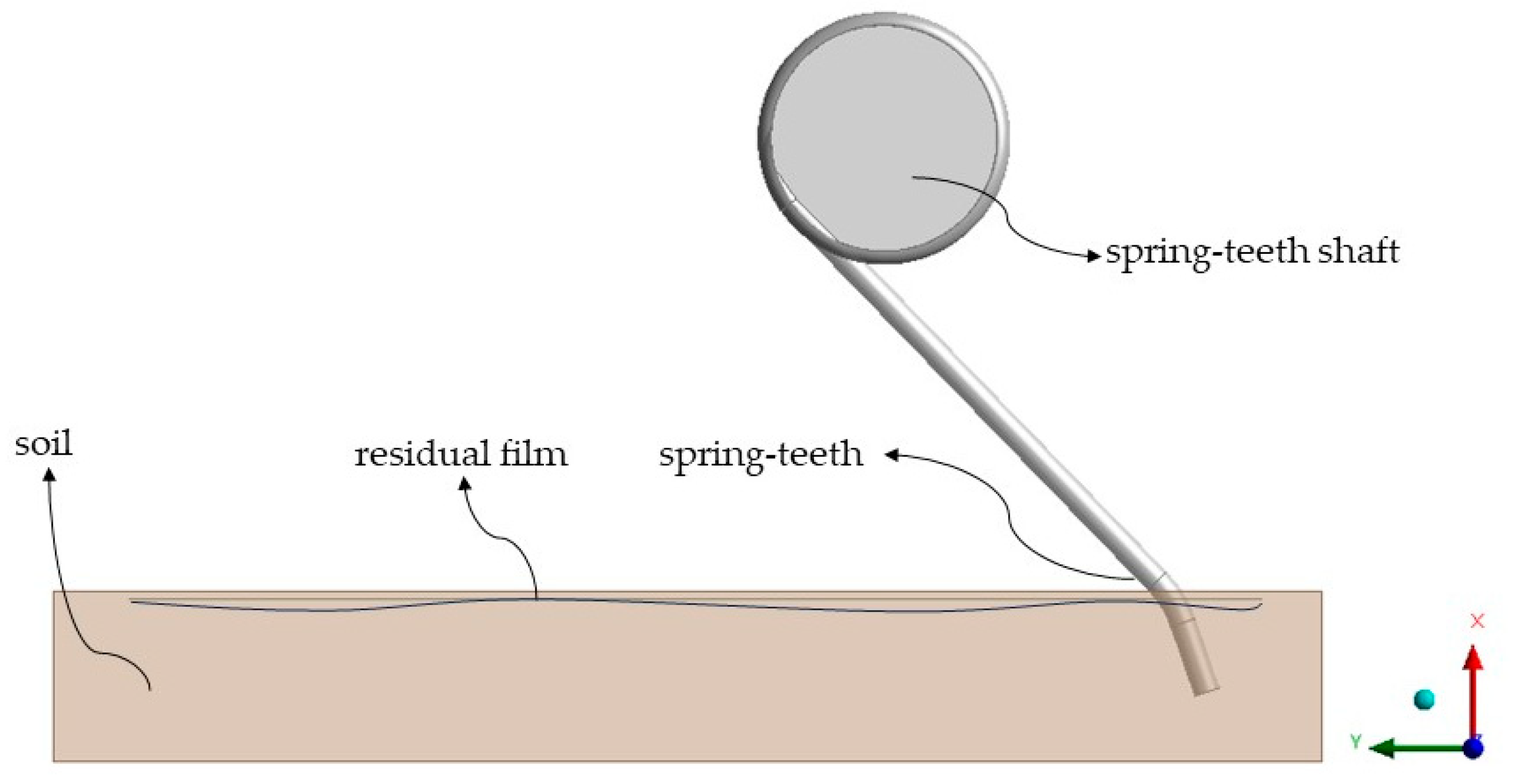
2.2.2. Pickup Process
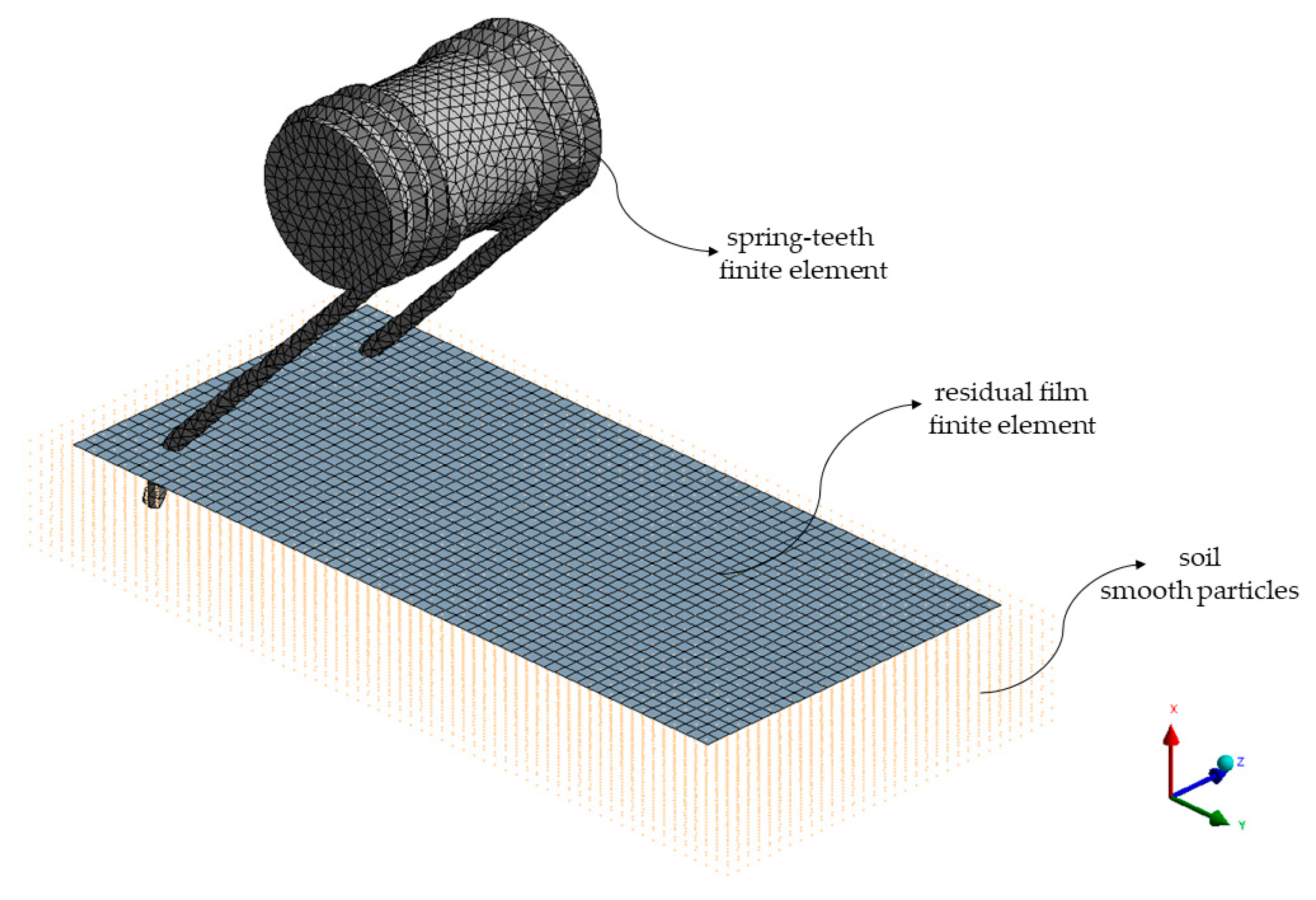
2.3. Finite Element Model Establishments
2.3.1. Parametric Model
2.3.2. Boundary Condition Setting and Solution Calculation
3. Results and Analysis
3.1. Properties of Residual Film in Process of Picking Up
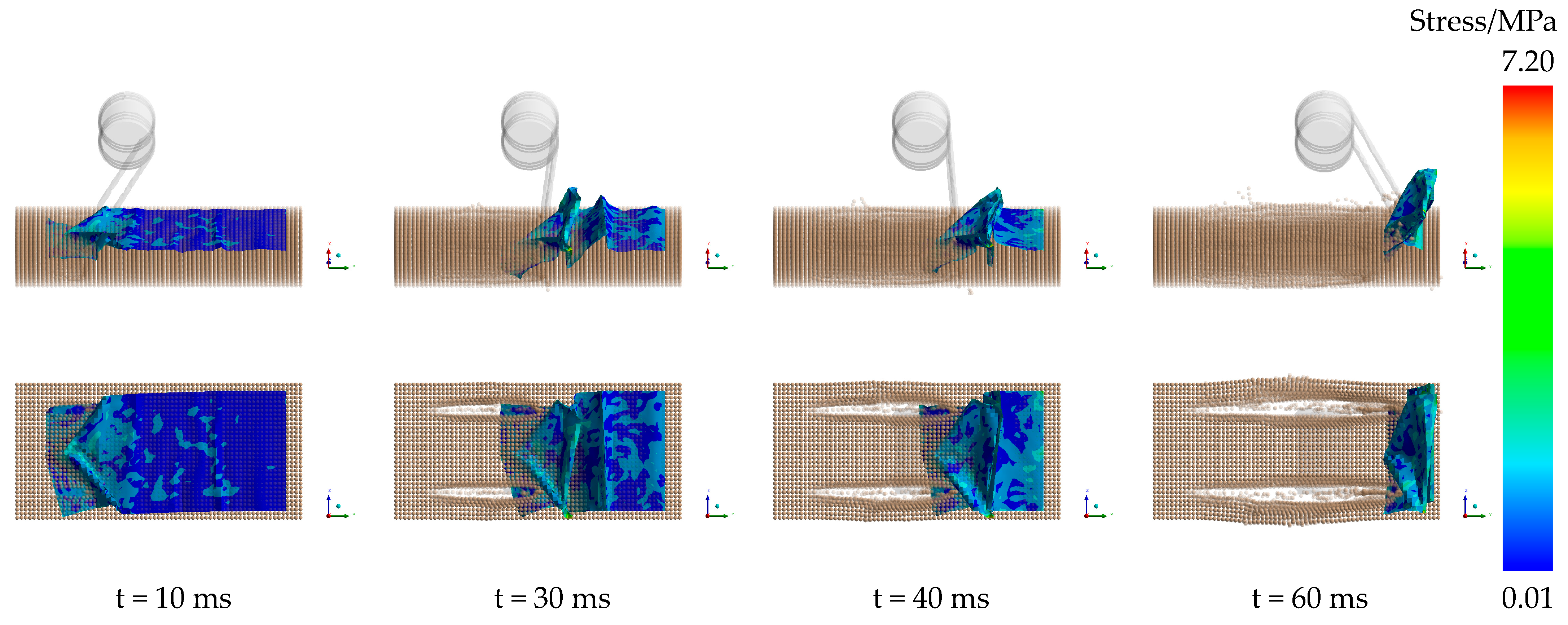
3.1.1. Residual Film Dynamic Characteristics
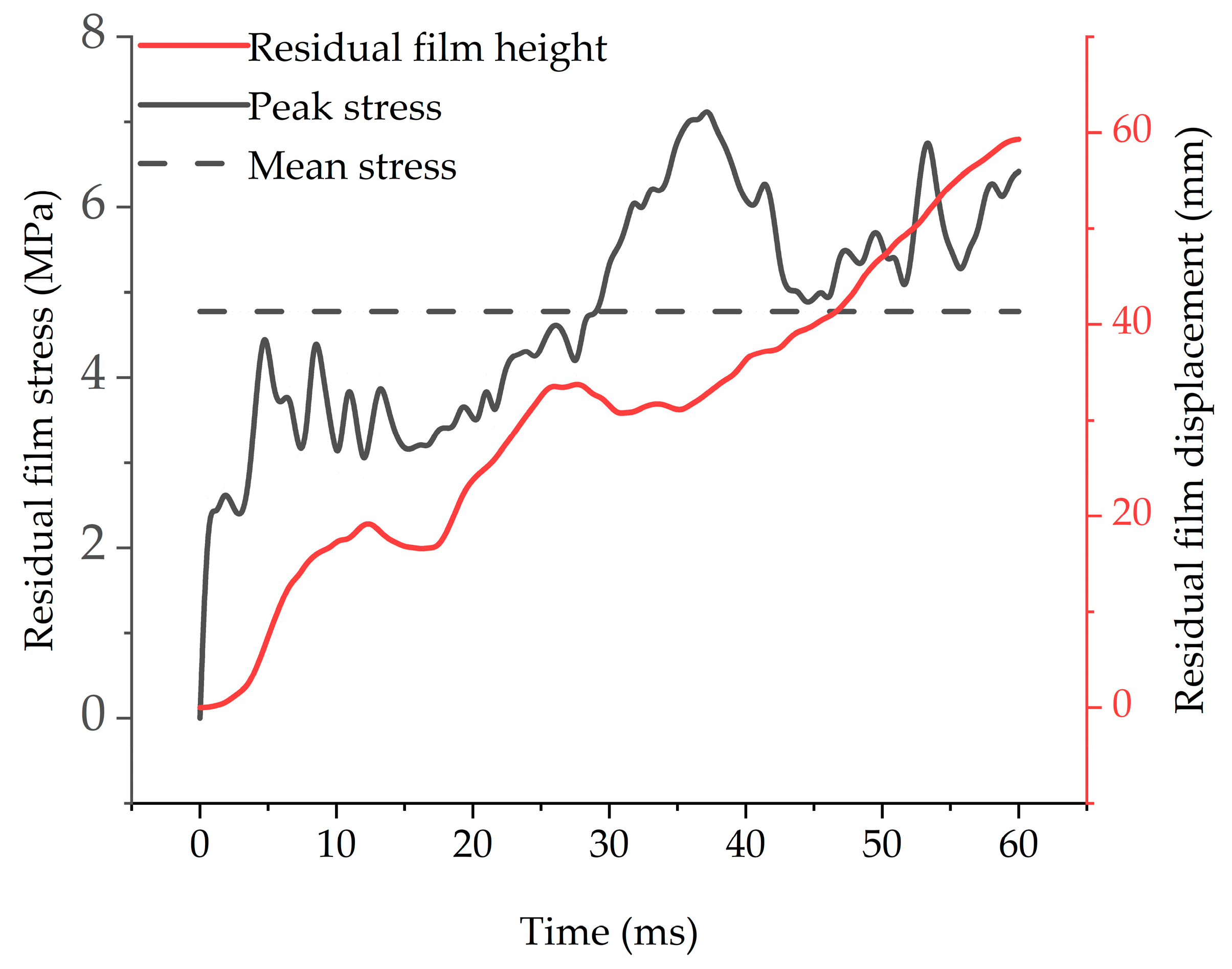
3.1.2. Residual Film Stress Changes
3.1.3. Residual Film Deformation Changes
3.2. Multi-Factor Simulation Optimization Tests
3.2.1. Simulation Test Program
3.2.2. Analysis of Test Results
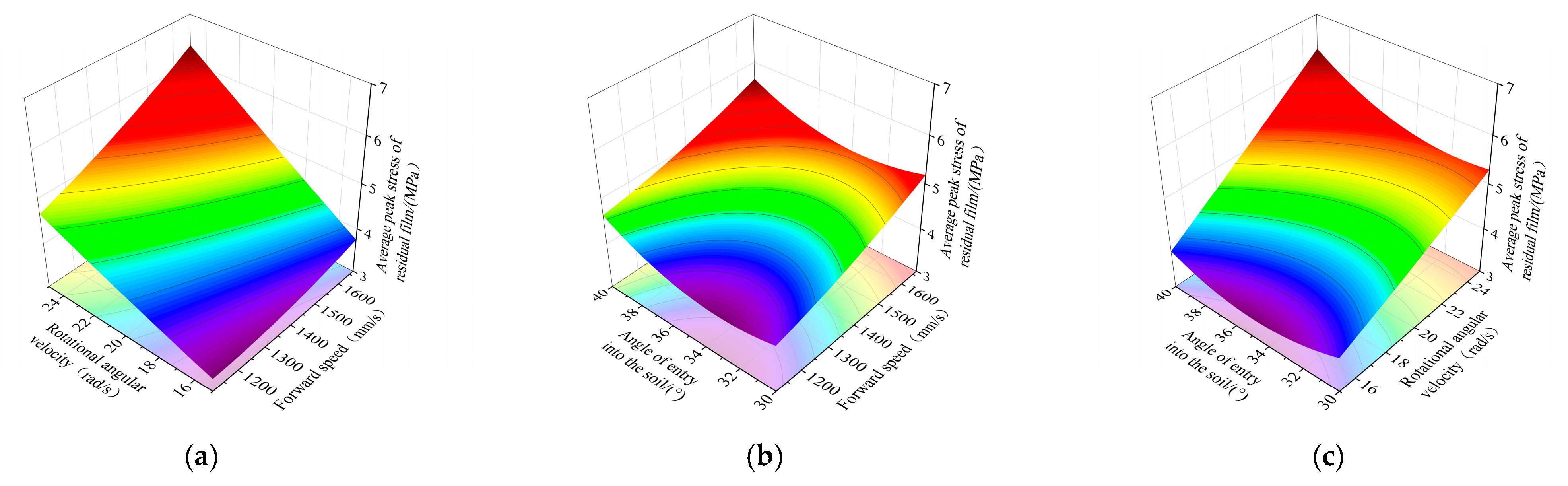
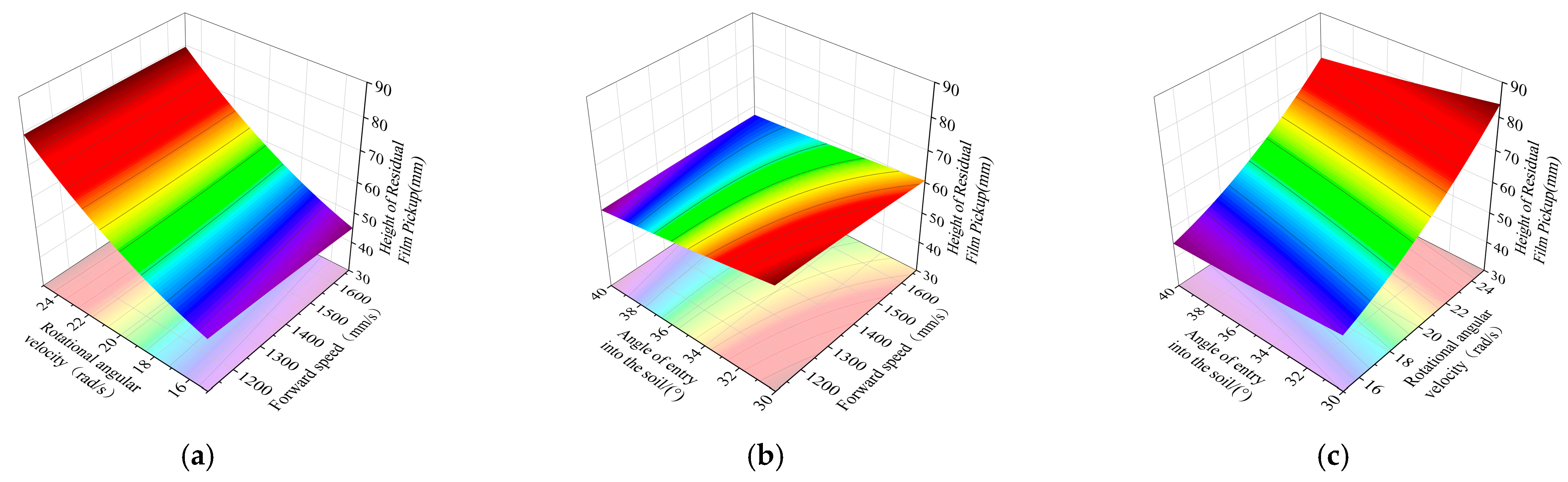
3.2.3. Response Surface Analysis
3.2.4. Optimization
3.3. Field Experiment
3.3.1. Test Conditions
3.3.2. Experimental Design
3.3.3. Test Result
3.4. Comparative Analysis with Previous Research Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, C.; Liu, E.; Shu, F.; Liu, Q.; Liu, S.; He, W. Review of agricultural plastic mulching and its residual pollution and prevention measures in China. J. Agric. Resour. Environ. 2014, 31, 95–102. [Google Scholar]
- Chen, Q.; Wu, C.; Chen, G.; Li, Z. The effect of the different overlay on growth and yield of spring peanut. J. Guangxi Agric. 2013, 28, 28–30. [Google Scholar]
- He, W.; Yan, C.; Liu, S.; Chang, R.; Wang, X.; Cao, S.; Liu, Q. The use of plastic mulch film in typical cotton planting regions and the associated environmental pollution. J. Agro-Environ. Sci. 2009, 28, 1618–1622. [Google Scholar]
- Zhou, T.; Jiang, Y.; Wang, X.; Xie, J.; Wang, C.; Shi, Q.; Zhang, Y. Detection of Residual Film on the Field Surface Based on Faster R-CNN Multiscale Feature Fusion. Agriculture 2023, 13, 6. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, X.; Yan, J.; Jiang, Y.; Yao, J. Experiment and Analysis of Film-Soil Separation Motion Characteristics of a Chain Drive Residual Film Recovery Mechanism for the Tillage Layer. Appl. Sci. 2022, 12, 5884. [Google Scholar] [CrossRef]
- Dai, F.; Guo, X.; Zhao, W.; Xin, S.; Liu, X.; Wu, Z. Design and experiment of canvas belt combined operation machine for potato digging and plastic film collecting. Trans. Chin. Soc. Agric. Mach. 2018, 49, 104–113. [Google Scholar]
- Peng, Q.; Li, K.; Wang, X.; Zhang, G.; Kang, J. Design and Test of Stripping and Impurity Removal Device for Spring-Tooth Residual Plastic Film Collector. Agriculture 2023, 13, 42. [Google Scholar] [CrossRef]
- You, J.; Zhang, B.; Wen, H.; Kang, J.; Song, Y.; Chen, X. Design and test optimization on spade and tine combined residual plastic film device. Trans. Chin. Soc. Agric. Mach. 2017, 48, 97–104. [Google Scholar]
- Zhang, Z.; Li, J.; Wang, X.; Zhao, Y.; Xue, S.; Su, Z. Effects of Biodegradable Plastic Film on Carbon Footprint of Crop Production. Agriculture 2022, 12, 5. [Google Scholar]
- Xue, S.; Chen, X.; Li, J.; Wang, X.; Zhang, Z. Design of and Experiment on a Film Removal Device of an Arc-Toothed Residual Film Recovery Machine before Sowing. Appl. Sci. 2021, 12, 8551. [Google Scholar] [CrossRef]
- Yang, W.; Yang, J.; Jia, F.; Wang, Q.; Huang, Y. Numerical simulation of cassava root excavation operation planted on red clay. J. Mech. Eng. 2013, 49, 135–143. [Google Scholar] [CrossRef]
- Qi, L.; Liang, Z.; Ma, X.; Tan, Y.; Jiang, L. Simulation Analysis and Verification of Fluid-Solid Coupling Interaction between Raking and Pressing Weeding Wheel and Paddy Soil. Trans. Chin. Soc. Agric. Eng. 2015, 31, 29–35+37+36. [Google Scholar]
- Zhang, S.; Zhao, W.; Dai, F.; Song, X.; Qu, J.; Zhang, F. Simulation analysis and experiment of the compaction process of the full film double ridge furrow ridging and laminating machine. Trans. Chin. Soc. Agric. Eng. 2020, 36, 20–30. [Google Scholar]
- Kang, J.; Li, S.; Yang, X.; Liu, L.; Li, C. Simulation analysis and experimental verification of power consumption for disc trenching machine operation. Trans. Chin. Soc. Agric. Eng. 2016, 32, 8–15. [Google Scholar]
- Zhang, Z.; Li, J.; Wang, X.; Zhao, Y.; Xue, S.; Su, Z. Parameters Optimization and Test of an Arc-Shaped Nail-Tooth Roller-Type Recovery Machine for Sowing Layer Residual Film. Agriculture 2022, 12, 660. [Google Scholar] [CrossRef]
- Jin, W.; Ding, Y.; Nong, F.; Zhang, X.; Bai, S. Design and test of excavating and conveying device with vibrating chain tooth and bar for residual film-soil-straw. Trans. Chin. Soc. Agric. Mach. 2023, 54, 72–82. [Google Scholar]
- Xie, J.; Tang, W.; Cao, F.; Han, Y.; Zhang, Y.; Yang, Y.; Li, K. Design and Experiment of a Tooth Chain Composite Residual Film Recycling Machine. Trans. Chin. Soc. Agric. Eng. 2020, 36, 11–19. [Google Scholar]
- Jin, X.; Ma, F.; Wang, D.; Zhu, Z. Simulation of Mouldboard Plough Soil Cutting Based on Smooth Particle Hydrodynamics Method and FEM-SPH Coupling Method. Agriculture 2023, 13, 1847. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, X.; Pan, R.; Guo, S.; Yang, J. Numerical Simulation of Spiral Cutter-Soil Interaction in Deep Vertical Rotary Tillage. Agriculture 2023, 13, 1850. [Google Scholar] [CrossRef]
- Tan, Q.; Fang, H.; Yang, Q.; Ren, Y.; Gao, T.; Bao, A.; Hu, M. Analysis of clay cutting characteristics by SPH method. Trans. Chin. Soc. Agric. Eng. 2023, 39, 49–57. [Google Scholar]
- Tong, J.; Zhang, Z.; Chen, D.; Zhang, Q.; Ma, Y. Three-dimensional dynamic finite element analysis of the interaction between a convex tooth suppressor and soil. Trans. Chin. Soc. Agric. Eng. 2014, 30, 48–58. [Google Scholar]
- Yang, W.; Li, X.; Wang, R.; Yang, J.; Pan, Q.; Li, J. Numerical simulation test of maximum stress of tuber in cassava lifting. Trans. Chin. Soc. Agric. Eng. 2016, 32, 58–64. [Google Scholar]
- Shi, Z.; Zhang, X.; Liu, X.; Guo, L.; Zhang, C.; Liu, L. Design and test of roll type surface layer residual film recovery machine. Trans. Chin. Soc. Agric. Mach. 2024, 55, 128–137. [Google Scholar]
- Xie, J.; Hou, S.; Zhang, X.; Zhang, T. Analysis and Experiment on the Contact of Spring Tooth Picking up Film Based on the Mechanical Properties of Residual Film. J. Agric. Mech. Res. 2016, 38, 177–181. [Google Scholar]
- Zhu, Z.; Zhao, H.; Cai, Y.; Qu, J. Damage analysis of plastic film under hail impact. Trans. Chin. Soc. Agric. Eng. 2022, 38, 246–253. [Google Scholar]
- Ma, L.; Wang, P.; Yang, X.; Li, J.; Li, X.; Li, X. Design and Experiment of a Vibration Type Root Cutting Device for Fruit Trees. J. Trans. Chin. Soc. Agric. Mach. 2020, 51, 281–291. [Google Scholar]
- Liu, H.; Han, J.; Chen, J.; Lu, J.; Zhao, S. Performance Simulation and Experiment on rigid Press Wheel for Hilly Area. Trans. Chin. Soc. Agric. Mach. 2018, 49, 115–122. [Google Scholar]
- Jin, W.; Wang, S.; Qian, H.; Li, W.; Yang, J.; Ma, L. Simulation Analysis of Soil Cutting by Interplant Weeding Claw in Paddy Fields Based on LS-DYNA. J. Agric. Mech. Res. 2023, 45, 203–209. [Google Scholar]
- Cao, S.; Xie, J.; Wang, H.; Yang, Y.; Zhang, Y.; Zhou, J.; Wu, S. Design and Operating Parameters Optimization of the Hook-and-Tooth Chain Rail Type Residual Film Picking Device. Agriculture 2022, 12, 10. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, L.; Chen, X.; Jian, J.; Hou, S. Optimization of Tooth Parameters for Residual Film Recycling Machine. J. Agric. Mech. Res. 2016, 38, 167–170+178. [Google Scholar]
- Chen, L.; Liang, X.; Cao, C. Virtual Simulation and Power Consumption Testing of Straw Returning Machine Based on Multibody Dynamics. Trans. Chin. Soc. Agric. Mach. 2016, 47, 106–111. [Google Scholar]
- Zhang, B.; Chen, X.; Liang, R.; Wang, X.; Meng, H.; Kan, Z. Calibration and Test of Contact Parameters between Chopped Cotton Stalks Using Response Surface Methodology. Agriculture 2022, 12, 1851. [Google Scholar] [CrossRef]
- NY/T 1227-2006; Operational Quality of Residual Mulch Recycling Machines. China Standards Press: Beijing, China, 2006.
- GB/T14290-2021; Round Straw Baling Machine. China Standards Press: Beijing, China, 2021.
- GB/T 25412-2010; Residual Film Recycling Machine. China Standards Press: Beijing, China, 2010.




| Material | Density (kg/m3) | Elastic Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|
| The residual film | 920 | 6.0 × 105 | 0.34 |
| The soil | 1430 | 7.1 × 106 | 0.38 |
| The spring teeth | 7850 | 2.1 × 1011 | 0.30 |
| Coded Value | Forward Speed x1/(mm/s) | Rotational Angular Velocity x2/(rad/s) | Angle of Entry into the Soil x3/(°) |
|---|---|---|---|
| −1.414 | 996.12 | 12.93 | 27.93 |
| −1 | 1111.11 | 15.00 | 30.00 |
| 0 | 1388.50 | 20.00 | 35.00 |
| 1 | 1666.67 | 25.00 | 40.00 |
| 1.414 | 1780.89 | 27.07 | 42.07 |
| No. | Forward Speed x1/(mm/s) | Rotational Angular Velocity x2/(rad/s) | Angle of Entry into the Soil x3/(°) | Average Peak Stress of Residual Film Y1/(MPa) | Height of Residual Film Pickup Y2/(mm) |
|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | 3.53 | 53.31 |
| 2 | 1 | −1 | −1 | 4.28 | 50.05 |
| 3 | −1 | 1 | −1 | 4.72 | 83.43 |
| 4 | 1 | 1 | −1 | 6.43 | 86.29 |
| 5 | −1 | −1 | 1 | 3.57 | 44.70 |
| 6 | 1 | −1 | 1 | 3.88 | 49.13 |
| 7 | −1 | 1 | 1 | 5.41 | 74.14 |
| 8 | 1 | 1 | 1 | 7.25 | 78.30 |
| 9 | −1.414 | 0 | 0 | 3.98 | 60.44 |
| 10 | 1.414 | 0 | 0 | 5.29 | 49.81 |
| 11 | 0 | −1.414 | 0 | 3.28 | 36.76 |
| 12 | 1 | 1.414 | 0 | 5.68 | 89.19 |
| 13 | 0 | 0 | −1.414 | 4.47 | 58.99 |
| 14 | 0 | 0 | 1.414 | 5.91 | 53.38 |
| 15 | 0 | 0 | 0 | 4.68 | 61.09 |
| 16 | 0 | 0 | 0 | 4.22 | 61.44 |
| 17 | 0 | 0 | 0 | 4.78 | 60.06 |
| 18 | 0 | 0 | 0 | 4.15 | 65.71 |
| 19 | 0 | 0 | 0 | 4.33 | 56.96 |
| 20 | 0 | 0 | 0 | 4.14 | 57.71 |
| Source of Variation | DOF | Average Peak Stress of Residual Film Y1/(MPa) | Height of Residual Film Pickup Y2/(mm) | ||||
|---|---|---|---|---|---|---|---|
| Sum of Squares | F | Significant Level p | Sum of Squares | F | Significant Level p | ||
| Models | 9 | 18.89 | 21.87 | <0.0001 ** | 3553.15 | 15.10 | 0.0001 ** |
| x1 | 1 | 3.48 | 36.28 | 0.0001 ** | 3.90 | 0.15 | 0.7074 |
| x2 | 1 | 11.89 | 123.91 | <0.0001 ** | 3303.93 | 126.35 | <0.0001 ** |
| x3 | 1 | 0.85 | 8.82 | 0.0141 * | 100.60 | 3.85 | 0.0783 |
| x1x2 | 1 | 0.78 | 8.08 | 0.0175 * | 4.28 | 0.16 | 0.6944 |
| x1x3 | 1 | 0.01 | 0.13 | 0.7308 | 10.10 | 0.39 | 0.5481 |
| x2x3 | 1 | 0.44 | 4.56 | 0.0586 | 7.51 | 0.29 | 0.6038 |
| x12 | 1 | 0.09 | 0.94 | 0.3549 | 0.40 | 0.02 | 0.9035 |
| x22 | 1 | 0.01 | 0.05 | 0.8201 | 119.24 | 4.56 | 0.0585 |
| x32 | 1 | 1.25 | 13.02 | 0.0048 ** | 0.85 | 0.03 | 0.8602 |
| Residual | 10 | 0.96 | 261.49 | ||||
| Lack of fit | 5 | 0.57 | 1.47 | 0.3416 | 212.60 | 4.35 | 0.0663 |
| Pure error | 5 | 0.39 | 48.88 | ||||
| Total | 19 | 19.84 | 3814.64 | ||||
| Test Serial Number | Recovery Rate (%) | Winding Rate (%) |
|---|---|---|
| 1 | 92.3 | 0.9 |
| 2 | 93.5 | 1.1 |
| 3 | 90.6 | 1.3 |
| Average value | 92.1 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Guo, L.; Yan, J.; Shi, Z.; Kang, M.; Yao, J. Simulation Analysis and Parameter Optimization of Residual Film Pickup Process Based on Finite Element Method. Agriculture 2024, 14, 524. https://doi.org/10.3390/agriculture14040524
Zhang X, Guo L, Yan J, Shi Z, Kang M, Yao J. Simulation Analysis and Parameter Optimization of Residual Film Pickup Process Based on Finite Element Method. Agriculture. 2024; 14(4):524. https://doi.org/10.3390/agriculture14040524
Chicago/Turabian StyleZhang, Xuejun, Lei Guo, Jinshan Yan, Zenglu Shi, Mengchen Kang, and Jieting Yao. 2024. "Simulation Analysis and Parameter Optimization of Residual Film Pickup Process Based on Finite Element Method" Agriculture 14, no. 4: 524. https://doi.org/10.3390/agriculture14040524




