Enhancing Predictive Accuracy in European Agricultural Tractor Residual Value Estimation: A Double Square Root Regression Reappraisal
Abstract
:1. Introduction
1.1. Current Issues
1.1.1. Limited Original Source Data Availability
1.1.2. Diesel Emission Regulation Compliance Cost Fosters Price Increase
1.1.3. Original Equipment Manufacturer (OEM) Size Increase
1.1.4. Original Equipment Manufacturer (OEM) Portfolio Complexity Increase
1.2. Previous Studies
1.3. Goals
2. Materials and Methods
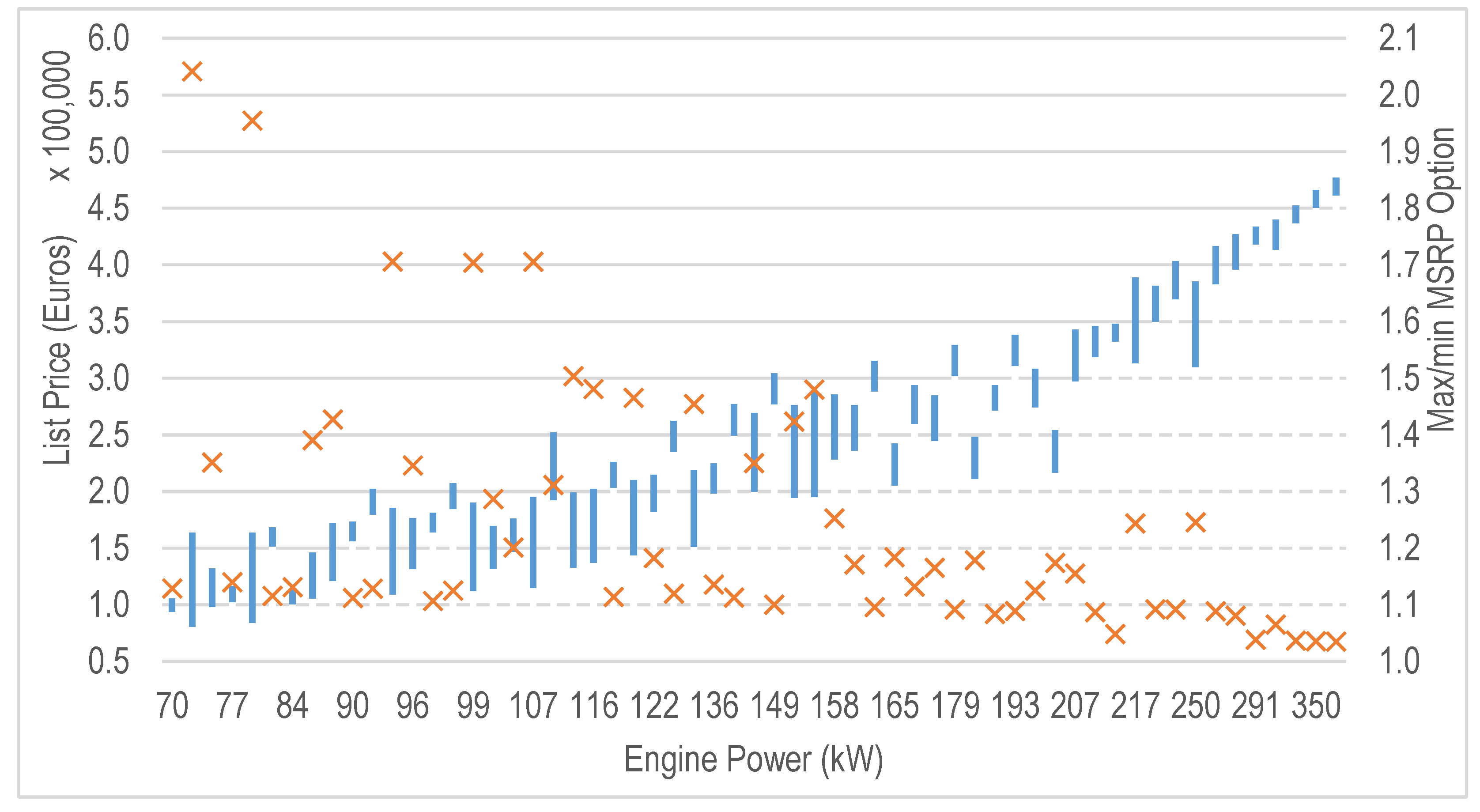
2.1. Dataset
2.2. Data Systemization and Preprocessing
2.3. Data Analysis
2.4. Regressin Analysis
3. Results
3.1. Regression Analysis
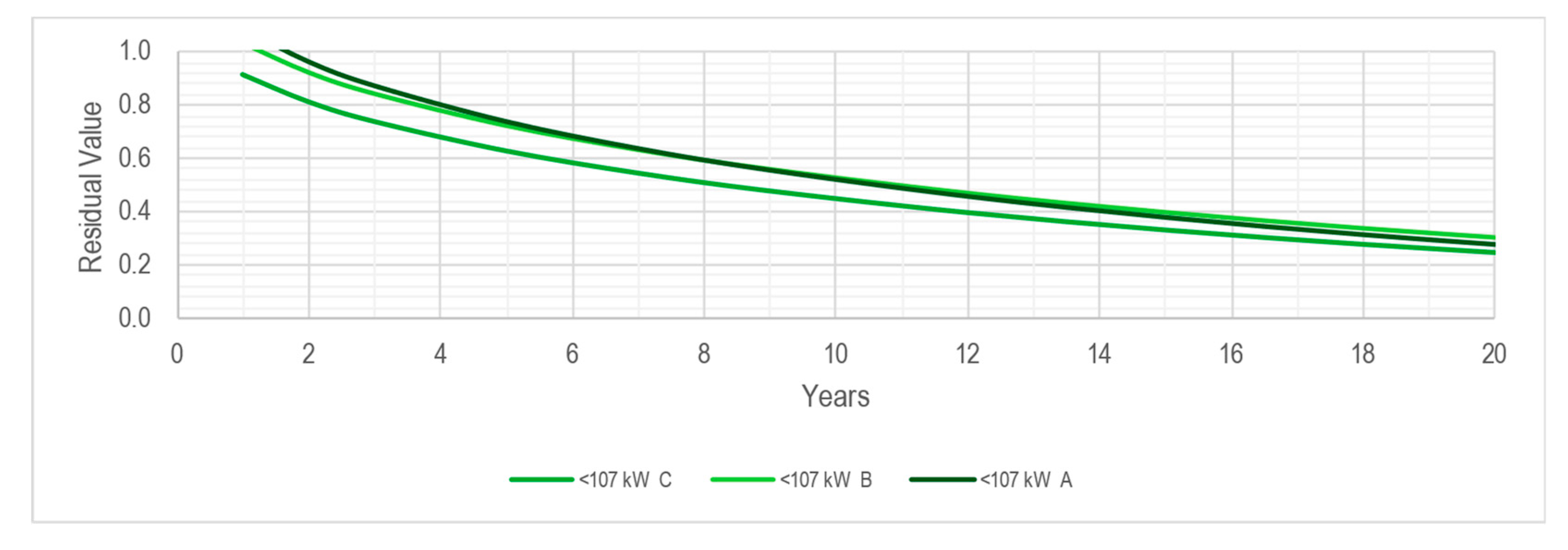
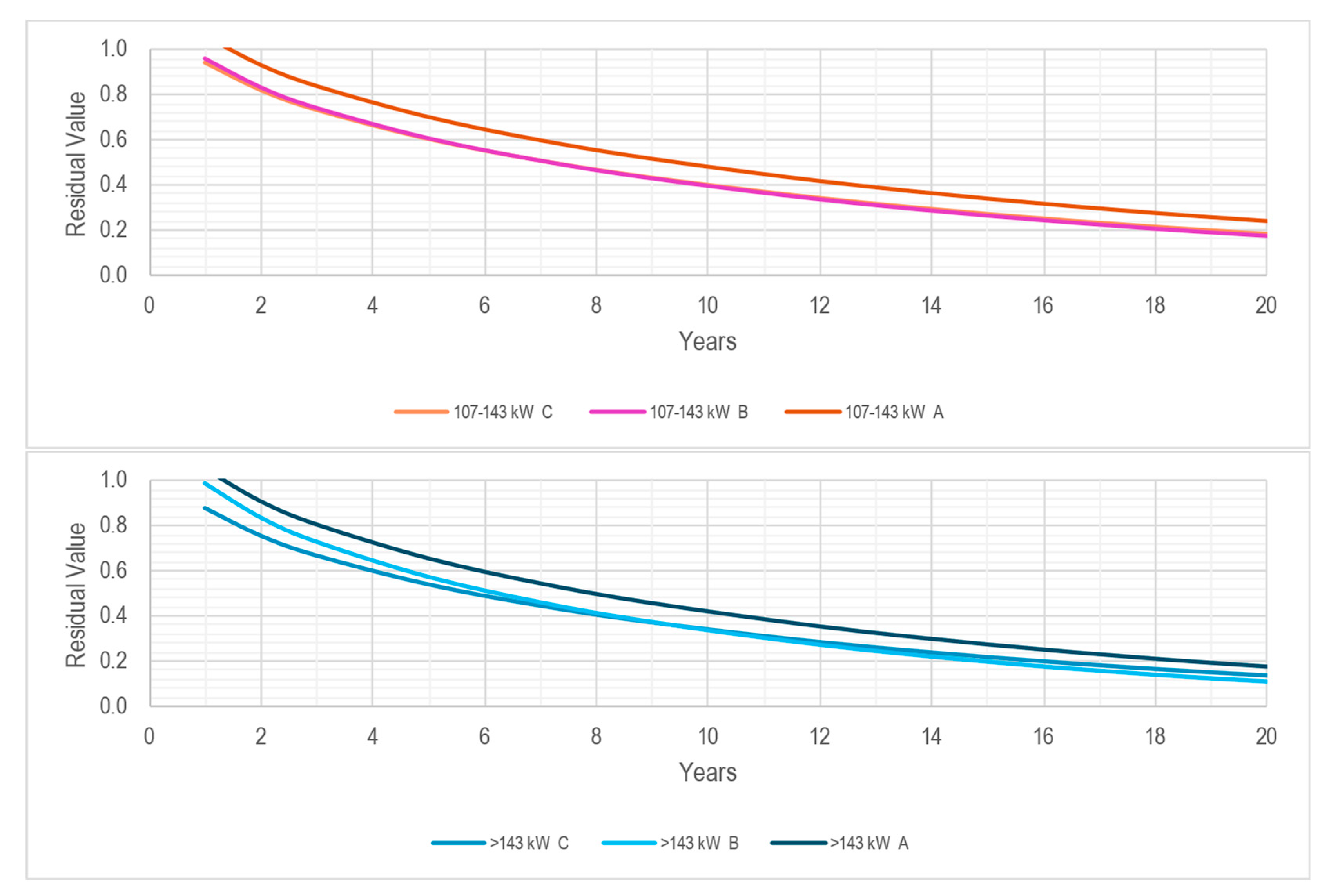
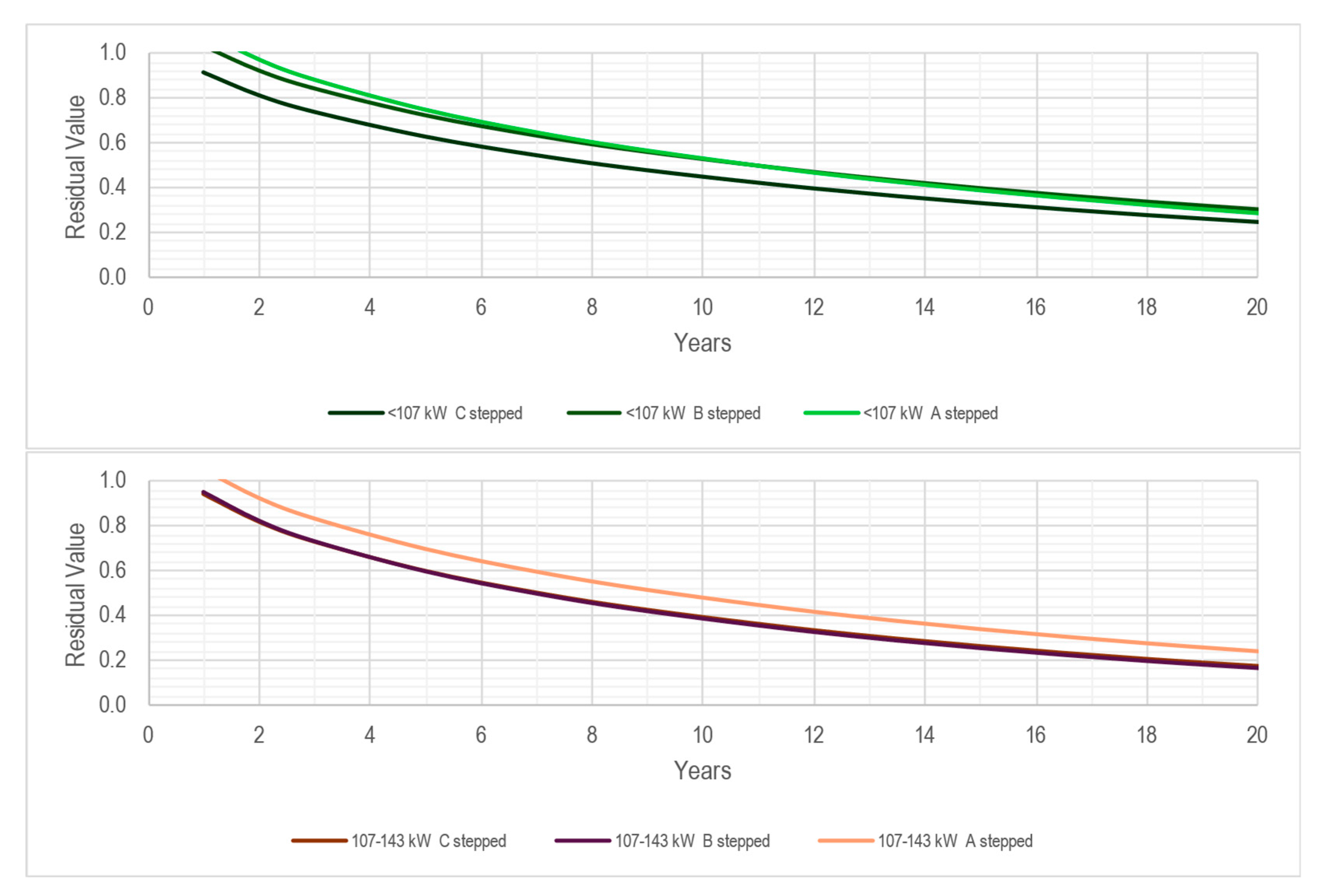
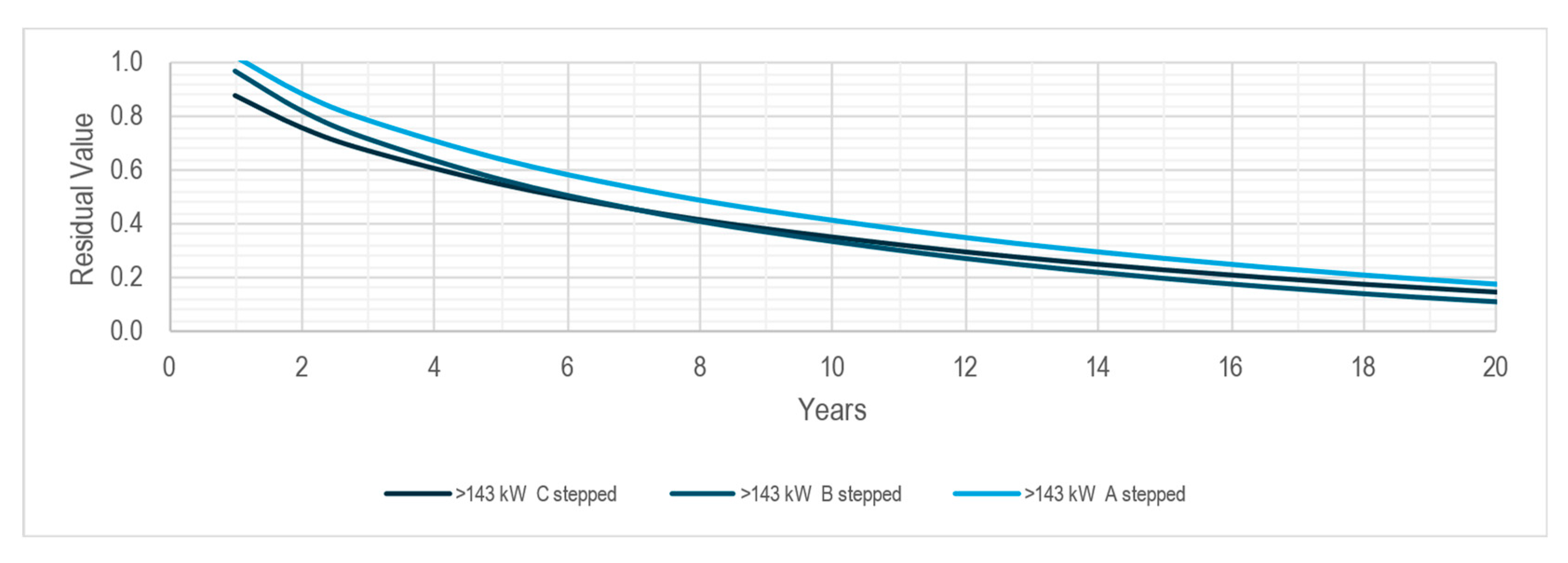
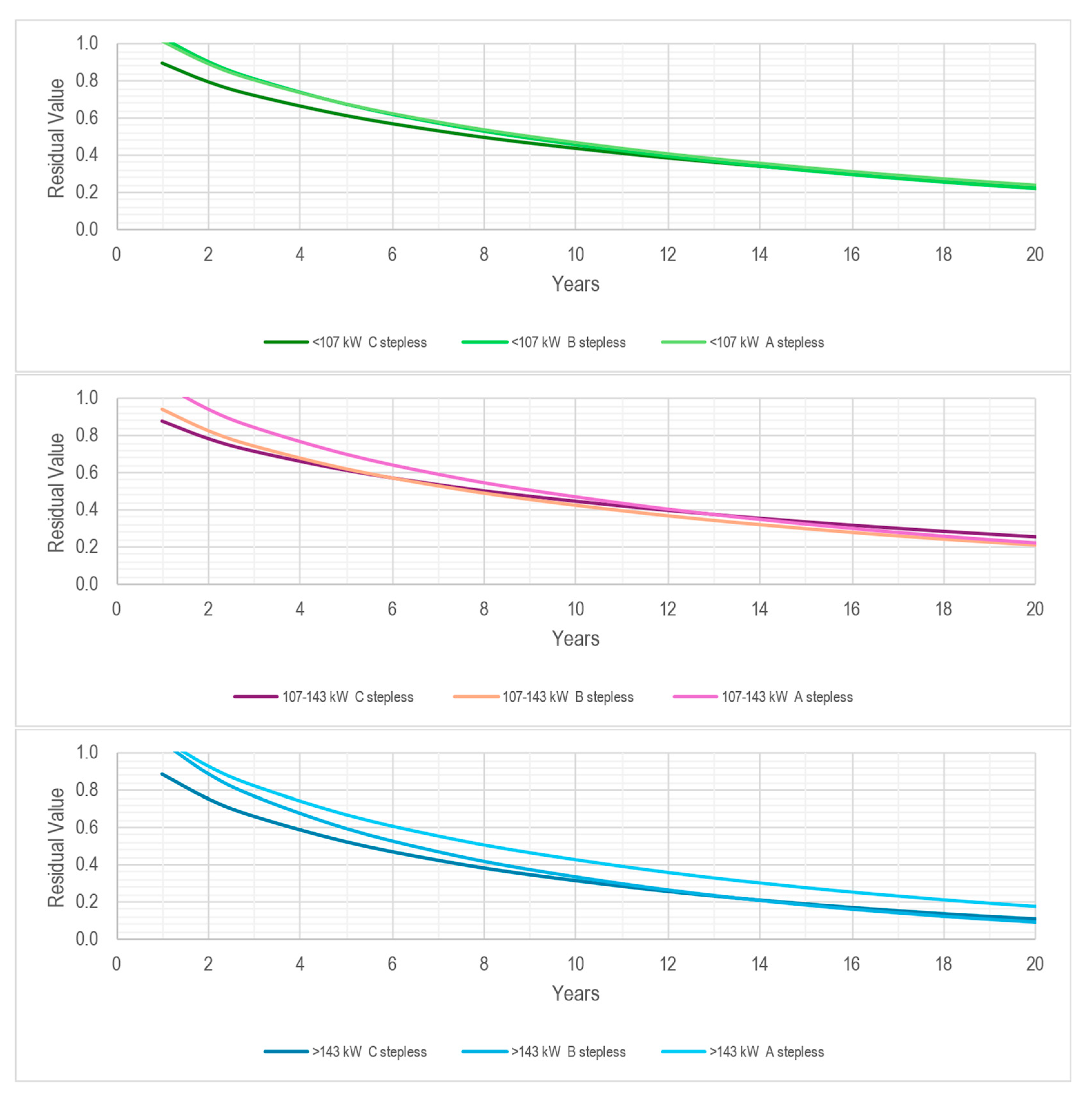
3.2. Residual Value
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. Handbook on Agricultural Cost of Production Statistics; FAO: Rome, Italy, 2016. [Google Scholar]
- Kay, R.D.; Edwards, W.M.; Duffy, P.A. Farm Management, 7th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- Kastens, T. Farm Machinery Operations Cost Calculations; Kansas State University Agricultural Experiment Station and Cooperative Extension Service: Manhattan, KS, USA, 1997. [Google Scholar]
- ASABE. Agricultural Machinery Management Data ASAE Standard EP496.2 Agricultural Machinery Management; ASABE: Joseph, MI, USA, 1999. [Google Scholar]
- ASABE. Agricultural Machinery Management Data ASAE Standard D497.7 Agricultural Machinery Management Data; American Society of Agricultural and Biological Engineers: Joseph, MI, USA, 2020. [Google Scholar]
- Gransberg, D.D.; Popescu, C.M.; Ryan, R. Construction Equipment Management for Engineers, Estimators, and Owners; CRC Press: Boca Raton, FL, USA, 2006; ISBN 0429136250. [Google Scholar]
- Edwards, W. FM1900/AgDM A3-30, Replacement Strategies for Farm Machinery; Iowa State University. Extension and Outreach: Ames, IA, USA, 2019. [Google Scholar]
- ECB Haircuts. Available online: https://www.ecb.europa.eu/ecb/educational/explainers/tell-me-more/html/haircuts.en.html (accessed on 24 December 2023).
- ACEA. Economic and Market Report. State of the EU Auto Industry. Full-Year 2021; European Automobile Manufacturers’ Association (ACEA): Brussels, Belgium, 2022. [Google Scholar]
- CEMA. Economic Press Release Tractor Registrations 2021; CEMA aisbl—European Agricultural Machinery: Brussels, Belgium, 2022. [Google Scholar]
- Wilson, P. Estimating Tractor Depreciation: The Impact of Choice of Functional Form. J. Farm Manag. 2010, 13, 799–818. [Google Scholar]
- Posada, F.; Isenstadt, A.; Badshah, H. Estimated Cost of a Diesel Emissions-Control Technology to Meet Future California Low NOx Standards in 2024 and 2027; The International Council of Clean Transportation: Washington, DC, USA, 2020. [Google Scholar]
- EC Directive 97/68/EC of the European Parliament and of the Council of 16 December 1997; European Commission (EC): Brussels, Belgium, 1997.
- EC Directive 2000/25/EC of the European Parliament; European Commission (EC): Brussels, Belgium, 2000.
- EC Directive 2004/26/EC of the European Parliament and of the Council of 21 April 2004 Amending Directive 97/68/EC; European Commission (EC): Brussels, Belgium, 2004.
- EC Directive 2009/30/EC of the European Parliament and of the Council of 23 April 2009 Amending Directive 98/70/EC; European Commission (EC): Brussels, Belgium, 2009.
- Herranz-Matey, I.; Ruiz-Garcia, L. New Agricultural Tractor Manufacturer’s Suggested Retail Price (MSRP) Model in Europe. Agriculture 2024, 14, 342. [Google Scholar] [CrossRef]
- Weersink, A.; Stauber, S. Optimal Replacement Interval and Depreciation Method for a Grain Combine. West. J. Agric. Econ. 1988, 13, 18–28. [Google Scholar]
- Leatham, D.J.; Baker, T.G. Empirical Estimates of the Effects of Inflation on Salvage Values, Cost and Optimal Replacement of Tractors and Combines. North Cent. J. Agric. Econ. 1981, 3, 109–117. [Google Scholar] [CrossRef]
- Reid, D.W.; Bradford, G.L. On Optimal Replacement of Farm Tractors. Am. J. Agric. Econ. 1983, 65, 326–331. [Google Scholar] [CrossRef]
- Perry, G.M.; Bayaner, A.; Nixon, C.J. The Effect of Usage and Size on Tractor Depreciation. Am. J. Agric. Econ. 1986, 72, 317–325. [Google Scholar] [CrossRef]
- Perry, G.M.; Glyer, D.J. Durable Asset Depreciation: A Reconciliation between Hypothesis. Rev. Econ. Stat. 1990, 72, 524–529. [Google Scholar] [CrossRef]
- Cross, T.L.; Perry, G.M. Depreciation Patterns for Agricultural Machinery. Am. J. Agric. Econ. 1995, 77, 194–204. [Google Scholar] [CrossRef]
- Cross, T.L.; Perry, G.M. Remaining Value Functions for Farm Equipment. Appl. Eng. Agric. 1996, 12, 547–553. [Google Scholar] [CrossRef]
- Unterschultz, J.; Mumey, G. Reducing Investment Risk in Tractors and Combines with Improved Terminal Asset Value Forecasts. Can. J. Agric. Econ. 1996, 44, 295–309. [Google Scholar] [CrossRef]
- Wu, J.; Perry, G.M. Estimating Farm Equipment Depreciation: Which Functional Form Is Best? Am. J. Agric. Econ. 2004, 86, 483–491. [Google Scholar] [CrossRef]
- Fenollosa, M.; Guadalajara, N. An Empirical Depreciation Model for Agricultural Tractors in Spain. Span. J. Agric. Res. 2007, 5, 130–141. [Google Scholar] [CrossRef]
- Daninger, N.; Gunderson, M.A. The Pricing and Depreciation Patterns of Used Tractors. In Proceedings of the Agricultural and Applied Economics Association 2017 Annual Meeting, Chicago, IL, USA, 30 July–1 August 2017. [Google Scholar]
- Ruiz-Garcia, L.; Sanchez-Guerrero, P. A Decision Support Tool for Buying Farm Tractors, Based on Predictive Analytics. Agriculture 2022, 12, 331. [Google Scholar] [CrossRef]
- Witte, F.; Back, H.; Sponagel, C.; Bahrs, E. Remaining Value Development of Tractors—A Call for the Application of a Differentiated Market Value Estimation. Agric. Eng. 2022, 77. [Google Scholar] [CrossRef]
- Herranz-Matey, I.; Ruiz-Garcia, L. A New Method and Model for the Estimation of Residual Value of Agricultural Tractors. Agriculture 2023, 13, 409. [Google Scholar] [CrossRef]
- Herranz-Matey, I.; Ruiz-Garcia, L. Agricultural Tractor Retail and Wholesale Residual Value Forecasting Model in Western Europe. Agriculture 2023, 13, 2002. [Google Scholar] [CrossRef]
- Herranz-Matey, I.; Ruiz-Garcia, L. Agricultural Combine Remaining Value Forecasting Methodology and Model (and Derived Tool). Agriculture 2023, 13, 894. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill: New York, NY, USA, 2005; ISBN 0072386886. [Google Scholar]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 1119122732. [Google Scholar]






| Brand | OEM | Brand Tier |
|---|---|---|
| Brand I | OEM I | B |
| Brand II | OEM II | B |
| Brand III | OEM III | A |
| Brand IV | OEM IV | A |
| Brand V | OEM III | C |
| Brand IV | OEM I | C |
| Brand | Powertrain | Powertrain Type |
|---|---|---|
| Brand I | Multimode continuous transmission | Stepless |
| Input coupled continuous variable transmission | Stepless | |
| Full power shift transmission | Stepped | |
| 8 speed dual clutch partial powershift transmission | Stepped | |
| 6 speed partial powershift transmission | Stepped | |
| 4 speed partial powershift transmission | Stepped | |
| 2 speed partial powershift transmission | Stepped | |
| Power shuttle transmission | Stepped | |
| Brand II | Multimode infinite variable transmission | Stepless |
| Input coupled infinite variable transmission | Stepless | |
| 6 speed partial powershift transmission | Stepped | |
| 4 speed partial powershift transmission | Stepped | |
| Brand III | Output coupled infinite variable transmission | Stepless |
| Brand IV | Multimode infinite variable transmission | Stepped |
| Input coupled infinite variable transmission | Stepped | |
| Full power shift transmission | Stepped | |
| 8 speed dual clutch partial powershift transmission | Stepped | |
| 4 speed partial powershift transmission | Stepped | |
| 2 speed partial powershift transmission | Stepped | |
| Power shuttle transmission | Stepped | |
| Brand V | Output coupled infinite variable transmission | Stepless |
| 8 speed dual clutch partial powershift transmission | Stepped | |
| 7 speed partial powershift transmission | Stepped | |
| 6 speed partial powershift transmission | Stepped | |
| 4 speed partial powershift transmission | Stepped | |
| Brand VI | Multimode continuous transmission | Stepless |
| Input coupled continuous variable transmission | Stepless | |
| Full power shift transmission | Stepped | |
| 8 speed dual clutch partial powershift transmission | Stepped | |
| 6 speed partial powershift transmission | Stepped | |
| 4 speed partial powershift transmission | Stepped | |
| 2 speed partial powershift transmission | Stepped | |
| Power shuttle transmission | Stepped |
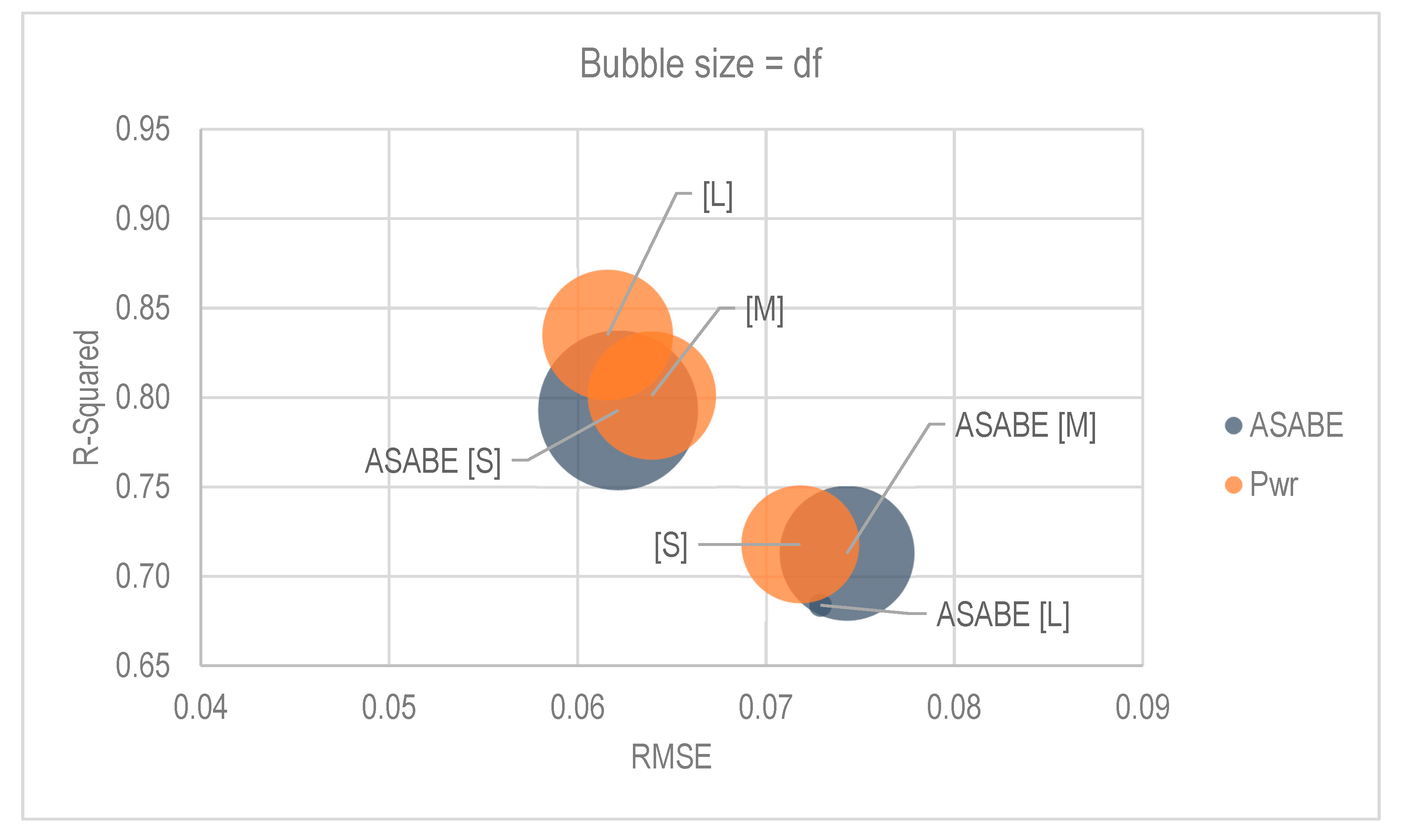
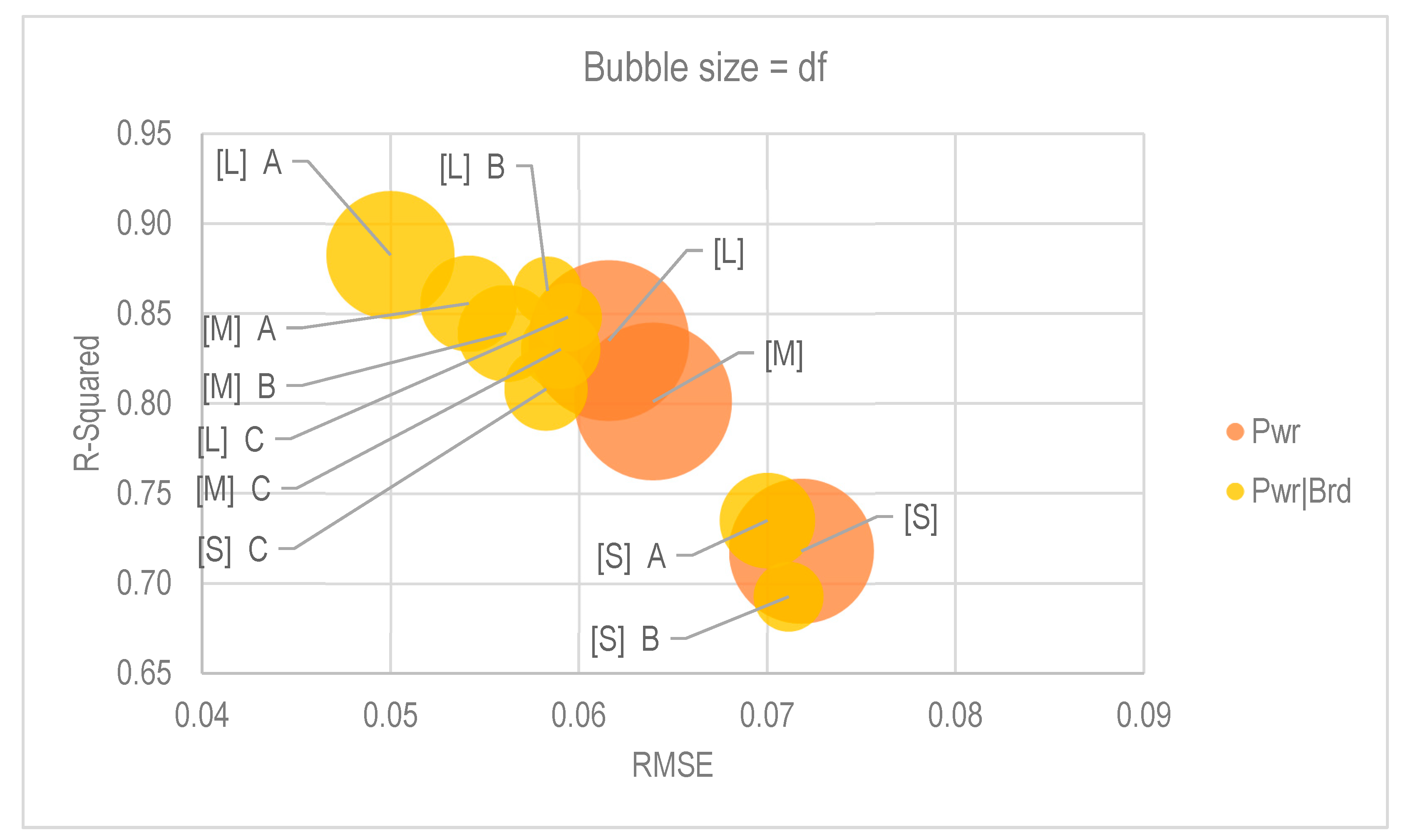
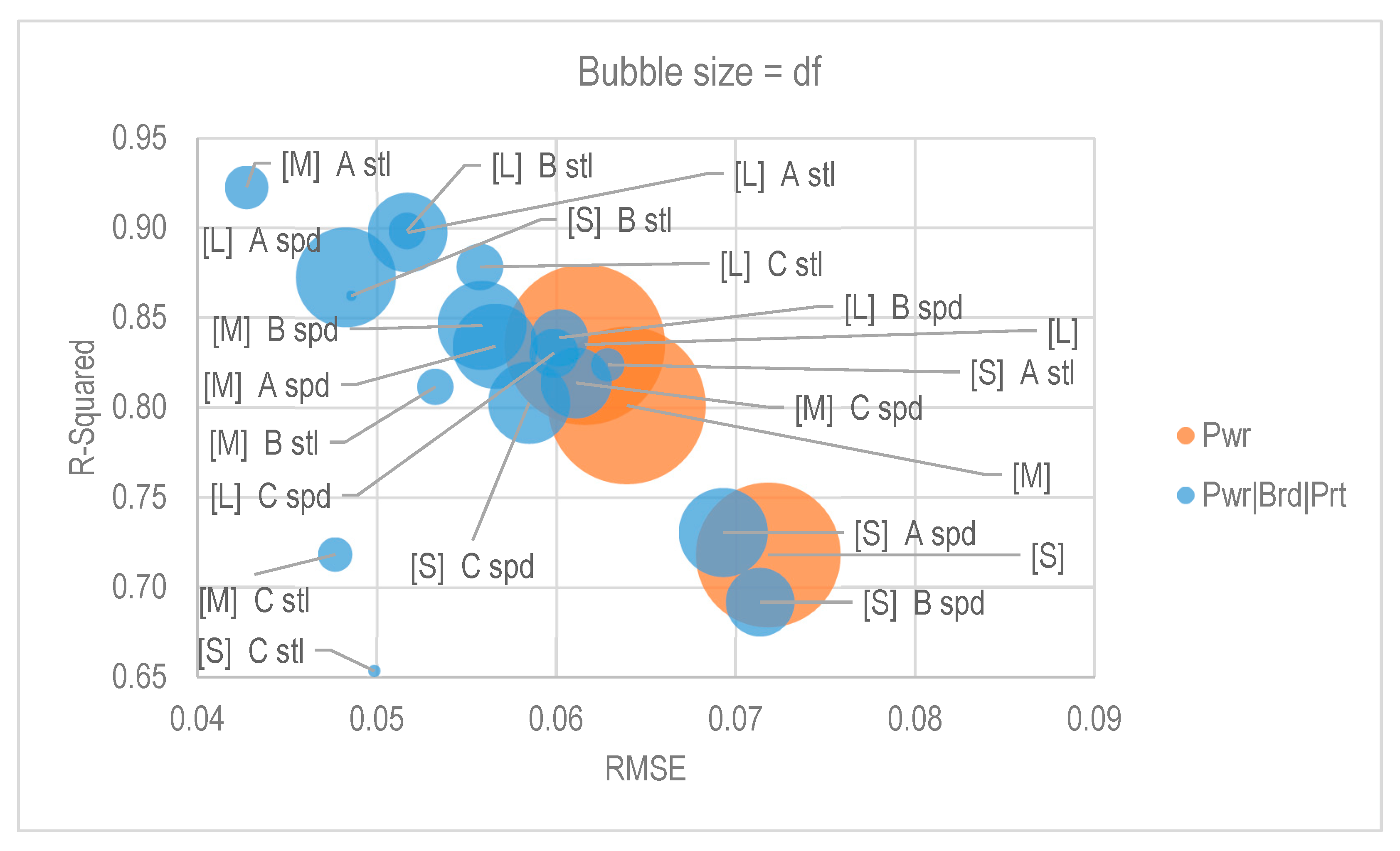
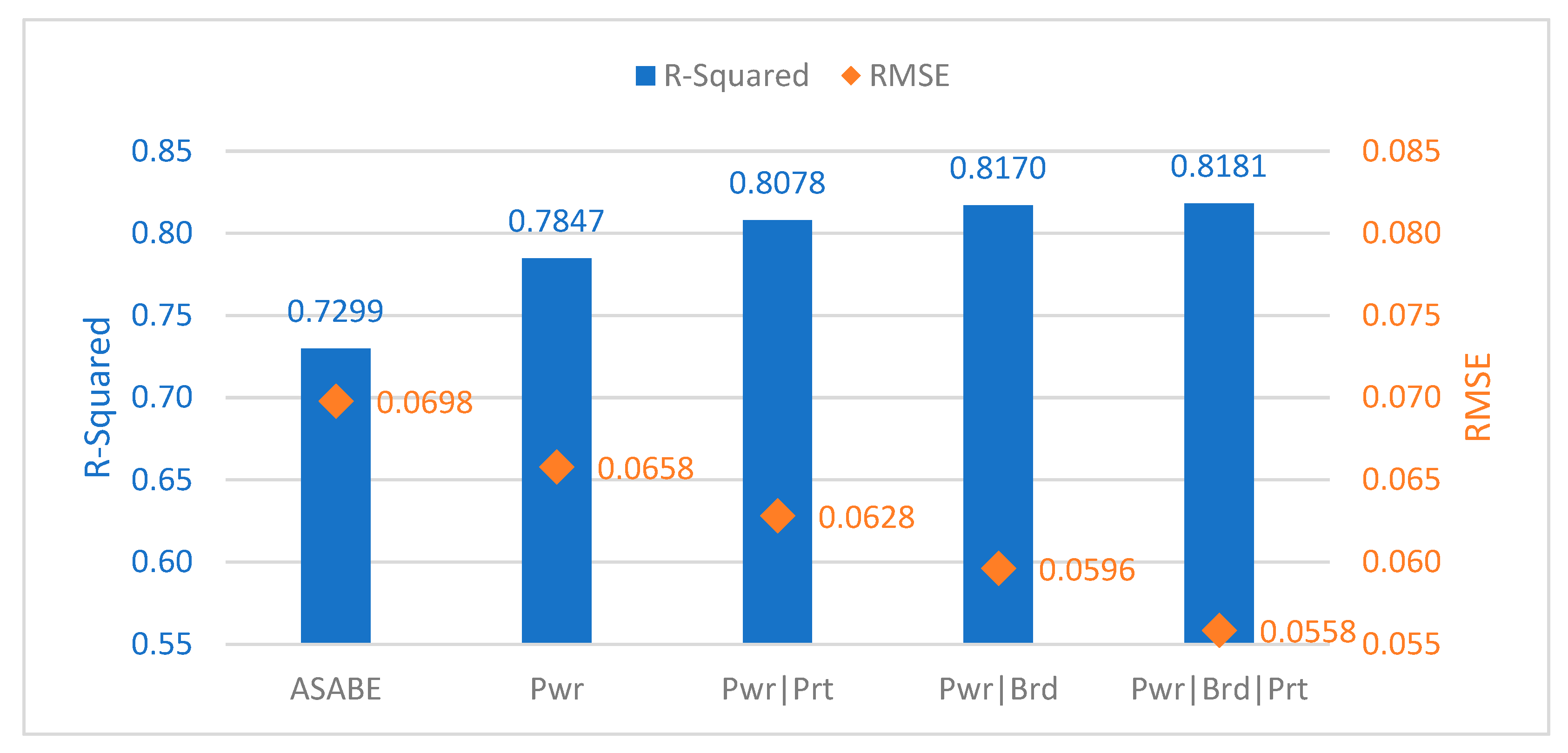
| Cohort Criteria | Cohort Regression | RMSE | R-Squared |
|---|---|---|---|
| ASABE | ASABE [≥112 kW] | 0.06215 | 0.79288 |
| ASABE [60–112 kW] | 0.07430 | 0.71295 | |
| ASABE [<112 kW] | 0.07289 | 0.68387 | |
| Pwr | >143 kW | 0.06159 | 0.83499 |
| 107–143 kW | 0.06394 | 0.80116 | |
| <107 kW | 0.07182 | 0.71795 | |
| Pwr|Prt | >143 kW stepless | 0.06542 | 0.84204 |
| 107–143 kW stepless | 0.05341 | 0.84314 | |
| <107 kW stepless | 0.06120 | 0.82763 | |
| >143 kW stepped | 0.05886 | 0.83028 | |
| 107–143 kW stepped | 0.06572 | 0.79290 | |
| <107 kW stepped | 0.07225 | 0.71085 | |
| Pwr|Brd | >143 kW C | 0.05941 | 0.84793 |
| 107–143 kW C | 0.05904 | 0.83011 | |
| <107 kW C | 0.05826 | 0.80803 | |
| >143 kW B | 0.05834 | 0.86266 | |
| 107–143 kW B | 0.05615 | 0.83892 | |
| <107 kW B | 0.07114 | 0.69262 | |
| >143 kW A | 0.05000 | 0.88252 | |
| 107–143 kW A | 0.05415 | 0.85558 | |
| <107 kW A | 0.07001 | 0.73496 | |
| Pwr|Brd|Prt | >143 kW C stepless | 0.05574 | 0.87824 |
| 107–143 kW C stepless | 0.04768 | 0.71821 | |
| <107 kW C stepless | 0.04986 | 0.65347 | |
| >143 kW B stepless | 0.05168 | 0.89827 | |
| 107–143 kW B stepless | 0.05326 | 0.81155 | |
| <107 kW B stepless | 0.04858 | 0.86220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herranz-Matey, I.; Ruiz-Garcia, L. Enhancing Predictive Accuracy in European Agricultural Tractor Residual Value Estimation: A Double Square Root Regression Reappraisal. Agriculture 2024, 14, 654. https://doi.org/10.3390/agriculture14050654
Herranz-Matey I, Ruiz-Garcia L. Enhancing Predictive Accuracy in European Agricultural Tractor Residual Value Estimation: A Double Square Root Regression Reappraisal. Agriculture. 2024; 14(5):654. https://doi.org/10.3390/agriculture14050654
Chicago/Turabian StyleHerranz-Matey, Ivan, and Luis Ruiz-Garcia. 2024. "Enhancing Predictive Accuracy in European Agricultural Tractor Residual Value Estimation: A Double Square Root Regression Reappraisal" Agriculture 14, no. 5: 654. https://doi.org/10.3390/agriculture14050654
APA StyleHerranz-Matey, I., & Ruiz-Garcia, L. (2024). Enhancing Predictive Accuracy in European Agricultural Tractor Residual Value Estimation: A Double Square Root Regression Reappraisal. Agriculture, 14(5), 654. https://doi.org/10.3390/agriculture14050654






