Abstract
The operational complexities of the elastic tooth drum pepper harvester (ETDPH), characterized by variable drum loads that are challenging to recognize due to varying pepper densities, significantly impact pepper loss rates and mechanical damage. This study proposes a novel method integrating complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), kernel principal component analysis (KPCA), and a support vector machine (SVM) to enhance drum load recognition. The method consists of three principal steps: the initial experiments with ETDPHs to identify the critical factors affecting drum load and to formulate classification criteria; the development of a CEEMDAN-KPCA-SVM model for ETDPH drum load recognition, where drum spindle torque signals are processed by CEEMDAN for decomposition and reconstruction, followed by feature extraction and dimensionality reduction via KPCA to refine the model’s accuracy and training efficiency; and evaluation of the model’s performance on real datasets, highlighting the improvements brought by CEEMDAN and KPCA, as well as comparative analysis with other machine learning models. The results describe four load conditions—no load (mass of pepper intake (MOPI) = 0 kg/s), low load (0 < MOPI ≤ 0.658 kg/s), normal load (0.658 < MOPI ≤ 1.725 kg/s), and high load (MOPI > 1.725 kg/s)—with the CEEMDAN-KPCA-SVM model achieving 100% accuracy on both training and test sets, outperforming the standalone SVM by 6% and 12.5%, respectively. Additionally, it reduced the training time to 2.88 s, a 10.9% decrease, and reduced the prediction time to 0.0001 s, a 63.6% decrease. Comparative evaluations confirmed the superiority of the CEEMDAN-KPCA-SVM model over random forest (RF) and gradient boosting machine (GBM) in classification tasks. The synergistic application of CEEMDAN and KPCA significantly improved the accuracy and operational efficiency of the SVM model, providing valuable insights for load recognition and adaptive control of ETDPH drum parameters.
1. Introduction
Pepper, a globally cultivated crop with diverse applications, is primarily harvested using various types of machinery, including ETDPHs, twin-screw roller harvesters, and comb tooth harvesters [1]. Among these, the ETDPH is particularly favored due to its method of operation, which involves rotating a drum equipped with elastic teeth to brush-remove peppers from the plants [2]. The drum plays a key role in this harvesting process. Field conditions, particularly variations in the density of pepper fruits, can lead to fluctuations in the drum load, impacting both the efficiency of the harvest and the potential for fruit damage. To optimize the performance and minimize damage in the ETDPH, it is essential to regulate the drum load to remain within an acceptable range.
The drum is a type of rotating component, and monitoring the operating condition of rotating components is critical to ensuring the normal operation of machinery [3]. In the agricultural field, load condition is a crucial aspect of monitoring the operating condition of rotating components. Many researchers have conducted research on the load condition recognition of rotating components of harvesters [4]. Traditional methods of recognizing the load conditions of rotating components of harvesters involve the installation of sensors to monitor changes in sensor values. For example, combine harvesters recognize load conditions by sensing the rotational speed of the threshing drum, measuring the tension of the drive belt or chain that drives the threshing drum, and using torque sensors to measure the output torque of the threshing drum shaft [5,6]. Liu et al. [7] measured the load on the twin threshing drums of small pre-harvest threshers by using speed sensors to detect changes in drum speed. Lu et al. [8] determined the load on the threshing drum by analyzing the hydraulic pressure of the variable speed cylinder, which correlates with the drum’s torque. You et al. [9] used tension sensors to indirectly measure the load on the threshing drum by evaluating the tension in the drive belt. However, most of these methods rely on manual judgement of the drum load, depending on the experience of the operator. With the deepening research on machine learning algorithms, these techniques have started to be widely applied to the load recognition of agricultural rotating machinery. The current trend in load condition recognition methods for rotating components of agricultural machinery is shifting towards collecting signal data during the operation of rotating components and building machine learning models to achieve load condition recognition [10].
However, relying solely on collecting signal data and then training models can limit model performance [11,12]. To improve model performance, it is essential to process the signal data prior to model training. The signals collected from agricultural machinery are often non-stationary and non-linear, with mixed noise. Traditional signal processing typically uses wavelet analysis to remove the noise [13]. Although it has multi-scale analysis capabilities and can remove noise from signals, it requires manual selection of the base wavelet and the number of decomposition levels [14,15,16,17]. To address this problem, Huang et al. proposed the empirical mode decomposition (EMD) method [18]. It is an adaptive signal processing method that can decompose the original signal into multiple intrinsic mode functions (IMFs), making it more suitable for non-stationary and non-linear signals. However, this method can suffer from mode mixing problems. Subsequently, Wu et al. proposed the ensemble empirical mode decomposition (EEMD) method to address this problem [19]. This method addresses mode mixing by adding Gaussian white noise during the decomposition process. However, it introduces new disadvantages. Because the added noise is not completely removed during decomposition, it can increase signal reconstruction errors. After identifying this problem, Torres et al. proposed the CEEMDAN method. By adding white noise at each stage of EMD, CEEMDAN can suppress mode mixing while reducing residual noise. This method is now widely used in signal processing. By decomposing and reconstructing signals with CEEMDAN, the noise contained in the signals can be effectively removed [20].
The combination of machine learning and signal processing techniques has been increasingly explored and is now widely applied in areas such as pattern recognition, fault diagnosis, and condition prediction [21,22]. Yang et al. [23] developed a method combining CEEMDAN, RCMDE, and SRNN for load identification in wet ball mills, achieving high accuracy in load detection. Tang et al. [24] proposed a fault diagnosis method for wind turbine bearings using CEEMDAN for signal decomposition and recursive feature elimination for feature selection, which significantly improved diagnostic accuracy. Guo et al. [25] introduced a CEEMDAN and BiLSTM-based approach for predicting the remaining useful life of lithium-ion batteries, demonstrating significant improvements in prediction accuracy. Guo et al. [26] developed a prognostic method for lithium-ion battery health using CEEMDAN and demonstrated its effectiveness in accurately predicting battery life. Huang et al. [27] introduced a quality diagnosis method for gas metal arc welding (GMAW) based on CEEMDAN and the extreme learning machine (ELM), which significantly improved the accuracy of weld quality classification. The combination of signal processing and machine learning to recognize the load condition of rotating components in agricultural machinery is a feasible technical method. However, the ETDPH still relies mainly on manual recognition of drum load conditions during operation, which lacks the necessary technology. To address this issue, this paper proposes a drum-load condition recognition method for an ETDPH based on CEEMDAN-KPCA-SVM. The main contributions of this paper are as follows:
- Integrating the CEEMDAN technique, the correlation coefficient method, and the variance contribution rate to decompose and reconstruct the original signal. This method evaluates the interplay between the IMFs and the original signal from dual viewpoints, eliminating components with negligible correlation to the original signal, thus effectively filtering noise from the original torque signal and improving the precision of the model.
- Extracting features across time, frequency, and time–frequency domains, and evaluating the impact of three distinct dimensionality reduction algorithms. Given the necessity for the extracted features to reflect variations under four different conditions, a holistic set of signal characteristics is derived. Additionally, the influence of dataset dimensions on model training is considered, and the efficacy of various dimensionality reduction algorithms is contrasted.
- Proposing a novel method for recognizing drum load for an EDTPH. Drum load experiments were performed to establish a classification system. The CEEMDAN technique was used to filter noise from the raw data, and a thorough analysis of the extracted signal features was conducted. The KPCA algorithm was applied to reduce the dimensionality of the feature set, which was then fed into an SVM model for training, resulting in a drum load recognition model specific to the ETDPH. Moreover, the effectiveness of combining CEEMDAN and KPCA was evaluated, and a comparative analysis of different models for drum load recognition was carried out.
The structure of this paper is organized as follows. Section 2 describes the drum load experiments carried out on the ETDPH, details the basis for drum load classification, and explains the CEEMDAN-KPCA-SVM-based drum load analysis method. Section 3 compares the effectiveness of the CEEMDAN and KPCA methods combined with three different machine learning models in identifying ETDPH drum loads. Finally, Section 4 summarizes the main contributions of this paper, discusses the limitations of this study, and outlines plans for future research.
2. Materials and Methods
2.1. Drum Load Test and Classification
During field operations, the ETDPH experiences continuous variations in drum load due to the complex work conditions, which impact its harvesting performance. To maintain the drum load within an optimal range and ensure efficient harvesting, it is essential to monitor the drum load condition. To identify the factors influencing drum load and to provide a basis for classifying these conditions, as well as to facilitate subsequent signal collection, an ETDPH drum load test platform was established, and drum load tests were conducted.
2.1.1. Test Platform
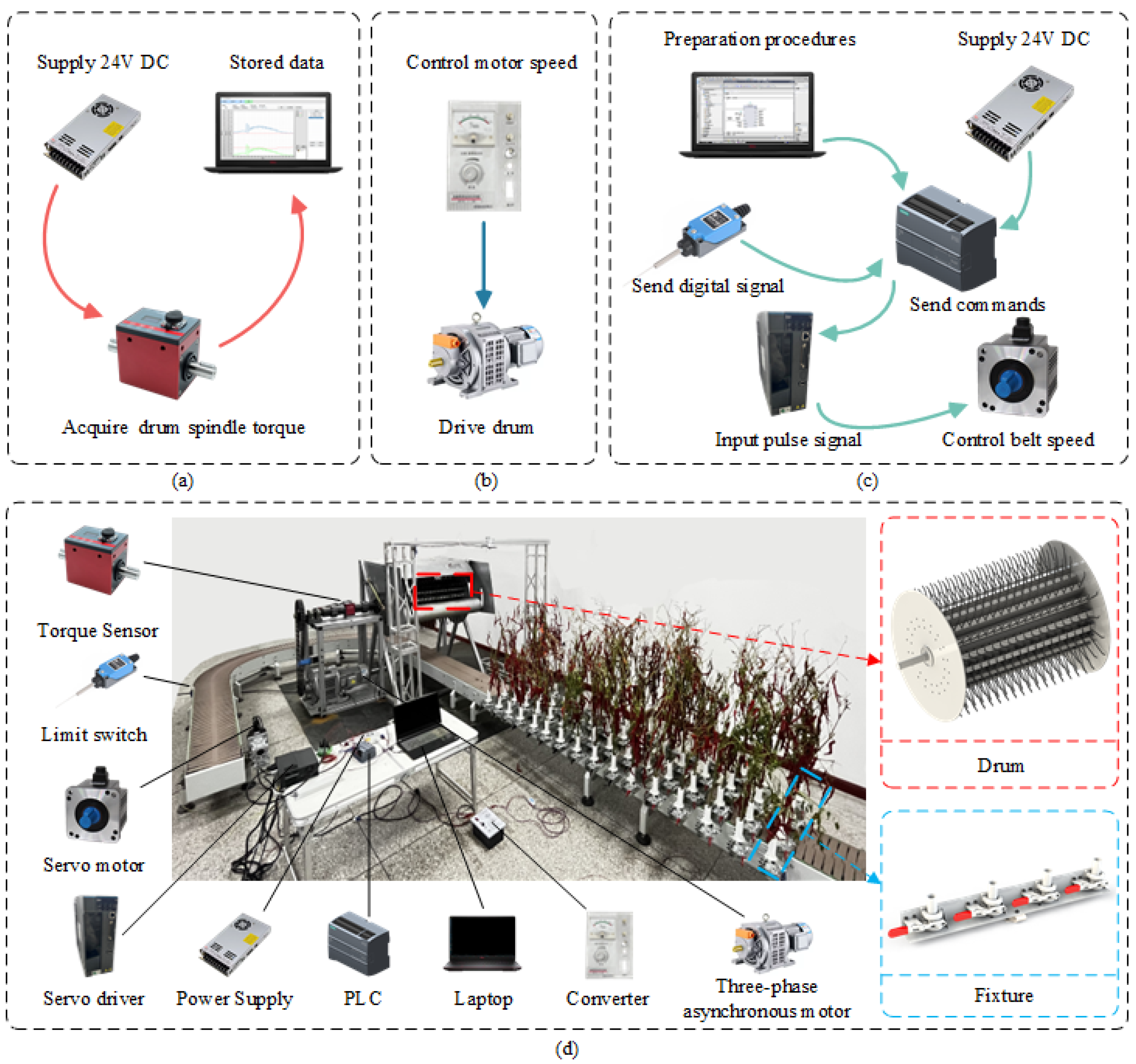
The drum load test platform of the ETDPH mainly consists of the picking device and the conveyor device, as shown in Figure 1. The picking device can be divided into the mechanical structure, data acquisition, and control system parts. The conveyor device can be divided into the mechanical structure and control system parts.
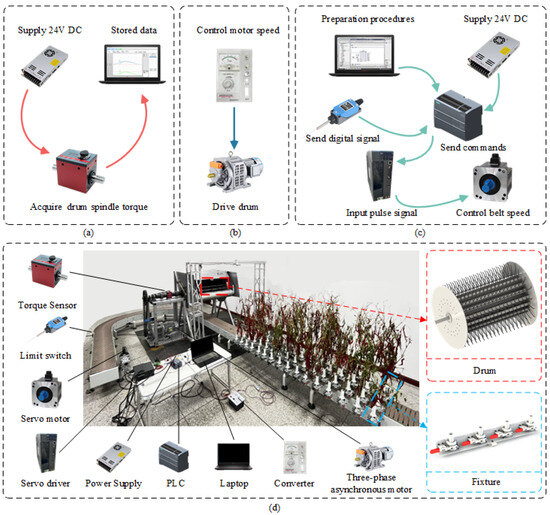
Figure 1.
ETDPH test platform hardware installation, signal acquisition system, and control system. (a) The signal acquisition system; (b) the drum rotation speed control system; (c) the conveyor device control system; (d) the ETDPH test platform hardware installation.
The mechanical structure of the picking device is centered around the drum itself, consisting of side discs and elastic teeth mounting plates installed between the discs. The drum radius is set to 425 mm to ensure that the harvesting area of the drum covers all fruit-bearing areas. The length of the drum is set to 1042 mm to allow several rows of peppers to be harvested in a single pass. Elastic teeth are mounted on the elastic tooth mounting plates, with three adjacent rows arranged in a staggered pattern. The elastic tooth mounting plates and elastic teeth are removable, allowing the number of rows, number of teeth per row, spacing or type of elastic teeth to be adjusted. The drum has a hollow structure to prevent the pepper fruits from becoming stuck inside during harvesting. The data acquisition part is installed on the front of the drum and consists of a DYN-200 torque sensor and an upper computer. The DYN-200 torque sensor is connected to the main shaft of the drum by means of a coupling, which enables real-time acquisition of torque, speed, and power signals from the main shaft. The DYN-200 torque sensor has a range of 0 to 2000 N·m and an accuracy of 0.1%, which meets the experimental requirements. The control system consists of a YCT200 three-phase asynchronous motor and a frequency converter. The frequency converter controls the speed of the three-phase asynchronous motor, which in turn controls the drum speed via a chain drive. The drum speed can be adjusted from 0 to 260 rpm.
The mechanical structure of the conveyor device consists of clamps and a conveyor belt. The clamp section consists of U-bolts, clamps, Polycarbonate (PC) tubes, and angle irons. The pepper plants are inserted into the PC tubes and then held in place by the clamps, which are bolted to the angle irons. Each PC tube is 20 mm apart, and the row spacing is designed according to Xinjiang’s line pepper planting agronomy, which can simulate row spacing for both single-membrane four-row and single-membrane two-row planting methods. The conveyor belt is 12 m long, simulating sufficient harvesting time. The control structure of the conveyor device includes a servo motor, a servo driver, a servo electronic transformer, a Programmable Logic Controller (PLC), a limit switch, and an upper computer. This setup can control the end position and the conveying speed of the conveyor belt. The limit switch is mounted on the side of the conveyor belt. When the first row of clamp-mounting plates contacts the limit switch, the entire conveyor belt stops immediately. The speed of the conveyor belt is controlled by the PLC, which sends instructions to the servo driver, which controls the start, stop, and speed of the servo motor. It controls the start, stop, and speed adjustment of the conveyor belt, with an adjustable speed range of 0 to 1.4 m/s.
2.1.2. Drum Load Test
The drum load of the ETDPH comes from two main sources. The first source is the load generated by the rotation of the drum itself, which is related to the speed of the drum. The second source is the load generated by the interaction between the plants and the drum during the harvesting of peppers. The magnitude of this load is related to the mass of peppers entering the drum per unit time. Previous experiments have often used operating speed to simulate this variation, but this method overlooks the issue of uneven pepper fruit density in real fields. The mass of pepper entering the ETDPH drum per second is defined as the MOPI, according to the different field pepper yields and work speeds. For the above reasons, therefore, this study will use rotation speed and MOPI as the two factors for conducting this experiment.
The experiment was conducted in October 2023 at the College of Mechanical and Electrical Engineering, Shihezi University, located in Shihezi City, Xinjiang Uygur Autonomous Region. The experimental plants, a variety of Shanzaohong line pepper, were sourced from Yaziquan Village, Shawan City, Tarbagatay Prefecture, Xinjiang Uygur Autonomous Region. Using the ETDPH drum load test platform, the investigation focused on the effects of drum speed and MOPI on the ETDPH’s drum load. A single-factor experimental design was employed, with the levels of the factors detailed in Table 1.

Table 1.
ETDPH drum load test factor level table.
The evaluation metrics for the experiment were established from two aspects. The first aspect is the indicator reflecting the load carried by the drum. The motor power that drives the drum rotation is an important parameter for evaluating the drum load of the ETDPH. The greater the drum load, the higher the motor power. In this study, the average motor power, after subtracting the average no-load motor power at the corresponding speed was selected as the indicator. The second indicator reflects the operating quality of the ETDPH, which is also affected when the drum load of the ETDPH is not in normal condition. According to the indicators in the applicability evaluation of the Agricultural Machinery Extension Appraisal Syllabus DG/T 114-2019 [28], mechanical breakage rate and loss rate are selected as the evaluation indicators for this test. The calculation of machine breakage rate and loss rate is shown in Equations (1) and (2).
where is the mechanical breakage rate, is the loss rate, is the mass of mechanically broken peppers, is the mass of unbroken peppers, is the mass of missed peppers, is the mass of crashed peppers, and is the mass of peppers picked up in the measurement area.
2.1.3. Drum Load Condition Division
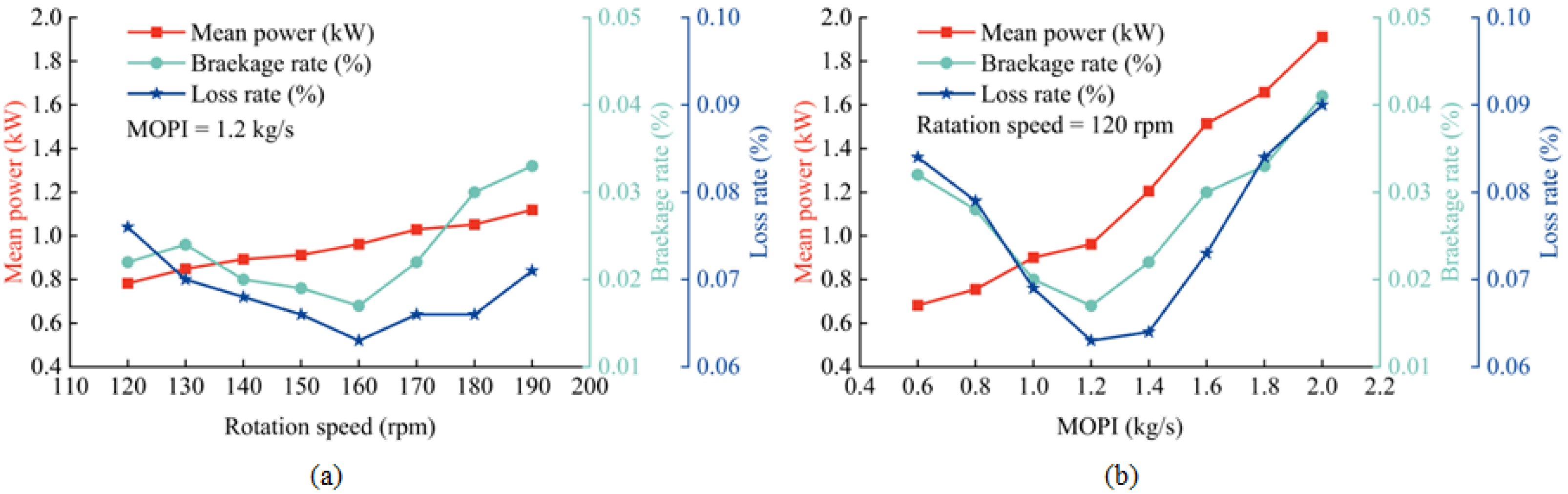
The effect of drum speed on the average drive motor power, mechanical breakage rate, and loss rate is shown in Figure 2a. It can be seen that the drive motor power increases as the ETDPH drum speed increases. This increase is due to the increased impact and friction between the stalks and peppers and the drum, which requires more resistance and therefore more motor power. At lower speeds, the force exerted by the elastic tooth on some peppers does not exceed the adhesion between the peppers and the stalks, resulting in unharvested or unripe peppers and increased losses. Conversely, at higher speeds, some pepper stalks lift off the ground, preventing the attached peppers from being harvested and increasing the loss rate. Similarly, the mechanical breakage rate tends to decrease before increasing; at lower speeds, inadequate acceleration causes some peppers to remain in the drum after picking, suffering multiple impacts and resulting in breakage. At higher speeds, the excessive impact of the elastic tooth causes the pepper to be crushed, increasing the mechanical breakage rate.
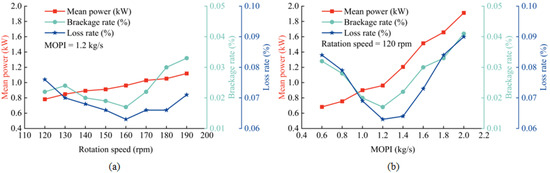
Figure 2.
Variation in mean drive motor power, mechanical breakage, and loss rate with rotation speed and ETDPH pepper feed. (a) Variation in mean value of drive motor power, mechanical breakage rate, and loss rate with rotation speed; (b) variation in mean value of drive motor power, mechanical breakage rate, and loss rate with MOPI.
As shown in Figure 2a, the variations in speed have a minimal effect on the average motor power. In an operational environment, the speed of the ETDPH is usually constant or subject to minor adjustments at short intervals to facilitate performance. Consequently, this study excludes speed from its scope and concentrates only on the effect of pepper intake rate on the drum load of the ETDPH. In addition, the graph shows that both breakage and loss are minimized at a speed of 160 rpm, and therefore 160 rpm is adopted for subsequent experiments.
The effect of MOPI on the mean power of the drive motor, mechanical breakage rate, and loss rate is depicted in Figure 2b. An increase in MOPI results in a higher rate of pepper entry into the drum per second, increasing the interaction between the drum’s elastic teeth and the peppers. Consequently, the drum’s rotation must overcome increased resistance, which elevates the motor’s power. The loss rate initially declines before rising; this pattern occurs because, at a low MOPI, the limited amount of pepper results in substantial gaps between the stalks and peppers as they enter the drum. In these gaps, some elastic teeth penetrate without contacting the peppers, thereby increasing the loss rate. Conversely, at a high MOPI, the excessive pepper density prevents the elastic teeth from thoroughly brushing each pepper, leading to leakage. The mechanical breakage rate similarly shows a trend of an initial decrease followed by an increase. At a low MOPI, the large gaps between the plants, the peppers, and the drum cause multiple collisions, which damage the peppers. At a high MOPI, the peppers and stalks are densely packed, preventing the elastic teeth from fully contacting the peppers and resulting in incomplete picking, which increases the mechanical breakage rate.
As shown in Figure 2, the MOPI variation has a large effect on the mean value of the motor’s power, and in this study, the MOPI is used as a variable to classify the load conditions. The mechanical breakage rate and loss rate with the MOPI variation curves were fitted using Origin 2022 [29], resulting in the following regression equation. A 2nd order polynomial function was chosen for this fit because of its ability to accurately capture the non-linear relationships inherent in the data. This function effectively balances complexity and computational efficiency, providing a reliable fit without the risk of overfitting that higher order polynomials might introduce.
where the for Equation (3) is 0.8773 and the for Equation (4) is 0.8888. According to the criteria of the Agricultural Machinery Extension Appraisal Syllabus DG/T 114-2019 [28], which stipulate a loss rate of no more than 8% and a mechanical breakage rate of no more than 3%, the range of MOPI that complies with these requirements for applicability evaluation is classified as normal load. The remaining ranges are categorized as low load and high load, respectively. Specifically, no load corresponds to an MOPI of 0 kg/s, low load corresponds to an MOPI between 0 and 0.658 kg/s, normal load corresponds to an MOPI between 0.658 and 1.725 kg/s, and high load corresponds to an MOPI exceeding 1.725 kg/s.
2.2. Overview of the Methodological Process
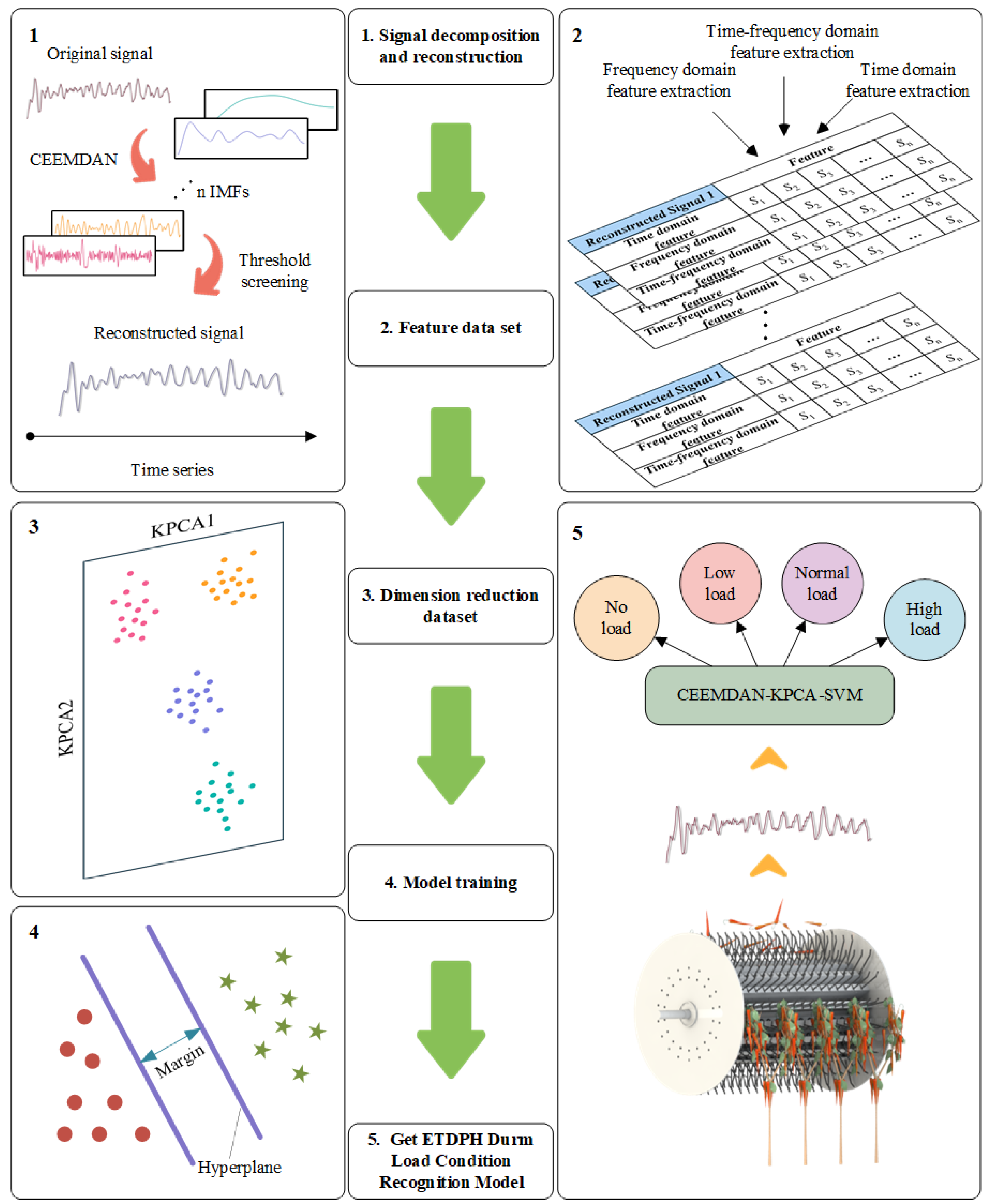
We introduce a novel method for recognizing the drum load of the ETDPH, using a CEEMDAN-KPCA-SVM methodology. This method addresses the limitations of single-model ETDPH drum load recognition, as single models cannot effectively remove noise from the original signal. The CEEMDAN technique excels in denoising signals and extracting instantaneous signal features, thereby improving data accuracy and reliability. By combining KPCA for dimensionality reduction and a SVM for classification, our method is not only more effective at feature extraction, but also significantly improves the recognition accuracy of the model. The overall framework of the proposed method is depicted in Figure 3.
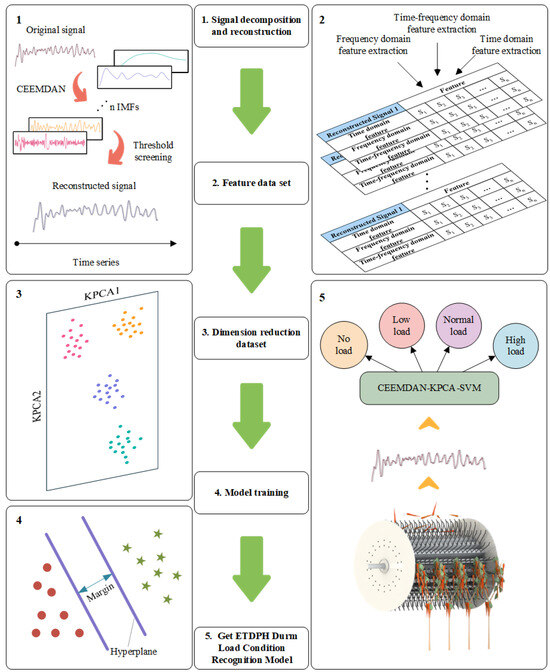
Figure 3.
Process based on the CEEMDAN-KPCA-SVM ETDPH drum load condition recognition method.
Step 1: Spindle torque signals under four conditions—no load, low load, normal load, and high load—were decomposed using CEEMDAN to obtain multiple IMFs. These IMFs were then filtered using the correlation coefficient method and the variance contribution rate, selecting only those exceeding predetermined thresholds for signal reconstruction.
Step 2: Statistical features in the time domain of the reconstructed torque signal were extracted, alongside frequency domain features obtained by fast Fourier transform and power spectral density function processing. Wavelet packet analysis was used to decompose the signal, facilitating the extraction of time–frequency domain features post-decomposition.
Step 3: The feature dataset was reduced in dimensionality using KPCA.
Step 4: The reduced-dimensionality dataset was partitioned into training and testing subsets, on which an SVM model was trained.
Step 5: The resulting model, integrating CEEMDAN, KPCA, and the SVM, was established as an effective ETDPH drum load recognition system.
2.3. CEEMDAN-Based Signal Decomposition and Reconstruction
CEEMDAN, a signal processing technique, effectively decomposes non-linear and non-smooth torque signals into a series of smoother IMFs. Through the decomposition and subsequent reconstruction of the signal using the CEEMDAN algorithm, noise is effectively eliminated.
2.3.1. CEEMDAN
Let the initial torque signal be denoted as , where represents Gaussian white noise satisfying the normal distribution, is the th IMF obtained by using the EMD decomposition, is the obtained by averaging, is the amplitude coefficient of the added Gaussian white noise [19]. The specific steps of the CEEMDAN algorithm are as follows:
- 1.
- Add Gaussian white noise to the original signal to obtain a new signal :
- 2.
- Use the EMD method to decompose . The mean value of is subsequently calculated as
- 3.
- Use the original signal minus . The residual component is obtained as
- 4.
- Decompose the signal , , then obtain :
- 5.
- When , the above steps are repeated to obtain the th residual component and the , as follows:
- 6.
- Stop decomposition when the extreme point of is no more than two. The result of the decomposition is obtained as follows:where is the number of all IMFs.
2.3.2. Signal Reconstruction Based on Correlation Coefficient Method and Variance Contribution Rate
The IMFs were screened using the correlation coefficient method and the variance contribution rate together. The IMFs that met the requirements were selected for reconstruction. The specific steps are as follows:
- Decompose the ETDPH drum spindle torque signals into several IMFs using the CEEMDAN technique.
- Use Pearson’s correlation coefficient to determine the correlation between the original signal and the IMFs [23].where is the correlation coefficient, and x are the observations; and are the sample means of samples and , respectively, and is the number of observations.
- Calculate the variance contribution rate for each IMF [30].where is the time series’ length, is the mean of , is the time, and is the mean of the original signal.
- Select IMFs above the correlation coefficient and variance contribution thresholds for signal reconstruction.
2.4. Feature Extraction and Dimensionality Reduction
2.4.1. Feature Extraction
The operation of the ETDPH drum takes place in a diverse environment, and the spindle torque signal exhibits non-linear and non-smooth characteristics. Consequently, it is of paramount importance to extract features from the original signal that effectively represent the various load conditions of the drum [31,32]. Recognizing that different domains of the torque signal provide complementary insights, this research seeks to extract features from the time, frequency, and time–frequency domains of the torque signal that are instrumental in delineating the load state of the ETDPH drum.
A comprehensive selection of 11 temporal statistical features were used in our study: mean, standard deviation, variance, peak value, peak factor, kurtosis, skewness, root mean square (RMS), waveform factor, impulse factor, and shape factor. Table 2 provides a description of the time domain features extracted above. These factors provide multi-dimensional data support for accurately recognizing the load condition of the ETDPH drum.

Table 2.
Description of time domain features.
In this study, the time domain signals were converted to the frequency domain using the fast Fourier transform and the power spectral density functions, resulting in a set of 10 frequency domain features. These features include mean, RMS, standard deviation, variance, and peak value. Table 3 provides a description of the frequency domain features extracted above.

Table 3.
Description of frequency domain features.
In addition, this study not only extracts time and frequency domain features from the reconstructed signal, but also applies wavelet packet analysis to the signal. DB1 is chosen as the base wavelet, with three levels of decomposition, and the energy value of each node is considered as a feature, resulting in eight features. The energy serves as a basic quantitative indicator of the signal, with high energy correlating with high load conditions and vice versa. Torque signals under different load conditions have different energy distribution patterns.
In summary, this research has extracted eleven time domain, ten frequency domain, and eight time–frequency domain features, for a total of twenty-nine features.
2.4.2. KPCA Dimensionality Reduction
It is crucial to perform dimensionality reduction on the extracted feature dataset to avoid excessive data dimensionality and computational complexity during model training [33,34,35]. KPCA is a widely used nonlinear dimensionality reduction technique. It non-linearly transforms the original features into a high-dimensional space using a kernel function, with the aim of making the original feature data structure as linearly separable as possible. The specific steps of KPCA are outlined below:
- 1.
- Suppose the data set consisting of samples of the ETDPH’s drum spindle torque signal is , . Here, is the number of samples, and is the dimension of each sample .
- 2.
- Assume there is a non-linear mapping, . The original data can be mapped onto a higher dimensional space, and the covariance matrix of the mapped data set is :where is the mean mapped vector.
- 3.
- Since it is not possible to directly calculate and decompose the covariance matrix in high-dimensional space to find its principal components, it is necessary to be aided by the kernel function, which is defined ashere, the Gaussian Radial Basis Function (RBF) is selected as the kernel function. This function is defined as
- 4.
- Construct a nuclear matrix , where the elements are .
- 5.
- Centre the data on the origin in the high-dimensional feature space by centering the kernel matrix :where is an matrix whose elements are all .
- 6.
- Decomposing the kernel matrix yields eigenvalues with their corresponding eigenvectors .
- 7.
- Select the most important eigenvectors based on the size of the eigenvalues. These eigenvectors correspond to the main directions of change of the data in the high-dimensional feature space.
- 8.
- Obtain the coordinates of each original sample in low-dimensional space by calculating its inner product with the selected eigenvectors, and project the sample onto the th principal component:where is the projection of sample onto the th principal component, and is the th element of the th kernel eigenvector of the kernel matrix .
2.5. Usage of SVM
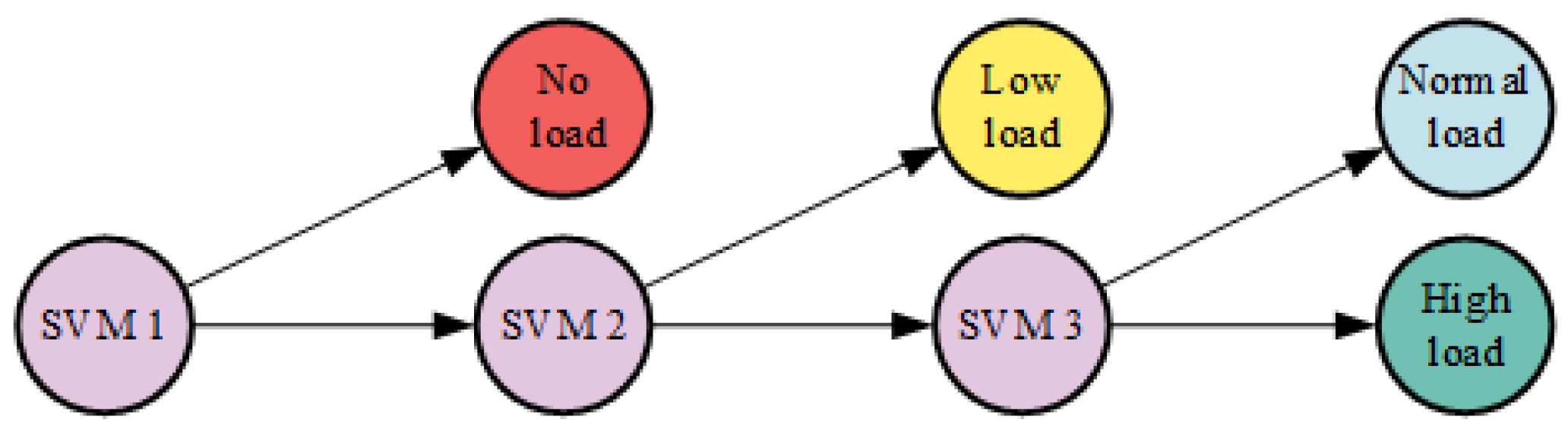
The SVM is a widely used supervised learning method designed for classification tasks [36]. It works by transforming data into a high-dimensional space using a kernel function and then constructing a hyperplane to maximize the separation between different classes. Typical kernel functions include linear, polynomial, RBF, and sigmoid kernels. Since the basic SVM is limited to binary classification, this research develops a multi-classification SVM, as shown in Figure 4. The RBF kernel is selected for this study due to its adaptable decision boundary, superior classification efficiency, and reasonable number of features.
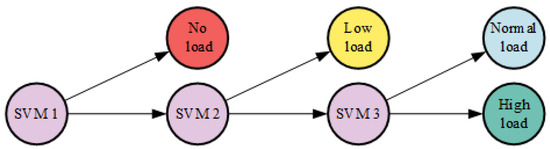
Figure 4.
Multiclassification SVM structure.
3. Results and Discussion
In this study, the torque signals of the drum spindle were collected under different load conditions: no load (MOPI = 0 kg/s), low load (0 < MOPI < 0.658 kg/s), normal load (0.658 ≤ MOPI ≤ 1.725 kg/s), and high load (MOPI ≥ 1.725 kg/s). Due to the complex and rapidly changing field conditions, short signal sequences better reflect the actual operating condition of the drum. Therefore, only the stable 0.6 s segment of each collected signal was selected for subsequent analysis.
3.1. Analysis of Torque Signal Decomposition and Reconstruction
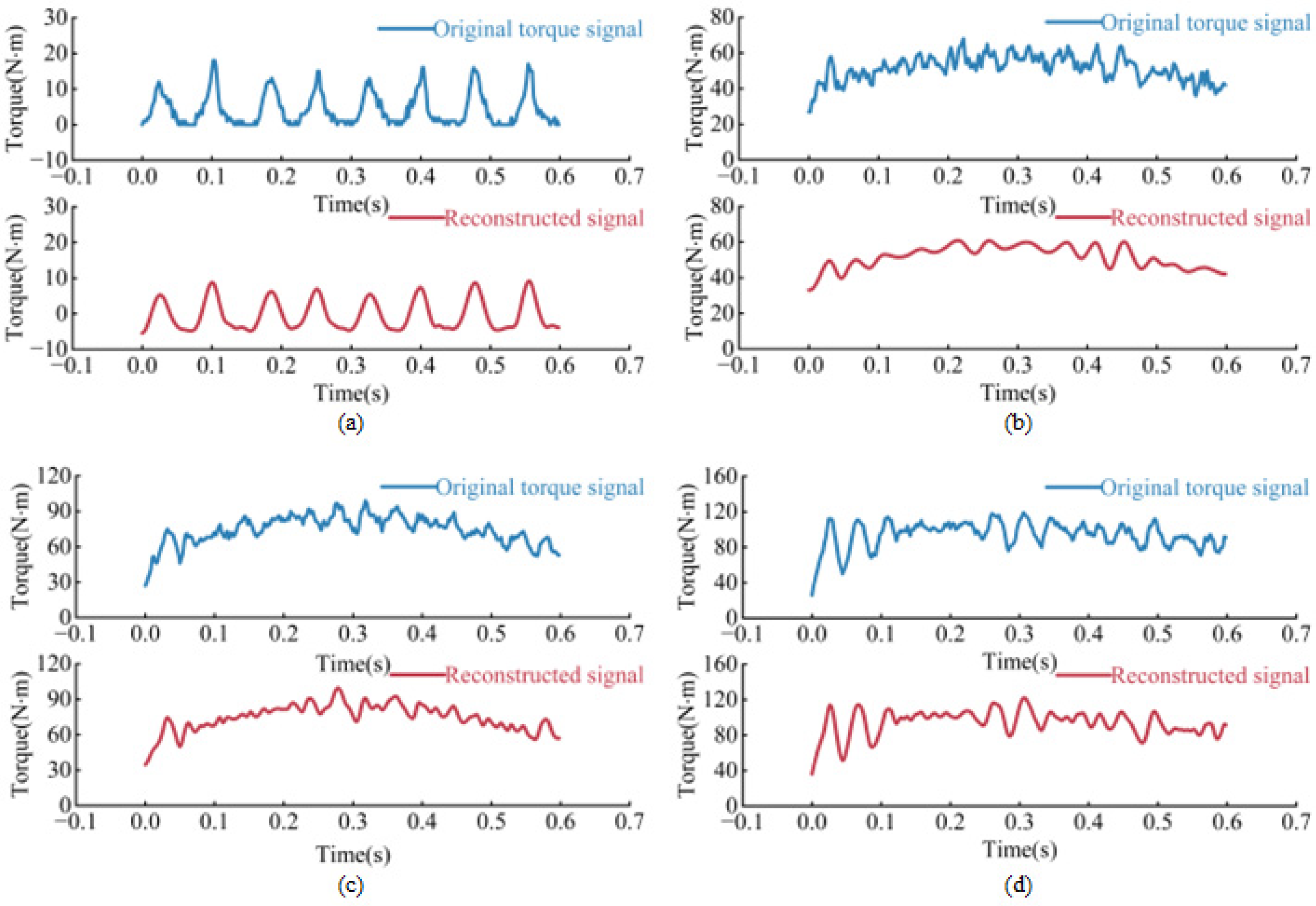
As shown in Figure 5, the original torque signals contain some noise. To better extract the related load features from the torque signals, it is necessary to remove the noise contained in the original signals. The specific steps for this operation are as follows:
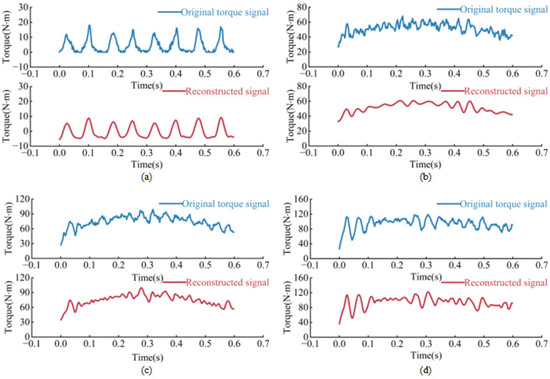
Figure 5.
Comparison between the original signal and the signal waveforms after CEEMDAN decomposition and reconstruction under four load conditions. (a) No load; (b) low load; (c) normal load; (d) high load.
- Use the CEEMDAN method and decompose the original signals under each load condition to obtain five IMFs.
- Calculate the correlation coefficients and variance contributions of the IMFs and the original signals using Equation (17) and Equation (19), respectively.
- Select the IMFs with correlation coefficients greater than 0.4 and variance contributions rates greater than 0.1 for signal reconstruction.
These criteria ensure that the selected IMFs are sufficiently correlated with the original signal and contribute significantly to the overall variance, thereby improving the accuracy and reliability of the signal reconstruction. A correlation coefficient greater than 0.4 indicates a significant linear relationship between the IMFs and the original signal, ensuring that the extracted modal functions effectively reflect the main characteristics of the signal. A variance contribution rate greater than 0.1 indicates that the IMFs account for a significant proportion of the total energy, preventing the retention of low-energy noise components. The application of these criteria can effectively filter out irrelevant noise components. According to the calculation, the correlation coefficients for IMF3 and IMF4 were 0.5576 and 0.6183, respectively, with variance contributions of 0.4902 and 0.5647. Other components did not satisfy the requirements. Therefore, IMF3 and IMF4 were selected for signal reconstruction under no load condition. Under low load conditions, the correlation coefficients for IMF2 and IMF5 were 0.7451 and 0.5720, with variance contributions rates of 0.5416 and 0.2886, respectively. Other components did not meet the requirements, so IMF2 and IMF5 were selected for reconstruction. Under normal load conditions, the correlation coefficients for IMF2 and IMF5 were 0.6244 and 0.7041, with variance contribution rates of 0.3858 and 0.4472, respectively. Other components did not meet the requirements, so IMF2 and IMF5 were selected for reconstruction. Under high load conditions, the correlation coefficients for IMF2 and IMF5 were 0.7858 and 0.5934, with variance contribution rates of 0.6012 and 0.2672. Other components did not meet the requirements, so IMF2 and IMF5 were selected for reconstruction. The comparison between the original signals and the reconstructed signals is shown in Figure 5. As shown in the Figure 5, in all four cases, the noise in the reconstructed signal is significantly removed compared to the original signal. This indicates that the signal processing method used is very effective and successfully separates the meaningful components of the signal from the noise. The clarity of the signal after CEEMDAN decomposition and reconstruction is significantly improved and the extraneous fluctuations are reduced for all four load conditions, indicating that the method was effectively applied to denoise the original drum torque signal.
In order to quantify the denoising effect of the CEEMDAN algorithm, we calculated the signal-to-noise ratio (SNR) for both the original and the reconstructed signals. Table 4 shows the results of these calculations. The SNR of the reconstructed signal is 9.8 dB, 12.62 dB, 9.19 dB, and 5.24 dB higher than that of the original signal, indicating that the noise was significantly reduced by the CEEMDAN algorithm.

Table 4.
SNR of original signal and SNR of reconstructed signal.
3.2. Analysis of Signal Feature of Different Load Conditions
Eleven time domain features were extracted from the ETDRH drum spindle torque signals across four load conditions, as detailed in Table 5. Notably, features such as mean, standard deviation, variance, peak value, and RMS showed a pronounced upward trend, from no load to high load, with significant fluctuations. Conversely, the peak factor and skewness showed a gradual decrease, with relatively small fluctuations. The kurtosis showed a pattern of an initial increase, followed by a decrease and then a further increase, from no load to high load. In contrast, the waveform factor showed the opposite trend, initially decreasing, then increasing and finally decreasing again, from no load to high load. These three indicators shared the characteristic of relatively stable variations. The shape factor gradually decreased from no load to high load, maintaining a smooth variation. The impulse factor showed minimal differences under low, normal, and high load conditions, but was significantly higher under no load compared to the other conditions.

Table 5.
Time domain features for four load conditions.
Ten frequency domain features were extracted from the ETDRH drum spindle torque signals under the same four load conditions, following fast Flourier transform and power spectral density function processing, as listed in Table 6. All these features, including the mean, RMS, standard deviation, variance, and peak value of the spectrum and power spectral density, showed a consistent upward trend. The mean and RMS of the signal spectrum increased moderately, while the standard deviation, variance, and peak value increased rapidly. Similarly, the mean, RMS, and standard deviation of the power spectral density increased more slowly, while the variance and peak value increased rapidly.

Table 6.
Frequency domain features for four load conditions.
Eight time–frequency domain features were extracted from the ETDPH drum spindle torque signals under four load conditions by decomposing the signals into three levels using DB1 wavelet packet decomposition and calculating the energy values of each node, as shown in Table 7. These eight time–frequency domain features consistently show the pattern no load < low load < normal load < high load.

Table 7.
Time–frequency features for four load conditions.
3.3. Dimensionality Reduction Analysis
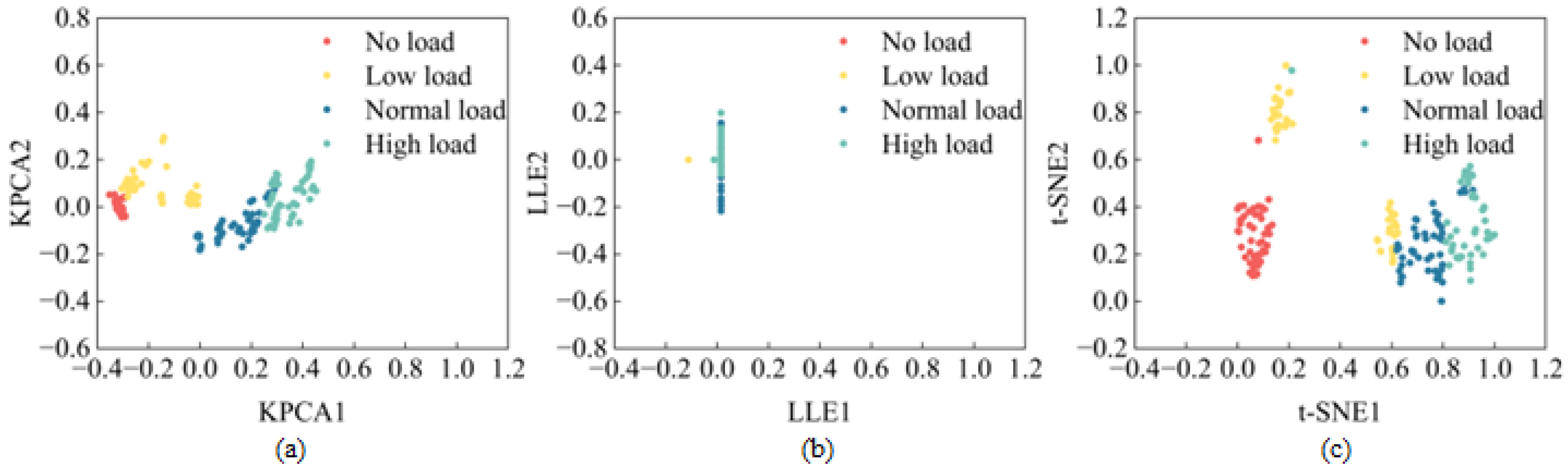
Dimension reduction is a crucial preliminary step in model training, especially when dealing with high-dimensional datasets. This process simplifies the complexity of the data, minimizes noise and redundancy, and mitigates the curse of dimensionality, thereby increasing the efficiency of the algorithm. The goal of dimension reduction is to preserve the similarities and disparities of the original data, ensuring that intra-class distances are minimal and inter-class distances are substantial. Nonlinear dimension reduction methods such as KPCA, Locally Linear Embedding (LLE), and t-Distributed Stochastic Neighbor Embedding (t-SNE) are often used in different contexts to meet different requirements. KPCA extends the applicability of traditional PCA by incorporating kernel techniques, enabling nonlinear dimension reduction and revealing the structure of nonlinear data. LLE reveals the intrinsic geometric structure by preserving the local neighborhood relationships between data points. t-SNE excels in visualizing high-dimensional data sets by optimizing similarity in both low- and high-dimensional spaces.
In this study, the three methods mentioned above were applied to reduce the dimensionality of a feature dataset. The results shown in Figure 6 and the corresponding reduction times shown in Table 8 illustrate different categorizations: red for no load, yellow for low load, blue for normal load, and green for high load. The two-dimensional KPCA plot shows minimal distances between samples, within the no load, normal load, and high load groups, with no overlap or mixing of samples between categories. Although the low load category shows slightly greater distances, it remains distinct from the other categories. This method not only effectively reduces dimensions, but also requires minimal time. Conversely, the two-dimensional LLE plot fails to separate different categories, resulting in significant sample mixing and a suboptimal reduction effect, accompanied by a longer processing time. The t-SNE algorithm shows small intra-class distances for no load, normal load, and high load, but larger distances for low load, along with some sample mixing between these categories. This method gives a suboptimal reduction effect and takes a significantly longer time than the others.
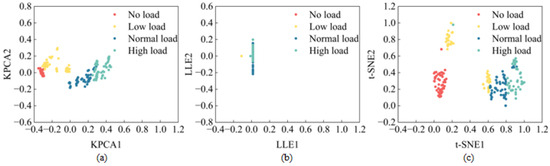
Figure 6.
Dimension reduction effect of KPCA, LLE, and t-SNE. (a) KPCA; (b) LLE; (c) t-SNE.

Table 8.
Time required for different dimensionality reduction algorithms.
Based on these findings, KPCA was selected as the preferred dimension reduction algorithm. The use of KPCA to reduce the dimensionality of the dataset laid the foundation for the subsequent recognition of the ETDPH drum load conditions.
3.4. Load State Recognition Model Construction and Accuracy Comparison Based on Three Algorithms
3.4.1. Load Recognition Model Based on SVM Algorithm
The SVM is a robust machine learning technique that uses one or more hyperplanes in a high-dimensional space to categorize data, improving classification accuracy and generalization by maximizing the margin between different classes of data points. In the present research, the Radial Basis Function (RBF) kernel was adopted. In the RBF kernel, the “penalty parameter c” and “gamma” are crucial parameters that affect the performance of the model. This study used a total of 200 datasets for training and validation of the SVM model, with 160 datasets (40 from each of the four conditions: no load, low load, normal load, and high load) for training and 40 datasets (10 from each condition) for testing. The datasets were labelled as follows: no load was labelled as 0, low load was labelled as 1, normal load was labelled as 2, and high load was labelled as 3. Using automatic optimization for model training, it was found that the highest accuracy, reaching 100% for both training and test sets, was achieved when c = 61.5848 and gamma = 0.4833.
3.4.2. Load Recognition Model Based on RF Algorithm
RF is an ensemble learning method that improves model accuracy and robustness by constructing multiple decision trees and aggregating their predictions. For this study, a total of 200 datasets were used, divided into training and test sets. Specifically, 40 datasets from each of the four conditions (no load, low load, normal load, and high load) were used as the training set, making a total of 160 training datasets. Similarly, 10 datasets from each condition were used as the test set, making a total of 40 test datasets. The number of decision trees (n_estimators) and the minimum number of samples per leaf node (min_samples_leaf) are two important parameters for the RF algorithm. The maximum number of decision trees was set to 101, and the maximum value for the minimum number of samples per leaf node was set to 21. Thus, 160 datasets were used to train the model, and 40 datasets were used to test the classification performance. The conditions—no load, low load, normal load, and high load—were labelled as 0, 1, 2, and 3, respectively. The optimal performance of the RF model was achieved with n_estimators set at 90 and min_samples_leaf at 1, resulting in a training set accuracy of 100% and a test set accuracy of 97%.
3.4.3. Load Recognition Model Based on GBM Algorithm
GBM is a powerful ensemble learning technique that improves the predictive power of models by sequentially building decision trees, where each tree attempts to correct the errors of the previous one. The number of decision trees (n_estimators) and the learning rate are critical parameters that affect model accuracy. In this study, these two parameters were continuously adjusted during the training process. To train and test the model, a total of 200 samples were used, divided into training and test sets. Specifically, 160 samples were used for training, with 40 samples each for the no load, low load, normal load, and high load conditions. For testing, 40 samples were used, with 10 samples each for the no load, low load, normal load, and high load conditions. The labels 0, 1, 2, and 3 correspond to the reduced dimensional samples. These parameters were used to train the GBM model. The optimal parameters were found to be n_estimators = 160 and learning_rate = 0.0734. With these settings, the accuracy of the training set was 100%, and the accuracy of the test set was 95%.
3.5. Comparison of Diagnostic Accuracy and Speed of SVM and Other Algorithms
The integration of signal processing with machine learning for the detection of the operating states of agricultural machinery components represents a sophisticated technical method. Using CEEMDAN for signal decomposition and reconstruction, together with KPCA for global feature dimensionality reduction, and training three different machine learning algorithms significantly improved both training and test set accuracies, as shown in Table 9 and Figure 7. When applied individually, CEEMDAN significantly improved training and test set accuracy for the SVM and RF, with a slight increase in test set accuracy for GBM, despite the lack of change in training set accuracy. In addition, CEEMDAN resulted in a marginal reduction in training time for RF and GBM. Independently, KPCA resulted in a slight increase in training set accuracy for the SVM and RF, although the test set accuracy remained unchanged for the SVM and decreased for RF. For GBM, KPCA caused a slight decrease in training set accuracy but an improvement in test set accuracy. When combined with KPCA, all three algorithms experienced significant reductions in training times and predication times. The test accuracies of CEEMDAN-KPCA-SVM and CEEMDAN-SVM were the same. This is because after CEEMDAN decomposition and reconstruction, the irrelevant components in the original signal were removed. The global features extracted from the reconstructed signal can adequately represent different load conditions, so that KPCA only serves to reduce the training time. Compared to single models, the combination of CEEMDAN and KPCA shows significant advantages in noise removal, feature extraction, and model performance improvement. The simultaneous application of both techniques not only effectively removes noise from the original signal, but also significantly improves the accuracy of training and testing sets and reduces the time required to train and predict.

Table 9.
Comparison of accuracy and training time of three different algorithmic models when combining CEEMDAN and KPCA.
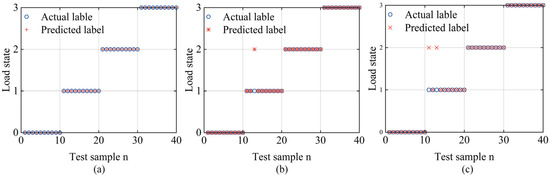
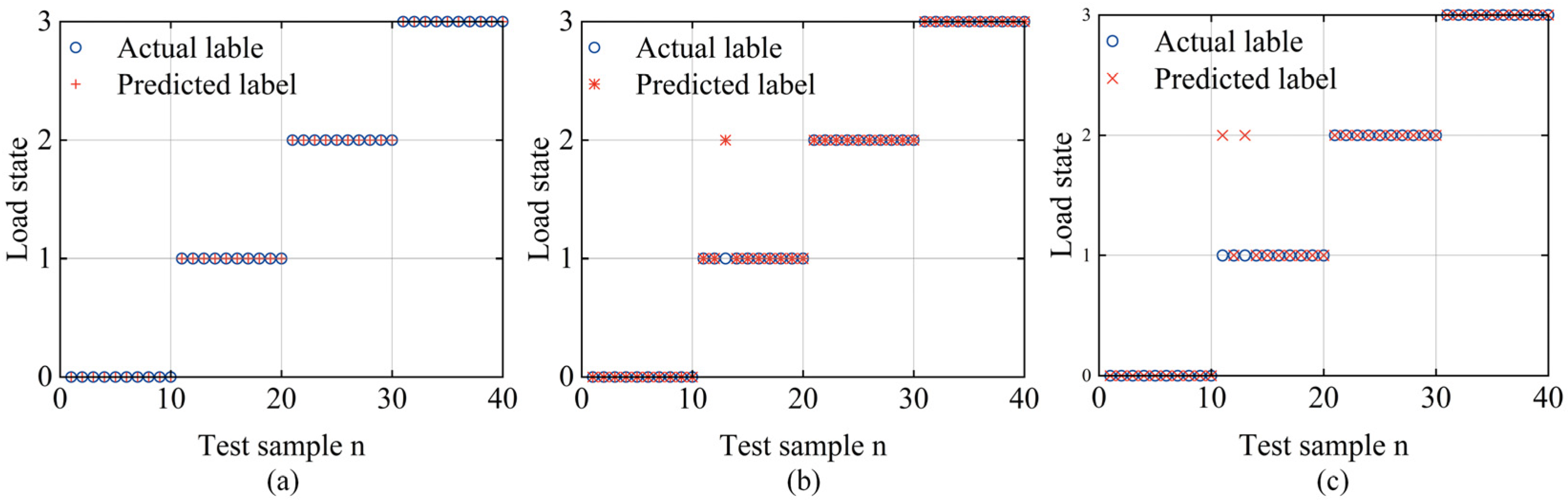
Figure 7.
Comparing the results of three models for recognizing load conditions. (a) CEEMDAN-KPCA-SVM; (b) CEEMDAN-KPCA-RF; (c) CEEMDAN-KPCA-GBM.
Further examination of the performance of the three algorithms shows that the CEEMDAN-KPCA-SVM combination has a significantly shorter training time and a predication time of 2.88 s compared to CEEMDAN-KPCA-GBM and CEEMDAN-KPCA-RF. In terms of test set accuracy, CEEMDAN-KPCA-SVM achieved a perfect 100%, surpassing the 97% of CEEMDAN-KPCA-RF and the 95% of CEEMDAN-KPCA-GBM. Given the complex operating environment of the ETDPH, where the drum load varies with pepper density and is sensitive to short-term conditions, a model that combines short training time and predication time with high classification accuracy is essential. Considering these factors, CEEMDAN-KPCA-SVM emerges as the superior choice in terms of both accuracy, training time, and prediction time, making it the optimal model for ETDPH drum load condition recognition.
4. Conclusions
In this study, drum load experiments were performed, and a novel method for drum load condition recognition method was proposed by integrating CEEMDAN, KPCA, and SVM. This method addresses the current reliance on manual identification of ETDPH drum load, improves model recognition accuracy, reduces computational burden, and lays the groundwork for the deployment of this method on actual ETDPH systems. This study included the identification of critical factors influencing drum load and the establishment of a framework for classifying load conditions. Torque signals from the drum spindle were acquired and processed using CEEMDAN to decompose and reconstruct the signals, effectively eliminating noise. Load-sensitive features were extracted to create a dataset, which was then reduced in dimensionality and utilized for model training. After evaluating the effectiveness of various models, the CEEMDAN-KPCA-SVM model emerged as the optimal choice for recognizing drum load. The research findings can be distilled into three principal points:
- Noise reduction through CEEMDAN combined with correlation coefficient and variance contribution rate methods: The original signal was subjected to noise reduction via CEEMDAN, complemented by the correlation coefficient and variance-contribution-rate methods. CEEMDAN decomposed the signal into multiple IMFs, and the correlation coefficients and variance contribution rates between each IMF and the original signal were computed across varying loads. The IMFs falling below the threshold were discarded, and the signal was reconstructed. This process effectively mitigated noise, enhancing the accuracy of subsequent model training. The accuracies of SVM, RF, and GBM on the test set improved by 12.5%, 9%, and 8%, respectively, after training with CEEMDAN-decomposed and reconstructed signals.
- Feature extraction and dimensionality reduction: Time domain, frequency domain, and time–frequency domain features were extracted from the signals, and dimensionality reduction was achieved using KPCA, LLE, and t-SNE. The global statistical features showed distinct patterns under different loading conditions, and the data retained its discriminability post-dimensionality reduction. KPCA outperformed LLE and t-SNE, yielding smaller inter-class distances and a swift dimensionality reduction time of 0.14 s. The training times and predication times for SVM, RF, and GBM were also accelerated after KPCA reduction, with training time decreases of 10.9%, 83.6%, and 57.6%, predication time decreases of 63.6%, 43.4%, and 33.3%, respectively.
- Development of a CEEMDAN-KPCA-SVM model for discerning the load conditions of ETDPH: A drum load experiment was executed to delineate load conditions based on the MOPI. It was found that an MOPI of 0 kg/s corresponds to no load, 0 to 0.658 kg/s to low load, 0.658 to 1.725 kg/s to normal load, and over 1.725 kg/s to high load. CEEMDAN was employed to filter noise from the original torque signals obtained under these four load conditions. Time domain, frequency domain, and time–frequency domain statistical features were extracted from the reconstructed signals. KPCA was then utilized to reduce the feature set’s dimensionality, and the SVM was applied to train the drum load condition recognition model. The comparative analysis of the three models before and after implementing CEEMDAN and KPCA revealed that the CEEMDAN-KPCA-SVM method was superior, boasting the briefest training time of 2.88 s and a predication time of 0.0001 s, while attaining 100% accuracy for both the training and test sets.
The ETDPH drum loading experiments and signal data collection were primarily conducted in controlled laboratory conditions, allowing precise control of variables and accurate measurements. However, real-world conditions present additional challenges, such as variable environments, machine wear, and crop density. To address this, we have designed an ETDPH drum load test rig that simulates real-world conditions, taking into account noise effects and computational costs. By integrating signal processing, dimensionality reduction, and machine learning, we aimed to improve the real-world applicability of the method.
Our algorithm performed well on test bench torque signal data, but has not been tested on field ETDPH data, which challenges model generalization. We plan to collect diverse field data to develop a more robust algorithm that integrates multi-source data, considering real-time processing and low latency for effective use on real ETDPHs. These improvements aim to improve the performance and efficiency of ETDPHs in practical applications.
Author Contributions
Conceptualization, X.Z. and J.L.; methodology, X.Z. and J.L.; software, X.Z. and J.Z.; validation, X.Z., J.L. and Z.Z.; formal analysis, X.Z.; investigation, X.Z., Z.W. and J.L.; resources, X.Z. and X.Q.; data curation, X.Z. and Z.W.; writing—original draft preparation, X.Z., J.L. and Z.Z.; writing—review and editing, X.Z., J.L. and X.Q.; visualization, X.Z. and J.L.; supervision, X.Z., J.L. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (grant nos. 62163032 and 62063030), the Financial Science and Technology Program of the XPCC (grant nos. 2022CB011 and 2022CB002-07) and National Key Research and Development Program of China (No. 2022YFD2002003-2).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, X.; Cao, Y.; Fang, W.; Sheng, H. Vibration Test and Analysis of Crawler Pepper Harvester under Multiple Working Conditions. Sustainability 2023, 15, 8112. [Google Scholar] [CrossRef]
- Jin, L.; Xinyan, Q.; Chen, Y. Design and Analysis on Key Components of a Novel Chili Pepper Harvester’s Picking Device. Open Mech. Eng. J. 2015, 9, 540–545. [Google Scholar] [CrossRef]
- Gomez-Gil, F.J.; Martínez-Martínez, V.; Ruiz-Gonzalez, R.; Martínez-Martínez, L.; Gomez-Gil, J. Vibration-Based Monitoring of Agro-Industrial Machinery Using a k-Nearest Neighbors (kNN) Classifier with a Harmony Search (HS) Frequency Selector Algorithm. Comput. Electron. Agric. 2024, 217, 108556. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, X.; Zhang, J.; Wang, L.; Wang, D.; Zhang, P. Fault Diagnosis of Silage Harvester Based on a Modified Random Forest. Inf. Process. Agric. 2023, 10, 301–311. [Google Scholar] [CrossRef]
- Ren, L.; Qi, Y.Q.; Zhai, X.J.; Jin, Y.; Wang, G.Q. Combine Harvester Threshing Drum Load Control System. Ind. Control Comput. 2016, 29, 153–154+156. [Google Scholar]
- Zhang, J.; Wang, Y.; Huang, M.; Wang, S.H. Experiment and Simulation of Cole Seed Filling Angle Based on ADAMS. J. Chin. Agric. Mech. 2015, 05, 46–49. [Google Scholar]
- Liu, H.; He, P.; Jiang, M.; Yuan, Y.; Kang, J.; Zhao, J.; Zhu, K. The Study on Constant Speed Control of Dual Threshing Drums in Small Pre-Harvest Threshing Machines. J. Agric. Mech. Res. 2016, 38, 210–213+223. [Google Scholar]
- Lu, W.; Zhang, D.; Deng, Z. Constant Load PID-Control of Threshing Cylinderin Combine. Trans. Chin. Soc. Agric. Mach. 2008, 39, 49–51+55. [Google Scholar]
- You, Y.; Li, W. Fuzzy Constant Load Control of Threshing Drum in Combine Harvester. J. Chin. Agric. Mech. 2015, 36, 33–35+49. [Google Scholar]
- Ma, Z.; Jiang, S.; Li, Y.; Xu, L.; Zhu, Y.; Shi, M.; Nfamoussa Traore, S. Recognition Methods of Threshing Load Conditions Based on Machine Learning Algorithms. Comput. Electron. Agric. 2022, 200, 107250. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, X.; Wen, G.; Lei, Z.; Dong, S.; Zhang, P.; Chen, X. Construction of Health Indicators for Condition Monitoring of Rotating Machinery: A Review of the Research. Expert Syst. Appl. 2022, 203, 117297. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine Learning Methods for Wind Turbine Condition Monitoring: A Review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Yang, Y.; Li, S.; Li, C.; He, H.; Zhang, Q. Research on Ultrasonic Signal Processing Algorithm Based on CEEMDAN Joint Wavelet Packet Thresholding. Measurement 2022, 201, 111751. [Google Scholar] [CrossRef]
- Aharamuthu, K.; Ayyasamy, E.P. Application of Discrete Wavelet Transform and Zhao-Atlas-Marks Transforms in Non Stationary Gear Fault Diagnosis. J. Mech. Sci. Technol. 2013, 27, 641–647. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, F.; Zhang, C.; Zhang, L.; Li, P. Evaluation of Rolling Bearing Performance Degradation Using Wavelet Packet Energy Entropy and RBF Neural Network. Symmetry 2019, 11, 1064. [Google Scholar] [CrossRef]
- Zhou, Z.; Zejun, W.; Yingyong, B. Application Study of Wavelet Analysis on Ultrasonic Echo Wave Noise Reduction. Chin. J. Sci. Instrum. 2009, 30, 237–241. [Google Scholar]
- Chen, Y.; Li, S. Application of Improved Threshold Denoising Based on Wavelet Transform to Ultrasonic Signal Processing. J. Beijing Univ. Aeronaut. Astronaut. 2006, 32, 466–470. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shi, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing. Biomed. Signal Process. 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Hu, Y.; Ouyang, Y.; Wang, Z.; Yu, H.; Liu, L. Vibration Signal Denoising Method Based on CEEMDAN and Its Application in Brake Disc Unbalance Detection. Mech. Syst. Signal Process. 2023, 187, 109972. [Google Scholar] [CrossRef]
- Karijadi, I.; Chou, S.-Y.; Dewabharata, A. Wind Power Forecasting Based on Hybrid CEEMDAN-EWT Deep Learning Method. Renew. Energy. 2023, 218, 119357. [Google Scholar] [CrossRef]
- Yang, L.; Cai, J. A Method to Identify Wet Ball Mill’s Load Based on CEEMDAN, RCMDE and SRNN Classification. Miner. Eng. 2021, 165, 106852. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, M.; Ouyang, T.; Che, F. A Wind Turbine Bearing Fault Diagnosis Method Based on Fused Depth Features in Time–Frequency Domain. Energy Rep. 2022, 8, 12727–12739. [Google Scholar] [CrossRef]
- Guo, X.; Wang, K.; Yao, S.; Fu, G.; Ning, Y. RUL Prediction of Lithium Ion Battery Based on CEEMDAN-CNN BiLSTM Model. Energy Rep. 2023, 9, 1299–1306. [Google Scholar] [CrossRef]
- Guo, L.; He, H.; Ren, Y.; Li, R.; Jiang, B.; Gong, J. Prognostics of Lithium-Ion Batteries Health State Based on Adaptive Mode Decomposition and Long Short-Term Memory Neural Network. Eng. Appl. Artif. Intell. 2024, 127, 107317. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, D.; Wang, K.; Wang, L.; Fan, J. A Quality Diagnosis Method of GMAW Based on Improved Empirical Mode Decomposition and Extreme Learning Machine. J. Manuf. Process. 2020, 54, 120–128. [Google Scholar] [CrossRef]
- DG/T 114-2019; Agricultural Machinery Extension Appraisal Syllabus. Ministry of Agriculture and Rural Affairs of the People’s Republic of China: Beijing, China, 2019.
- Software for Data Analysis and Graphing, version 2022; OriginLab Corporation: Northampton, MA, USA, 2022.
- Chen, W.; Li, J.; Wang, Q.; Han, K. Fault Feature Extraction and Diagnosis of Rolling Bearings Based on Wavelet Thresholding Denoising with CEEMDAN Energy Entropy and PSO-LSSVM. Measurement 2021, 172, 108901. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Ping, W.; Jian, W.; Cheng, J. A Bearing Fault Diagnosis Scheme with Statistical-Enhanced Covariance Matrix and Riemannian Maximum Margin Flexible Convex Hull Classifier. ISA Trans. 2021, 111, 323–336. [Google Scholar] [CrossRef]
- Dhamande, L.S.; Chaudhari, M.B. Compound Gear-Bearing Fault Feature Extraction Using Statistical Features Based on Time-Frequency Method. Measurement 2018, 125, 63–77. [Google Scholar] [CrossRef]
- Liu, X.; Xie, J.; Luo, Y.; Yang, D. A Novel Power Transformer Fault Diagnosis Method Based on Data Augmentation for KPCA and Deep Residual Network. Energy Rep. 2023, 9, 620–627. [Google Scholar] [CrossRef]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and Empirical Comparison of Dimensionality Reduction Algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Yang, J.; Cheng, F.; Liu, Z.; Duodu, M.M.; Zhang, M. A Novel Semi-Supervised Fault Detection and Isolation Method for Battery System of Electric Vehicles. Appl. Energy 2023, 349, 121650. [Google Scholar] [CrossRef]
- Kok, Z.H.; Mohamed Shariff, A.R.; Alfatni, M.S.M.; Khairunniza-Bejo, S. Support Vector Machine in Precision Agriculture: A Review. Comput. Electron. Agric. 2021, 191, 106546. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).