Modelling Soil Moisture Content with Hydrus 2D in a Continental Climate for Effective Maize Irrigation Planning
Abstract
1. Introduction
2. Materials and Methods
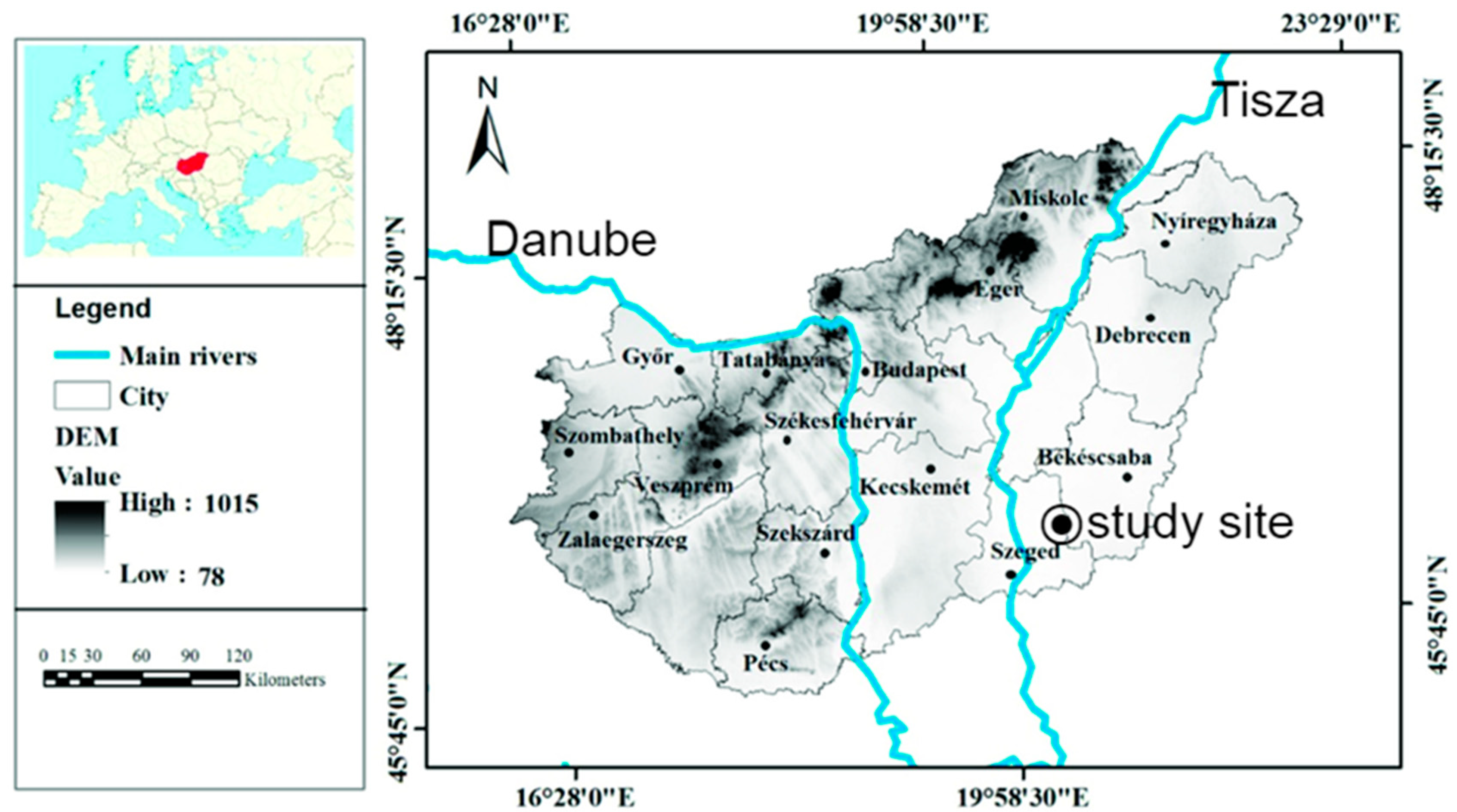
2.1. Description of the Study Area
2.2. Soil Data
2.3. Crop Data
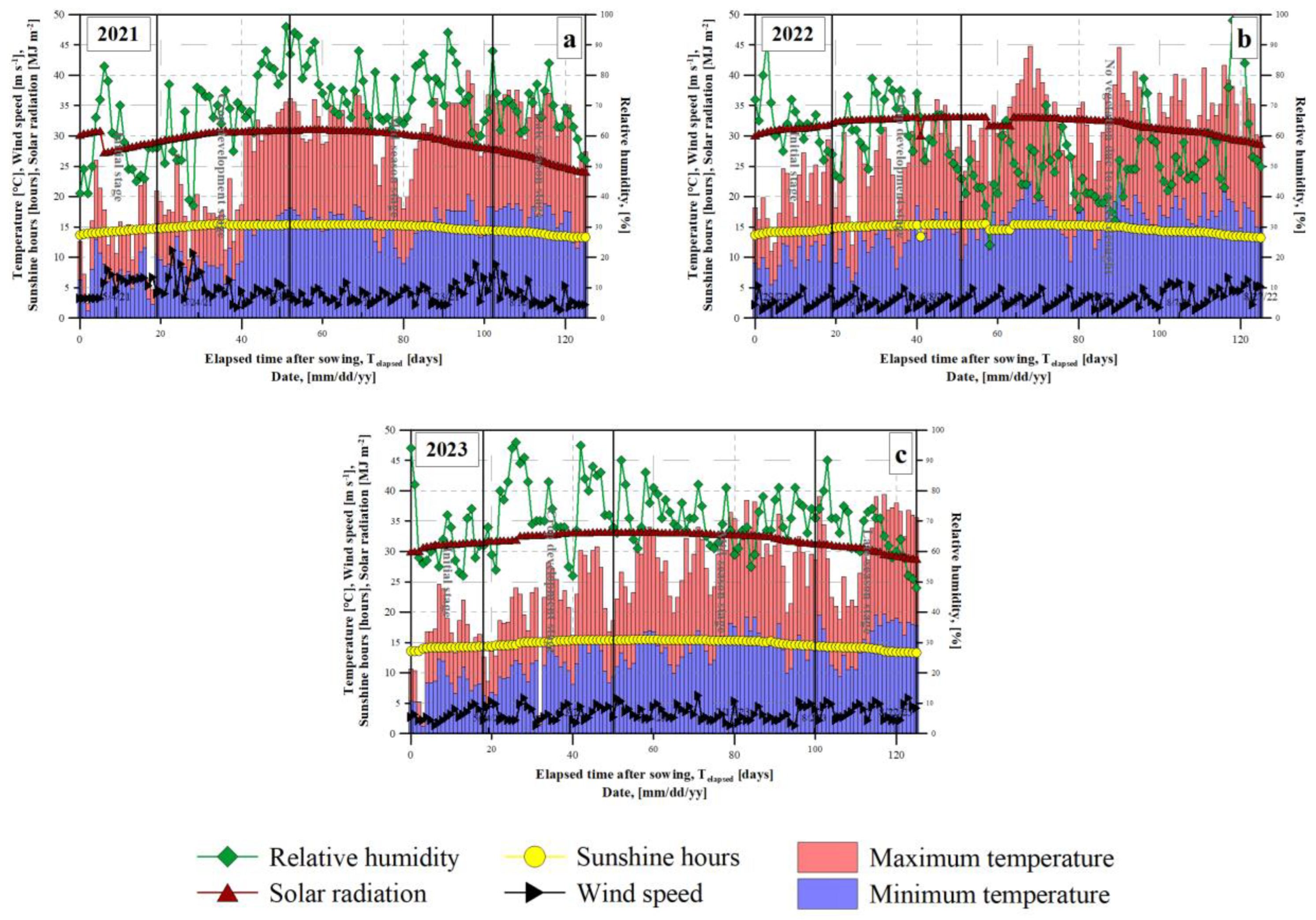
2.4. Meteorological Data
- ET0—reference evapotranspiration [mm day−1],
- Rn—net radiation at the crop surface [MJ m−2 day−1],
- G—soil heat flux density [MJ m−2 day−1],
- T—mean daily air temperature at 2 m height [°C],
- U2—wind speed at 2 m height [m s−1],
- es—saturation vapor pressure [kPa],
- ea—actual vapor pressure [kPa],
- es–ea—saturation vapor pressure deficit [kPa],
- D—slope vapor pressure curve [kPa °C−1],
- g—psychrometric constant [kPa °C−1].
2.5. HYDRUS Modeling Environment
2.5.1. Description of the Model
- θ is the volumetric water content of the soil (fraction of soil volume occupied by water) [-]
- t is time [s],
- K is the hydraulic conductivity of the soil [mm s−1],
- S represents sources/sinks of water in the soil term due to the water uptake of plants, rainfall, or geochemical reaction [s−1],
- Kij(h) is the anisotropic hydrological conductivity tensor [m s−1],
- xi is the Cartesian coordinate [m].
2.5.2. Model Parameters
2.5.3. Boundaries and Domain Discretization
2.5.4. Developing the Model
- θ(h) is the volumetric water content at soil suction pressure h [L3L−3],
- θr is the residual volumetric water content [L3L−3]
- θs is the saturated volumetric water content, [L3L−3],
- α is a fitting parameter related to the inverse of the air entry suction, α > 0, [L−1] /cm−3
- n is a dimensionless empirical fitting parameter, n > 1 [-]
| Soil Physical Properties / Depth | Measured Hydraulic Conductivity, k [m·s−1] | Measured Bulk Density, ρB [g·cm−3] | Measured Porosity, θP [V/V%] | Field Capacity, θFC [V/V%] | USDA Soil Classification Based on the PSD Analysis | ||
|---|---|---|---|---|---|---|---|
| Sand, [m/m%] | Silt, [m/m%] | Clay, [m/m%] | |||||
| Average of 0–60 cm | 0.4272 | 1.3 | 47.38 | 32.2 | 37 | 29 | 34 |
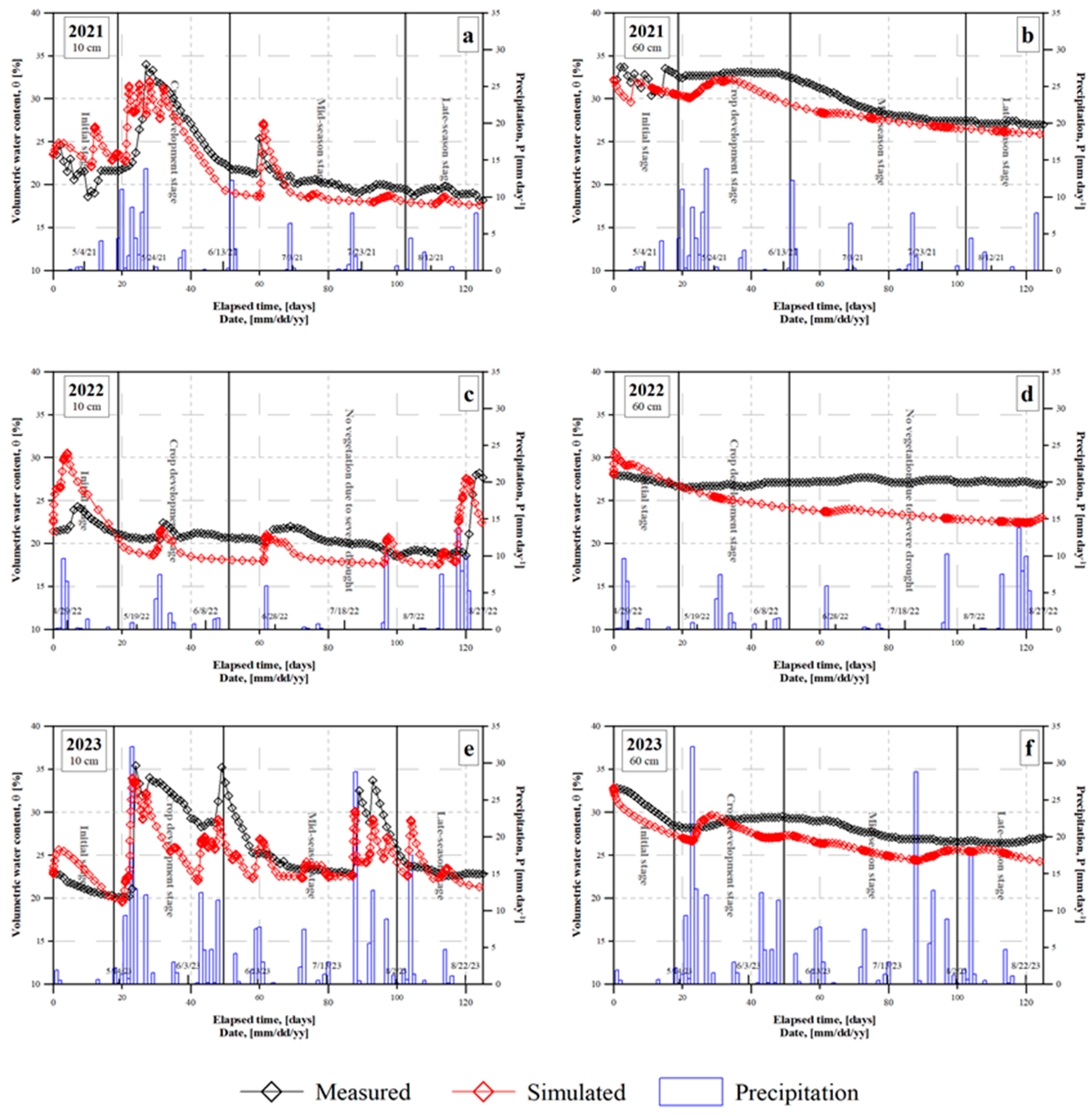
2.5.5. Validation of the HYDRUS 2D Model
3. Results
3.1. Meteriological Conditions
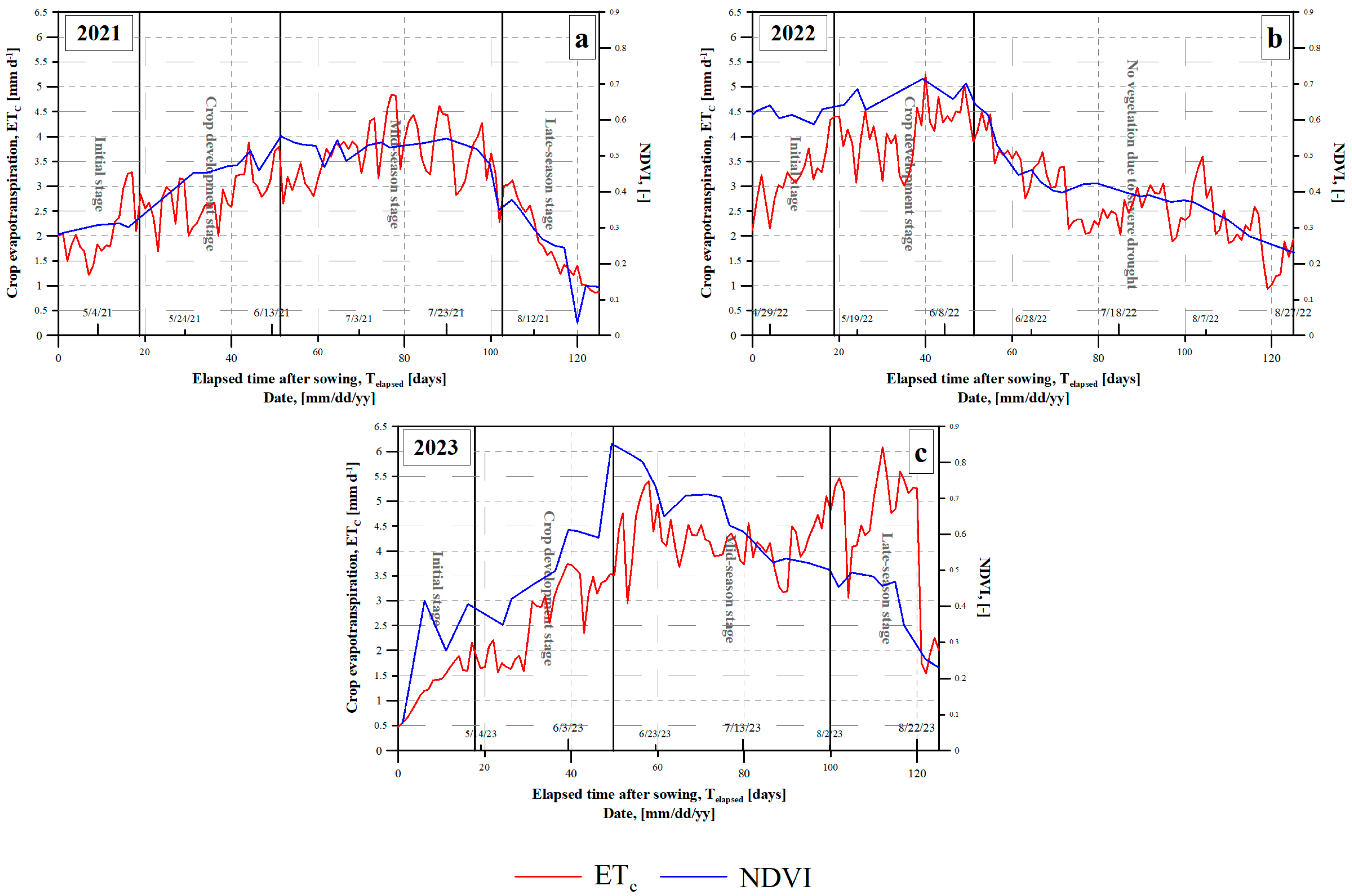
3.2. Maize Biomass and Crop Evapotranspiration (ETc)
3.3. HYDRUS 2D Model Performance
3.4. Water Productivity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Steensland, A. 2021 Global Agricultural Productivity Report: Climate for Agricultural Growth; Virginia Tech College of Agriculture and Life Sciences: Blacksburg, VA, USA, 2021. [Google Scholar]
- Ponnampalam, E.N.; Bekhit, A.E.D.; Bruce, H.; Scollan, N.D.; Muchenje, V.; Silva, P.; Jacobs, J.L. Production strategies and processing systems of meat: Current status and future outlook for innovation—A global perspective. In Sustainable Meat Production and Processing; Academic Press: Cambridge, MA, USA, 2019; pp. 17–44. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. How unusual is the 2022 European compound drought and heatwave event? Geophys. Res. Lett. 2023, 50, e2023GL105453. [Google Scholar] [CrossRef]
- Toreti, A.; Bavera, D.; Acosta Navarro, J.; Cammalleri, C.; de Jager, A.; Di Ciollo, C.; Hrast Essenfelder, A.; Maetens, W.; Magni, D.; Masante, D.; et al. Drought in Europe August 2022; Publications Office of the European Union: Luxembourg, 2022; JRC130493. [Google Scholar] [CrossRef]
- Fu, Z.; Ciais, P.; Feldman, A.F.; Gentine, P.; Makowski, D.; Prentice, I.C.; Stoy, P.C.; Bastos, A.; Wigneron, J.P. Critical soil moisture thresholds of plant water stress in terrestrial ecosystems. Sci. Adv. 2022, 8, 7827. [Google Scholar] [CrossRef] [PubMed]
- Yillia, P.T. Water-Energy-Food nexus: Framing the opportunities, challenges and synergies for implementing the SDGs. Osterr. Wasser-Und Abfallwirtsch. 2016, 68, 86–98. [Google Scholar] [CrossRef]
- Hertel, T.W. The challenges of sustainably feeding a growing planet. Food Secur. 2015, 7, 185–198. [Google Scholar] [CrossRef]
- McKenzie, F.C.; Williams, J. Sustainable food production: Constraints, challenges and choices by 2050. Food Secur. 2015, 7, 221–233. [Google Scholar] [CrossRef]
- Tamás, J. Precision Agriculture (Precíziós Mezőgazdaság); Szaktudás Kiadó Ház ZRt.: Budapest, Hungary, 2001. (In Hungarian) [Google Scholar]
- Cai, X.; McKinney, D.C.; Rosegrant, M.W. Sustainability analysis for irrigation water management in the Aral Sea region. Agric. Syst. 2003, 76, 1043–1066. [Google Scholar] [CrossRef]
- Szépszó, G.; Horányi, A. Transient simulation of the REMO regional climate model and its evaluation over Hungary. Időjárás 2008, 112, 203–231. [Google Scholar]
- Bakucs, Z.; Fertő, I.; Vígh, E. Crop Productivity and Climatic Conditions: Evidence from Hungary. Agriculture 2020, 10, 421. [Google Scholar] [CrossRef]
- European Commission. The EU Environmental Implementation Review 2019 Country Report: Hungary; European Commission: Brussels, Belgium, 2019; Available online: https://ec.europa.eu/environment/eir/pdf/report_hu_en.pdf (accessed on 12 November 2023).
- FAO (Food and Agriculture Organisation of the United Nations). FAO Aquastat; FAO: Rome, Italy, 2020; Available online: http://www.fao.org/aquastat/en/ (accessed on 11 October 2023).
- Haacker, E.M.; Sharda, V.; Cano, A.M.; Hrozencik, R.A.; Núñez, A.; Zambreski, Z.; Nozari, S.; Smith, G.E.B.; Moore, L.; Sharma, S.; et al. Transition pathways to sustainable agricultural water management: A review of integrated modeling approaches. JAWRA J. Am. Water Resour. Assoc. 2019, 55, 6–23. [Google Scholar] [CrossRef]
- Levidow, L.; Zaccaria, D.; Maia, R.; Vivas, E.; Todorovic, M.; Scardigno, A. Improving water-efficient irrigation: Prospects and difficulties of innovative practices. Agric. Water Manag. 2014, 146, 84–94. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Srivastava, A.; Kushwaha, N.L.; Juhász, C.; Tamás, J.; Nagy, A. Meteorological Data Fusion Approach for Modeling Crop Water Productivity Based on Ensemble Machine Learning. Water 2023, 15, 30. [Google Scholar] [CrossRef]
- Datta, S.; Taghvaeian, S.; Stivers, J. Understanding Soil Water Content and Thresholds for Irrigation Management; Oklahoma Cooperative Extension Service; Oklahoma State University: Stillwater, OK, USA, 2017. [Google Scholar]
- Barker, J.B.; Franz, T.E.; Heeren, D.M.; Neale, C.M.; Luck, J.D. Soil water content monitoring for irrigation management: A geostatistical analysis. Agric. Water Manag. 2017, 188, 36–49. [Google Scholar] [CrossRef]
- Lascano, R.J. Irrigation of Agricultural Crops, 2nd ed.; American Society of Agronomy: Madison, WI, USA, 2007. [Google Scholar]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Smart irrigation monitoring and control strategies for improving water use efficiency in precision agriculture: A review. Agric. Water Manag. 2022, 260, 107324. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Griffiths, H.M.; Dorigo, W.; Xaver, A.; Gruber, A. Surface soil moisture estimation: Significance, controls, and conventional measurement techniques. In Remote Sensing of Energy Fluxes and Soil Moisture Content; Petropoulos, G.P., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 29–48. [Google Scholar]
- Dwevedi, A.; Kumar, P.; Kumar, P.; Kumar, Y.; Sharma, Y.K.; Kayastha, A.M. Soil sensors: Detailed insight into research updates, significance, and future prospects. In New Pesticides and Soil Sensors; Academic Press: Cambridge, MA, USA, 2017; pp. 561–594. [Google Scholar] [CrossRef]
- Fernández, J.E. Plant-based methods for irrigation scheduling of woody crops. Horticulturae 2017, 3, 35. [Google Scholar] [CrossRef]
- Jones, H.G. Irrigation scheduling: Advantages and pitfalls of plant-based methods. J. Exp. Bot. 2004, 55, 2427–2436. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Imran Khan, M.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil moisture measuring techniques and factors affecting the moisture dynamics: A comprehensive review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigation scheduling focusing on the FAO56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of evapotranspiration and soil moisture content across different scales of observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [PubMed]
- Massman, W.; Lee, X. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges. Agric. For. Meteorol. 2002, 113, 121–144. [Google Scholar] [CrossRef]
- Gebler, S.; Hendricks Franssen, H.J.; Pütz, T.; Post, H.; Schmidt, M.; Vereecken, H. Actual evapotranspiration and precipitation measured by lysimeters: A comparison with eddy covariance and tipping bucket. Hydrol. Earth Syst. Sci. 2015, 19, 2145–2161. [Google Scholar] [CrossRef]
- Rajan, N.; Maas, S.J. Spectral crop coefficient approach for estimating daily crop water use. Adv. Remote Sens. 2014, 3, 197. [Google Scholar] [CrossRef]
- Tegos, A.; Efstratiadis, A.; Koutsoyiannis, D. A parametric model for potential evapotranspiration estimation based on a simplified formulation of the Penman-Monteith equation. In Evapotranspiration—An Overview; Shahid, S., Ed.; IntechOpen: London, UK, 2013; pp. 143–165. [Google Scholar] [CrossRef]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Owusu-Sekyere, J.D.; Ampofo, E.A.; Asamoah, O. Comparison of five different methods in estimating reference evapotranspiration in Cape Coast, Ghana. Afr. J. Agric. Res. 2017, 12, 2976–2985. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Mhawej, M.; Nasrallah, A.; Abunnasr, Y.; Fadel, A.; Faour, G. Better irrigation management using the satellite-based adjusted single crop coefficient (aKc) for over sixty crop types in California, USA. Agric. Water Manag. 2021, 256, 107059. [Google Scholar] [CrossRef]
- Mebrie, D.W.; Assefa, T.T.; Yimam, A.Y.; Belay, S.A. A remote sensing approach to estimate variable crop coefficient and evapotranspiration for improved water productivity in the Ethiopian highlands. Appl. Water Sci. 2023, 13, 168. [Google Scholar] [CrossRef]
- Yimer, N.M. Assessment of Performance of SWAP and CROPWAT Model simulating Irrigation Water Requirement on Sugarcane Yield of Kuraz Irrigation Project. Master’s Thesis, Kuraz University, Addis Ababa, Ethiopia, 2022. [Google Scholar]
- Kumar, S.; Meena, R.S.; Sheoran, S.; Jangir, C.K.; Jhariya, M.K.; Banerjee, A.; Raj, A. Remote sensing for agriculture and resource management. In Natural Resources Conservation and Advances for Sustainability; Academic Press: Cambridge, MA, USA, 2022; pp. 91–135. [Google Scholar] [CrossRef]
- Ahmad, U.; Alvino, A.; Marino, S. A review of crop water stress assessment using remote sensing. Remote Sens. 2021, 13, 4155. [Google Scholar] [CrossRef]
- Nagy, A.; Riczu, P.; Gálya, B.; Tamás, J. Spectral estimation of soil water content in visible and near infra-red range. Eurasian J. Soil Sci. 2014, 3, 163–171. [Google Scholar] [CrossRef][Green Version]
- Melton, F.S.; Johnson, L.F.; Lund, C.P.; Pierce, L.L.; Michaelis, A.R.; Hiatt, S.H.; Guzman, A.; Adhikari, D.D.; Purdy, A.J.; Rosevelt, C.; et al. Satellite irrigation management support with the terrestrial observation and prediction system: A framework for integration of satellite and surface observations to support improvements in agricultural water resource management. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1709–1721. [Google Scholar] [CrossRef]
- Tamás, J.; Lénárt, C. Analysis of a small agricultural watershed using remote sensing techniques. Int. J. Remote Sens. 2006, 27, 3727–3738. [Google Scholar] [CrossRef]
- Burgerné Gimes, A. Előadásaim [My presentations]; Agroinform: Budapest, Hungary, 2014. (In Hungarian) [Google Scholar]
- Mezősi, G.; Bata, T.; Meyer, B.C.; Blanka, V.; Ladányi, Z. Climate change impacts on environmental hazards on the Great Hungarian Plain, Carpathian Basin. Int. J. Disaster Risk Sci. 2014, 5, 136–146. [Google Scholar] [CrossRef][Green Version]
- Lennert, J.; Kovács, K.; Koós, B.; Swain, N.; Bálint, C.; Hamza, E.; Király, G.; Rácz, K.; Váradi, M.M.; Kovács, A.D. Climate Change, Pressures, and Adaptation Capacities of Farmers: Empirical Evidence from Hungary. Horticulturae 2024, 10, 56. [Google Scholar] [CrossRef]
- Szedlák, L. Fekete év a Magyar Mezőgazdaságban: Tényleg Lehúzhatják a Rolót Ezek a Termelők? 2022. Available online: https://www.agrarszektor.hu/noveny/20221228/fekete-ev-a-magyar-mezogazdasagban-tenyleg-lehuzhatjak-a-rolot-ezek-a-termelok-41820 (accessed on 1 November 2023).
- Széles, A.; Horváth, É.; Simon, K.; Zagyi, P.; Huzsvai, L. Maize production under drought stress: Nutrient supply, yield prediction. Plants 2023, 12, 3301. [Google Scholar] [CrossRef] [PubMed]
- Szolnoky, T.; Nagy, A. WaterAgri D 1.2 Stakeholder Training Material; 2023. Available online: https://wateragri.eu/wp-content/uploads/2023/09/D1.2.pdf (accessed on 2 January 2024).
- IUSS Working Group WRB. World Reference Base for Soil Resources 2006. A Framework for International Classification Correlation and Communication. World Soil Resources Reports 2006, 103. FAO: Rome. Electronic update. 2007. Available online: http://www.fao.org/ag/agl/agll/wrb/ (accessed on 24 March 2022).
- Gee, G.W.; Bauder, J.W. Particle size analysis by hydrometer: A simplified method for routine textural analysis and a sensitivity test of measurement parameters. Soil Sci. Soc. Am. J. 1979, 43, 1004–1007. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis: Part 3 Chemical Methods; Sparks, D.L., Ed.; SSSA Book Series No. 5; ASA and SSSA: Madison, WI, USA, 1996; pp. 961–1010. [Google Scholar] [CrossRef]
- Thomas, G.W. Soil pH and soil acidity. In Methods of Soil Analysis: Part 3 Chemical Methods; Sparks, D.L., Ed.; SSSA Book Series No. 5; ASA and SSSA: Madison, WI, USA, 1996; pp. 475–490. [Google Scholar] [CrossRef]
- ASTM D4373; Standard Test Method for Rapid Determination of Carbonate Content of Soils. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D2937; Standard Test Method for Density of Soil in Place by the Drive-Cylinder Method. ASTM International: West Conshohocken, PA, USA, 2009.
- Reynolds, S.G. The gravimetric method of soil moisture determination Part III An examination of factors influencing soil moisture variability. J. Hydrol. 1970, 11, 288–300. [Google Scholar] [CrossRef]
- Nagy, J. Maize Production; Akadémiai Kiadó: Budapest, Hungary, 2006. [Google Scholar]
- Štěpánek, P.; Trnka, M.; Chuchma, F.; Zahradníček, P.; Skalák, P.; Farda, A.; Fiala, R.; Hlavinka, P.; Balek, J.; Semerádová, D.; et al. Drought prediction system for Central Europe and its validation. Geosciences 2018, 8, 104. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Meier, U. Growth Stages of Mono and Dicotyledonous Plants; BBCH Monograph; Federal Biological Research Centre for Agriculture and Forestry: Bonn, Germany, 2001; Available online: https://www.politicheagricole.it/flex/AppData/WebLive/Agrometeo/MIEPFY800/BBCHengl2001.pdf (accessed on 22 November 2023).
- Ramachandran, J.; Lalitha, R.; Kannan, S.V. Estimation of site-specific crop coefficients for major crops of lal-gudi block in tamil nadu using remote sensing based algorithms. J. Agric. Eng. 2021, 58, 62–72. [Google Scholar] [CrossRef]
- Li, X.; Zhu, W.; Xie, Z.; Zhan, P.; Huang, X.; Sun, L.; Duan, Z. Assessing the effects of time interpolation of NDVI composites on phenology trend estimation. Remote Sens. 2021, 13, 5018. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- Magyar, T.; Fehér, Z.; Buday-Bódi, E.; Tamás, J.; Nagy, A. Modelling of soil moisture and water fluxes in a maize field for the optimization of irrigation. Comput. Electron. Agric. 2023, 213, 108159. [Google Scholar] [CrossRef]
- Šimunek, J.; Šejna, M.; Saito, H.; Sakai, M.; Van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Version 4.17; Department of Environmental Sciences University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Han, M.; Zhao, C.; Feng, G.; Yan, Y.; Sheng, Y. Evaluating the effects of mulch and irrigation amount on soil water distribution and root zone water balance using HYDRUS-2D. Water 2015, 7, 2622–2640. [Google Scholar] [CrossRef]
- Jones, C.D. Assessing Efficiencies in Vegetable Production: Hydrological Modeling of Soil-Water Dynamics and Estimation of Greenhouse Gas Emissions; University of Florida: Gainesville, FL, USA, 2013. [Google Scholar]
- van Dam, J.; van der Zee, S.E.A.T.M.; Vogel, H.J.; Vrugt, J.A.; Wöhling, T.; Young, I.M. Modeling Soil Processes: Review, Key Challenges, and New Perspectives. Soil Sci. 2016, 15, vzj2015-09. [Google Scholar]
- VIZUGY. 2024. Available online: https://www.vizugy.hu/?mapModule=OpFkGrafikon&AllomasVOA=E0A4A0FC-A9AD-11D4-BB66-00508BA24287&mapData=KutIdosor#mapModule (accessed on 14 March 2024).
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Wesseling, J.G. Meerjarige simulaties van grondwateronttrekking voor verschillende bodemprofielen, grondwatertrappen en gewassen met het model SWATRE. SC-DLO Rep. 1991, 152, 40. [Google Scholar]
- Assouline, S. The Effects of Microdrip and Conventional Drip Irrigation on Water Distribution and Uptake. Soil Sci. Soc. Am. J. 2002, 66, 1630–1636. [Google Scholar] [CrossRef]
- Feddes, R.A. Simulation of Field Water Use and Crop Yield. In Penning de Vries, F.W.T.; van Laar, H.H., Ed.; Simulation of Plant Growth and Crop Production; Pudoc: Wageningen, The Netherlands, 1982; pp. 194–209. Available online: https://edepot.wur.nl/172222 (accessed on 1 June 2024).
- Yu, J.; Wu, Y.; Xu, L.; Peng, J.; Chen, G.; Shen, X.; Lan, R.; Zhao, C.; Zhangzhong, L. Evaluating the Hydrus-1D Model Optimized by Remote Sensing Data for Soil Moisture Simulations in the Maize Root Zone. Remote Sens. 2022, 14, 6079. [Google Scholar] [CrossRef]
- Seo, H.S.; Šimunek, J.; Poeter, E.P. Documentation of the Hydrus Package for Modflow-2000, the US Geological Survey Modular Ground-water Model; IGWMC-International Ground Water Modeling Center: Princeton, NJ, USA, 2007; p. 96. [Google Scholar]
- Wang, X.; Li, Y.; Chau, H.W.; Tang, D.; Chen, J.; Bayad, M. Reduced root water uptake of summer maize grown in water-repellent soils simulated by HYDRUS-1D. Soil Tillage Res. 2021, 209, 104925. [Google Scholar] [CrossRef]
- Wang, Z.L.; Feng, H.; Wen, G.G. Effects of different water and nutrient schedules on farmland moisture and seed maize yield. J. Drain. Irrig. Mach. Eng. 2015, 33, 152–157. [Google Scholar]
- Wei, Z.; Yu, G.; Wang, Q.; Liu, Y. Separating transpiration and evaporation by stable isotopes in a maize field. Agric. For. Meteorol. 2014, 195–196, 108–117. [Google Scholar]
- Crow, W.T.; Van den Berg, M.J. An improved approach for estimating observation and model error parameters in soil moisture data assimilation. Water Resour. Res. 2010, 46, W12519. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- Hungarian Meteorological Service. 2024. Available online: https://odp.met.hu/climate/station_data_series/ (accessed on 15 January 2024).
- Singh, R. Water Productivity Analysis from Field to Regional Scale; Wageningen University: Wageningen, The Netherlands, 2005. [Google Scholar]
- Hopmans, J.W.; Bristow, K.L. Current capabilities and future needs of root water and nutrient uptake modeling. Adv. Agron. 2002, 77, 103–183. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Allen, R.G.; Droogers, P.; D’Urso, G.; Steduto, P. Twenty-five years modeling irrigated and drained soils: State of the art. Agric. Water Manag. 2007, 92, 111–125. [Google Scholar] [CrossRef]
- Kirda, C. Deficit irrigation scheduling based on plant growth stages showing water stress tolerance. In Deficit Irrigation Practices; Water Reports; Food and Agricultural Organization of the United Nations: Rome, Italy, 2002; Volume 22, pp. 3–10. [Google Scholar]
- Allen, L.N.; MacAdam, J.W. Irrigation and water management. In Forages: The Science of Grassland Agriculture; Wiley: Hoboken, NJ, USA, 2020; Volume 2, pp. 497–513. [Google Scholar] [CrossRef]
- Arbat, G.; Puig-Bargués, J.; Duran-Ros, M.; Barragán, J.; de Cartagena, F.R. Drip-Irriwater: Computer software to simulate soil wetting patterns under surface drip irrigation. Comput. Electron. Agric. 2013, 98, 183–192. [Google Scholar] [CrossRef]
- Nikam, B.R.; Garg, V.; Thakur, P.K.; Aggarwal, S.P. Application of remote sensing and GIS in performance evaluation of irrigation project at disaggregated level. J. Indian Soc. Remote Sens. 2020, 48, 979–997. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Li, J.; Lei, Y.; Li, C.; Manevski, K.; Shen, Y. Using NDVI percentiles to monitor real-time crop growth. Comput. Electron. Agric. 2019, 162, 357–363. [Google Scholar] [CrossRef]
- Hari, M.; Tyagi, B.; Huddar, M.S.K.; Harish, A. Satellite-based regional-scale evapotranspiration estimation mapping of the rice bowl of Tamil Nadu: A little water to spare. Irrig. Drain. 2021, 70, 958–975. [Google Scholar] [CrossRef]
- Nagy, A.; Kiss, N.É.; Buday-Bódi, E.; Magyar, T.; Cavazza, F.; Gentile, S.L.; Abdullah, H.; Tamás, J.; Fehér, Z.Z. Precision Estimation of Crop Coefficient for Maize Cultivation Using High-Resolution Satellite Imagery to Enhance Evapotranspiration Assessment in Agriculture. Plants 2024, 13, 1212. [Google Scholar] [CrossRef]
- Bausch, W.C. Soil background effects on reflectance-based crop coefficients for corn. Remote Sens. Environ. 1993, 46, 213–222. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef] [PubMed]
- Gobin, A.; Kersebaum, K.C.; Eitzinger, J.; Trnka, M.; Hlavinka, P.; Takáč, J.; Kroes, J.; Ventrella, D.; Marta, A.D.; Deelstra, J.; et al. Variability in the water footprint of arable crop production across European regions. Water 2017, 9, 93. [Google Scholar] [CrossRef]
- Aina, R.M.N.; Grósz, J.; Waltner, I. Estimation of Crop Evapotranspiration Using AquaCrop for the Rákos and Szilas Stream Watersheds, Hungary. In Proceedings of the 3rd International Conference on Water Sciences, Szarvas, Hungary, 7–9 January 2020. [Google Scholar]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Kamal, M.R.; Che Man, H.; Wayayok, A. HYDRUS-1D simulation of soil water dynamics for sweet corn under tropical rainfed condition. Appl. Sci. 2020, 10, 1219. [Google Scholar] [CrossRef]
- Ukoh Haka, I.B. Quantifying Evaporation and Transpiration in Field Lysimeters Using the Soil Water Balance. Ph.D. Thesis, University of the Free State, Bloemfontein, South Africa, 2010. [Google Scholar]
- Zsembeli, J.; Czellér, K.; Sinka, L.; Kovács, G.; Tuba, G. Application of Lysimeters in Agricultural Water Management. Creating a Platform to Address the Techniques Used in Creation and Protection of Environment and in Economic Management of Water in the Soil. 2019, pp. 5–21. Available online: https://raumberg-gumpenstein.at/jdownloads/Tagungen/Lysimetertagung/Lysimetertagung_2021/2l_2021_zsembeli.pdf. (accessed on 22 July 2023).
- Gebler, S.; Franssen, H.J.H.; Kollet, S.J.; Qu, W.; Vereecken, H. High resolution modelling of soil moisture patterns with TerrSysMP: A comparison with sensor network data. J. Hydrol. 2017, 547, 309–331. [Google Scholar] [CrossRef]
- Pinheiro, E.A.R.; van Lier, Q.D.J.; Inforsato, L.; Šimůnek, J. Measuring full-range soil hydraulic properties for the prediction of crop water availability using gamma-ray attenuation and inverse modeling. Agric. Water Manag. 2019, 216, 294–305. [Google Scholar] [CrossRef]
- Moore, C.; Doherty, J. Role of the calibration process in reducing model predictive error. Water Resour. Res. 2005, 41, W05020. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Varga, B.; Varga-László, E.; Bencze, S.; Balla, K.; Veisz, O. Water use of winter cereals under well-watered and drought-stressed conditions. Plant Soil Environ. 2013, 59, 150–155. [Google Scholar] [CrossRef]
- Biró, K.; Kovács, E. Impact of the 2022 Drought Shock on the Adaptive Capacity of Hungarian Agriculture. Preprints, 2023. [Google Scholar] [CrossRef]


| Parameter | Measured Mean Value |
|---|---|
| Sand content (%) | 44.00 |
| Silt content (%) | 34.00 |
| Clay content (%) | 22.00 |
| Salt (% m/m) | 0.06 |
| Soil pH (H2O) | 8.15 |
| Soil CaCO3 (% m/m) | 8.80 |
| Soil humus (% m/m) | 3.84 |
| Soil bulk density (g/cm3) | 1.30 |
| Soil temperature (°C) | 17.00 |
| Year | Stage | Period, T [Days] | Kc Range, [–] |
|---|---|---|---|
| 2021 | Initial | 25th of April 2021–14th of May 2021 | 0.32–0.43 |
| Crop development | 15th of May 2021–15th of June 2021 | 0.44–0.66 | |
| Mid-season | 16th of June 2021–2nd of August 2021 | 0.67–1.05 | |
| Late-season | 3rd of August 2021–27th of August 2021 | 0.52–0.16 | |
| 2022 | Initial | 25th of April 2022–13th of May 2022 | 0.63–0.72 |
| Crop development | 14th of May 2022–13th of June 2022 | 0.71–0.51 | |
| Mid-season (dry vegetation *) | |||
| Late-season (no vegetation *) | |||
| 2023 | Initial | 25th of April 2023–19th of May 2023 | 0.19–0.42 |
| Crop development | 20th of May 2023–13th of June 2023 | 0.43–0.84 | |
| Mid-season | 14th of June 2023–2nd of August 2023 | 1.08–0.51 | |
| Late-season | 3rd of August 2023–27th of August 2023 | 0.50–0.23 |
| Depth | 2021 | 2022 | 2023 |
|---|---|---|---|
| 10 cm | 23.5 | 21.4 | 22.8 |
| 60 cm | 32.2 | 28.0 | 32.8 |
| Parameter | Value | Description |
|---|---|---|
| P0 | −0.150 | Value of the pressure head [L] below which roots start to extract water from the soil (h1). |
| Popt | −0.300 | Value of the pressure head [L] below which roots extract water at the maximum possible rate (h2). |
| P2H | −3.250 | Value of the limiting pressure head [L] below which roots can no longer extract water at the maximum rate (assuming a potential transpiration rate of r2H) (h3hight). |
| P2L | −6.000 | As above, but for a potential transpiration rate of r2L (h3low). |
| P3 | −80.000 | Value of the pressure head [L] below which root water uptake ceases (usually taken at the wilting point) (h4). |
| r2H | 0.005 | Potential transpiration rate [LT−1] (currently set at 0.5 cm/day) (Tp). |
| r2L | 0.001 | Potential transpiration rate [LT−1] (currently set at 0.1 cm/day) (Tp). |
| Stage | Depth (R2) | NRMSE | MAE | MBE | RMSE | MSE |
|---|---|---|---|---|---|---|
| 2021 | ||||||
| Initial | 10 cm 0.03 60 cm 0.10 | 14.42 6.00 | 2.47 1.57 | 2.47 1.32 | 3.24 1.94 | 9.56 3.75 |
| Crop development | 10 cm 0.46 60 cm 0.14 | 12.36 6.30 | 2.90 1.88 | 1.08 1.88 | 3.31 2.07 | 10.97 4.29 |
| Mid-season | 10 cm 0.42 60 cm 0.93 | 9.41 5.78 | 1.74 1.41 | 1.37 1.42 | 1.93 1.68 | 3.74 2.83 |
| Late-season | 10 cm 0.48 60 cm 0.31 | 6.79 8.12 | 1.26 0.97 | 1.26 0.97 | 1.30 2.21 | 1.69 4.87 |
| Full vegetation period | 10 cm 0.65 60 cm 0.85 | 11.23 5.72 | 2.06 1.47 | 0.66 1.43 | 2.47 1.73 | 6.11 2.98 |
| 2022 | ||||||
| Initial | 10 cm 0.13 60 cm 0.81 | 17.71 0.95 | 2.86 0.79 | 2.78 0.79 | 3.96 0.95 | 1.57 0.90 |
| Crop development | 10 cm 0.21 60 cm 0.68 | 10.04 6.89 | 2.02 1.65 | 1.36 1.65 | 2.11 1.85 | 4.44 3.41 |
| Mid-season (dry vegetation *) | ||||||
| Late-season (no vegetation *) | ||||||
| Full vegetation period | 10 cm 0.51 60 cm 0.50 | 20.34 19.08 | 5.61 7.29 | 2.26 6.69 | 4.37 5.16 | 19.13 26.59 |
| Stage | Depth (R2) | NRMSE | MAE | MBE | RMSE | MSE |
| 2023 | ||||||
| Initial | 10 cm 0.48 60 cm 0.79 | 3.39 5.75 | 2.27 1.61 | 1.71 1.55 | 3.39 1.73 | 11.46 2.99 |
| Crop development | 10 cm 0.22 60 cm 0.83 | 17.22 5.58 | 4.92 1.42 | 4.92 1.00 | 5.39 1.62 | 29.10 2.63 |
| Mid-season | 10 cm 0.28 60 cm 0.78 | 12.36 7.998 | 2.36 2.18 | 1.77 2.18 | 12.36 2.23 | 10.28 4.96 |
| Late-season | 10 cm 0.22 60 cm 0.55 | 7.63 6.06 | 1.249 1.47 | 1.45 1.47 | 1.46 1.61 | 2.12 2.60 |
| Full vegetation period | 10 cm 0.38 60 cm 0.72 | 13.95 6.73 | 2.63 1.68 | 1.37 1.78 | 3.59 1.91 | 12.85 3.63 |
| Meteorological Parameter | Period | Quantity of the Parameter |
|---|---|---|
| Mean relative humidity (%) | June to August 2021 | 73.1 |
| Cummulative precipitation (mm) | 114.2 | |
| Mean relative humidity (%) | June to August 2022 | 54.3 |
| Cummulative precipitation (mm) | 88.5 | |
| Mean relative humidity (%) | June to August 2023 | 70.6 |
| Cummulative precipitation(mm) | 162.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siphiwe, N.G.; Magyar, T.; Tamás, J.; Nagy, A. Modelling Soil Moisture Content with Hydrus 2D in a Continental Climate for Effective Maize Irrigation Planning. Agriculture 2024, 14, 1340. https://doi.org/10.3390/agriculture14081340
Siphiwe NG, Magyar T, Tamás J, Nagy A. Modelling Soil Moisture Content with Hydrus 2D in a Continental Climate for Effective Maize Irrigation Planning. Agriculture. 2024; 14(8):1340. https://doi.org/10.3390/agriculture14081340
Chicago/Turabian StyleSiphiwe, Nxumalo Gift, Tamás Magyar, János Tamás, and Attila Nagy. 2024. "Modelling Soil Moisture Content with Hydrus 2D in a Continental Climate for Effective Maize Irrigation Planning" Agriculture 14, no. 8: 1340. https://doi.org/10.3390/agriculture14081340
APA StyleSiphiwe, N. G., Magyar, T., Tamás, J., & Nagy, A. (2024). Modelling Soil Moisture Content with Hydrus 2D in a Continental Climate for Effective Maize Irrigation Planning. Agriculture, 14(8), 1340. https://doi.org/10.3390/agriculture14081340







