Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter
Abstract
:1. Introduction
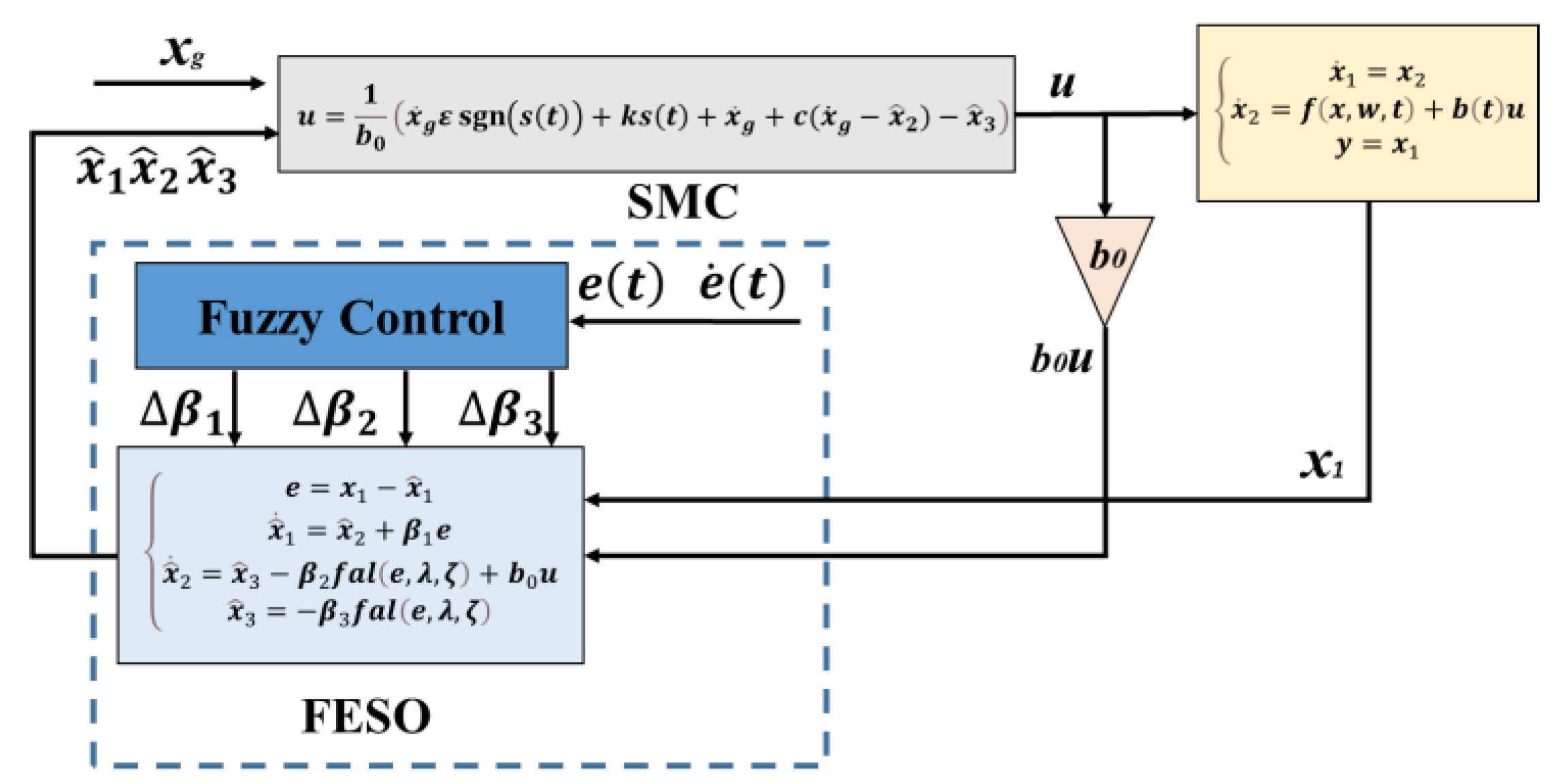
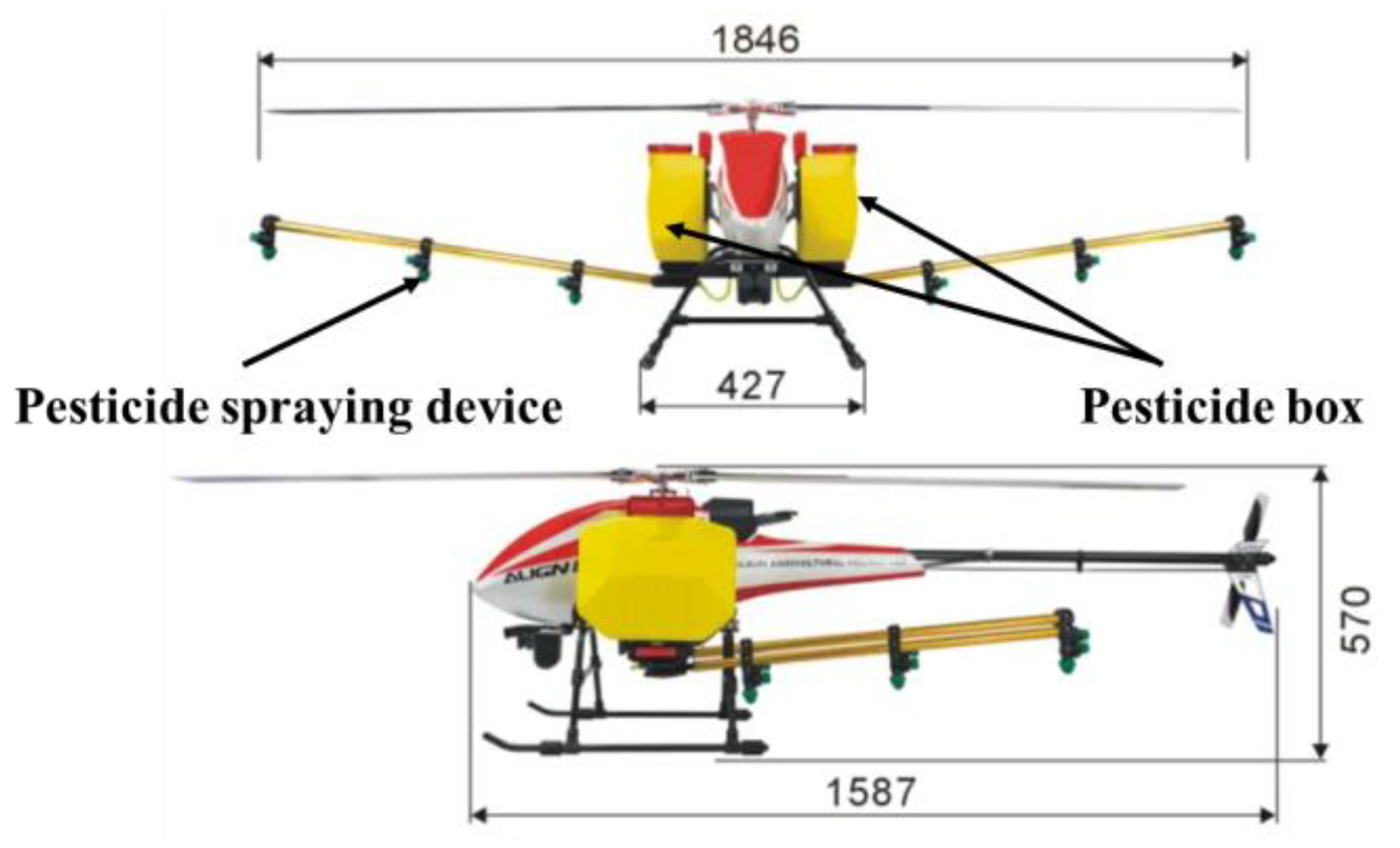
2. Materials and Methods
2.1. Second-Order Nonlinear Expansion System
2.2. Sliding Mode Function of Second-Order Nonlinear Extended System
2.3. Sliding Mode Control (SMC) Law
2.4. Fuzzy Extended State Observer (FESO)
2.4.1. Fuzzy Rules
2.4.2. Fuzzy Reasoning
2.4.3. Defuzzification
2.5. Stability Analysis
2.6. Design of the Trajectory Control System
3. Results and Discussion
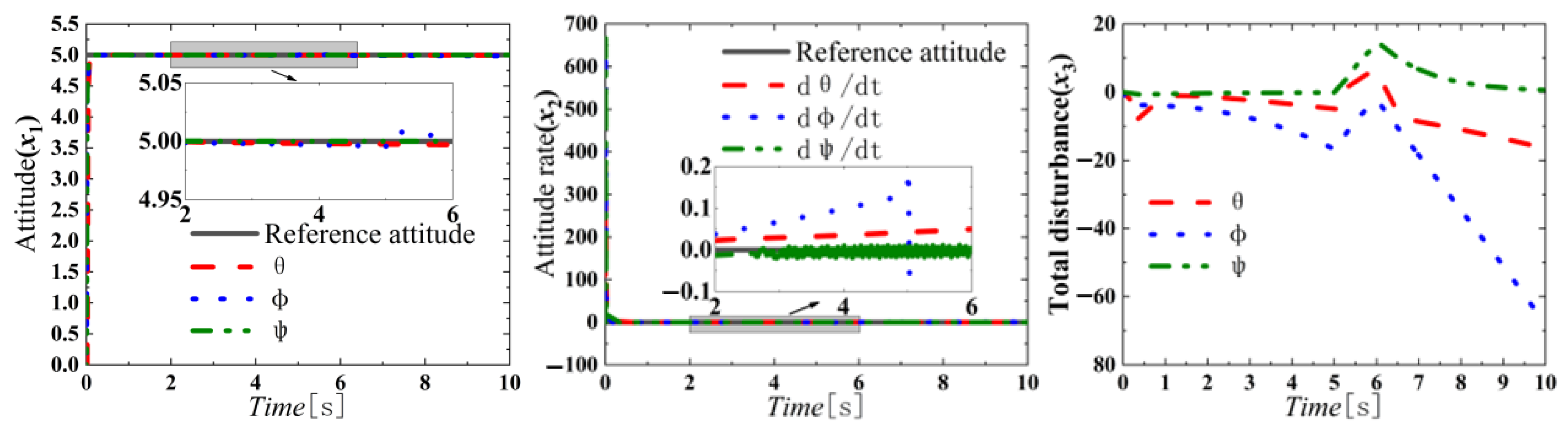
3.1. Simulation Results of Attitude Control
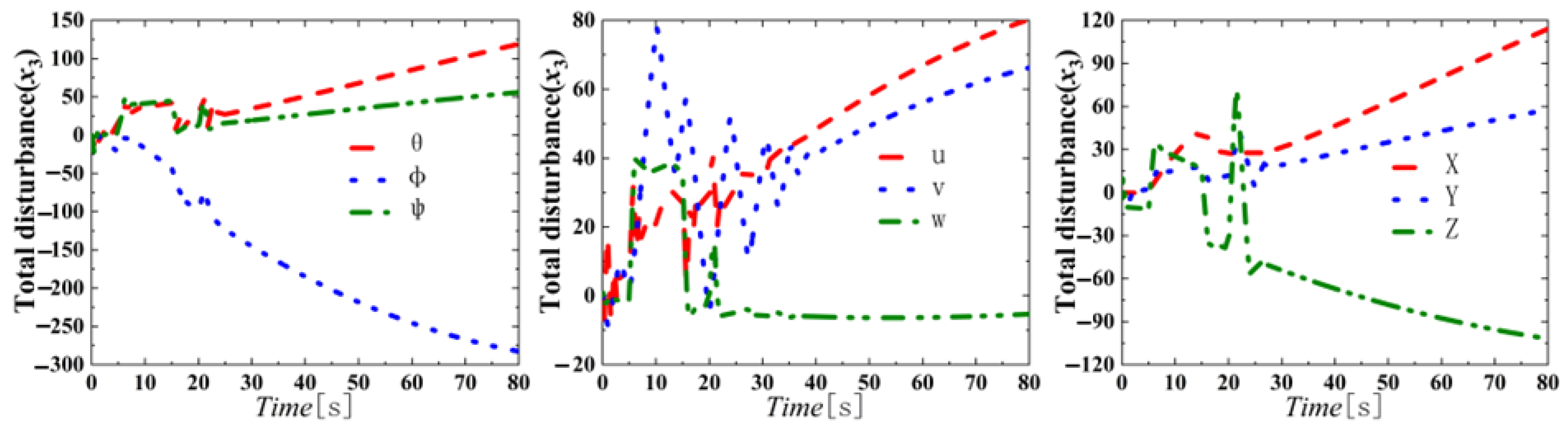
3.1.1. Anti-Disturbance Test
3.1.2. Robustness Test
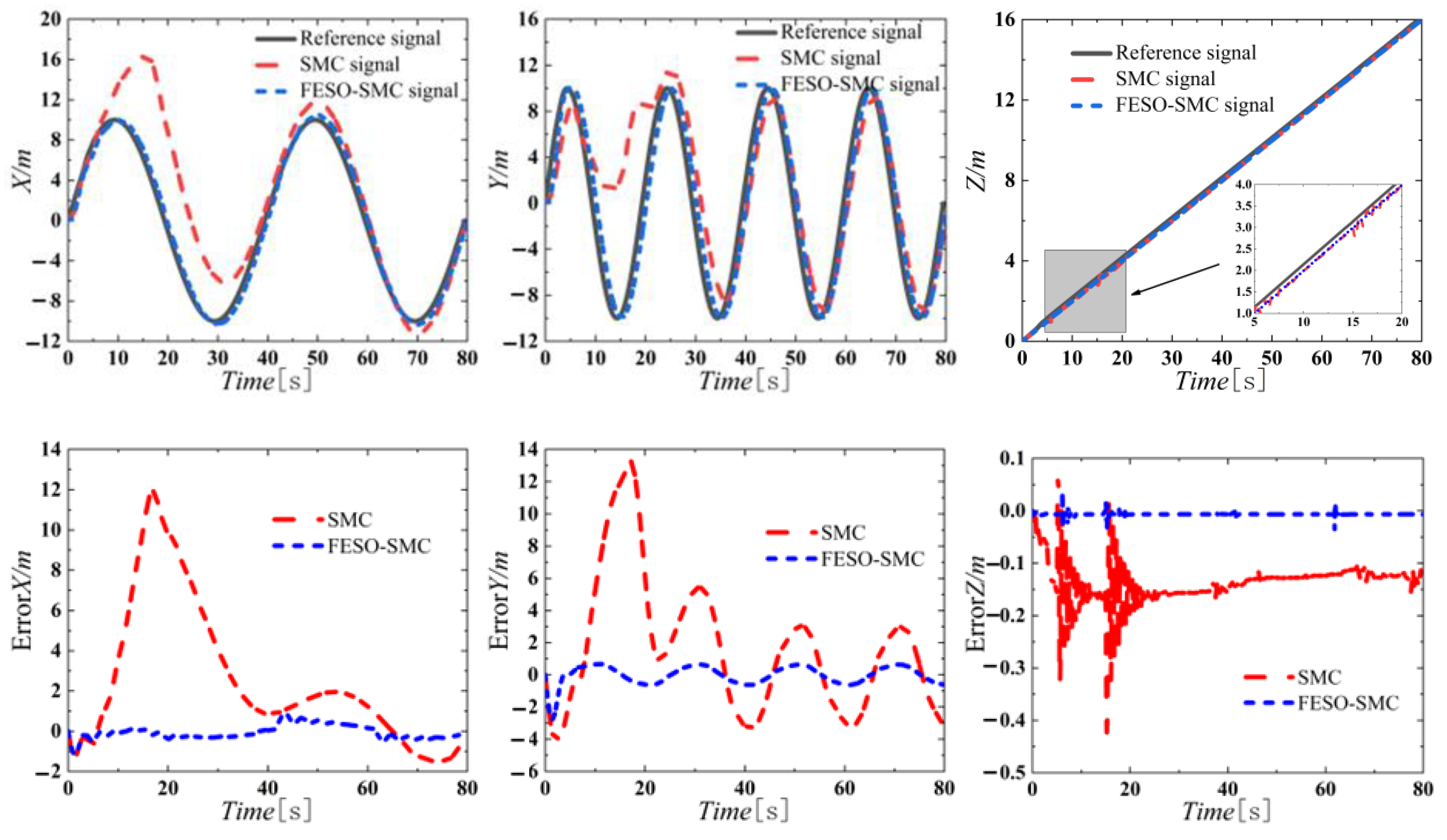
3.2. Simulation Results of Trajectory Control
4. Conclusions
- (1)
- The FESO exhibits robust adaptive capabilities, effectively managing significant disturbances. Upon a change in disturbance, the FESO rapidly estimates and compensates for this variation within a single second, ensuring prompt disturbance rejection;
- (2)
- The FESO-SMC controller proposed in this study maintains attitude stability and achieves high-precision trajectory tracking for agricultural unmanned helicopters. Notably, even under conditions of strong wind disturbances and structural perturbations, the FESO-SMC controller sustains high-precision tracking control. Specifically, the attitude control error of the FESO-SMC controller is merely one-fifth that of the traditional SMC controller, while its position control accuracy exceeds twice that of the SMC controller when subjected to disturbances. These findings highlight the superior anti-disturbance capabilities and enhanced robustness of the FESO-SMC controller compared to conventional SMC methods, underscoring its effectiveness in improving the operational reliability and precision of agricultural unmanned helicopters.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, D.; Simon, C.; Parmjit, C. Development and characterization of a contact-charging electrostatic spray UAV system. Agriculture 2024, 14, 467. [Google Scholar] [CrossRef]
- Fuentealba, A.; Dupont, A.; Hébert, C.; Berthiaume, R.; Quezada-García, R.; Bauce, É. Comparing the efficacy of various aerial spraying scenarios using Bacillus thuringiensis to protect trees from spruce budworm defoliation. For. Ecol. Manag. 2019, 432, 1013–1021. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Tian, T.; Yin, J. A review of unmanned aerial vehicle low-altitude remote sensing (UAV-LARS) use in agricultural monitoring in China. Remote Sens. 2021, 13, 1221. [Google Scholar] [CrossRef]
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the technological development and application of UAV systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Aleksandra, P.; Bogusława, B.; Jerzy, C. Propellers spin rate effect of a spraying drone on quality of liquid deposition in a crown of young spruce. Agriculture 2023, 13, 1584. [Google Scholar] [CrossRef]
- Martins, L.; Carlos, C.; Oliveira, P. Inner-outer feedback linearization for quadrotor control: Two-step design and validation. Nonlinear Dyn. 2022, 110, 479–495. [Google Scholar] [CrossRef]
- Zhang, X.; Xian, B.; Zhao, B. Autonomous flight control of a nano quadrotor helicopter in a GPS-denied environment using on-board vision. IEEE Trans. Ind. Electron. 2015, 62, 6392–6403. [Google Scholar] [CrossRef]
- Case, C.; Suresh, B.; Coates, A. Autonomous sign reading for semantic mapping. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Ghadiri, H.; Emam, M.; Khodadadi, H. Adaptive super-twisting non-singular terminal sliding mode control for tracking of quadrotor with bounded disturbances. Aerosp. Sci. Technol. 2021, 112, 106616. [Google Scholar] [CrossRef]
- Ifassiouen, H.; Guisser, M.; Medromi, H. Robust nonlinear control of a miniature autonomous helicopter using sliding mode control structure. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2007, 1, 84–89. [Google Scholar]
- Ramirez-Rodriguez, H.; Parra-Vega, V.; Sanchez-Orta, A. Robust backstepping control based on integral sliding modes for tracking of quadrotors. J. Intell. Robot. Syst. 2014, 73, 51–66. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst.-Eng. Appl. Math. 2012, 349, 685–699. [Google Scholar] [CrossRef]
- Liu, B.; Wang, P.; Sha, L. Attitude control for QTR using exponential nonsingular terminal sliding mode control. J. Syst. Eng. Electron. 2019, 30, 191–200. [Google Scholar]
- Liu, H.; Wang, H.; Shen, L. Attitude control for vertical take off and landing mode of QTR based on fractional order sliding mode control. Syst. Eng. Electron. 2017, 39, 156–161. [Google Scholar]
- Maqsood, H.; Qu, Y. Nonlinear disturbance observer based sliding mode control of quadrotor helicopter. J. Electr. Eng. Technol. 2020, 15, 1453–1461. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Wang, X. Time and FOV constraint guidance applicable to maneuvering target via sliding mode control. Aerosp. Sci. Technol. 2023, 133, 108104. [Google Scholar] [CrossRef]
- Zhang, N.; Qi, W.; Park, J.H. Sliding mode control for discrete-time singular semi-Markovian jumping models. Inf. Sci. 2023, 624, 554–566. [Google Scholar] [CrossRef]
- Han, J. State feedback realization of nonlinear control systems. Control Decis. 1991, 21, 161–167. [Google Scholar]
- Han, J. A new type of controller: NLPID. Control Decis. 1994, 24, 401–407. [Google Scholar]
- Han, J. From PID to active disturbances rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Guo, B.; Wu, Z.; Zhou, H. Active disturbance rejection control approach to output-feedback stabilization of a class of uncertain nonlinear systems subject to stochastic disturbance. IEEE Trans. Autom. Control 2016, 61, 1613–1618. [Google Scholar] [CrossRef]
- Shen, S.; Xu, J. Trajectory tracking active disturbance rejection control of the unmanned helicopter and its parameters tuning. IEEE Access 2021, 9, 56773–56785. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G. Low-computation adaptive fuzzy tracking control of unknown nonlinear systems with unmatched disturbances. IEEE Trans. Fuzzy Syst. 2020, 28, 321–332. [Google Scholar] [CrossRef]
- Navabi, M.; Hashkavaei, N.S.; Reyhanoglu, M. Satellite attitude control using optimal adaptive and fuzzy controllers. Acta Astronaut. 2023, 204, 434–442. [Google Scholar] [CrossRef]
- Cui, D.; Xiang, Z. Nonsingular fixed-time fault-tolerant fuzzy control for switched uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2023, 31, 174–183. [Google Scholar] [CrossRef]
- Lu, W.; Li, Q.; Lu, K. Load adaptive PMSM drive system based on an improved ADRC for manipulator joint. IEEE Access 2021, 9, 33369–33384. [Google Scholar] [CrossRef]
- Qi, B.; Wang, P.; Chai, X. Mirror milling trajectory planning for large thin-walled parts based on Fuzzy-ADRC controlled force pre-supporting. J. Manuf. Process. 2023, 85, 192–204. [Google Scholar]
- Wu, Y.; Chen, Z.; Su, L. Longitudinal attitude control of quad tilt-rotor UAV based on fuzzy LADRC. Flight Dyn. 2020, 38, 28–33. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996; p. 274. [Google Scholar]
- Liu, J. Sliding Mode Control Design and MATLAB Simulation, 3rd ed.; Tsinghua University Press: Beijing, China, 2015; p. 46. [Google Scholar]
- Shen, S.; Xu, J. Adaptive neural network-based active disturbance rejection flight control of an unmanned helicopter. Aerosp. Sci. Technol. 2021, 119, 107062. [Google Scholar] [CrossRef]
- Wu, C.; Wang, H.; Zhang, Y. Trajectory tracking of Unmanned Helicopter based on LADRC. Acta Aeronaut. Sin. 2015, 36, 473–483. [Google Scholar]






| NB | NS | ZO | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | NB | NB | NS | NS | ZO | |
| NS | NS | NS | NS | ZO | ZO | |
| ZO | NS | ZO | ZO | ZO | PS | |
| PS | NS | ZO | PS | PS | PS | |
| PB | ZO | ZO | PS | PS | PB | |
| NB | NS | ZO | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | NB | NS | ZO | ZO | PS | |
| NS | NB | NS | ZO | PS | ZO | |
| ZO | NS | NS | ZO | PS | PB | |
| PS | ZO | ZO | ZO | PS | PB | |
| PB | PS | PS | PS | PB | PB | |
| NB | NS | ZO | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | NB | NB | NS | NS | ZO | |
| NS | NS | NS | ZO | ZO | PS | |
| ZO | NS | Z0 | ZO | PS | PB | |
| PS | ZO | ZO | PS | PS | PB | |
| PB | PS | PS | PS | PS | PB | |
| Parameter | Unit | Initial Value | Modify Value |
|---|---|---|---|
| Mass | 30 | 15 | |
| Rotor radius | m | 0.923 | 0.923 |
| Tail rotor radius | m | 0.157 | 0.157 |
| Rotor speed | 195 | 195 | |
| Tail rotor speed | 1146 | 1146 | |
| Inertia coefficient | 0.51 | 0.42 | |
| Inertia coefficient | 0.69 | 0.57 | |
| Inertia coefficient | 1.26 | 0.91 |
| ] | SMC | FESO-SMC |
|---|---|---|
| c | [92 114 105] | [108 129 95] |
| [0.52 2.15 0.55] | [0.65 2.74 0.45] | |
| k | [187 126 209] | [268 96 175] |
| [1.54 0.39 0.65] | [1.65 0.52 0.69] | |
| dL | [−50 −20 −20] | - |
| dU | [20 20 50] | - |
| - | [79 49 127] | |
| - | [470 71 190] | |
| - | [52 41 55] | |
| - | [0.005 0.01 0.01] |
| Attitude (SMC) | Attitude (FESO-SMC) | Velocity (SMC) | Velocity (FESO-SMC) | Position (SMC) | Position (FESO-SMC) | |
|---|---|---|---|---|---|---|
| c | [67 81 77] | [52 78 65] | [52 57 72] | [45 46 95] | [99 121 110] | [87 85 91] |
| [0.45 1.56 0.58] | [0.35 1.24 0.71] | [1.42 0.79 0.55] | [1.15 1.12 0.52] | [0.77 4.35 1.28] | [1.25 5.01 2.32] | |
| k | [156 150 170] | [124 128 165] | [121 136 52] | [101 105 56] | [57 60 98] | [41 65 86] |
| [1.55 0.41 0.58] | [1.15 0.32 0.65] | [7.22 9.45 1.24] | [7.21 9.35 1.27] | [1.25 0.84 0.87] | [2.41 0.79 0.92] | |
| dL | [−50 −20 −20] | - | [−10 −20 −70] | - | [−60 −50 −40] | - |
| dU | [20 20 50] | - | [80 50 50] | - | [180 20 100] | - |
| - | [74 65 145] | - | [412 105 27] | - | [30 45 96] | |
| - | [505 61 208] | - | [124 112 53] | - | [212 79 180] | |
| - | [64 32 51] | - | [42 45 72] | - | [101 97 82] | |
| - | [0.005 0.01 0.01] | - | [0.01 0.01 0.01] | - | [0.01 0.01 0.01] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Li, J.; Chen, Y.; Lv, J. Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter. Agriculture 2025, 15, 306. https://doi.org/10.3390/agriculture15030306
Shen S, Li J, Chen Y, Lv J. Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter. Agriculture. 2025; 15(3):306. https://doi.org/10.3390/agriculture15030306
Chicago/Turabian StyleShen, Suiyuan, Jiyu Li, Yu Chen, and Jia Lv. 2025. "Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter" Agriculture 15, no. 3: 306. https://doi.org/10.3390/agriculture15030306
APA StyleShen, S., Li, J., Chen, Y., & Lv, J. (2025). Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter. Agriculture, 15(3), 306. https://doi.org/10.3390/agriculture15030306








