Parameter Optimization and Experimental Study of Drum with Elastic Tooth Type Loss-Reducing Picking Mechanism of Pepper Harvester
Abstract
:1. Introduction
- The kinematic and dynamic models of the pepper picking process were established by using the projectile motion theory, the Hertz contact theory, and the von Mises criterion. The interaction mechanisms between the pepper stalks and the elastic tooth drum, and between the pepper fruits and the elastic teeth were analyzed. A kinematic model was established to determine the critical conditions for fruit detachment and breakage, while a post-picking trajectory model identified the key factors influencing picking efficiency, breakage rate, and loss rate.
- An optimization method for the picking parameters was developed using AHP and RSM. A model of pepper stalks and fruits was created, validated by measurements, and integrated into the picking mechanism model for dynamic simulations in LS-DYNA of ANSYS Workbench. A three-factor, three-level Box–Behnken design in RSM was employed to analyze the influence of interaction terms of the factors on the target values. A multi-objective optimization model was obtained through RSM optimization after AHP weighting, which yielded optimal parameter combinations to minimize pepper loss. This method enhances factor importance reflection and optimization precision, for a multi-objective decision-making problem.
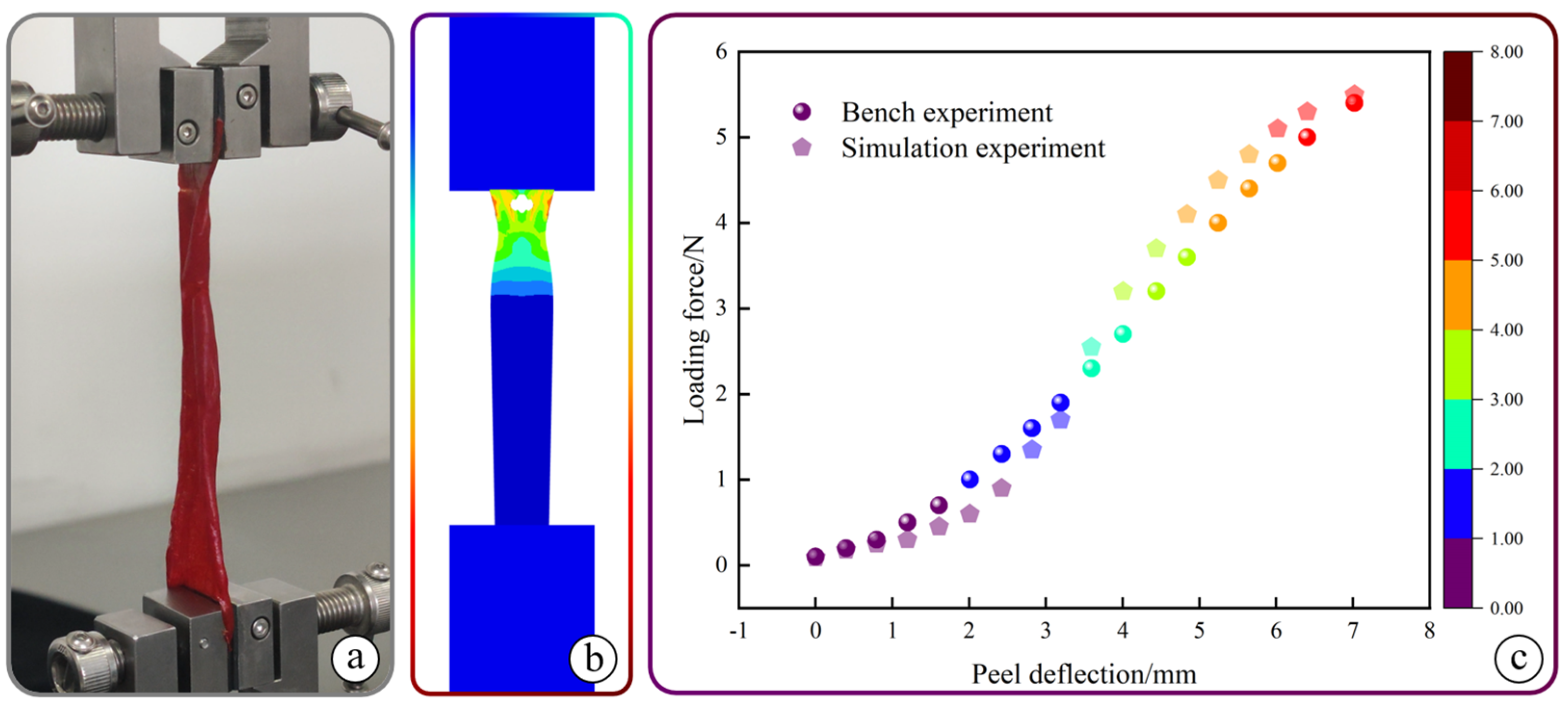
- A pepper picking test bench with an elastic tooth drum was designed to simulate harvest operations under actual growing conditions, minimizing the effects of vibration and uncontrollable factors. The bench, fixing the picking mechanism and moving the pepper plant, was designed based on the cultivation technique. The accuracy of the bench was validated by comparing predicted values from regression equations with actual measurements, confirming the effectiveness of the loss-reducing mechanism under optimal parameters. This solution effectively reduces fruit loss by minimizing the influence of uncontrollable factors in complex environments.
2. Materials and Methods
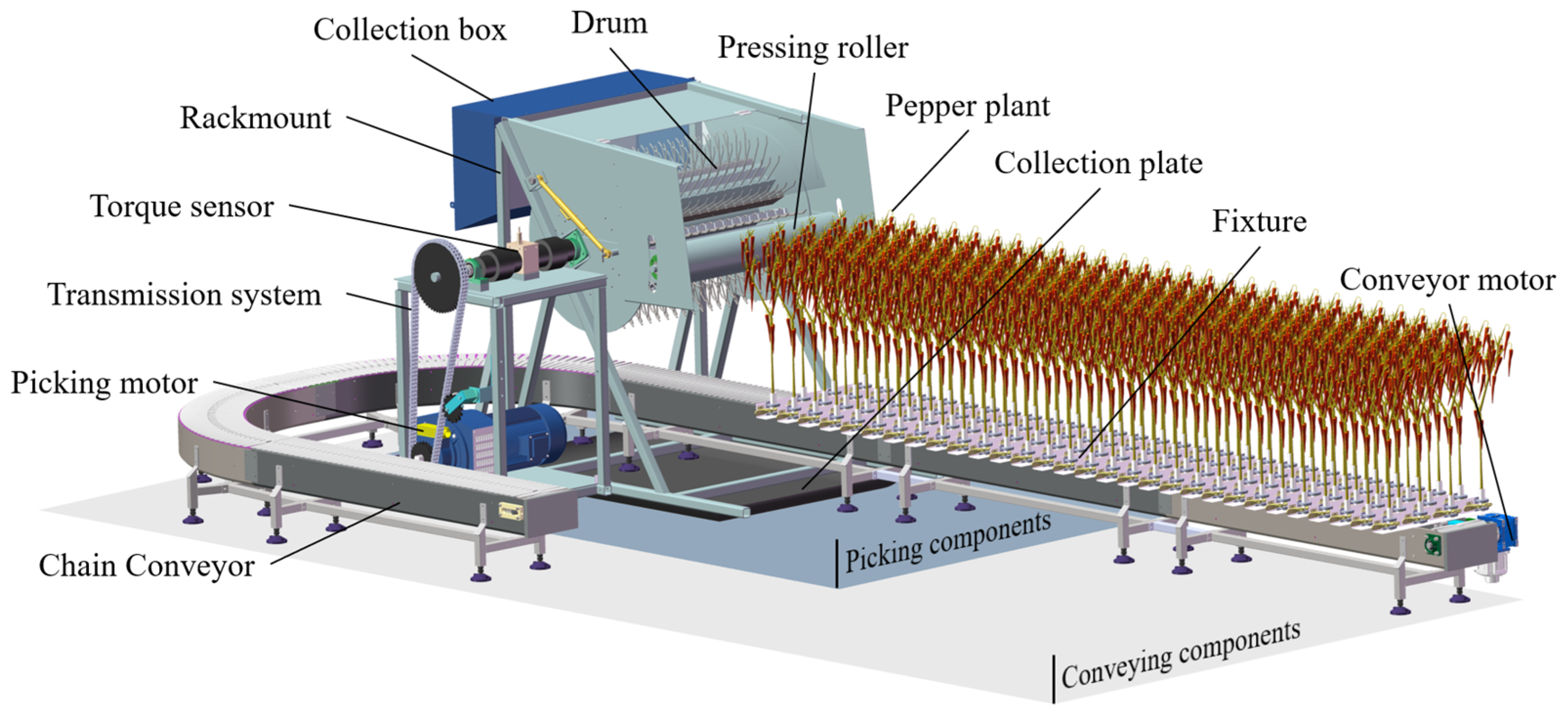
2.1. Structure of the Whole Harvester and Working Principle
2.1.1. Cultivation Technique and Harvester Structure
2.1.2. Pepper Harvester Working Principle
2.1.3. Pepper Harvester Technical Parameters
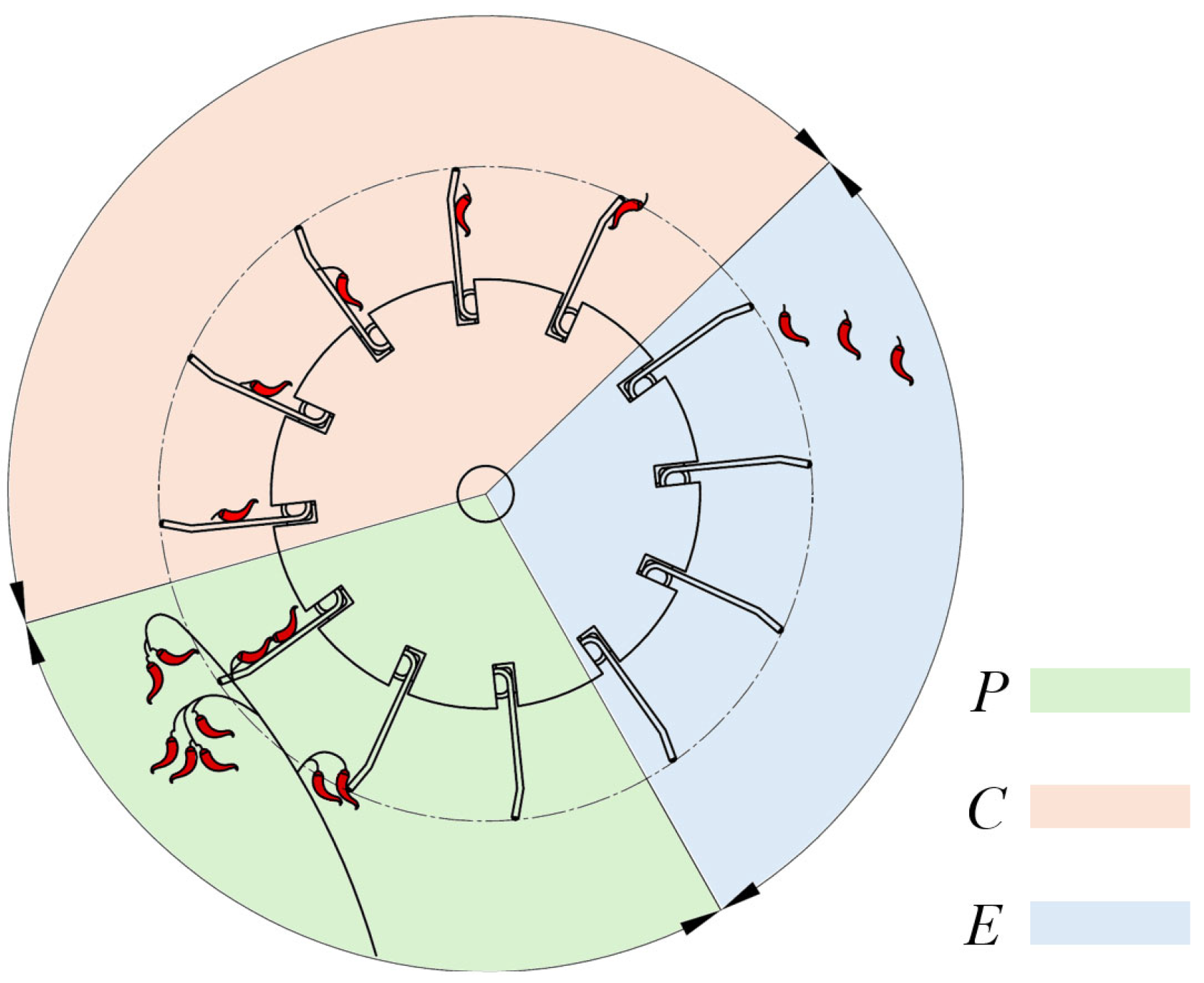
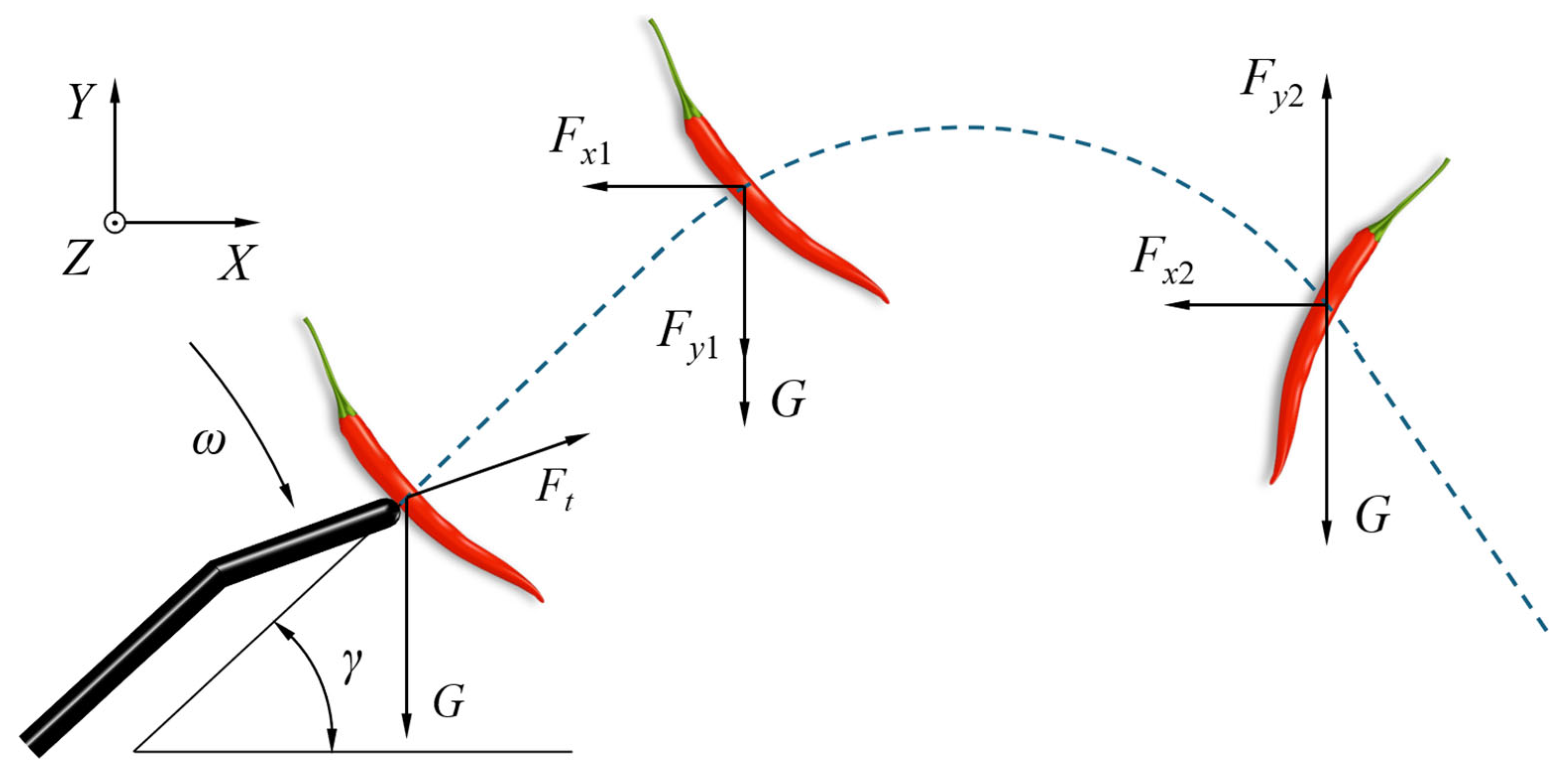
2.2. Analysis of the Interaction Mechanism Between Pepper Plants and Elastic Tooth Drum
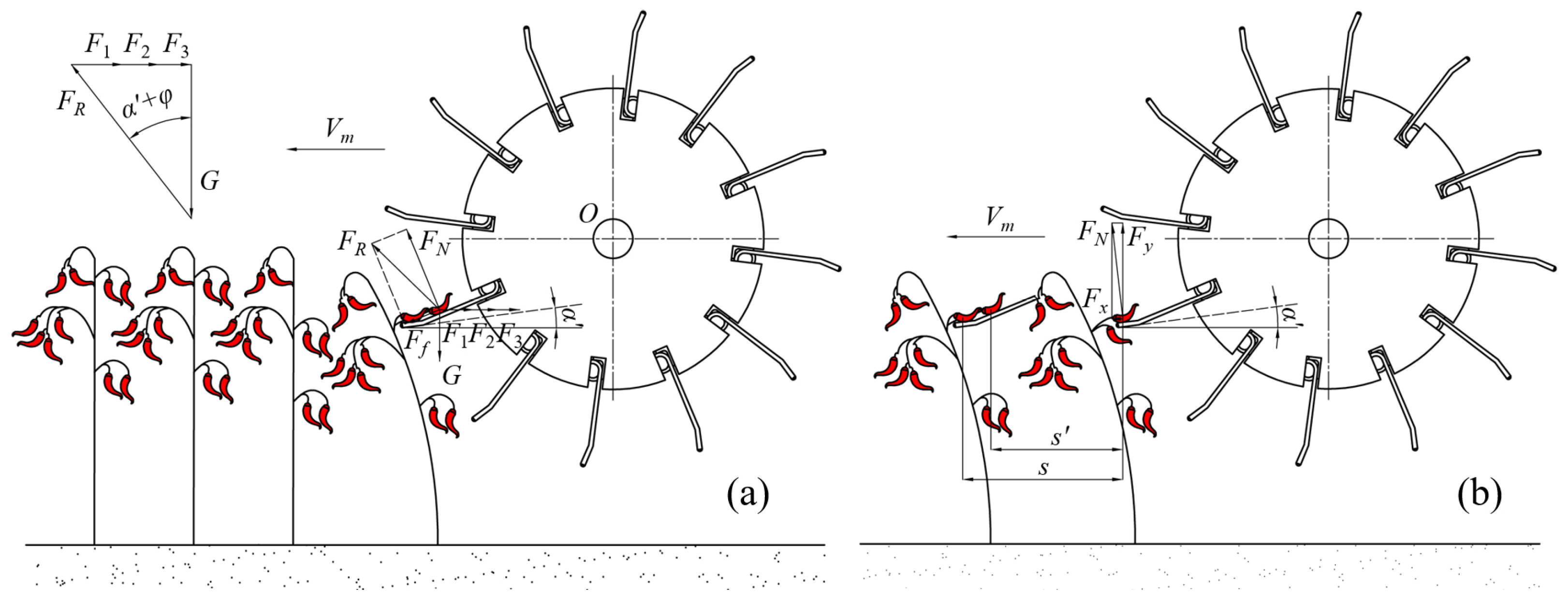
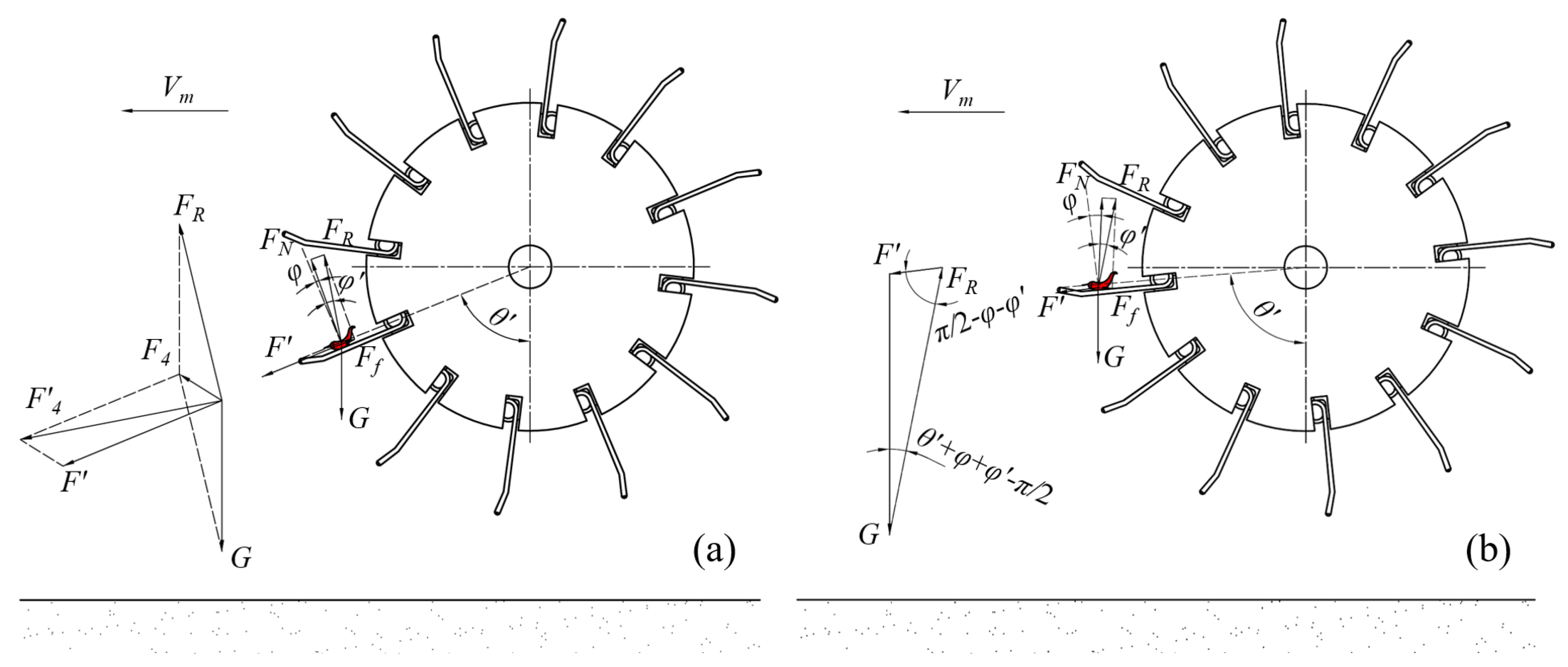
2.2.1. Analysis of Stresses on Pepper Stalks
2.2.2. Analysis of Stresses on Pepper Fruits in Picking Section
- There is no interaction between pepper fruits, branches, and leaves except for the connecting force, ignoring the influence of airflow;
- The initial velocity of pepper fruits is 0;
- The impact force is the orthogonal direction of the impact force.
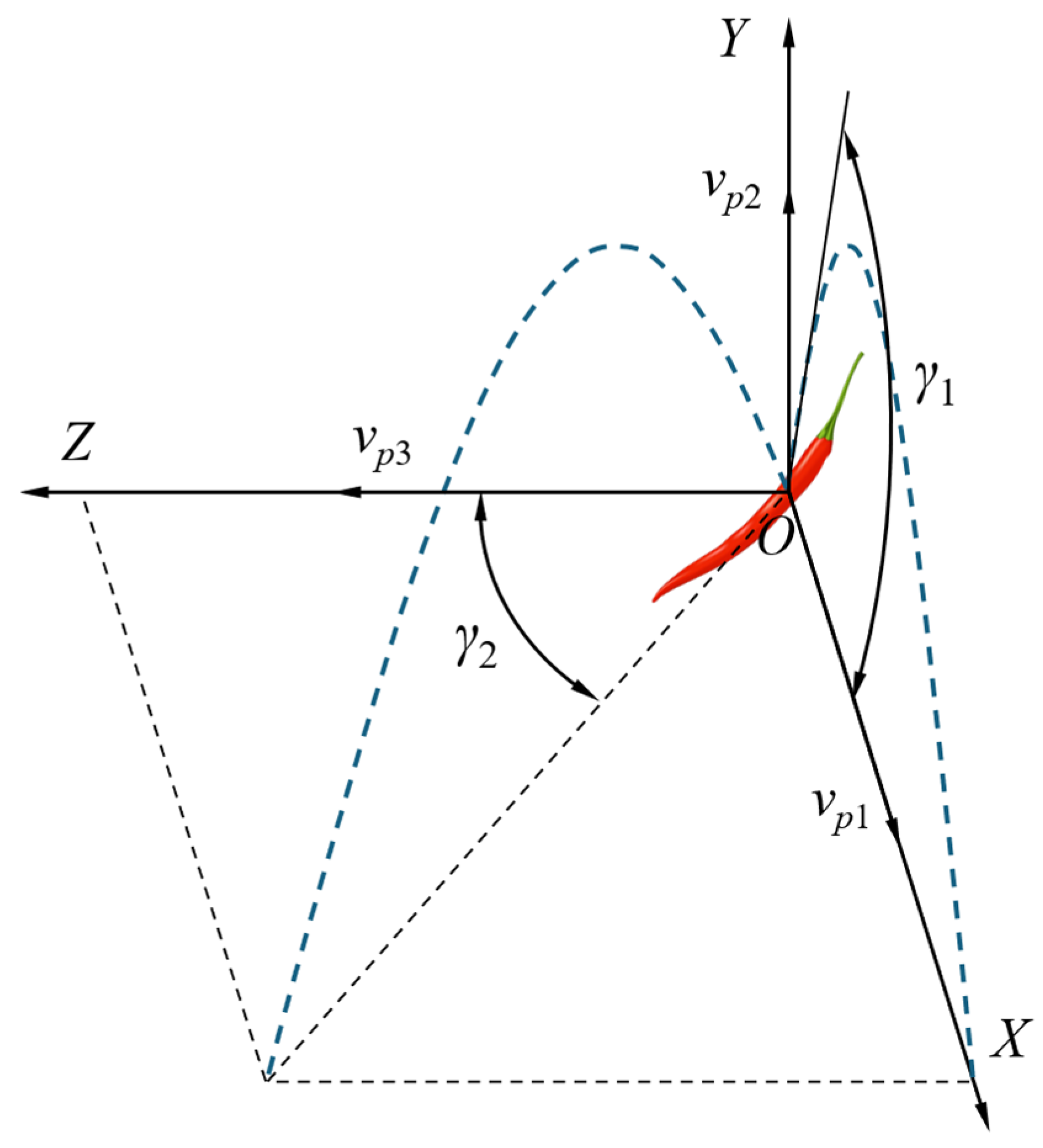
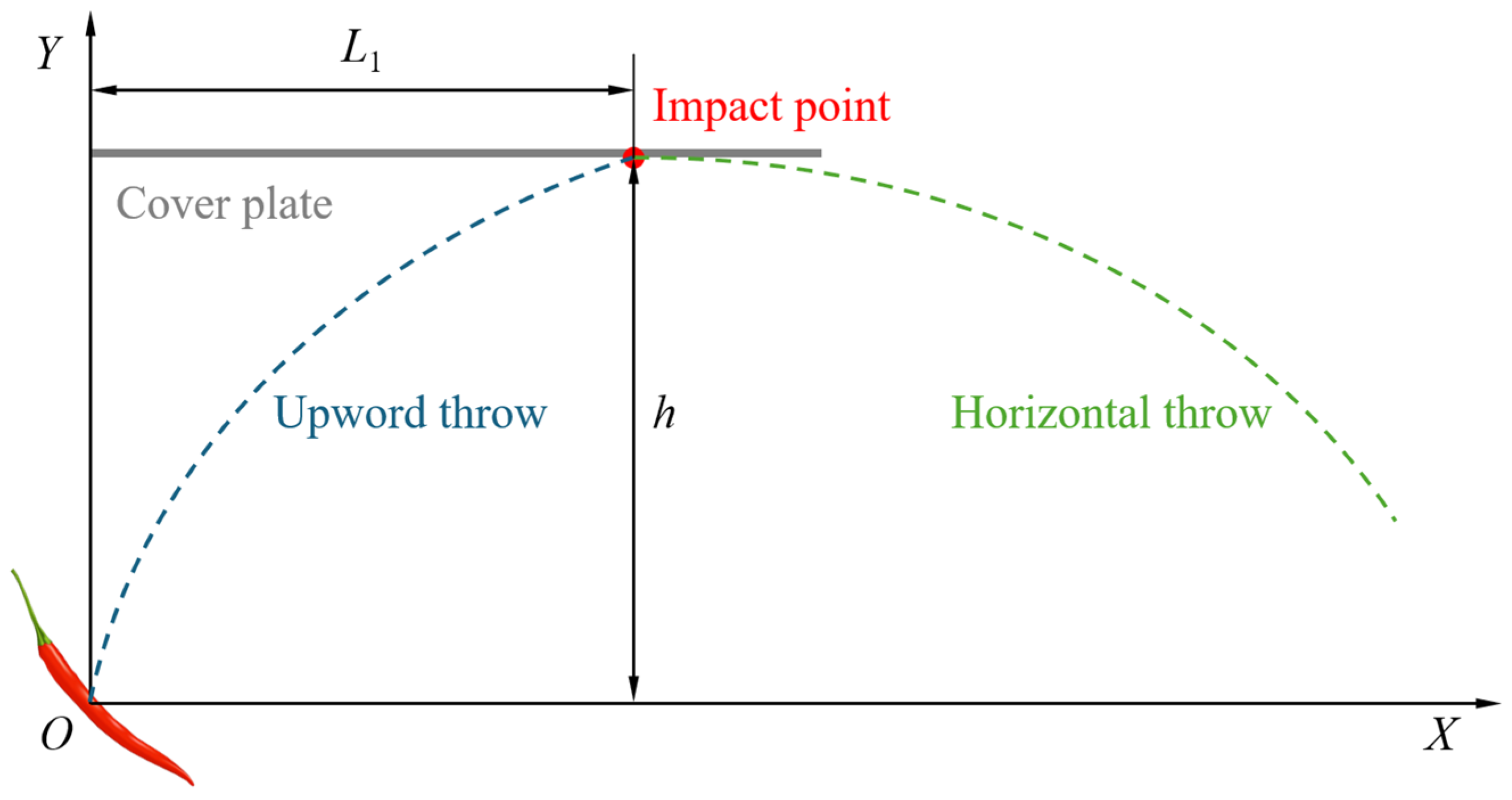
2.2.3. Analysis of Kinematics on Pepper Fruits in Casting Section
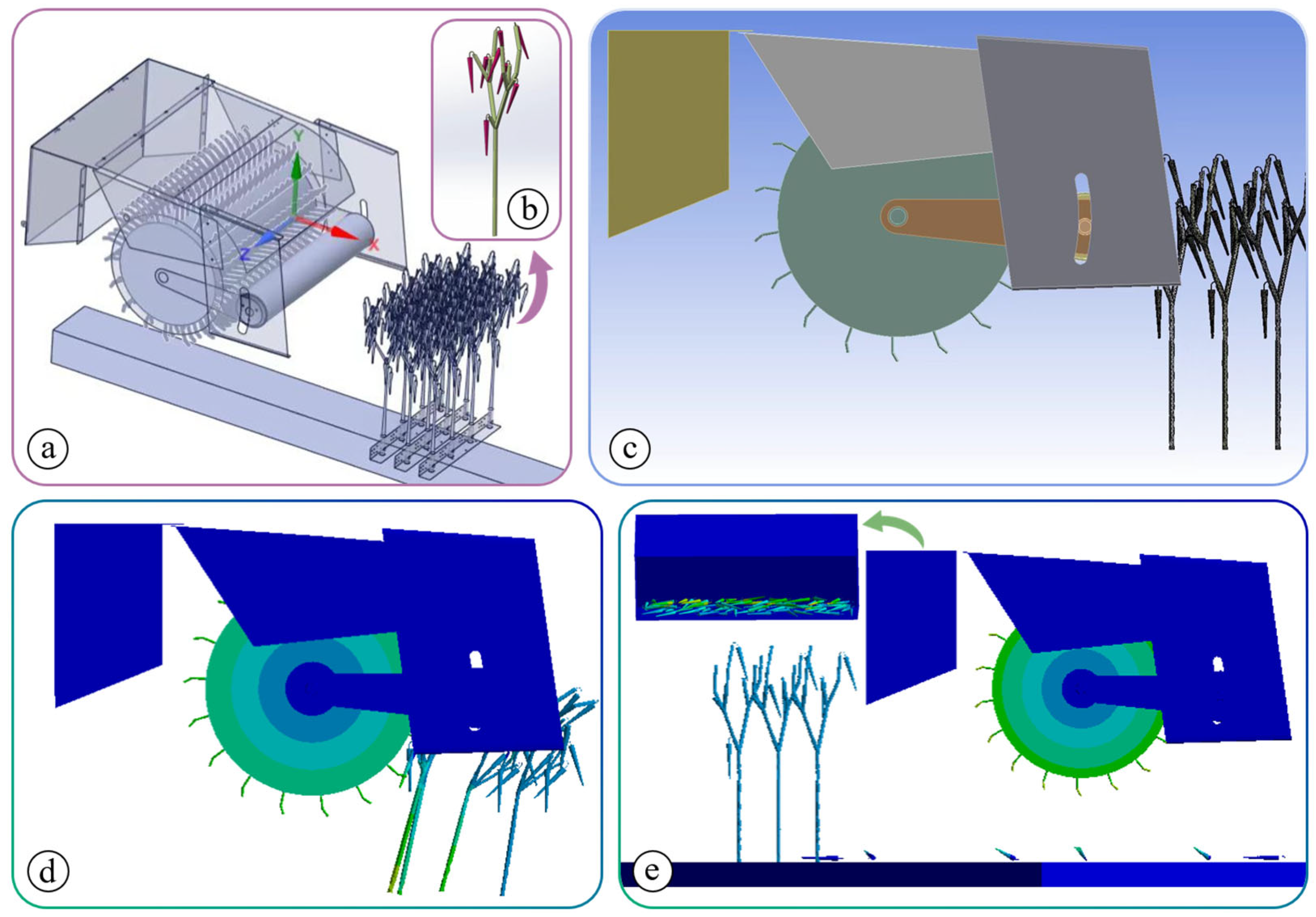
2.3. Simulation Test Design
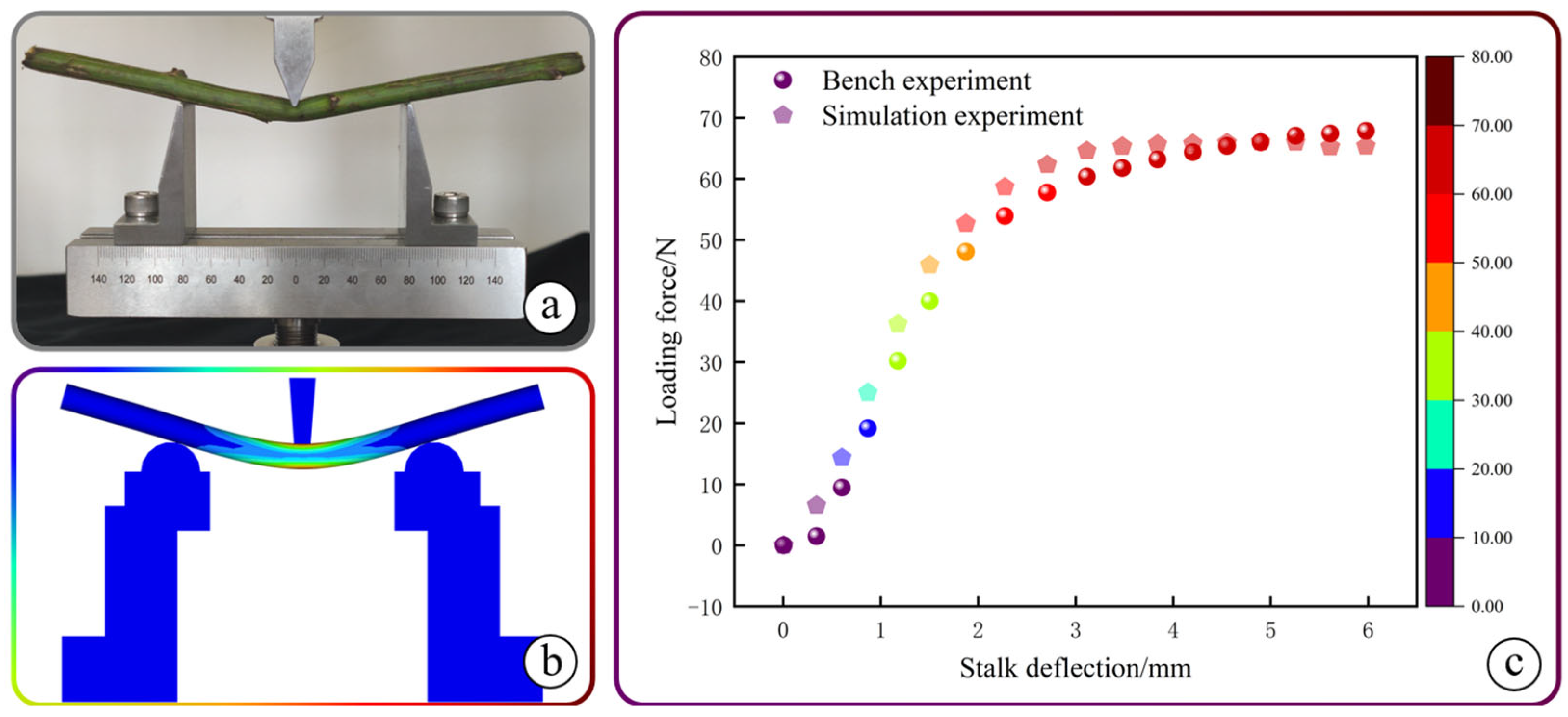
2.3.1. Materials and Equipment
2.3.2. Test Indicator
2.3.3. Test Factors and Levels
2.3.4. Test Program and Method
- Contact force definition: In ANSYS Workbench 2021R1, within the contact definition in the Explicit Dynamics module, the contact type is set as FLEX TO SOLID (flexible body to rigid body). Based on the parameters of the pepper plant, the contact force parameters are set as follows: normal force type is chosen as impact, stiffness is defined as 1.5 × 105, force exponent is set to 2.0, damping is defined as 150, penetration depth is set to 0.05. The friction force is selected as static, and the friction coefficient is set to 0.3 to simulate the friction between the pepper fruit and the drum.
- Traction force and resistance: Considering the traction force Fq and resistance Fz acting on the pepper plant during the harvest process, the total resistance Fm is defined as the combined force of both, with its magnitude being the product of the plant mass m and the friction coefficient f between the pepper fruit and the branches, i.e., , where v is the plant’s movement speed.
- Drive definition: A drive is applied to the drum to define its rotational motion during the harvest process, with the rotational speed set according to the parameters in Table 4, ensuring that the actual operational state of the harvester is simulated. In addition, a slip joint is defined between the pepper plant and the ground to simulate the plant’s movement during harvesting, and a linear drive is added to achieve the forward motion of the harvester.
- Fruit stalk separation sensor: This sensor detects whether the pepper fruit has successfully separated from the stalk. When the sensor detects that the relative position between the fruit and the stalk is zero, it indicates that the fruit has separated from the stalk, and the harvest process is completed. This sensor allows the picking rate to be calculated in real-time.
- Fruit stress monitoring sensor: This sensor is used to detect if the fruit is subjected to stress exceeding the threshold, thereby determining if the fruit has been broken. A breakage stress threshold is set, and once the stress on the fruit exceeds this threshold, the fruit is considered broken, allowing for the calculation of the breakage rate.
- Fruit drop sensor: In the simulation, the sensor at the collection box entrance is used to monitor the collection of the fruit. If the fruit falls outside the collection box, it is recorded as a lost fruit, allowing the loss rate to be calculated.
3. Results
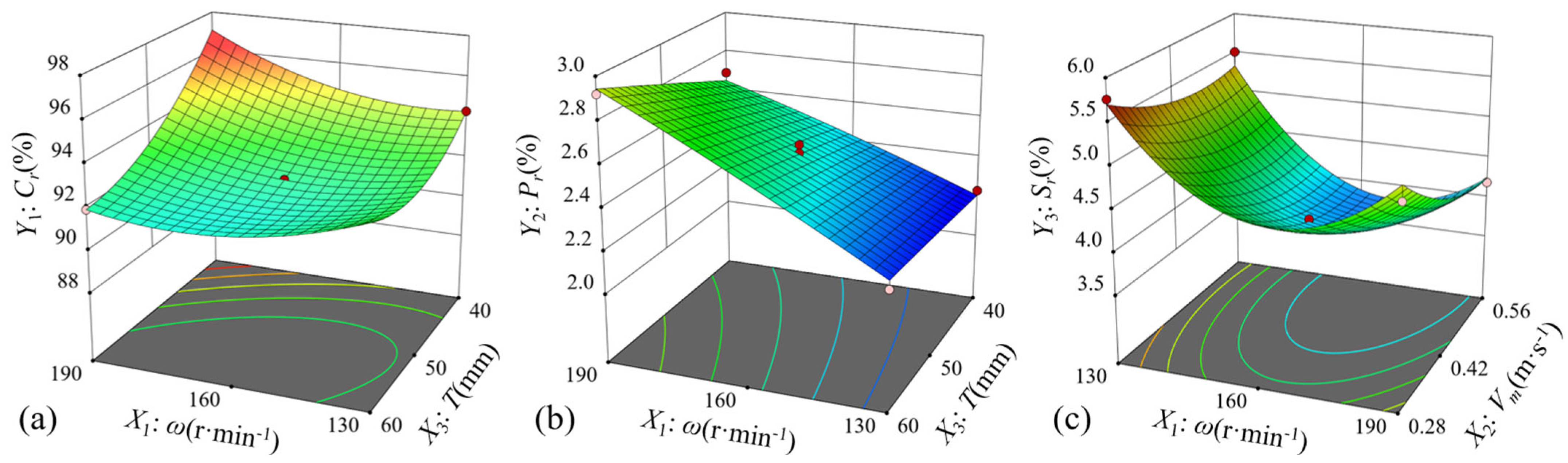
3.1. Regression Modeling and Analysis of Variance
3.2. Impact of Factors on Test Indicators
3.3. Parameter Optimization and Test Validation
3.3.1. Parameter Optimization
3.3.2. Test Bench Design and Test Validation
- Drum rotational speed adjustment: The drum speed is adjusted by adjusting the electromagnetic controller of the drum drive motor. The drum drive motor is a three-phase asynchronous electromagnetic AC motor; the electromagnetic controller rotates the control knob to adjust the speed and the torque sensor installed in the drum spindle reads the drum rotational speed and displays it on the computer and adjusts the knob to the predetermined speed to complete the adjustment of the drum rotational speed.
- Operating speed adjustment: The feed speed adjustment is made by adjusting the servo control software of the conveyor drive motor. The conveyor drive motor is a servo motor; the speed is adjusted by the servo control software, the proportionality between the operating speed and the motor speed is calculated through the transmission ratio, the operating speed is calculated by combining the time used in the calibrated displacement range, and the speed of the motor in the software is set to complete the adjustment of the operating speed.
- Tooth spacing adjustment: Replacement of tooth spacing of 40 mm, 50 mm, 60 mm, 3 specifications of the elastic tooth mounting plate. Elastic teeth are pre-installed in different specifications of the elastic tooth mounting plate.
4. Discussion
4.1. Discussion of Results
- Due to the simulation accuracy and time limitations, the mutual entanglement force between pepper plants is added as a constant value force in this paper, which increases the relative error between the simulation test and the bench test. In actual harvesting, the mutual entanglement force is affected by several factors such as overlap coefficient, moisture content, friction coefficient, etc. Further research is needed to investigate the change in the pepper plant–plant interaction force in the harvest process and its impact on the quality of the harvesting operation to further improve the reliability of the simulation results.
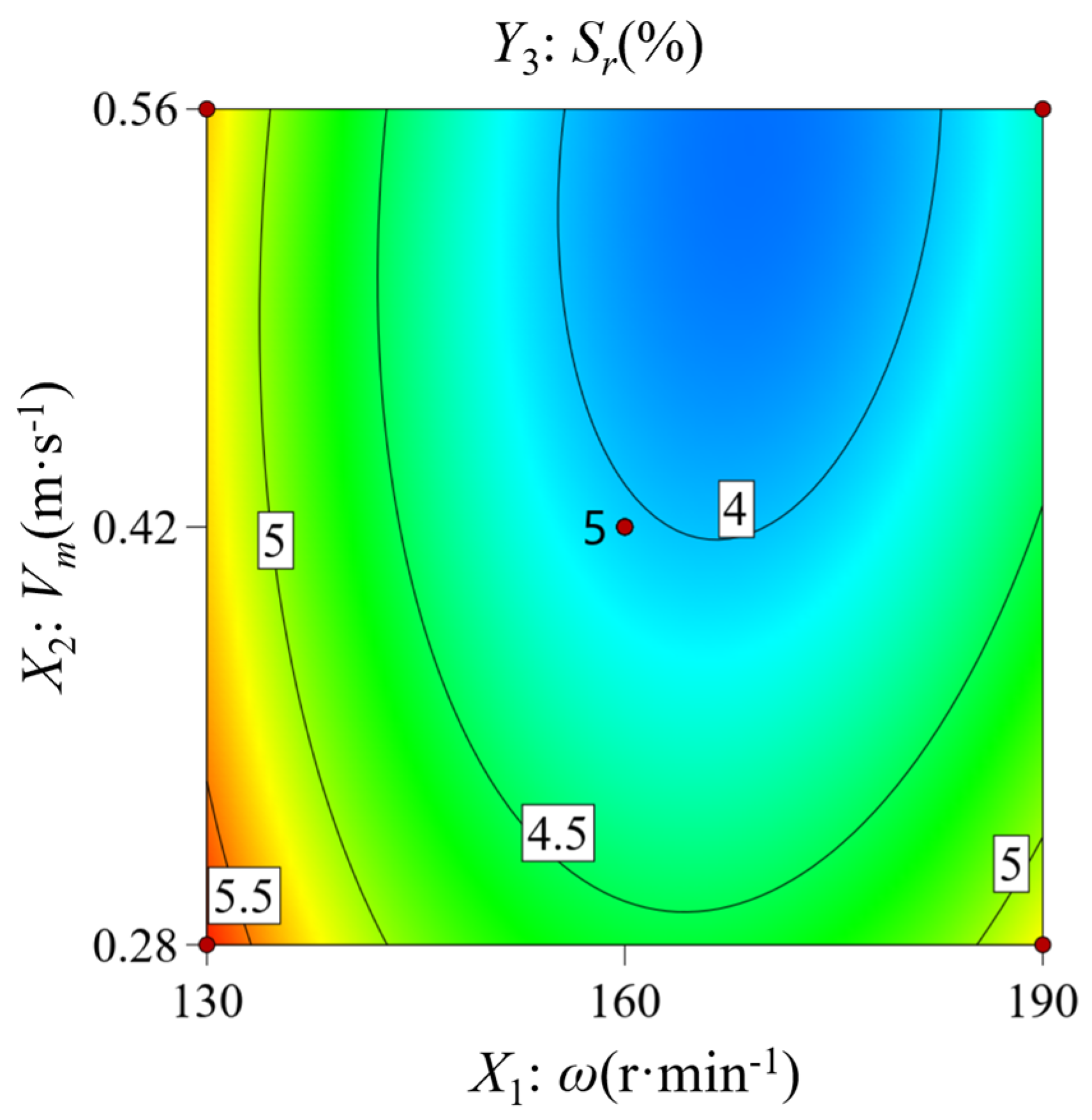
- Based on the test results, it was found that the ratio of drum rotational speed to feed speed is an important parameter affecting the quality of the picking operation. Among them, the picking speed ratio has the most obvious effect on the picking loss rate. According to the previous simulation test results, the contour plots of drum rotational speed X1 and operating speed X2 on the target value loss rate X2 were generated using Design-Expert13 software, as shown in Figure 15.
4.2. Discussion of Bench Test
4.3. Limitations and Prospects
- Due to the time constraints of the pepper harvest period, the test samples in this paper were selected without considering factors such as the variety, fall, and growth of the pepper plants. Therefore, the test results are only applicable to peppers with good uprightness and favorable growth. The adaptive adjustment of pepper varieties, collapse, growth, and other factors and institutional parameters is also a research direction that should be considered in the future.
- The peppers in the simulation were uniformly arranged with consistent morphological parameters. Although the pepper plants were randomly grouped to complete picking in the test bench, only plants with better growth were selected for sampling. Therefore, the effect of the fruit density of the pepper was not considered in this study. In the actual working conditions, the change in pepper growth density will cause random load fluctuation on the elastic teeth, resulting in harvest loss. Future loss reduction studies should consider the effect of pepper density.
- The AHP-RSM integrated optimization framework adopted in this study aligns with the target dimensions and research requirements. Future studies will further validate the generalizability of the conclusions through multi-algorithm comparisons and hybrid optimization strategies, aiming to extend its applicability to complex agricultural machinery optimization scenarios.
5. Conclusions
- Based on Hertz contact theory, the interaction between the drum and the pepper plant is analyzed, with the main influencing factors identified as drum rotational speed and tooth spacing. By combining Hertz contact theory with the von Mises criterion, the interaction between the elastic tooth drum and the pepper fruits is examined from the point of view of fruit loss and breakage mechanisms. It is found that the critical operating speed for pepper fruit detachment is 0.7 m/s, and the critical drum rotational speed for pepper fruit breakage is 220 r/min. Using projectile motion theory, a trajectory and velocity model for the pepper fruits during the ejection phase is established, showing that the drum rotational speed is the key factor affecting the pepper loss rate during the casting section.
- A Box–Behnken multi-factor response surface simulation is performed through the LS-DYNA module of ANSYS Workbench. Variance analysis of the test results identifies the influence patterns of the interacting factors on the target values. The ranking of the factors affecting the picking rate is as follows: tooth spacing, operating speed, and drum rotational speed. The ranking of factors affecting the breakage rate is as follows: drum rotational speed, tooth spacing, and operating speed. The ranking of factors affecting loss rate is as follows: drum rotational speed, operating speed, and tooth spacing.
- By determining the weights of each objective value through the AHP, a multi-objective optimization equation is established with RSM. The optimal harvesting parameters for minimizing pepper loss are found to be a drum rotational speed of 182 r/s, an operating speed of 0.42 m/s, and a tooth spacing of 40 mm. Under these conditions, the predicted picking rate is 93.36%, the breakage rate is 2.6%, and the loss rate is 3.99%. Bench tests show that the relative error between predicted and measured values for each target is less than 5%. Under the optimized parameter combination, the picking rate increases from 89.73% to 95.13%, the breakage rate decreases from 3.21% to 2.66%, and the loss rate decreases from 5.16% to 3.95%. Validation tests confirm the accuracy of the simulation results and the effectiveness of the optimal parameter combination.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Zhou, S.; Li, X. The Research Progresses on Pepper in 2019. J. China Capsicum 2020, 18, 1–11. [Google Scholar]
- Spence, C. Why is piquant/spicy food so popular? Int. J. Gastron. Food Sci. 2018, 12, 16–21. [Google Scholar] [CrossRef]
- Zhu, N. Analysis of the Comprehensive Development and Utilization Perspective of Pepper Seeds. J. China Condiment 2014, 39, 120–123. [Google Scholar]
- Hernández Pérez, T.; Gómez García, M.D.R.; Valverde, M.E. Capsicum annuum (hot pepper): An ancient Latin-American crop with outstanding bioactive compounds and nutraceutical potential. J. Compr. Rev. Food Sci. Food Saf. 2020, 19, 2972–2993. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, Y.; Zhao, L. Research Progress on Pepper Seeds and Their High Value-Added Utilization. J. Technol. Food Ind. 2018, 39, 320–327. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 20 September 2022).
- Wang, L.; Zang, B.; Zhang, Z. Status in Breeding and Production of Capsicum spp. in China During ‘The Thirteenth Five-Year Plan’ Period and Future Prospect. J. China Veg. 2021, 2, 21–29. [Google Scholar]
- Zou, X.; Ma, Y.; Dai, X. Spread and Industry Development of Pepper in China. J. Acta Hortic. Sin. 2020, 47, 1715–1726. [Google Scholar]
- Lin, Q.; Xin, Z.; Kong, L. The Current Status of Pepper Industry Development and Breeding Countermeasures in China. J. China Agric. Univ. 2023, 28, 82–95. [Google Scholar]
- Gentry, J.P.; Miles, J.A.; Hinz, W.W. Development of a Chili Pepper Harvester. J. Trans. ASAE 1978, 21, 52–54. [Google Scholar] [CrossRef]
- Marshall, D.E. Designing a Pepper for Mechanical Harvest. J. Capsicum Eggplant Newsl. 1997, 16, 15–27. [Google Scholar]
- Shooter, S.B.; Buffinton, K.W. Design and Development of the Pik Rite Chili Pepper Harvester: A Collaborative Project with the University, Industry, and Government. In Proceedings of the 29th ASEE/IEEE Frontiers in Education Conference, San Juan, PR, USA, 10–13 November 1999. [Google Scholar]
- Hawkes, J.G.; Libbin, J.D.; Eastman, R.; Diemer, J.; Jones, R. Challenges in Pepper Harvest Mechanization. In Proceedings of the Pepper Industry Conference, Las Cruces, NM, USA, 15–17 October 2000. [Google Scholar]
- Xue, S.; Li, Q.; Huang, Q. Analysis of Factors Affecting Mechanised Harvesting of Pepper. J. Xinjiang Agric. Mech. 2020, 4, 9–11. [Google Scholar]
- Meng, Q. Analysis of Production Cost and Income of Pepper in Main Production Areas in China—Based on the Investigation of Five Provinces Such as Guizhou and Hunan. Master’s Thesis, Hebei Agricultural University, Baoding, China, 2018. [Google Scholar]
- Xinjiang Uygur Autonomous Region Bureau of Statistics. Xinjiang Statistical Yearbook; China Statistics Press: Beijing, China, 2019.
- Song, W.; Wang, C.; Li, J. The Main Dried Pepper Varieties in Xinjiang and Their Adaptability. Rural Sci. Technol. 2003, 4, 31. [Google Scholar]
- Yang, H.; Shao, Z.; Gao, Y. Research on the Development Model of Xinjiang Agricultural Industrialization Consortium—Taking the Pepper Industry in Yanqi County as an Example. J. Anhui Agric. Sci. 2020, 648, 233–237. [Google Scholar]
- Gao, X. Research on the Health Function of Chili Pepper and the Development of Its Products. J. Food Res. Dev. 2004, 3, 115–116. [Google Scholar]
- Ding, H.; Dong, H.; Zhao, K. Talking about the Selection of Harvesting Machinery and Its Advantages and Disadvantages in the Process of Harvesting Pigmented Peppers. J. Hebei Agric. Mach. 2019, 252, 21–22. [Google Scholar]
- Wang, G. Discussion on the Problem of Mechanical Harvesting of Pepper. J. Rural Sci. Technol. 2014, 347, 65. [Google Scholar]
- Ge, J.; Yan, T.; Ouyang, W. Current Status of the Pepper Industry in Xinjiang and Suggestions for Development Strategies. J. Pepper Mag. 2010, 8, 8–10. [Google Scholar]
- Fan, S.; Sun, R.; Hong, X. Current Status and Research Strategies of Mechanization Technology for Pepper Harvesting in China. J. Zhongzhou Univ. 2023, 40, 116–120. [Google Scholar]
- Sun, G. Development of 4JZ-3600/2600 Self-Propelled Pepper Harvesting Machine. Agric. Eng. 2012, 2, 69–71. [Google Scholar]
- Xu, D. Design and Research of Line Pepper Harvester. Master’s Thesis, Gansu Agricultural University, Lanzhou, China, 2017. [Google Scholar]
- Abudulah, R. Design and Research of Tracked Miniature Pepper Harvester Hydraulic System. Master’s Thesis, Shihezi University, Shihezi, China, 2022. [Google Scholar]
- Yang, J.; Qin, X.; Lei, J.; Lu, L.; Zhang, J.; Wang, Z. Design and Experiment of a Crawler-Type Harvester for Red Cluster Peppers in Hilly and Mountainous Regions. J. Agric. 2024, 14, 1742. [Google Scholar] [CrossRef]
- Ning, Z.; Luo, L.; Ding, X.; Dong, Z.; Yang, B.; Cai, J.; Chen, W.; Lu, Q. Recognition of Sweet Peppers and Planning the Robotic Picking Sequence in High-Density Orchards. J. Comput. Electron. Agric. 2022, 196, 106878. [Google Scholar] [CrossRef]
- Liu, S.; Liu, M.; Chai, Y.; Li, S.; Miao, H. Recognition and Location of Pepper Picking Based on Improved Yolov5s and Depth Camera. J. Appl. Eng. Agric. 2023, 39, 179–185. [Google Scholar] [CrossRef]
- Deng, L.; Liu, T.; Jiang, P.; Qi, A.; He, Y.; Li, Y.; Yang, M.; Deng, X. Design and Testing of Bionic-Feature-Based 3D-Printed Flexible End-Effectors for Picking Horn Peppers. Agronomy 2023, 13, 2231. [Google Scholar] [CrossRef]
- Islam, M.N.; Iqbal, M.Z.; Ali, M.; Chowdhury, M.; Kabir, M.S.N.; Park, T.; Kim, Y.-J.; Chung, S.-O. Kinematic Analysis of a Clamp-Type Picking Device for an Automatic Pepper Transplanter. Agriculture 2020, 10, 627. [Google Scholar] [CrossRef]
- Zou, D.; Maimaiti Turson, A.; Han, C.; Li, Q.; Li, Y.; Zhang, J. Design and Experiment of Picking Platform of Pepper Harvester. J. Agric. Mech. Res. 2022, 44, 105–109. [Google Scholar]
- Li, X.; Li, Y.; Gao, H.; Qiu, Z.; Ma, F.; Gao, L. Bionic Threshing Process Analysis of Seed Corn Kernel. Trans. Chin. Soc. Agric. Mach. 2011, 42, 99–103. [Google Scholar]
- Sun, G. Study on Optimization of Snapping Roller Based on Bionic Corn Ear Picking Device. Master’s Thesis, Jilin University, Changchun, China, 2018. [Google Scholar]
- Lei, M.; Kong, L.; Chen, Y. Research on the Chili Picking Device of Spring Tooth Roller-Type. J. Chin. Agric. Mech. 2014, 35, 161–165. [Google Scholar]
- Lei, M.; Wang, F.; Wang, M. Experimental Study on Performance of Chili Picking Device Based on Spring Tooth Roller-Type. J. Agric. Mech. Res. 2018, 40, 142–146,152. [Google Scholar]
- Duan, Y.; Kong, L.; Chen, Y. Tine Drum Pepper Picking Device: Picking Hot Pepper Mechanical Damage Characteristics and Mechanism. J. Chin. Agric. Mech. 2014, 35, 79–82. [Google Scholar]
- Zhang, X.; Qin, X.; Lei, J.; Zhai, Z.; Zhang, J.; Wang, Z. A Novel Method on Recognizing Drum Load of Elastic Tooth Drum Pepper Harvester Based on CEEMDAN-KPCA-SVM. J. Agric. 2024, 14, 1114. [Google Scholar] [CrossRef]
- He, J.; Hu, W.; Guo, Y.F. Kinematic Simulation of No-Row Feed-in Mechanism with Guide-Rod for Corn Harvester. J. Trans. Chin. Soc. Agric. Eng. 2007, 23, 125–129. [Google Scholar]
- Du, Y.; Mao, E.; Song, Z. Simulation on Corn Plants in Harvest process Based on ADAMS. J. Trans. Chin. Soc. Agric. Mach. 2012, 43, 106–111. [Google Scholar]
- Wu, S.; Huang, W.; Yuan, X.; Li, X.; Mu, G.; Zhang, H. Design and Test of Stem-Leaf Separation Device for Salted Wakame (Undaria pinnatifida). J. Trans. Chin. Soc. Agric. Mach. 2024, 55, 348–360,+388. [Google Scholar]
- Cao, W.; Sun, W.; Niu, C.; Jiao, H.; Chen, B. Combed safflower picking device based on ANSYS/LS-DYNA. J. Trans. Chin. Soc. Agric. Mach. 2018, 49, 123–131. [Google Scholar]
- Li, X.; Fang, X.; Han, Z.; Zhang, Z.; Liu, G.; Cui, J.; Qiao, X.; Han, K. Dynamic Simulation of Sweet Sorghum Cutting Based on ANSYS/LS-DYNA. J. Trans. J. Agric. Sci. Technol. Mach. 2015, 17, 70–76. [Google Scholar]
- DG/T 114-2019; Agricultural Machinery Extension Appraisal Syllabus. Ministry of Agriculture and Rural Affairs of the People’s Republic of China: Beijing, China, 2019.
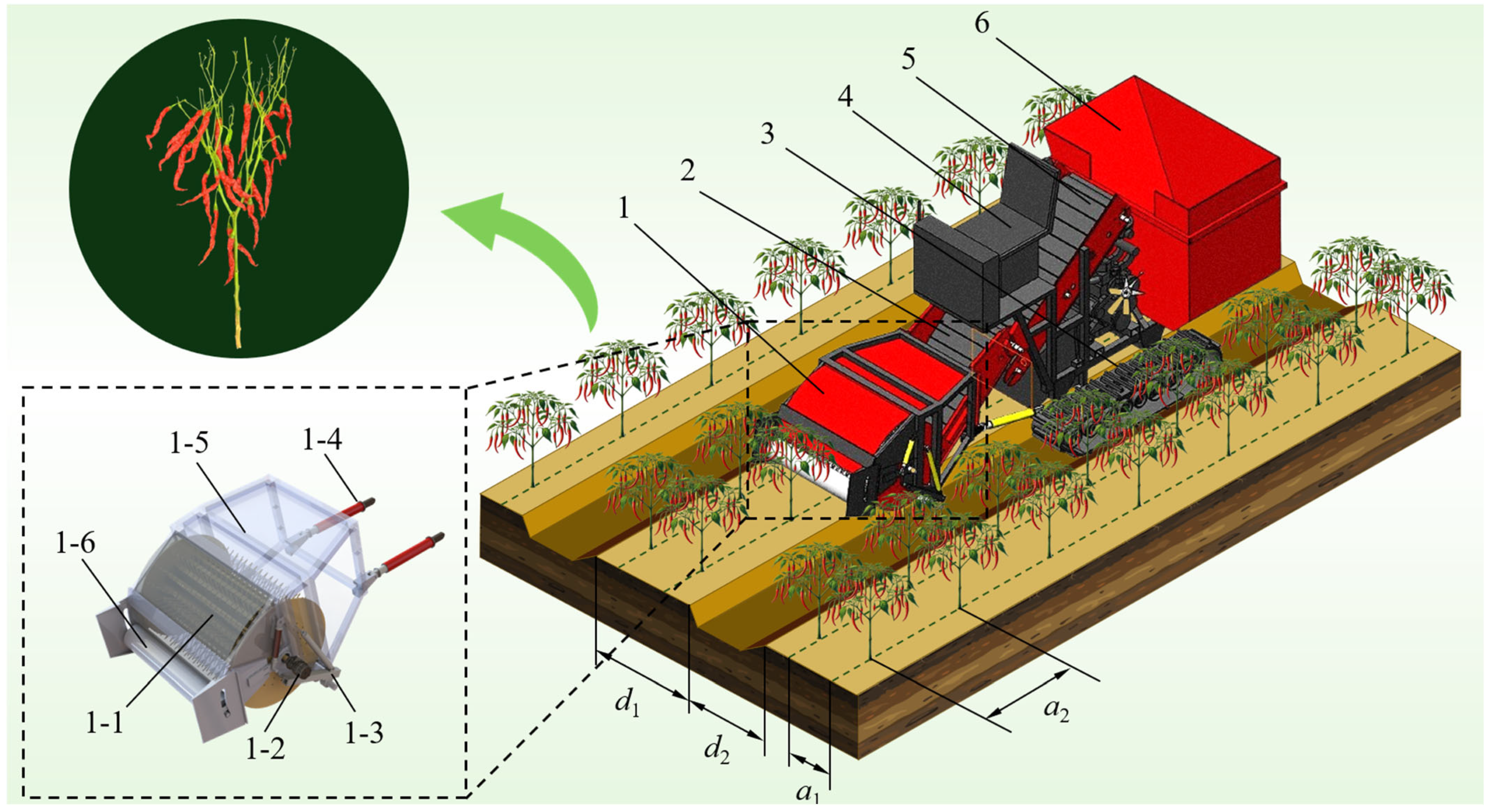



| Parameters | Value (mm) |
|---|---|
| Ridge width d1 | 600 |
| Ridge trench width d2 | 300~500 |
| Row spacing a1 | 350~450 |
| Plant spacing a2 | 212~347 |
| Item | Design Parameters |
|---|---|
| Structure form | Crawler self-propelled |
| Size (L × W × H) (mm × mm × mm) | 5138 × 1694 × 2634 |
| Structure quality (kg) | 1500 |
| Type of diesel engine | 4TE45 |
| Rated power of engine (kW) | 39 |
| Rated speed of engine (r·min−1) | 2400 |
| Driving speed (m·s−1) | 0~8 |
| Wheelbase (mm) | 1300 |
| Working rows | 1 |
| Working width (mm) | 1100 |
| Parameter | Maximum Value | Minimum Value | Average Value |
|---|---|---|---|
| Culm diameter at fruiting/mm | 6 | 3.5 | 4.9 |
| Plant height/mm | 900 | 700 | 780 |
| Fruit height above ground/mm | 500 | 320 | 407 |
| Maximum diameter/mm | 440 | 200 | 293 |
| Pepper fruit length/mm | 210 | 140 | 176 |
| Pepper fruit width/g | 22 | 10 | 15.5 |
| Water content of pepper fruits (%) | 84.20 | 30.60 | 53.13 |
| Water content of pepper stalks (%) | 82.25 | 26.07 | 51.11 |
| Levels | Drum Rotational Speed ω/(r∙min−1) | Operating Speed Vm/(m∙s−1) | Tooth Spacing T/mm |
|---|---|---|---|
| −1 | 130 | 0.28 | 40 |
| 0 | 160 | 0.42 | 50 |
| 1 | 190 | 0.56 | 60 |
| NO. | X1 (ω) | X2 (Vm) | X3 (T) | Y1 (Cr) | Y2 (Pr) | Y3 (Sr) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 92.08 | 2.53 | 4.03 |
| 2 | 0 | 1 | 1 | 89.54 | 2.95 | 3.96 |
| 3 | 0 | 1 | −1 | 93.72 | 2.71 | 3.58 |
| 4 | −1 | 0 | −1 | 94.31 | 2.23 | 5.12 |
| 5 | 0 | 0 | 0 | 92.11 | 2.50 | 4.00 |
| 6 | 0 | −1 | −1 | 96.36 | 2.84 | 4.41 |
| 7 | −1 | 0 | 1 | 94.31 | 2.47 | 5.51 |
| 8 | 0 | 0 | 0 | 92.05 | 2.54 | 4.06 |
| 9 | 0 | −1 | 1 | 92.19 | 3.09 | 4.72 |
| 10 | 0 | 0 | 0 | 92.07 | 2.58 | 4.02 |
| 11 | 1 | 1 | 0 | 92.43 | 3.09 | 4.19 |
| 12 | 1 | −1 | 0 | 94.95 | 3.22 | 5.04 |
| 13 | 1 | 0 | 1 | 91.93 | 2.92 | 4.73 |
| 14 | 1 | 0 | −1 | 96.01 | 2.69 | 4.41 |
| 15 | 0 | 0 | 0 | 92.09 | 2.52 | 4.05 |
| 16 | −1 | 1 | 0 | 90.55 | 2.47 | 5.51 |
| 17 | −1 | −1 | 0 | 93.18 | 2.76 | 5.76 |
| Response Values | Source | Sum of Squares | Degree of Freedom | F-Value | p-Value |
|---|---|---|---|---|---|
| Y1 | Model | 47.77 | 9 | 8.03 | 0.0060 |
| X2 | 13.62 | 1 | 20.61 | 0.0027 | |
| X3 | 19.31 | 1 | 29.22 | 0.0010 | |
| X1X3 | 4.16 | 1 | 6.30 | 0.0404 | |
| X12 | 3.74 | 1 | 5.66 | 0.0490 | |
| X32 | 5.26 | 1 | 7.95 | 0.0258 | |
| Residual | 4.63 | 7 | |||
| Lack of fit | 4.63 | 3 | |||
| Pure error | 0.0020 | 4 | |||
| R2 | 0.9117 | ||||
| Cor total | 52.40 | 16 | |||
| Y2 | Model | 1.33 | 9 | 67.17 | <0.0001 |
| X1 | 0.6216 | 1 | 282.64 | <0.0001 | |
| X2 | 0.0595 | 1 | 27.06 | 0.0013 | |
| X3 | 0.0648 | 1 | 29.46 | 0.0010 | |
| X1X3 | 0.0132 | 1 | 6.01 | 0.0440 | |
| X22 | 0.5625 | 1 | 255.76 | <0.0001 | |
| Residual | 0.0154 | 7 | |||
| Lack of fit | 0.0119 | 3 | |||
| Pure error | 0.0035 | 4 | |||
| R2 | 0.9886 | ||||
| Cor total | 1.34 | 16 | |||
| Y3 | Model | 5.95 | 9 | 28.97 | 0.0001 |
| X1 | 1.23 | 1 | 53.97 | 0.0002 | |
| X2 | 0.9045 | 1 | 39.61 | 0.0004 | |
| X12 | 3.30 | 1 | 144.49 | <0.0001 | |
| X22 | 0.1817 | 1 | 7.96 | 0.0257 | |
| Residual | 0.1599 | 7 | |||
| Lack of fit | 0.1576 | 3 | |||
| Pure error | 0.0023 | 4 | |||
| R2 | 0.9739 | ||||
| Cor total | 6.11 | 16 |
| Item | Design Parameters |
|---|---|
| Drum rotational speed/(rad·s−1) | 0~300 |
| Plant operating speed/(m·s−1) | 0~3 |
| Power of picking/kW | 7.5 |
| Power of conveying/kW | 2.5 |
| Picking width/mm | 1050 |
| Drum diameter/mm | 850 |
| Conveyor belt length/mm | 12,000 |
| NO. | ω /(r·min−1) | Vm /(m·s−1) | T /(mm) | Measured Value | Projected Value | Relative Error | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cr (%) | Pr (%) | Sr (%) | Cr (%) | Pr (%) | Sr (%) | Cr (%) | Pr (%) | Sr (%) | ||||
| T1 | 160 | 0.56 | 60 | 89.73 | 2.96 | 3.99 | 90.34 | 2.90 | 3.90 | 0.68 | 2.02 | 2.25 |
| T2 | 190 | 0.28 | 50 | 94.71 | 3.21 | 5.16 | 92.53 | 3.27 | 5.08 | 2.30 | 1.87 | 1.55 |
| T3 | 130 | 0.56 | 50 | 90.62 | 2.43 | 5.45 | 91.71 | 2.53 | 5.18 | 1.20 | 4.12 | 4.95 |
| T4 | 182 | 0.42 | 40 | 95.13 | 2.66 | 3.95 | 93.36 | 2.60 | 3.99 | 1.86 | 2.26 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Qin, X.; Lei, J.; Yang, J.; Zhang, J.; Lu, L.; Wang, Z. Parameter Optimization and Experimental Study of Drum with Elastic Tooth Type Loss-Reducing Picking Mechanism of Pepper Harvester. Agriculture 2025, 15, 600. https://doi.org/10.3390/agriculture15060600
Wang B, Qin X, Lei J, Yang J, Zhang J, Lu L, Wang Z. Parameter Optimization and Experimental Study of Drum with Elastic Tooth Type Loss-Reducing Picking Mechanism of Pepper Harvester. Agriculture. 2025; 15(6):600. https://doi.org/10.3390/agriculture15060600
Chicago/Turabian StyleWang, Bingpeng, Xinyan Qin, Jin Lei, Jiaxuan Yang, Jianglong Zhang, Lijian Lu, and Zhi Wang. 2025. "Parameter Optimization and Experimental Study of Drum with Elastic Tooth Type Loss-Reducing Picking Mechanism of Pepper Harvester" Agriculture 15, no. 6: 600. https://doi.org/10.3390/agriculture15060600
APA StyleWang, B., Qin, X., Lei, J., Yang, J., Zhang, J., Lu, L., & Wang, Z. (2025). Parameter Optimization and Experimental Study of Drum with Elastic Tooth Type Loss-Reducing Picking Mechanism of Pepper Harvester. Agriculture, 15(6), 600. https://doi.org/10.3390/agriculture15060600






