Field Ridge Segmentation and Navigation Line Coordinate Extraction of Paddy Field Images Based on Machine Vision Fused with GNSS
Abstract
:1. Introduction
- (1)
- Embedded Real-time Semantic Segmentation System: A bilateral semantic segmentation network model (BiSeNet) is utilized to detect paddy field ridges. The system is optimized and deployed on the Jetson AGX Xavier platform, employing the TensorRT inference engine to facilitate the real-time detection of paddy field ridges.
- (2)
- Multi-sensor Dynamic Perception Architecture: By integrating machine vision, GNSS, and AHRS (Attitude and Heading Reference System), a dynamic measurement model for the camera’s height above the ground is developed. An advanced, comprehensive inverse perspective mapping (IPM) algorithm is formulated to enable real-time transformation from image coordinates to navigation coordinates, irrespective of the camera’s pose.
- (3)
- Comprehensive Terrain Validation and Systematic Evaluation: A visual navigation testing platform for the rice transplanter is established, and field experiments are performed without prior boundary information. The results of these experiments validate the system’s accuracy, real-time performance, and stability in autonomously acquiring navigation and positioning data for paddy field ridges.
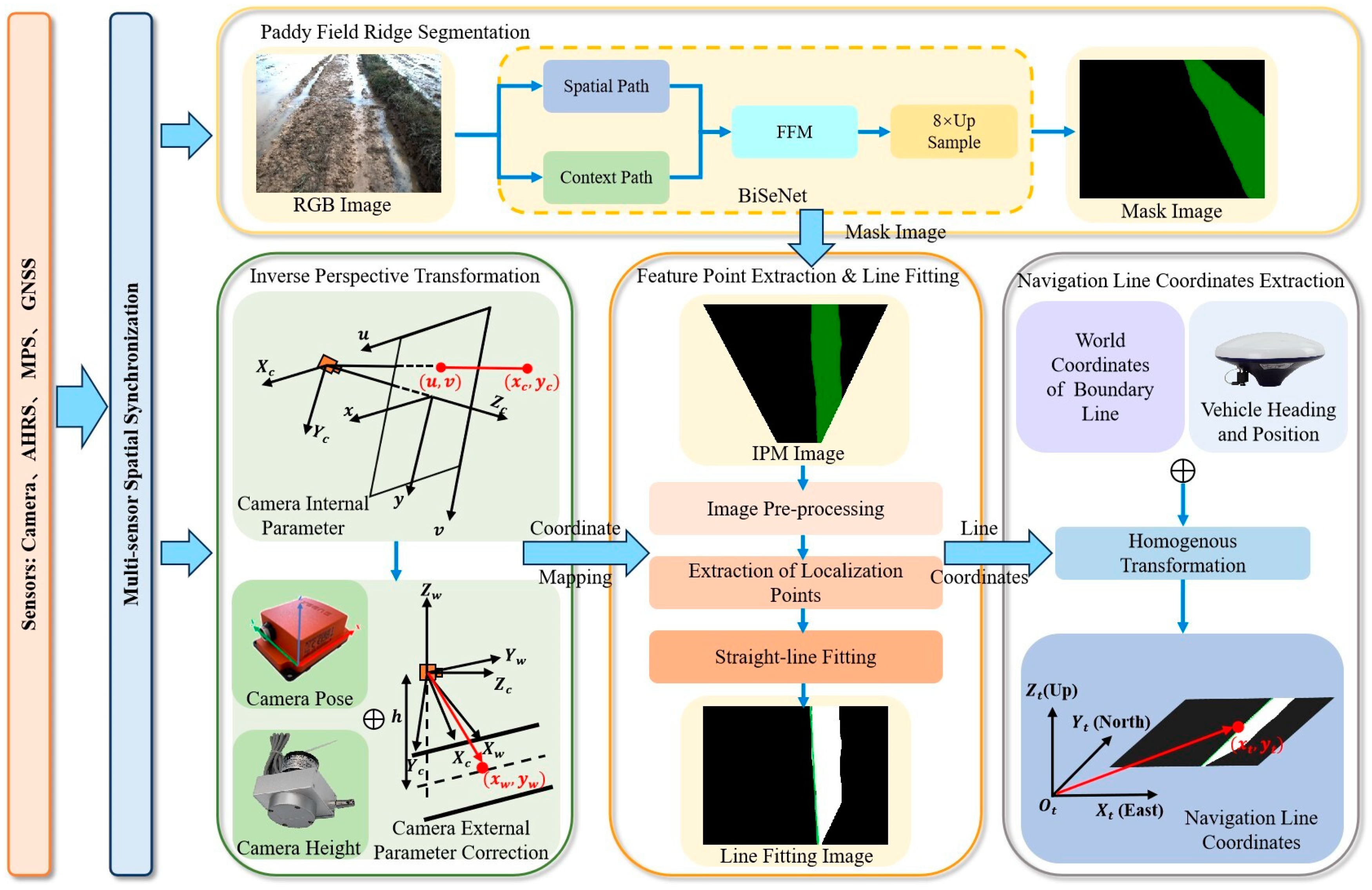
2. Materials and Methods
2.1. Platform Configuration
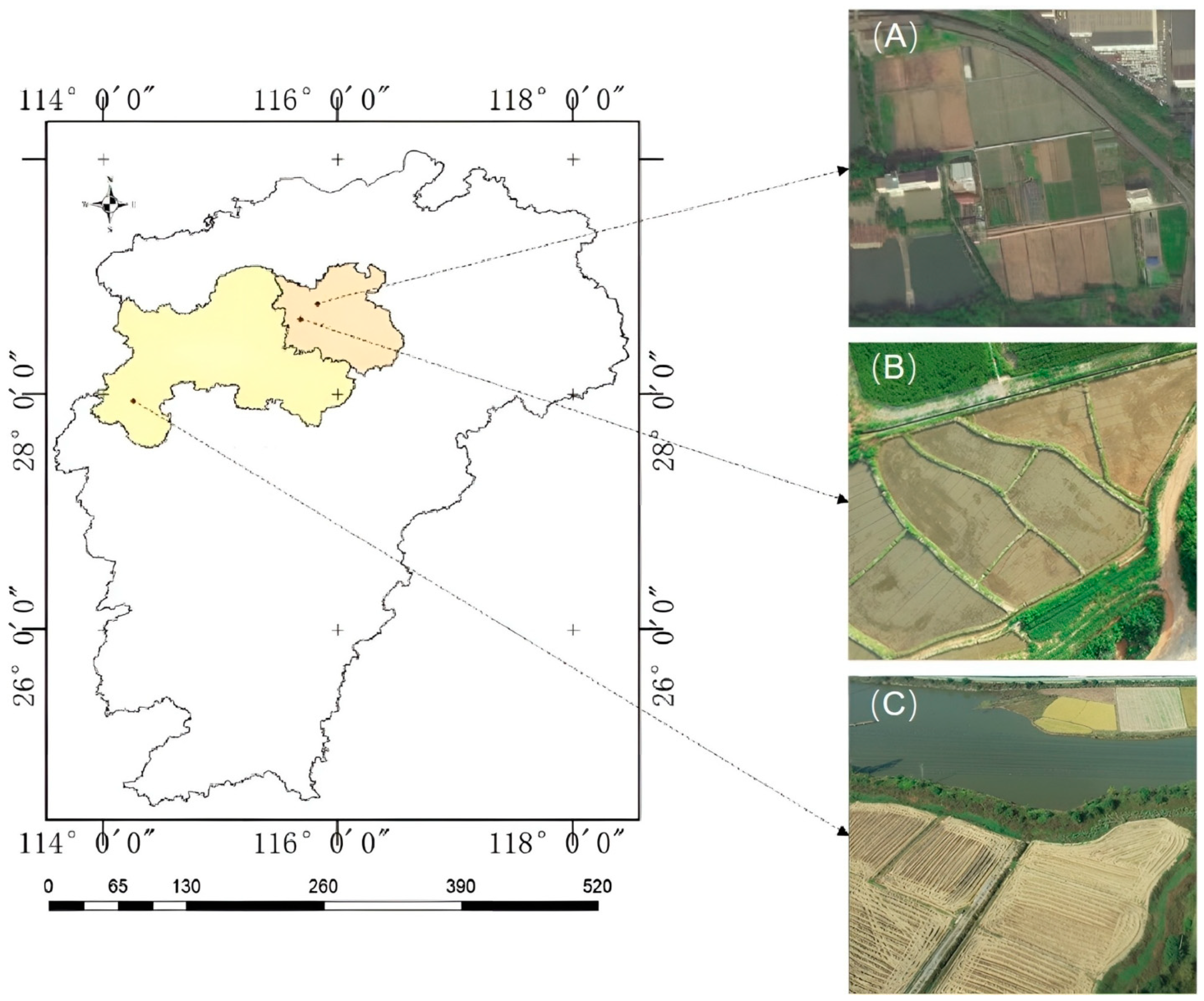
2.2. Image Acquisition and Dataset Construction
- (1)
- Image Acquisition
- (2)
- Dataset construction
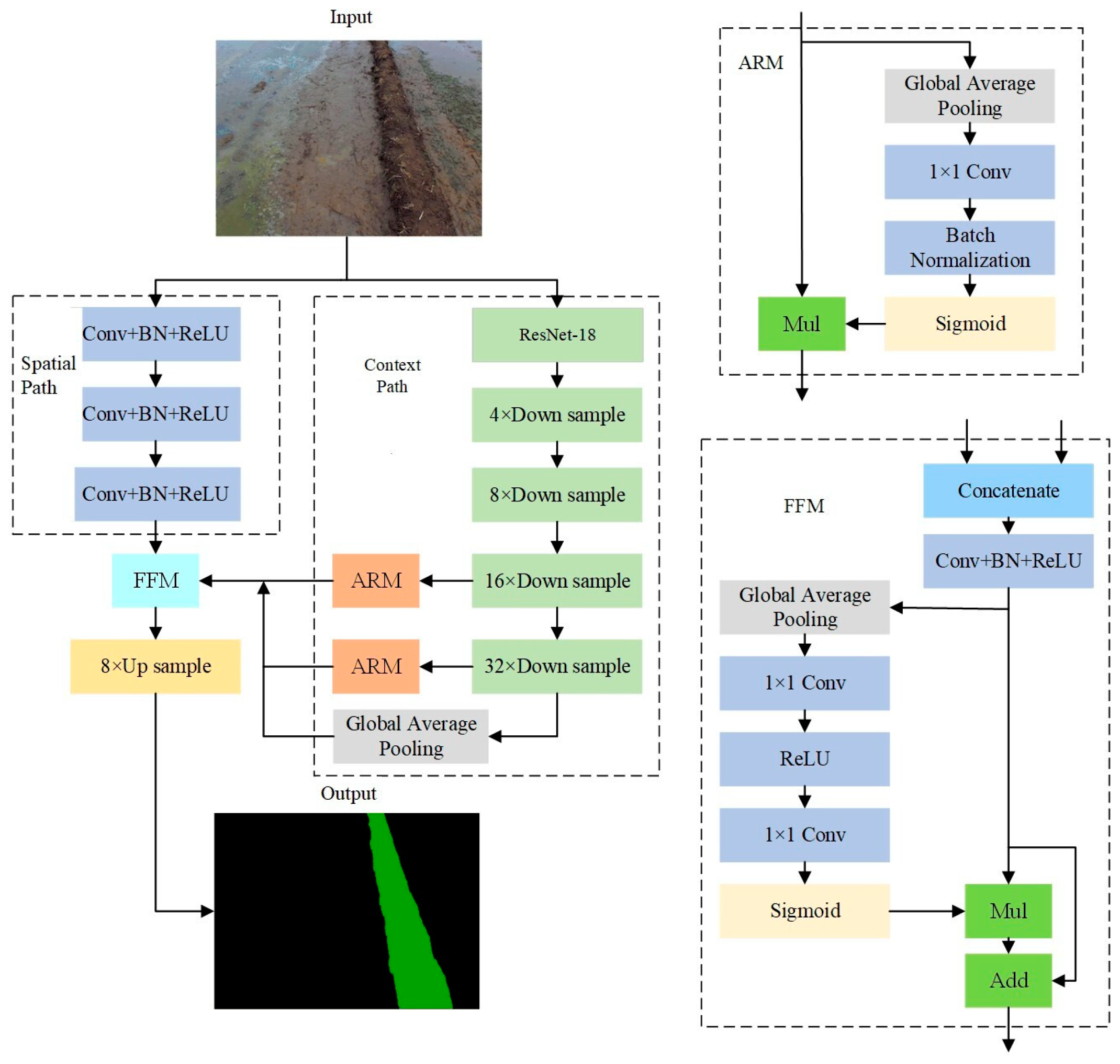
2.3. BiSeNet Network Model
2.4. Navigation Line Fitting for Paddy Field Ridges
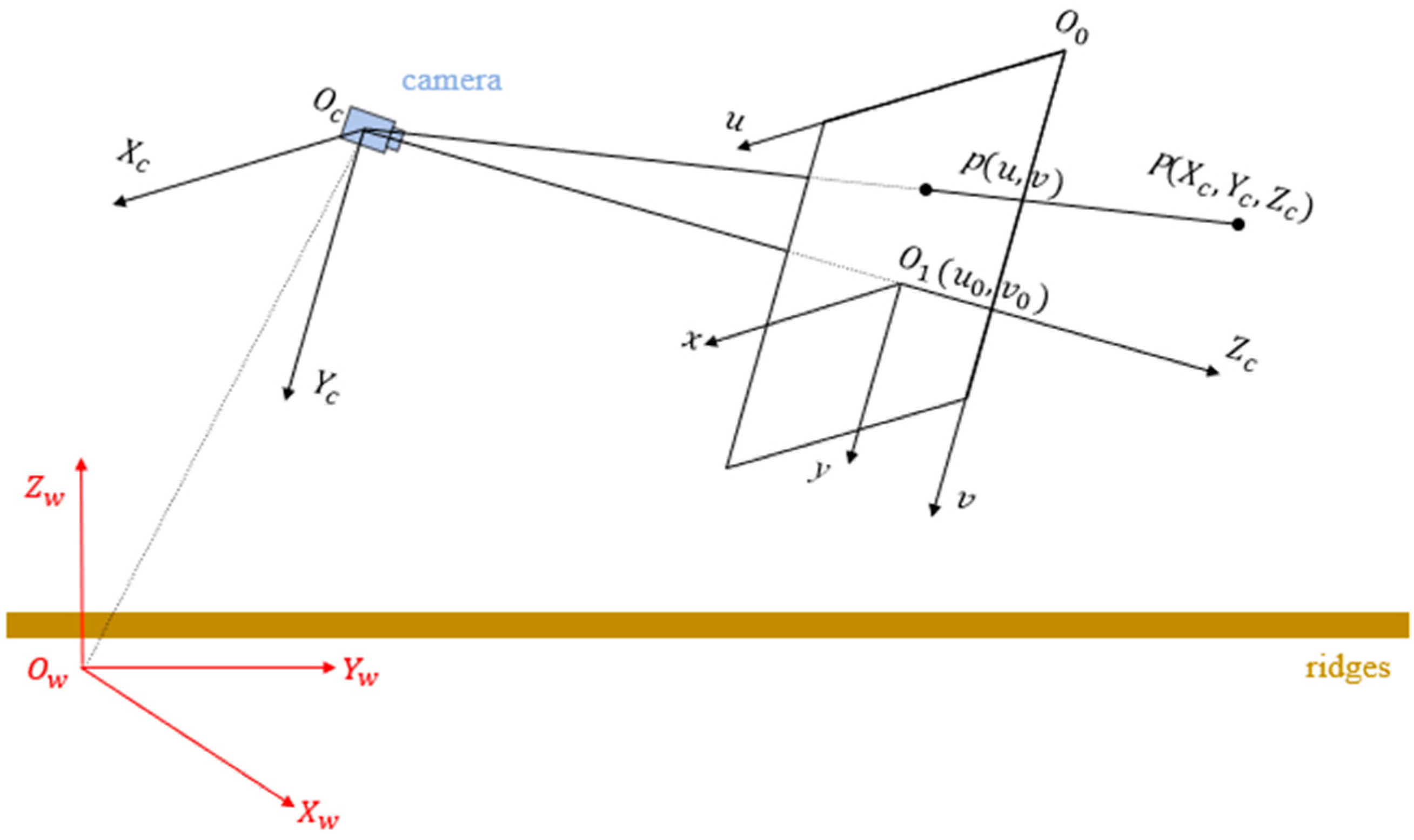
2.5. Acquisition of an Aerial View of Paddy Field Ridges Based on Inverse Perspective Transformation
- (1)
- Inverse perspective transformation
- (2)
- Camera roll attitude correction
- (3)
- Camera height parameter correction
2.6. Straight-Line Fitting of Paddy Field Ridges Based on Distance Transformation
- (1)
- Image pre-processing
- (2)
- Extraction of localization points for paddy field ridges
- (3)
- Straight-line fitting of paddy field ridges
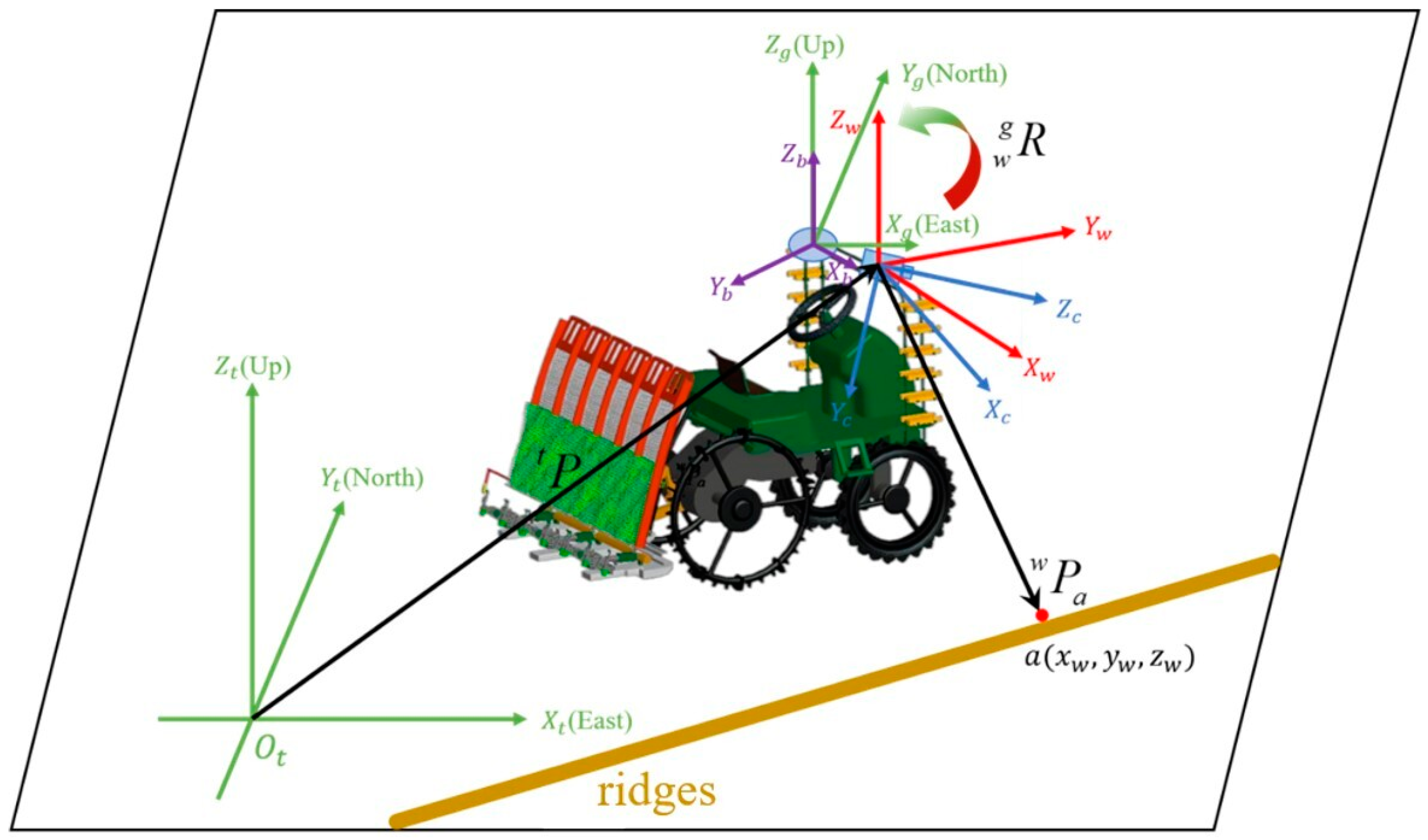
2.7. Coordinate Extraction of Navigation Lines of Paddy Field Ridges Based on Homogeneous Coordinate Transformation
3. Results and Analysis
3.1. Recognition of Paddy Field Ridges
- (1)
- Model training
- (2)
- Model deployment
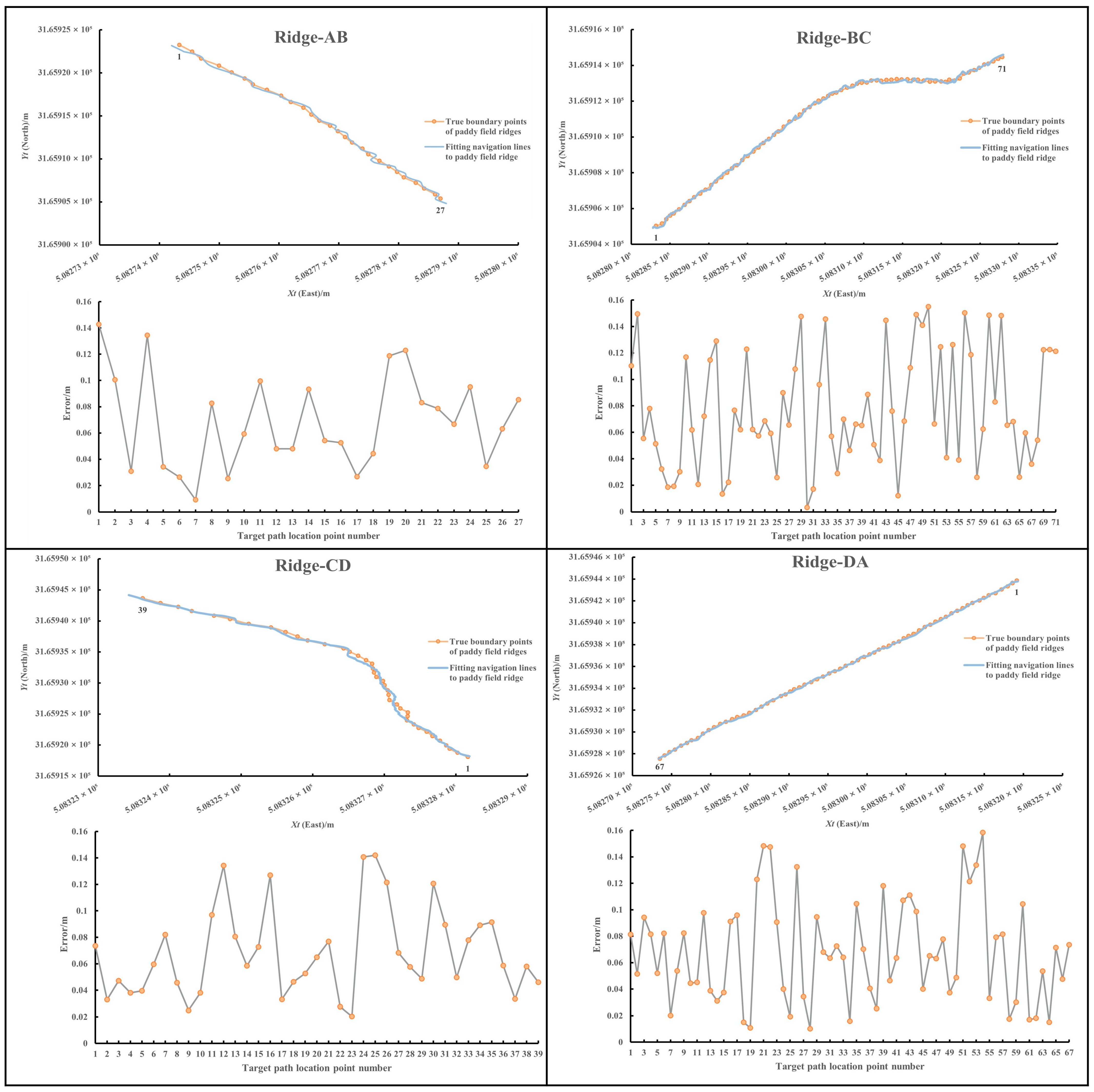
3.2. Navigation Line Coordinate Extraction
4. Discussion
- (1)
- Constraints in Data-Driven Generalization: The limited availability of open benchmark datasets for agricultural environments presents a substantial challenge. The self-constructed paddy field dataset exhibits constraints in both sample size and environmental diversity [32]. To address these limitations, future research will focus on developing a heterogeneous agricultural scene dataset through data acquisition across multiple regions and climatic conditions. Furthermore, the integration of self-supervised learning and domain adaptation techniques will be explored to minimize dependence on manual annotations and enhance the model’s generalization capabilities.
- (2)
- Navigation Integrity in Complex Environments: Effective field path planning and autonomous navigation for rice transplanters necessitate improved detection and localization of field headlands, facilitating precise distance estimation between the transplanter and the headland to enable automated turning maneuvers. Achieving this objective requires the refinement of the transplanter-to-headland distance estimation model, the development of autonomous steering control algorithms, and the online calibration of system parameters. Future investigations will integrate an extended Kalman filter (EKF) within a multi-sensor data fusion framework, with the system’s performance validated through autonomous field navigation experiments.
- (3)
- Challenges in Energy-Efficiency Optimization: The high computational demands of the Jetson AGX Xavier platform are accompanied by substantial energy consumption, constraining its deployment in resource-limited agricultural machinery. To mitigate this issue, subsequent research will prioritize algorithm optimization for computational efficiency, hardware acceleration (e.g., NVIDIA Jetson Xavier NX), and dynamic load scheduling strategies to achieve a balanced trade-off between system performance and energy efficiency across diverse operational scenarios.
5. Conclusions
- (1)
- To overcome the difficulty in extracting complex paddy field boundary information in hilly areas and the limitation in applying GNSS agricultural navigation, a semantic segmentation network was used to extract the paddy field boundary, and a paddy field ridge image dataset and a BiSeNet semantic segmentation model were constructed. The model training and testing results showed that the model’s pixel accuracy is 92.61%, the average intersection and merger ratio is 90.88%, and the model segmentation speed is up to 18.87 fps. In addition, we deployed the model on the Jetson AGX Xavier embedded development platform and optimized the BiSeNet model deployment using the TensorRT model inference framework. The experimental data showed that the optimized model deployment using TensorRT with FP16 data accuracy and a 1024 × 1024 model image input size had the best performance, with a real-time model segmentation speed of 26.31 fps, an average intersection and merger ratio of 90.62%, and a model pixel segmentation accuracy of 92.43%, which meets the requirements of the real-time segmentation of paddy field ridges in terms of speed and accuracy.
- (2)
- Since existing navigation line extraction techniques lack high-precision coordinate localization to support global path planning, we proposed a method that combines inverse perspective transformation and homogeneous coordinate transformation to accurately and reliably extract the navigation line coordinates of paddy field ridges. As inverse perspective transformation is not applicable to the unevenness of the hard bottom layer of paddy fields, we obtained the camera’s 3D attitude angle through the AHRS and designed a method and device to measure the height of the rice transplanter’s on-board camera from paddy fields based on a hydraulic profiling system so as to obtain the camera’s dynamic external parameter and improve the inverse perspective transformation.
- (3)
- The proposed method was realized on a rice transplanter, and tests were carried out in the actual field. The accuracy and real-time performance of the method for paddy field segmentation and navigation line coordinate extraction were verified by calculating the distance error between the fitted navigation line of the paddy field ridges and their real boundary. The test results showed that the average distance error is 0.071 m, the standard deviation is 0.039 m, and the overall time consumed is about 100 ms, which basically meets the accuracy and real-time requirements of navigation line extraction under a rice transplanter operation speed of 0.7 m s−1.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khadatkar, A.; Mathur, S.M.; Dubey, K.; BhusanaBabu, V. Development of Embedded Automatic Transplanting System in Seedling Transplanters for Precision Agriculture. Artif. Intell. Agric. 2021, 5, 175–184. [Google Scholar] [CrossRef]
- Duckett, T.; Pearson, S.; Blackmore, S.; Grieve, B.; Chen, W.-H.; Cielniak, G.; Cleaversmith, J.; Dai, J.; Davis, S.; Fox, C.; et al. Agricultural Robotics: The Future of Robotic Agriculture. arXiv 2018, arXiv:1806.06762. Available online: https://arxiv.org/abs/1806.06762 (accessed on 18 January 2024).
- Reddy Maddikunta, P.K.; Hakak, S.; Alazab, M.; Bhattacharya, S.; Gadekallu, T.R.; Khan, W.Z.; Pham, Q.-V. Unmanned Aerial Vehicles in Smart Agriculture: Applications, Requirements, and Challenges. IEEE Sens. J. 2021, 21, 17608–17619. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Cracknell, A.P. Remote Sensing Letters Contribution to the Success of the Sustainable Development Goals—N 2030 Agenda. Remote Sens. Lett. 2020, 11, 715–719. [Google Scholar] [CrossRef]
- Idoje, G.; Dagiuklas, T.; Iqbal, M. Survey for Smart Farming Technologies: Challenges and Issues. Comput. Electr. Eng. 2021, 92, 107104. [Google Scholar] [CrossRef]
- Bechar, A.; Vigneault, C. Agricultural Robots for Field Operations. Part 2: Operations and Systems. Biosyst. Eng. 2017, 153, 110–128. [Google Scholar] [CrossRef]
- dos Santos, A.F.; da Silva, R.P.; Zerbato, C.; de Menezes, P.C.; Kazama, E.H.; Paixão, C.S.S.; Voltarelli, M.A. Use of Real-Time Extend GNSS for Planting and Inverting Peanuts. Precis. Agric. 2019, 20, 840–856. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, H.; Fu, W.; Liu, M.; Yin, Y.; Zhao, C. Research Status and Prospects of Agricultural Machinery Autonomous Driving. Trans. Chin. Soc. Agric. Mach. 2023, 54, 1–24. [Google Scholar] [CrossRef]
- Zhou, J.; He, Y. Research Progress on Navigation Path Planning of Agricultural Machinery. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–14. [Google Scholar] [CrossRef]
- Zhang, H.; He, B.; Xing, J. Mapping Paddy Rice in Complex Landscapes with Landsat Time Series Data and Superpixel-Based Deep Learning Method. Remote Sens. 2022, 14, 3721. [Google Scholar] [CrossRef]
- Xie, B.; Jin, Y.; Faheem, M.; Gao, W.; Liu, J.; Jiang, H.; Cai, L.; Li, Y. Research Progress of Autonomous Navigation Technology for Multi-Agricultural Scenes. Comput. Electron. Agric. 2023, 211, 107963. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, B.; Xu, N.; Zhou, J.; Shi, J.; Diao, Z. Vision-Based Navigation and Guidance for Agricultural Autonomous Vehicles and Robots: A Review. Comput. Electron. Agric. 2023, 205, 107584. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, Z.; Zhang, X.; He, Y.; Fang, H. Application of Visual Inertia Fusion Technology in Rice Transplanter Operation. Comput. Electron. Agric. 2024, 221, 108990. [Google Scholar] [CrossRef]
- Alsalam, B.H.Y.; Morton, K.; Campbell, D.; Gonzalez, F. Autonomous UAV with Vision Based On-Board Decision Making for Remote Sensing and Precision Agriculture. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–12. [Google Scholar]
- Adhikari, S.P.; Kim, G.; Kim, H. Deep Neural Network-Based System for Autonomous Navigation in Paddy Field. IEEE Access 2020, 8, 71272–71278. [Google Scholar] [CrossRef]
- Sevak, J.S.; Kapadia, A.D.; Chavda, J.B.; Shah, A.; Rahevar, M. Survey on Semantic Image Segmentation Techniques. In Proceedings of the 2017 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, Thirupur, India, 7–8 December 2017; pp. 306–313. [Google Scholar]
- Alsaeed, D.; Bouridane, A.; El-Zaart, A. A Novel Fast Otsu Digital Image Segmentation Method. Int. Arab. J. Inf. Technol. 2016, 13, 427–434. [Google Scholar]
- Wang, Q.; Liu, H.; Yang, P.; Meng, Z. Detection Method of Headland Boundary Line Based on Machine Vision. Trans. Chin. Soc. Agric. Mach. 2020, 51, 18–27. [Google Scholar]
- Pandey, R.; Lalchhanhima, R. Segmentation Techniques for Complex Image: Review. In Proceedings of the 2020 International Conference on Computational Performance Evaluation (ComPE), Shillong, India, 2–4 July 2020; pp. 804–808. [Google Scholar]
- Li, Y.; Hong, Z.; Cai, D.; Huang, Y.; Gong, L.; Liu, C. A SVM and SLIC Based Detection Method for Paddy Field Boundary Line. Sensors 2020, 20, 2610. [Google Scholar] [CrossRef]
- Jafari, M.H.; Samavi, S. Iterative Semi-Supervised Learning Approach for Color Image Segmentation. In Proceedings of the 2015 9th Iranian Conference on Machine Vision and Image Processing (MVIP), Tehran, Iran, 18–19 November 2015; pp. 76–79. [Google Scholar]
- Jiang, Q.; Fang, S.; Peng, Y.; Gong, Y.; Zhu, R.; Wu, X.; Ma, Y.; Duan, B.; Liu, J. UAV-Based Biomass Estimation for Rice-Combining Spectral, TIN-Based Structural and Meteorological Features. Remote Sens. 2019, 11, 890. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation Nowcasting Using a Small Attention-UNet Architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Zhang, Z.; Fang, H. Automated Detection of Boundary Line in Paddy Field Using MobileV2-UNet and RANSAC. Comput. Electron. Agric. 2022, 194, 106697. [Google Scholar] [CrossRef]
- Liu, X.; Qi, J.; Zhang, W.; Bao, Z.; Wang, K.; Li, N. Recognition Method of Maize Crop Rows at the Seedling Stage Based on MS-ERFNet Model. Comput. Electron. Agric. 2023, 211, 107964. [Google Scholar] [CrossRef]
- Choi, K.H.; Han, S.K.; Han, S.H.; Park, K.-H.; Kim, K.-S.; Kim, S. Morphology-Based Guidance Line Extraction for an Autonomous Weeding Robot in Paddy Fields. Comput. Electron. Agric. 2015, 113, 266–274. [Google Scholar] [CrossRef]
- Chen, J.; Qiang, H.; Wu, J.; Xu, G.; Wang, Z. Navigation Path Extraction for Greenhouse Cucumber-Picking Robots Using the Prediction-Point Hough Transform. Comput. Electron. Agric. 2021, 180, 105911. [Google Scholar] [CrossRef]
- Fu, D.; Jiang, Q.; Qi, L.; Xing, H.; Chen, Z.; Yang, X. Detection of the centerline of rice seedling belts based on region growth sequential clustering-RANSAC. Trans. CSAE 2023, 39, 47–57. [Google Scholar] [CrossRef]
- Fragoso, V.; Sweeney, C.; Sen, P.; Turk, M. ANSAC: Adaptive Non-Minimal Sample and Consensus. arXiv 2017, arXiv:1709.09559. Available online: https://arxiv.org/abs/1709.09559 (accessed on 21 November 2024).
- Diao, Z.; Guo, P.; Zhang, B.; Zhang, D.; Yan, J.; He, Z.; Zhao, S.; Zhao, C. Maize Crop Row Recognition Algorithm Based on Improved UNet Network. Comput. Electron. Agric. 2023, 210, 107940. [Google Scholar] [CrossRef]
- Wang, T.; Chen, B.; Zhang, Z.; Li, H.; Zhang, M. Applications of Machine Vision in Agricultural Robot Navigation: A Review. Comput. Electron. Agric. 2022, 198, 107085. [Google Scholar] [CrossRef]
- Hong, Z.; Li, Y.; Lin, H.; Gong, L.; Liu, C. Field Boundary Distance Detection Method in Early Stage of Planting Based on Binocular Vision. Field Boundary Distance Detection Method. in Early Stage of Plantin Based on Binocular Vision. Trans. Chin. Soc. Agric. Mach. 2022, 53, 27–33+56. [Google Scholar]
- Masiero, A.; Sofia, G.; Tarolli, P. Quick 3D With UAV and TOF Camera For Geomorphometric Assessment. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Nice, France, 31 August–2 September 2020; XLIII-B1. pp. 259–264. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, H.; Zhang, M.; Li, S.; Cao, R.; Li, H. Design of Point Cloud Acquisition System for Farmland Environment Based on LiDAR. Trans. Chin. Soc. Agric. Mach. 2019, 50, 1–7. [Google Scholar]
- Wang, S.; Song, J.; Qi, P.; Yuan, C.; Wu, H.; Zhang, L.; Liu, W.; Liu, Y.; He, X. Design and Development of Orchard Autonomous Navigation Spray System. Front. Plant Sci. 2022, 13, 960686. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Liu, Z.; Huang, F.; Liu, C. Rice Rows Detection and Navigation Information Extraction Method—Based on Camera Pose. J. Agric. Mech. Res. 2024, 46, 15–21. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Zhu, Z.; Li, Z.; Du, Y.; Mao, E. Tractor Path Tracking Control Based on Binocular Vision. Inf. Process. Agric. 2018, 5, 422–432. [Google Scholar] [CrossRef]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. BiSeNet: Bilateral Segmentation Network for Real-Time Semantic Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 325–341. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Aly, M. Real Time Detection of Lane Markers in Urban Streets. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 7–12. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- He, J.; He, J.; Luo, X.; Li, W.; Man, Z.; Feng, D. Rice Row Recognition and Navigation Control Based on Multi-sensor Fusion. Trans. Chin. Soc. Agric. Mach. 2022, 53, 18–26+137. [Google Scholar] [CrossRef]
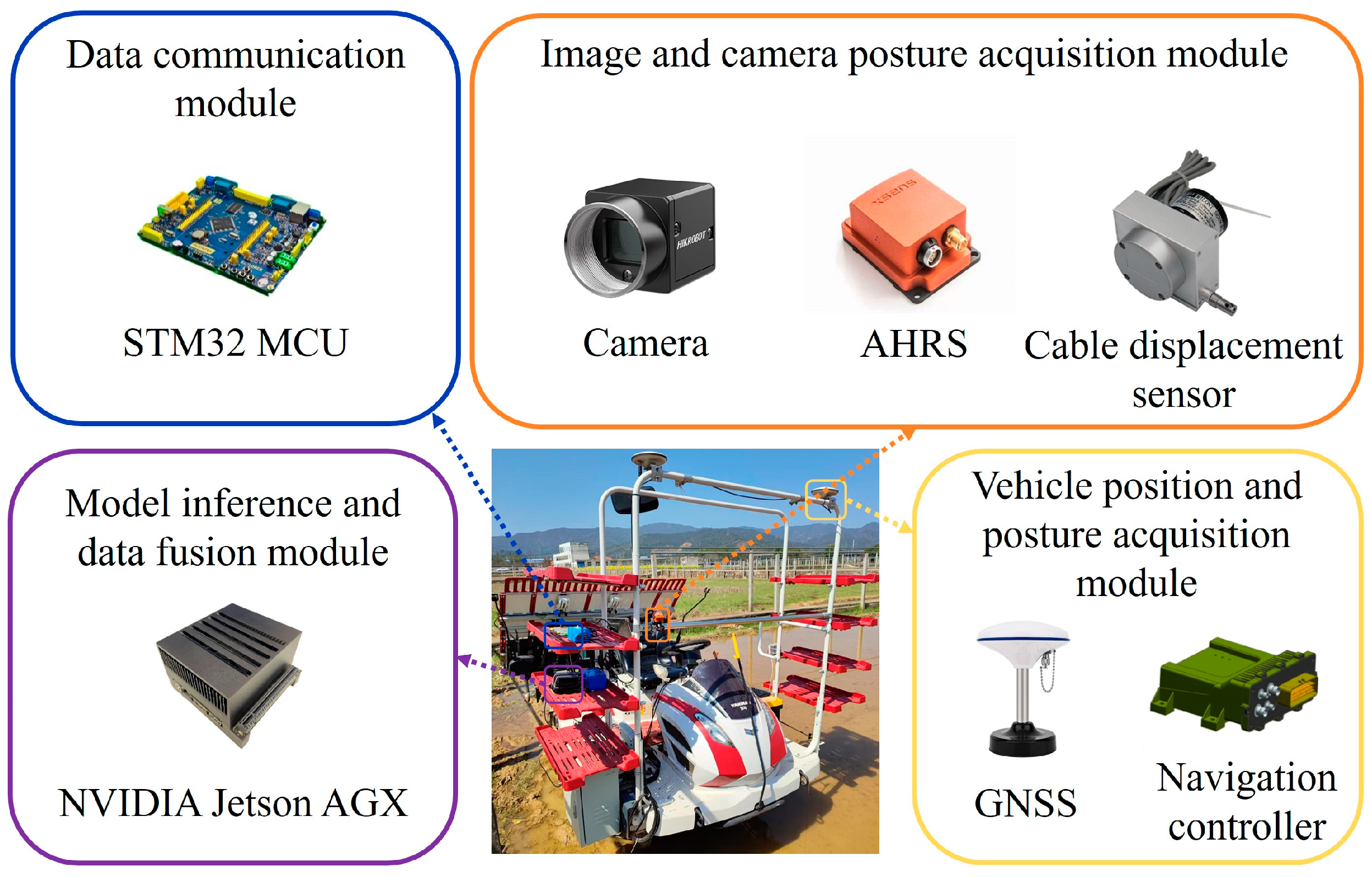
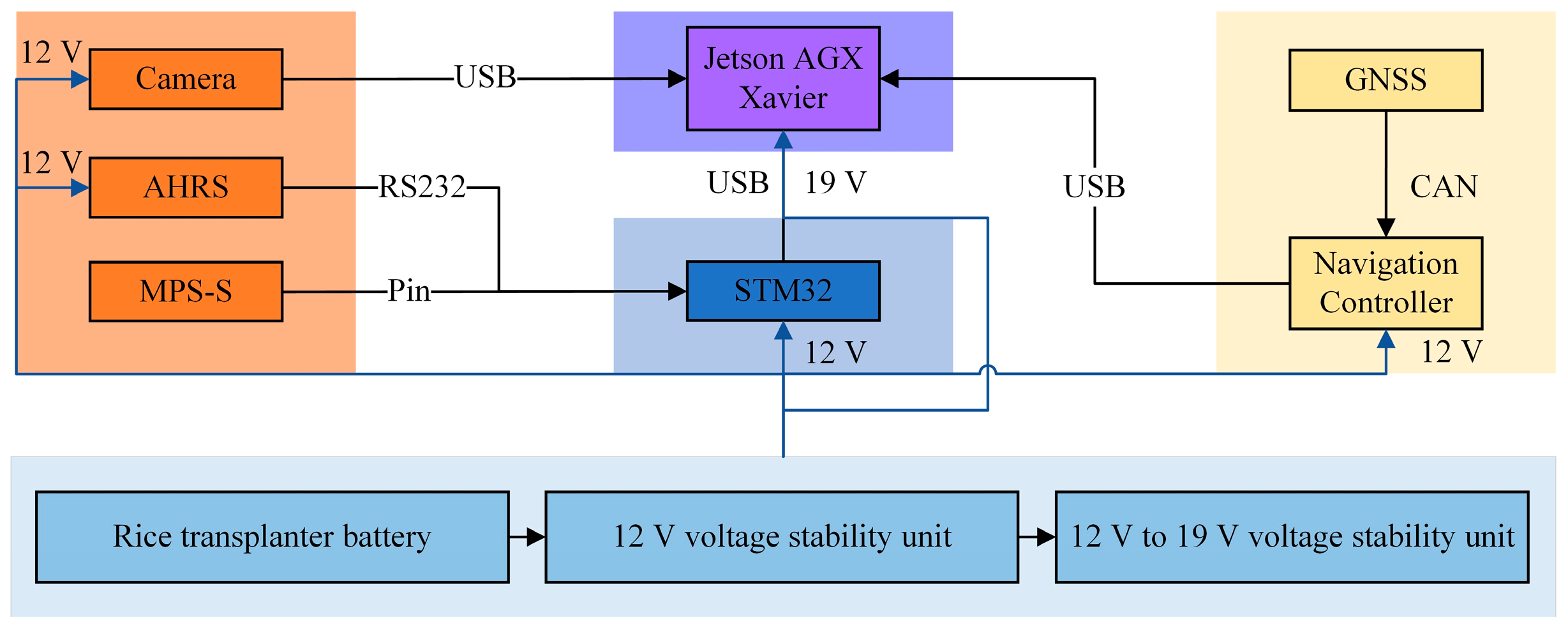







| Sensors | Models | Parameters |
|---|---|---|
| Camera | MV-CA016-10UC | Sensor model: IMX273 |
| Sensor type: CMOS | ||
| Resolution: 1440 × 1080 | ||
| Maximum frame rate: 249.1 fps | ||
| Connector: USB3.0 | ||
| AHRS | MTi-300 (Xsens) | Roll (RMS): 0.2° |
| Pitch (RMS): 0.2° | ||
| Yaw (RMS): 1.0° | ||
| Cable displacement sensor | MPS-S-1000-V2 | Sensor range (mm): 100–2500 mm |
| Signal output (V): 0–10 V | ||
| GNSS | UM982 | Channels: 1408 |
| Satellite: BDS/GPS/GLONASS/Galileo/QZSS | ||
| Orientation Accuracy: 0.1°/1 m Baseline | ||
| RTK(RMS): 0.8 cm ± 1 ppm (horizontal), 1.5 cm ± 1 ppm (vertical) | ||
| Output frequency: 20 Hz |
| Model | Acc (%) | mIoU (%) | Segmentation Speed (fps) |
|---|---|---|---|
| PSPNet | 89.39 | 82.89 | 6.67 |
| UNet | 89.86 | 84.24 | 6.81 |
| Deeplabv3+ | 93.12 | 86.41 | 6.46 |
| BiSeNet | 92.61 | 90.88 | 18.87 |
| Model | Performance Indicator | Image Resolution | |
|---|---|---|---|
| 1024 × 1024 | 512 × 1024 | ||
| PyTorch-FP32 | fps | 5.4933 | 5.6395 |
| MB | 102.55 | 102.55 | |
| mIoU | 90.8403% | 88.9504% | |
| Acc | 92.5697% | 90.1361% | |
| TensorRT-FP32 | fps | 11.2456 | 20.3995 |
| MB | 130.56 | 128.84 | |
| mIoU | 90.6256% | 81.7504% | |
| Acc | 92.4321% | 86.1361% | |
| TensorRT-FP16 | fps | 26.31269 | 38.6020 |
| MB | 26.76 | 26.91 | |
| mIoU | 90.6245% | 81.7621% | |
| Acc | 92.4313% | 86.1439% | |
| TensorRT-INT8 | fps | 34.8101 | 42.6858 |
| MB | 16.02 | 14.54 | |
| mIoU | 86.5943% | 78.0418% | |
| Acc | 88.4083% | 82.3285% | |
| Ridge | Distance Error (m) | |||
|---|---|---|---|---|
| Maximum | Minimum | Average | Standard Deviation | |
| AB | 0.143 | 0.009 | 0.069 | 0.036 |
| BC | 0.155 | 0.003 | 0.077 | 0.043 |
| CD | 0.142 | 0.020 | 0.068 | 0.033 |
| DA | 0.158 | 0.010 | 0.068 | 0.039 |
| Total | 0.158 | 0.003 | 0.071 | 0.039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wu, X.; Fang, P.; Zhang, W.; Chen, X.; Zhao, R.; Liu, Z. Field Ridge Segmentation and Navigation Line Coordinate Extraction of Paddy Field Images Based on Machine Vision Fused with GNSS. Agriculture 2025, 15, 627. https://doi.org/10.3390/agriculture15060627
Liu M, Wu X, Fang P, Zhang W, Chen X, Zhao R, Liu Z. Field Ridge Segmentation and Navigation Line Coordinate Extraction of Paddy Field Images Based on Machine Vision Fused with GNSS. Agriculture. 2025; 15(6):627. https://doi.org/10.3390/agriculture15060627
Chicago/Turabian StyleLiu, Muhua, Xulong Wu, Peng Fang, Wenyu Zhang, Xiongfei Chen, Runmao Zhao, and Zhaopeng Liu. 2025. "Field Ridge Segmentation and Navigation Line Coordinate Extraction of Paddy Field Images Based on Machine Vision Fused with GNSS" Agriculture 15, no. 6: 627. https://doi.org/10.3390/agriculture15060627
APA StyleLiu, M., Wu, X., Fang, P., Zhang, W., Chen, X., Zhao, R., & Liu, Z. (2025). Field Ridge Segmentation and Navigation Line Coordinate Extraction of Paddy Field Images Based on Machine Vision Fused with GNSS. Agriculture, 15(6), 627. https://doi.org/10.3390/agriculture15060627






