Experimental Study on Loosening and Vibration Characteristics of Vibrating Screen Bolts of Combine Harvester
Abstract
1. Introduction
2. Materials and Methods
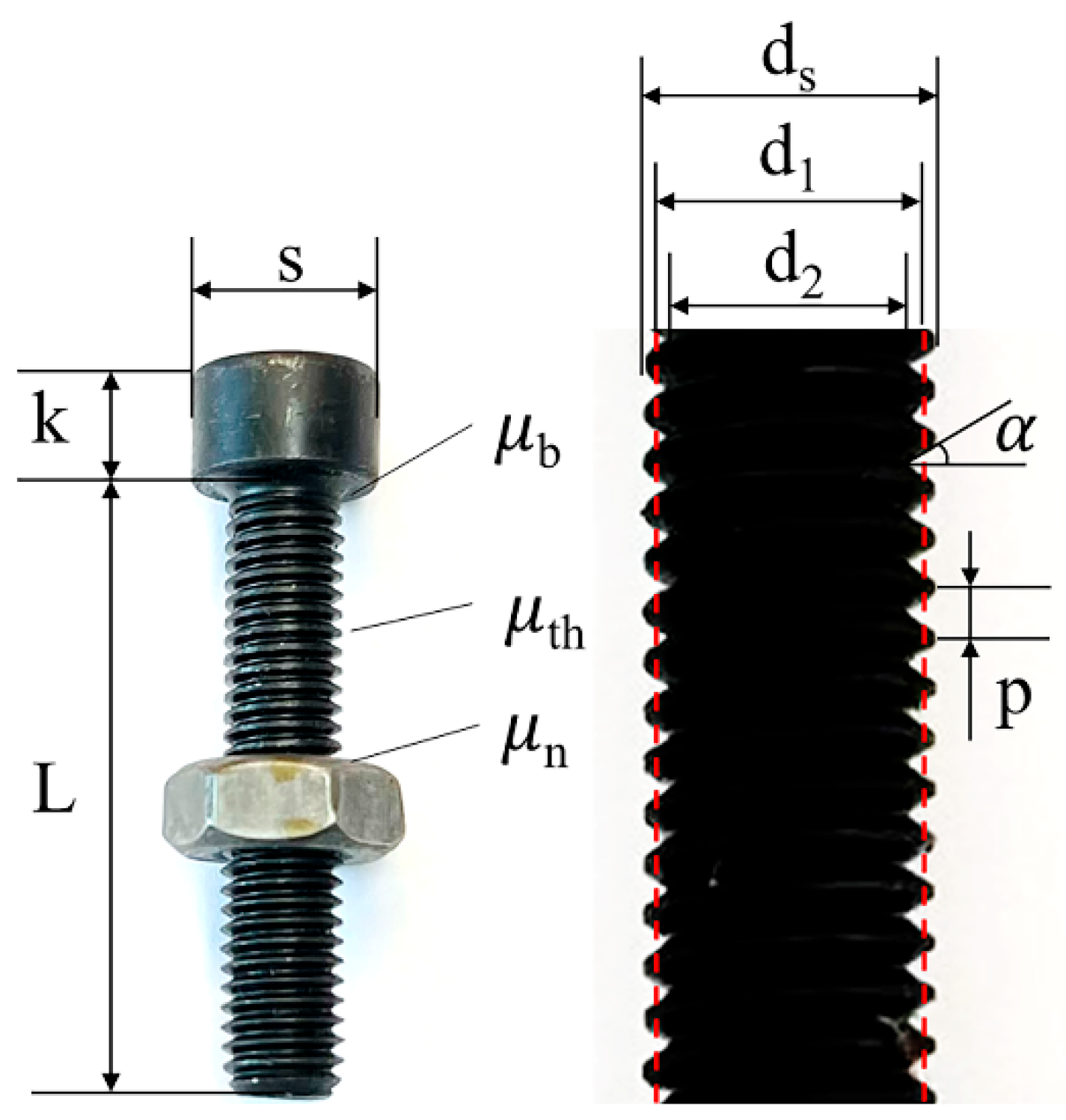
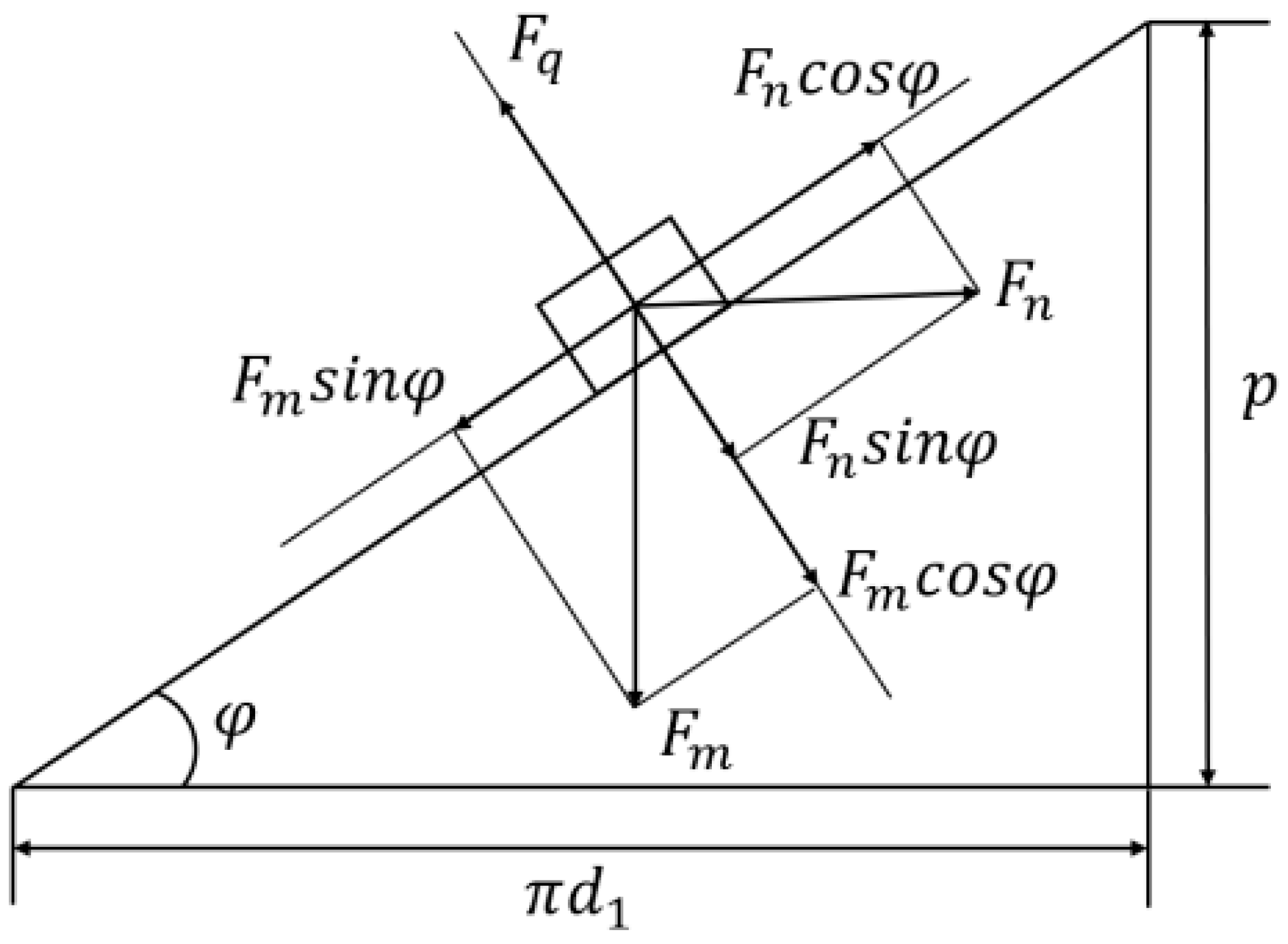
2.1. Mechanical Model of Bolt Tightening
- (1)
- Friction Torque of the Bolt-Nut Mating Thread Pair (ML)
- (2)
- Friction Torque (MK) Between the Nut or Bolt Head and the Connection Plate
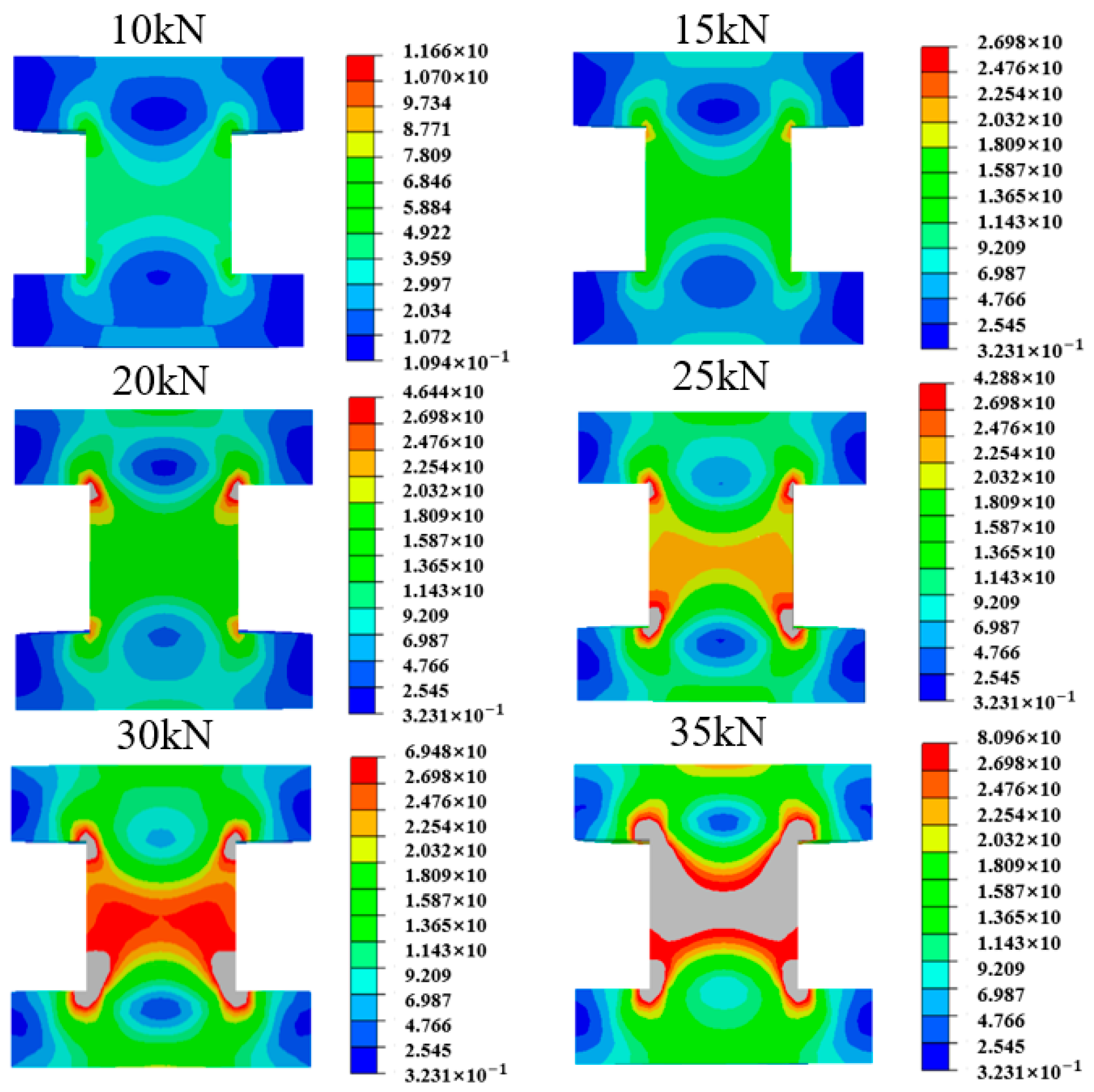
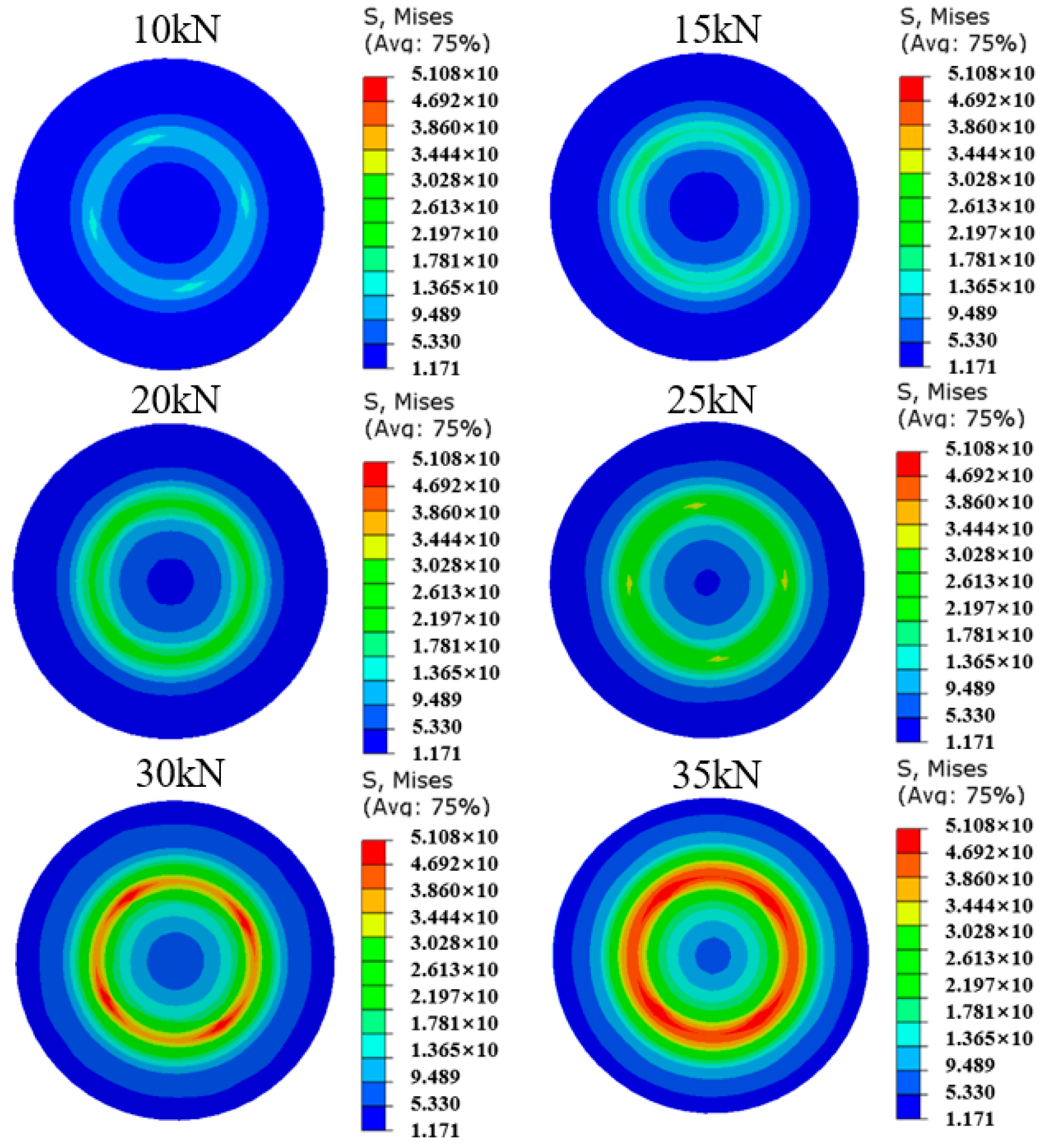
2.2. Finite Element Simulation of Bolt Preload
Determination of Bolt Preload
2.3. Simulation Analysis of Bolt Axial Preload
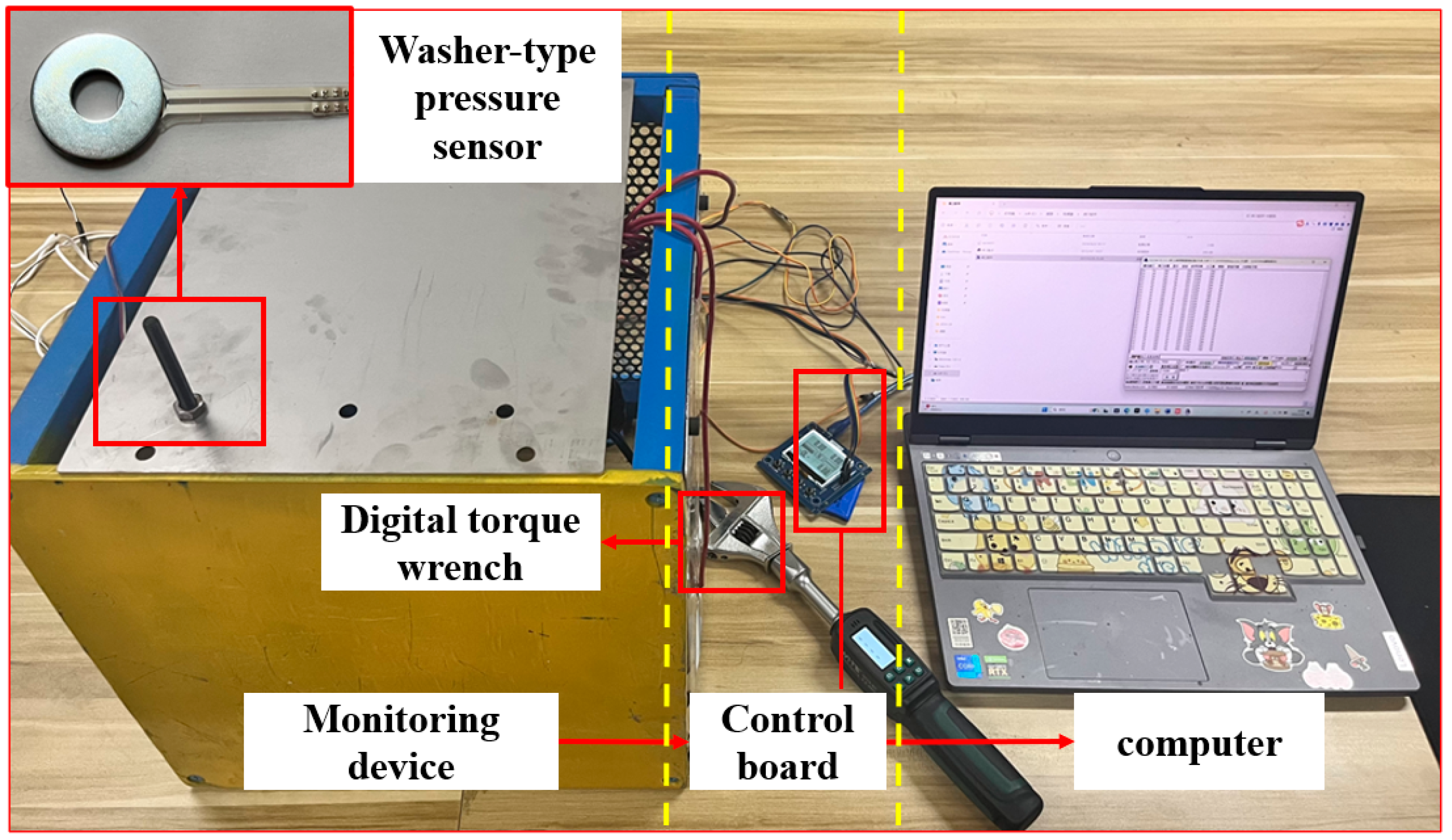
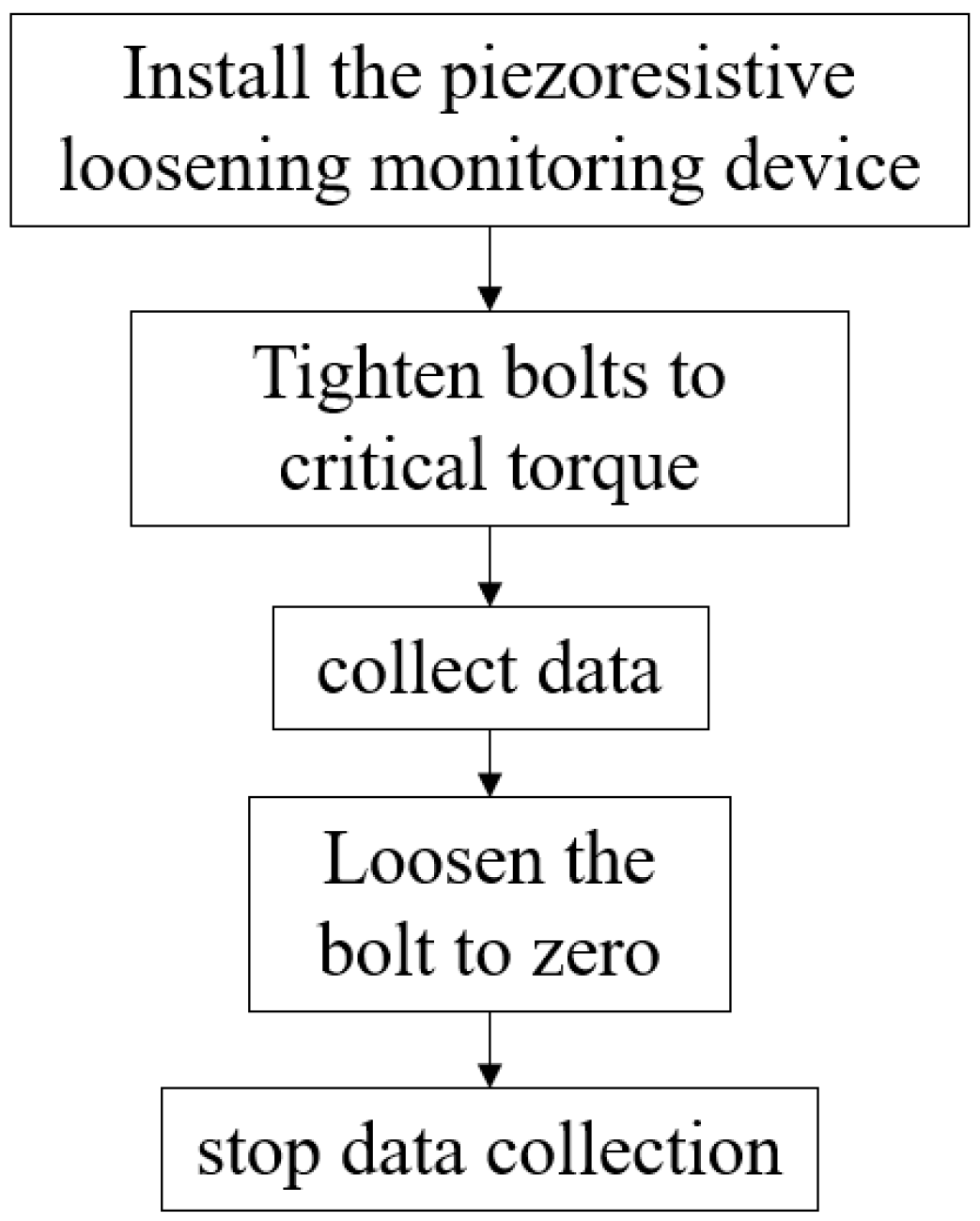
2.4. Single-Bolt Loosening Test
Single-Bolt Loosening Condition Setting
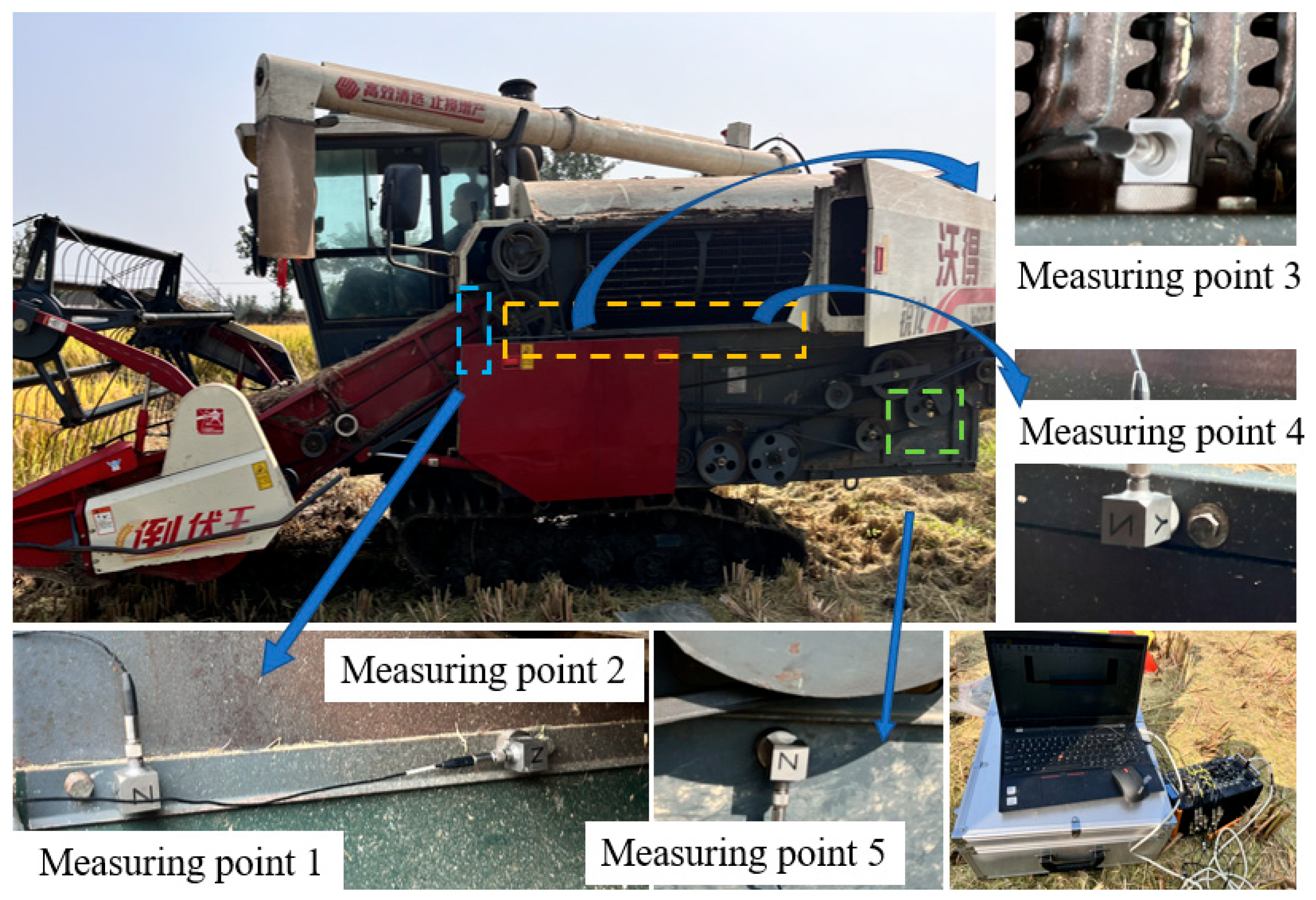
2.5. Vibration Test of Vibrating Screen Connection Bolts
2.5.1. Composition of Vibration Testing System
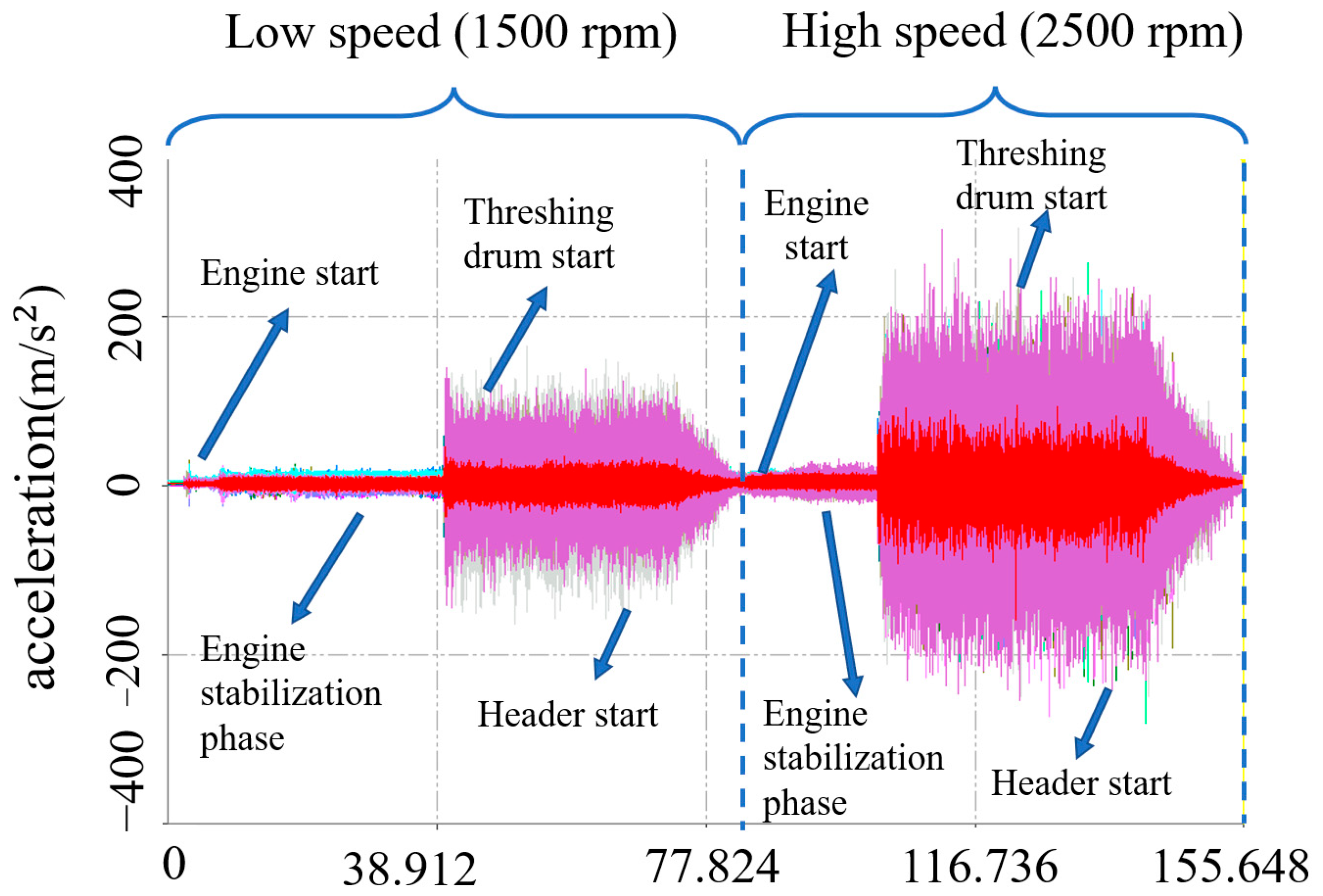
2.5.2. Experimental Plan and Procedure
3. Results and Discussion
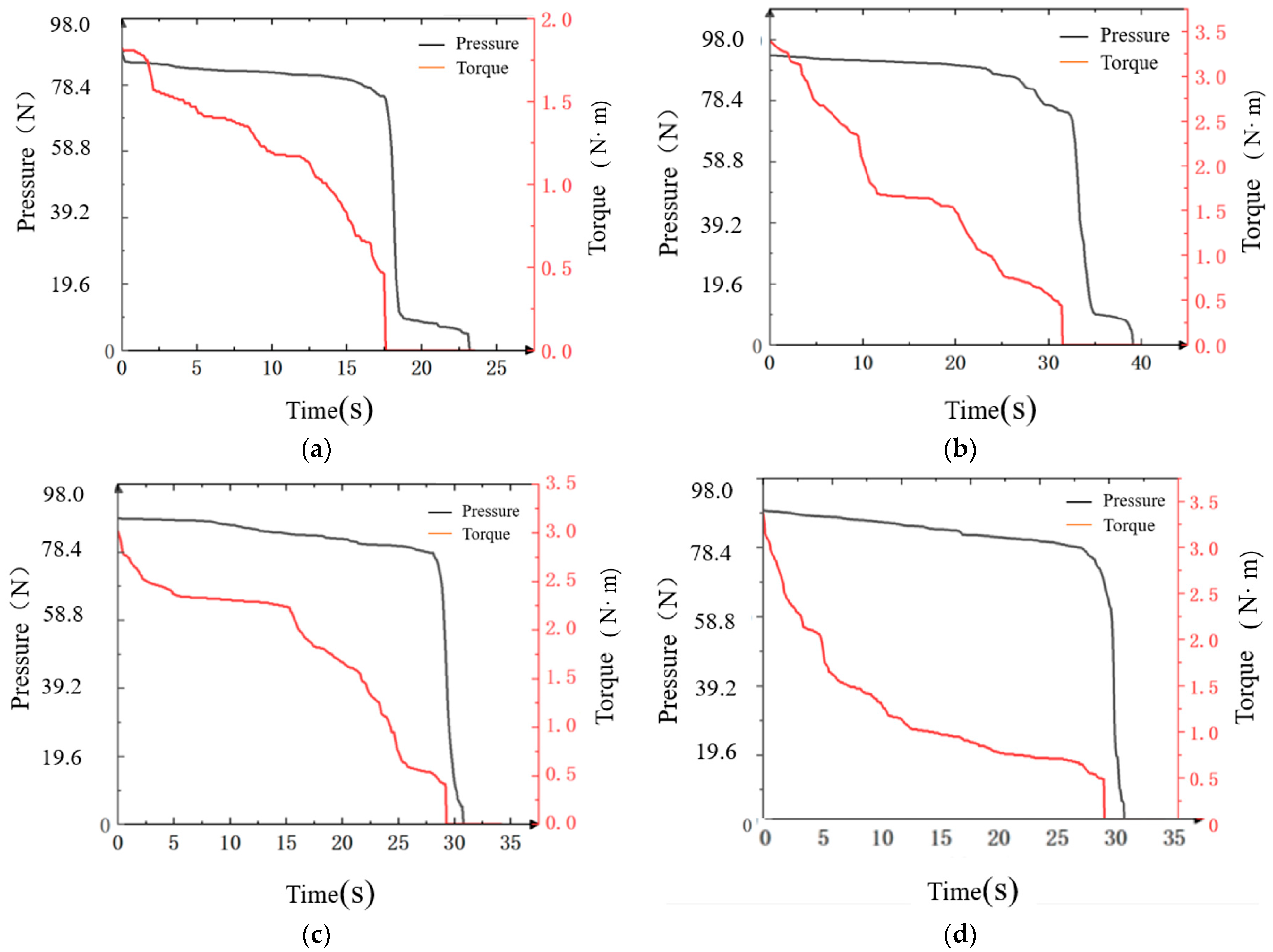
3.1. Analysis of Single-Bolt Test Data
3.2. Vibration Characteristics Analysis of Connection Bolts
3.2.1. Kurtosis Factor Analysis of Vibration Response
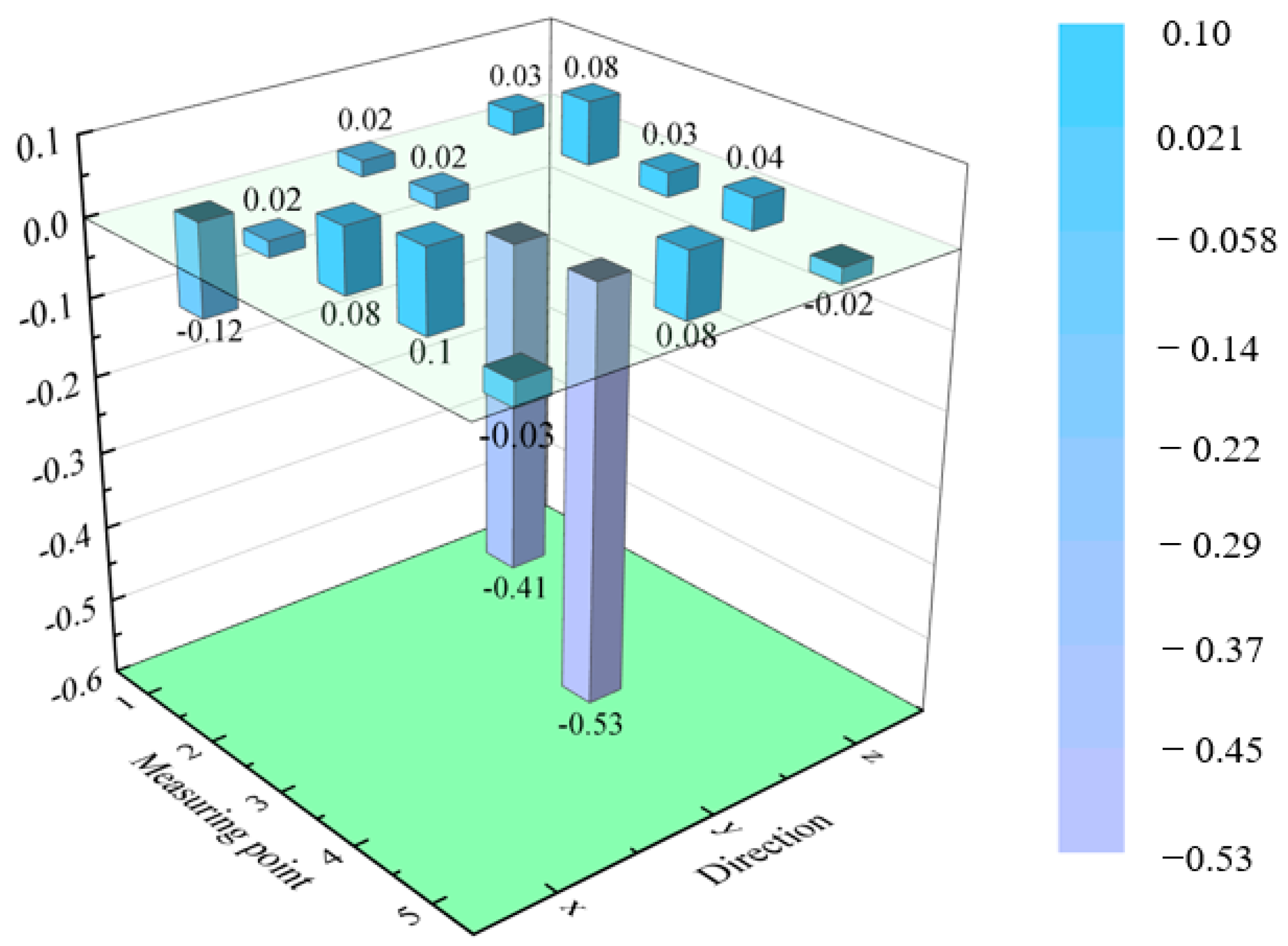
3.2.2. Skewness Factor Analysis of Vibration Response
3.2.3. Analysis of Vibration Response Margin Factor
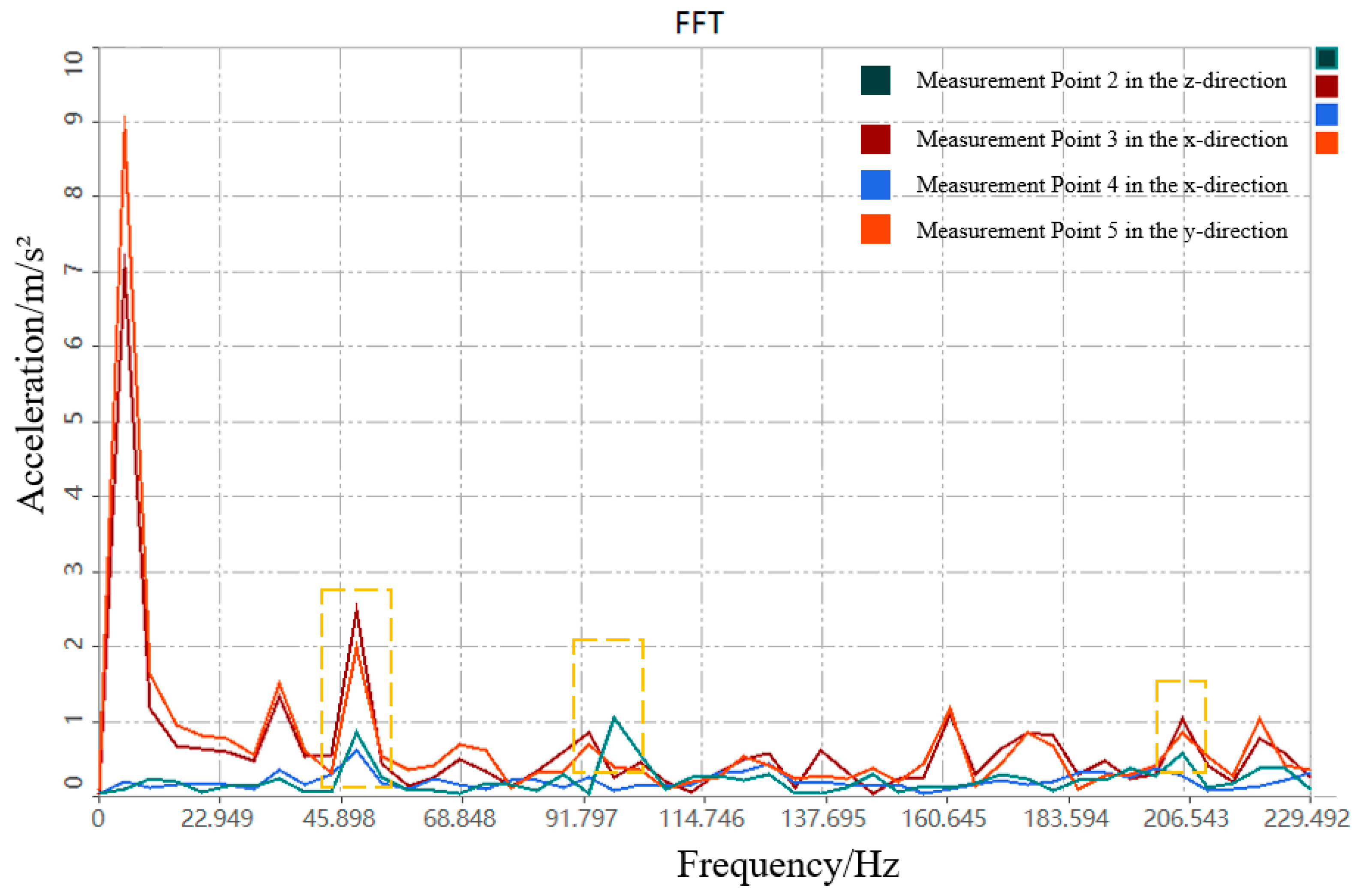
3.2.4. Frequency Spectrum Analysis of Vibration Response
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, M.; Liang, Z.; Zhang, J.; Xu, L.; Song, X. A robust prediction method based on Kriging method and fuzzy c-means algorithm with application to a combine harvester. Struct. Multidiscip. Optim. 2022, 65, 260. [Google Scholar] [CrossRef]
- Lu, E.; Tian, Z.; Xu, L.; Ma, Z.; Luo, C. Observer-based robust cooperative formation tracking control for multiple combine harvesters. Nonlinear Dyn. 2023, 111, 15109–15125. [Google Scholar]
- Wang, Y.; Liu, X.; Li, Z.; Feng, Z.; Pan, C.; Zhang, J.; Xu, J. Nitsche-based isogeometric approach for free vibration analysis of laminated plate with multiple stiffeners and cutouts. Int. J. Mech. Sci. 2023, 244, 108041. [Google Scholar]
- Cao, Z.; Dai, J.; Xu, W.; Chang, C. Bearing Fault Diagnosis with Frequency Sparsity Learning. Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar]
- Zhou, Y.; Ji, J.; Zhao, W.; Zhu, S.; Liu, H. Modulated Vibration Reduction Design for Integral-Slot Interior Permanent Magnet Synchronous Machines. Trans. Ind. Electron. 2022, 69, 12249–12260. [Google Scholar]
- Qi, G.; Ma, L.; Bortolotti Rossini, M.; Schroeder, K. Vibration of a Satellite Structure with Composite Lattice Truss Core Sandwich Panels. Aia J. 2022, 60, 3389–3401. [Google Scholar] [CrossRef]
- Zhang, B.; Tan, C.A.; Liu, Z.; Hu, Z. Nonstationary time-frequency characteristics of vehicle suspension systems based on evolutionary power spectral density. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Fan, W.; Chen, Z.; Li, Y.; Zhu, F.; Xie, M. A Reinforced Noise Resistant Correlation Method for Bearing Condition Monitoring. Trans. Autom. Sci. Eng. 2023, 20, 995–1006. [Google Scholar] [CrossRef]
- Yuan, Y.; Jin, R.; Tang, L. Numerical Investigation on the Flow-Induced Vibration Characteristics of Fire Turbopump with the Turbine-Pump Structure. Appl. Sci. 2022, 12, 4650. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Shen, X.; Liu, X.; Zhang, J.; Ren, N. Free vibration analysis of stiffened rectangular plate with cutouts using Nitsche based IGA method. Thin-Walled Struct. 2022, 181, 109975. [Google Scholar]
- Sakai, T. Investigations of Bolt Loosening Mechanisms: 1st Report, On the Bolts of Transversely Loaded Joints. Bull. JSME 1978, 21, 1385–1390. [Google Scholar]
- Yamamoto, K. Investigations on the Self-loosening of Threaded Fasteners under Transverse Vibration—A Solution for Self-loosening Mechanism. Precis. Mach. 1977, 43, 82–87. [Google Scholar]
- Jiang, W.Q.; Mo, Z.; Wang, T.; Zhang, Q.; Yang, L.Q.; Zhang, W. Loosening process of bolted connection in transmission tower under transverse cyclic load. Structures 2025, 73, 108399. [Google Scholar]
- Sun, C.Y.; Liu, C.H.; Yuan, J.H. Mechanical behavior analysis of fully grouted bolts under shear throughout the entire elastic–plastic process. Eng. Fail. Anal. 2025, 171, 109340. [Google Scholar]
- Chen, H.; Dai, S.; Ou, M.; Li, S.; Wang, C.; Li, Z.; Wang, G.; Chen, Y.; Jia, W. Multibody Dynamics Simulation and Vibration Test for High Clearance Orchard Sprayer. Appl. Sci. 2022, 12, 8058. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, S.; Guo, L.H.; Qu, J.Y.; Wang, S. Ultimate tensile behavior of bolted T-stub connections with preload. Build. Eng. 2022, 47. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans. 2022, 129, 555–563. [Google Scholar] [CrossRef]
- Jiménez-Peña, C.; Lavatelli, A.; Balcaen, R.; Zappa, E.; Debruyne, D. A Novel Contactless Bolt Preload Monitoring Method Using Digitallmage Correlation. J. Nondestruct. Eval. 2021, 40, 54. [Google Scholar]
- Li, J.; Liang, Z.; Zhu, F.; Liu, C. Optimum of Grain Loss Sensors by Analyzing Effects of Grain Collision Attitude on Signal Characteristics. Electronics 2022, 11, 3187. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, J.; Xu, L.; Cai, Q.; Yu, X.; Liu, P. Impurity/Breakage Assessment of Vehicle-Mounted Dynamic Rice Grain Flow on Combine Harvester Based on Improved Deeplabv3+ and YOLOv4. IEEE Access 2023, 11, 49273–49288. [Google Scholar]
- Zhao, W.; Zhu, S.; Ji, J.; Liu, G.; Mao, Y. Analysis and Reduction of Electromagnetic Vibration in Fractional-Slot Concentrated-Windings PM Machines. Trans. Ind. Electron. 2022, 69, 3357–3367. [Google Scholar]
- Xue, H.; Ding, D.; Zhang, Z.; Wu, M.; Wang, H. A Fuzzy System of Operation Safety Assessment Using Multimodel Linkage and Multistage Collaboration for In-Wheel Motor. Trans. Fuzzy Syst. 2022, 30, 999–1013. [Google Scholar]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault identification of hydraulic pump using deep adaptive normalized CNN and synchrosqueezed wavelet transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar]
- Tang, S.; Zhu, Y.; Yuan, S. An adaptive deep learning model towards fault diagnosis of hydraulic piston pump using pressure signal. Eng. Fail. Anal. 2022, 138, 106300. [Google Scholar]
- Zhou, H.T.; Jia, W.D.; Li, Y.; Ou, M.X. Method for Estimating Canopy Thickness Using Ultrasonic Sensor Technology. Agriculture 2022, 11, 1011. [Google Scholar]
- Zhang, F.; Chen, Z.J.; Wang, Y.F.; Bao, R.F.; Chen, X.G.; Fu, S.L.; Tian, M.M.; Zhang, Y.K. Research on Flexible End-Effectors with Humanoid Grasp Function for Small Spherical Fruit Picking. Agriculture 2023, 13, 123. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Srivastava, A.; Deng, J.; Li, Z.; Raza, A.; Khadke, L.; Yu, Z.; El-Rawy, M. Forecasting vapor pressure deficit for agricultural water management using machine learning in semi-arid environments. Agric. Water Manag. 2023, 283, 108302. [Google Scholar]
- Huda, F.; Kajiwara, I.; Hosoya, N.; Kawamura, S. Bolt loosening analysis and diagnosis by non-contact laser excitation vibration tests. Mech. Syst. Signal Process. 2013, 40, 589–604. [Google Scholar]
- Xu, Z.; Yu, X.C.; Li, H.; Xu, P.Y.; Gu, D.W.; Han, Q.K.; Wen, B.C. Nonlinear vibration characteristics of fiber-reinforced composite thin-walled conical-cylindrical coupled shells under partial bolt looseness. Thin-Walled Struct. 2025, 209, 112874. [Google Scholar]
- Wu, P.H.; Zhao, Y.; Mao, C.Y. A frequency-time approach of random vibration analysis for bolted structures based on a semi-analytic Jacobian matrix. Mech. Syst. Signal Process. 2024, 218, 111562. [Google Scholar]
- Wu, C.X.; Yan, Q.W. Dynamic modeling and vibration analysis of bolted flange joint disk-drum structures: Theory and experiment. Int. J. Mech. Sci. 2024, 272, 109186. [Google Scholar]
- Liu, X.F.; Sun, W.; Liu, H.H.; Ma, H.W.; Du, D.X.; Li, H. Modeling and vibration analysis of bolted composite conical-conical shells with flanges. Thin-Walled Struct. 2024, 200, 111955. [Google Scholar]
- Valdez-Yepez, R.; Tutivén, C.; Vidal, Y. Structural health monitoring of jacket-type support structures in offshore wind turbines: A comprehensive dataset for bolt loosening detection through vibrational analysis. Data Brief 2024, 53, 110222. [Google Scholar] [PubMed]
- Kreutz, M.; Trainotti, F.; Gimpl, V.; Rixen, D.J. On the robust experimental multi-degree-of-freedom identification of bolted joints using frequency-based substructuring. Mech. Syst. Signal Process. 2023, 203, 110626. [Google Scholar]
- Pirdayr, A.; Mohammadi, M.; Kazemzadeh-Parsi, M.J.; Rajabi, M. Self-loosening effects on vibration characteristics of plates with bolted joints: An experimental and finite element analysis. Measurement 2021, 185, 109922. [Google Scholar]
- Liu, H.H.; Sun, W.; Du, D.X.; Liu, X.F. Modeling and free vibration analysis for bolted composite plate under inconsistent pre-tightening condition. Compos. Struct. 2022, 292, 115634. [Google Scholar]
- Madan, A.; Zhao, C.; Han, C.; Dong, Y.; Yang, Y. Monitoring rail track bolt loosening using fiber-optic distributed acoustic sensing. Sens. Actuators A Phys. 2025, 382, 116176. [Google Scholar]
- Wang, X.; Yue, Q.R.; Liu, X.G. Bolted lap joint loosening monitoring and damage identification based on acoustic emission and machine learning. Mech. Syst. Signal Process. 2024, 220, 111690. [Google Scholar]
- Hu, M.P.; Avval, S.S.P.; He, J.; Yue, N.; Groves, R.M. Explainable artificial intelligence study on bolt loosening detection using Lamb waves. Mech. Syst. Signal Process. 2025, 225, 112285. [Google Scholar]
- Tong, T.; Hua, J.D.; Du, D.Y.; Gao, F.; Lin, J. Bolt looseness detection in lap joint based on phase change of Lamb waves. Mech. Syst. Signal Process. 2025, 223, 111840. [Google Scholar]
- Tan, B.H.; Wang, T.; Fang, Q.; Yang, D.; Wang, H.; Lu, G.T. Bolt looseness monitoring using dynamic mode decomposition with piezoelectric active sensing. Measurement 2024, 238, 115204. [Google Scholar]
- Zhou, C.; He, J.; Xiong, X.; Yang, S.X.; Sun, J.H. Simulation data-driven attention fusion network with multi-similarity metric: A single-domain generalization diagnostic method for tie rod bolt loosening of a rod-fastening rotor system. Measurement 2025, 240, 115565. [Google Scholar]
- Liu, Z.C.; Huang, X.B.; Zhao, L.; Wen, G.R.; Feng, G.Z.; Zhang, Y. Research on online monitoring technology for transmission tower bolt looseness. Measurement 2023, 223, 113703. [Google Scholar]
- Du, F.; Tian, Z.X.; Nan, Y.; Zhang, X.; Xu, C.; Wang, S.F.; Su, Z.Q. A modified virtual time reversal method for enhancing monitoring sensitivity of bolt preloads based on ultrasonic guided waves. J. Sound Vib. 2024, 585, 118475. [Google Scholar]
- Liu, P.T.; Wang, X.P.; Wang, Y.Q.; Zhu, J.; Ji, X.Y. Research on percussion-based bolt looseness monitoring under noise interference and insufficient samples. Mech. Syst. Signal Process. 2024, 208, 111013. [Google Scholar]
- Yuan, B.; Sun, W.; Wang, Y.Q.; Zhao, R.X.; Mu, X.K.; Sun, Q.C. Study on bolt preload measurement: An error compensation model for ultrasonic detection based on solid coupling. Measurement 2023, 221, 113484. [Google Scholar]
- Liu, H.; Wei, S.; Xiao, F.L.; Hong, W.M.; Dong, X.D.; Hui, L. Modeling and free vibration analysis of bolted composite flanged cylindrical-cylindrical shells under partial bolt loosening conditions. Thin-Walled Struct. 2024, 199, 111853. [Google Scholar]
- Liu, F.; Sun, W.; Hong, H.L.; Hong, W.M.; Dong, X.D.; Hui, L. An investigation of vibration responses for bolted composite flanged-cylindrical shells considering material and joint nonlinearity. Thin-Walled Struct. 2024, 204, 112335. [Google Scholar]
- Fan, J.S.; Yuan, Q.; Wei, L.L.; Zhang, L.; Zhang, D.D.; Zhang, D.S.; Wang, L. Experimental study of anchor bolt stress evaluation with hybrid optical fiber monitoring. Opt. Fiber Technol. 2023, 80, 103415. [Google Scholar]
- ISO 4014:2014; Hexagon Head Bolts—Product Grades A and B. International Organization for Standardization: Geneva, Switzerland, 2014.
- Yuan, Y.L. Rolling bearing fault diagnosis based on kurtosis wavelet packet analysis. New Technol. New Technol. 2008, 43–46. [Google Scholar]
- Ding, W.S.; Tang, Q.; Huang, F. Failure Analysis of Bolted Connection under Lateral Vibration. Mech. Res. Appl. 2022, 35, 190–192. [Google Scholar]
- Tang, W.H.; Hong, S.; Wang, Y. Technical analysis of railway bearing performance test based on kurtosis and spectral kurtosis. J. Dalian Jiaotong Univ. New Technol. New Technol. 2020, 41, 69–73. [Google Scholar]




| Serial Number | Technical Index | Main Specification |
|---|---|---|
| 1 | Number of channels | 4 channels/card, up to 32 channels per unit, wireless channel expansion through Ethernet |
| 2 | Communication mode | Gigabit Ethernet and wireless WIFI communication |
| 3 | Voltage range | ±20 mV, ±50 mV, ±100 mV, ±200 mV, ±500 mV |
| 4 | Voltage indication error | Not more than 0.3% |
| 5 | Continuous sampling rate | Single box does not exceed 16 channels synchronous acquisition, up to 256 KHz channel |
| 6 | Analog-to-digital converter | 24-bit varepsilon-∆ AD converter |
| 7 | Environmental suitability | Maximum 100 g impact, −20~60 °C wide temperature |
| 8 | Supports capture card types | Voltage/IEPE/Strain/speed/counter/Signal source/CAN/DIO/RS485 |
| 9 | Access type | Supports intelligent wire identification and TEDS sensor access |
| Test Conditions | Measuring Point Locations | Triaxial Channel Directions | Testing Time | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| Full/Partial Throttle No-Load–Threshing–Header Engagement–Gradual Shutdown | 1 | Vertical Direction | Lateral Direction | Forward Direction | Two groups per test, sampling time is 2 min of response signals during the stable operation phase. |
| 2 | Lateral Direction | Vertical Direction | Forward Direction | ||
| 3 | Vertical Direction | Forward Direction | Lateral Direction | ||
| 4 | Vertical Direction | Forward Direction | Lateral Direction | ||
| 5 | Vertical Direction | Forward Direction | Lateral Direction | ||
| Measuring Point | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 5.22 | 3.26 | 3.75 | 3.83 | 2.85 |
| 5.12 | 3.25 | 3.83 | 3.87 | 2.87 | |
| 5.04 | 3.31 | 3.84 | 3.88 | 2.85 | |
| y | 3.06 | 3.27 | 3.27 | 4.38 | 2.99 |
| 3.05 | 3.27 | 3.23 | 4.43 | 3.00 | |
| 3.06 | 3.27 | 3.25 | 4.41 | 3.00 | |
| z | 3.41 | 4.10 | 3.87 | 4.51 | 3.12 |
| 3.50 | 4.16 | 3.83 | 4.41 | 3.10 | |
| 3.43 | 4.20 | 3.82 | 4.34 | 3.12 |
| Measuring Point | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | −0.12 | 0.02 | 0.08 | 0.10 | −0.03 |
| −0.13 | 0.01 | 0.08 | 0.08 | −0.03 | |
| −0.10 | 0.01 | 0.08 | 0.07 | −0.03 | |
| y | 0.02 | 0.02 | −0.41 | −0.53 | 0.08 |
| 0.02 | 0.03 | −0.40 | −0.53 | 0.09 | |
| 0.01 | 0.03 | −0.40 | −0.53 | 0.09 | |
| z | 0.03 | 0.08 | 0.00 | 0.04 | −0.02 |
| 0.04 | 0.08 | 0.03 | 0.03 | −0.03 | |
| 0.05 | 0.08 | 0.00 | 0.02 | −0.03 |
| Measuring Point | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 68.17 | 63.71 | 187.17 | 199.66 | 199.15 |
| 67.95 | 63.08 | 190.60 | 206.16 | 206.41 | |
| 69.87 | 63.88 | 195.59 | 190.44 | 201.73 | |
| y | 59.07 | 63.36 | 122.00 | 191.54 | 188.55 |
| 60.05 | 61.67 | 123.35 | 187.75 | 190.53 | |
| 59.66 | 63.35 | 121.51 | 186.60 | 183.29 | |
| z | 45.32 | 95.86 | 170.42 | 221.93 | 245.77 |
| 47.63 | 96.75 | 169.92 | 211.11 | 244.20 | |
| 47.60 | 96.02 | 160.12 | 195.69 | 247.35 |
| Characteristic Value | Measuring Point with Maximum Value | Measuring Point with Maximum Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| RMS Value | 16 | 18 | 37 | 37 | 58 | 5 |
| kurtosis | 3 | 4 | 3.8 | 4.4 | 3 | 4 |
| skewness | 0.1 | 0.08 | 0.4 | 0.5 | 0.09 | 4 |
| margin | 68 | 96 | 190 | 200 | 240 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Sun, M.; Yan, G.; Que, K.; Wang, B.; Xu, S.; Lian, Y.; Tang, Z. Experimental Study on Loosening and Vibration Characteristics of Vibrating Screen Bolts of Combine Harvester. Agriculture 2025, 15, 749. https://doi.org/10.3390/agriculture15070749
Yuan L, Sun M, Yan G, Que K, Wang B, Xu S, Lian Y, Tang Z. Experimental Study on Loosening and Vibration Characteristics of Vibrating Screen Bolts of Combine Harvester. Agriculture. 2025; 15(7):749. https://doi.org/10.3390/agriculture15070749
Chicago/Turabian StyleYuan, Lulu, Meiyan Sun, Guangen Yan, Kexin Que, Bangzhui Wang, Sijia Xu, Yi Lian, and Zhong Tang. 2025. "Experimental Study on Loosening and Vibration Characteristics of Vibrating Screen Bolts of Combine Harvester" Agriculture 15, no. 7: 749. https://doi.org/10.3390/agriculture15070749
APA StyleYuan, L., Sun, M., Yan, G., Que, K., Wang, B., Xu, S., Lian, Y., & Tang, Z. (2025). Experimental Study on Loosening and Vibration Characteristics of Vibrating Screen Bolts of Combine Harvester. Agriculture, 15(7), 749. https://doi.org/10.3390/agriculture15070749







