Predicting Cyperus esculentus Biomass Using Tiller Number: A Comparative Analysis of Growth Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Area and Sample Collection
2.2. Establishment and Goodness of Fit Evaluation
2.3. The Significance of Model Parameters
2.4. Statistical Analysis
3. Results
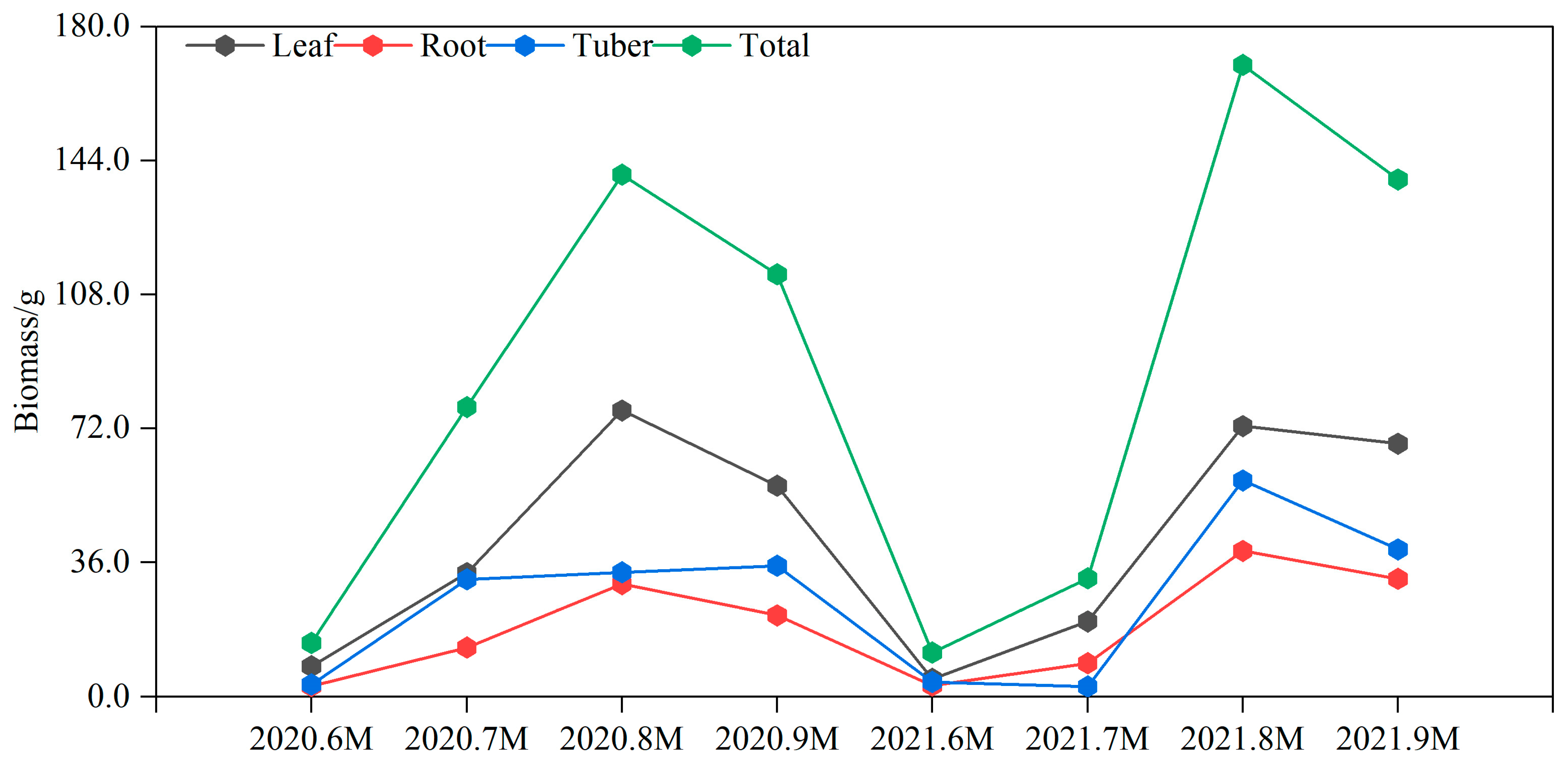
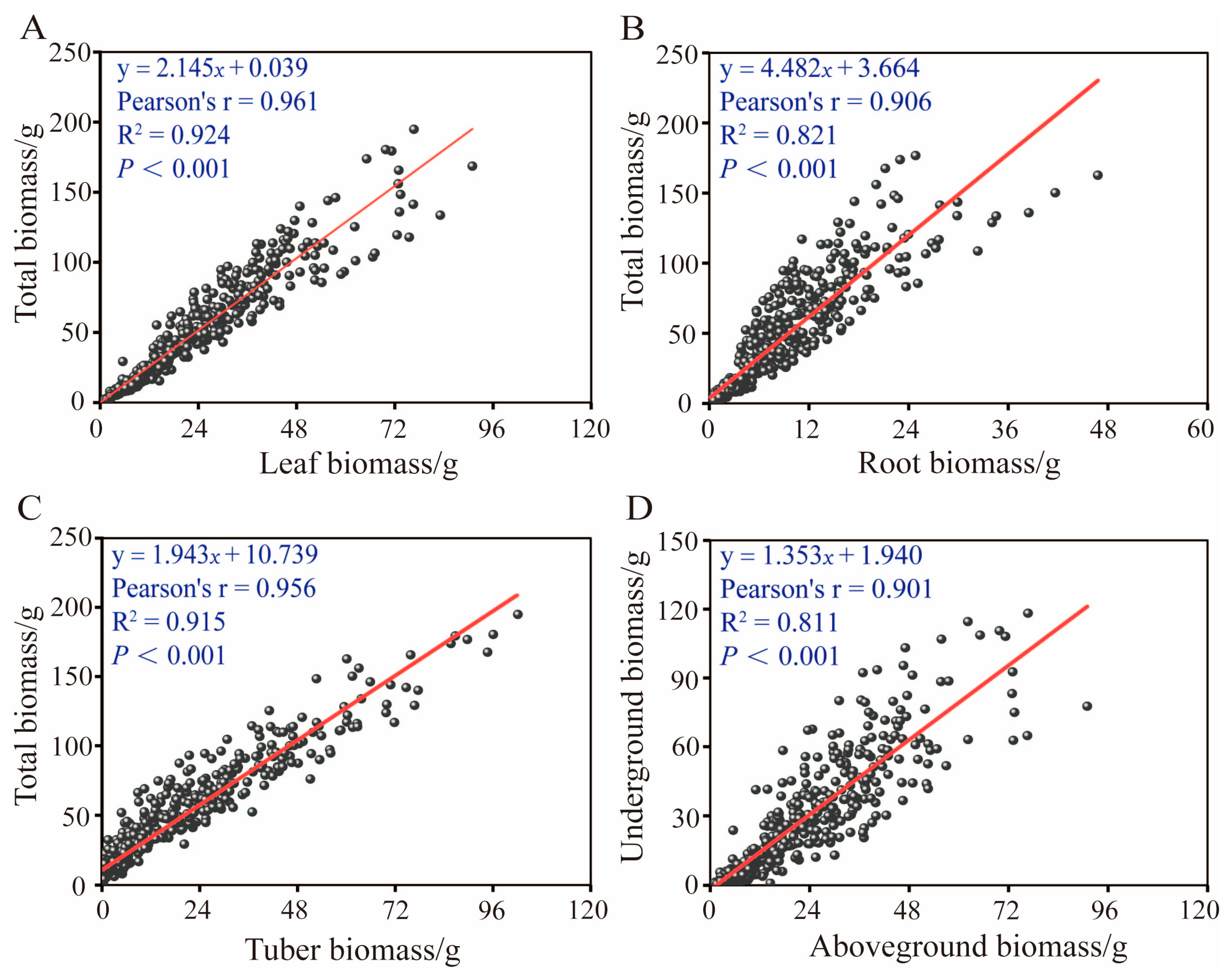
3.1. Basic Description and Biomass Allocation
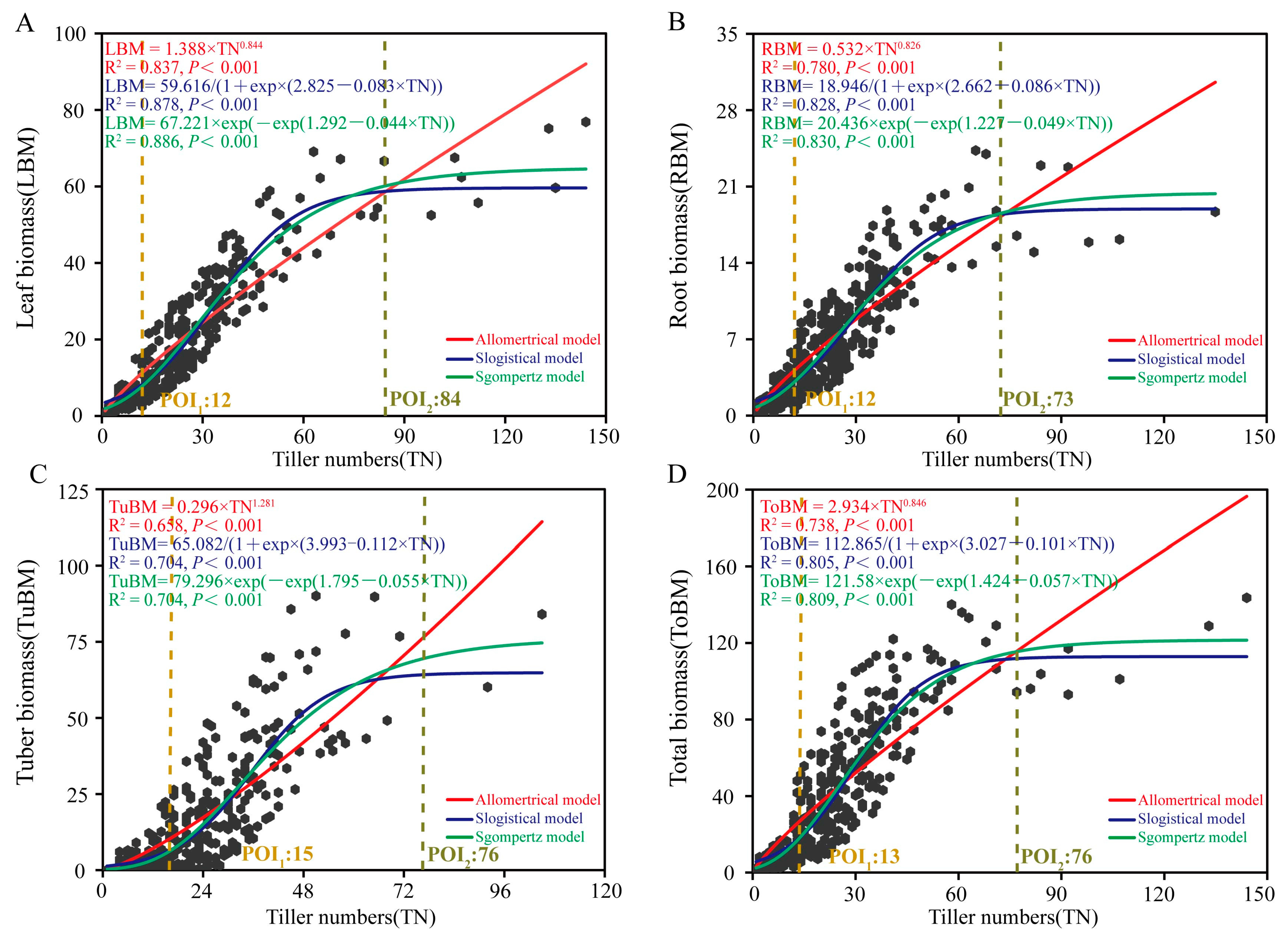
3.2. Construction of Different Biomass Models
3.3. Comparison and Validation of Measured and Estimated Values of Different Biomass Models
3.4. Comparison of the Ecological Significance of Different Biomass Models
4. Discussion
4.1. Introduction of Parameters to Explain Biomass Models
4.2. Response of Inflection Points to Biomass Change Trends
4.3. Comparison of Differences Between Different Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Follak, S.; Belz, R.; Bohren, C.; De Castro, O.; Del Guacchio, E.; Pascual-Seva, N.; Schwarz, M.; Verloove, F.; Essl, F. Biological Flora of Central Europe: Cyperus esculentus L. Perspect. Plant Ecol. Evol. Syst. 2016, 23, 33–51. [Google Scholar] [CrossRef]
- Ezeh, O.; Gordon, M.H.; Niranjan, K. Yellow Nutsedge (Cyperus esculentus) Growth and Reproduction in Response to Nitrogen and Irrigation. Eur. J. Lipid Sci. Technol. 2014, 116, 783–794. [Google Scholar] [CrossRef]
- Peerzada, A.M. Biology, Agricultural Impact, and Management of Cyperus rotundus L.: The World’s Most Tenacious Weed. Acta Physiol. Plant 2017, 39, 270. [Google Scholar] [CrossRef]
- Bohren, C.; Wirth, J. Implementation of Control Strategies against Yellow Nutsedge (Cyperus esculentus L.) into Practice. Jul.-KüHn-Arch. 2018, 458, 189–197. [Google Scholar] [CrossRef]
- Nwosu, L.C.; Edo, G.I.; Özgör, E. The Phytochemical, Proximate, Pharmacological, GC-MS Analysis of Cyperus esculentus (Tiger Nut): A Fully Validated Approach in Health, Food and Nutrition. Food Biosci. 2022, 46, 101551. [Google Scholar] [CrossRef]
- Wang, M.; Su, Y.-Z.; Yang, R.; Yang, X. Allocation Patterns of Above- and Belowground Biomass in Desert Grassland in the Middle Reaches of Heihe River, Gansu Province, China. Chin. J. Plant Ecol. 2013, 37, 209–219. [Google Scholar] [CrossRef]
- Rathore, A.C.; Kumar, A.; Tomar, J.M.S.; Jayaprakash, J.; Mehta, H.; Kaushal, R.; Alam, N.M.; Gupta, A.K.; Raizada, A.; Chaturvedi, O.P. Predictive Models for Biomass and Carbon Stock Estimation in Psidium Guajava on Bouldery Riverbed Lands in North-Western Himalayas, India. Agrofor. Syst. 2018, 92, 171–182. [Google Scholar] [CrossRef]
- Das, M.; Chandra Nath, P.; Sileshi, G.W.; Pandey, R.; Nath, A.J.; Das, A.K. Biomass Models for Estimating Carbon Storage in Areca Palm Plantations. Environ. Sustain. Ind. 2021, 10, 100115. [Google Scholar] [CrossRef]
- Batbaatar, A.; Carlyle, C.N.; Bork, E.W.; Chang, S.X.; Cahill, J.F. Differential Sensitivity of Above- and Belowground Plant Biomass to Drought and Defoliation in Temperate Grasslands. Agric. Ecosyst. Environ. 2023, 356, 108660. [Google Scholar] [CrossRef]
- Gebremeskel, D.; Birhane, E.; Rannestad, M.M.; Gebre, S.; Tesfay, G. Biomass and Soil Carbon Stocks of Rhamnus Prinoides Based Agroforestry Practice with Varied Density in the Drylands of Northern Ethiopia. Agrofor. Syst. 2021, 95, 1275–1293. [Google Scholar] [CrossRef]
- Nie, X.; Yang, Y.; Yang, L.; Zhou, G. Above- and Belowground Biomass Allocation in Shrub Biomes across the Northeast Tibetan Plateau. PLoS ONE 2016, 11, e0154251. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Xue, X.; You, Q.; Sun, J.; Zhou, J.; Wang, T.; Tsunekawa, A. Change in the Trade-off between Aboveground and Belowground Biomass of Alpine Grassland: Implications for the Land Degradation Process. Land Degrad. Dev. 2020, 31, 105–117. [Google Scholar] [CrossRef]
- Peng, Y.; Fornara, D.A.; Yue, K.; Peng, X.; Peng, C.; Wu, Q.; Ni, X.; Liao, S.; Yang, Y.; Wu, F.; et al. Globally Limited Individual and Combined Effects of Multiple Global Change Factors on Allometric Biomass Partitioning. Glob. Ecol. Biogeogr. 2022, 31, 454–469. [Google Scholar] [CrossRef]
- Webster, T.M. Mulch Type Affects Growth and Tuber Production of Yellow Nutsedge (Cyperus esculentus) and Purple Nutsedge (Cyperus rotundus). Weed Sci. 2005, 53, 834–838. [Google Scholar] [CrossRef]
- Barko, J.W.; Smart, R.M. The Growth and Biomass Distribution of Two Emergent Freshwater Plants, Cyperus esculentus and Scirpus validus, on Different Sediments. Aquat. Bot. 1978, 5, 109–117. [Google Scholar] [CrossRef]
- Li, B.; Shibuya, T.; Yogo, Y.; Hara, T. Effects of Ramet Clipping and Nutrient Availability on Growth and Biomass Allocation of Yellow Nutsedge. Ecol. Res. 2004, 19, 603–612. [Google Scholar] [CrossRef]
- Westendorff, N.d.R.; Agostinetto, D.; da Ulguim, A.R.; Perboni, L.T.; da Silva, B.M. Yield Loss and Economic Thresholds of Yellow Nutsedge in Irrigated Rice as a Function of the Onset of Flood Irrigation. Bragantia 2014, 73, 32–38. [Google Scholar] [CrossRef]
- Larue, F.; Fumey, D.; Rouan, L.; Soulié, J.-C.; Roques, S.; Beurier, G.; Luquet, D. Modelling Tiller Growth and Mortality as a Sink-Driven Process Using Ecomeristem: Implications for Biomass Sorghum Ideotyping. Ann. Bot. 2019, 124, 675–690. [Google Scholar] [CrossRef]
- Veenstra, R.L.; Messina, C.D.; Berning, D.; Haag, L.A.; Carter, P.; Hefley, T.J.; Prasad, P.V.V.; Ciampitti, I.A. Tiller Biomass in Low Plant-Density Corn Enhances Transient C Sink without Direct Harvest Index Detriment. Field Crops Res. 2023, 292, 108804. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, X.; Ma, Q.; Li, F.; Tao, R.; Zhu, M.; Li, C.; Zhu, X.; Guo, W.; Ding, J. Tiller Fertility Is Critical for Improving Grain Yield, Photosynthesis, and Nitrogen Efficiency in Wheat. J. Integr. Agric. 2023, 22, 2054–2066. [Google Scholar] [CrossRef]
- Xie, W.; Furusawa, C.; Miyata, H.; Ata-Ul-Karim, S.T.; Yamasaki, Y.; Shiotsu, F.; Kato, Y. Genotypic Differences in the Agronomic Performance of Ratoon Rice in a Cool-Temperate Environment in Central Japan. Field Crops Res. 2024, 317, 109487. [Google Scholar] [CrossRef]
- Dimobe, K.; Goetze, D.; Ouédraogo, A.; Mensah, S.; Akpagana, K.; Porembski, S.; Thiombiano, A. Aboveground Biomass Allometric Equations and Carbon Content of the Shea Butter Tree (Vitellaria Paradoxa C.F. Gaertn., Sapotaceae) Components in Sudanian Savannas (West Africa). Agrofor. Syst. 2019, 93, 1119–1132. [Google Scholar] [CrossRef]
- Bem, C.M.; Cargnelutti Filho, A.; Facco, G.; Schabarum, D.E.; Silveira, D.L.; Simões, F.M.; Uliana, D.B. Growth Models for Morphological Traits of Sunn Hemp. Semin. Agrar. 2016, 38, 2933. [Google Scholar] [CrossRef]
- Eker, M.; Poudel, K.; Özçelik, R. Aboveground Biomass Equations for Small Trees of Brutian Pine in Turkey to Facilitate Harvesting and Management. Forests 2017, 8, 477. [Google Scholar] [CrossRef]
- Jian, L.I.; Wang, M.; Wang, Y.; Zhang, M.; Yao, N. Fitting Model of Jilin Quinoa Growth Model Based on Meteorological Factors. J. Jilin Agric. Univ. 2017, 39, 743–747. [Google Scholar] [CrossRef]
- Nyamjav, J.; Batsaikhan, M.-E.; Li, G.; Li, J.; Luvsanjamba, A.; Jin, K.; Xiao, W.; Wu, L.; Indree, T.; Qin, A. Allometric Equations for Estimating Above-Ground Biomass of Nitraria sibirica Pall. in Gobi Desert of Mongolia. PLoS ONE 2020, 15, e0239268. [Google Scholar] [CrossRef]
- Hossain, M.; Siddique, M.R.H.; Saha, S.; Abdullah, S.M.R. Allometric Models for Biomass, Nutrients and Carbon Stock in Excoecaria agallocha of the Sundarbans, Bangladesh. Wetl. Ecol. Manag. 2015, 23, 765–774. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Fahandezh-Saadi, S.; Zand-Parsa, S. Logistic Model Application for Prediction of Maize Yield under Water and Nitrogen Management. Agric. Water Manag. 2011, 99, 51–57. [Google Scholar] [CrossRef]
- Cheng, Y.; Wei, Z.M.; Liu, J.Y.; Xu, F.; Wang, Z.; Chen, T. Logistic Equation Based Fitting and Analysis of the Growth Index of Cyperus esculentus. J. Northeast Agric. Sci. 2024, 49, 47–51. [Google Scholar] [CrossRef]
- Fourcaud, T.; Zhang, X.; Stokes, A.; Lambers, H.; Korner, C. Plant Growth Modelling and Applications: The Increasing Importance of Plant Architecture in Growth Models. Ann. Bot. 2008, 101, 1053–1063. [Google Scholar] [CrossRef]
- Tanwar, S.P.S.; Verma, A.; Kumar, P.; Alam, N.M.; Bhatt, R.K. Biomass and Carbon Projection Models in Hardwickia Binata Roxb. Vis a Vis Estimation of Its Carbon Sequestration Potential under Arid Environment. Arch. Agron. Soil Sci. 2020, 66, 1925–1935. [Google Scholar] [CrossRef]
- Liu, A.N.; Zhang, Y.; Hou, Z.F.; Lu, G.H. Allometric Scaling of Biomass with Nitrogen and Phosphorus Above- and below-Ground in Herbaceous Plants Varies along Water-Salinity Gradients. AoB Plants 2021, 13, plab030. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Wang, X. Aboveground and Belowground Biomass and Its’ Allometry for Salsola Passerina Shrub in Degraded Steppe Desert in Northwestern China. Land Degrad. Dev. 2021, 32, 714–722. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, L.; liu, M.; Li, J. Simulation of Rice Biomass Accumulation by an Extended Logistic Model Including Influence of Meteorological Factors. Int. J. Biometeorol. 2002, 46, 185–191. [Google Scholar] [CrossRef]
- Meade, K.A.; Cooper, M.; Beavis, W.D. Modeling Biomass Accumulation in Maize Kernels. Field Crops Res. 2013, 151, 92–100. [Google Scholar] [CrossRef]
- Dou, Y.; Yang, Y.; An, S. Above-Ground Biomass Models of Caragana Korshinskii and Sophora Viciifolia in the Loess Plateau, China. Sustainability 2019, 11, 1674. [Google Scholar] [CrossRef]
- Gambín, B.L.; Borrás, L.; Otegui, M.E. Kernel Weight Dependence upon Plant Growth at Different Grain-Filling Stages in Maize and Sorghum. Aust. J. Agric. Res. 2008, 59, 280. [Google Scholar] [CrossRef]
- Pepler, S.; Gooding, M.J.; Ellis, R.H. Modelling Simultaneously Water Content and Dry Matter Dynamics of Wheat Grains. Field Crops Res. 2006, 95, 49–63. [Google Scholar] [CrossRef]
- Song, Y.; Wan, G.-Y.; Wang, J.-X.; Zhang, Z.-S.; Xia, J.-Q.; Sun, L.-Q.; Lu, J.; Ma, C.-X.; Yu, L.-H.; Xiang, C.-B.; et al. Balanced Nitrogen–Iron Sufficiency Boosts Grain Yield and Nitrogen Use Efficiency by Promoting Tillering. Mol. Plant 2023, 16, 2004–2010. [Google Scholar] [CrossRef]
- Okamura, M.; Aoki, N. Effect of Two Alleles of Tiller Angle Control 1 on Grain Yield and Dry Matter Production in Rice. Field Crops Res. 2024, 309, 109325. [Google Scholar] [CrossRef]
- Li, J.; Han, G.; Kang, S.; Zhang, X.; Li, C. Responses of Tillering Stipa Breviflora Traits to a Long-Term Grazing Gradient. Acta Soc. Bot. Pol. 2022, 91, 13. [Google Scholar] [CrossRef]
- Křen, J.; Klem, K.; Svobodová, I.; Míša, P.; Neudert, L. Yield and Grain Quality of Spring Barley as Affected by Biomass Formation at Early Growth Stages. Plant Soil Environ. 2014, 60, 221–227. [Google Scholar] [CrossRef]
- Boe, A.; Beck, D.L. Yield Components of Biomass in Switchgrass. Crop Science 2008, 48, 1306–1311. [Google Scholar] [CrossRef]
- R: The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 28 December 2024).
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Isler, K.; Barbour, A.D.; Martin, R.D. Line-Fitting by Rotation: A Nonparametric Method for Bivariate Allometric Analysis. Biom. J. 2002, 44, 289. [Google Scholar] [CrossRef]
- Pareja, G. Fitting a Logistic Curve to Population Size Data; Iowa State University: Ames, IA, USA, 1984. [Google Scholar] [CrossRef]
- Winsor, C.P. The Gompertz Curve as a Growth Curve. Proc. Natl. Acad. Sci. USA 1932, 18, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Bayen, P.; Noulèkoun, F.; Bognounou, F.; Lykke, A.M.; Faso, B. Models for Estimating Aboveground Biomass of Four Dryland Woody Species in Burkina Faso, West Africa. J. Arid. Environ. 2020, 180, 104205. [Google Scholar] [CrossRef]
- Shu, M.; Shen, M.; Dong, Q.; Yang, X.; Li, B.; Ma, Y. Estimating the Maize Above-Ground Biomass by Constructing the Tridimensional Concept Model Based on UAV-Based Digital and Multi-Spectral Images. Field Crop. Res. 2022, 282, 108491. [Google Scholar] [CrossRef]
- Mello, A.; Toebe, M.; Marchioro, V.S.; de Souza, R.R.; Paraginski, J.A.; Somavilla, J.C.; Martins, V.; Manfio, G.L.; Junges, D.L.; da Rocha Borges, M.E. Nonlinear Models in the Description of Sunflower Cultivars Growth Considering Heteroscedasticity. J. Plant Growth Regul. 2023, 42, 7215–7228. [Google Scholar] [CrossRef]
- Niklas, K.J. Modelling Below- and Above-Ground Biomass for Non-Woody and Woody Plants. Ann. Bot. 2005, 95, 315–321. [Google Scholar] [CrossRef]
- Chaturvedi, R.K.; Raghubanshi, A.S. Allometric Models for Accurate Estimation of Aboveground Biomass of Teak in Tropical Dry Forests of India. For. Sci. 2015, 61, 938–949. [Google Scholar] [CrossRef]
- Weiner, J. Allocation, Plasticity and Allometry in Plants. Perspect. Plant Ecol. Evol. Syst. 2004, 6, 207–215. [Google Scholar] [CrossRef]
- Prusinkiewicz, P. Modeling Plant Growth and Development. Curr. Opin. Plant Biol. 2004, 7, 79–83. [Google Scholar] [CrossRef]
- Nguimkeu, P. A Simple Selection Test between the Gompertz and Logistic Growth Models. Technol. Forecast. Soc. Change 2014, 88, 98–105. [Google Scholar] [CrossRef]
- Wang, W.; Quanjiu, W.; Jun, F.; Lijun, S.; Xinlei, S. Logistic Model Analysis of Winter Wheat Growth on China’s Loess Plateau. Can. J. Plant Sci. 2014, 94, 1471–1479. [Google Scholar] [CrossRef]
- de Bem, C.M.; Cargnelutti Filho, A.; Chaves, G.G.; Kleinpaul, J.A.; Pezzini, R.V.; Lavezo, A. Gompertz and Logistic Models to the Productive Traits of Sunn Hemp. JAS 2017, 10, 225. [Google Scholar] [CrossRef]
- Ma, J.; Yuan, C.; Zhou, J.; Li, Y.; Gao, G.; Fu, B. Logistic Model Outperforms Allometric Regression to Estimate Biomass of Xerophytic Shrubs. Ecol. Indic. 2021, 132, 108278. [Google Scholar] [CrossRef]
- Randriamalala, J.R.; Radosy, H.O.; Ramanakoto, M.; Razafindrahanta, H.; Ravoninjatovo, J.-M.; Haingomanantsoa, R.S.; Ramananantoandro, T. Allometric Models to Predict the Individual Aboveground Biomass of Shrubs of Malagasy Xerophytic Thickets. J. Arid. Environ. 2022, 202, 104751. [Google Scholar] [CrossRef]
- Kuyah, S.; Sileshi, G.W.; Rosenstock, T.S. Allometric Models Based on Bayesian Frameworks Give Better Estimates of Aboveground Biomass in the Miombo Woodlands. Forests 2016, 7, 13. [Google Scholar] [CrossRef]
- Saha, C.; Mahmood, H.; Nayan, S.N.S.; Siddique, M.R.H.; Abdullah, S.M.R.; Islam, S.M.Z.; Iqbal, M.Z.; Akhter, M. Allometric Biomass Models for the Most Abundant Fruit Tree Species of Bangladesh: A Non-Destructive Approach. Environ. Chall. 2021, 3, 100047. [Google Scholar] [CrossRef]
- Liu, R.; Yang, X.; Gao, R.; Hou, X.; Huo, L.; Huang, Z.; Cornelissen, J.H.C. Allometry Rather than Abiotic Drivers Explains Biomass Allocation among Leaves, Stems and Roots of Artemisia across a Large Environmental Gradient in China. J. Ecol. 2021, 109, 1026–1040. [Google Scholar] [CrossRef]
- Carini, F.; Filho, A.C.; Bandeira, C.T.; Neu, I.M.M.; Pezzini, R.V.; Pacheco, M.; Thomasi, R.M. Growth Models for Lettuce Cultivars Growing in Spring. J. Agric. Sci. 2017, 11, 147. [Google Scholar] [CrossRef]
- Connor, D.J.; Fereres, E. A Dynamic Model of Crop Growth and Partitioning of Biomass. Field Crops Res. 1999, 63, 139–157. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.; Zhu, J.-K. Thriving under Stress: How Plants Balance Growth and the Stress Response. Dev. Cell 2020, 55, 529–543. [Google Scholar] [CrossRef]
- Lin, Z.; Fan, D.; Ma, S.; Miao, W.; Wang, X. Relative Growth Rate for Trees at the Growth Stage Is Coordinated with Leaf Bulk Modulus of Elasticity and Osmotic Potential in a Subtropical Forest of China. Ecol. Indic. 2022, 141, 109135. [Google Scholar] [CrossRef]
- Li, G.; Si, M.; Zhang, C.; Shen, Z.; Wang, S.; Shao, J. Responses of Plant Biomass and Biomass Allocation to Experimental Drought: A Global Phylogenetic Meta-Analysis. Agric. For. Meteorol. 2024, 347, 109917. [Google Scholar] [CrossRef]
- Acciaresi, H.A.; Guiamet, J.J. Below- and Above-ground Growth and Biomass Allocation in Maize and Sorghum Halepense in Response to Soil Water Competition. Weed Res. 2010, 50, 481–492. [Google Scholar] [CrossRef]
- Dolezal, J.; Jandova, V.; Macek, M.; Liancourt, P. Contrasting Biomass Allocation Responses across Ontogeny and Stress Gradients Reveal Plant Adaptations to Drought and Cold. Funct. Ecol. 2021, 35, 32–42. [Google Scholar] [CrossRef]
- Deprá, M.S.; Lopes, S.J.; Noal, G.; Reiniger, L.R.S.; Cocco, D.T. Modelo Logístico de Crescimento de Cultivares Crioulas de Milho e de Progênies de Meios-Irmãos Maternos Em Função Da Soma Térmica. Cienc. Rural. 2016, 46, 36–43. [Google Scholar] [CrossRef][Green Version]
- Noulèkoun, F.; Khamzina, A.; Naab, J.B.; Lamers, J.P.A. Biomass Allocation in Five Semi-Arid Afforestation Species Is Driven Mainly by Ontogeny Rather than Resource Availability. Ann. Sci. 2017, 74, 78. [Google Scholar] [CrossRef]
- Soliveres, S.; Maestre, F.T. Plant–Plant Interactions, Environmental Gradients and Plant Diversity: A Global Synthesis of Community-Level Studies. Perspect. Plant Ecol. Evol. Syst. 2014, 16, 154–163. [Google Scholar] [CrossRef]
- Cleland, E.E.; Lind, E.M.; DeCrappeo, N.M.; DeLorenze, E.; Wilkins, R.A.; Adler, P.B.; Bakker, J.D.; Brown, C.S.; Davies, K.F.; Esch, E.; et al. Belowground Biomass Response to Nutrient Enrichment Depends on Light Limitation Across Globally Distributed Grasslands. Ecosystems 2019, 22, 1466–1477. [Google Scholar] [CrossRef]
- Ma, X.; Wang, X. Biomass Partitioning and Allometric Relations of the Reaumuria Soongorica Shrub in Alxa Steppe Desert in NW China. For. Ecol. Manag. 2020, 468, 118178. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Z.; Li, Y.; He, J.; Wu, X. Dynamic Growth Models for Caragana Korshinskii Shrub Biomass in China. J. Environ. Manag. 2020, 269, 110675. [Google Scholar] [CrossRef] [PubMed]
- Naik, S.K.; Sarkar, P.K.; Das, B.; Singh, A.K.; Bhatt, B.P. Biomass Production and Carbon Stocks Estimate in Mango Orchards of Hot and Sub-Humid Climate in Eastern Region, India. Carbon. Manag. 2019, 10, 477–487. [Google Scholar] [CrossRef]
- Ge, H.; Yuepeng, S.; Xuehui, S.; Deqiang, Z.; Xiaoyu, Z. Optimal Growth Model of Populus Simonii Seedling Combination Based on Logistic and Gompertz Models. bjlydxxb 2020, 42, 59–70. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, L.; liu, M. A Nonlinear Mixed-Effects Model to Predict Stem Cumulative Biomass of Standing Trees. Procedia Environ. Sci. 2011, 10, 215–221. [Google Scholar] [CrossRef]


| Index | Min Value | Max Value | Mean Value | Standard Error | Allocation Proportion |
|---|---|---|---|---|---|
| Tiller numbers | 1.00 | 144.00 | 24.91 | 0.89 | - |
| Leaf biomass | 0.31 | 97.86 | 18.41 | 0.82 | 46.03% |
| Root biomass | 0.21 | 65.87 | 7.42 | 0.36 | 18.55% |
| Tuber biomass | 0.00 | 96.08 | 14.18 | 0.88 | 35.45% |
| Total biomass | 0.55 | 217.39 | 40.00 | 1.88 | - |
| Index | Tiller Numbers | Leaf Biomass | Root Biomass | Tuber Biomass | Total Biomass |
|---|---|---|---|---|---|
| Tiller numbers | 1.00 | ||||
| Leaf biomass | 0.853 *** | 1.00 | |||
| Root biomass | 0.721 ** | 0.831 *** | 1.00 | ||
| Tuber biomass | 0.567 ** | 0.749 ** | 0.663 ** | 1.00 | |
| Total biomass | 0.773 ** | 0.924 *** | 0.824 *** | 0.915 *** | 1.00 |
| Index | Models | Parameters | Goodness-of-Fit Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | k | R2 | R2* | p | Q | RMSE | AIC | RSS | ||
| LBM | LBM = a × (TN)b | 1.388 | 0.844 | - | 0.837 | 0.836 | <0.0001 | 2 | 9.617 | 801.926 | 15,151.86 |
| LBM = k/(1 + exp(a − b × TN)) | 2.825 | 0.083 | 59.616 | 0.878 | 0.877 | <0.0001 | 3 | 9.43 | 799.716 | 14,967.01 | |
| LBM = k × exp(−exp(a − b × TN)) | 1.304 | 0.046 | 64.856 | 0.886 | 0.885 | <0.0001 | 3 | 9.312 | 788.744 | 14,081.93 | |
| RBM | RBM = a × (TN)b | 0.532 | 0.826 | - | 0.78 | 0.779 | <0.0001 | 2 | 5.994 | 645.918 | 6368.82 |
| RBM = k/(1 + exp(a − b × TN)) | 2.662 | 0.086 | 18.946 | 0.828 | 0.826 | <0.0001 | 3 | 5.904 | 638.997 | 6128.59 | |
| RBM = k × exp(−exp(a − b × TN)) | 1.227 | 0.049 | 20.465 | 0.83 | 0.828 | <0.0001 | 3 | 5.861 | 636.54 | 6045.50 | |
| TuBM | TuBM = a × (TN)b | 0.296 | 1.281 | - | 0.658 | 0.655 | <0.0001 | 2 | 18.689 | 1049.292 | 59,882.31 |
| TuBM = k/(1 + exp(a − b × TN)) | 3.993 | 0.112 | 65.082 | 0.740 | 0.739 | <0.0001 | 3 | 15.384 | 967.379 | 37,989.40 | |
| TuBM = k × exp(−exp(a − b × TN)) | 1.795 | 0.055 | 76.296 | 0.738 | 0.737 | <0.0001 | 3 | 15.703 | 977.13 | 40,104.14 | |
| ToBM | TOBM = a × (TN)b | 2.934 | 0.846 | - | 0.738 | 0.737 | <0.0001 | 2 | 24.665 | 1157.94 | 109,506.20 |
| TOBM = k/(1 + exp(a − b × TN)) | 3.027 | 0.101 | 112.865 | 0.805 | 0.803 | <0.0001 | 3 | 23.764 | 1146.535 | 101,646.89 | |
| TOBM = k × exp(−exp(a − b × TN)) | 1.424 | 0.057 | 121.581 | 0.809 | 0.807 | <0.0001 | 3 | 23.293 | 1137.33 | 97,658.60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Lu, Y.; Tariq, A.; Zeng, F.; Gao, Y.; Sardans, J.; Al-Bakre, D.A.; Peñuelas, J. Predicting Cyperus esculentus Biomass Using Tiller Number: A Comparative Analysis of Growth Models. Agriculture 2025, 15, 946. https://doi.org/10.3390/agriculture15090946
Ding Y, Lu Y, Tariq A, Zeng F, Gao Y, Sardans J, Al-Bakre DA, Peñuelas J. Predicting Cyperus esculentus Biomass Using Tiller Number: A Comparative Analysis of Growth Models. Agriculture. 2025; 15(9):946. https://doi.org/10.3390/agriculture15090946
Chicago/Turabian StyleDing, Ya, Yan Lu, Akash Tariq, Fanjiang Zeng, Yanju Gao, Jordi Sardans, Dhafer A. Al-Bakre, and Josep Peñuelas. 2025. "Predicting Cyperus esculentus Biomass Using Tiller Number: A Comparative Analysis of Growth Models" Agriculture 15, no. 9: 946. https://doi.org/10.3390/agriculture15090946
APA StyleDing, Y., Lu, Y., Tariq, A., Zeng, F., Gao, Y., Sardans, J., Al-Bakre, D. A., & Peñuelas, J. (2025). Predicting Cyperus esculentus Biomass Using Tiller Number: A Comparative Analysis of Growth Models. Agriculture, 15(9), 946. https://doi.org/10.3390/agriculture15090946








