Modeling Yields Response to Shading in the Field-to-Forest Transition Zones in Heterogeneous Landscapes
Abstract
:1. Introduction
2. Methodology
2.1. Shadow Modeling
2.1.1. Calculation of the Azimuth and the Altitude
2.1.2. Solar Irradiance and the Canopy Transmittance for Modeling
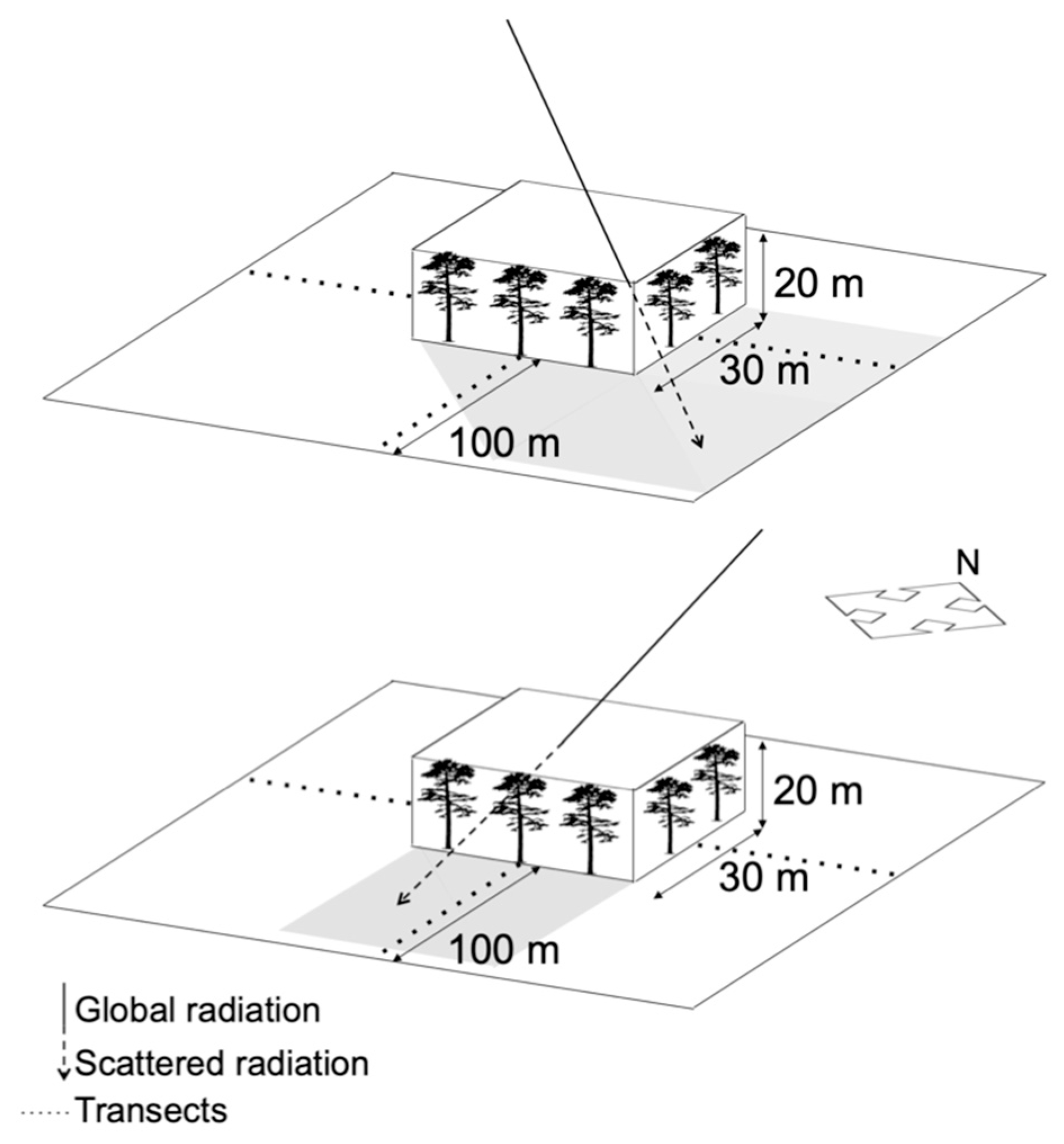
2.1.3. Simulation of the Shading Using the Geographical Information Systems
2.2. Crop Modeling
2.2.1. Simulation
2.2.2. Climate Data
2.2.3. Spatial Extent of the Transition Zones
3. Results
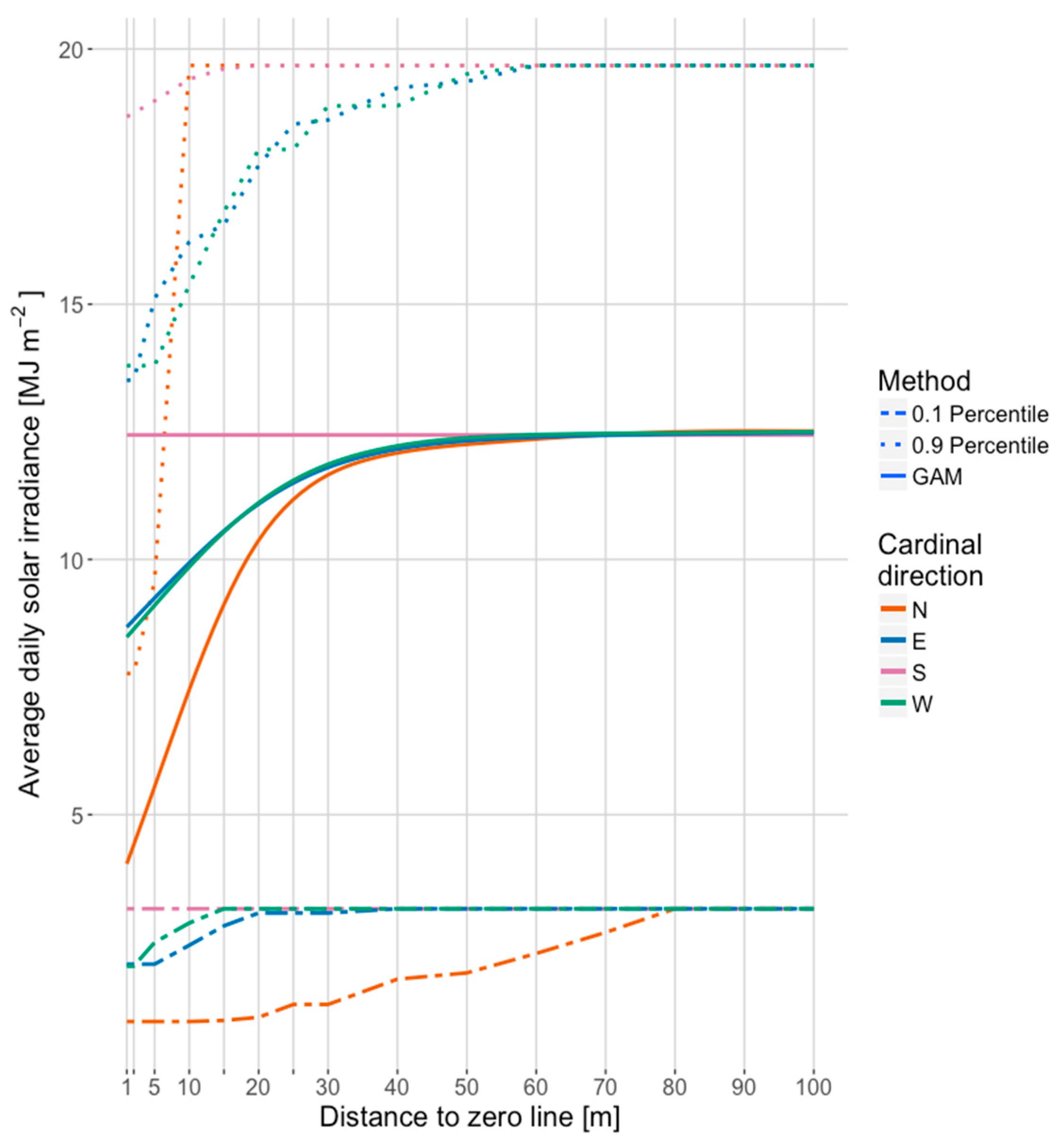
3.1. Solar Irradiance
3.2. Soil Moisture
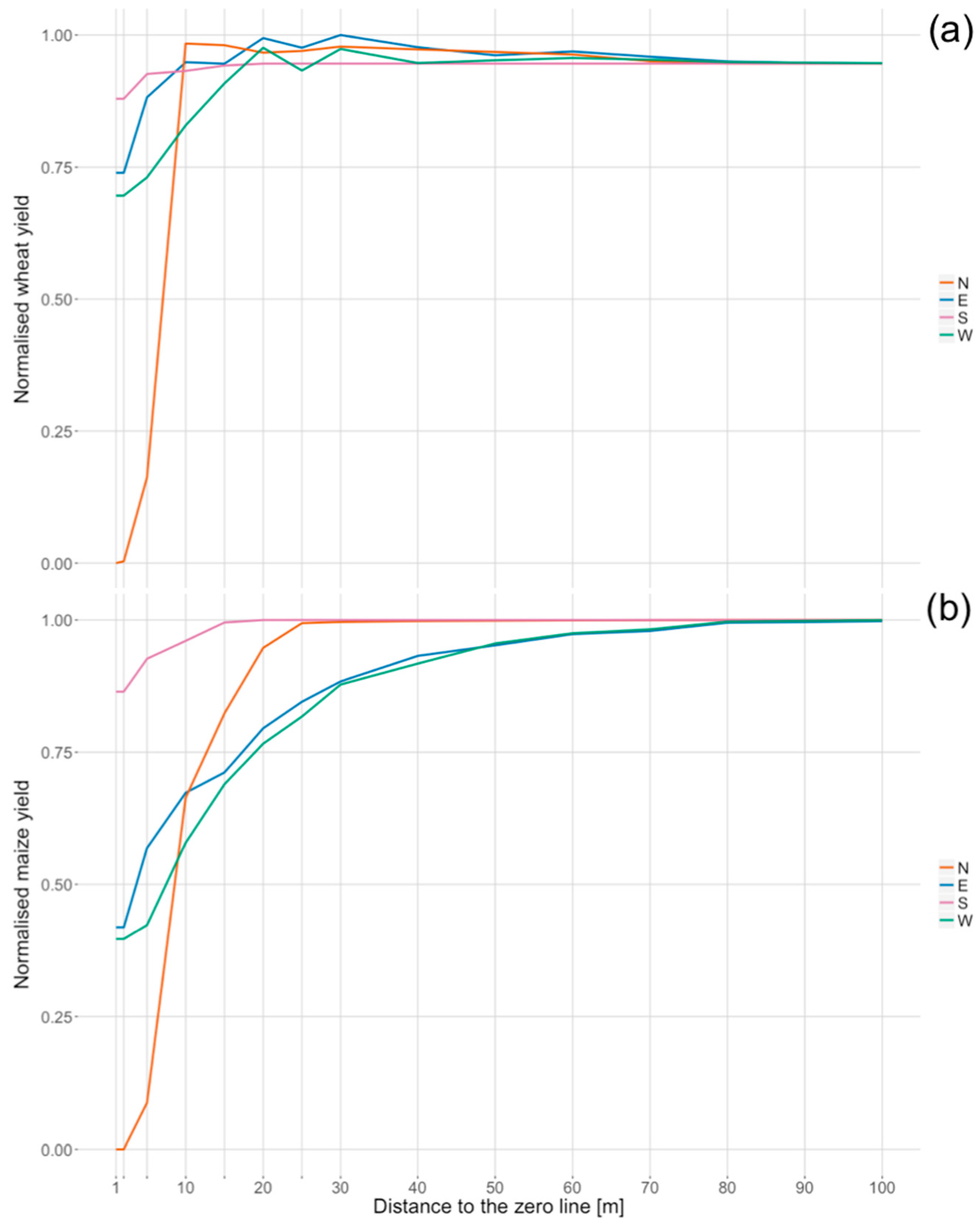
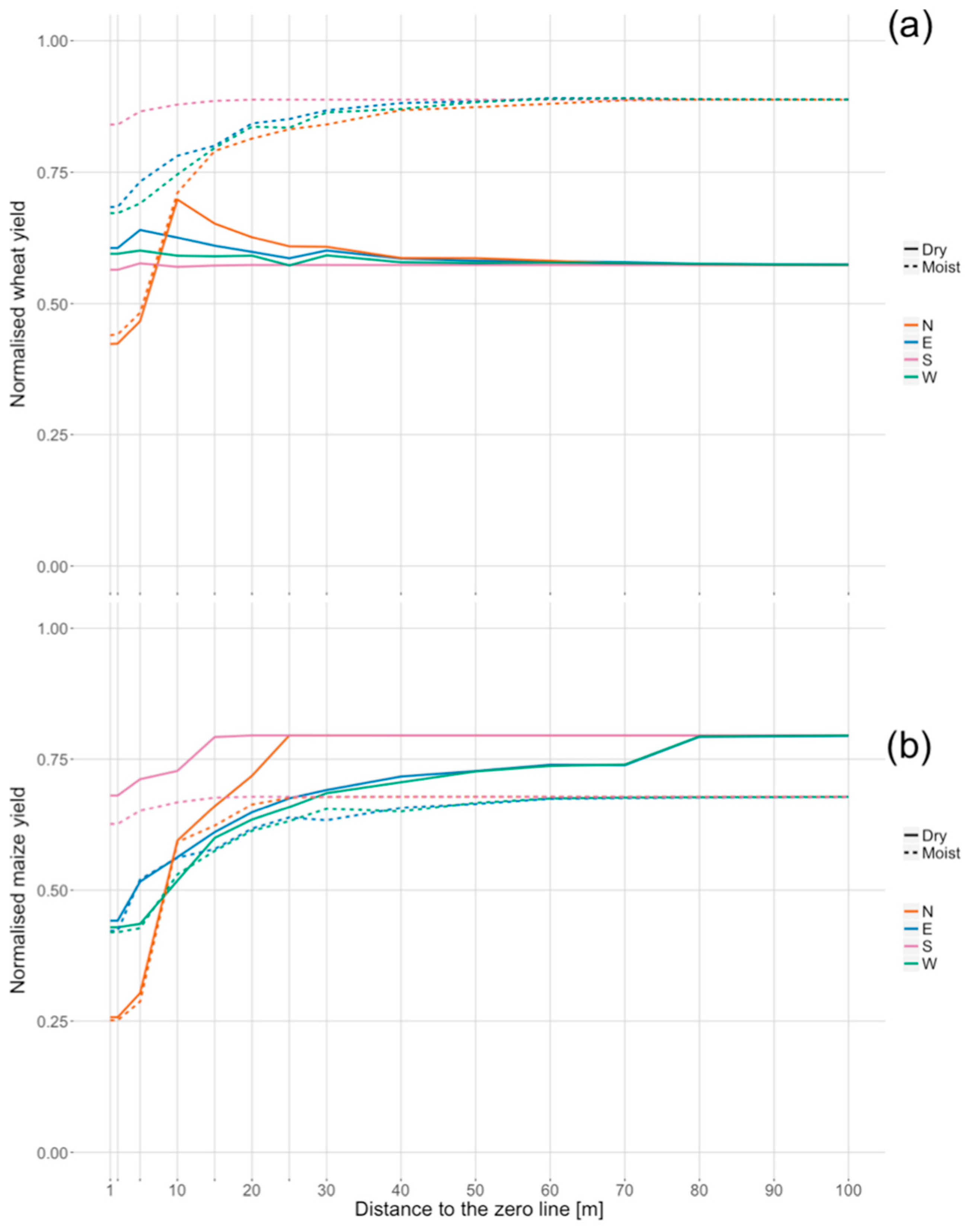
3.3. Yield
3.4. Upscaling the Shading Effects on the Crop Yield
4. Discussion
4.1. Relation between Yield Reduction, Soil Moisture, and Solar Irradiance
4.2. Magnitude of the Shading Effects on the Yield
4.3. The Spatial Extent of the Shading Effects on the Yield
5. Conclusions and Outlook
- Solar irradiance and yield have a strong correlation; with increasing distance to forest, solar irradiance and yield increase.
- The main influencing factors for the reduction of solar irradiance and the accompanying yield are tree height, distance to the forest, and cardinal direction.
- Crop varieties react differently, according to their physiological disposition.
- In dry years, the shading effects in the transition zones can be beneficial for the crop growth.
- On a regional level, a yield reduction of 5% to 8% can be considered to have been caused by shading in the transition zones.
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Schmidt, M.; Jochheim, H.; Kersebaum, K.-C.; Lischeid, G.; Nendel, C. Gradients of microclimate, carbon and nitrogen in transition zones of fragmented landscapes—A review. Agric. For. Meteorol. 2017, 232, 659–671. [Google Scholar] [CrossRef]
- Haddad, N.M.; Brudvig, L.A.; Clobert, J.; Davies, K.F.; Gonzalez, A.; Holt, R.D.; Lovejoy, T.E.; Sexton, J.O.; Austin, M.P.; Collins, C.D.; et al. Habitat fragmentation and its lasting impact on Earth’s ecosystems. Sci. Adv. 2015, 1, e1500052. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Lischeid, G.; Nendel, C. Microclimate and matter dynamics in transition zones of forest to arable land. Agric. For. Meteorol. 2019. submitted for publication. [Google Scholar]
- Laurance, W.; Camargo, J.; Luizão, R.; Laurance, S.; Pimm, S.; Bruna, E.; Stouffer, P.; Williamson, G.; Benítez-Malvido, J.; Vasconcelos, H.; et al. The fate of Amazonian forest fragments: A 32-year investigation. Biol. Conserv. 2011, 144, 56–67. [Google Scholar] [CrossRef]
- Nuberg, I.K. Effect of shelter on temperate crops: A review to define research for Australian conditions. Agrofor. Syst. 1998, 41, 3–34. [Google Scholar] [CrossRef]
- Gray, A.N.; Spies, T.A.; Easter, M.J. Microclimatic and soil moisture responses to gap formation in coastal Douglas-fir forests. Can. J. Res. 2002, 32, 332–343. [Google Scholar] [CrossRef]
- Kort, J. 9. Benefits of windbreaks to field and forage crops. Agric. Ecosyst. Environ. 1988, 22, 165–190. [Google Scholar] [CrossRef]
- Kapos, V. Effects of isolation on the water status of forest patches in the Brazilian Amazon. J. Trop. Ecol. 1989, 5, 173–185. [Google Scholar] [CrossRef]
- Matlack, G.R. Microenvironment variation within and among forest edge sites in the eastern United States. Biol. Conserv. 1993, 66, 185–194. [Google Scholar] [CrossRef]
- Gholz, H.L.; Vogel, S.A.; Cropper, W.P.; McKelvey, K.; Ewel, K.C.; Teskey, R.O.; Curran, P.J. Dynamics of canopy structure and light interception in Pinus Elliottii Stands, North Florida. Ecol. Monogr. 1991, 61, 33–51. [Google Scholar] [CrossRef]
- Voicu, M.F.; Comeau, P.G. Microclimatic and spruce growth gradients adjacent to young aspen stands. For. Ecol. Manag. 2006, 221, 13–26. [Google Scholar] [CrossRef]
- Dufour, L.; Metay, A.; Talbot, G.; Dupraz, C. Assessing light competition for cereal production in temperate agroforestry systems using experimentation and crop modeling. J. Agron. Crop Sci. 2013, 199, 217–227. [Google Scholar] [CrossRef]
- Ghaffari, A.; Cook, H.F.; Lee, H.C. Simulating winter wheat yields under temperate conditions: Exploring different management scenarios. Eur. J. Agron. 2001, 15, 231–240. [Google Scholar] [CrossRef]
- Juin, S.; Brisson, N.; Clastre, P.; Grand, P. Impact of global warming on the growing cycles of three forage systems in upland areas of southeastern France. Agronomie 2004, 24, 327–337. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.E. Tree and crop selection and management to optimize overall system productivity, especially light utilization, in agroforestry. In Meteorology and Agroforestry, Proceedings of an International Workshop on the Application of Meteorology to Agroforestry Systems Planning and Management, Nairobi, Kenya, 9–13 February 1987; International Council for Research in Agroforestry (ICRAF): Nairobi, Kenya, 1989; pp. 163–173. [Google Scholar]
- Chirko, C.P.; Gold, M.A.; Nguyen, P.V.; Jiang, J.P. Influence of direction and distance from trees on wheat yield and photosynthetic photon flux density (Qp) in a Paulownia and wheat intercropping system. For. Ecol. Manage. 1996, 83, 171–180. [Google Scholar] [CrossRef]
- Li, F.; Meng, P.; Fu, D.; Wang, B. Light distribution, photosynthetic rate and yield in a Paulownia-wheat intercrop-ping system in China. Agrofor. Syst. 2008, 74, 163–172. [Google Scholar] [CrossRef]
- Huxley, P.A.; Pinney, A.; Akunda, E.P.; Muraya, P. A tree/crop interface orientation experiment with a Grevillea robusta hedgerow and maize. Agrofor. Syst. 1994, 26, 23–45. [Google Scholar] [CrossRef]
- Reynolds, P.E.; Simpson, J.A.; Thevathasan, N.V.; Gordon, A.M. Effects of tree competition on corn and soy- bean photosynthesis, growth, and yield in a temperate tree- based agroforestry intercropping system in southern Ontario, Canada. Ecol. Eng. 2007, 29, 362–371. [Google Scholar] [CrossRef]
- Reuter, H.I.; Kersebaum, K.C.; Wendroth, O. Modeling of solar radiation influenced by topographic shading—Evaluation and application for precision farming. Phys. Chem. Earth Parts ABC 2005, 30, 143–149. [Google Scholar] [CrossRef]
- Brisson, N.; Bussière, F.; Ozier-Lafontaine, H.; Tournebize, R.; Sinoquet, H. Adaptation of the crop model STICS to intercropping. Theoretical basis and parameterisation. Agronomie 2004, 24, 409–421. [Google Scholar] [CrossRef]
- Corre-Hellou, G.; Faure, M.; Launay, M.; Brisson, N.; Crozat, Y. Adaptation of the STICS intercrop model to simulate crop growth and N accumulation in pea–barley intercrops. Field Crops Res. 2009, 113, 72–81. [Google Scholar] [CrossRef]
- Knörzer, H.; Grözinger, H.; Graeff-Hönninger, S.; Hartung, K.; Piepho, H.-P.; Claupein, W. Integrating a simple shading algorithm into CERES-wheat and CERES-maize with particular regard to a changing microclimate within a relay-intercropping system. Field Crops Res. 2011, 121, 274–285. [Google Scholar] [CrossRef]
- Artru, S.; Dumont, B.; Ruget, F.; Launay, M.; Ripoche, D.; Lassois, L.; Garré, S. How does STICS crop model simulate crop growth and productivity under shade conditions? Field Crops Res. 2018, 215, 83–93. [Google Scholar] [CrossRef]
- Artru, S.; Garré, S.; Dupraz, C.; Hiel, M.-P.; Blitz-Frayret, C.; Lassois, L. Impact of spatio-temporal shade dynamics on wheat growth and yield, perspectives for temperate agroforestry. Eur. J. Agron. 2017, 82, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Bithell, M.; Brasington, J. Coupling agent-based models of subsistence farming with individual-based forest models and dynamic models of water distribution. Environ. Model. Softw. 2009, 24, 173–190. [Google Scholar] [CrossRef]
- McNider, R.T.; Handyside, C.; Doty, K.; Ellenburg, W.L.; Cruise, J.F.; Christy, J.R.; Moss, D.; Sharda, V.; Hoogenboom, G.; Caldwell, P. An integrated crop and hydrologic modeling system to estimate hydrologic impacts of crop irrigation demands. Environ. Model. Softw. 2015, 72, 341–355. [Google Scholar] [CrossRef]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Brandle, J.R.; Hodges, L.; Zhou, X.H. Windbreaks in North American agricultural systems. Agrofor. Syst. 2004, 61. [Google Scholar] [CrossRef]
- ESRL Global Monitoring Division—Global Radiation Group. Available online: https://www.esrl.noaa.gov/gmd/grad/solcalc/index.html (accessed on 13 August 2018).
- Nendel, C.; Berg, M.; Kersebaum, K.C.; Mirschel, W.; Specka, X.; Wegehenkel, M.; Wenkel, K.O.; Wieland, R. The MONICA model: Testing predictability for crop growth, soil moisture and nitrogen dynamics. Ecol. Model. 2011, 222, 1614–1625. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.; Boote, K.J.; Thorburn, P.; Rötter, R.P.; Cammarano, D.; et al. Quantifying uncertainties in simulating wheat yields under climate change. Nat. Clim. Change. 2013, 3, 827–832. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.J.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pirttioja, N.; Fronzek, S.; Bindi, M.; Carter, T.R.; Hoffmann, H.; Palosuo, T.; Ruiz Ramos, M.; Trnka, M.; Acutis, M.; Asseng, S.; et al. Temperature and precipitation effects on wheat yield across a European transect: A crop model ensemble analysis using impact response surfaces. Clim. Res. 2015, 65, 87–105. [Google Scholar] [CrossRef]
- Mitchell, M.G.E.; Bennett, E.M.; Gonzalez, A. Forest fragments modulate the provision of multiple ecosystem services. J. Appl. Ecol. 2014, 51, 909–918. [Google Scholar] [CrossRef] [Green Version]
- Malik, R.S.; Sharma, S.K. Moisture extraction and crop yield as a function of distance from a row of Eucalyptus tereticornis. Agrofor. Syst. 1990, 12, 187–195. [Google Scholar] [CrossRef]
- Lyles, L.; Tatarko, J.; Dickerson, J.D. Windbreak effects on soil water and wheat yield. Trans. ASAE 1984, 27, 0069–0072. [Google Scholar] [CrossRef]
- Emmingham, W.H.; Waring, R.H. Conifer growth under different light environments in the Siskiyou Mountains of southwestern Oregon. Northwest Sci. 1973, 47, 88–99. [Google Scholar]
- Bulir, P. Effects of shelterbelts on winter wheat yields. Zadradnictvi 1992, 163–175. [Google Scholar]
- Groot, A.; Carlson, D.W. Influence of shelter on night temperatures, frost damage, and bud break of white spruce seedlings. Can. J. For. Res. 1996, 26, 1531–1538. [Google Scholar] [CrossRef]
- Riitters, K.H.; Wickham, J.D.; O’Neill, R.V.; Jones, K.B.; Smith, E.R.; Coulston, J.W.; Wade, T.G.; Smith, J.H. Fragmentation of continental united states forests. Ecosystems 2002, 5, 815–822. [Google Scholar] [CrossRef]
- Riutta, T.; Slade, E.M.; Morecroft, M.D.; Bebber, D.P.; Malhi, Y. Living on the edge: Quantifying the structure of a fragmented forest landscape in England. Landsc. Ecol 2014, 29, 949–961. [Google Scholar] [CrossRef]


| Depth (cm) | Soil Organic Carbon (%) | Texture Class | Raw Density (kg m−3) |
|---|---|---|---|
| 0 to 30 | 0.8 | loamy sand | 1446 |
| 30 to 40 | 0.15 | loamy sand | 1446 |
| 40 to 200 | 0.05 | loamy sand | 1446 |
| 10 m * | 15 m | 20 m | 30 m * | 40 m * | 50 m | 100 m | |
|---|---|---|---|---|---|---|---|
| Non-forest | 4.8% | 6% | 7% | 9.6% | 12% | 15.2% | 26.3% |
| Crop | Area (ha) | Average Yield (kg ha−1) | TZ (m) | TZ Share (%) | Yield Reduction in TZ (%) | Yield Reduction in Brandenburg (%) |
|---|---|---|---|---|---|---|
| Winter wheat | 129,000 | 6314 | 15 | 6 | 10.4 | 5.4 |
| Silage maize | 178,600 | 2564 | 30 | 9.6 | 12.3 | 8.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, M.; Nendel, C.; Funk, R.; Mitchell, M.G.E.; Lischeid, G. Modeling Yields Response to Shading in the Field-to-Forest Transition Zones in Heterogeneous Landscapes. Agriculture 2019, 9, 6. https://doi.org/10.3390/agriculture9010006
Schmidt M, Nendel C, Funk R, Mitchell MGE, Lischeid G. Modeling Yields Response to Shading in the Field-to-Forest Transition Zones in Heterogeneous Landscapes. Agriculture. 2019; 9(1):6. https://doi.org/10.3390/agriculture9010006
Chicago/Turabian StyleSchmidt, Martin, Claas Nendel, Roger Funk, Matthew G. E. Mitchell, and Gunnar Lischeid. 2019. "Modeling Yields Response to Shading in the Field-to-Forest Transition Zones in Heterogeneous Landscapes" Agriculture 9, no. 1: 6. https://doi.org/10.3390/agriculture9010006
APA StyleSchmidt, M., Nendel, C., Funk, R., Mitchell, M. G. E., & Lischeid, G. (2019). Modeling Yields Response to Shading in the Field-to-Forest Transition Zones in Heterogeneous Landscapes. Agriculture, 9(1), 6. https://doi.org/10.3390/agriculture9010006