Temporal Sensitivity Analysis of the MONICA Model: Application of Two Global Approaches to Analyze the Dynamics of Parameter Sensitivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Crop Growth Model
2.2. Study Sites and Management Settings
2.3. Parameter Selection and Model Outputs
2.4. Parameter Screening
2.5. The Extended FAST Method
2.6. Top-Down Concordance Coefficients
2.7. Implementation of the SA
3. Results
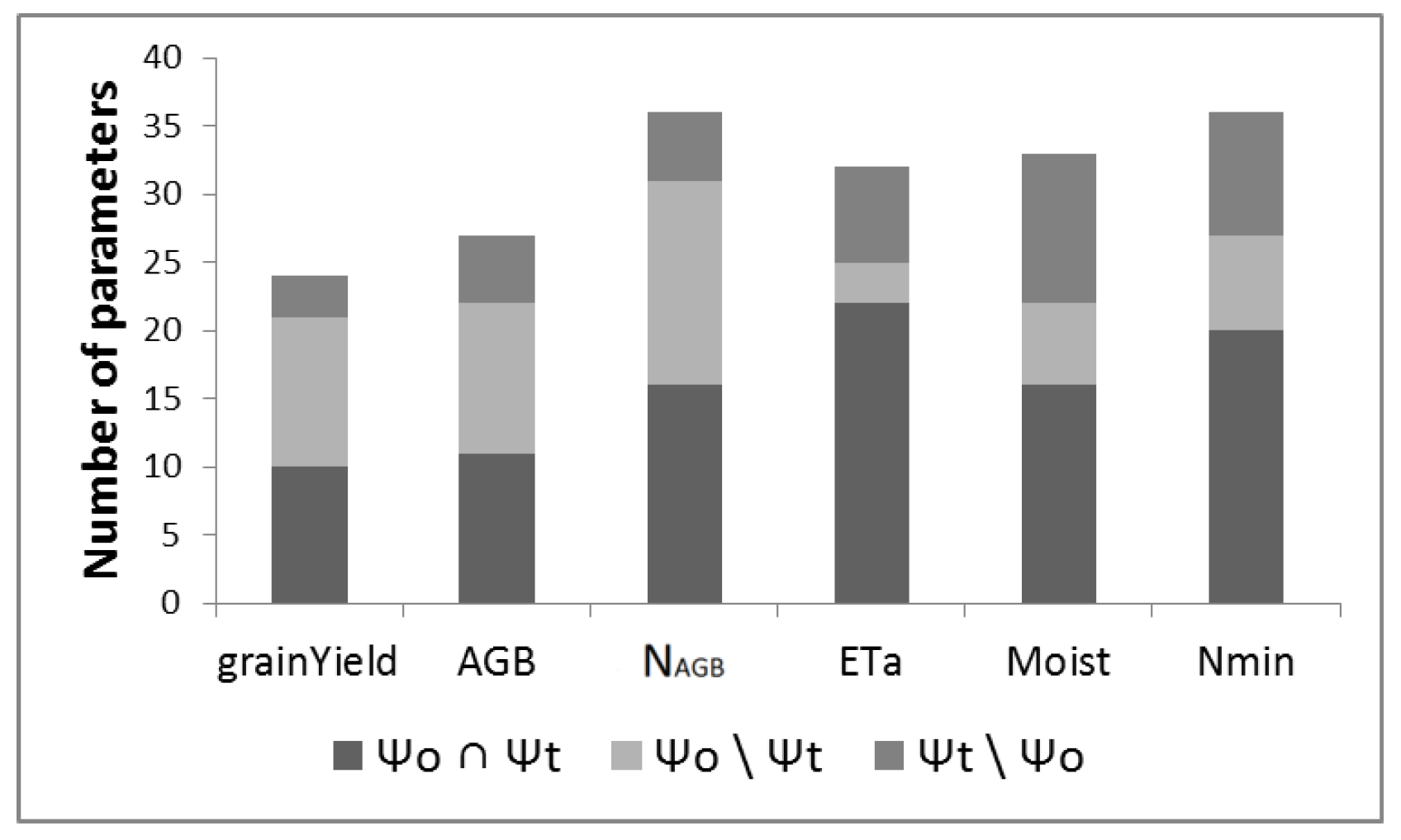
3.1. Parameter Screening
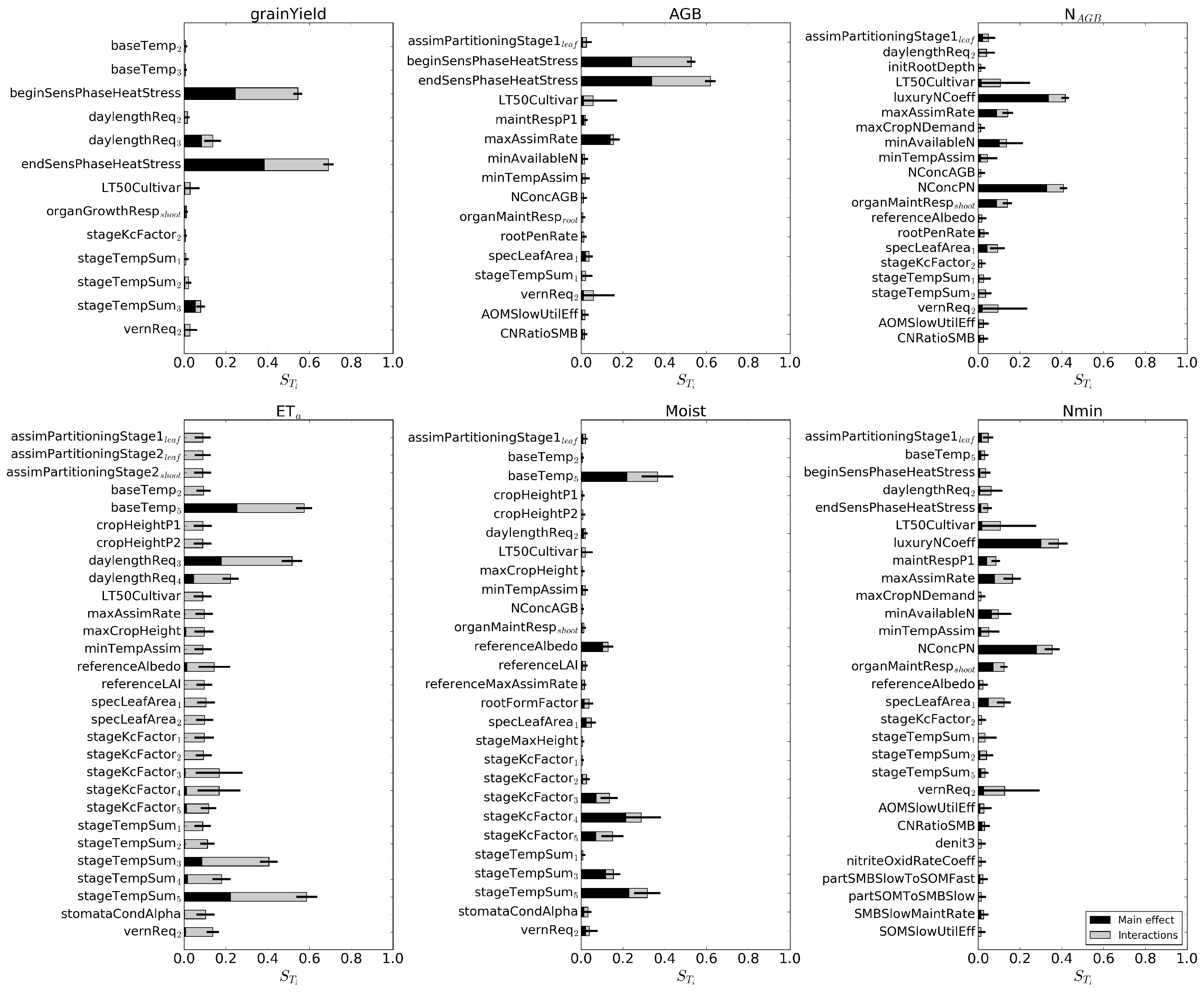
3.2. Extended FAST Method
3.2.1. Original Approach
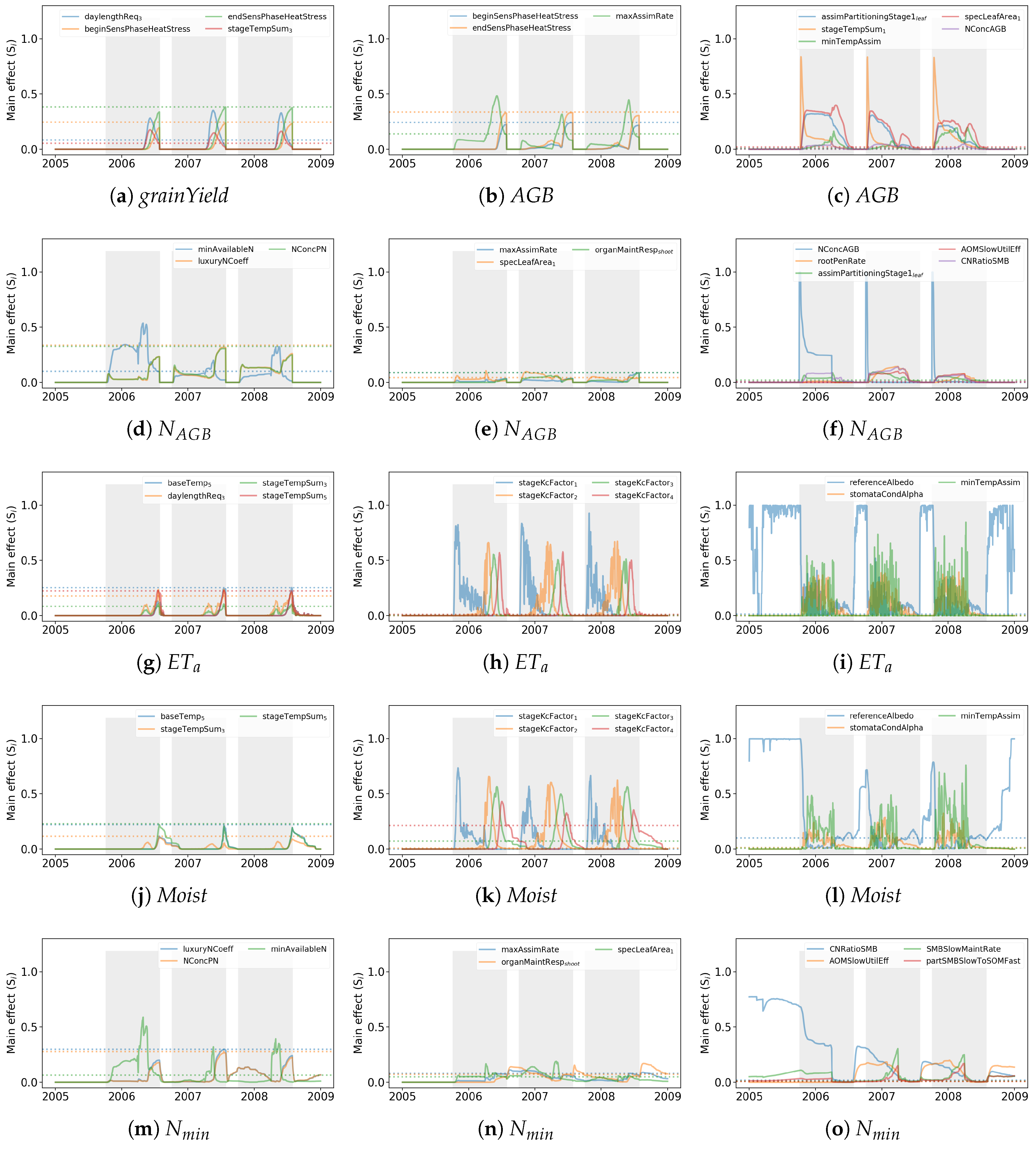
3.2.2. Time-Dependent Main Effects
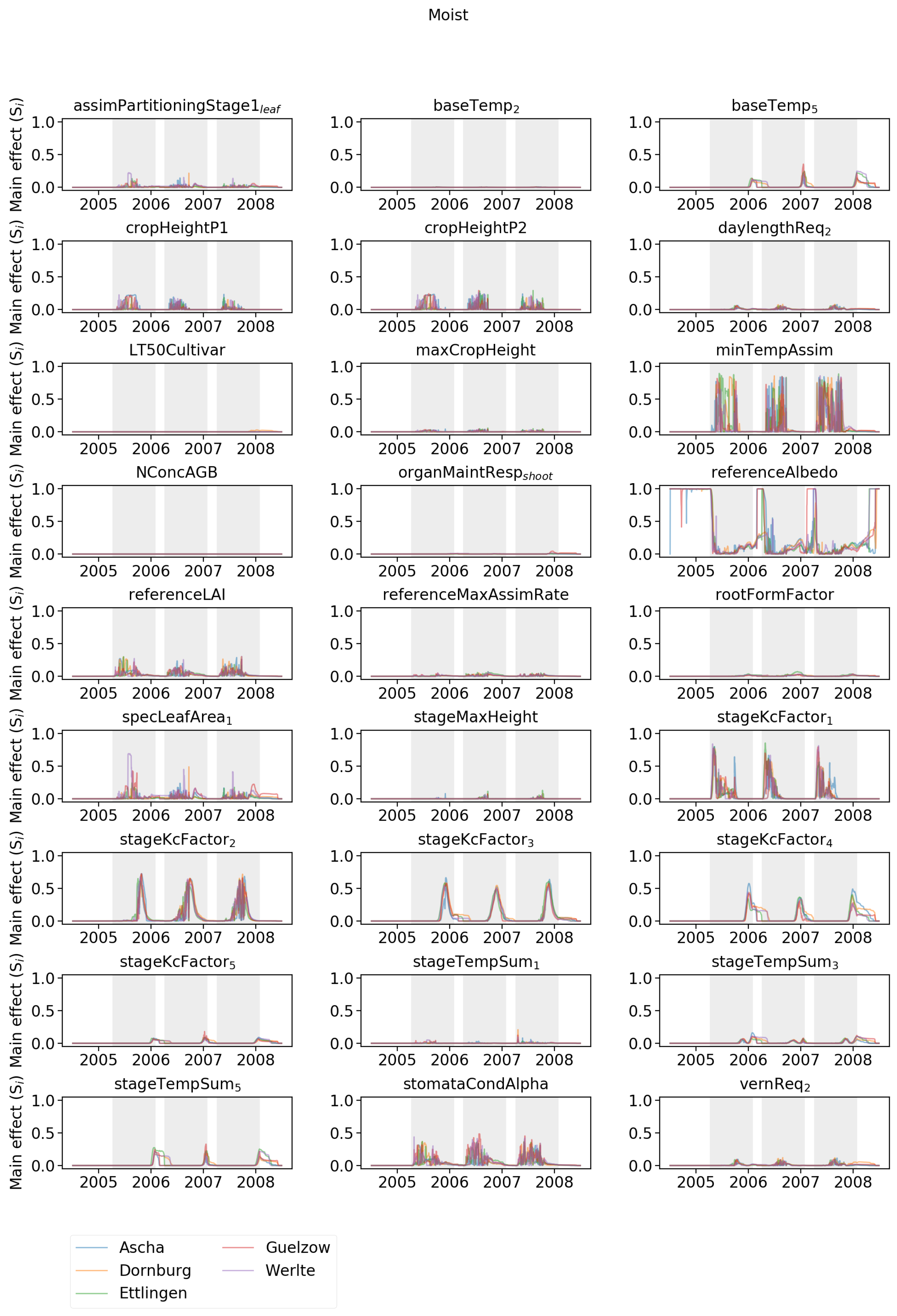
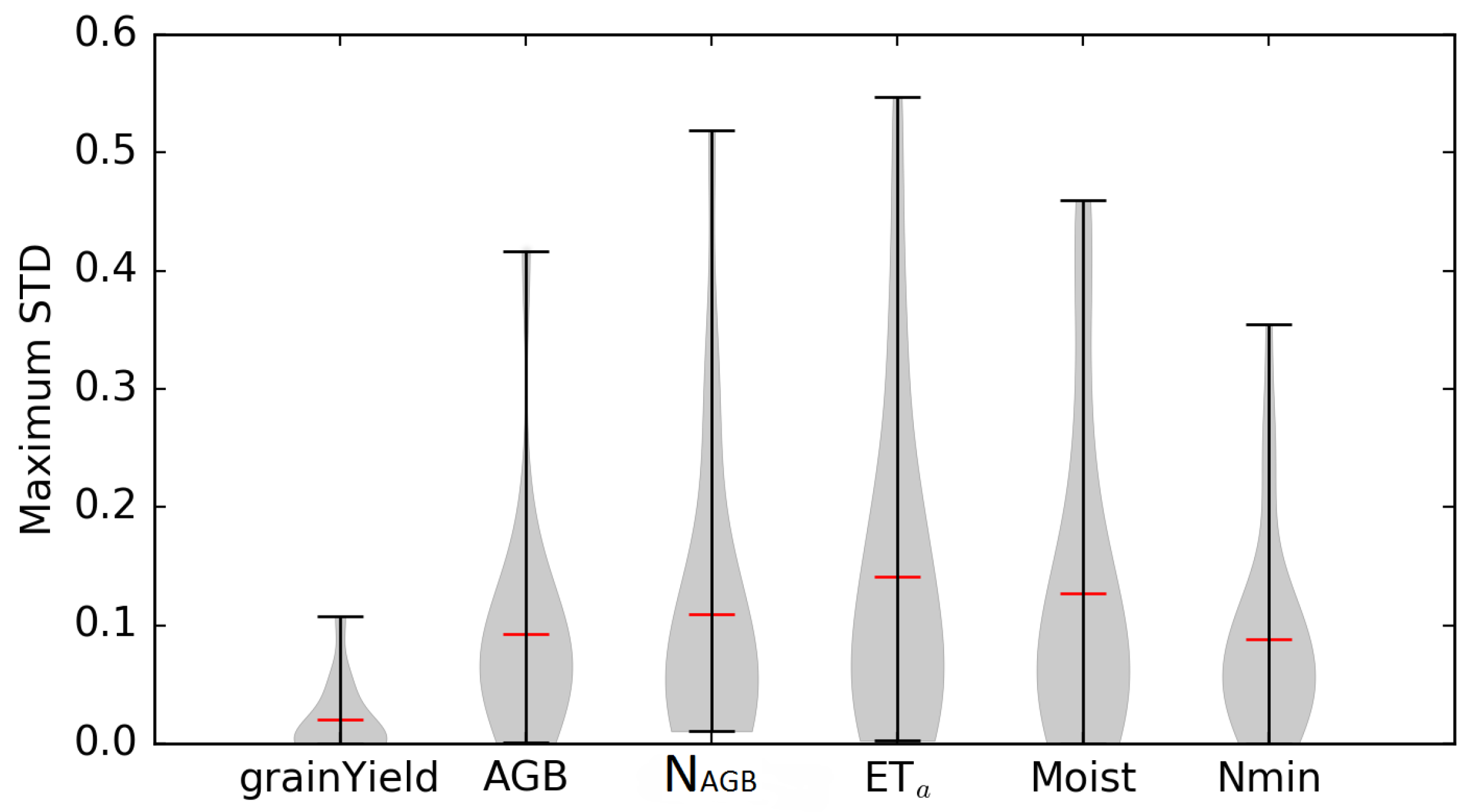
3.2.3. Temporal Sensitivity Patterns
3.2.4. Influence of the Different Sites
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AGB | Above-ground biomass |
| C | Organic carbon |
| CAN | Calcium-ammonium-nitrate-based fertilizer |
| EE | Elementary effect |
| ET | Potential evapotranspiration |
| ET | Actual evapotranspiration |
| FAST | Fourier amplitude sensitivity test |
| HPC | High-performance computer |
| Moist | Soil moisture |
| MONICA | Model for Nitrogen and Carbon dynamics in Agro-ecosystems |
| N | N content in above-ground biomass |
| N | Soil mineral nitrogen |
| SA | Sensitivity analysis |
| S | First-order sensitivity index |
| S | Total sensitivity index |
| TDCC | Top-down concordance coefficients |
| TDSA | Time-dependent sensitivity analysis |
Software availability
| Name of Software | MONICA—Model for Nitrogen and Carbon dynamics in Agro-ecosystems |
| Version | 1.2 |
| Developer | Claas Nendel |
| Contact | Claas Nendel, Leibniz Centre for Agricultural Landscape Research (ZALF), Research Platform ’Models’, Eberswalder Straße 84, 15374 Müncheberg, Germany Email: nendel@zalf.de Tel.: +49-33432 82-355 Fax: +49-33432-82-181 |
| Year first available | 2011 |
| Required hardware and software | MONICA will run on Windows or Linux machines. When building the model directly from the source code MONICA requires Boost.Python Version 1.0. For Windows systems the compilation process requires Visual Studio 2015 (Community Edition). |
| Availability and Cost | Information about the MONICA model can be found at http://monica.agrosystem-models.com. For Windows an installation wizard can be downloaded at http://monica.agrosystem-models.com. The source code of the model is available at Github (https://github.com/zalf-rpm/monica). |
| Cost and License | Free. MONICA is distributed under the Mozilla Public License, v.2.0 (http://mozilla.org/MPL/2.0/) |
| Program Language | MONICA was developed using the programming language C/C++. Model parameters are stored in a separate SQLite database that comes with the model. |
| Program size | Source code: approx. 20 MB Windows installer: 2.6 MB |
Appendix A. Daily Parameter Sensitivities Based on SI Differentiated among the Different Sites





References
- Martre, P.; Wallach, D.; Asseng, S.; Ewert, F.; Jones, J.W.; Rötter, R.P.; Boote, K.J.; Ruane, A.C.; Thorburn, P.J.; Cammarano, D.; et al. Multimodel ensembles of wheat growth: Many models are better than one. Glob. Chang. Biol. 2015, 21, 911–925. [Google Scholar] [CrossRef] [PubMed]
- Asseng, S.; Ewert, F.; Martre, P.; Roetter, R.P.; Lobell, D.B.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ewert, F.; Rötter, R.; Bindi, M.; Webber, H.; Trnka, M.; Kersebaum, K.; Olesen, J.; van Ittersum, M.; Janssen, S.; Rivington, M.; et al. Crop modelling for integrated assessment of risk to food production from climate change. Environ. Model. Softw. 2014. [Google Scholar] [CrossRef]
- Makowski, D.; Naud, C.; Jeuffroy, M.H.; Barbottin, A.; Monod, H. Global sensitivity analysis for calculating the contribution of genetic parameters to the variance of crop model prediction. Reliab. Eng. Syst. Saf. 2006, 91, 1142–1147. [Google Scholar] [CrossRef]
- Mirzaei, M.; Huang, Y.F.; El-Shafie, A.; Shatirah, A. Application of the generalized likelihood uncertainty estimation (GLUE) approach for assessing uncertainty in hydrological models: A review. Stoch. Environ. Res. Risk Assess. 2015, 29, 1265–1273. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of Eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
- Ma, S.; Churkina, G.; Wieland, R.; Gessler, A. Optimization and evaluation of the ANTHRO-BGC model for winter crops in Europe. Ecol. Model. 2011, 222, 3662–3679. [Google Scholar] [CrossRef]
- Muleta, M.; Nicklow, J. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Confalonieri, R.; Bregaglio, S.; Acutis, M. Quantifying plasticity in simulation models. Ecol. Model. 2012, 225, 159–166. [Google Scholar] [CrossRef]
- Jakeman, A.; Letcher, R.; Norton, J. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Specka, X.; Nendel, C.; Wieland, R. Analyzing the parameter sensitivity of the agro-ecosystem model MONICA for different crops. Eur. J. Agron. 2015, 71, 73–87. [Google Scholar] [CrossRef]
- Richter, G.M.; Acutis, M.; Trevisiol, P.; Latiri, K.; Confalonieri, R. Sensitivity analysis for a complex crop model applied to Durum wheat in the Mediterranean. Eur. J. Agron. 2010, 32, 127–136. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; John Wiliey & Sons, Ltd.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Dzotsi, K.; Basso, B.; Jones, J. Development, uncertainty and sensitivity analysis of the simple SALUS crop model in DSSAT. Ecol. Model. 2013, 260, 62–76. [Google Scholar] [CrossRef]
- Makler-Pick, V.; Gal, G.; Gorfine, M.; Hipsey, M.R.; Carmel, Y. Sensitivity analysis for complex ecological models—A new approach. Environ. Model. Softw. 2011, 26, 124–134. [Google Scholar] [CrossRef]
- Zhao, G.; Bryan, B.; Song, X. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar, environmental, and management parameters. Ecol. Model. 2014, 279, 1–11. [Google Scholar] [CrossRef]
- Song, X.; Bryan, B.; Almeida, A.; Paul, K.; Zhao, G.; Ren, Y. Time-dependent sensitivity of a process-based ecological model. Ecol. Model. 2013, 265, 114–123. [Google Scholar] [CrossRef]
- Song, X.; Bryan, B.; Paul, K.; Zhao, G. Variance-based sensitivity analysis of a forest growth model. Ecol. Model. 2012, 247, 135–143. [Google Scholar] [CrossRef]
- Lamboni, M.; Monod, H.; Makowski, D. Multivariate sensitivity analysis to measure global contribution of input factors in dynamic models. Reliab. Eng. Syst. Saf. 2011, 96, 450–459. [Google Scholar] [CrossRef]
- Lamboni, M.; Makowski, D.; Lehuger, S.; Gabrielle, B.; Monod, H. Multivariate global sensitivity analysis for dynamic crop models. Field Crops Res. 2009, 113, 312–320. [Google Scholar] [CrossRef]
- Nendel, C.; Berg, M.; Kersebaum, K.; Mirschel, W.; Specka, X.; Wegehenkel, M.; Wenkel, K.; Wieland, R. The MONICA model: Testing predictability for crop growth, soil moisture and nitrogen dynamics. Ecol. Model. 2011, 222, 1614–1625. [Google Scholar] [CrossRef]
- Kersebaum, K. Application of a simple management model to simulate water and nitrogen dynamics. Ecol. Model. 1995, 81, 145–156. [Google Scholar] [CrossRef]
- Greenwood, D.; Stone, D.; Draycott, A. Weather, nitrogen-supply and growth rate of field vegetables. Plant Soil 1990, 124, 297–301. [Google Scholar] [CrossRef]
- Wegehenkel, M. Test of a modelling system for simulating water balances and plant growth using various different complex approaches. Ecol. Model. 2000, 129, 39–64. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; FAO: Roma, Italy, 1998; Volume 56. [Google Scholar]
- Hansen, S.; Jensen, H.; Nielsen, N.; Svendsen, H. Simulation of nitrogen dynamics and biomass production in winter wheat using the Danish simulation model DAISY. Fertili. Res. 1991, 27, 245–259. [Google Scholar] [CrossRef]
- Glemnitz, M.; Eckner, J.; Aurbacher, J.; Kornatz, P.; Müller, J.; Heiermann, M.; Peter, C. Crop rotations as “cornerstone” of sustainable energy cropping—Integrative evaluation of their agronomic, ecologic, economic and resource efficiency effects. In Biomass and Energy Crops V; Association of Applied Biologists: Brussels, Belgium, 2015; pp. 117–128. [Google Scholar]
- Nehring, A.; Vetter, A. Entwicklung und Vergleich von Optimierten Anbausystemen für die landwirtschaftliche Produktion von Energiepflanzen unter den Verschiedenen Standortbeding ungen Deutschlands (EVA)—Abschlussbericht 2009 zum Teilprojekt 1; Technical Report; Thüringer Landesanstalt für Landwirtschaft: Jena, Germany, 2009.
- Vetter, A.; Nehring, A.; Ebel, G.; Peters, J.; Grunewald, J.; Kruse, S.; Deiglmayr, K.; Wilken, F. Schriftliche Mitteilung. Datenmaterial aus den Bonituren des deutschlandweiten Verbundprojektes EVA; Technical Report; Thüringer Landesanstalt für Landwirtschaft: Jena, Germany, 2011; FKZ 22013008.
- Esprey, L.; Sands, P.; Smith, C. Understanding 3-PG using a sensitivity analysis. For. Ecol. Manag. 2004, 193, 235–250. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef] [Green Version]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V. Improving the Morris method for sensitivity analysis by scaling the elementary effects. In 19th European Symposium on Computer Aided Process Engineering; Jezowski, J., Thullie, J., Eds.; Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2009; Volume 26, pp. 925–930. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W. A measure of top-down correlation. Technometrics 1987, 29, 351–357. [Google Scholar]
- Helton, J.; Johnson, J.; Sallaberry, C.; Storlie, C. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Confalonieri, R.; Bellocchi, G.; Bregaglio, S.; Donatelli, M.; Acutis, M. Comparison of sensitivity analysis techniques: A case study with the rice model WARM. Ecol. Model. 2010, 221, 1897–1906. [Google Scholar] [CrossRef]
- Savage, I. Contributions to the theory of rank order statistics—The two-sample case. Ann. Math. Stat. 1956, 27, 590–615. [Google Scholar] [CrossRef]
- Lutz, M. Programming Python, 4th ed.; O’Reilly: Sebastopol, CA, USA, 2010. [Google Scholar]
- Beazley, D. Automated scientific software scripting with SWIG. Future Gener. Comput. Syst. 2003, 19, 599–609. [Google Scholar] [CrossRef]
- Dalcín, L.; Paz, R.; Storti, M. MPI for Python. J. Parallel Distrib. Comput. 2005, 65, 1108–1115. [Google Scholar] [CrossRef]
- Dalcín, L.; Paz, R.; Storti, M.; D’Elía, J. MPI for Python: Performance improvements and MPI-2 extensions. J. Parallel Distrib. Comput. 2008, 68, 655–662. [Google Scholar] [CrossRef]
- Confalonieri, R.; Bellocchi, G.; Tarantola, S.; Acutis, M.; Donatelli, M.; Genovese, G. Sensitivity analysis of the rice model WARM in Europe: Exploring the effects of different locations, climates and methods of analysis on model sensitivity to crop parameters. Environ. Model. Softw. 2010, 25, 479–488. [Google Scholar] [CrossRef] [Green Version]
- Estrada, V.; Diaz, M. Global sensitivity analysis in the development of first principle-based eutrophication models. Environ. Model. Softw. 2010, 25, 1539–1551. [Google Scholar] [CrossRef]
- Francos, A.; Elorza, F.J.; Bouraoui, F.; Bidoglio, G.; Galbiati, L. Sensitivity analysis of distributed environmental simulation models: understanding the model behavior in hydrological studies at the catchment scale. Reliab. Eng. Syst. Saf. 2003, 79, 205–218. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A. Sensitivity analysis of an environmental model an application of different analysis methods. Reliab. Eng. Syst. Saf. 1997, 57, 49–69. [Google Scholar] [CrossRef]
- Simons-Legaard, E.; Legaard, K.; Weiskittel, A. Predicting aboveground biomass with LANDIS-II: A global and temporal analysis of parameter sensitivity. Ecol. Model. 2015, 313, 325–332. [Google Scholar] [CrossRef] [Green Version]
- Garambois, P.A.; Roux, H.; Larnier, K.; Castaings, W.; Dartus, D. Characterization of process-oriented hydrologic model behavior with temporal sensitivity analysis for flash floods in Mediterranean catchments. Hydrol. Earth Syst. Sci. 2013, 17, 2305–2322. [Google Scholar] [CrossRef] [Green Version]
- Reusser, D.E.; Buytaert, W.; Zehe, E. Temporal dynamics of model parameter sensitivity for computationally expensive models with the Fourier amplitude sensitivity test. Water Resour. Res. 2011, 47, W07551. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W. (Eds.) Working with Dynamic Crop Modells; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wang, E.; Martre, P.; Asseng, S.; Ewert, F.; Zhao, Z.; Maiorano, A.; Rötter, R.; Kimball, B.; Ottman, M.; Wall, G.; et al. Generic temperature response functions reduce uncertainty in crop yield projections. Nat. Plants 2016. in revision. [Google Scholar]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rotter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827–832. [Google Scholar] [CrossRef]
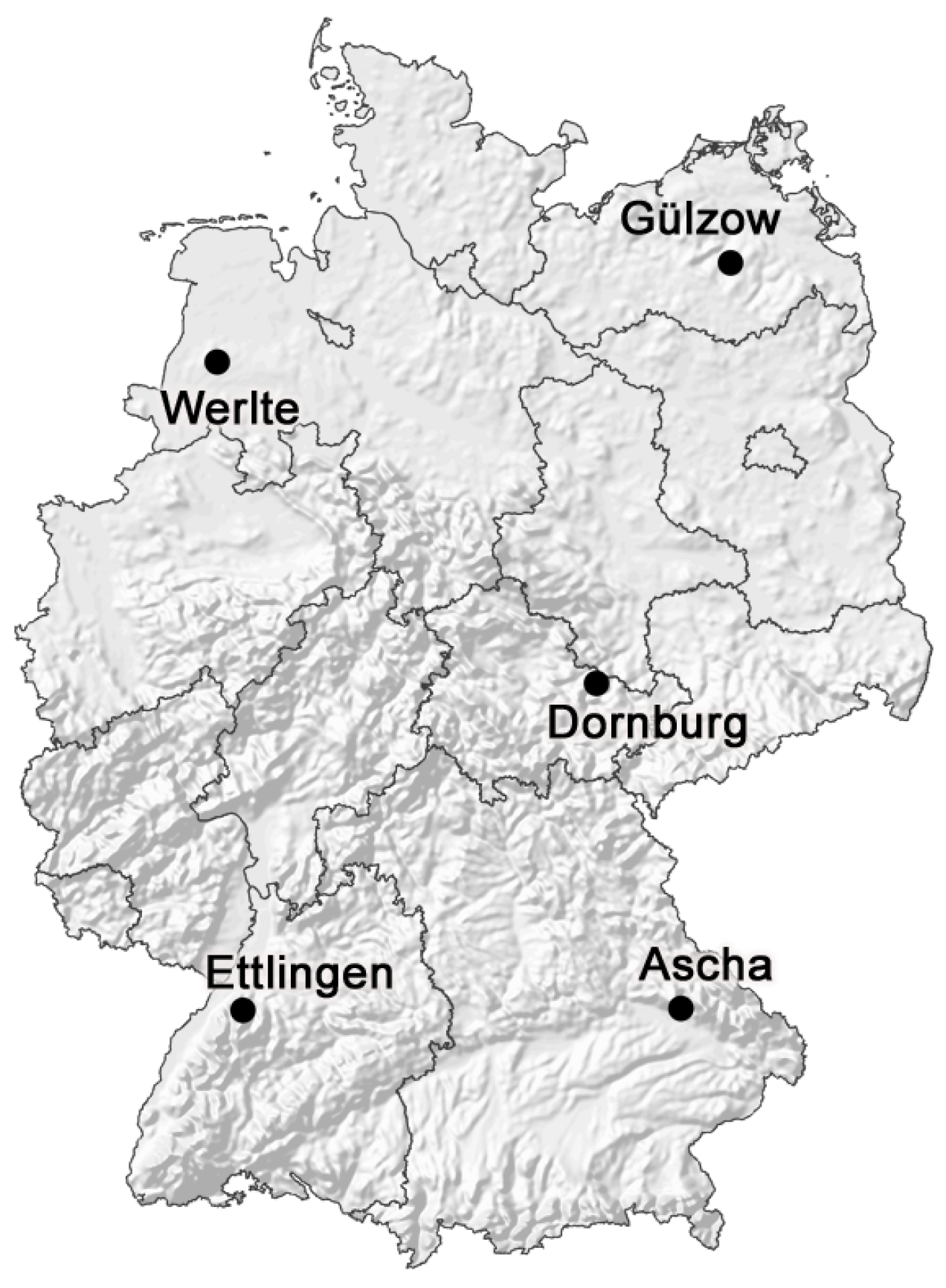


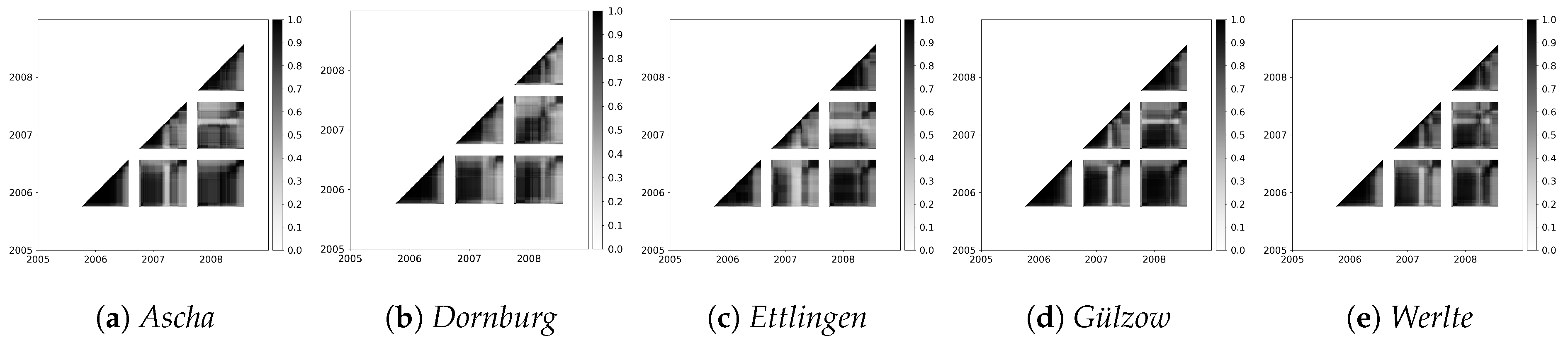
| Name | Ascha | Dornburg | Ettlingen | Gülzow | Werlte |
|---|---|---|---|---|---|
| Geographical location | ′ N | ′ N | ′ N | ′ N | ′ N |
| ′ E | ′ E | ′ E | ′ E | ′ E | |
| Height above sea level | 430 m | 250 m | 170 m | 10 m | 32 m |
| Soil type | Stagnic Cambisol | Luvisol | Regosol-Luvisol | Planosol | Stagnic Cambisol |
| Soil texture | Loamy sand | Silty clayey loam | Loamy silt | Sandy loam | Loamy sand |
| Available water capacity | 117 mm | 189–215 mm | 199 mm | 120 mm | 105 mm |
| C | 1.3% | 1.0% | 0.76% | 0.7% | 1.3% |
| pH value | 6.4 | 7.2 | 7.3 | 6.4 | 5.2 |
| Total annual precipitation | 807 mm | 474 mm | 742 mm | 559 mm | 797 mm |
| Mean temperature | 7.5 C | 8.8 C | 11.1 C | 8.4 C | 9.57 C |
| Ploughing | Sowing | Fertilization | Harvesting | ||
|---|---|---|---|---|---|
| 3 October | 4 October | 31 March | 70 kg N | CAN | 29 July |
| 30 April | 30 kg N | CAN | |||
| 22 May | 60 kg N | CAN | |||
| Parameter | Description | Unit | Nominal | grainYield | AGB | N | ET | Moist | N |
|---|---|---|---|---|---|---|---|---|---|
| AOMSlowUtilEff | Added organic matter slow utilization efficiency | 0.4 | x | x | x | ||||
| assimPartitioningStage1 | Portion of assimilates assigned for leaf growth in Stage 1 | % | 0.5 | x | x | x | x | x | |
| assimPartitioningStage2 | Portion of assimilates assigned for leaf growth in Stage 2 | % | 0.2 | x | |||||
| assimPartitioningStage2 | Portion of assimilates assigned for shoot growth in Stage 2 | % | 0.6 | x | |||||
| baseTemp | Base temperature for assimilation in Stage 2 | C | 1 | x | x | x | |||
| baseTemp | Base temperature for assimilation in stage 3 | C | 1 | x | |||||
| baseTemp | Base temperature for assimilation in Stage 5 | C | 9 | x | x | x | |||
| beginSensPhaseHeatStress | Temperature sum marking the start of the sensitive phase for heat stress | C | 620 | x | x | x | |||
| CNRatioSMB | C-to-N ratio of the soil microbial biomass | − | 6.7 | x | x | x | |||
| cropHeightP1 | Factor for crop height | − | 6 | x | x | ||||
| cropHeightP2 | Reduction factor for crop height | − | 0.5 | x | x | ||||
| daylengthReq | Day length required for maximum growth in Stage 2 | h | 20 | x | x | x | x | ||
| daylengthReq | Day length required for maximum growth in stage 3 | h | 20 | x | x | ||||
| daylengthReq | Day length required for maximum growth in Stage 4 | h | 20 | x | |||||
| denit3 | Denitrification coefficient | 0.9 | x | ||||||
| endSensPhaseHeatStress | Temperature sum marking the end of the sensitive phase for heat stress | C | 740 | x | x | x | |||
| initRootingDepth | Initial root depth of the crop | m | 0.1 | x | |||||
| LT50Cultivar | Threshold temperature below which 50% of the crop dies from frost injury | C | −24 | x | x | x | x | x | x |
| luxuryNCoeff | Coefficient describing the maximum N concentration relative to the critical N concentration in the crop tissue | − | 1.3 | x | x | ||||
| maintRespP1 | Q factor for maintenance respiration | − | 0.08 | x | x | ||||
| maxAssimRate | Maximum assimilation rate per leaf area | kg CO ha | 52 | x | x | x | x | ||
| maxCropHeight | Maximum crop height | m | 0.83 | x | x | ||||
| maxCropNDemand | Maximum amount of soil mineral N to be taken up by the crop | 6 | x | x | |||||
| minAvailableN | Mineral N concentration in the soil that is not available for crop N uptake | 0.0008 | x | x | x | ||||
| minTempAssim | Minimum temperature required for assimilation | C | 4 | x | x | x | x | x | |
| NConcAGB | Default N concentration in above-ground biomass | kg kg | 0.06 | x | x | x | |||
| nConcPN | Shape factor for the critical N curve | − | 1.6 | x | x | ||||
| nitrRateCoeffStand | Nitrification rate default coefficient | d | 0.2 | x | |||||
| organMaintResp | Maintenance respiration factor for shoots | kg CO kg DM | 0.15 | x | x | x | x | x | |
| partSMBSlowToSOMFast | Portion of the soil microbial biomass that is added to the fast soil organic matter pool | 0.6 | x | ||||||
| partSOMToSMBSlow | Portion of the soil organic matter that is added to the slow soil microbial biomass pool | 0.015 | x | ||||||
| referenceAlbedo | FAO reference albedo for green grass | − | 0.23 | x | x | x | x | ||
| referenceLAI | Leaf area index of the reference crop | mkg | 1.44 | x | x | ||||
| referenceMaxAssimRate | Maximum assimilation rate of the reference crop | kg CO ha | 30 | x | |||||
| rootFormFactor | Factor describing the root mass distribution pattern with respect to depth | − | 3 | x | |||||
| rootPenRate | Vertical root growth rate | m C d | 0.0011 | x | x | ||||
| SMBSlowMaintRateStand | Maintenance rate for slowly-reproducing soil microbial biomass | d | 0.001 | x | |||||
| SOMSlowUtilEff | Microbial utilization efficiency for the slowly-decomposing soil organic matter pool | 0.4 | x | ||||||
| specificLeafArea | Specific leaf area for calculating the leaf area index for stage 1 | m kg | 0.002 | x | x | x | x | x | |
| specificLeafArea | Specific leaf area for calculating the leaf area index for stage 2 | m kg | 0.0018 | x | |||||
| stageAtMaxHeight | Stage of maximal crop height | − | 3 | x | |||||
| stageKcFactor | factor for Stage 1 | − | 0.4 | x | x | ||||
| stageKcFactor | factor for Stage 2 | − | 0.7 | x | x | x | x | x | |
| stageKcFactor | factor for Stage 3 | − | 1.1 | x | x | ||||
| stageKcFactor | factor for stage 4 | − | 1.1 | x | x | ||||
| stageKcFactor | factor for Stage 5 | − | 0.8 | x | x | ||||
| stageTempSum | Temperature sum for Stage 1 | C | 148 | x | x | x | x | x | x |
| stageTempSum | Temperature sum for Stage 2 | C | 284 | x | x | x | x | ||
| stageTempSum | Temperature sum for Stage 3 | C | 380 | x | x | x | |||
| stageTempSum | Temperature sum for Stage 4 | C | 180 | x | |||||
| stageTempSum | Temperature sum for Stage 5 | C | 420 | x | x | x | |||
| stomataCondAlpha | Stomata conductivity parameter | − | 40 | x | x | ||||
| vernReq | Temperature sum required for optimum vernalization in Stage 2 | C | 50 | x | x | x | x | x | x |
| Number of relevant parameters | 13 | 16 | 21 | 29 | 27 | 29 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Specka, X.; Nendel, C.; Wieland, R. Temporal Sensitivity Analysis of the MONICA Model: Application of Two Global Approaches to Analyze the Dynamics of Parameter Sensitivity. Agriculture 2019, 9, 37. https://doi.org/10.3390/agriculture9020037
Specka X, Nendel C, Wieland R. Temporal Sensitivity Analysis of the MONICA Model: Application of Two Global Approaches to Analyze the Dynamics of Parameter Sensitivity. Agriculture. 2019; 9(2):37. https://doi.org/10.3390/agriculture9020037
Chicago/Turabian StyleSpecka, Xenia, Claas Nendel, and Ralf Wieland. 2019. "Temporal Sensitivity Analysis of the MONICA Model: Application of Two Global Approaches to Analyze the Dynamics of Parameter Sensitivity" Agriculture 9, no. 2: 37. https://doi.org/10.3390/agriculture9020037
APA StyleSpecka, X., Nendel, C., & Wieland, R. (2019). Temporal Sensitivity Analysis of the MONICA Model: Application of Two Global Approaches to Analyze the Dynamics of Parameter Sensitivity. Agriculture, 9(2), 37. https://doi.org/10.3390/agriculture9020037






