Research on Sailing Efficiency of Hybrid-Driven Underwater Glider at Zero Angle of Attack
Abstract
:1. Introduction
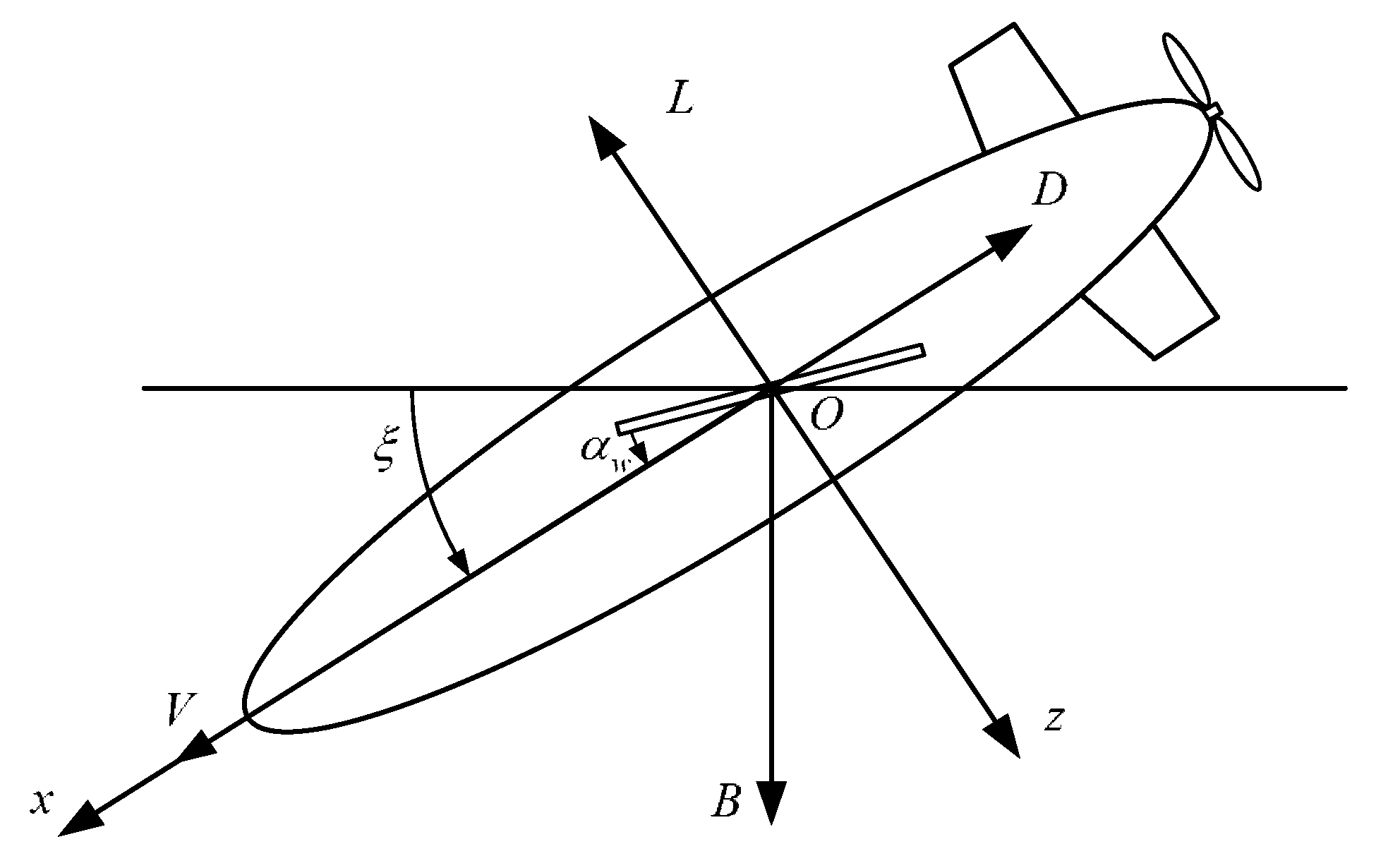
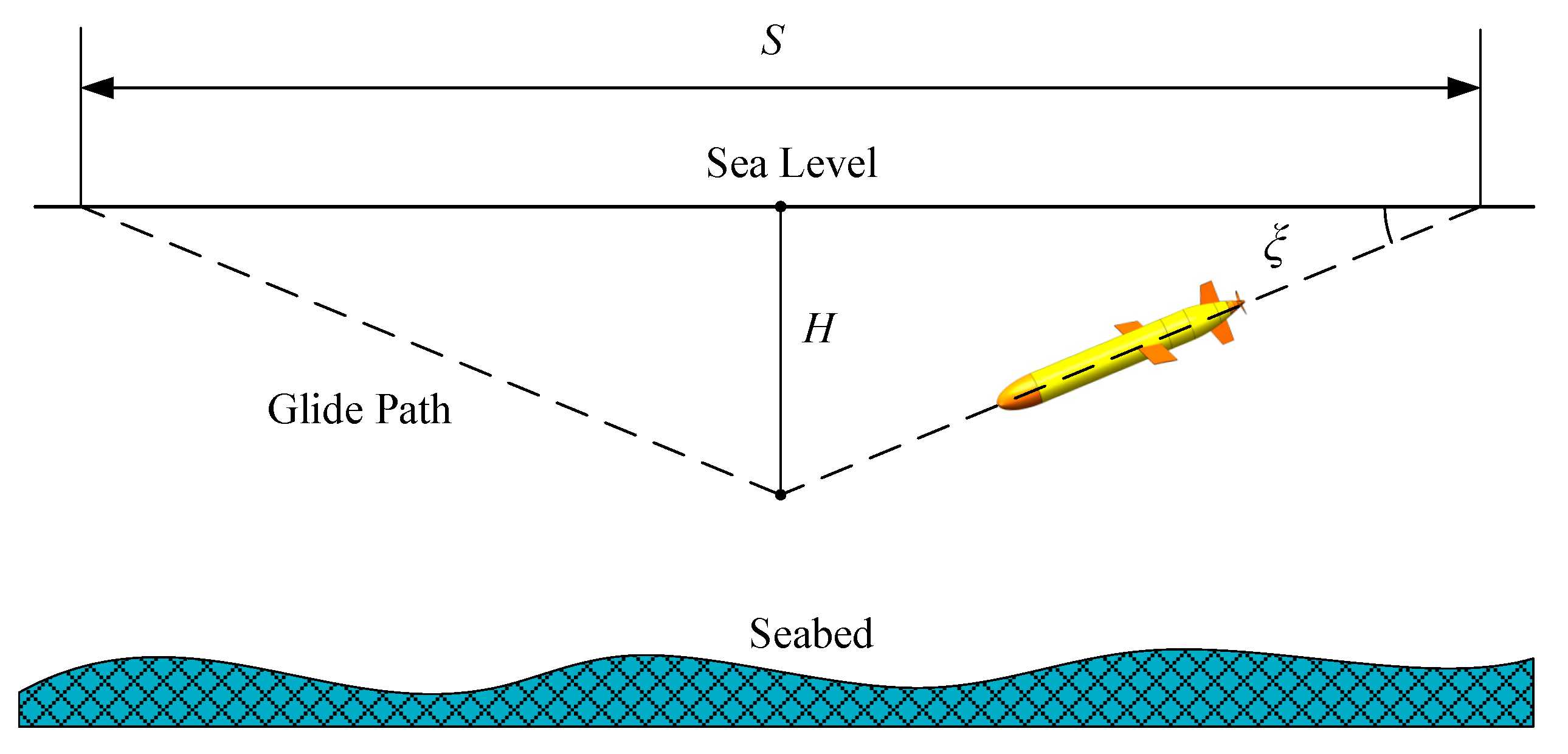
2. Glide Angle Range of the Zero-Angle-of-Attack Glider in Different Driving Modes
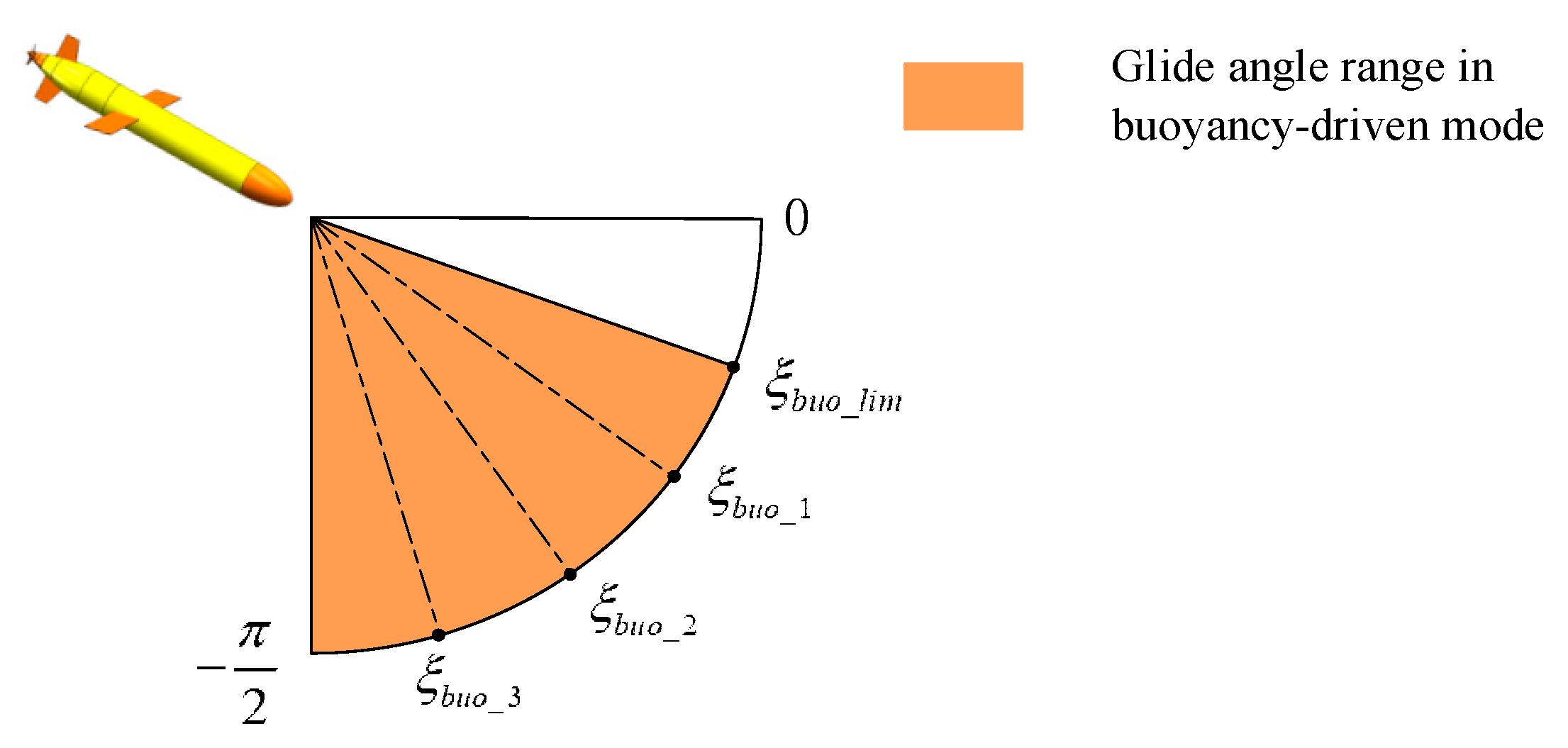
2.1. The Glide Angle Range in Buoyancy-Driven Mode
2.2. The Glide Angle Range in Hybrid-Driven Mode
2.3. The Glide Angle Range of the Zero-Angle-of-Attack Glider
3. Energy Consumption per Meter and Sailing Efficiency
3.1. Energy Consumption Model
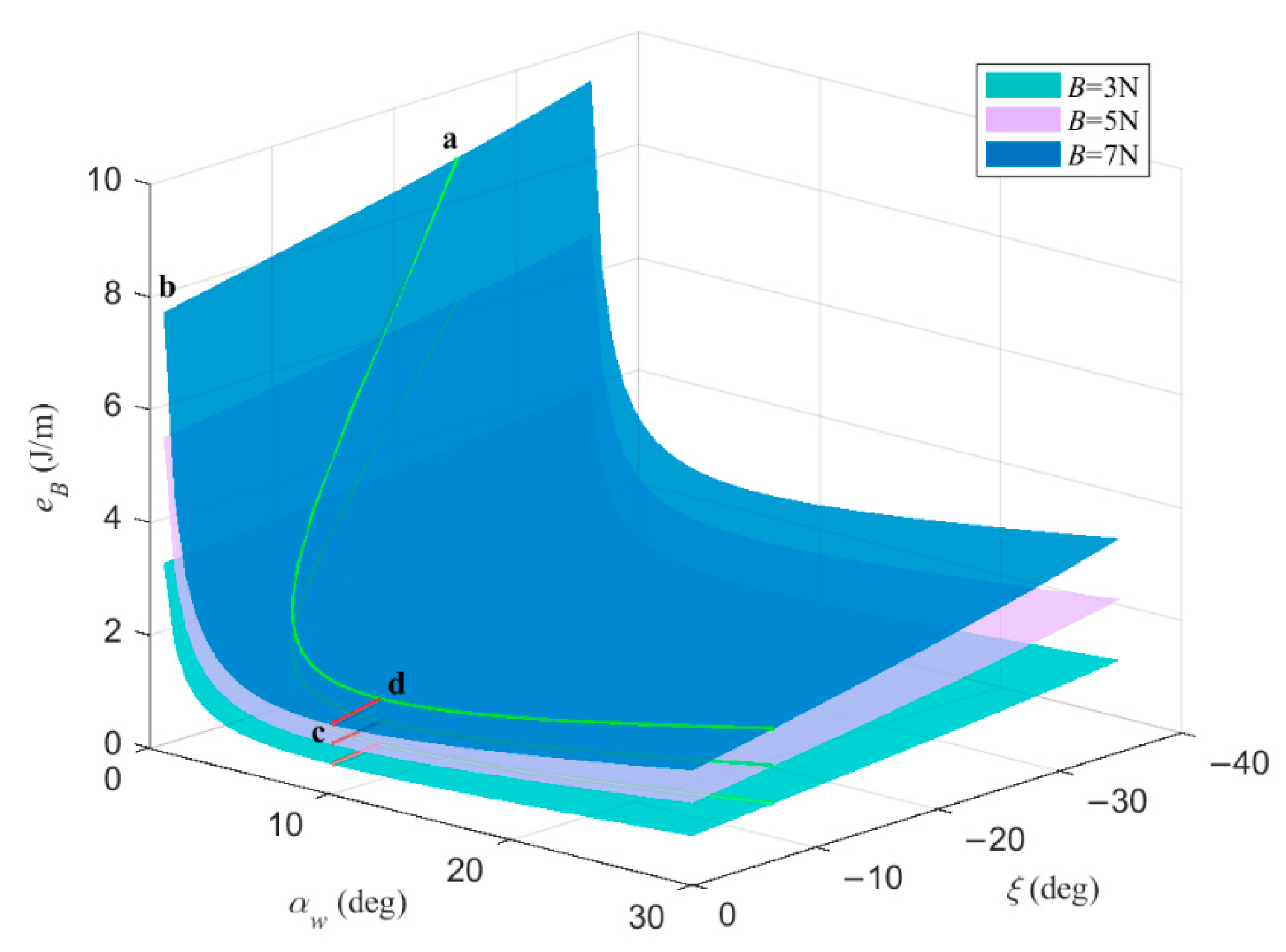
3.1.1. Discussion on the Efficiency of Two Driving Systems
3.1.2. The Influence of Wing Installation Angle on under Given Net Buoyancy
3.1.3. The Influence of Glide Angle on under Given Net Buoyancy
3.2. Energy Consumption Model
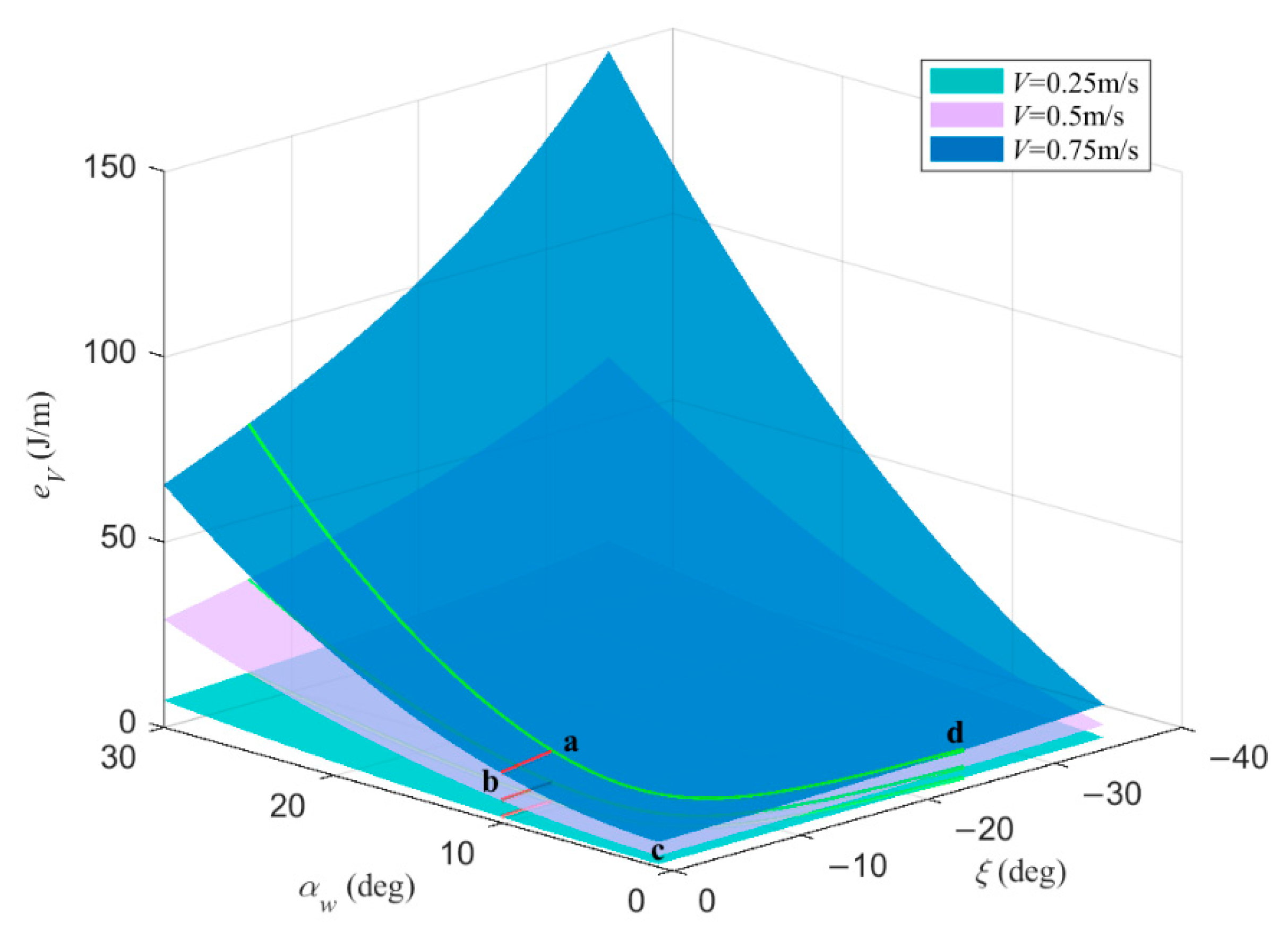
3.2.1. The Influence of Wing Installation Angle on under Given Speed
3.2.2. The Influence of Glide Angle on under Given Speed
3.3. Summary and Discussion
4. Conclusions
- At a given wing installation angle , the available glide angle range for a hybrid-driven glider to achieve zero-angle-of-attack gliding is . In buoyancy-driven mode, the glide angle corresponding to the wing installation angle is exactly the lower limit of the range. In hybrid-driven mode, the glide angle range can be achieved by adjusting the thrust.
- Under given net buoyancy and glide angle, the zero-angle-of-attack glider has a wider speed range but a lower sailing efficiency in hybrid-driven mode than in buoyancy-driven mode.
- Under given speed and glide angle, the zero-angle-of-attack glider has a higher sailing efficiency in hybrid-driven mode than in buoyancy-driven mode.
- When the wing installation angle is determined, the zero-angle-of-attack glider will have a higher sailing efficiency in hybrid-driven mode than in buoyancy-driven mode, under both given net buoyancy and given speed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Glide angle | |
| Wing installation angle | |
| Net buoyancy | |
| Lift force | |
| Drag force | |
| Glide speed | |
| Drag of the wings | |
| Lift of the wings | |
| Drag of the hull | |
| Lift of the hull | |
| Drag coefficient of the hull | |
| , | Drag coefficients of the wing |
| Slope of lift coefficient of the wing | |
| Area of the wings | |
| Cross-sectional area of the hull | |
| Seawater density | |
| Drag correction factor | |
| Lift correction factor | |
| Glide angle in buoyancy-driven mode | |
| Limit glide angle in buoyancy-driven mode | |
| Thrust force | |
| Working depth | |
| Horizontal distance in each profile | |
| Efficiency of the propulsion system | |
| Efficiency of the variable buoyancy system | |
| Buoyancy volume change | |
| Work done by thrust during the downward process | |
| Energy consumption of the variable buoyancy system | |
| Energy consumption model including net buoyancy term | |
| Energy consumption model including speed term | |
| Propeller speed | |
| Wake fraction | |
| Thrust deduction fraction | |
| , | Voltage |
| , | Current |
| Time of oil discharge | |
| Time of the downward process |
References
- Stommel, H. The slocum mission. Oceanography 1989, 2, 22–25. [Google Scholar] [CrossRef]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Sherman, J.; Davis, R.E.; Owens, W.B.; Valdes, J. The autonomous underwater glider “Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A long-range autonomous underwater vehicle for oceanographic research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef] [Green Version]
- D’Spain, G.L.; Jenkins, S.A.; Zimmerman, R.; Luby, J.C.; Thode, A.M. Underwater acoustic measurements with the Liberdade/X-Ray flying wing glider. J. Acoust. Soc. Am. 2005, 117, 2624. [Google Scholar] [CrossRef]
- Osse, T.J.; Eriksen, C.C. The deepglider: A full ocean depth glider for oceanographic research. In Proceedings of the Oceans-2007, Vancouver, BC, Canada, 29 September–4 October 2007. [Google Scholar] [CrossRef]
- Nakamura, M.; Hyodo, T.; Koterayama, W. LUNA testbed vehicle for virtual mooring. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Claustre, H.; Beguery, L.; Patrice, P.L.A. SeaExplorer Glider Breaks Two World Records Multisensor UUV Achieves Global Milestones for Endurance, Distance. Sea Technol. 2014, 55, 19–22. [Google Scholar]
- Graver, J.G. Underwater gliders: Dynamics, Control, and Design. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2005. [Google Scholar]
- Chen, Z.; Yu, J.; Zhang, A.; Song, S. Control system for long-range survey hybrid-driven underwater glider. In Proceedings of the OCEANS-2015—Genova, Genova, Italy, 18–21 May 2015. [Google Scholar] [CrossRef]
- Bachmayer, R.; Leonard, N.E.; Graver, J.; Fiorelli, E.; Bhatta, P.; Paley, D. Underwater gliders: Recent developments and future applications. In Proceedings of the 2004 International Symposium on Underwater Technology, Taipei, Taiwan, 20–23 April 2004. [Google Scholar] [CrossRef] [Green Version]
- Furlong, M.E.; Paxton, D.; Stevenson, P.; Pebody, M.; Mcphail, S.D.; Perrett, J. Autosub Long Range: A Long Range Deep Diving AUV for Ocean Monitoring. In Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles (AUV), Southampton, UK, 24–27 September 2012. [Google Scholar] [CrossRef]
- Hobson, B.W.; Bellingham, J.G.; Kieft, B.; McEwen, R.; Godin, M.; Zhang, Y. Tethys-class long range AUVs—Extending the endurance of propeller-driven cruising AUVs from days to weeks. In Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles (AUV), Southampton, UK, 24–27 September 2012. [Google Scholar] [CrossRef]
- Bellingham, J.G.; Zhang, Y.; Kerwin, J.E.; Erikson, J.; Hobson, B.; Kieft, B.; Godin, M.; McEwen, R.; Hoover, T.; Paul, J.; et al. Efficient propulsion for the Tethys long-range autonomous underwater vehicle. In Proceedings of the 2010 IEEE/OES Autonomous Underwater Vehicles, Monterey, CA, USA, 1–3 September 2010. [Google Scholar] [CrossRef]
- Jenkins, S.A.; Humphreys, D.E.; Sherman, J.; Osse, J.; Jones, C.; Leonard, N.; Graver, J.; Bachmayer, R.; Clem, T.; Carroll, P.; et al. Underwater Glider System Study. Scripps Institution of Oceanography Technical Report. 2003. Available online: https://escholarship.org/uc/item/1c28t6bb (accessed on 15 December 2021).
- Wolowicz, C.H.; Yancey, R.B. Longitudinal Aerodynamic Characteristics of Light, Twin-Engine, Propeller-Driven Airplanes; NASA Technical Note, 1972. Available online: https://www.nasa.gov/centers/dryden/pdf/87800main_H-646.pdf (accessed on 15 December 2021).
- Editorial Board of “Aeronautical Aerodynamics Manual”. Aviation Aerodynamics Manual; National Defense Industry Press: Beijing, China, 1983; Volume 2. [Google Scholar]
- Tian, X.; Zhang, L.; Zhang, H.; Wang, Y.; Liu, Y.; Yang, Y.; Song, L. The Optimal Lift–Drag Ratio of Underwater Glider for Improving Sailing Efficiency. IEEE J. Ocean. Eng. 2021, 46, 808–816. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, Z. Ship Propulsion, 1st ed.; National Defense Industry Press: Beijing, China, 1980. [Google Scholar]
- Griffiths, G. Technology and Applications of Autonomous Underwater Vehicles; CRC Press: Boca Raton, FL, USA, 2002; Volume 2. [Google Scholar]
- Davis, R.E.; Eriksen, C.C.; Jones, C.P. Autonomous buoyancy-driven underwater gliders. In Technology and Applications of Autonomous Underwater Vehicles; Griffiths, G., Ed.; Taylor & Francis: London, UK, 2002; Chapter 3; pp. 37–58. [Google Scholar]
- Furlong, M.E.; Mcphail, S.D.; Stevenson, P. A concept design for an ultra-long-range survey class AUV. In Proceedings of the IEEE Oceans 2007—Europe, Aberdeen, UK, 18–21 June 2007. [Google Scholar] [CrossRef] [Green Version]
- Miller, T.F. A bio-inspired climb and glide energy utilization strategy for undersea vehicle transit. Ocean. Eng. 2018, 149, 78–94. [Google Scholar] [CrossRef]
- Hockley, C.; Butka, B. Can a Conventional Propulsion System Match the Efficiency of an Underwater Glider Buoyancy Engine? Mar. Technol. Soc. J. 2019, 53, 75–82. [Google Scholar] [CrossRef]
- Hu, R. Research on the Motion of Underwater Glider in Vertical Plane. Master’s Dissertation, Shanghai Jiao Tong University, Shanghai, China, 2008. [Google Scholar]


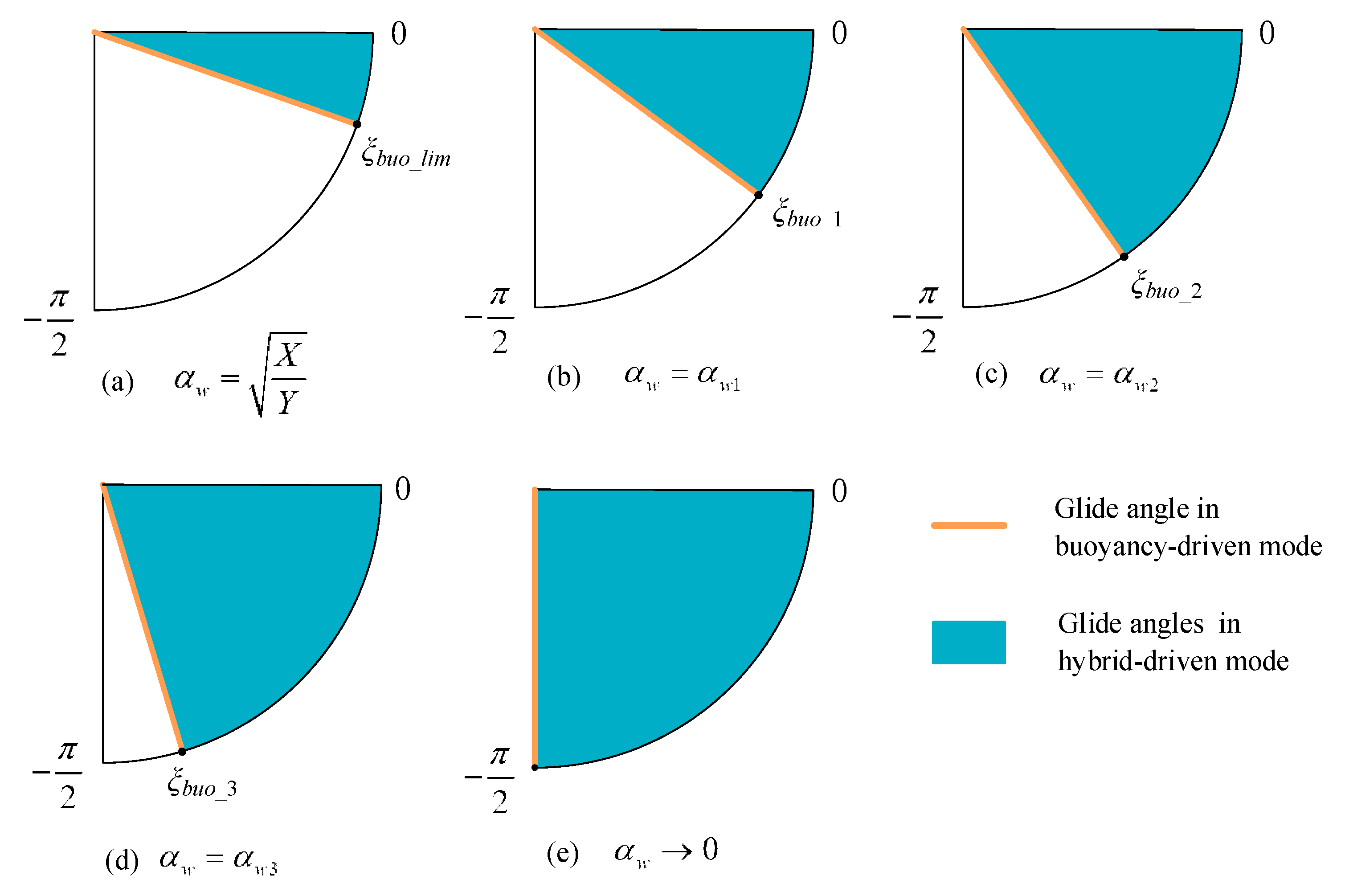

| Condition | Given Net Buoyancy B | Given Glide Speed V |
|---|---|---|
| Given glide angle | Buoyancy-driven mode | Propulsion mode |
| Given wing installation angle | Hybrid-driven mode | Hybrid-driven mode |
| Condition | Given Net Buoyancy B | Given Glide Speed V | |
|---|---|---|---|
| Driving Mode | |||
| Buoyancy-driven mode | Equal | Higher | |
| Hybrid-driven mode | Lower | Higher | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Zhang, L.; Zhang, H. Research on Sailing Efficiency of Hybrid-Driven Underwater Glider at Zero Angle of Attack. J. Mar. Sci. Eng. 2022, 10, 21. https://doi.org/10.3390/jmse10010021
Tian X, Zhang L, Zhang H. Research on Sailing Efficiency of Hybrid-Driven Underwater Glider at Zero Angle of Attack. Journal of Marine Science and Engineering. 2022; 10(1):21. https://doi.org/10.3390/jmse10010021
Chicago/Turabian StyleTian, Xin, Lianhong Zhang, and Hongwei Zhang. 2022. "Research on Sailing Efficiency of Hybrid-Driven Underwater Glider at Zero Angle of Attack" Journal of Marine Science and Engineering 10, no. 1: 21. https://doi.org/10.3390/jmse10010021
APA StyleTian, X., Zhang, L., & Zhang, H. (2022). Research on Sailing Efficiency of Hybrid-Driven Underwater Glider at Zero Angle of Attack. Journal of Marine Science and Engineering, 10(1), 21. https://doi.org/10.3390/jmse10010021






